Highlights

  • Assessment of melting heat transfer and non-uniform heat source on magnetic Cu–H2O nanofluid flow through a porous cylinder was studied.

  • The governing equations are solved by KBM (Keller box method).

  • A good agreement was created with the experimental results.

  • With increase in porous parameter values, the heat transfer rate declined near the surface.

  • The coefficient of surface drag force depreciated with enhancing melting parameter values.

Introduction

The nanofluids are liquid suspensions of nano-sized solid particles into the base liquids. In the last few decades, the term nanofluid has become an interesting topic among the different research communities because of its rapid capacity of heat exchange. This has resulted in broad utilization of nanofluids in several manufacturing and technology applications such as energy storage, cancer therapy, melts of polymer paints, drug delivery, asphalts and glues. Choi and Eastman [1] were the first who proposed the term nanofluid and observed that the addition of nanoparticles in traditional fluids fairly improved the thermal conductivity of fluid. The utilization of heat exchange is in various industrial applications such as pasteurization of food, fuel cells, biomedicine/pharmaceutical processes and microelectronics. Wang [2] modeled the fluid transportation from a stretchable cylinder and found that temperature and velocity decay with higher variations of Reynolds number. Ishak et al. [3] examined the fluid motion and heat transfer via a stretching tube in the occurrence of suction/injection. Their results showed that the heat exchange declines with higher Pr values. Wang and Ng [4] elaborated fluid flow via a stretchable cylinder due to slip, and they stated that velocities as well as shear drag force reduced drastically with slip. Ashorynejad et al. [5] proposed heat transfer motion of nanoliquid via a stretching geometry in the occurrence of magnetic effects. Their outcomes revealed that heat exchange rate augments by an increment in variation of both nanoparticle volume fraction and Reynolds number, while it reduces by an increment in magnetic parameter values. Majeed et al. [6] discussed the mixed influence of prescribed heat flux at surface and partial slip on fluid flow along stretchable cylinder. From their results, they examined that velocity diminishes, while temperature boosts by the slip parameter. The analytic results of axisymmetric third-grade fluid flow via a stretchable cylinder in the occurrence of magnetic effects have been computed by Hayat et al. [7]. Their results demonstrated that axial velocity is a lessening function of magnetic field. Butt et al. [8] evaluated the role of magnetic field on the viscous flow and entropy generation via a porous stretching cylinder and observed that the permeability and magnetic field parameters have diminishing impacts on velocity; however, temperature amplifies with a rise in same parameters. Pandey and Kumar [9, 10] and Mishra et al. [11] inspected the boundary-layer transport and heat exchange of nanofluid via stretching cylinder influenced by different effects. Hayat et al. [12] deliberated the motion of viscoelastic liquid due to stretchable cylinder because of mixed convection impact. Ebrahimi et al. [13] discussed the role of melting heat exchange in fluid flow in the presence of heat exchanger influenced by U-shaped heat pipe. Khan and Malik [14, 15] investigated the behavior of Sisko nanofluid flow and heat exchange through a stretchable cylinder due to forced convective impact. Malik et al. [16] modeled the flow of Sisko liquid via a nonlinear stretching cylinder in the existence of Cattaneo–Christov heat flux. Ahmed et al. [17] created a model to study the influence of heat source/sink on boundary-layer transport of nanoliquid along stretchable and permeable tube. Pandey and Kumar [18] analyzed the effects of magnetic field in Cu–water nanoliquid motion through stretching/shrinking channel due to ohmic heating and heat absorption–generation. The characteristics of thermal radiation and heat absorption/generation transportation of nanoliquid from unsteady stretchable surface have been considered by Pandey and Kumar [19]. Singh and Kumar [20] analyzed the mixed effects of melting on the boundary-layer transport and heat exchange due to stretching sheet in micro-polar liquid. Singh and Kumar [21] formulated a problem to examine the impact of melting heat exchange in motion of micro-polar fluid via stretching/shrinking surface due to magnetic field effect. Pandey and Kumar [22] proposed the mixed impacts of melting and suction–blowing on the magnetic nanoliquid flow in a wedge implanted in porous medium with slip impact. Singh et al. [23] analyzed the stagnation point slip flow and heat exchange of micro-polar liquid due to shrinking surface. Hayat et al. [24] considered the role of slip effects and Joule heating on the peristaltic motion of MHD tangent hyperbolic nanofluid along inclined channel. Hayat et al. [25] observed the influence of Joule heating and melting heat transfer on Cu–water fluid flow. The influence of magnetic field on several geometries was done by [26,27,28,29,30,31,32].

Mathematical formulation

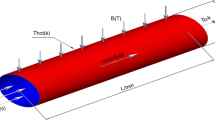
The model deals with a laminar, steady, incompressible and axisymmetric motion of a Cu–water nanofluid via a porous flat stretching pipe with diameter 2a, r-axis is perpendicular to the pipe, and z-axis is along the direction of the pipe. The pipe is being stretched with velocity \(W_{w} = 2cz\) along z-axis where stretching rate is c. The model is in the existence of the melting heat transfer, non-uniform heat source and a uniform magnetic field of strength of \(B_{0}\) imposed in the direction of r-axis. The graphical depiction of the model is exhibited together with configuration of flow and coordinate system in Fig. 1. The temperature of melting surface and free stream is \(T_{{\text{m}}}\) and \(T_{\infty }\). It is also considered that \(T_{{\text{s}}}\) is solid medium temperature distanced the interface, and \(T_{{\text{s}}} < T_{{\text{m}}}\). The thermal radiation, ohmic dissipation and ohmic heating effects are assumed to be negligible. The physical properties of H2O and nanoparticles are depicted in Table 1. Under these all above postulations, the boundary-layer equations are given as follows:

$$\frac{\partial (ru)}{{\partial r}} + \frac{\partial (rw)}{{\partial z}} = 0$$
(1)
$$uw_{r} + ww_{z} = \nu_{{{\text{nf}}}} \left( {w_{rr} + \frac{1}{r}w_{r} } \right) - \frac{{\sigma_{{{\text{nf}}}} B_{0}^{2} }}{{\rho_{{{\text{nf}}}} }}w - \frac{{\nu_{{{\text{nf}}}} }}{K}w$$
(2)
$$uu_{r} + wu_{z} = - \frac{1}{{\rho_{{{\text{nf}}}} }}p_{r} + \nu_{{{\text{nf}}}} \left( {u_{rr} + \frac{1}{r}u_{r} - \frac{u}{{r^{2} }}} \right)$$
(3)
$$\left( {\rho C_{p} } \right)_{{{\text{nf}}}} \left( {wT_{z} + uT_{r} } \right) = k_{{{\text{nf}}}} \left( {T_{rr} + \frac{1}{r}T_{r} } \right) + q^{\prime \prime \prime }.$$
(4)
Fig. 1
figure 1

Flow configuration and coordinate system

Full size image
Table 1 Thermophysical properties of water and nanoparticle
Full size table

Boundary conditions of the model are

$$\begin{aligned} u & = 0,\,w = 2cz,\,k\frac{\partial T}{{\partial r}} = \rho \left[ {\lambda + C_{{\text{s}}} \left( {T_{{\text{m}}} - T_{{\text{s}}} } \right)} \right]u \quad {\text{at}}\quad r = a, \\ u & = 0 = w,\quad T = T_{\infty } \quad {\text{as}}\,r = \infty . \\ \end{aligned}$$
(5)

Now, \(q^{\prime \prime \prime }\) is defined as

$$q^{\prime \prime \prime } = \frac{{k_{{{\text{nf}}}} W_{w} }}{{z\nu_{{\text{f}}} }}\left( {Q\left( {T_{w} - T_{\infty } } \right)f^{\prime } + Q_{0} \left( {T - T_{\infty } } \right)} \right)$$
(6)

where \(Q\) and \(Q_{0}\) are internal heat source parameters.

The theoretical model for nanofluid transport is defined as follows [11, 18, 32,33,34]:

$$\begin{aligned} \mu_{{{\text{nf}}}} & = \frac{{\mu_{f} }}{{\left( {1 - \phi } \right)^{2.5} }},\,\nu_{{{\text{nf}}}} = \frac{{\mu_{{{\text{nf}}}} }}{{\rho_{{{\text{nf}}}} }},\,\rho_{{{\text{nf}}}} = \rho_{{\text{f}}} \left( {1 - \phi } \right) + \rho_{{\text{s}}} \phi ,\;\sigma_{{{\text{nf}}}} \; = \phi \sigma_{{\text{s}}} + \left( {1 - \phi } \right)\sigma_{{\text{f}}} , \\ \left( {\rho c_{p} } \right)_{{{\text{nf}}}} & = \left( {\rho c_{p} } \right)_{{\text{f}}} \left( {1 - \phi } \right) + \left( {\rho c_{p} } \right)_{{\text{s}}} \phi ,\,\frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }} = \frac{{k_{{\text{s}}} + 2k_{{\text{f}}} - 2\phi \left( {k_{{\text{f}}} - k_{{\text{s}}} } \right)}}{{k_{{\text{s}}} + 2k_{{\text{f}}} + 2\phi \left( {k_{{\text{f}}} - k_{{\text{s}}} } \right)}}. \\ \end{aligned}$$
(7)

The partial differential Eqs. (1)–(4) of the governing flow of nanofluid are changed into the ordinary differential equations by utilizing the similarity variable as

$$u = - ca\frac{f\left( \eta \right)}{{\sqrt \eta }},\quad w = 2czf^{\prime}\left( \eta \right) \quad \eta = \left( \frac{r}{a} \right)^{2} ,\quad \theta = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty }. }}$$
(8)

The changed ordinary differential equations of flow and thermal field are as follows:

$$\frac{A}{B}\left( {\eta f^{\prime \prime \prime } + f^{\prime \prime } - \Lambda f^{\prime } } \right) - \frac{M}{B}f^{\prime } - {\text{Re}} f^{\prime 2} + {\text{Re}} ff^{\prime \prime } = 0$$
(9)
$$\left( {\eta \theta ^{\prime\prime} + \theta ^{\prime}} \right) + {\text{Re}} \left( {\frac{C}{D}\Pr f\theta ^{\prime} + Qe^{ - \eta } + Q_{0} \theta } \right) = 0.$$
(10)

The boundary equations reduced to

$$\begin{aligned} f\left( {\eta = 1} \right) & = 0,\;f^{\prime}\left( {\eta = 1} \right) = 1,\;\Pr f\left( {\eta = 1} \right) + m\theta ^{\prime}\left( {\eta = 1} \right) = 0, \\ f^{\prime}\left( {\eta = \infty } \right) & = 0 = \;\theta \left( {\eta = \infty } \right). \\ \end{aligned}$$
(11)

Here,

$$\begin{aligned} {\text{Re}} & = \frac{{ca^{2} }}{{2v_{{\text{f}}} }},\,\Pr = \frac{{v_{{\text{f}}} }}{\alpha },\,M = \frac{{a^{2} \sigma_{{\text{f}}} B_{0}^{2} }}{{4\rho_{{\text{f}}} }}\Lambda = \frac{{a^{2} }}{4K},\,m = \frac{{C_{p} \left( {T_{w} - T_{\infty } } \right)}}{{\left( {\lambda + C_{{\text{s}}} \left( {T_{m} - T_{s} } \right)} \right)}}, \\ A & = \frac{1}{{\left( {1 - \phi } \right)^{2.5} }},B = \left( {1 - \phi } \right) + \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}\phi ,C = \left( {1 - \phi } \right) + \frac{{\left( {\rho C_{p} } \right)_{{\text{s}}} }}{{\left( {\rho C_{p} } \right)_{{\text{f}}} }}\phi , \\ D & = \left( {k_{{\text{s}}} + 2k_{{\text{f}}} + \phi \left( {k_{{\text{f}}} - k_{{\text{s}}} } \right)} \right)^{ - 1} \times \left( {k_{{\text{s}}} + 2k_{{\text{f}}} - 2\phi \left( {k_{{\text{f}}} - k_{{\text{s}}} } \right)} \right). \\ \end{aligned}$$
(12)

Now, the nanofluid pressure can be computed from Eq. (3) as follows:

$$\frac{p}{\rho } = \frac{{p_{\infty } }}{\rho } - \frac{{c^{2} a^{2} }}{{2\eta }}f^{2} \left( \eta \right) - 2cv_{{{\text{nf}}}} f^{\prime} \left( \eta \right){\mkern 1mu} {\text{i.e.}}{\mkern 1mu} \frac{{p - p_{\infty } }}{{\rho cv_{{{\text{nf}}}} }} = - \frac{B}{A}\frac{{{\text{Re}}}}{{2\eta }}f^{2} \left( \eta \right) - 2f^{\prime} \left( \eta \right).$$
(13)

The physical quantities of the most importance are Nusselt number and surface drag force (skin friction coefficient) and written as

$${\text{Nu}} = \frac{{aq_{w} }}{{k_{{{\text{nf}}}} \left( {T_{w} - T_{\infty } } \right)}},\,C_{f} = \frac{{\tau_{w} }}{{2\rho_{{{\text{nf}}}} (ca)^{2} }},$$
(14)

where \(q_{w}\) is the heat transfer and \(\tau_{w}\) is the skin friction of cylindrical pipe, which are given as follows:

$$q_{w} = - k_{{{\text{nf}}}} \left( {\frac{\partial T}{{\partial r}}} \right)_{r = a} \,\tau_{w} = \mu_{{{\text{nf}}}} \left( {\frac{\partial w}{{\partial r}}} \right)_{r = a}.$$
(15)

By the use of Eqs. (8) and (15), Eq. (14) reduces as follows:

$${\text{Nu}} = - 2\theta ^{\prime}\left( {\eta = 1} \right),\,C_{{\text{f}}} \frac{{aB{\text{Re}} }}{zA} = f^{\prime\prime}\left( 1 \right).$$
(16)

Results and discussion

The transformed ordinary differential Eqs. (9) and (10) with Eq. (11) have been handled with the assistance of finite-difference method called Keller box method formed by Cebeci and Bradshaw [35]. To analyze impacts of assorted physical parameters on the motion of the micro-polar fluid, a numerical computation has been carried out for \(0 \le \Lambda \le 15,\) \(0.5 \le Q = Q_{0} \le 10,\) \(1 \le {\text{Re}} \le 10,\) \(0 \le m \le 0.2\) and \(0 \le \phi \le 0.25\). In the whole computation, values of some parameters are fixed as \(\Pr = 7,\) \(M = 1,\) \(S = 0.6\). In order to authenticate the numerical outcomes obtained, a comparison of present data with those of past studies is illustrated in Table 2 and is observed to be in a good conformity.

Table 2 Comparison of f″ (1) for different values of Re when P = 0.7 (for pure water)
Full size table

The impact of porosity parameter \(\Lambda\) on flow and thermal field is shown in Figs. 2 and 3, respectively. Figure 2 explain that as the value of porous parameter increased velocity boundary thickness of nanofluid constantly declined near the surface but there was no variation when the nanofluid moved away from the wall. The nanofluid temperature accelerates in the range of \(\eta \in \left[ {1,\;2} \right]\), but after this range there are no changes in thermal field of nanofluid as porosity parameter \(\Lambda\) escalates, which is observed in Fig. 3.

Fig. 2
figure 2

Velocity versus \(\Lambda\)

Full size image
Fig. 3
figure 3

Temperature versus \(\Lambda\)

Full size image

The outlines of velocity and thermal field of Cu–H2O nanofluid due to several values of \({\text{Re}}\) are revealed in Figs. 4 and 5, respectively. These asymptotic outlines verify the solutions for each value of pertinent parameter. The Cu–H2O nanofluid flow and thermal distributions are depreciated very fast as \({\text{Re}}\) escalates.

Fig. 4
figure 4

Velocity versus \({\text{Re}}\)

Full size image
Fig. 5
figure 5

Temperature versus \({\text{Re}}\)

Full size image

The activity of the thermal and flow field due to melting parameter \(m\) is demonstrated in Figs. 6 and 7, respectively. It is apparent from Fig. 6 that fluid velocity retards with escalating values of melting parameter. It is seen from Fig. 7 that the thermal layer width plus fluid temperature declines with enhancing melting parameter \(m\).

Fig. 6
figure 6

Velocity versus m

Full size image
Fig. 7
figure 7

Temperature versus m

Full size image

The distributions of velocity and temperature for the several values of space and temperature-dependent internal heat source parameters (\(Q\) and \(Q_{0}\)) are exhibited in Figs. 8 and 9, respectively. It is viewed from Fig. 8 that the velocity reduces slightly with growing \(Q\) and \(Q_{0}\). It is depicted from Fig. 9 that fluid thermal field diminishes monotonically with rising values of \(Q\) and \(Q_{0}\).

Fig. 8
figure 8

Velocity versus \(Q = Q_{0}\)

Full size image
Fig. 9
figure 9

Temperature versus \(Q = Q_{0}\)

Full size image

Figures 10 and 11 depict variation in velocity \(f^{\prime}(\eta )\) and temperature \(\theta (\eta )\) graphs, respectively, for various estimates of Cu particle volume fraction \(\phi\). It is evident from Fig. 10 that \(f^{\prime}(\eta )\) minimizes with escalating \(\phi\) values. It is seen from Fig. 11 that influence of mounting \(\phi\) is to enhance thermal boundary layer as well as nanofluid temperature \(\theta (\eta )\).

Fig. 10
figure 10

Velocity versus \(\phi\)

Full size image
Fig. 11
figure 11

Temperature versus \(\phi\)

Full size image

The influence of \({\text{Re}}\) and \(\Lambda\) on surface drag force (skin factor) is shown in Fig. 12. It is illustrated from these curves that the surface drag force monotonically lessens with a climb in \({\text{Re}}\) and \(\Lambda\) values. The deviation in Nusselt number \(- \theta ^{\prime}(1)\) (the surface heat transfer rate) with Reynolds number \({\text{Re}}\) and porous parameter \(\Lambda\) is shown in Fig. 13. The outlines illustrate that heat transfer rate boosts with a climb in Reynolds number \({\text{Re}}\), while this rate retards with mounting porous parameter \(\Lambda\).

Fig. 12
figure 12

Variation in \(f^{\prime\prime}\left( 1 \right)\) due to \({\text{Re}}\) and \(\Lambda\)

Full size image
Fig. 13
figure 13

Variation in \(- \theta ^{\prime}\left( 1 \right)\) due to \({\text{Re}}\) and \(\Lambda\)

Full size image

Figure 14 explains the distribution of surface drag force (skin factor) \(f^{\prime\prime}(1)\) with respect to \({\text{Re}}\) for different estimates of \(Q = Q_{0}\). It is observed from these outlines \(f^{\prime\prime}(1)\) trim down with an augmentation in both \({\text{Re}}\) and \(Q = Q_{0}\) values; also from this figure, it is clear that reduction in \(f^{\prime\prime}(1)\) is more pronouncing for higher values of \({\text{Re}}\), i.e., for \({\text{Re}} > 4\). The profile of heat transfer rate \(\theta ^{\prime}(1)\) is described for relatable parameters in Fig. 15. Figure 15 portrays the actions of the heat transfer rate in opposition to Reynolds number \({\text{Re}}\) for various estimates of \(Q = Q_{0}\). These curves show that heat transfer rate mounts monotonically with enhancing values of \({\text{Re}}\) and \(Q = Q_{0}\). Table 3 demonstrates deviation in the surface drag force \(f^{\prime\prime}\left( 1 \right)\) and Nusselt Number \(- \theta ^{\prime}(1)\) (rate of heat exchange) for diverse numerical values of the used parameters in the present model. The data of this table are obtained by Keller box method. From this table, both skin factor and rate of heat exchange decline with the increasing values of porous parameter \(\Lambda\). Further, it is obvious that values of \(f^{\prime\prime}\left( 1 \right)\) retard with the higher Reynolds number \({\text{Re}}\) values, while Nusselt number boosts with the same values of Reynolds number. In addition, the rising values of melting parameter \(m\) cause a down fall in skin friction coefficient, while speeding up the rate of heat exchange. Moreover, it is obvious from this table that the heat exchange rate is proportional to internal heat source parameters (\(Q\) and \(Q_{0}\)), whereas there is a slight moderate in skin friction coefficient with \(Q = Q_{0}\) values.

Fig. 14
figure 14

Variation in \(f^{\prime\prime}(1)\) due to \({\text{Re}}\) and \(Q = Q_{0}\)

Full size image
Fig. 15
figure 15

Variation in \(- \theta ^{\prime}(0)\) due to \({\text{Re}}\) and \(Q = Q_{0}\)

Full size image
Table 3 Values of f″ and −θ′(1) for different values of Λ, Re, m and Q = Q0 when Pr = 7, M = 1, S = 0.6 and ϕ = 0.05
Full size table

Conclusions

The assessment of non-uniform heat source and melting heat transfer on magnetized Cu–H2O nanofluid via a stretching cylinder saturated in porous medium has been investigated. The outcomes of relatable parameters are achieved numerically by utilizing Keller box method. It is expected that the current investigations may be beneficial in several industrial applications. The main outcomes of this research are summarized as follows:

  • With increase in porous parameter values, the surface drag force and heat transfer rate declined  near the surface.

  • It is seen that the surface drag force declines with augment in Reynolds number, whereas the upshot is contrary for Nusselt number \(- \theta ^{\prime}(1)\).

  • The coefficient of surface drag force depreciated with enhancing melting parameter values. Moreover, the rate of heat exchange also hikes.

  • The values of \(f^{\prime\prime}\left( 1 \right)\) reduce slightly with space and temperature-dependent internal heat source parameters, but the rate of heat exchange is proportional to same parameters.