Bound state solutions of the Schrodinger equation for the modified Kratzer potential plus screened Coulomb potential

Abstract

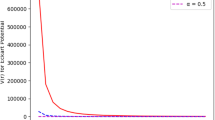
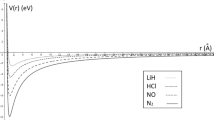
We obtained an approximate solution of the Schrodinger equation for the modified Kratzer potential plus screened Coulomb potential model, within the framework of Nikiforov–Uvarov method. The bound state energy eigenvalues for N₂, CO, NO, and CH diatomic molecules were computed for various vibrational and rotational quantum numbers. Special cases were considered when the potential parameters were altered, resulting into modified Kratzer potential, screened Coulomb potential, and standard Coulomb potential, respectively. Their energy eigenvalues expressions and numerical computations agreed with the already existing literatures.

Appendix: Review of Nikiforov–Uvarov (NU) method

The NU method was proposed by Nikiforov and Uvarov [65] to transform Schrodinger-like equations into a second-order differential equation via a coordinate transformation $s = s(r),$ of the form

$$ \psi^{\prime\prime}(s) + \frac{{\tilde{\tau }(s)}}{\sigma (s)}\psi^{\prime}(s) + \frac{{\tilde{\sigma }(s)}}{{\sigma^{2} (s)}}\psi (s) = 0 $$

(41)

where $\tilde{\sigma }(s),\,\,\sigma (s)$ are polynomials, at most second degree and $\tilde{\tau }(s)$ is a first-degree polynomial. The exact solution of Eq. (41) can be obtained by using the transformation

$$ \psi (s) = \varPhi (s)y_{n} (s) $$

(42)

This transformation reduces Eq. (41) into a hypergeometric-type equation of the form

$$ \sigma (s)y^{\prime\prime}_{n} (s) + \tau (s)y^{\prime}_{n} (s) + \lambda y_{n} (s) = 0 $$

(43)

The function $\varPhi (s)$ can be defined as the logarithm derivative [65]

$$ \frac{{\varPhi^{\prime}(s)}}{\varPhi (s)} = \frac{\pi (s)}{\sigma (s)} $$

(44)

with $\pi (s)$ being at most a first-degree polynomial. The second part of $\psi (s)$ being $y_{n} (s)$ in Eq. (42) is the hypergeometric function with its polynomial solution given by Rodrigues relation

$$ y_{n} (s) = \frac{{B_{n} }}{\rho (s)}\frac{{{\text{d}}^{n} }}{{{\text{d}}s^{n} }}\left[ {\sigma^{n} (s)\rho (s)} \right] $$

(45)

Here, $B_{n}$ is the normalization constant and $\rho (s)$ is the weight function which must satisfy the condition

$$ \frac{\text{d}}{{{\text{d}}s}}\left[ {\sigma (s)\rho (s)} \right] = \tau (s)\rho (s) $$

(46)

with

$$ \tau (s) = \tilde{\tau }(s) + 2\pi (s) $$

(47)

It should be noted that the derivative of $\tau (s)$ with respect to s should be negative. The eigenfunctions and eigenvalues can be obtained using the definition of the following function $\pi (s)$ and parameter $\lambda$, respectively:

$$ \pi (s) = \frac{{\sigma^{\prime}(s) - \tilde{\tau }(s)}}{2} \pm \sqrt {\left( {\frac{{\sigma^{\prime}(s) - \tilde{\tau }(s)}}{2}} \right)^{2} - \tilde{\sigma }(s) + k\sigma (s)} $$

(48)

and

$$ \lambda = k + \pi^{\prime}(s) $$

(49)

The value of $k$ can be obtained by setting the discriminant of the square root in Eq. (48) equal to zero. As such, the new eigenvalue equation can be given as

$$ \lambda + n\tau^{\prime}(s) + \frac{n(n - 1)}{2}\sigma^{\prime\prime}(s) = 0,\,\,(n = 0,1,2, \ldots ) $$

(50)