Introduction

Mathematical modelling of viral dynamics is studied in many recent articles and surveys [4, 22, 24, 36]. Models of immune response and infection dynamics can be governed by ordinary or partial differential equations including delay reaction-diffusion equations [1, 17, 25, 26, 28]. If we neglect time delay in immune response and the spatial distribution of immune cells and viruses, then we obtain an ordinary differential equation or systems of equations [17, 25, 26]. Models taking into consideration the duration of clonal expansion of immune cells lead to delay differential equations. To study the qualitative behaviour of solutions, many approaches and theories can be applied including dynamical systems theory. In a previous work by R. H Martin and H.L Smith [19], the authors showed that under some hypothesis, the delay reaction-diffusion equation and its homogeneous in space equation have the same asymptotic properties of solutions. In this paper we study the local and global stability of the homogeneous in space solution of the delay reaction-diffusion equation for infection dynamics recently proposed in [1].

Delay reaction–diffusion equation

$$\begin{aligned} \begin{array}{ll} {\displaystyle \frac{\partial u}{\partial t} = K \Delta u+ u(1-u-f(u_{\tau })),}\\ \end{array} \end{aligned}$$
(1.1)

is introduced in [3] as a model of viral infection spreading in tissues. Here u is the virus density distribution, f(u) is a continuous positive function which will be specified below. Virus reproduction is described by the logistic term \(u(1-u)\) and its elimination by the immune cells is given by the term \(u f(u_\tau )\), where \(u_\tau (x,t)=u(x,t-\tau )\), and the function f(u) specifies the efficiency of immune response-mediated virus elimination. The strength of the antiviral immune response given by the value of \(f(\cdot )\) depends on virus concentration at time \(t -\tau\) due to the duration of proliferation and maturation of immune cells. As detailed in [1], the homogeneous in space delay reaction-diffusion equation is

$$\begin{aligned} \;\;\left\{ \begin{array}{ll} {\displaystyle u'(t)= u(t) (1-u(t)-f(u(t-\tau )))\; \text { for }\; t\ge 0,}\\ {\displaystyle u(t)=\phi (t) \;\; \text { for } -\tau \le t\le 0.}\\ \end{array} \right. \end{aligned}$$
(1.2)

The two above equations were considered by authors in [1]. They studied their dynamics and stability and gave significant numerical simulations in 1D and 2D cases. They identified various new regimes in the dynamics of delay reaction-diffusion equation and established that the dynamics of space dependent solutions are described by a combination of various waves, notably, bistable, mono-stable, periodic and quasi-waves. However, they discussed more briefly the stability of steady states for the associated delay differential equation.

Motivated by their work, we focus particularly on the given delay differential equation corresponding to the delayed reaction-diffusion Eq. (1.2). Our purpose is to establish a non-classical stability result using the monotone dynamical systems approach rarely applied to equations arising from immune response models. We recall as pointed out before that in a previous work of Martin and Smith [19], the authors showed that under some hypothesis, the delayed reaction-diffusion equation and its homogeneous in space equation have the same asymptotic behaviour of solutions.

In the late twenties and early thirties of the last century, pioneering ideas on monotonicity for ordinary differential equations have been the subject of two famous and important research articles written by Muller and Kamke [13, 23]. Then the work of Krasnoselskii [14, 15] opens new opportunities for understanding the qualitative behaviour of positive solutions of operator equations and their trajectories. The transition to a rigorous mathematical theory of monotonicity for dynamical systems is largely due to the results proved by Hirsch in a series of articles entitled “Systems of differential equations that are competitive or cooperative" [9,10,11]. Many concepts, definitions and theorems have been proved and presented in Hirsch’s works above, such as generic convergence under strong monotonicity and compactness assumption and properties of strongly order preserving semi-flows associated with ordinary differential equations. It should be noted that the notion of strongly order preserving semi-flow was first introduced by Matano in [20].

The complete final version of the theory in its general aspect on metric ordered spaces has been the subject of the fundamental work of Smith and Thieme [31,32,33,34]. In this work, the ideas of Kamke, Muller, Krasnoselskii, Matano and Hirsch have been generalised, streamlined and simplified. The book of Smith [30] may serve as a background reference for readers who are interested in learning or applying the classical theory of monotone dynamical systems. We should also cite the important article of Pituk [27] where local stability of non-quasimonotone scalar autonomous delay differential equations was detailed and ameliorated. Later, Yi and collaborators introduced the concept of essentially strongly order-preserving semi-flows and provided a simplified compactness assumption [39, 40]. Recently, and using the results of [40], Niri and El Karkri have established a simplified framework for stability analysis of equilibriums for nonquasimonotone autonomous scalar delay differential equations [5, 6]. The obtained theorems have been applied in the same articles to an SIS compartmental epidemiological model with infection period, variable population size and deaths caused by infection [5, 6].

In the present paper, the method is mainly based on the framework developed in [5, 6]. We aim to establish sufficient conditions of local and global asymptotic stability for the equilibria of the Eq. (1.2). We prove that for certain values of this model’s parameters the equilibriums are asymptotically stable and under particular conditions we get the global stability of nonzero equilibrium.

It is important to verify that monotone dynamical systems theory has its special definitions of stability. The reader is referred to a short comparative study published in [7] where authors prove that an equilibrium \(x^{*}\) is asymptotically stable in the sense of the monotone dynamical systems theory if and only if it is uniformly asymptotically stable in the sense of the classical theory of stability (see Proposition 3 in [7]).

We organize the rest of this paper as follows. The next section provides some preliminary results concerning existence, regularity and smoothness of solutions of autonomous scalar delay differential equations as well as a reminder of some important results of monotone dynamical systems theory for non-quasimonotone scalar delay differential equations. Most of the results and definitions in this section are taken from [5, 6, 8, 27, 30, 40]. In Sect. 3, the delay differential equation is presented, related existence, equilibria and regularity results are provided. In Sect. 4, we study asymptotic stability, in first place for the infection free equilibrium \(v_{0}=0\), then for the nonzero equilibrium \(( 0<v^{* }<1)\) in the cases of strictly positive and strictly negative derivative \(f'(v^{*})\). Global stability results are presented in Sects. 5 and  6 with distinction of two forms of the function f namely for nondecreasing function and for changing monotonicity one. Numerical simulations illustrate theoretical results of global stability. In Sect. 7, real clinical data of a COVID-19 patient have been used to calibrate models parameters for two particular forms of f(u), and numerical simulations have been exploited to forecast the immunological behaviour of the patient. We summarize our conclusion and discuss our findings at the end of the paper.

Preliminaries

For readers’ convenience, we recall some concepts, definitions and theorems which will be used in the rest of this paper. For \(\tau >0\), let \(\left( C,\parallel .\parallel _{\infty }\right)\) denote the Banach space of continuous functions mapping \([-\tau ,0]\) into \({\mathbb {R}}\) with the maximum norm \(\parallel .\parallel _{\infty }\) defined by \(\parallel \varphi \parallel _{\infty }=\underset{x\in \left[ -\tau ,0\right] }{sup}\mid \varphi (x)\mid\) for all \(\varphi \in C\). Let \(\Pi\) be an open subset of C and \(h:\Pi \rightarrow {\mathbb {R}}\) be continuous and Lipschitzian in every compact subset of \(\Pi\). Consider the autonomous functional differential equation

$$\begin{aligned} \left\{ \begin{array}{ll} x{'}(t)=h(x_{t}) \quad \text { for } \quad t\ge 0,\\ x(t)=\varphi (t)\quad \text { for } \quad -\tau \le t\le 0, \\ \end{array}\right. \end{aligned}$$
(2.3)

where \(\varphi \in \Pi\) is the initial condition and \(x_{t}(\theta )=x(t+\theta )\) for all \(\left( t,\theta \right) \in [0,+\infty [\times \left[ -\tau ,0\right]\).

Theorem 2.1

(Existence, continuity and smoothness of solutions [8]) Let \(\Pi\) be an open subset of C and suppose that \(h:\Pi \rightarrow {\mathbb {R}}\) is continuous and Lipschitzian in every compact subset of \(\Pi\). If \(\varphi \in \Pi\), then problem (2.3) has a unique solution \(x(.,\varphi )=x_{\varphi }\) defined for \(t\ge -\tau\). If h is \(C^{k}\) on \(\Pi\) then \(x_{\varphi }\) is \(C^{k+1}\) on \([k.\tau ,+\infty [\).

Put \(\Omega =\overline{\Pi }\), and assume that h is defined on \(\Omega\). The delay differential Eq. (2.3) is said to satisfy the Assumption (TD1) on \(\Omega\) if h maps bounded subsets of \(\Omega\) to bounded subsets of \({\mathbb {R}}\), and the positive semi-orbit of every solution of (2.3) with \(\varphi \in \Omega\) is bounded. See for instance [5, 40]. For \(\mu > 0\), consider the set

$$\begin{aligned} C_{\mu }=\left\{ \phi \in C;\;\phi \ge 0\; and\;s\longmapsto \phi (s)e^{\mu s}\; is\; nondecreasing\; on\;\left[ -\tau ,0\right] \right\} . \end{aligned}$$

As pointed out in [27, 30], \(C_{\mu }\) is a closed cone in the Banach space C with empty interior. \(C_{\mu }\) generates a closed partial order denoted by \(\le _{\mu }\) and defined as follows:

$$\begin{aligned} \forall \phi ,\varphi \in C: \phi \le _{\mu }\psi \Longleftrightarrow \psi -\phi \in C_{\mu } , \end{aligned}$$

i.e, \(\phi \le _{\mu }\psi \Longleftrightarrow \phi \le \psi \; and\;s\longmapsto (\phi (s)-\psi (s))e^{\mu s}\) is non-increasing on \(\left[ -\tau ,0\right]\). We write \(\phi <_{\mu }\psi\) if \(\phi \le _{\mu }\psi\) and \(\phi \ne \psi\). The reader is referred to [5, 27, 30] for further details on the partial order \(\le _{\mu }.\)

Definition 2.2

A continuous linear functional \(G:C\longrightarrow {\mathbb {R}}\) is said to satisfy the \((L_{\mu })\) property if for some \(\mu >0\): \((L_{\mu }):\qquad G(\phi )+\mu \phi (0)\ge 0\quad whenever\;\phi \in C\;\; and\; \phi \ge _{\mu } 0\).

For all \(v\in {\mathbb {R}}\) we denote \(\,\hat{v}\in C\) the constant function \(\,\hat{v}\) defined by \(\hat{v}\left( \theta \right) =v\) for all \(\theta \in \left[ -\tau ,0\right]\). Consider the function \(\tilde{h}\) defined on \(\left\{ v\in {\mathbb {R}}/\,\hat{v}\in \Omega \right\}\) by

$$\begin{aligned} \tilde{h}(v)=h(\hat{v}(t)) \end{aligned}$$
(2.4)

for all v in \(\left\{ s\in {\mathbb {R}}/\,\hat{s}\in \Omega \right\}\). The delay differential equation (2.3)is said to satisfy the \((SM_{\mu })\) property on \(\Omega\) if there exists \(\mu >0\) such that for all \(\phi ,\psi \in \Omega\):

$$\begin{aligned} \quad \phi <_{\mu }\psi \quad \Longrightarrow \quad \mu (\psi (0)-\phi (0))+h(\psi )-h(\phi )>0. \end{aligned}$$

The theorem bellow illustrates the importance of the \((L_{\mu })\) assumption in the asymptotic stability analysis of equilibriums [27, 30].

Theorem 2.3

Consider the delay differential Eq. (2.3). Let \(\tilde{h}\) defined by (2.4). Suppose that h is continuously differentiable in a neighbourhood of an equilibrium \(x^{*}\) of (2.3) and \(dh(x^{*})\) verifies \((L_{\mu })\) for some \(\mu >0\), then:

  1. (i)

    If \(\tilde{h}'(x^{*})<0\) then \(x^{*}\) is asymptotically stable.

  2. (ii)

    If \(\tilde{h}'(x^{*})>0\) then \(x^{*}\) is unstable.

We recall, as mentioned in the previous section, that here we mean by asymptotically stable, asymptotic stability in the sense of monotone dynamical systems theory which is equivalent to uniform asymptotic stability in the sense of the classical theory of stability. As explained in [27], under the assumption \((L_{\mu })\) satisfied by \(dh(x^{*})\), the stability of the equilibrium \(x^{*}\) of (2.3) is exactly the same as for the ordinary differential equation obtained from (2.3) by ‘‘ignoring the delays’’. A subset H of C is said to be order convex if for all \(\nu _{1}\) , \(\nu _{2}\in H\) such that \(\nu _{1}\le _{\mu }\nu _{2}\) we have \(\left\{ \nu \in C/\nu _{1}\le _{\mu }\nu \le _{\mu }\nu _{2}\right\} \subset H\) (see [30]). An efficient tool for obtaining global convergence for the delay differential Eq. (2.3) has been obtained by J.El Karkri et al by combining results of [30] and [40]. More precisely, we have the theorem recently formulated and proved in [5] where we assume that initial values of the delay differential Eq. (2.3) belong to \(\Omega\).

Theorem 2.4

Let E denote the set of equilibriums of the delay differential Eq. (2.3). Assume that f satisfies the assumptions \((SM_{\mu })\) and (TD1). Then \(\Omega\) contains an open and dense subset of convergent points. If the set of equilibriums E consists of a single point, then it attracts all solutions of (2.3). If \(\Omega\) is order convex and E consists of two points, then each solution of (2.3) converges to one of them.

The Model and the Delay Differential Equation

The delay differential Eq. (1.2) can be written as

$$\begin{aligned} \;\;\left\{ \begin{array}{ll} {\displaystyle u'(t)= F(u_{t})\;\; \text { for }\; t\ge 0,}\\ {\displaystyle u(t)=\phi (t) \;\; \text { for } -\tau \le t\le 0,}\\ \end{array} \right. \end{aligned}$$
(3.5)

where \(u_{t}(\theta )=u(t+\theta )\) for all \(\left( t,\theta \right) \in [0,+\infty [\times \left[ -\tau ,0\right]\), and

$$\begin{aligned} \begin{aligned} F\,:\,&C([-\tau ,0],{\mathbb {R}})\longrightarrow {\mathbb {R}} \\&\psi \longmapsto F(\psi )=\psi (0)(1-\psi (0)-f(\psi (-\tau ))). \end{aligned} \end{aligned}$$

In all this article the function f is assumed to be of class \(C^1\) on an interval ]a, b[ such that \(\left[ 0,1\right] \subset ]a,b[\), with \(\; f\left( x\right) >0\) for all \(x\in \left[ a,b\right] .\)

Theorem 3.1

(Existence, continuity and smoothness of solutions) For all \(\varphi \in C([-\tau ,0],[0,1])\), the delay differential Eq. (3.5) has a unique solution \(u(\varphi ,.)\,:\,t\longmapsto u(\varphi ,t)\) defined on \([-\tau ,+\infty [\). Furthermore, \(u(\varphi ,.)\) is continuous on \([-\tau ,+\infty [\) and of class \(C^1\) on \([0,+\infty [\) and \(u\left( \varphi ,t\right) =u_{\varphi }\left( t\right) \in \left[ 0,1\right]\) for all \(t\ge 0\).

Proof

Let \(\psi \in C([-\tau ,0],[0,1])\). Then \(\psi \in C([-\tau ,0],]a,b[)\). Since f is \(C^{1}\) on ]a, b[,

$$\begin{aligned} F:\,\psi \mapsto F(\psi )=\psi (0)(1-\psi (0)-f(\psi (-\tau )) \end{aligned}$$

is \(C^{1}\) on the open subset \(C\left( [-\tau ,0],]a,b[\right)\) of C. Then F is continuous and Lipschitzian on all compact subsets of \(C\left( \left[ -\tau ,0\right] ,]a,b[\right)\). According to Theorem 2.1, the delay differential Eq. (3.5) has a unique continuous solution \(u\left( \psi ,.\right) =u_{\psi }(.)\) on \([-\tau ,+\infty [\). By the same theorem, we have \(u\left( \psi ,.\right)\) is \(C^{1}\) on \([0+\infty [\). \(\square\)

Theorem 3.2

Under hypothesis of Theorem 3.1, we have \(u_{\varphi }(t)\in \left[ 0,1\right]\) for all \(t\in [0,+\infty [,\) that is \(C\left( \left[ -\tau ,0\right] ,\left[ 0,1\right] \right)\) is positively invariant for the semi-flow generated by the delay differential Eq. (3.5) (see [30] for the definition and the properties of positively invariant subsets).

Proof

Assume that \(\varphi \in C\left( [-\tau ,0],]0,1[\right)\). Let us prove that \(u_{\varphi }(t)\in \left[ 0,1\right]\) for all \(t\in [0,+\infty [.\) Assume that \(\left\{ t\ge 0 : u_{\varphi }(t)>1\right\} \ne \emptyset\). Put \(t_{0}=\inf \left\{ t\ge 0 : u_{\varphi }(t)>1\right\}\) and \(u=u_{\varphi }\). We have \(t_{0}\ge 0\) , \(u(t_{0})=1\) and \(u'(t_{0})=u(t_{0})(1-u(t_{0})-f(u\left( t_{0}-\tau \right) ))\). Thus,

$$\begin{aligned} u'(t_{0})= & {} u(t_{0})\left( 1-u(t_{0})-f(u\left( t_{0}-\tau \right) \right) \\= & {} 1\left( 1-1-f(u\left( t_{0}-\tau \right) \right) = -f\left( u\left( t_{0}-\tau \right) \right) < 0. \end{aligned}$$

The inequality \(u'(t_{0})<0\) is in contradiction with the minimality of \(t_{0}\). Consequently, \(\left\{ t\ge 0 : u_{\varphi }(t)>1\right\} =\emptyset\), and then \(\; u_{\varphi }\left( t\right) \le 1\) for any \(t\ge 0\).

Now assume that \(\left\{ t\ge 0/u_{\varphi }(t)=0\right\} \ne \emptyset\). Put \(t_{1}=\inf \left\{ t>0/u_{\varphi }(t)=0\right\}\) and \(u=u_{\varphi }\). We have \(u(t_{1})=0\) for \(t_{1}\ge 0\) and \(u(t)>0\) for all \(t<t_{1}\). Thus, \(u(t)>0\) for all \(t<t_{1}\), and

$$\begin{aligned} \frac{u'(t)}{u(t)}=1-u(t)-f(u\left( t-\tau \right) . \end{aligned}$$

Thus, \(u(t)>0\) and \(\displaystyle \frac{d\,\ln \left( u(t)\right) }{dt}=1-u(t)-f\left( u\left( t-\tau \right) \right) ,\) for all \(t<t_{1}\). Then,

$$\begin{aligned} \underset{t<t_{1}}{\underset{t\rightarrow t_{1}}{lim}}\frac{d\,\ln \left( u(t)\right) }{dt}=1-u(t_{1})-f\left( u\left( t_{1}-\tau \right) \right) =1-f\left( u\left( t_{1}-\tau \right) \right) . \end{aligned}$$

On the other hand, \(\underset{t<t_{1}}{\underset{t\rightarrow t_{1}}{lim}}u(t)=u(t_{1})=0\). Thus, \(\underset{t<t_{1}}{\underset{t\rightarrow t_{1}}{lim}}ln\left( u\left( t\right) \right) =-\infty\), in contradiction with \({\displaystyle \underset{t<t_{1}}{\underset{t\rightarrow t_{1}}{lim}}\frac{d\,ln\left( u(t)\right) }{dt}\left( t=t_{1}\right) =1-f\left( u\left( t_{1}-\tau \right) \right) \in {\mathbb {R}}}\). This means that the assumption \(\left\{ t\ge 0/u_{\varphi }(t)<0\right\} \ne \emptyset\) fails. Consequently \(\left\{ t\ge 0/u_{\varphi }(t)<0\right\} =\emptyset\) which means that \(u_{\varphi }(t)\ge 0\) for all \(t\in [-\tau ,+\infty [\). We conclude that \(u_{\varphi }(t)\in \left[ 0,1\right]\) for all \(t\in [0,+\infty [\). In other words, \(u_{\varphi }(t)\in \left[ 0,1\right]\) for all \(\varphi \in C([-\tau ,0],]0,1[)\) and all \(t\in [0,+\infty [\). Take now \(\psi \text { in } C\left( [-\tau ,0],[0,1]\right) =\overline{C\left( [-\tau ,0],]0,1[\right) }\). There exists \(\left( \psi _{n}\right) _{n\in {\mathbb {N}}}\) in \(\left( C([-\tau ,0],]0,1[)\right) ^{{\mathbb {N}}}\) such that \(\underset{n\rightarrow +\infty }{lim}\Vert \psi _{n}-\psi \Vert _{\infty }=0\). By the previous result we have \(u_{\psi _{n}}(t)\in \left[ 0,1\right]\) for all \(n\in {\mathbb {N}}\) and all \(t\ge 0\). By continuity of solutions we have \(\underset{n\rightarrow +\infty }{lim}u_{\psi _{n}}(t)=u_{\psi }(t)\) for all \(t\ge 0\), with \(0\le u_{\psi _{n}}(t)\le 1\) for all \(n\in {\mathbb {N}}\). Thus, \(0\le \underset{n\rightarrow +\infty }{lim}u_{\psi _{n}}(t)\le 1\) for all \(t\ge 0\). Then we have \(0\le u_{\psi }(t)\le 1\) for all \(t\ge 0\). We have proved that \(0\le u_{\psi }(t)\le 1\) for all \(\psi \in \overline{C\left( [-\tau ,0],]0,1[\right) }\) and all \(t\ge 0\). \(\square\)

It is clearly seen that the function F is differentiable on \(C\left( [-\tau ,0],[0,1]\right)\). Moreover,

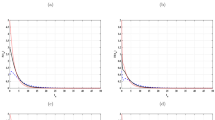
$$\begin{aligned} dF\left( \varphi \right) \left( \psi \right) =\left( 1-2.\varphi (0)-f(\varphi (-\tau ))\right) .\psi \left( 0\right) -\varphi (0).f\,'(\varphi (-\tau )).\psi \left( -\tau \right) , \end{aligned}$$

for any \(\left( \varphi ,\psi \right)\) in \(C\left( [-\tau ,0],[0,1]\right) \times C.\) As pointed out in [1], the function f has two typical forms in our context (see Fig. 1 in [1]).

Equilibrium points: The steady state equation is \(F(u)=0\) which has the solutions \(v_0 = 0\), and all \(v^{*}\in \left. \right] 0,1\left. \right]\) satisfying \(f(v^{*})=1-v^{*}\). The existence and the number of nontrivial equilibriums \(v^{*}\) depend on the form of the function f. In the next section we provide an asymptotic stability analysis of all equilibriums without any additional restriction on the form or on the smoothness of the \(C^{1}\) nonnegative function f. Contrariwise, for global convergence and global asymptotic stability analysis supplementary hypothesis on f will be indispensable.

Asymptotic Stability of Equilibriums

In this section, we discuss the conditions for the local stability of the zero and nonzero steady states of the delay differential Eq. (3.5). The technique of proofs is an application of the results of Theorem 2.3. More precisely, in Sect. 4.1 we prove that asymptotic stability of the zero equilibrium depends on the sign of \(f(0)-1\). Conditions of asymptotic stability of the nonzero equilibrium \(v^{*}\) are formulated in Sect.  4.2 in the case \(f'(v^{*})<0\) and in Sect.  4.3 for the case \(f'(v^{*})>0\).

Asymptotic Stability of the Zero Equilibrium

Theorem 4.1

If the nonnegative \(C^{1}\) function f satisfies the condition \(f(0)>1\), then the equilibrium 0 is asymptotically stable. If \(f(0)<1\), then the equilibrium 0 is unstable.

Proof

It is clearly seen that F is differentiable in 0 and the linearised equation at \(u=0\) is \(v'=\left( 1-f(0)\right) .v\). Furthermore, \(dF(0)(\psi ) = (1- f(0))\psi (0)\) for all \(\psi \in C\). Thus, for \(\mu > 1+ \Vert f\Vert _{\infty }\) and all \(\psi \;_{\mu }>0\) we have \(dF(0)(\psi ) +\mu \psi (0)>0\). Hence, \((L_{\mu })\) holds for dF(0). As in Eq. (2.4), one can write \(\widetilde{F}\left( x\right) =F\left( \hat{x}\right)\) for all \(x\in \left[ 0,1\right]\), where \(\hat{x}\left( \theta \right) =x\) for all \(\theta \in \left[ -\omega ,0\right]\). It is clearly seen that

$$\begin{aligned} \hat{x}\in \overline{C\left( [-\tau ,0],]0,1[\right) }=C\left( [-\tau ,0],[0,1]\right) ,\;\forall x\in \left[ 0,1\right] . \end{aligned}$$

Since \(\tilde{F}(x) = x(1-x-f(x))\) for all \(x\in [0,1]\), we have \(\tilde{F}'(x) = 1-2x-f(x)-xf'(x)\) for all \(x\in [0,1]\). Particularly \(\tilde{F}'(0)= 1- f(0)\). It follows that, if \(f(0)>1\), then \(\tilde{F}'(0)<0.\) In other words and by Theorem 2.3, 0 is asymptotically stable. Otherwise, if \(f(0)<1\), then \(\tilde{F}'(0)>0\), and then 0 is unstable. The proof is completed. \(\square\)

Asymptotic Stability of the Equilibrium \(v^{*}\) if \(f'(v^{*})<0\)

Let \(v^{*}\) be a nonzero equilibrium of the delay differential Eq. (3.5). In this section we assume that \(f\,'\left( v^{*}\right) <0\). We have

$$\begin{aligned} \left\{ \begin{array}{ll} \tilde{F}'(v^{*})=1-2.v^{*}-f(v^{*})-v^{*}.f'(v^{*})\\ dF\left( v^{*}\right) \left( \psi \right) =\left( 1-2.v^{*}-f(v^{*})\right) .\psi \left( 0\right) -v^{*}.f\,'(v^{*}).\psi \left( -\tau \right) \qquad for\;all\;\psi \in C \end{array}\right. \end{aligned}$$

However, \(1-v^{*} - f(v^{*} )=0\), as \(v^{*}\) is an equilibrium. Thus,

$$\begin{aligned} \left\{ \begin{array}{ll} \tilde{F}'(v^{*} ) = -v^{*} -v^{*} f'(v^{*} )= -v^{*} (1+ f'(v^{*} ))\\ dF\left( v^{*}\right) \left( \psi \right) =-v^{*}.\psi \left( 0\right) -v^{*}.f\,'(v^{*}).\psi \left( -\tau \right) \qquad for\;all\;\psi \in C \end{array}\right. \end{aligned}$$

Theorem 4.2

Let \(v^{*}\) be a non zero equilibrium of the delay differential Eq. (3.5) such that \(f'(v^{*})<0\).

  • If \(-1<f'(v^{*})<0\), then the equilibrium \(v^{*}\) is asymptotically stable.

  • If \(f'(v^{*})<-1\), then \(v^{*}\) is unstable.

Proof

Let \(\mu >0\) and \(\psi \;_{\mu }>0\). We have

$$\begin{aligned} \;\;\left\{ \begin{array}{ll} {\psi \ge 0 \text { and } \psi \ne 0}\\ {s\mapsto \psi (s)e^{\mu s} \quad is \quad increasing}\\ \end{array} \right. \end{aligned}$$

Obviously, \(\psi (0)>0\) and \(\psi \left( -\tau \right) \ge 0\). Since \(f'\left( v^{*}\right) <0\), we have

$$\begin{aligned} dF(v^{*})(\psi )+\mu .\psi (0)=[\mu -v^{*}]\psi (0)-v^{*}f'(v^{*})\psi (-\tau )\ge (\mu -v^{*})\psi (0). \end{aligned}$$

Then, for \(\mu > v^{*}\), we have \(d F(v^{*} )(\psi ) + \mu .\psi (0)>0\). Hence, the property \((L_{\mu })\) holds for \(dF(v^{*} )\). We can clearly see that

$$\begin{aligned} \tilde{F}'(v^{*} ) < 0 \Leftrightarrow 1 + f'(v^{*} )>0 \Leftrightarrow f'(v^{*} ) >-1 . \end{aligned}$$

Moreover, \(\tilde{F}'(v^{*} ) > 0 \Leftrightarrow f'(v^{*} ) <-1\). The theorem is then proved. \(\square\)

Asymptotic Stability of the Equilibrium \(v^{*}\) if \(f'(v^{*})>0\)

Let \(v^{*}\) be an equilibrium of the delay differential Eq. (3.5) such that \(v^{*}>0\). In this section we assume that \(f\,'\left( v^{*}\right) >0\). Consider the following assumption:

$$\begin{aligned} ln\left( \frac{1}{\tau v^{*}f\,'\left( v^{*}\right) }\right) >1+\tau v^{*}. \;\;\;\;\; (H^1) \end{aligned}$$

Theorem 4.3

Let \(v^{*}\) be a non zero equilibrium of the delay differential Eq. (3.5) such that \(f'(v^{*})>0\). If the condition \((H^1)\) is satisfied, then \(v^{*}\) is asymptotically stable.

Proof

We have

$$\begin{aligned} dF\left( v^{*}\right) \left( \psi \right) =-v^{*}.\psi \left( 0\right) -v^{*}.f\,'(v^{*}).\psi \left( -\tau \right) \qquad for\;all\;\psi \in C. \end{aligned}$$

Let us set

$$\begin{aligned} \;\;\left\{ \begin{array}{ll} {\lambda = - v^{*},}\\ {\eta = -v^{*}f'(v^{*} ),}\\ {\eta ^{-}=min\left( \eta ,0\right) .} \end{array} \right. \end{aligned}$$

We have \(dF(v^{*})(\psi ) = \lambda \psi (0) + \eta \psi (-\tau )\) for all \(\psi \in C\). According to Theorem.1.1 of [5], \(dF(v^{*})\) satisfies \((L_{\mu })\) if and only if one of the two following statements hold:

$$\begin{aligned} \left\{ \begin{array}{ll} (a)\quad \lambda +\eta ^{-}>0,\\ (b)\quad \lambda +\eta ^{-}<0,\;\tau |\eta |<1\text { and }\tau \lambda -ln(\tau |\eta |)>1. \end{array}\right. \end{aligned}$$

Here (a) is not satisfied. It is clearly seen that \((H^1)\) implies that hypothesis (b) holds, and then \(dF(v^{*})\) verifies \((L_{\mu })\). Since \(f'(v^{*})>0\), we have

$$\begin{aligned} \tilde{F}'(v^{*} ) =-v^{*} (1+ f'(v^{*} ))<0. \end{aligned}$$

Then, Theorem 2.3 applies and the equilibrium \(v^{*}\) is asymptotically stable. \(\square\)

Fig. 1
figure 1

The two typical forms of the function f as presented in [1]

Full size image

Global Stability of the Non-Zero Equilibrium for the First Typical Form of f

Here the function f is assumed to be non decreasing, (Fig. 1, left). The function is assumed to be sufficiently small, such that \(f_{1}=f\left( 0\right) <1\). Consider the following assumption

$$\begin{aligned} ln\left( \frac{1}{\tau .\parallel f\,'\parallel _{\infty }}\right) >\tau (\Vert f\Vert _{\infty }+1)+1.\quad \left( HG\right) \end{aligned}$$

Proposition 5.1

If \(\left( HG\right)\) holds, then the assumption \(\left( SM_{\mu }\right)\) holds for the delay differential Eq. (3.5) on \(C\left( [-\tau ,0],[0,1]\right)\).

Proof

Assume that \(\left( HG\right) \,\) holds. Let \(\phi ,\psi \in \overline{C\left( [-\tau ,0],]0,1[\right) }= C\left( [-\tau ,0],[0,1]\right)\) be such that \(\phi <_{\mu }\psi\) for \(\mu >0\). By the same arguments as in the proof of Theorem 4.1 in [5], one can affirm that there exists \(\lambda \in \left[ 0,1\right]\) such that

$$\begin{aligned} F\left( \psi \right) -F\left( \phi \right)= & {} dF\left( \nu \right) \left( \psi -\phi \right) \\= & {} [1-2.\nu (0)-f(\nu (-\tau ))]\left( \psi -\phi \right) (0)-\nu (0)f\;'(\nu (-\tau )).\left( \psi -\phi \right) (-\tau ), \; \end{aligned}$$

where \(\nu =\lambda .\psi +\left( 1-\lambda \right) .\phi\). Thus,

$$\begin{aligned} F\left( \psi \right) -F\left( \phi \right) +\mu \left( \psi -\phi \right) (0)= & {} [1-2.\nu (0)-f(\nu (-\tau ))+\mu ].\left( \psi -\phi \right) (0)\\&- \nu (0)f\;'(\nu (-\tau )).\left( \psi -\phi \right) (-\tau ). \end{aligned}$$

Since \(\phi <_{\mu }\psi\), we have \(\left( \psi -\phi \right) (-\tau )\le e^{\mu .\tau }.\left( \psi -\phi \right) (0)\). Moreover, as \(f\;'(\nu (-\tau ))\ge 0\), we get

$$\begin{aligned} -\nu (0)f\;'(\nu (-\tau )).\left( \psi -\phi \right) (-\tau )\ge -\nu (0).f\;'(\nu (-\tau )).e^{\mu .\tau }.\left( \psi -\phi \right) (0). \end{aligned}$$

Then,

$$\begin{aligned}&F\left( \psi \right) -F\left( \phi \right) +\mu \left( \psi -\phi \right) (0)\\&\quad \ge \left[ \mu +1-2.\nu (0)-f(\nu (-\tau ))-\nu (0).f\;'(\nu (-\tau )).e^{\mu .\tau }\right] .\left( \psi -\phi \right) (0). \end{aligned}$$

Since \(f(\nu (-\tau ))\le \parallel f\parallel _{\infty }\),      \(0\le \nu \left( 0\right) \le 1\)   and     \(0\le f\;'(\nu (-\tau ))\le \parallel f\,'\parallel _{\infty }\), we have

$$\begin{aligned}&[\mu +1-2.\nu (0)-f(\nu (-\tau ))-\nu (0).f\;'(\nu (-\tau )).e^{\mu .\tau }].\left( \psi -\phi \right) (0)\ge \\&\quad [\mu -1-\parallel f\parallel _{\infty }-\parallel f\,'\parallel _{\infty }.e^{\mu .\tau }].\left( \psi -\phi \right) (0). \end{aligned}$$

It results that,

$$\begin{aligned} F\left( \psi \right) -F\left( \phi \right) +\mu \left( \psi -\phi \right) (0)\ge [\mu -1-\parallel f\parallel _{\infty }-\parallel f\,'\parallel _{\infty }.e^{\mu .\tau }].\left( \psi -\phi \right) (0). \end{aligned}$$

It can be clearly seen that \(\left( HG\right) \Longleftrightarrow \left[ \exists \mu>0\;/\quad \mu -1-\parallel f\parallel _{\infty }-\parallel f\,'\parallel _{\infty }.e^{\mu .\tau }>0\right]\). Consequently, the condition \(\left( HG\right)\) implies that there exists \(\mu >0\) such that, for all \(\phi <_{\mu }\psi\) in \(C\left( [-\tau ,0],[0,1]\right)\), we have

$$\begin{aligned} F\left( \psi \right) -F\left( \phi \right) +\mu \left( \psi -\phi \right) (0)>0. \end{aligned}$$

That is \(\left( HG\right)\) implies that \(\left( SM_{\mu }\right)\) holds for the delay differential Eq. (3.5) on \(\overline{C\left( [-\tau ,0],]0,1[\right) }=C\left( [-\tau ,0],[0,1]\right)\). \(\square\)

Theorem 5.2

If hypothesis \(\left( HG\right)\) holds, then for all \(\varphi \in C([-\tau ,0],]0,1])\), we have

$$\begin{aligned} \displaystyle \lim _{t\rightarrow \infty } u(\varphi ,t) = v^{*}. \end{aligned}$$

Proof

F is clearly continuous on \(\overline{C\left( [-\tau ,0],]0,1[\right) }=C\left( [-\tau ,0],[0,1]\right)\). Furthermore, from Theorem 3.1, all solutions of Eq. (3.5) starting from \(\overline{C\left( [-\tau ,0],]0,1[\right) }=C\left( [-\tau ,0],[0,1]\right)\) are bounded. Thus, condition \(\left( TD1\right)\) above is fulfilled by the delay differential Eq. (3.5). From Proposition 5.1, the assumption \(\left( SM_{\mu }\right)\) holds for the delay differential Eq. (3.5) on \(C\left( [-\tau ,0],[0,1]\right)\). The delay differential equation (3.5) has two equilibriums in the convex order subset \(C\left( [-\tau ,0],[0,1]\right)\) of C. Thus, by Theorem 2.4 , each solution of Eq. (3.5) starting from \(C\left( [-\tau ,0],[0,1]\right)\) converges to an equilibrium. Let \(\varphi \in C([-\tau ,0],]0,1])\) and assume by contradiction that \(\displaystyle \lim _{t\rightarrow \infty } u(\varphi ,t) = 0.\) We set \(u(t) = u(t,\varphi )\). By the same arguments used in the proof of Theorem 3.2, we have \(u(t)>0, \;\forall t \ge -\tau .\) This allows us to write

$$\begin{aligned} \frac{u'(t)}{u(t)} =1-u(t) - f(u(t-\tau )),\;\forall t \ge -\tau . \end{aligned}$$

Introducing the limit when t goes to infinity, we obtain

$$\begin{aligned} \frac{u'(t)}{u(t)} \rightarrow _{t\rightarrow +\infty }1-0 - f(0). \end{aligned}$$

While \(1- f(0) >0.\) Thus,

$$\begin{aligned} \exists \,\tilde{t}>0 \text { such that } \forall t\ge \tilde{t}, \; \displaystyle \frac{u'(t)}{u(t)} >0. \end{aligned}$$

Which means that u is strictly increasing on \([\tilde{t}, +\infty [\) with

$$\begin{aligned} \;\;\left\{ \begin{array}{ll} { u(t)>0,\;\forall t\ge \tilde{t};}\\ { \displaystyle \lim _{t\rightarrow +\infty } u(t) =0.}\\ \end{array} \right. \end{aligned}$$

This is contradictory. In other words, the hypothesis that \(\displaystyle \lim _{t\rightarrow +\infty }u(t) =0\) is false. Since the solution converges to an equilibrium, we the have \(\displaystyle \lim _{t\rightarrow +\infty } u(t) =v^{*}\). Therefore, the assertion of the theorem holds. \(\square\)

Theorem 5.3

If \(\left( HG\right)\) holds, then the positive equilibrium \(v^{*}\) is globally asymptotically stable on \(C\left( [-\tau ,0],]0,1]\right)\).

Proof

By \(\left( HG\right)\) we have

$$\begin{aligned} ln\left( \frac{1}{\tau .\parallel f\,'\parallel _{\infty }}\right) >\tau (\Vert f\Vert _{\infty }+1)+1. \end{aligned}$$

Since \(0<v^{*}\le 1\) and \(0<f\,'\left( v^{*}\right) \le \parallel f\,'\parallel _{\infty }\), we have

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle \ln \left( \frac{1}{\tau v^{*}f\,'\left( v^{*}\right) }\right) \ge \ln \left( \frac{1}{\tau .\parallel f\,'\parallel _{\infty }}\right) ,\\ \displaystyle \tau (\Vert f\Vert _{\infty }+1)+1\ge 1+\tau v^{*}. \end{array}\right. \end{aligned}$$

Thus,

$$\begin{aligned} \displaystyle \ln \left( \frac{1}{\tau v^{*}f\,'\left( v^{*}\right) }\right) >1+\tau v^{*}. \end{aligned}$$

Hence, condition \(\left( H^{1}\right)\) holds. Then, by Theorem 4.3 we have the asymptotic stability of \(v^{*}\). From Theorem 5.2, all solutions starting from \(C\left( [-\tau ,0],]0,1]\right)\) converge to \(v^{*}\). Finally, \(v^{*}\) is globally asymptotically stable on \(C\left( [-\tau ,0],]0,1]\right)\). \(\square\)

Let study now the convergence of solutions starting from \(C\left( [-\tau ,0],[0,1]\right)\).

Theorem 5.4

Assume that \(\left( HG\right)\) holds. The following statements are equivalent.

  • \(\left( H1\right)\) \(\underset{t\rightarrow +\infty }{lim}u(t)=0\)

  • \(\left( H2\right)\) \(\left( \forall a,b\in [-\tau ,+\infty [\right) \quad /b-a\ge \tau\) we have \(\left\{ a\le t\le b/\,u(t)=0\right\} \ne \emptyset\).

Proof

We have implicitly showed in the proof of Theorem 3.2 that \(C\left( [-\tau ,0],]0,1]\right)\) is positively invariant. Assume that condition \(\left( H2\right)\) fails. Then, there exists \(b\ge 0\) such that for all \(t\in \left[ b-\tau ,b\right]\) we have \(0<u(t)\le 1\). That is \(u_{b}:\theta \mapsto u(t+b)\) on \(\left[ -\tau ,0\right]\) is in the positively invariant subset \(C\left( [-\tau ,0],]0,1]\right)\) of C. By Theorem 5.2, we have \(\underset{\underset{t\rightarrow +\infty }{t\ge b}}{lim}u(t)=v^{*}\). That is \(\underset{t\rightarrow +\infty }{lim}u(t)=v^{*}\). Then, assumption \(\left( H1\right)\) fails. Finally “\(Non \left( H2\right) \Longrightarrow Non\left( H1\right)\)”. Then \(\left( H1\right) \Longrightarrow \left( H2\right)\). Assume now that \(\left( H2\right)\) is satisfied. It’s clearly seen that there exists a sequence \(\left( t_{n}\right) _{n\in {\mathbb {N}}}\) such that \(\underset{n\rightarrow +\infty }{lim}t_{n}=+\infty\) and \(\left( \forall n\in {\mathbb {N}}\right)\) \(u(t_{n})=0\). Then, \(\underset{n\rightarrow +\infty }{lim}u\left( t_{n}\right) =0\) . Since \(\underset{t\rightarrow +\infty }{lim}u\left( t\right)\) exists and belongs to \(\left\{ 0,v^{*}\right\}\) , obviously \(\underset{t\rightarrow +\infty }{lim}u\left( t\right) =0\). That is \(\left( H1\right)\) holds. Thus, \(\left( H2\right) \Longrightarrow \left( H1\right)\). The proof is completed. \(\square\)

Example of the First Typical Form of f: Linear Function

Consider \(f\left( u\right) =k_{1}u+k_{2}\), with \(k_{1}>0\) and \(0<k_{2}<1\). The unique nonzero equilibrium is \(\displaystyle v^{*}=\frac{1-k_{2}}{1+k_{1}}\). We have \(\parallel f\,'\parallel _{\infty }=k_{1}\) and \(\parallel f\parallel _{\infty }=k_{1}+k_{2}\). Condition \(\left( HG\right)\) in this case is

$$\begin{aligned} \displaystyle \ln \left( \frac{1}{\tau .\parallel f\,'\parallel _{\infty }}\right)>\tau (\Vert f\Vert _{\infty }+1)+1\Longleftrightarrow \displaystyle \ln \left( \frac{1}{\tau .k_{1}}\right) >\tau (k_{1}+k_{2}+1)+1. \end{aligned}$$

Let take \(\tau =1\), \(k_{2}=f\left( 0\right) =0.1\) and \(k_{1}=0.1\). \(\left( HG\right)\) is clearly satisfied. The nonzero equilibrium is \(v^{*}\simeq 0.82\). In Fig. 2, numerical simulations for different initial values illustrate the global stability. As we see, solutions converge to the non zero equilibrium.

Fig. 2
figure 2

Numerical simulations for a linear function \(f= 0.1x + 0.1\)

Full size image

Global Stability of the Non-Zero Equilibrium for the Second Typical Form of f

As explained in [3], experimental observations show that, in many cases, the intensity of the immune response has a bell-shaped dependence on the concentration of virus, i.e., it increases at low and decays at high infection levels [3]. This illustrates the fact that when virus concentration u(t) increases for the first time, the function f(u(t)) should increase quickly so as that the concentration of virus at time \(t+\tau\), \(u(t+\tau )\), decreases as illustrated in Eq. (1.2). Here f is assumed to have the form in the right hand side of Fig. 1 (bell-shaped form).

Put \(\parallel f\,'\parallel _{\infty }^{+}=max\left\{ f\,'\left( x\right) :\quad x\in \left[ 0,1\right] ,\quad f\,'(x)\ge 0\right\}\). It is clearly seen that

$$\begin{aligned} \left( \forall x\in \left[ 0,1\right] \right) \;max(0,f\,'(x))\le \parallel f\,'\parallel _{\infty }^{+}. \end{aligned}$$

Denote by \(\left( HG^{+}\right)\) the assumption

$$\begin{aligned} \ln \left( \frac{1}{\tau .\parallel f\,'\parallel _{\infty }^{+}}\right) >\tau (\Vert f\Vert _{\infty }+1)+1. \end{aligned}$$

Proposition 6.1

If \(\left( HG^{+}\right)\) holds, then the assumption \(\left( SM_{\mu }\right)\) holds for the delay differential Eq. (3.5) on \(C\left( [-\tau ,0],[0,1]\right)\).

Proof

Assume that \(\left( HG^{+}\right)\) holds. Take \(\phi ,\psi \in \overline{C\left( [-\tau ,0],]0,1[\right) }=C\left( [-\tau ,0],[0,1]\right)\) such that \(\phi <_{\mu }\psi\) for \(\mu >0\). As in the proof of Proposition 5.1, we have

$$\begin{aligned}&F\left( \psi \right) -F\left( \phi \right) +\mu \left( \psi -\phi \right) (0)\ge [\mu +1-2.\nu (0)-f(\nu (-\tau ))\\&\quad -\nu (0).f\;'(\nu (-\tau )).e^{\mu .\tau }].\left( \psi -\phi \right) (0) \end{aligned}$$

Where \(\nu =\lambda .\psi +\left( 1-\lambda \right) .\phi\) with \(\lambda \in \left[ 0,1\right]\). We have

$$\begin{aligned} f\;'(\nu (-\tau ))\le max(0,f\;'(\nu (-\tau )))\le \parallel f\,'\parallel _{\infty }^{+}. \end{aligned}$$

Thus,

$$\begin{aligned} F\left( \psi \right) -F\left( \phi \right) +\mu \left( \psi -\phi \right) (0)\ge [\mu -1-\parallel f\parallel _{\infty }-\parallel f\,'\parallel _{\infty }^{+}.e^{\mu .\tau }].\left( \psi -\phi \right) (0). \end{aligned}$$

It is clearly seen that \(\left( HG\right) \quad \Longleftrightarrow \left[ \exists \mu>0\;/\quad \mu -1-\parallel f\parallel _{\infty }-\parallel f\,'\parallel _{\infty }^{+}.e^{\mu .\tau }>0\right]\). Finally, condition \(\left( HG^{+}\right)\) implies that there exists \(\mu >0\) such that for all \(\phi <_{\mu }\psi\) in \(C\left( [-\tau ,0],[0,1]\right)\), we have \(F\left( \psi \right) -F\left( \phi \right) +\mu \left( \psi -\phi \right) (0)>0\). That is \(\left( HG^{+}\right)\) implies that \(\left( SM_{\mu }\right)\) holds for the delay differential Eq. (3.5) on \(\overline{C\left( [-\tau ,0],]0,1[\right) }=C\left( [-\tau ,0],[0,1]\right)\) completing the proof. \(\square\)

Theorem 6.2

If \(\left( HG^{+}\right)\) holds, then the positive equilibrium \(v^{*}\) is globally asymptotically stable on \(C\left( [-\tau ,0],]0,1]\right)\).

Proof

The proof is identical to that of Theorem 5.3. \(\square\)

Example of the Second Typical Form of f: \(f\left( x\right) =\left( ax+b\right) .e^{-cx}\)

Consider \(f\left( x\right) =\left( ax+b\right) .e^{-cx}\) with \(a>0\) , \(b>0\) and \(0<\frac{1}{c}-\frac{b}{a}<1\) . We have \(\parallel f'\parallel _{\infty }^{+}=f'(0)=a-cb>0\) and \(\parallel f\parallel _{\infty }=f(x_{0})=f\left( \frac{1}{c}-\frac{b}{a}\right) =\frac{a}{c}e^{\left( \frac{bc-a}{a}\right) }\). The condition \(\left( HG^{+}\right)\) can be rewritten as

$$\begin{aligned} \left( HG^{+}\right) \;ln\left( \frac{1}{\tau .\left( a-cb\right) }\right) >\tau (\frac{a}{c}e^{\left( \frac{bc-a}{a}\right) }+1)+1. \end{aligned}$$

For \(\tau =0.1\), \(a=1\),\(b=0.4\) and \(c=1\), \(\left( HG^{+}\right)\) is fulfilled. In this case we have \(v^{*}\simeq 0.45\). As we see in Fig. 3, solutions converge to the equilibrium \(v^{*}\) for different initial values.

For \(\tau =0.1\), \(a=10\), \(b=0.4\) and \(c=1\), we have

$$\begin{aligned} ln\left( \frac{10}{a-cb}\right) -\frac{a}{c.10}e^{\left( \frac{bc-a}{a}\right) }-1.1\simeq -1.44<0, \end{aligned}$$

and condition \(\left( HG^{+}\right)\) is not satisfied.

Fig. 3
figure 3

Numerical simulations for \(f\left( x\right) =\left( 0.1.x+0.01\right) e^{-0.2.x}\)

Full size image
Fig. 4
figure 4

Oscillations in time for \(f\left( u\right) =\left( -0.05.u+0.05\right) e^{6.5.u}\)

Full size image

Numerical simulations in Fig. 4 show that for some parameters which do not satisfy the stability conditions, there are periodic oscillations. Period doubling bifurcations and transition to chaos are observed in Fig. 2 of [1].

Application to SARS-COV-2 Immune Response

Table 1 The normalised (divided  by \(10^6\)) number of copies per \(10^3\) cells during 16 days from the day of virus detection (day 8)
Full size table

In order to illustrate the obtained analytical results, we use the clinical case measures of SARS-CoV-2 for patient 3 represented in Fig. 2 of [16]. The data in Table 1 has been obtained after transforming the logarithmic representations into the number of virus copies per \(10^3\) cells (divided by \(10^6\) for normalisation) and denoted u(t). It has been then used to calibrate the equation in order to obtain optimized parameters. We have used the values from day 9 to day 23. This was performed in R software using the library “deSolve”. Then, simulations for different initial values are established using MATLAB solver “dde23”.

Delay \(\tau\) represents the duration of clonal expansion of antigen-specific lymphocytes in the adaptive immune response. According to the biological data, we set \(\tau =7\). It should be noted that the incubation period of SARS-CoV-2 is in average 5 days (less for the Omicron variant) [21, 29]. Therefore, disease symptoms appear before the onset of the adaptive immune response, and further disease progression is determined by the interplay of these two processes.

Fig. 5
figure 5

Numerical simulations corresponding to a COVID-19 case with \(f\left( u\right) =0.28u+0.989\) and \(\tau = 7 \; days\)

Full size image
Fig. 6
figure 6

Numerical simulations corresponding to a COVID-19 case with \(f\left( u\right) =\left( 0.517 u+0.988\right) .e^{-0.173u}\) and \(\tau = 7 \;days\)

Full size image

Calibration and Simulation in the Case \(f\left( u\right) =k_{1}u+k_{2}\)

After calibrating the model for the form \(f\left( u\right) =k_{1}u+k_{2}\), with \(k_{1}>0\) and \(0<k_{2}<1\) to the COVID-19 data, we obtained the following parameters values \(k_{1}\simeq 0.28\) and \(k_{2}\simeq 0.989\). The assumption of asymptotic stability (H1) is satisfied for those parameters with \(\tau = 7\). Four different cases of initial values are considered, \(\varphi _1 = 0.005 ,\;\varphi _2 (t)= 0.01\exp {t} + 0.008 ,\;\varphi _3 = 0.01\exp {t} + 0.02,\) and \(\varphi _4 = 0.01\exp {t} + 0.05\). We observe that the four solutions \(u_1 ,\;u_2 ,\;u_3\), and \(u_4\) corresponding respectively to the initial values \(\varphi _1 ,\;\varphi _2 ,\;\varphi _3 ,\) and \(\varphi _4\), converge monotonically to the non-zero equilibrium (or endemic equilibrium) which is \({v^*}_{cov} \simeq 0.00859\) as shown in Fig. 5.

Calibration and Simulation in the Case \(f\left( u\right) =\left( a.u+b\right) .e^{-c.u}\)

The calibration of COVID-19 data with the case where \(f\left( x\right) =\left( ax+b\right) .e^{-cx}\), leads to the following parameters : \(a\simeq 0.517\), \(b\simeq 0.988\) and \(c\simeq 0.173\). Equation \(f\left( x\right) =1-x\) has a unique positive solution \(v_{cov}^{*}\simeq 0.01\) which is the unique non zero equilibrium of the system. With the same delay \(\tau = 7 \;\; days\), and for the four different initial values \(\varphi _1(t) = 0.008,\;\varphi _2 (t)= 0.025 ,\;\varphi _3(t) = 0.01\exp {t} + 0.04,\;\) and \(\varphi _4(t) = 0.01\exp {t} + 0.15\), we observe that the four respectively corresponding solutions \(u_1 ,\;u_2 ,\;u_3\), and \(u_4\) converge monotonically to the endemic equilibrium \({v^*}_{cov} \simeq 0.0089\) as shown in Fig. 6.

Here we have \(f'\left( v_{cov}^{*}\right) \simeq 0.344>0\), that means biologically that when the virus concentration is close to the nonzero equilibrium \({v^*}_{cov}\), the function \(f\left( u\right) =1-\frac{\psi \left( u\right) }{\varPhi \left( u\right) }>0\) is increasing, where \(\psi \left( u\right)\) is the cell mortality factor and \(\varPhi \left( u\right)\) corresponds to the proliferation dynamic. That happens when proliferation increases faster than mortality. Obviously, an analogous interpretation corresponds to the case \(f'\left( v_{cov}^{*}\right) <0\). We refer the reader to [2] for further details on \(\varPhi\), \(\psi\) and on how the original model of two equations can be reduced to a scalar DDE model.

Discussion and Conclusion

Based on a monotonicity approach, our study provided new results on the qualitative behaviour of solutions for a homogeneous in space delay equation arising in mathematical immunology. The exponential ordering and its properties allowed us to use the framework developed in [5, 6, 8, 27, 30, 40]. The problem of the zero equilibrium asymptotic stability in the sense of the monotone dynamical systems theory has been completely resolved in the case where f is of class \(C^1\). For the nonzero equilibrium \(v^{*}\) when \(f'(v^{*})<0\), a complete characterisation of asymptotic stability has been provided in Theorem  4.2. In the case where \(f'(v^{*})>0\), the study leaded to a sufficient condition on f. The generalization of those conditions to the case where f is continuous and Lipschiz using the results of [27], can be the subject of other works in the future.

Condition of global stability obtained in Sect. 5 depends on the delay \(\tau\) and on the maximum norms of the function f and its derivative \(f'\). The factor \(\Vert f\Vert _{\infty }\) reflects the intensity of immune response, while \(\Vert f ' \Vert _{\infty }\) corresponds to the speed of reaction. Condition in Sect. 6 is similar to that of Sect. 5 except that \(\Vert f ' \Vert _{\infty }\) is replaced by \(\Vert f'\Vert _{\infty }^{+}=\underset{}{Sup\left\{ f'(u): u\in \left[ 0,1\right] \cap \left( f'\right) ^{-1}\left( [0,+\infty [\right) \right\} }\). Here we see that the global stability condition depends only on the increasing branch of the function f. Those results can be used in the study of the reaction-diffusion equation taking into account the spacial diffusion of immune cells and viruses.

Some monotone approaches for the study of reaction-diffusion delayed equations with space dependence have been the subject of many articles and surveys. In their research on abstract functional differential equations and reaction-diffusion systems [18], Martin and Smith applied the idea of quasi-monotone functions to some particular reaction–diffusion delayed functional equations. In 1991, they proved in [19] that under some hypothesis, the solutions of the reaction–diffusion delayed equation \(\frac{\partial u}{\partial t}(x,t)=\Delta u\left( x,t\right) +F\left( x,u_{t}\left( x\right) \right)\) and its corresponding homogeneous in space delayed equation \(u'\left( t\right) =F\left( u_{t}\right)\) have the same asymptotic behaviour. The reader is referred to the introduction of [19] for further details. A more recent development of these ideas is in the work by Yi and Huang [39], where the topic has been introduced as a second application of the theoretical results in the paper (Subsection 2.2). A sophisticated framework has been established by Wang and Zhao in [38] for non delayed partial differential reaction-diffusion equations. The generalization of the obtained results to delayed equations can be the subject of interesting works. The book of Zhao [41] is an excellent reference for the theoretical framework of those systems and their applications in population biology. The reader is particularly referred to Chapters 2 and 9 for useful results and explanations. We cite also the relatively recent article of Wu and Zhao [37].

It should be noted that the equation studied here is not specific to immune reaction systems and that many models are governed by such delayed equations in epidemiology, electronics, ecology and others. We should also point out that the method above can be applied to other forms of the function f, for example the delayed systems studied by Volpert and Trofimchuk in [35], where f is assumed to satisfy the condition \(f(1)=0\) and \(f(0)>1\).

For reader’s convenience, we summarise the main features of the proposed approach. First, the monotone dynamical systems framework leads to local and global stability with order conservation as seen in Figs.  2, 3,  5 and  6. Hence, the asymptotic behaviour of the system is more controllable. This technical advantage is not fulfilled, for example, in [1, 3, 4]. Second, the obtained stability conditions are explicit expressions of systems parameters. That is, stability regions of parameters can be represented geometrically. And then, biologists and clinicians can forecast the evolution of the viral infection. In the recent work [1], for instance, important conditions of stability have been obtained in a more general modeling context, but they can not be used in practical situations since they are not explicit. Moreover, and as it was established in numerical simulations, the method can also be applied to the study of COVID-19 dynamics. We tested the global stability for two specific forms of the efficiency of the immune response for virus elimination f and for different forms of the initial condition. The epidemiological implication of this result can be interpreted as that the viral load dynamic is related monotonically to the initial viral load value, the most this latest is near the equilibrium value the fast it tends to this equilibrium which can be null in several cases and means the extinction of virus. Finally, the asymptotic stability and the global asymptotic stability established using the monotone approach are stronger than those obtained by the classical Lyapunov and characteristic equation’s approach. The method presented in Sect. 7 enables us to forecast the evolution of the viral infection in the future. Indeed, the calibration techniques allow the determination of the optimal parameters fitting the clinical data. Then numerical simulation with the obtained parameters leads to graphical illustrations of the virus concentration dynamics. As we see in Fig. 5, using a linear form of the function f(u), we have obtained a small steady state virus concentration \(v_{cov}^{*}\simeq 0.00859\) that absorbs all the eventual orbits of the system. That means that patient 3 will recover from infection but a small viral concentration will persist in his body.

The approach presented in this paper can lead to deeper assimilation of other more complex immunological models and consequently, better clinical strategies and protocols may be established.