Skip to main content
SpringerLink
Log in

Identification-based Adaptive Tracking Control of Uncertain Bistable Electromechanical Duffing Oscillator

  • Regular Papers
  • Control Theory and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

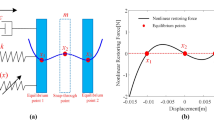
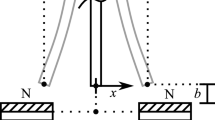
This paper presents a backstepping-based adaptive control design for bistable Duffing-Holmes oscillators. The system parameters are assumed to be uncertain, and the controller uses an adaptation rule to estimate them and to achieve an asymptotic tracking performance. The convergence of the tracking and parameter estimation errors is studied using the Contraction theory. The practical utility of the proposed control scheme is illustrated by applying it to a vibration energy harvester, modeled as a bistable Duffing oscillator, to increase its power level under various external excitations. Moreover, a procedure to increase the harvested energy by reducing the control effort is proposed. Simulation studies are carried out to show the validity and feasibility of the proposed controller.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. Kovacic and M. J. Brennan, The Duffing Equation: Nonlinear Oscillators and Their Behaviour, John Wiley & Sons, Chichester, United Kingdom, 2011.

    Book  Google Scholar 

  2. P. Holmes, “A nonlinear oscillator with a strange attractor,” Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, vol. 292, no. 1394, pp. 419–448, 1979.

    MathSciNet  MATH  Google Scholar 

  3. R. L. Harne and K.-W. Wang, Harnessing Bistable Structural Dynamics: For Vibration Control, Energy Harvesting and Sensing, John Wiley & Sons, Chichester, United Kingdom, 2017.

    Book  Google Scholar 

  4. R. L. Harne and K. Wang, “A review of the recent research on vibration energy harvesting via bistable systems,” Smart Materials and Structures, vol. 22, no. 2, p. 023001, 2013.

    Article  Google Scholar 

  5. A. Khaligh, P. Zeng, and C. Zheng, “Kinetic energy harvesting using piezoelectric and electromagnetic technologies — State of the art,” IEEE Transactions on Industrial Electronics, vol. 57, no. 3, pp. 850–860, 2010.

    Article  Google Scholar 

  6. V. G. Lopes, J. V. L. Peterson, and A. Cunha Jr, “Nonlinear characterization of a bistable energy harvester dynamical system,” Topics in Nonlinear Mechanics and Physics, pp. 71–88, Springer, 2019.

  7. M. F. Daqaq, R. Masana, A. Erturk, and D. Dane Quinn, “On the role of nonlinearities in vibratory energy harvesting: A critical review and discussion,” Applied Mechanics Reviews, vol. 66, no. 4, July 2014.

  8. A. Erturk and D. J. Inman, “Broadband piezoelectric power generation on high-energy orbits of the bistable duffing oscillator with electromechanical coupling,” Journal of Sound and Vibration, vol. 330, no. 10, pp. 2339–2353, May 2011.

    Article  Google Scholar 

  9. B. Zhang, Q. Zhang, W. Wang, J. Han, X. Tang, F. Gu, and A. D. Ball, “Dynamic modeling and structural optimization of a bistable electromagnetic vibration energy harvester,” Energies, vol. 12, no. 12, p. 2410, 2019.

    Article  Google Scholar 

  10. J. P. Udani and A. F. Arrieta, “Sustaining high-energy orbits of bi-stable energy harvesters by attractor selection,” Applied Physics Letters, vol. 111, no. 21, p. 213901, 2017.

    Article  Google Scholar 

  11. C. Lan, L. Tang, and W. Qin, “Obtaining high-energy responses of nonlinear piezoelectric energy harvester by voltage impulse perturbations,” The European Physical Journal Applied Physics, vol. 79, no. 2, p. 20902, 2017.

    Article  Google Scholar 

  12. S. Zhou, J. Cao, D. J. Inman, S. Liu, W. Wang, and J. Lin, “Impact-induced high-energy orbits of nonlinear energy harvesters,” Applied Physics Letters, vol. 106, no. 9, p. 093901, 2015.

    Article  Google Scholar 

  13. J. Wang and W.-H. Liao, “Attaining the high-energy orbit of nonlinear energy harvesters by load perturbation,” Energy Conversion and Management, vol. 192, pp. 30–36, July 2019.

    Article  Google Scholar 

  14. A. H. Hosseinloo, J.-J. Slotine, and K. Turitsyn, “Robust and adaptive control of coexisting attractors in nonlinear vibratory energy harvesters,” Journal of Vibration and Control, vol. 24, no. 12, pp. 2532–2541, 2018.

    Article  MathSciNet  Google Scholar 

  15. G. Sebald, H. Kuwano, D. Guyomar, and B. Ducharne, “Simulation of a duffing oscillator for broadband piezoelectric energy harvesting,” Smart Materials and Structures, vol. 20, no. 7, p. 075022, 2011.

    Article  Google Scholar 

  16. K. Makihara, Y. Yamamoto, C. Horiguchi, H. Sakaguchi, and K. Fujimoto, “An innovative controller to increase harvested energy,” in Journal of Physics: Conference Series, vol. 557, p. 012023, IOP Publishing, 2014.

  17. R. Dehghani and H. Khanlo, “Radial basis function neural network chaos control of a piezomagnetoelastic energy harvesting system,” Journal of Vibration and Control, vol. 25, no. 16, pp. 2191–2203, 2019.

    Article  MathSciNet  Google Scholar 

  18. A. Yousefpour, A. Haji Hosseinloo, M. R. H. Yazdi, and A. Bahrami, “Disturbance observer-based terminal sliding mode control for effective performance of a nonlinear vibration energy harvester,” Journal of Intelligent Material Systems and Structures, vol. 31, no. 12, pp. 1495–1510, 2020.

    Article  Google Scholar 

  19. J. Qin, H. Gao, and W. X. Zheng, “Exponential synchronization of complex networks of linear systems and nonlinear oscillators: A unified analysis,” IEEE Transactions on Neural Networks and Learning Systems, vol. 26, no. 3, pp. 510–521, March 2015.

    Article  MathSciNet  Google Scholar 

  20. X. Jin, S. Lü, and J. Yu, “Adaptive NN-based consensus for a class of nonlinear multiagent systems with actuator faults and faulty networks,” IEEE Transactions on Neural Networks and Learning Systems, pp. 1–13, 2021. DOI: https://doi.org/10.1109/TNNLS.2021.3053112

  21. K. Vijayaraghavan and R. Rajamani, “Ultra-low power control system for maximal energy harvesting from short duration vibrations,” IEEE Transactions on Control Systems Technology, vol. 18, no. 2, pp. 252–266, 2010.

    Article  Google Scholar 

  22. R. A. Rojas and A. Carcaterra, “An approach to optimal semi-active control of vibration energy harvesting based on MEMS,” Mechanical Systems and Signal Processing, vol. 107, pp. 291–316, July 2018.

    Article  Google Scholar 

  23. T. T. Le, F. Jost, and S. Sager, “Optimal control of vibration-based micro-energy harvesters,” Journal of Optimization Theory and Applications, vol. 179, no. 3, pp. 1025–1042, 2018.

    Article  MathSciNet  Google Scholar 

  24. H. Adloo and M. Roopaei, “Review article on adaptive synchronization of chaotic systems with unknown parameters,” Nonlinear Dynamics, vol. 65, no. 1–2, pp. 141–159, 2011.

    Article  MathSciNet  Google Scholar 

  25. Z. Chen, X. Yuan, Y. Yuan, H. H.-C. Iu, and T. Fernando, “Parameter identification of chaotic and hyper-chaotic systems using synchronization-based parameter observer,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 63, no. 9, pp. 1464–1475, September 2016.

    Article  MathSciNet  Google Scholar 

  26. W. Lohmiller and J.-J. E. Slotine, “On contraction analysis for non-linear systems,” Automatica, vol. 34, no. 6, pp. 683–696, June 1998.

    Article  MathSciNet  Google Scholar 

  27. F. Forni and R. Sepulchre, “A differential lyapunov framework for contraction analysis,” IEEE Transactions on Automatic Control, vol. 59, no. 3, pp. 614–628, 2014.

    Article  MathSciNet  Google Scholar 

  28. P. A. Ioannou and J. Sun, Robust Adaptive Control, Prentice-Hall, Upper Saddle River, USA, 1996.

    MATH  Google Scholar 

  29. J. Jouffroy and J.-J. E. Slotine, “Methodological remarks on contraction theory,” Proc. of 43rd IEEE Conference on Decision and Control (CDC), vol. 3, pp. 2537–2543, 2004.

    Google Scholar 

  30. B. B. Sharma and I. N. Kar, “Design of asymptotically convergent frequency estimator using contraction theory,” IEEE Transactions on Automatic Control, vol. 53, no. 8, pp. 1932–1937, September 2008.

    Article  MathSciNet  Google Scholar 

  31. A. H. Nayfeh and D. T. Mook, Nonlinear Oscillations, John Wiley & Sons, New York, USA, 1995.

    Book  Google Scholar 

  32. L. G. Costa, L. L. da Silva Monteiro, P. M. C. L. Pacheco, and M. A. Savi, “A parametric analysis of the nonlinear dynamics of bistable vibration-based piezoelectric energy harvesters,” Journal of Intelligent Material Systems and Structures, vol. 32, no. 7, pp. 699–723, April 2021.

    Article  Google Scholar 

  33. C. Zhang, R. L. Harne, B. Li, and K. Wang, “Harmonic analysis and experimental validation of bistable vibration energy harvesters interfaced with rectifying electrical circuits,” Communications in Nonlinear Science and Numerical Simulation, vol. 82, p. 105069, March 2020.

    Article  MathSciNet  Google Scholar 

  34. W. Q. Liu, A. Badel, F. Formosa, Y. P. Wu, and A. Agbossou, “Wideband energy harvesting using a combination of an optimized synchronous electric charge extraction circuit and a bistable harvester,” Smart Materials and Structures, vol. 22, no. 12, p. 125038, 2013.

    Article  Google Scholar 

  35. T. Huguet, M. Lallart, and A. Badel, “Orbit jump in bistable energy harvesters through buckling level modification,” Mechanical Systems and Signal Processing, vol. 128, pp. 202–215, August 2019.

    Article  Google Scholar 

  36. F. L. Huang, X. M. Wang, Z. Q. Chen, X. H. He, and Y. K. Ni, “A new approach to identification of structural damping ratios,” Journal of Sound and Vibration, vol. 303, no. 1, pp. 144–153, March 2007.

    Article  Google Scholar 

  37. Y. Li, S. Zhou, and G. Litak, “Uncertainty analysis of bistable vibration energy harvesters based on the improved interval extension,” Journal of Vibration Engineering & Technologies, vol. 8, no. 2, pp. 297–306, 2020.

    Article  Google Scholar 

  38. S.-H. Yu, H. S. Kang, Y.-T. Kim, C.-H. Hyun, and M. Park, “Fuzzy adaptive modular design of uncertain chaotic duffing oscillators,” International Journal of Control, Automation, and Systems, vol. 12, no. 1, pp. 188–194, February 2014.

    Article  Google Scholar 

  39. P. Kim, M. S. Nguyen, O. Kwon, Y.-J. Kim, and Y.-J. Yoon, “Phase-dependent dynamic potential of magnetically coupled two-degree-of-freedom bistable energy harvester,” Scientific Reports, vol. 6, p. 34411, 2016.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Facultad de Ingeniería, Universidad Autónoma de Querétaro, Querétaro, 76010, Mexico

    Suresh Thenozhi

  2. Facultad de Ingeniería Mecánica y Eléctrica, Universidad de Colima, Coquimatlán, Colima, 28400, Mexico

    Antonio Concha

Authors
  1. Suresh Thenozhi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Antonio Concha
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Antonio Concha.

Additional information

Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The authors acknowledge the reviewers for their helpful comments that improve the quality of this manuscript.

Suresh Thenozhi received his Ph.D. degree in automatic control from CINVES-TAV, Mexico City, in 2014. Since 2017, he has been a Professor with the Faculty of Engineering, Autonomous University of Queretaro. His research focuses on control theory.

Antonio Concha received his Ph.D. degree in automatic control from CINVES-TAV, Mexico, in 2013. Since 2016, he has been a Professor with the Faculty of Mechanical and Electrical Engineering, University of Colima. He focuses on system estimation and control.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Thenozhi, S., Concha, A. Identification-based Adaptive Tracking Control of Uncertain Bistable Electromechanical Duffing Oscillator. Int. J. Control Autom. Syst. 20, 2191–2201 (2022). https://doi.org/10.1007/s12555-021-0386-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-021-0386-4

Keywords

Search

Navigation