Introduction

As the rapid development of new materials and electronics in the last 10 years, more and more low-powered embedded electromechanical devices and wireless sensors are used for structural health monitoring [1,2,3,4]. In order to power them continuously and realize autonomic health monitoring, energy harvesting techniques and fault diagnosis methods have been developed recently [5,6,7,8]. For example, different flow energy harvesters were designed to power the sensors embedded in high buildings or underwater environments [9,10,11,12,13,14,15]. For the high-performance energy harvesting from base vibrations, nonlinear mechanisms have been widely used to design suitable energy harvesters, such as internal resonance mechanism [16, 17], bistable mechanism [18, 19], tristable mechanism [20, 21], and multi-stable mechanism [22, 23].

Fairly high-energy oscillations of the mechanical resonator and large-amplitude output voltage from a Duffing-like bistable energy harvester were experimentally found by Erturk and Inman [24]. This demonstrates the high-efficiency advantage of the bistable energy harvester (BEH) over the traditional linear one. Zhou et al. [25] designed a rotatable nonlinear magnetic coupled energy harvester, which exhibits bistable characteristics for a suitable angle of inclination. Under different harmonic base excitations, the hysteresis and the multi-solution range of the BEH were numerically and experimentally observed. Based on this design, Cao et al. [26] developed a BEH with the nonlinear time-varying potential to efficiently harvest energy from human motions. Litak et al. [27] numerically and experimentally verified the high-efficiency energy harvesting performance of BEHs from random base excitations. Stanton et al. [28] derived a distributed parameter model of magnetic coupled cantilever-based BEH to predict the output voltage and nonlinear response characteristics. Meanwhile, plate-based BEH was presented by Arrieta et al. [29], and this BEH performs well under very high-level base excitations.

For processing and manufacturing of BEHs, the errors cannot be totally eliminated in practice. Therefore, the geometrical variables, material properties and other parameters should be treated as uncertainties in analysis and are bound to their design. For the piezoelectric energy harvester, the mass, the stiffness, the damping, the capacitance, the electromechanical coupling coefficient, etc., are all uncertain variables in design, and these uncertainties can make the output voltage fluctuate around its expected value. In order to analyze this problem, Ali et al. [30] used the Monte Carlo simulation (MCS) to study the effect of parametric uncertainty in the piezoelectric energy harvester on the harvested power and found that the maximum of the mean harvested power decreases with increasing uncertainty. Franco and Varoto [31] used the MCS to research the effects of uncertainties on the performance of the cantilever-based piezoelectric energy harvesters, and they strongly suggested that uncertainties must be accounted for in the design. Brian et al. [32] presented systematic uncertainty propagation studies for both linear and nonlinear energy harvesters. In these studies, uncertainties from the system and environmental excitation were all simulated.

However, in above researches, the probabilistic uncertain analysis method, the MCS, was adopted to obtain accurate distributions of responses. In this case, numerous samples of uncertain variables are needed to define the probability density functions of the uncertain parameters. Therefore, it is very difficult to obtain the enough samples in practice. To partly ameliorate this problem, the interval analysis may be more suitable, because it just needs to know the upper and lower bounds of uncertain variables. Many interval analysis methods have been developed, among which the Taylor expansion [33, 34] is a popular one. It can give the bounds of function based on the sensitivities with respect to the uncertain variables and the deviations, and it does not need to modify the governing function of system. When the dependence of the response on uncertain parameters is non-monotonic in interval, the interval of response will exhibit significant errors; to limit the errors, Li and Xu [35] defined several cases according to the relationship between the response and uncertain parameter and improved the formats of interval extension based on the first Taylor series correspondingly. To solve practical complex problem, Li et al. recently used parameter \( \sin \alpha \) to improve the interval extension based on the first-order Taylor series and provided an opportunity to account for the different categories of uncertainties by defining multiple \( \alpha_{i} \;(i = 1,2, \ldots ) \), and consequently the accurate interval of response was obtained by maximizing and minimizing a continuous function [36, 37], respectively. Therefore, this improved interval extension method is used in this paper to investigate the effect of uncertain parameters on the output voltage in the BEH.

In this paper, we use the improved interval extension to make uncertainty analysis of the BEH with uncertain parameters. In “Theoretical Solutions of the Output Voltage of the BEH,” the theoretical solutions of the BEH are provided. In “Improved Interval Extension Based on the First-Order Taylor Series,” the improved interval extension based on the first-order Taylor series is introduced in detail. In “Effect of the Structural and Electric Parameters on the Output Voltage,” the effect of the structural and electric parameters on the output voltage is analyzed. In “Uncertainty Analysis of the BEH with Uncertain Parameters,” the detailed uncertainty analysis of the BEH with uncertain parameters is provided. Conclusions follow in “Conclusions.”

Theoretical Solutions of the Output Voltage of the BEH

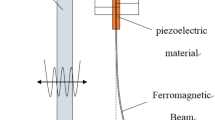
The schematic diagram of a general magnetic coupled BEH is shown in Fig. 1. The middle position of the BEH is unstable, while the two bilateral positions are stable. Under the base displacement excitation \( x_{b} (t) \), the electromechanical model of the BEH can be described by the following equations [38, 39]:

$$ m\ddot{x}(t) + c\dot{x}\left( t \right) - k_{1} x\left( t \right) + k_{3} x^{3} \left( t \right) - \theta V\left( t \right) = - Nm\ddot{x}_{b} \left( t \right), $$
(1)
$$ C_{p} \dot{V}\left( t \right) + V\left( t \right)\left( R \right)^{ - 1} + \theta \dot{x}\left( t \right) = 0, $$
(2)

where \( x\left( t \right) \), \( m \) and \( c \) are the tip displacement, the equivalent mass and the equivalent damping of the BEH, respectively.\( C_{p} \), R, \( \theta \) and \( V\left( t \right) \) are the equivalent capacitance, the load resistance, the electromechanical coupling coefficient, the output voltage across R, respectively.\( - k_{1} \) and \( k_{3} \) are the coefficients of the equivalent linear and nonlinear terms, respectively. N is called the amplitude-wise correction factor for the lumped parameter model [38].

Fig. 1
figure 1

Schematic diagram of the magnetic coupled BEH in the horizontally moving frame. The piezoelectric bimorph component (PZT) converts the mechanical energy into electrical one

Full size image

If the BEH is subjected to the base acceleration excitation \( A\cos \left( {\omega t} \right) \), the electromechanical model can be rewritten for analysis, as follows:

$$ \ddot{x}\left( t \right) + \bar{c}\dot{x}\left( t \right) - \bar{k}_{1} x\left( t \right) + \bar{k}_{3} x^{3} \left( t \right) - \bar{\theta }V\left( t \right) = NA\cos \left( {\omega t} \right), $$
(3)
$$ C_{p} \dot{V}\left( t \right) + V\left( t \right)\left( R \right)^{ - 1} + \theta \dot{x}\left( t \right) = 0, $$
(4)

where the new parameters are defined as: \( \bar{c} = c/m \), \( \bar{k}_{1} = k_{1} /m \), \( \bar{k}_{3} = k_{3} /m \), \( \bar{\theta } = \theta /m. \)NA is an effective amplitude of the inertial force.

It is known that the high-energy interwell oscillation of the resonator leads to the large-amplitude output voltage. Therefore, this paper focuses on the steady-state interwell displacement solutions and voltage solutions of the BEH under harmonic-based excitations. For the interwell oscillation, the BEH under base harmonic excitation, the steady-state response displacement and voltage of are assumed to have slowly varying coefficients, described as [39]:

$$ x\left( t \right) = a\left( t \right)\sin \left( {\omega t} \right) + b\left( t \right)cos\left( {\omega t} \right) , $$
(5)
$$ \dot{x}\left( t \right) = (\dot{a}\left( t \right) - b\left( t \right)\omega )\sin \left( {\omega t} \right) + (\dot{b}\left( t \right) - a\left( t \right)\omega )cos\left( {\omega t} \right) , $$
(6)
$$ V\left( t \right) = C\left( t \right)\sin \left( {\omega t} \right) + d\left( t \right)cos\left( {\omega t} \right) , $$
(7)
$$ \ddot{x}\left( t \right) = - (2\dot{b}\left( t \right) + a\left( t \right)\omega )\omega \sin \left( {\omega t} \right) + (2\dot{a}\left( t \right) - b\left( t \right)\omega )\omega cos\left( {\omega t} \right) , $$
(8)
$$ \dot{V}\left( t \right) = (\dot{C}\left( t \right) - d\left( t \right)\omega )\sin \left( {\omega t} \right) + (\dot{d}\left( t \right) - C\left( t \right)\omega )cos\left( {\omega t} \right) , $$
(9)

Substituting Eqs. (6), (7) and (9) into Eq. (4), balancing the terms multiplied by \( \sin (\omega t) \) and \( \cos (\omega t) \), and neglecting all the time derivatives terms, the following equations are obtained:

$$ C = \frac{\theta \omega }{{\frac{1}{{R^{2} }} + (C_{p} \omega )^{2} }}\left( { - C_{p} \omega a + \frac{b}{R}} \right) , $$
(10)
$$ d = \frac{\theta \omega }{{\frac{1}{{R^{2} }} + (C_{p} \omega )^{2} }}\left( { - \frac{a}{R} - C_{p} \omega b} \right) , $$
(11)

Substituting Eqs. (5)–(8), (10), (11) into Eq. (3), balancing the terms multiplied by \( \sin (\omega t) \) and \( \cos (\omega t) \) and neglecting all the time derivatives terms, the following equations are obtained:

$$ \left( {\frac{3}{4}\bar{k}_{3} r^{2} - \omega^{2} - \bar{k}_{1} + SC_{p} \omega } \right)a - \left( {\omega \bar{c} + \frac{S}{R}} \right)b = 0 , $$
(12)
$$ \left( {\frac{3}{4}\bar{k}_{3} r^{2} - \omega^{2} - \bar{k}_{1} + SC_{p} \omega } \right)b + \left( {\omega \bar{c} + \frac{S}{R}} \right)a = NA , $$
(13)

where \( S = \frac{{\bar{\theta }\theta \omega }}{{\frac{1}{{R^{2} }} + (C_{p} \omega )^{2} }} \).

The final expression of the response displacement and the output voltage are shown as follows:

$$ \left( {\frac{3}{4}\bar{k}_{3} r^{2} - \omega^{2} - \bar{k}_{1} + SC_{p} \omega } \right)^{2} r^{2} + \left( {\omega \bar{c} + \frac{S}{R}} \right)^{2} r^{2} = (NA)^{2} $$
(14)
$$ V = \left| {\left. {\frac{\theta \omega }{{\sqrt {\frac{1}{{R^{2} }} + \left( {C_{p} \omega } \right)^{2} } }}} \right|} \right.r $$
(15)

where r is the response displacement amplitude. V is the response voltage amplitude, \( S = \frac{{\bar{\theta }\theta \omega }}{{\frac{1}{{R^{2} }} + (C_{p} \omega )^{2} }} \).

Improved Interval Extension Based on the First-Order Taylor Series

Based on Eqs. (14) and (15), the uncertainty analysis will be performed. This paper will use the improved interval extension based on the first-order Taylor series [36].

In Ref. [36], each uncertain parameter can be described by the interval variable:

$$ x^{I} = [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} , \bar{x}], $$
(16)

\( {\text{where}} \)\( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} \) and \( \bar{x} \) are the lower and upper bounds of interval, respectively. In addition, \( x^{I} \) can be represented by its central value and deviation, as follows:

$$ x_{c} = \frac{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} + \bar{x}}}{2}, $$
(17)
$$ \Delta x = \frac{{\bar{x} - \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} }}{2}. $$
(18)

Equation (16) can be rewritten based on the parameterized interval analysis (PIA) [40, 41], as follows:

$$ x^{I} = x_{c} + \Delta x\sin \alpha , $$
(19)
$$ \alpha \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]. $$
(20)

The first-order Taylor expansion of \( f(X^{I} ) \) around the central value \( X_{c} \) can be expressed as:

$$ f(X^{I} ) \approx f\left( {X_{c} } \right) + \mathop \sum \limits_{i = 1}^{n} \frac{{\partial f\left( {X_{c} } \right)}}{{\partial x_{i} }}(x_{i}^{I} - x_{ic} ) , $$
(21)

where \( f(X_{c} ) \) and \( \frac{{\partial f\left( {X_{c} } \right)}}{{\partial x_{i} }} \) are the response at the central values of intervals and the first-order sensitivity of response (at the central values) with respect to the interval variable, respectively.

We substitute Eqs. (19) and (20) into Eq. (21) to build a continuous function with the first-order independent variables, as follows:

$$ f(X^{I} ) \approx f(\alpha_{j} ) = f\left( {X_{c} } \right) + \mathop \sum \limits_{i = 1}^{n} \frac{{\partial f\left( {X_{c} } \right)}}{{\partial x_{i} }}[\Delta x_{i} \sin \alpha_{j} ]. $$
(22)

Equation (22) can be rewritten:

$$ f(X^{I} ) \approx f(\alpha_{j} ) = f\left( {X_{c} } \right) + G(\alpha_{j} ), $$
(23)
$$ G(\alpha_{j} ) = \mathop \sum \limits_{i = 1}^{n} \frac{{\partial f\left( {X_{c} } \right)}}{{\partial x_{i} }}[\Delta x_{i} \sin \alpha_{j} ] , $$
(24)

where \( j \) is defined according to the number of categories of uncertainties. The same type of uncertain variables should be expressed by a single \( \alpha \). The bounds of function \( f(X^{I} ) \) can be obtained based on the following two equations:

$$ \underline{{f(X^{I} )}} = f(X_{c} ) + {\text{minimum}}(G(\alpha_{j} )), $$
(25)
$$ \overline{{f(X^{I} )}} = f\left( {X_{c} } \right) + {\text{maximum}}(G(\alpha_{j} )). $$
(26)

Meanwhile, the first-order sensitivities can be calculated by the common finite-difference method.

$$ f^{\prime}\left( x \right) = \frac{f(x + h) - f(x - h)}{2h}, $$
(27)

where \( h \) is called the finite-difference interval.

Effect of the Structural and Electric Parameters on the Output Voltage

Pervious to uncertain analysis, the effect of the structural and electric variables of the BEH on the output voltage is studied by changing values of these parameters. The base values of the parameters are referred to Ref. [25, 38]. More specifically, the variables are the mass, the nonlinear stiffness, the damping, the capacitance, and the electromechanical coupling coefficient of the BEH. Next, five groups of simulations will be performed. In each case, a specific parameter will be changed by ± 2%, and the corresponding stable output voltages will calculate based on Eqs. (14) and (15). For system parameters, we used k1 = − 15.17 N/m and other specified as central value parameters in Table 1. In additions, only the stable output voltages are plotted in this paper. When the excitation frequency is changing from 8 to 10 Hz to be close to the resonance of interwell solution (the excitation level is \( 4\;{\text{m/s}}^{2} \)), the results are shown in Figs. 2, 3, 4, 5 and 6.

Table 1 The uncertain parameters
Full size table
Fig. 2
figure 2

The output voltage versus frequency for various mass m

Full size image
Fig. 3
figure 3

The output voltage versus frequency for various nonlinear stiffness term \( k_{3} \)

Full size image
Fig. 4
figure 4

The output voltage versus frequency for various damping c

Full size image
Fig. 5
figure 5

The output voltage versus frequency for various capacitance \( C_{p} \)

Full size image
Fig. 6
figure 6

The output voltage versus frequency for various electromechanical coupling coefficient \( \theta \)

Full size image

It can be found from these figures, the electrical parameters (\( C_{p} \), \( \theta \)) have stronger influences on the stable output voltages than the structural parameters (m, \( k_{3} \), c). Among all these parameters, the influence of the damping c is weakest. Results show that the stable output voltage is increased when we add extra a mass. However, the increase in other parameters makes the output voltage to decrease. In practice, these parameters may be slightly changed at the same time because of manufacturing errors, which will make the output voltage be apart away from the design value. This will bring a negative influence on the energy harvesting performance of the BEH. We should analyze this problem carefully. In the following section, we use the improved interval extension method to study this effect.

Uncertainty Analysis of the BEH with Uncertain Parameters

According to the results in “Effect of the Structural and Electric Parameters on the Output Voltage,” it is found out that the structural parameters and the electric parameters have remarkable effects on the high-energy interwell output voltage of the BEH. In practical engineering, these parameters may be uncertain due to manufacturing errors. It makes the output voltage deviate from the designed value and become the uncertain variable. Upper and lower bounds of the output voltage can be predicted by the improved interval extension (IIE) based on the first-order Taylor series. The structural uncertainties and the electric uncertainties are described by interval numbers \( x^{I} \), and they are expressed by \( m^{I} \), \( k_{3}^{I} \), \( c^{I} \), \( C_{p}^{I} \) and \( \theta^{I} \) to facilitate the understanding, as listed in Table 1. The function \( f(X^{I} ) \) is used to calculate the stable output voltage amplitude \( V \).

According to the method illustrated in “Improved Interval Extension Based on the 1st Order Taylor Series,” these interval variables can be expressed by the interval number. \( m^{I} \) and \( c^{I} \) are structural design variables and expressed by the parameter \( \alpha_{1} \). \( k_{3}^{I} \) is strongly influenced by magnets; thus, we use another parameter \( \alpha_{2} \) to describe it. The rest electrical design variables \( C_{p}^{I} \) and \( \theta^{I} \) are expressed by the parameter \( \alpha_{3} \):

$$ m^{I} = [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{m} , \bar{m}] = m_{c} + \Delta m \cdot sin\alpha_{1} , $$
(28)
$$ c^{I} = [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{c} , \bar{c}] = c_{c} + \Delta c \cdot sin\alpha_{1} , $$
(29)
$$ k_{3}^{I} = [\underline{{k_{3} }} , \overline{{k_{3} }} ] = (k_{3} )_{c} + \Delta k_{3} \cdot sin\alpha_{2} , $$
(30)
$$ C_{p}^{I} = [\underline{{C_{p} }} , \overline{{C_{p} }} ] = (C_{p} )_{c} + \Delta C_{p} \cdot sin\alpha_{3} , $$
(31)
$$ \theta^{I} = [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } , \bar{\theta }] = \theta_{c} + \Delta \theta \cdot sin\alpha_{3} , $$
(32)

where \( \begin{array}{*{20}c} \\ {\alpha_{1} \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]} \\ \end{array} \), \( \begin{array}{*{20}c} \\ {\alpha_{2} \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]} \\ \end{array} \), \( \begin{array}{*{20}c} \\ {\alpha_{3} \in \left[ { - \frac{\pi }{2},\frac{\pi }{2}} \right]} \\ \end{array} \).

The bounds of the output voltage can be calculated based on Eqs. (25) and (26), as follows:

$$ f(m^{I} , k_{3}^{I} , c^{I} , C_{p}^{I} ,\theta^{I} ) \approx f\left( {\alpha_{1} ,\alpha_{2} ,\alpha_{2} } \right) = f(m_{c} ,\left( {k_{3} } \right)_{c} ,c_{c} ,(C_{p} )_{c} ,\theta_{c} ) + G\left( {\alpha_{1} ,\alpha_{2} ,\alpha_{3} } \right), $$
(33)
$$ \begin{aligned} G\left( {\alpha_{1} ,\alpha_{2} ,\alpha_{3} } \right) = \frac{{\partial f(m_{c} ,\left( {k_{3} } \right)_{c} ,C_{c} ,(C_{p} )_{c} ,\theta_{c} )}}{\partial m}\Delta m \cdot \sin \alpha_{1} + \frac{{\partial f(M_{c} ,\left( {k_{3} } \right)_{c} ,c_{c} ,(C_{p} )_{c} ,\theta_{c} )}}{\partial c}\Delta c \cdot \sin \alpha_{1} \hfill \\ + \frac{{\partial f(m_{c} ,\left( {k_{3} } \right)_{c} ,c_{c} ,(C_{p} )_{c} ,\theta_{c} )}}{{\partial k_{3} }}\Delta k_{3} \cdot \sin \alpha_{2} + \frac{{\partial f(m_{c} ,\left( {k_{3} } \right)_{c} ,c_{c} ,(C_{p} )_{c} ,\theta_{c} )}}{{\partial C_{p} }}\Delta C_{p} \cdot \sin \alpha_{3} \hfill \\ + \frac{{\partial f(m_{c} ,(k_{3} )_{c} ,c_{c} ,(C_{p} )_{c} ,\theta_{c} )}}{\partial \theta }\Delta \theta \cdot \sin \alpha_{3} \hfill \\ \end{aligned} $$
(34)

Therefore, the lower and upper bounds of the output voltage can be obtained:

$$ \underline{{f(m^{I} , k_{3}^{I} , c^{I} , C_{p}^{I} ,\theta^{I} )}} = f(m_{c} ,(k_{3} )_{c} ,c_{c} ,(C_{p} )_{c} ,\theta_{c} ) + {\text{minimum}}\left( {G\left( {\alpha_{1} ,\alpha_{2} ,\alpha_{3} } \right)} \right), $$
(35)
$$ \overline{{f(m^{I} , k_{3}^{I} , c^{I} , C_{p}^{I} ,\theta^{I} )}} = f(m_{c} ,\left( {k_{3} } \right)_{c} ,c_{c} ,(C_{p} )_{c} ,\theta_{c} ) + {\text{maximum}}\left( {G\left( {\alpha_{1} ,\alpha_{2} ,\alpha_{3} } \right)} \right). $$
(36)

The finite-difference method is used to calculate the sensitivities in above equations. The bounds of the output voltage are obtained at the different cases, and these cases are described in Table 2.

Table 2 The simulation cases
Full size table

Firstly, only the uncertain parameter m is considered, and it is expressed by the interval number \( m^{I} \). The bounds of the output voltages are predicted by the IIE based on the first-order Taylor series, when the excitation frequency is 8 Hz, 9 Hz and 10.5 Hz (the excitation level is 4 m/s2). The lower and upper bounds of the output voltages under different excitation frequencies can be connected with line segments separately. The numerical results from case-1 are plotted in Fig. 7. In order to demonstrate the accuracy of the interval analysis, we assume the uncertain variables listed in Table 1 to be distributed uniformly within their intervals. Then, the Monte Carlo simulation (MCS) is carried out, and the number of simulations is 10,000. In each simulation, the space of the excitation frequencies is 0.02 Hz. The samples obtained via the MCS are also plotted in the same graph with bounds form the IIE. It is found that the samples are all distributed within the bounds from the IIE. This shows that the IIE can obtain the accurate bounds of the output voltage with the much less cost of calculation than the MCS.

Fig. 7
figure 7

Bounds of the output voltage in case 1 (results obtained from improved interval extension—IIE and Monte Carlo simulations—MCS)

Full size image

In case 2, the uncertain structural parameters m, \( k_{3} \) and c are taken into consideration. The interval analysis and the MCS are conducted, and the results are plotted in Fig. 8. It shows that the bounds of the output voltage from the IIE matches well will that from the MCS. The interval of the output voltage becomes wider as the number of uncertainties is increased from 1 to 3.

Fig. 8
figure 8

Bounds of the output voltage in case 2

Full size image

In case 3, the uncertain electric parameters \( C_{p} \) and \( \theta \) are considered, as the results shown in Fig. 9. Comparing with the results in Fig. 8, it is found that the interval in Fig. 9 is wider than that in Fig. 8. This means that the uncertain electric parameters have a stronger influence on the output voltage of the BEH than the uncertain structural parameters.

Fig. 9
figure 9

Bounds of the output voltage in case 3

Full size image

Finally, we take all five uncertain parameters listed in Table 1 into consideration and carry out simulations at different excitation levels (4 m/s2 in case 4; 5 m/s2 in case 5). Note that the acceleration levels 4 m/s2 and 5 m/s2 are large enough to ensure the large amplitude oscillation of the BEH. The results show that the accuracy of the interval analysis is good, and the width of the interval is almost same for different excitation levels. However, the central value slightly moves up at the high level of excitation (5 m/s2), as shown in Figs. 10 and 11. From the uncertain analysis [20, 21], it is found that the higher vibration orbit of the nonlinear energy harvesters needs the higher excitation level. From above uncertain analysis, which parameter leads to a higher vibration orbit can be determined. Therefore, the nonlinear energy harvesters can be designed based on the real-application environments.

Fig. 10
figure 10

Bounds of the output voltage in case 4

Full size image
Fig. 11
figure 11

Bounds of the output voltage in case 5

Full size image

Conclusions

This paper uses the improved interval extension based on the first-order Taylor series to predict the lower and upper bounds of the stable high-energy interwell output voltage of the BEH with uncertain mass, nonlinear stiffness term, damping, capacitance and electromechanical coupling coefficient. Meanwhile, the Monte Carlo simulation is used to verify the suitability and the accuracy of this method. Particularly, this method allows researchers to define the number of parameter \( \alpha_{j} \) according to the categories of uncertain variables. For example, the structural uncertainties and the electrical uncertainties should be expressed by two parameters \( \alpha_{1} \) and \( \alpha_{3} \). Consequently, accurate bounds of output voltage can be predicted. It is found that interval of the output voltage of the BEH can be limited by reducing the number of uncertain variables, and the bounds of the output voltage is more sensitive to the electrical uncertain variables than the structural uncertainties. Therefore, designers of the BEH should pay enough attention on the errors and tolerances of the electrical output design variables. Specifically, in the design of the BEH, it is more effective to improve the accuracy of the output voltage by limiting the uncertainties of electric parameters than structural parameters. Reducing the number of uncertain parameters through increasing processing precision in production of the BEH can also improve the accuracy of the output voltage.