A hierarchy of spectral relaxations for polynomial optimization

Abstract

We show that (1) any constrained polynomial optimization problem (POP) has an equivalent formulation on a variety contained in an Euclidean sphere and (2) the resulting semidefinite relaxations in the moment-SOS hierarchy have the constant trace property (CTP) for the involved matrices. We then exploit the CTP to avoid solving the semidefinite relaxations via interior-point methods and rather use ad-hoc spectral methods for minimizing the largest eigenvalue of a matrix pencil. Convergence to the optimal value of the semidefinite relaxation is guaranteed. As a result we obtain a hierarchy of nonsmooth “spectral relaxations” of the initial POP. Efficiency and robustness of this spectral hierarchy is tested against several equality constrained POPs on a sphere as well as on a sample of randomly generated quadratically constrained quadratic problems.

Appendix

1.1 Spectral minimizations of SDP

In this section, we provide the proofs of lemmas stated in Sects. 2.6.1 and 2.6.3. First we recall the following useful properties of ${\mathcal {S}}$ and ${\mathcal {S}}^+$:

• If ${\textbf{X}}={{\,\textrm{diag}\,}}({\textbf{X}}_1,\dots ,{\textbf{X}}_l)\in {\mathcal {S}}$,

  $$\begin{aligned} {\textbf{X}}\succeq 0\Longleftrightarrow {\textbf{X}}_j\succeq 0,\,j\in [l]\qquad \text { and }\qquad {{\,\textrm{trace}\,}}({\textbf{X}})=\sum _{j=1}^l {{\,\textrm{trace}\,}}({\textbf{X}}_j). \end{aligned}$$

  (49)

• If ${\textbf{A}}={{\,\textrm{diag}\,}}({\textbf{A}}_1,\dots ,{\textbf{A}}_l)\in {\mathcal {S}}$ and ${\textbf{B}}={{\,\textrm{diag}\,}}({\textbf{B}}_1,\dots ,{\textbf{B}}_l)\in {\mathcal {S}}$,

  $$\begin{aligned} \langle {\textbf{A}}, {\textbf{B}}\rangle = \sum _{j=1}^l\langle {\textbf{A}}_j, {\textbf{B}}_j\rangle . \end{aligned}$$

  (50)

1.1.1 SDP with constant trace property

Proof of Lemma 3

The proof of (20) is similar in spirit to the one of Helmberg and Rendl in [17, Sect. 2]. Here, we extend this proof for SDP (13), which involves a block-diagonal positive semidefinite matrix. From (13),

$$\begin{aligned} -\tau = \sup _{{\textbf{X}}\in {\mathcal {S}}}\{ \langle {\textbf{C}},{\textbf{X}}\rangle :\,{\mathcal {A}} {\textbf{X}}={\textbf{b}},\,{{\,\textrm{trace}\,}}({\textbf{X}})=a,\, {\textbf{X}} \succeq 0\}. \end{aligned}$$

The dual of this SDP reads:

$$\begin{aligned} -\rho = \inf _{({\textbf{z}},\zeta )} \{ {\textbf{b}}^\top {\textbf{z}}+a\zeta :\, {\mathcal {A}}^\top {\textbf{z}}+\zeta {\textbf{I}}-{\textbf{C}}\succeq 0 \}, \end{aligned}$$

where ${\textbf{I}}$ is the identity matrix of size s. From this,

$$\begin{aligned} \begin{array}{rl} -\rho &{}= \inf _{({\textbf{z}},\zeta )} \{ {\textbf{b}}^\top {\textbf{z}}+a\zeta :\, \zeta \ge \lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}})\} \\ &{} = \inf \{a\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}})+ {\textbf{b}}^\top {\textbf{z}} :\,{\textbf{z}}\in {{\mathbb {R}}}^m \}. \end{array} \end{aligned}$$

Since $\rho =\tau$, (20) follows. For the second statement, let ${\textbf{z}}^\star$ be an optimal solution of SDP (14). Then ${\textbf{b}}^\top {\textbf{z}}^\star =-\rho =-\tau$. In addition, ${\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}}^\star \preceq 0$ implies that

$$\begin{aligned} \lambda _1({\textbf{C}}-{\mathcal {A}}^\top {{\textbf{z}}^\star })\le 0, \end{aligned}$$

so that $\varphi ({\textbf{z}}^\star )\le -\tau$. Note that (20) indicates that $\varphi ({\textbf{z}}^\star )\ge -\tau$. Thus, $\varphi ({\textbf{z}}^\star )=-\tau$, yielding the second statement. $\square$

The following proposition recalls the differentiability properties of $\varphi$.

Proposition 8

The function $\varphi$ in (19) has the following properties:

• 1. $\varphi$ is convex and continuous but not differentiable.

• 2. The subdifferential of $\varphi$ at ${\textbf{z}}$ reads:

  $$\begin{aligned} \partial \varphi ({\textbf{z}})=\{{\textbf{b}}-a{\mathcal {A}}{\textbf{W}} \,\ {\textbf{W}}\in {{\,\textrm{conv}\,}}({\varGamma }({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}}))\}, \end{aligned}$$

  (51)

  where for each ${\textbf{A}}\in {\mathcal {S}}$,

  $$\begin{aligned} {\varGamma }({\textbf{A}}):=\{{\textbf{u}}{\textbf{u}}^\top \,\ {\textbf{A}}{\textbf{u}}=\lambda _1({\textbf{A}}){\textbf{u}}\,\ \Vert {\textbf{u}}\Vert _2=1\}. \end{aligned}$$

  (52)

Proof

Properties 1–2 are from Helmberg–Rendl [17, Sect. 2] (see also [44, (4)]). $\square$

The following result is useful to recover an optimal solution of SDP (13) from an optimal solution of NSOP (20).

Lemma 8

Let ${\bar{\textbf{z}}}$ be an optimal solution of NSOP (20). Then:

• 1. There exists ${\textbf{X}}^\star \in a{{\,\textrm{conv}\,}}({\varGamma }({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}}))$ such that ${\mathcal {A}}{\textbf{X}}^\star ={\textbf{b}}$.

• 2. Let ${\textbf{u}}$ be a normalized eigenvector corresponding to $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})$. If $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})$ has multiplicity 1 then ${\textbf{X}}^\star =a{\textbf{u}}{\textbf{u}}^\top$, thus ${\textbf{X}}^\star$ is an optimal solution of SDP (13).

Proof

By [1, Theorem 4.2], ${\textbf{0}}\in \partial \varphi ({\bar{\textbf{z}}})$. Combining this with Proposition 8.2, the first statement follows.

We next prove the second statement. Assume that $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})$ has multiplicity 1. Then ${\varGamma }({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})=\{{\textbf{u}} {\textbf{u}}^\top \}$. The first statement implies that ${\textbf{X}}^\star =a{\textbf{u}}{\textbf{u}}^\top$. From this, ${\textbf{X}}^\star \succeq 0$ and ${\mathcal {A}}{\textbf{X}}^\star ={\textbf{b}}$, so that ${\textbf{X}}^\star$ is a feasible solution of SDP (13). Moreover,

$$\begin{aligned} \begin{array}{rl} \langle {\textbf{C}}, {\textbf{X}}^\star \rangle &{}=\langle {\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}}, {\textbf{X}}^\star \rangle +\langle {\mathcal {A}}^\top {\bar{\textbf{z}}}, {\textbf{X}}^\star \rangle \\ &{}=a \langle {\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}},{\textbf{u}}{\textbf{u}}^\top \rangle +{\bar{\textbf{z}}}^\top ( {\mathcal {A}} {\textbf{X}}^\star )\\ &{}=a{\textbf{u}}^\top ( {\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}}){\textbf{u}}+{\bar{\textbf{z}}}^\top {\textbf{b}}\\ &{}=a\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})\Vert {\textbf{u}}\Vert _2^2+{\bar{\textbf{z}}}^\top {\textbf{b}}\\ &{}=a\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})+{\bar{\textbf{z}}}^\top {\textbf{b}}=\varphi ({\bar{\textbf{z}}})=-\tau . \end{array} \end{aligned}$$

Thus, $\langle {\textbf{C}}, {\textbf{X}}^\star \rangle =-\tau$, yielding the second statement. $\square$

To obtain a convergence guarantee when solving NSOP (20) by LMBM [15, Algorithm 1], we need the following technical lemma:

Lemma 9

When applied to problem NSOP (20), the LMBM algorithm is globally convergent.

Proof

The convexity of $\varphi$ yields that $\varphi$ is weakly upper semismooth on ${{\mathbb {R}}}^m$ according to [37, Proposition 5]. From this, $\varphi$ is upper semidifferentiable on ${{\mathbb {R}}}^m$ by using [3, Theorem 3.1]. Combining this with the fact that $\varphi$ is bounded from below on ${{\mathbb {R}}}^m$, the result follows thanks to [3, Sect. 5] (see also the final statement of [1, Sect. 14.2]). $\square$

1.1.2 SDP with bounded trace property

Proof of Lemma 4

Let ${\textbf{X}}^\star$ be an optimal solution of SDP (13) and set . By Condition 4 of Assumption 1, one has

(53)

Similarly to the proof of Lemma 3, one obtains:

(54)

Let us prove that

$$\begin{aligned} \psi ({\textbf{z}})\ge -\tau ,\,\forall {\textbf{z}}\in {{\mathbb {R}}}^m. \end{aligned}$$

(55)

Let ${\textbf{z}}\in {{\mathbb {R}}}^m$ be fixed and consider the following two cases:

• Case 1 $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}})>0$. By (53) and (54),

  

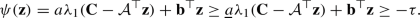
  Thus, $\psi ({\textbf{z}})\ge -\tau$.

• Case 2 $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}})\le 0$. Then ${\mathcal {A}}^\top {\textbf{z}}-{\textbf{C}}\succeq 0$ and $\psi ({\textbf{z}})={\textbf{b}}^\top {\textbf{z}}\ge -\rho =-\tau$ by (14).

Let $({\textbf{z}}^{(j)})_{j\in {{\mathbb {N}}}}$ be a minimizing sequence of SDP (14). Then $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}}^{(j)})\le 0$, $j\in {{\mathbb {N}}}$, since ${\mathcal {A}}^\top {\textbf{z}}^{(j)}-{\textbf{C}}\succeq 0$ and ${\textbf{b}}^\top {\textbf{z}}^{(j)}\rightarrow -\tau$ as $j\rightarrow \infty$ since $\tau =\rho$. It implies that $\psi ({\textbf{z}}^{(j)})={\textbf{b}}^\top {\textbf{z}}^{(j)}\rightarrow -\tau$ as $j\rightarrow \infty$. From this and by (55), the first statement follows.

For the second statement, let ${\textbf{z}}^\star$ be an optimal solution of SDP (14). Since ${\mathcal {A}}^\top {\textbf{z}}-{\textbf{C}}\succeq 0$, $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}})\le 0$ and thus $\psi ({\textbf{z}}^\star )={\textbf{b}}^\top {\textbf{z}}^\star = -\rho =-\tau$. Thus, ${\textbf{z}}^\star$ is an optimal solution of (26), yielding the second statement. $\square$

We consider the differentiability properties of $\psi$ in the following proposition:

Proposition 9

The function $\psi$ has the following properties:

• 1. $\psi$ is convex and continuous but not differentiable.

• 2. The subdifferential of $\psi$ at ${\textbf{z}}$ reads:

  $$\begin{aligned} \partial \psi ({\textbf{z}})={\left\{ \begin{array}{ll} \{{\textbf{b}}\}\text { if }\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}})< 0 ,\\ \{{\textbf{b}}-a{\mathcal {A}}{\textbf{W}} \,\ {\textbf{W}}\in {{\,\textrm{conv}\,}}({\varGamma }({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}}))\}\text { if }\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}})> 0,\\ \{{\textbf{b}}-\zeta a{\mathcal {A}}{\textbf{W}} \,\ \zeta \in [0,1],\,{\textbf{W}}\in {{\,\textrm{conv}\,}}({\varGamma }({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}}))\}\text { otherwise},\\ \end{array}\right. } \end{aligned}$$

  where ${\varGamma }(.)$ is defined as in (52).

Proof

Note that $\psi$ is the maximum of two convex functions, i.e.,

$$\begin{aligned} \psi ({\textbf{z}})=\max \{\varphi _1({\textbf{z}}),\varphi _2({\textbf{z}})\} , \end{aligned}$$

with $\varphi _1({\textbf{z}})=a\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\textbf{z}})+{\textbf{b}}^\top {\textbf{z}}$ and $\varphi _2({\textbf{z}})={\textbf{b}}^\top {\textbf{z}}$. Thus, $\psi$ is convex and

$$\begin{aligned} \partial \psi ({\textbf{z}})= {\left\{ \begin{array}{ll} \partial \varphi _1({\textbf{z}}) &{}\text { if }\varphi _1({\textbf{z}})>\varphi _2({\textbf{z}}),\\ {{\,\textrm{conv}\,}}(\partial \varphi _1({\textbf{z}})\cup \partial \varphi _2({\textbf{z}}))&{}\text { if }\varphi _1({\textbf{z}})=\varphi _2({\textbf{z}}),\\ \partial \varphi _2({\textbf{z}}) &{}\text { otherwise}. \end{array}\right. } \end{aligned}$$

Note that $\partial \varphi _2({\textbf{z}})=\{{\textbf{b}}\}$ and $\partial \varphi _1({\textbf{z}})$ is computed as in formula (51). Thus, the result follows. $\square$

The following theorem is useful to recover an optimal solution of SDP (13) from an optimal solution of NSOP (26).

Lemma 10

Assume that ${\bar{\textbf{z}}}$ is an optimal solution of NSOP (26). The following statements are true:

• 1. There exists

  $$\begin{aligned} {\textbf{X}}^\star {\left\{ \begin{array}{ll} = {\textbf{0}}&{} \text { if } \lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})< 0,\\ \in \zeta a{{\,\textrm{conv}\,}}({\varGamma }({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})) &{}\text { if } \lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})=0,\\ \in a{{\,\textrm{conv}\,}}({\varGamma }({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}}))&{} \text { otherwise}, \end{array}\right. } \end{aligned}$$

  for some $\zeta \in [0,1]$ such that ${\mathcal {A}}{\textbf{X}}^\star ={\textbf{b}}$.

• 2. Let ${\textbf{u}}$ be a normalized eigenvector corresponding to $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})$. If $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})$ has multiplicity 1, then ${\textbf{X}}^\star = {{\bar{\xi }}}{\textbf{u}}{\textbf{u}}^\top$ with ${{\bar{\xi }}}$ defined as in (27) and ${\textbf{X}}^\star$ is an optimal solution of SDP (13).

Proof

Due to [1, Theorem 4.2], ${\textbf{0}}\in \partial \varphi ({\bar{\textbf{z}}})$. From this and by Proposition 9.2, the first statement follows. Let us prove the second statement. Assume that $\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})$ has multiplicity 1. Then one has ${\varGamma }({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}})=\{{\textbf{u}}{\textbf{u}}^\top \}$, yielding ${\textbf{X}}^\star ={{\bar{\xi }}}{\textbf{u}}{\textbf{u}}^\top$ with ${{\bar{\xi }}}$ defined as in (27), so that ${\textbf{X}}^\star \succeq 0$. From this and since ${\mathcal {A}}{\textbf{X}}^\star ={\textbf{b}}$, ${\textbf{X}}^\star$ is a feasible solution of SDP (13). Moreover,

$$\begin{aligned} \begin{array}{rl} \langle {\textbf{C}}, {\textbf{X}}^\star \rangle &{}=\langle {\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}}, {\textbf{X}}^\star \rangle +\langle {\mathcal {A}}^\top {\bar{\textbf{z}}}, {\textbf{X}}^\star \rangle \\ &{}={{\bar{\xi }}}\langle {\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}},{\textbf{u}}{\textbf{u}}^\top \rangle +{\bar{\textbf{z}}}^\top ( {\mathcal {A}} {\textbf{X}}^\star )\\ &{}= {{\bar{\xi }}}{\textbf{u}}^\top ( {\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}}){\textbf{u}}+{\bar{\textbf{z}}}^\top {\textbf{b}}\\ &{}=\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}}) {{\bar{\xi }}}\Vert {\textbf{u}}\Vert _2^2+{\bar{\textbf{z}}}^\top {\textbf{b}}\\ &{}=\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}}){{\bar{\xi }}}+{\bar{\textbf{z}}}^\top {\textbf{b}}\\ &{}=a\max \{\lambda _1({\textbf{C}}-{\mathcal {A}}^\top {\bar{\textbf{z}}}),0\}+{\bar{\textbf{z}}}^\top {\textbf{b}}=\psi ({\bar{\textbf{z}}})=-\tau . \end{array} \end{aligned}$$

Thus, $\langle {\textbf{C}}, {\textbf{X}}^\star \rangle =-\tau$, yielding the second statement. $\square$

The next result proves that when applied to NSOP (26), the LMBM algorithm [15, Algorithm 1] converges.

Lemma 11

LMBM applied to NSOP (26) is globally convergent.

The proof of Lemma 11 is similar to Lemma 9.

1.2 Converting moment relaxations to standard SDP

We will present a way to transform SDP (31) to the form (33) recalled as follows:

$$\begin{aligned} -\tau _k = \sup _{{\textbf{X}}\in {\mathcal {S}}_k} \{ \langle {\textbf{C}},{\textbf{X}}\rangle :\,\langle {\textbf{A}}_j, {\textbf{X}}\rangle ={\textbf{b}}_j,\,j\in [m],\, {\textbf{X}} \succeq 0\}. \end{aligned}$$

Let $k\in {{\mathbb {N}}}$ be fixed. We will prove that there exists ${\textbf{A}}_j\in {\mathcal {S}}_k$, $j\in [r]$, such that ${\textbf{X}}={\textbf{P}}_k{\textbf{M}}_k({\textbf{y}}){\textbf{P}}_k$ for some if and only if $\langle {\textbf{A}}_j, {\textbf{X}}\rangle =0$, $j\in [r]$. Let . Then ${\mathcal {V}}$ is a linear subspace of ${\mathcal {S}}_k$ and . We take a basis ${\textbf{A}}_1,\dots ,{\textbf{A}}_r$ of the orthogonal complement ${\mathcal {V}}^\bot$ of ${\mathcal {V}}$. Notice that

(56)

with ${\textbf{X}}\in {\mathcal {S}}_k$, it implies that ${\textbf{X}}\in {\mathcal {V}}$ if and only if $\langle {\textbf{A}}_j, {\textbf{X}}\rangle =0$, $j\in [r]$.

Let us find such a basis ${\textbf{A}}_1,\dots ,{\textbf{A}}_r$. Let ${\textbf{A}}=(A_{\alpha ,\beta })_{\alpha ,\beta \in {{\mathbb {N}}}^n_k}\in {\mathcal {V}}^\bot$. Then for all ${\textbf{X}}=(X_{\alpha ,\beta })_{\alpha ,\beta \in {{\mathbb {N}}}^n_k}\in {\mathcal {V}}$, $\langle {\textbf{A}}, {\textbf{X}}\rangle =0$. Note that if ${\textbf{X}}={\textbf{P}}_k{\textbf{M}}_k({\textbf{y}}){\textbf{P}}_k$, then one has

$$\begin{aligned} X_{\alpha ,\beta }=w_{\alpha ,\beta }y_{\alpha +\beta },\,\forall \alpha ,\beta \in {{\mathbb {N}}}^n_k, \end{aligned}$$

with $w_{\alpha ,\beta }:=\theta _{k,\alpha }^{1/2}\theta _{k,\beta }^{1/2}$, for all $\alpha ,\beta \in {{\mathbb {N}}}^n_k$. It implies that

Let $\gamma \in {{\mathbb {N}}}^n_{2k}$ be fixed and let be such that for $\xi \in {{\mathbb {N}}}^n_{2k}$,

$$\begin{aligned} y_\xi ={\left\{ \begin{array}{ll} 0&{}\text { if }\xi \ne \gamma ,\\ 1&{}\text { otherwise.} \end{array}\right. } \end{aligned}$$

Then

If $\gamma \not \in 2{{\mathbb {N}}}^n$, we do not have the first term in the latter equality. Let us define

$$\begin{aligned} {\varLambda }_\gamma :=\{A_{\alpha ,\beta }:\,\alpha ,\beta \in {{\mathbb {N}}}^n_k,\, \alpha +\beta =\gamma ,\, \alpha \le \beta \}. \end{aligned}$$

Note that ${\varLambda }_\gamma$ consists of values of A indexed by pairs of vectors $(\alpha , \beta )$ satisfying the lexicographic order relation $\alpha \le \beta$. Moreover, it can be rewritten as ${\varLambda }_\gamma =\{A_{\alpha _j,\beta _j},\,j\in [t]\}$ where $(\alpha _1,\beta _1)<\dots <(\alpha _t,\beta _t)$ and $t=|{\varLambda }_\gamma |$. Thus, if $t\ge 2$, we can choose ${\textbf{A}}$ such that for all $\alpha ,\beta \in {{\mathbb {N}}}^n_k$,

$$\begin{aligned} A_{\alpha ,\beta }={\left\{ \begin{array}{ll} w_{\alpha _\mu ,\beta _\mu }&{} \text { if } \alpha _1=\beta _1 \text { and }(\alpha ,\beta ) =(\alpha _1,\beta _1),\\ \frac{1}{2} w_{\alpha _\mu ,\beta _\mu }&{} \text { if } \alpha _1< \beta _1 \text { and }(\alpha ,\beta ) \in \{(\alpha _1,\beta _1),(\beta _1,\alpha _1)\},\\ -w_{\alpha _1,\beta _1}&{} \text { if } \alpha _\mu =\beta _\mu \text { and }(\alpha ,\beta ) =(\alpha _\mu ,\beta _\mu ),\\ -\frac{1}{2} w_{\alpha _1,\beta _1}&{} \text { if } \alpha _\mu < \beta _\mu \text { and }(\alpha ,\beta ) \in \{(\alpha _\mu ,\beta _\mu ),(\beta _\mu ,\alpha _\mu )\},\\ 0 &{} \text { otherwise}, \end{array}\right. } \end{aligned}$$

for some $\mu \in [t]\backslash \{1\}$. We denote by ${\mathcal {B}}_\gamma$ the set of all such above $A_{\alpha ,\beta }$ satisfying $t=|{\varLambda }_\gamma |\ge 2$, otherwise let ${\mathcal {B}}_\gamma =\emptyset$. Then $|{\mathcal {B}}_\gamma |=|{\varLambda }_\gamma |-1$. From this and since $( {\mathcal {B}}_\gamma )_{\gamma \in {{\mathbb {N}}}^{n}_{2k}}$ is a sequence of pairwise disjoint subsets of ${\mathcal {S}}_k$,

It must be equal to r as in (56). We just proved that $\bigcup _{\gamma \in {{\mathbb {N}}}^{n}_{2k}} {\mathcal {B}}_\gamma$ is a basis of ${\mathcal {V}}^\bot$. Now we assume that $\bigcup _{\gamma \in {{\mathbb {N}}}^{n}_{2k}} {\mathcal {B}}_\gamma =\{{\textbf{A}}_1,\dots ,{\textbf{A}}_r\}$.

Let us rewrite the constraints

$$\begin{aligned} {\textbf{M}}_{k - \lceil h_j \rceil }(h_j\;{\textbf{y}}) = 0,\, j\in [l_h], \end{aligned}$$

(57)

as $\langle {\textbf{A}}_j,{\textbf{X}}\rangle =0$, $j=r+1,\dots ,m-1$ with ${\textbf{X}}={\textbf{P}}_k{\textbf{M}}_k({\textbf{y}}){\textbf{P}}_k$. From (57),

$$\begin{aligned} \sum _{\gamma \in {{\mathbb {N}}}^n_{2\lceil h_j \rceil }}h_{j,\gamma }y_{\alpha +\gamma }=0,\,\alpha \in {{\mathbb {N}}}^n_{2(k-\lceil h_j \rceil )},\,j\in [l_h]. \end{aligned}$$

(58)

Let $j\in [l_h]$ and $\alpha \in {{\mathbb {N}}}^n_{2(k-\lceil h_j \rceil )}$ be fixed. We define $\tilde{{\textbf{A}}}=({\tilde{A}}_{\mu ,\nu })_{\mu ,\nu \in {{\mathbb {N}}}^n_k}$ as follows:

$$\begin{aligned} {\tilde{A}}_{\mu ,\nu }={\left\{ \begin{array}{ll} h_{j,\gamma }&{}\text { if }\mu =\nu ,\,\mu +\nu =\alpha +\gamma ,\\ \frac{1}{2} h_{j,\gamma }&{}\text { if }\mu \ne \nu ,\,\mu +\nu =\alpha +\gamma ,\\ &{}\qquad \text { and } (\mu ,\nu )\le ({{\bar{\mu }}},{{\bar{\nu }}}),\,\forall {{\bar{\mu }}},{{\bar{\nu }}}\in {{\mathbb {N}}}^n_k\, \text { such that} \,{{\bar{\mu }}}+{{\bar{\nu }}}=\alpha +\gamma ,\\ 0&{}\text { otherwise.} \end{array}\right. } \end{aligned}$$

(59)

Then (58) implies that $\langle \tilde{{\textbf{A}}}, {\textbf{M}}_k({\textbf{y}})\rangle =0$. Since ${\textbf{M}}_k({\textbf{y}})={\textbf{P}}_k^{-1}{\textbf{X}}{\textbf{P}}_k^{-1}$,

$$\begin{aligned} 0=\langle \tilde{{\textbf{A}}}, {\textbf{P}}_k^{-1}{\textbf{X}}{\textbf{P}}_k^{-1}\rangle =\langle {\textbf{P}}_k^{-1}\tilde{{\textbf{A}}}{\textbf{P}}_k^{-1}, {\textbf{X}}\rangle =\langle {\textbf{A}}, {\textbf{X}}\rangle , \end{aligned}$$

where ${\textbf{A}}:={\textbf{P}}_k^{-1}\tilde{{\textbf{A}}}{\textbf{P}}_k^{-1}$, yielding the statement. Thus, we obtain the constraints $\langle {\textbf{A}}_j,{\textbf{X}}\rangle =0$, $j\in [m-1]$.

The final constraint $y_0=1$ can be rewritten as $\langle {\textbf{A}}_m, {\textbf{X}}\rangle =1$ with ${\textbf{A}}_m\in {\mathcal {S}}_k$ having zero entries except the top left one $[{\textbf{A}}_{m}]_{0,0}=1$. Thus, we select ${\textbf{b}}$ such that all entries of ${\textbf{b}}$ are zeros except $b_m=1$.

The number m (or $m_k$ when plugging the relaxation order k) of equality trace constraints $\langle {\textbf{A}}_j,{\textbf{X}}\rangle =b_j$ is:

(60)

The function $-L_{{\textbf{y}}}(f)=-\sum _\gamma f_\gamma y_{\gamma }$ is equal to $\langle {\textbf{C}}, {\textbf{X}}\rangle$ with ${\textbf{C}}:={\textbf{P}}_k^{-1}\tilde{{\textbf{C}}}{\textbf{P}}_k^{-1}$, where $\tilde{{\textbf{C}}}=({\tilde{C}}_{\mu ,\nu })_{\mu ,\nu \in {{\mathbb {N}}}^n_k}$ is defined by:

$$\begin{aligned} {\tilde{C}}_{\mu ,\nu }={\left\{ \begin{array}{ll} -f_{\gamma }&{}\text { if }\mu =\nu ,\,\mu +\nu =\gamma ,\\ -\frac{1}{2} f_{\gamma }&{}\text { if }\mu \ne \nu ,\,\mu +\nu =\gamma ,\\ &{}\qquad \text { and } (\mu ,\nu )\le ({{\bar{\mu }}},{{\bar{\nu }}}),\,\forall {{\bar{\mu }}},{{\bar{\nu }}}\in {{\mathbb {N}}}^n_k\, \text { such that}\,{{\bar{\mu }}}+{{\bar{\nu }}}=\gamma ,\\ 0&{}\text { otherwise.} \end{array}\right. } \end{aligned}$$

(61)