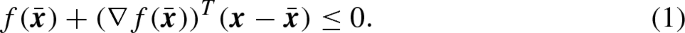Abstract
A mixed-integer convex (MI-convex) optimization problem is one that becomes convex when all integrality constraints are relaxed. We present a branch-and-bound LP outer approximation algorithm for an MI-convex problem transformed to MI-conic form. The polyhedral relaxations are refined with \({{\mathcal {K}}}^*\)cuts derived from conic certificates for continuous primal-dual conic subproblems. Under the assumption that all subproblems are well-posed, the algorithm detects infeasibility or unboundedness or returns an optimal solution in finite time. Using properties of the conic certificates, we show that the \({{\mathcal {K}}}^*\) cuts imply certain practically-relevant guarantees about the quality of the polyhedral relaxations, and demonstrate how to maintain helpful guarantees when the LP solver uses a positive feasibility tolerance. We discuss how to disaggregate\({{\mathcal {K}}}^*\) cuts in order to tighten the polyhedral relaxations and thereby improve the speed of convergence, and propose fast heuristic methods of obtaining useful \({{\mathcal {K}}}^*\) cuts. Our new open source MI-conic solver Pajarito (github.com/JuliaOpt/Pajarito.jl) uses an external mixed-integer linear solver to manage the search tree and an external continuous conic solver for subproblems. Benchmarking on a library of mixed-integer second-order cone (MISOCP) problems, we find that Pajarito greatly outperforms Bonmin (the leading open source alternative) and is competitive with CPLEX’s specialized MISOCP algorithm. We demonstrate the robustness of Pajarito by solving diverse MI-conic problems involving mixtures of positive semidefinite, second-order, and exponential cones, and provide evidence for the practical value of our analyses and enhancements of \({{\mathcal {K}}}^*\) cuts.








Similar content being viewed by others
Notes
Commercial mixed-integer second-order cone optimization (MISOCP) solvers use separation-based algorithms, but also occasionally solve SOCP subproblems to obtain feasible solutions and fathom nodes. SCIP-SDP offers both B&B-NL and separation-based B&B-OA methods for mixed-integer semidefinite problems.
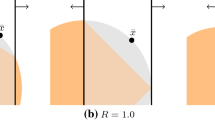
For a convex function \(f : {\mathbb {R}}^n \rightarrow {\mathbb {R}}\), the set \({\mathcal {X}}= \{\varvec{x}\in {\mathbb {R}}^n : f(\varvec{x}) \le 0\}\) is convex. If f is smooth, then given a point \(\bar{\varvec{x}} \in {\mathbb {R}}^n\), the following gradient cut yields a polyhedral relaxation of \({\mathcal {X}}\):
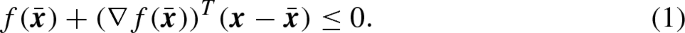
The new version of Pajarito that we implemented for this paper is the first conic-certificate-based OA solver. Although Pajarito solver was introduced in Lubin et al. [26], this early implementation used NLP solvers instead of primal-dual conic solvers for continuous subproblems, and was built to assess the value of extended formulations by counting iterations before convergence. To avoid confusing users, we recently moved this old NLP-based functionality out of Pajarito and into Pavito solver at github.com/JuliaOpt/Pavito.jl.
If \({{\mathcal {K}}}\) is polyhedral, then \({{\mathcal {K}}}^*\) is polyhedral, and hence \({\mathfrak {C}}(\varvec{l}, \varvec{u})\) and \({\mathfrak {C}}^* (\varvec{l}, \varvec{u})\) are both LPs. All LPs are well-posed.
We could instead remove lines 15–17 and solve the conic subproblem even if the LP solution is fractional, rather than branching. This variation may perform better if the conic subproblem solves are quite fast in practice.
From personal communications with Zonghao Gu of Gurobi Optimization and Felipe Serrano of ZIB in 2017, we learned that both the Gurobi and SCIP MISOCP implementations solve SOCP restrictions where \(\varvec{l}\ne \varvec{u}\) as heuristics to find feasible solutions. However, the dual information from these conic subproblem solves is discarded.
If Algorithm 1 branches on Line 34 after solving a bounded and feasible conic subproblem to get the tightest lower bound, then when examining a child node, this objective guarantee ensures the node’s lower bound L does not decrease when we update it to the optimal value of the LP OA on Line 12.
For example, if \({{\mathcal {K}}}_k\) is a positive semidefinite cone, we disaggregate \(\tilde{\varvec{z}}^k \in {{\mathcal {K}}}^*_k\) by performing an eigendecomposition on it; see “Appendix A.3.2”.
The LP solver may need to deal with more cuts at nodes visited early in the search tree, but is ultimately likely to need to examine fewer nodes overall and solve fewer expensive conic subproblems, so the tradeoff can be worthwhile.
For example, for a positive semidefinite cone, we use the extreme rays of the polyhedral cone of diagonally dominant symmetric matrices as initial fixed \({{\mathcal {K}}}^*\) extreme rays; see “Appendix A.3.1”.
However, to be able to recover the guarantees from Sect. 3.2 under an LP solver with a feasibility tolerance, we would need the ability to dynamically scale up the initial fixed \({{\mathcal {K}}}^*\) points.
For example, we obtain separation \({{\mathcal {K}}}^*\) extreme rays for a point that violates a positive semidefinite cone constraint by performing an eigendecomposition on it; see “Appendix A.3.3”.
MathProgBase is being replaced by a redesigned API, MathOptInterface. The process of building Pajarito has motivated many of the planned improvements in MathOptInterface.
MathProgBase documents the conic and linear/quadratic interfaces at mathprogbasejl.readthedocs.io/en/latest. JuMP is documented at juliaopt.org/JuMP.jl/0.18/.
As we note in “Appendix A.2”, Pajarito also recognizes rotated second-order cones, but for simplicity converts them to second-order cones during preprocessing.
Lubin et al. [26] first translated these instances from the MINLPLIB2 library into Convex.jl models. We used ConicBenchmarkUtilities.jl to translate these to CBF. The instances, available at github.com/mlubin/MICPExperiments, are 48 ‘rsyn’ instances, 48 ‘syn’ instances, 6 ‘tls’ instances, 12 ‘clay’ instances, and the challenging ‘gams01’ instance.
More Pajarito examples are at github.com/JuliaOpt/Pajarito.jl/blob/master/examples.
MathProgBase does not attempt to provide an abstraction for solver parameters like convergence tolerances. In cases where we need certain tolerances on the continuous conic and MIP solvers in order for Pajarito to converge to a requested tolerance, it is the user’s responsibility to set these tolerances. For example, we ask users to manually adjust the MIP solver’s linear feasibility tolerance and integer feasibility tolerance for improved convergence behavior. These cases are documented in Pajarito’s readme file.
This can be seen from a simple modification of the complementary solution case polyhedral relaxation guarantee we prove in Sect. 3.1.2, with trivial bounds on the integer variables.
We suggest the user set the MIP solver’s relative optimality gap tolerance to its smallest possible value.
Pajarito uses \(\theta = 10^{-5}\), to avoid division by zero. The gap tolerance \(\epsilon > 0\) is specified by the user, but defaults to \(\epsilon = 10^{-5}\).
Conic solvers typically do not use an absolute primitive constraint-wise feasibility tolerance, as Pajarito does for checking feasibility of OA solutions for the conic constraint. Our incumbent may not satisfy this notion of feasibility, since we do not perform a feasibility check on the conic solver’s primal subproblem solutions.
If the user sets a time limit, Pajarito may terminate with the status ‘user limit’. Pajarito sets the time limit on each MIP or conic solve to the remaining time. Note that the vast majority of Pajarito execution time is spent in MIP or conic solves.
If the user sets a time limit, Pajarito sets a time limit on the MIP solver, and terminates with a ‘user limit’ status if this limit is reached.
The MIP solver is not guaranteed to respect the cuts that we add, and we may need to re-add the same cuts during multiple lazy callbacks (unlike in the iterative method, where cuts previously added are respected). We actually store a dictionary from the integer sub-solution to the cuts. For each repeated integer sub-solution, we re-add these saved certificate cuts, in addition to the new separation cuts.
Note the user is responsible for setting the desired relative optimality gap tolerance on both the MIP solver and on Pajarito directly.
DCP modeling software implementations such as Convex.jl do not perform this transformation because they are simply designed to access conic solvers. Pajarito keeps the original second-order cone formulation in the conic subproblems because conic solvers are likely to perform better with this representation than with the higher-dimensional extended formulation.
For the MSD method, since most MISOCP solvers don’t currently allow adding lazy quadratic constraints, only the initial fixed cuts can be strengthened in this way.
We do not test the Pajarito’s MIP-solver-driven method with CBC or GLPK MIP solvers because their support for MathProgBase callbacks is limited.
We are unaware of any mainstream open source solvers designed for MISOCP. The functional representation of the second-order cone has points of nondifferentiability that may cause Bonmin to crash or suffer numerical issues.
CPLEX is available under an academic or commercial licence, and SCIP is an academic solver that is not released under an OSI-approved open source license. We use CPLEX version 12.7.0 and SCIP version 4.0.0.
However, for most of the 9 excluded instances from ‘Iter-CBC’, we verify that CBC is responsible for the significant integrality violations that result in exclusion.
For ‘MSD-CPLEX’, the two errors occur where Pajarito claims a solution is suboptimal and has an objective gap no worse than \(1.04 \times 10^{-5}\), and the one exclusion occurs where Pajarito’s solution violates a linear constraint by \(9.78 \times 10^{-6}\).
MOSEK 9 is the first version to recognize exponential cones.
This also projects \((u, v, w) \notin {\mathcal {E}}^*\) with \(u > 0, w < 0\) onto \({\mathcal {E}}^*\).
As noted in Sect. 5.2, Pajarito transforms any \({\mathcal {V}}\) constraints to equivalent \({\mathcal {L}}\) constraints during preprocessing.
This also projects \((u, \varvec{w}) \notin {\mathcal {L}}^*\) with \(u < \Vert \varvec{w}\Vert _2\) onto \({\mathcal {L}}^*\).
Note that for real symmetric matrices, all eigenvalues are real. We select the eigenvectors to be orthonormal.
By dropping any \(i \in \llbracket n \rrbracket : \lambda _i < 0\), this projects \(\varvec{W}\in {\mathbb {S}}\backslash {\mathbb {S}}_+^*\) onto \({\mathbb {S}}_+^*\).
Ben-Tal and Nemirovski [5] introduced an alternative extended formulation for the \({\mathcal {L}}^{1+n}\). See Vielma et al. [40] for a discussion and computational comparison of various \({\mathcal {L}}^{1+n}\) extended formulations in the context of a separation-based B&B-OA algorithm for MISOCP.
\({\mathcal {V}}^3\) is in fact a simple linear transformation of \({\mathbb {S}}_+^2\).
We do not explore how to scale these \({\mathcal {V}}\) constraints to recover the guarantees from Sect. 3.2 for an SOCP solver with an absolute feasibility tolerance.
For strengthening separation or certificate \({{\mathcal {K}}}^*\) cuts, Pajarito heuristically picks one of the n possible \({\mathcal {V}}\) constraints by choosing i as the coordinate of the largest absolute value in \(\varvec{\omega }\).
References
Achterberg, T.: SCIP: solving constraint integer programs. Math. Program. Comput. 1(1), 1–41 (2009)
Ahmadi, A.A., Hall, G.: Sum of squares basis pursuit with linear and second order cone programming. arXiv preprint arXiv:1510.01597 (2015)
Belotti, P., Kirches, C., Leyffer, S., Linderoth, J., Luedtke, J., Mahajan, A.: Mixed-integer nonlinear optimization. Acta Numer. 22, 1–131 (2013). ISSN 1474-0508
Ben-Tal, A., Nemirovski, A.: Lectures on Modern Convex Optimization. Society for Industrial and Applied Mathematics, Philadelphia (2001)
Ben-Tal, A., Nemirovski, A.: On polyhedral approximations of the second-order cone. Math. Oper. Res. 26(2), 193–205 (2001)
Bezanson, J., Edelman, A., Karpinski, S., Shah, V.B.: Julia: a fresh approach to numerical computing. SIAM Rev. 59(1), 65–98 (2017)
Bonami, P., Biegler, L.T., Conn, A.R., Cornuéjols, G., Grossmann, I.E., Laird, C.D., Lee, J., Lodi, A., Margot, F., Sawaya, N., Wächter, A.: An algorithmic framework for convex mixed integer nonlinear programs. Discrete Optim. 5(2), 186–204 (2008). ISSN 1572-5286
Bonami, P., Kılınç, M., Linderoth, J.: Algorithms and software for convex mixed integer nonlinear programs. In Lee, J., and Leyffer, S. (eds.) Mixed Integer Nonlinear Programming, Volume 154 of The IMA Volumes in Mathematics and Its Applications, pp. 1–39. Springer New York (2012). ISBN 978-1-4614-1926-6
Borchers, B.: CSDP, AC library for semidefinite programming. Optim. Methods Softw. 11(1–4), 613–623 (1999)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Diamond, S., Boyd, S.: CVXPY: a python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 17(83), 1–5 (2016)
Dolan, E.D., Moré, J.J.: Benchmarking optimization software with performance profiles. Math. Program. 91(2), 201–213 (2002). ISSN 0025-5610
Domahidi, A., Chu, E., Boyd, S.: ECOS: an SOCP solver for embedded systems. In: European Control Conference (ECC), pp. 3071–3076 (2013)
Drewes, S., Ulbrich, S.: Subgradient based outer approximation for mixed integer second order cone programming. In: Lee, J., Leyffer, S. (eds.) Mixed Integer Nonlinear Programming, Volume 154 of The IMA Volumes in Mathematics and Its Applications, pp. 41–59. Springer New York (2012). ISBN 978-1-4614-1926-6. https://doi.org/10.1007/978-1-4614-1927-3_2
Dunning, I., Huchette, J., Lubin, M.: JuMP: a modeling language for mathematical optimization. SIAM Rev. 59(2), 295–320 (2017). https://doi.org/10.1137/15M1020575
Friberg, H.A.: CBLIB 2014: a benchmark library for conic mixed-integer and continuous optimization. Math. Program. Comput. 8(2), 191–214 (2016). ISSN 1867-2957
Gally, T., Pfetsch, M.E., Ulbrich, S.: A framework for solving mixed-integer semidefinite programs. Optim. Methods Softw. 33(3), 594–632 (2018). https://doi.org/10.1080/10556788.2017.1322081
Gould, N., Scott, J.: A note on performance profiles for benchmarking software. ACM Trans. Math. Softw. (2016). https://doi.org/10.1145/2950048
Grant, M., Boyd, S.: CVX: Matlab software for disciplined convex programming, version 2.1. (2014). cvxr.com/cvx
Grant, M., Boyd, S., Ye, Y.: Disciplined convex programming. In: Liberti, L., Maculan, N. (eds.) Global Optimization, Volume 84 of Nonconvex Optimization and Its Applications, pp. 155–210. Springer US (2006). ISBN 978-0-387-28260-2
Günlük, O., Linderoth, J.: Perspective reformulation and applications. In: Lee, J., Leyffer, S. (eds.) Mixed Integer Nonlinear Programming, Volume 154 of The IMA Volumes in Mathematics and Its Applications, pp. 61–89. Springer, New York (2012). ISBN 978-1-4614-1926-6
Kim, S., Kojima, M., Yamashita, M.: Second order cone programming relaxation of a positive semidefinite constraint. Optim. Methods Softw. 18(5), 535–541 (2003)
Kröger, O., Coffrin, C., Hijazi, H., Nagarajan, H.: Juniper: an open-source nonlinear branch-and-bound solver in Julia. In: International Conference on the Integration of Constraint Programming, Artificial Intelligence, and Operations Research, pp. 377–386. Springer (2018)
Leyffer, S.: Deterministic Methods for Mixed Integer Nonlinear Programming. PhD thesis, Department of Mathematics and Computer Science, University of Dundee, Dundee (1993)
Lubin, M., Dunning, I.: Computing in operations research using Julia. INFORMS J. Comput. 27(2), 238–248 (2015)
Lubin, M., Yamangil, E., Bent, R., Vielma, J.P.: Extended formulations in mixed-integer convex programming. In: Louveaux, Q., Skutella, M. (eds.) Integer Programming and Combinatorial Optimization: 18th International Conference, IPCO 2016, Liège, Belgium, June 1–3, 2016, Proceedings, pp. 102–113. Springer International Publishing, Cham (2016). ISBN 978-3-319-33461-5. https://doi.org/10.1007/978-3-319-33461-5_9
Lubin, M., Zadik, I., Vielma, J.P.: Mixed-integer convex representability. In: Eisenbrand, F., Könemann, J.. (eds.) Integer Programming and Combinatorial Optimization—19th International Conference, IPCO 2017, Waterloo, ON, Canada, June 26–28, 2017, Proceedings, Volume 10328 of Lecture Notes in Computer Science, pp. 392–404. Springer (2017). ISBN 978-3-319-59249-7. https://doi.org/10.1007/978-3-319-59250-3_32
Lubin, M., Zadik, I., Vielma, J.P.: Regularity in mixed-integer convex representability. arXiv preprint arXiv:1706.05135 (2017)
Lubin, M., Yamangil, E., Bent, R., Vielma, J.P.: Polyhedral approximation in mixed-integer convex optimization. Math. Program. 172, 139–168 (2018)
Mosek ApS: Modeling Cookbook revision 2.0.1. docs.mosek.com/MOSEKModeling Cookbook-letter.pdf (2016). Accessed 12 Apr 2017
Nagarajan, H., Lu, M., Wang, S., Bent, R., Sundar, K.: An adaptive, multivariate partitioning algorithm for global optimization of nonconvex programs. arXiv preprint arXiv:1707.02514 (2017)
O’Donoghue, B., Chu, E., Parikh, N., Boyd, S.: Conic optimization via operator splitting and homogeneous self-dual embedding. J. Optim. Theory Appl. 169(3), 1042–1068 (2016). https://doi.org/10.1007/s10957-016-0892-3. ISSN 1573-2878
Parrilo, P.A.: Semidefinite programming relaxations for semialgebraic problems. Math. Program. 96(2), 293–320 (2003)
Permenter, F., Friberg, H.A., Andersen, E.D.: Solving conic optimization problems via self-dual embedding and facial reduction: a unified approach. Optimization Online (2015)
Quesada, I., Grossmann, I.: An LP/NLP based branch and bound algorithm for convex MINLP optimization problems. Comput. Chem. Eng. 16(10), 937–947 (1992). https://doi.org/10.1016/0098-1354(92)80028-8. ISSN 0098-1354
Saltzman, M., Ladáanyi, L., Ralphs, T.: The COIN-OR open solver interface: technology overview. Presented at CORS/INFORMS Banff., 5 (2004). https://www.coin-or.org/Presentations/CORS2004-OSI.pdf
Serrano, S.A.: Algorithms for unsymmetric cone optimization and an implementation for problems with the exponential cone. PhD thesis, Stanford University (2015)
Udell, M., Mohan, K., Zeng, D., Hong, J., Diamond, S., Boyd, S.: Convex optimization in Julia. In: Proceedings of HPTCDL ’14, pp. 18–28, Piscataway, NJ, USA. IEEE Press (2014). ISBN 978-1-4799-7020-9
Vielma, J.P.: Small and strong formulations for unions of convex sets from the Cayley embedding. Math. Program. 177, 21–53 (2018). https://doi.org/10.1007/s10107-018-1258-4. ISSN 1436-4646
Vielma, J.P., Dunning, I., Huchette, J., Lubin, M.: Extended formulations in mixed integer conic quadratic programming. Math. Program. Comput. 9(3), 369–418 (2017). https://doi.org/10.1007/s12532-016-0113-y. ISSN 1867-2957
Vigerske, S.: MINLPLIB2 library. www.gamsworld.org/minlp/minlplib2/html/ (2018). Accessed 13 May 2016
Witzig, J., Berthold, T., Heinz, S.: Experiments with conflict analysis in mixed integer programming. In: International Conference on AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, pp. 211–220. Springer (2017)
Zhang, S.: Lecture 4: the dual cone and dual problem. University Lecture. http://www.isye.umn.edu/courses/ie8534/pdf/Lecture-4.pdf (2014)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
M. Lubin is now at Google. The authors thank MOSEK for access to alpha releases of MOSEK 9 and Russell Bent and Emre Yamangil for support for and early contributions to Pajarito. This work has been partially funded by the National Science Foundation under Grant CMMI-1351619, the Department of Energy Computational Science Graduate Fellowship under Grant DE-FG02-97ER25308, and the Office of Naval Research under Grant N00014-18-1-2079.
Appendices
The standard primitive nonpolyhedral cones
As we discussed in Sect. 5.2, Pajarito recognizes three standard primitive nonpolyhedral cones defined by MathProgBase: exponential, second-order, and positive semidefinite cones. Here, we tailor the general techniques for tightening OAs from Sect. 4 to a primitive cone constraint involving one of these three cones. In particular, we describe the initial fixed OAs (see Sect. 4.2), extreme ray disaggregations (see Sect. 4.1), and separation procedures (see Sect. 4.3) implemented in Pajarito.
These ideas could be adapted to other primitive nonpolyhedral cones if the user desires. For example, consider a convex constraint (in NLP form) \(f(\varvec{t}) \le r\), where \(f : {\mathbb {R}}^n \rightarrow {\mathbb {R}}\) is a non-homogeneous convex function. If we define a closed convex cone using the closure of the epigraph of the perspective of f:
then the equivalent conic constraint is \((r, 1, \varvec{t}) \in {{\mathcal {K}}}_f\). From Zhang [43], the dual cone of \({{\mathcal {K}}}_f\) is the closure of the perspective of the epigraph of the convex conjugate of f, \(f^*(\varvec{w}) = \sup \{ -\varvec{w}^T \varvec{t}- f(\varvec{t}) : \varvec{t}\in {{\,\mathrm{dom}\,}}f \}\):
Note \({{\mathcal {K}}}_f^* \ne {{\mathcal {K}}}_{f^*}\) because of the permuting of the first two indices.
1.1 Exponential cone
The exponential cone \({\mathcal {E}}\) is defined from the convex univariate exponential function \(f(t) = \exp (t)\) in Eq. (28):
The convex conjugate is \(f^*(w) = w - w \log (-w)\), so by Eq. (29), the dual cone of the exponential cone is:
1.1.1 Initial fixed polyhedral relaxation
Suppose we have a primitive cone constraint \((r, s, t) \in {\mathcal {E}}\). We use the two \({\mathcal {E}}^*\) extreme rays (1, 0, 0), (0, 1, 0) to impose the simple bound constraints \(r, s \ge 0\). We use more \({\mathcal {E}}^*\) extreme rays of the form \((1, w - w \log (-w), w)\) by picking several different values \(w < 0\). Note the corresponding cuts separate any point (0, 0, t) satisfying \(t > 0\).
1.1.2 Extreme ray disaggregation
Suppose we have the \({\mathcal {E}}^*\) point (u, v, w). If \(w = 0\), the point is already a nonnegative combination of the initial fixed \({\mathcal {E}}^*\) points from “Appendix A.1.1”, so we discard it. If \(w < 0\), we use the \({\mathcal {E}}^*\) extreme ray \((u, w - w \log ({-}w/u), w)\), which when added to some nonnegative multiple of (0, 1, 0), gives (u, v, w).Footnote 38
1.1.3 Separation of an infeasible point
Suppose we want to separate a point \((r, s, t) \notin {\mathcal {E}}\) that satisfies the initial fixed cuts. Then \(r, s \ge 0\) and if \(r = s = 0\) then \(t \le 0\). If \(s = 0\), then \(t > 0\) and \(r > 0\), and we use the \({\mathcal {E}}^*\) extreme ray \((t/r, -2 + 2 \log (2r/t), -2)\). If \(s > 0\), then \(r < s \exp (t/s)\), and we use the \({\mathcal {E}}^*\) extreme ray \((1, (t/s - 1) \exp (t/s), -\exp (t/s))\).
1.2 Second-order cone
For \(n \ge 2\), the second-order cone is the epigraph of the \(\ell _2\)-norm, which is convex and homogeneous:
We sometimes drop the dimension \(1 + n\) when implied by context. This cone is self-dual (\({\mathcal {L}}^* = {\mathcal {L}}\)). We also define the (self-dual) rotated second-order cone:
Note that \({\mathcal {V}}\) is an invertible linear transformation of \({\mathcal {L}}\), since \((r, s, \varvec{t}) \in {\mathcal {V}}^{2+n}\) if and only if \((r + s, r - s, \sqrt{2} t_1, \ldots , \sqrt{2} t_n ) \in {\mathcal {L}}^{2+n}\), so for simplicity we restrict attention to \({\mathcal {L}}\).Footnote 39
1.2.1 Initial fixed polyhedral relaxation
Suppose we have a primitive cone constraint \((r, \varvec{t}) \in {\mathcal {L}}^{1+n}\). First, we note that the \(\ell _{\infty }\)-norm lower-bounds the \(\ell _2\)-norm, since for any \(\varvec{t}\in {\mathbb {R}}^n\) we have:
Let \(\varvec{e}(i) \in {\mathbb {R}}^n\) be the ith unit vector in n dimensions. We use the 2n\({\mathcal {L}}^*\) extreme rays \((1, \pm \varvec{e}(i)), \forall i \in \llbracket n \rrbracket \), which imply the conditions \(r \ge |t_i |, \forall i \in \llbracket n \rrbracket \), equivalent to the homogenized box relaxation \(r \ge \Vert \varvec{t}\Vert _{\infty }\). Second, we note that the \(\ell _1\)-norm also provides a lower bound for the \(\ell _2\)-norm, since for any \(\varvec{t}\in {\mathbb {R}}^n\) we have:
We use the \(2^n\)\({\mathcal {L}}^*\) extreme rays \((1, \varvec{\sigma }/\sqrt{n}), \forall \varvec{\sigma } \in \{-1, 1\}^n\), which imply the homogenized diamond relaxation \(r \ge \Vert \varvec{t}\Vert _1/\sqrt{n}\). Although the number of initial fixed cuts is exponential in the dimension n, in “Appendix B” we describe how to use an extended formulation introduced by Vielma et al. [40] with n auxiliary variables to imply an initial fixed OA that is no weaker but uses only a polynomial number of cuts. Note that the \({\mathcal {L}}^*\) point \((1, \varvec{0})\), which corresponds to the simple variable bound \(r \ge 0\), is a nontrivial conic combination of these initial fixed \({\mathcal {L}}^*\) extreme rays.
1.2.2 Extreme ray disaggregation
Suppose we have the \({\mathcal {L}}^*\) point \((u, \varvec{w})\). If \(\varvec{w}= \varvec{0}\), the point is already a nonnegative multiple of the \({\mathcal {L}}^*\) point \((1, \varvec{0})\), so we discard it. Otherwise, we use the \({\mathcal {L}}^*\) extreme ray \((\Vert \varvec{w}\Vert _2, \varvec{w})\), which when added to some nonnegative multiple of \((1, \varvec{0})\), gives the original point \((u, \varvec{w})\).Footnote 40
1.2.3 Separation of an infeasible point
Suppose we want to separate a point \((r, \varvec{t}) \notin {\mathcal {L}}\) that satisfies the initial fixed cuts. Then \(r \ge 0\) and so \(\varvec{t}\ne \varvec{0}\), and we use the \({\mathcal {L}}^*\) extreme ray \((1, {-}\varvec{t}/\Vert \varvec{t}\Vert _2)\).
1.3 Positive semidefinite cone
For \(n \ge 2\), we define the \(n \times n\)-dimensional positive semidefinite (PSD) matrix cone \({\mathbb {S}}^n_+\) as a subset of the symmetric matrices \({\mathbb {S}}^n = \{ \varvec{T}\in {\mathbb {R}}^{n \times n} : \varvec{T}= \varvec{T}^T \}\), avoiding the need to enforce symmetry constraints. From the minimum eigenvalue function \(\lambda _{\min } : {\mathbb {S}}^n \rightarrow {\mathbb {R}}\), we have:
For \(\varvec{W}, \varvec{T}\in {\mathbb {S}}^n\), we use the trace inner product \(\langle \varvec{W}, \varvec{T}\rangle = \sum _{i,j \in \llbracket n \rrbracket } W_{i,j} T_{i,j}\). \({\mathbb {S}}^n_+\) is self-dual and its extreme rays are the rank-1 PSD matrices [4], i.e. any \(\varvec{\omega }\varvec{\omega }^T\) for \(\varvec{\omega }\in {\mathbb {R}}^n\). An extreme ray \(({\mathbb {S}}^n_+)^*\) cut has the form:
In “Appendix C”, we describe how to strengthen extreme ray \({\mathbb {S}}_+^*\) cuts to rotated second-order cone constraints (for MISOCP OA; see Sect. 5.4).
Recall that our MI-conic form \({\mathfrak {M}}\) uses vector cone definitions, as does MathProgBase. Mosek ApS [30] refers to the matrix cone \({\mathbb {S}}^n_+ \subset {\mathbb {S}}^n\) as the smat PSD cone, and to its equivalent vectorized definition \({\mathcal {S}}^{n (n {+} 1)/2} \subset {\mathbb {R}}^{n (n {+} 1)/2}\) as the svec PSD cone. In svec space, we use the usual vector inner product, and \({\mathcal {S}}\) is also self-dual. The invertible linear transformations for an smat-space point \(\varvec{T}\in {\mathbb {S}}^n\) and an svec-space point \(\varvec{t}\in {\mathbb {R}}^{n (n {+} 1)/2}\) are:
1.3.1 Initial fixed polyhedral relaxation
Suppose we have a primitive cone constraint \(\varvec{T}\in {\mathbb {S}}_+^n\). Let \(\varvec{e}(i) \in {\mathbb {R}}^n\) be the ith unit vector in n dimensions. For each \(i \in \llbracket n \rrbracket \), we let \(\varvec{\omega }= \varvec{e}(i)\) in the extreme ray \({\mathbb {S}}^*_+\) cut (37), which imposes the diagonal nonnegativity condition \(T_{i,i} \ge 0\) necessary for PSDness. For each \(i,j \in \llbracket n \rrbracket : i > j\), we let \(\varvec{\omega }= \varvec{e}(i) \pm \varvec{e}(j)\) in (37), which enforces the condition \(T_{i,i} + T_{j,j} \ge 2 |T_{i,j} |\) necessary for PSDness. Ahmadi and Hall [2] discuss an LP inner approximation of the PSD cone called the cone of diagonally dominant (DD) matrices. Our initial fixed \({\mathbb {S}}^*_+\) points \(\varvec{\omega }\varvec{\omega }^T\) are exactly the extreme rays of the DD cone, so our initial fixed OA is the dual cone of the DD cone.
1.3.2 Extreme ray disaggregation
Suppose we have the \({\mathbb {S}}_+^*\) point \(\varvec{W}\), not necessarily and extreme ray of \({\mathbb {S}}_+^*\). We perform an eigendecomposition \(\varvec{W}= \sum _{i \in \llbracket n \rrbracket } \lambda _i \tilde{\varvec{\omega }}_i \tilde{\varvec{\omega }}_i^T\), where for all \(i \in \llbracket n \rrbracket \), \(\lambda _i\) is the ith eigenvalue and \(\tilde{\varvec{\omega }}_i\) is its corresponding eigenvector.Footnote 41 Since \(\varvec{W}\) is PSD, every eigenvalue is nonnegative, and there are \({{\,\mathrm{rank}\,}}(\varvec{W}) \le n\) positive eigenvalues. For each \(i \in \llbracket n \rrbracket : \lambda _i > 0\), we let \(\varvec{\omega }= \sqrt{\lambda _i} \tilde{\varvec{\omega }}_i\) in (37).Footnote 42 These extreme ray \({\mathbb {S}}^*_+\) cuts aggregate to imply the original \({\mathbb {S}}_+^*\) cut \(\langle \varvec{W}, \varvec{T}\rangle \ge 0\).
1.3.3 Separation of an infeasible point
Suppose we want to separate a point \(\varvec{T}\in {\mathbb {S}}^n \backslash {\mathbb {S}}^n_+\). We perform an eigendecomposition \(\varvec{T}= \sum _{i \in \llbracket n \rrbracket } \lambda _i \varvec{\tau }_i \varvec{\tau }_i^T\), for which at least one eigenvalue is negative. For each \(i \in \llbracket n \rrbracket : \lambda _i < 0\), we let \(\varvec{\omega }= \varvec{\tau }_i\) in (37) (note \(\langle \varvec{\tau }_i \varvec{\tau }_i^T, \varvec{T}\rangle = \varvec{\tau }_i^T \varvec{T}\varvec{\tau }_i = \lambda _i < 0\)).
The second-order cone extended formulation
Recall the definitions of the second-order cone \({\mathcal {L}}\) and the rotated-second-order cone \({\mathcal {V}}\) in “Appendix A.2”. Both \({\mathcal {L}}\) and \({\mathcal {V}}\) are self-dual. As discussed in Sect. 5.4, Pajarito can optionally use an extended formulation (EF) for second-order cone constraints, leading to tighter polyhedral relaxations. Vielma et al. [40] show that the constraint \((r, \varvec{t}) \in {\mathcal {L}}^{1+n}\) is equivalent to the following \(1 + n\) constraints on r, \(\varvec{t}\), and the auxiliary variables \(\varvec{\pi }\in {\mathbb {R}}^n\):
By projecting out the \(\varvec{\pi }\) variables, the equivalence is obvious. Constraints (39b) imply \(r \ge 0\) and \(\pi _i \ge 0\) and \(2 r \pi _i \ge t_i^2\) for all \(i \in \llbracket n \rrbracket \). Aggregating the latter conditions and using the linear inequality (39a), we see \(r^2 \ge \sum _{i \in \llbracket n \rrbracket } 2 r \pi _i \ge \sum _{i \in \llbracket n \rrbracket } t_i^2\), which is equivalent to the original constraint (for \(r \ge 0\)). We only use \({\mathcal {L}}^{1+n}\) and \({\mathcal {V}}^3\) here, so for convenience we drop the dimensions.Footnote 43
Suppose \((u, \varvec{w})\) is a \({\mathcal {L}}^*\) extreme ray, so from “Appendix A.2.2”, we have \(\varvec{w}\ne \varvec{0}\) and \(u = \Vert \varvec{w}\Vert _2 > 0\). Then \(u r + \varvec{w}^T \varvec{t}\ge 0\) is a \({\mathcal {L}}^*\) cut. Note that the linear constraint (39a) in the EF implies:
For each \(i \in \llbracket n \rrbracket \), consider the \({\mathcal {V}}^*\) extreme ray \((w_i^2/2u, u, w_i)\), which implies a \({\mathcal {V}}^*\) cut for the ith constraint (39b) in the EF. The RHS of (40) is an aggregation of these n\({\mathcal {V}}^*\) cuts, which means the \({\mathcal {V}}^*\) cuts imply the \({\mathcal {L}}^*\) cut condition \(u r + \varvec{w}^T \varvec{t}\ge 0\). Therefore, there is no loss of strength in the polyhedral relaxations, and we maintain the certificate \({{\mathcal {K}}}^*\) cut guarantees from Sect. 3.1.Footnote 44
We apply this lifting procedure to the initial fixed \({\mathcal {L}}^*\) points described in Sect. A.2.1. The \({\mathcal {L}}^*\) points for the \(\ell _{\infty }\)-norm relaxation are \((1, \pm \varvec{e}(i)), \forall i \in \llbracket n \rrbracket \); for each \(i \in \llbracket n \rrbracket \), we get three unique \({\mathcal {V}}^*\) extreme rays (0, 1, 0) (for \(w_i = 0\)) and \((1/2, 1, \pm 1)\) (for \(w_i = \pm 1\)). The \({\mathcal {L}}^*\) points for the \(\ell _1\)-norm relaxation are \((1, \varvec{\sigma }/\sqrt{n}), \forall \varvec{\sigma } \in \{-1, 1\}^n\); for each \(i \in \llbracket n \rrbracket \), we get two unique \({\mathcal {V}}^*\) extreme rays \((1/2n, 1, {\pm } 1/\sqrt{n})\) (for \(w_i = {\pm } 1/\sqrt{n}\)). The polyhedral relaxation implied by these 5n\({\mathcal {V}}^*\) points in the EF (39b) and (39a) is at least as strong as that implied by the \(2n + 2^n\)\({\mathcal {L}}^*\) points from Sect. A.2.1, so our initial fixed OA can be imposed much more economically with the EF.
SOCP outer approximation for PSD cones
Recall the definitions of the self-dual smat-space PSD cone \({\mathbb {S}}_+\) in “Appendix A.3” and the self-dual rotated-second-order cone \({\mathcal {V}}\) in “Appendix A.2”.Footnote 45 For a primitive cone constraint \(\varvec{T}\in {\mathbb {S}}_+^n\), we demonstrate how to strengthen an \(({\mathbb {S}}^n_+)^*\) extreme ray cut \(\langle \varvec{\omega }\varvec{\omega }^T, \varvec{T}\rangle \ge 0\) to up to n different \({\mathcal {V}}^3\) constraints. As discussed in Sect. 5.4, Pajarito can optionally solve an MISOCP OA model including these \({\mathcal {V}}^3\) constraints, leading to tighter relaxations of a challenging \({\mathbb {S}}_+^n\) constraint.
Fix the index \(i \in \llbracket n \rrbracket \). Let \(\underline{\omega } = \omega _i\) be the ith element of \(\varvec{\omega }\), and \(\underline{\varvec{\omega }} = (\omega _j)_{j \in \llbracket n \rrbracket \backslash \{i\}} \in {\mathbb {R}}^{n-1}\) be the (column) subvector of \(\varvec{\omega }\) with the ith element removed. Similarly, let \(\underline{t} = T_{i,i}\) and \(\underline{\varvec{t}} = (T_{i,j})_{j \in \llbracket n \rrbracket \backslash \{i\}} \in {\mathbb {R}}^{n-1}\), and let \(\underline{\varvec{T}} = (T_{k,j})_{k,j \in \llbracket n \rrbracket \backslash \{i\}} \in {\mathbb {S}}^{n-1}\) be the submatrix of \(\varvec{T}\) with the ith column and row removed. Kim et al. [22] prove a variant of the standard Schur-complement result that \(\varvec{T}\in {\mathbb {S}}^n_+\) if and only if \(\underline{t} \ge 0\) and:
Consider the 3-dimensional rotated second-order cone constraint:
By the definition of \({\mathcal {V}}\), constraint (42) is equivalent to the conditions \(\underline{t} \ge 0\) and:
Condition (41a) implies condition (43a), by the dual cone definition (5). Since \((\underline{\varvec{\omega }}^T \underline{\varvec{t}})^2 = \underline{\varvec{\omega }}^T \underline{\varvec{t}} \underline{\varvec{t}}^T \underline{\varvec{\omega }}\), condition (43b) is equivalent to \(\underline{\varvec{\omega }}^T (\underline{t} \underline{\varvec{T}} - \underline{\varvec{t}} \underline{\varvec{t}}^T) \underline{\varvec{\omega }} \ge 0\). Thus, by the dual cone definition again, condition (41b) implies condition (43b). Therefore, constraint (42) is a valid relaxation of the PSD constraint \(\varvec{T}\in {\mathbb {S}}^n_+\). Furthermore, from Theorem 3.3 of Kim et al. [22], constraint (42) holds if and only if:
Thus constraint (42) potentially implies an infinite family of \(({\mathbb {S}}^n_+)^*\) cuts, including the original \(({\mathbb {S}}^n_+)^*\) cut \(\langle \varvec{\omega }\varvec{\omega }^T, \varvec{T}\rangle \ge 0\).Footnote 46 Note that the choice of \(i \in \llbracket n \rrbracket \) is arbitrary, so we can derive n different \({\mathcal {V}}\) constraints of the form (42).Footnote 47
We now apply this strengthening procedure to the initial fixed \(({\mathbb {S}}^n_+)^*\) extreme rays described in “Appendix A.3.1”. Letting \(\varvec{\omega }= \varvec{e}(i) \pm \varvec{e}(j)\) for each \(i,j \in \llbracket n \rrbracket : j > i\) in constraint (42), we get the \(n (n {-} 1)/2\) initial fixed \({\mathcal {V}}\) constraints:
These constraints enforce that every \(2 \times 2\) principal matrix of \(\varvec{T}\) is PSD, a necessary but insufficient condition for \(\varvec{T}\in {\mathbb {S}}^n_+\). Ahmadi and Hall [2] discuss an SOCP inner approximation of the PSD cone called the cone of scaled diagonally dominant (SDD) matrices. Our initial fixed SOCP OA is the dual SDD matrix cone, a strict subset of the polyhedral dual DD matrix cone that corresponds to our initial fixed LP OA from “Appendix A.3.1”.
Rights and permissions
About this article
Cite this article
Coey, C., Lubin, M. & Vielma, J.P. Outer approximation with conic certificates for mixed-integer convex problems. Math. Prog. Comp. 12, 249–293 (2020). https://doi.org/10.1007/s12532-020-00178-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12532-020-00178-3