The Limit Cycles for a Class of Non-autonomous Piecewise Differential Equations

Abstract

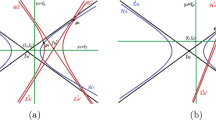
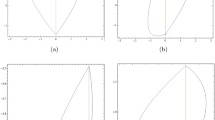
In this paper, we study a class of non-autonomous piecewise differential equations defined as follows: $dx/dt=a_{0}(t)+\sum _{i=1}^{n}a_{i}(t)|x|^{i}$, where $n\in \mathbb {N}^{+}$ and each $a_{i}(t)$ is real, 1-periodic, and smooth function. We deal with two basic problems related to their limit cycles $\big (\text {isolated solutions satisfying} x(0) = x(1)\big )$. First, we prove that, for any given $n\in \mathbb {N}^{+}$, there is no upper bound on the number of limit cycles of such equations. Second, we demonstrate that if $a_{1}(t),\ldots , a_{n}(t)$ do not change sign and have the same sign in the interval [0, 1], then the equation has at most two limit cycles. We provide a comprehensive analysis of all possible configurations of these limit cycles. In addition, we extend the result of at most two limit cycles to a broader class of general non-autonomous piecewise polynomial differential equations and offer a criterion for determining the uniqueness of the limit cycle within this class of equations.