Abstract
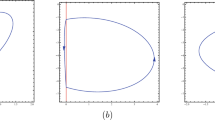
In this paper, we study the maximum number of limit cycles that can exhibit a planar discontinuous piecewise differential system separated by two parallel straight lines and formed by two arbitrary linear differential systems with isolated singularity in the lines of discontinuity and a linear Hamiltonian saddle. More precisely, we prove that when the piecewise differential systems are of type boundary focus-Hamiltonian linear saddle-boundary focus, then this class of systems has at most four crossing limit cycles. But when the piecewise differential system is of type boundary focus-Hamiltonian linear saddle-boundary center, we show that it can have at most three limit cycles, and when the piecewise differential system is of type boundary center-Hamiltonian linear saddle-boundary center, we show that it can have at most one limit cycle.









Similar content being viewed by others
Data availability
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
References
Berbache, A.: Two explicit non-algebraic crossing limit cycles for a family of piecewise linear systems. Mem. Differ. Equ. Math. Phys. 83, 13–29 (2021)
Braga, D., Fonseca, A.F., Mello, L.F., Ribeiro, R., Pessoa, C.: Crossing limit cycles bifurcating from two or three period annuli in discontinuous planar piecewise linear Hamiltonian differential systems with three zones. Int. J. Bifurc. Chaos Appl. Sci. Eng. 33(10), 17 (2023)
Cen, X., Liu, C., Yang, L., Zhang, M.: Limit cycles by perturbing quadratic isochronous centers piecewise polynomial differential systems. J. Differ. Equ. 265(12), 6083–6126 (2018)
Chen, X., Du, Z.: Limit cycles bifurcate from centers of discontinuous quadratic systems. Comput. Math. Appl. 59, 3836–3848 (2010)
da Cruz, L.P.C., Torregrosa, J.: Simultaneous bifurcation of limit cycles from a cubic piecewise center with two period annuli. J. Math. Anal. Appl. 461(1), 258–272 (2018)
Esteban, M., Llibre, J., Valls, C.: The 16th Hilbert problem for discontinuous piecewise isochronous centers of degree one or two separated by a straight line. Chaos 31, 043112 (2021)
Freire, E., Ponce, E., Rodrigo, F., Torres, F.: Bifurcation sets of continuous piecewise linear systems with two zones. Int. J. Bifur. Chaos Appl. Sci. Eng. 8, 2073–2097 (1998)
Filippov, A.F.: Differential Equations with Discontinuous Righthand Sides, Mathematics and its Applications (Soviet Series). Kluwer Academic Publishers, Dortrecht (1988)
Fonseca, A., Llibre, J., Mello, L.: Limit cycles in planar piecewise linear Hamiltonian systems with three zones without equilibrium points. Int. J. Bifur. Chaos Appl. Sci. Eng. 30, 2050157 (2020) (8 p)
Huang, B.: Limit cycles for a discontinuous quintic polynomial differential system. Qual. Theory Dyn. Syst. 18(3), 769–792 (2019) (pp. 301–354)
Llibre, J., Mereu, A.C.: Limit cycles for discontinuous quadratic differential systems with two zones. J. Math. Anal. Appl. 413, 763–775 (2014)
Llibre, J., Teixeira, M.A.: Piecewise linear differential systems with only centers can create limit cycles? Nonlinear Dyn. 91, 249–255 (2018)
Llibre, J., Valls, C.: Limit cycles of planar piecewise differential systems with linear Hamiltonian saddles. Symmetry 13, 1128 (2021)
Llibre, J., Novaes, D., Teixeira, M.: Maximum number of limit cycles for certain piecewise linear dynamical systems. Nonlinear Dyn. 82(3), 1159–1175 (2015)
Pessoa, C., Ribeiro, R.: Limit cycles of planar piecewise linear Hamiltonian differential systems with two or three zones. Electron. J. Qual. Theory Differ. Equ. 27, 19 (2022)
Pessoa, C., Ribeiro, R., Noves, D., Gouveia, M., Euzebio, R.: On cyclicity in discontinuous piecewise linear near-Hamiltonian differential systems with three zones having a saddle in the central one. Nonlinear Dyn. 111, 21153–21175 (2022)
Shafarevich, I.R.: Basic Algebraic Geometry. Springer, New York (1974)
Xiong, Y., Han, M.: Limit cycle bifurcations in discontinuous planar systems with multiple lines. J. Appl. Anal. Comput. 10, 361–377 (2020)
Xiong, Y., Wang, C.: Limit cycle bifurcations of planar piecewise differential systems with three zones. Nonlin. Anal. Real World Appl. 61, 103333 (2021) (18 p)
Xiong, Y.: Limit cycles bifurcations by perturbing piecewise smooth Hamiltonian systems with multiple parameters. J. Math. Anal. Appl. 421, 260–275 (2015)
Zhengkang, L., Xingbo, L.: Limit cycles in the discontinuous planar piecewise linear systems with three zones. Qual. Theory Dyn. Syst. 2021, 20–9 (2021)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Berbache, A., Tababouchet, I. Four crossing limit cycles of a family of discontinuous piecewise linear systems with three zones separated by two parallel straight lines. Bol. Soc. Mat. Mex. 30, 50 (2024). https://doi.org/10.1007/s40590-024-00623-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40590-024-00623-6
Keywords
- Discontinuous planar piecewise linear system
- Crossing limit cycles
- First integral
- Linear Hamiltonian saddles