Abstract
It is a well-known fact that there are continua X such that the inverse limit of any inverse sequence \(\{X,f_n\}\) with surjective continuous bonding functions \(f_n\) is homeomorphic to X. The pseudoarc or any Cook continuum are examples of such continua. Recently, a large family of continua X was constructed in such a way that X is \(\frac{1}{m}\)-rigid and the inverse limit of any inverse sequence \(\{X,f_n\}\) with surjective continuous bonding functions \(f_n\) is homeomorphic to X by Banič and Kac. In this paper, we construct an uncountable family of pairwise non-homeomorphic continua X such that X is 0-rigid and prove that for any sequence \((f_n)\) of continuous surjections on X, the inverse limit \(\varprojlim \{X,f_n\}\) is homeomorphic to X.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The rigidity of topological spaces has been studied in various ways by different authors, e.g., [1,2,3,4,5,6,7,8, 10,11,12]. Cook continua are basic examples of non-degenerate continua that are rigid, and therefore, they play an important role in the study of rigid continua, also in continuum theory and dynamical systems in general. There are many rigid continua or continua that are not 0-rigid that are constructed using Cook continua, see [2, 6, 10], where more references may be found. For example, in [2], Cook continua are used to construct stars, paths, and cycles of Cook continua. They are all examples of continua that are not 0-rigid. It was shown in [2] that for each positive integer m, X such that
-
1.
X is \(\frac{1}{m}\)-rigid, and
-
2.
for any inverse sequence \(\{X,f_n\}\) with surjective continuous bonding functions \(f_n\) the inverse limit \(\varprojlim \{X,f_n\}\) is homeomorphic to X.
Note that for any Cook continuum X and for any sequence \((f_n)\) of continuous surjections on X, the inverse limit \(\varprojlim \{X,f_n\}\) is homeomorphic to X (since each \(f_n\) is the identity on X), while  (since
(since  ).
).
The following problem is also presented in that paper.
Problem 1
[2, Problem 5.7] Find all non-degenerate continua X such that
-
1.
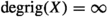 ,
, -
2.
\(\varprojlim \{X,f_n\}\) is homeomorphic to X for any sequence \((f_n)\) of continuous surjections \(f_n:X\rightarrow X\).
Note that the pseudoarc is one such continuum (see [2, Sect. 5] for a detailed explanation).
The main goal of family of pairwise non-homeomorphic continua X such that
-
1.
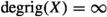 (or, equivalently, X is 0-rigid), and
(or, equivalently, X is 0-rigid), and -
2.
\(\varprojlim \{X,f_n\}\) is homeomorphic to X for any sequence \((f_n)\) of continuous surjections \(f_n:X\rightarrow X\).
We organize the paper in the following way. In Sect. 2, definitions and notations that are needed in the paper are given. In Sect. 3, we construct a large family of continua, and we call each of them a simple fan of Cook continua. They are then used in Sect. 4, where an uncountable family of pairwise non-homeomorphic continua X such that
-
1.
X is 0-rigid, and
-
2.
\(\varprojlim \{X,f_n\}\) is homeomorphic to X for any sequence \((f_n)\) of continuous surjections \(f_n:X\rightarrow X\)
is constructed. This partially answers Problem 1.
2 Definitions and Notation
Definitions and notation mostly follow [2, 9]. Note that all functions in the paper are assumed to be continuous.
A continuum is a non-empty connected compact metric space. A continuum is degenerate if it consists of only a single point. Otherwise, it is non-degenerate. A subcontinuum is a subspace of a continuum which itself is also a continuum.
Let (X, d) be a metric space. By \(B_X(x, \varepsilon )\) we denote the open ball of radius \(\varepsilon > 0\) with center \(x \in X\).
Definition 1
Let n be a positive integer, X a metric space, and \(f:X\rightarrow X\) a function. We use \(f^n\) to denote the composition:
Definition 2
An inverse sequence is a double sequence \(\{X_n,f_n\}_{n=1}^{\infty }\) of metric spaces \(X_n\) and functions \(f_n:X_{n+1}\rightarrow X_n\). The spaces \(X_n\) are called the coordinate spaces and the functions \(f_n\) are called the bonding functions. The inverse limit of an inverse sequence \(\{X_n,f_n\}_{n=1}^{\infty }\) is the subspace of the product space \(\prod _{n=1}^{\infty }X_n\) that consists of all points \({\textbf{x}}=(x_1,x_2,x_3,\ldots )\in \prod _{n=1}^{\infty }X_n\) such that \(x_n=f_n(x_{n+1})\) for each positive integer n:
Definition 3
Let n be a positive integer and let \((x_1,x_2,\ldots ,x_n,\ldots )\in \prod _{n=1}^\infty [0,1]\). A function \(\pi _n: \prod _{n=1}^\infty [0,1]\rightarrow [0,1]\) is defined as \(\pi _n(x_1,x_2,\ldots ,x_n,\ldots )=x_n\).
Definition 4
A metric d on a Hilbert cube \(\prod _{n=1}^{\infty } [0,1]\) is defined as
for each \(x = (x_1,x_2,x_3,\ldots ), y = (y_1,y_2,y_3,\ldots ) \in \prod _{n=1}^{\infty } [0,1]\).
Definition 5
Let X and Y be any metric spaces, S a subspace of X, and let \(f:X\rightarrow Y\) be a function. We use \(f|_S\) to denote the restriction \(f|_S:S\rightarrow Y\), defined by \(f|_S(x)=f(x)\) for any \(x\in S\).
Definition 6
A non-degenerate continuum X is a Cook continuum if for any non-degenerate subcontinuum S of X and any non-constant continuous function \(f:S\rightarrow X\), we have that
for any \(x\in S\).
The identity function on a metric space X will be denoted by \(1_{X}\).
Definition 7
Let n be a positive integer. A non-degenerate continuum X is \(\frac{1}{n}\)-rigid, if
for any continuous surjective function \(f:X\rightarrow X\). If a continuum X is not \(\frac{1}{n}\)-rigid for any positive integer n, then we say that X is 0-rigid. If a continuum X is \(\frac{1}{1}\)-rigid, then we also say that X is 1-rigid.
Definition 8
Let X be a continuum. The degree of rigidity,  , of the continuum X is:
, of the continuum X is:

In [2], examples of continua with the degree of rigidity equal to n for each positive integer n can be found.
Definition 9
Let X be a continuum and let \(x_0\in X\). The point \(x_0\) is called a cut-point if \(X\setminus \{x_0\}\) is not connected. Otherwise, it is called a non-cut point for the continuum X.
In [2], one can find the following result.
Lemma 1
[2, Lemma 3.2] Let K be a Cook continuum and let \(x\in K\) be any point. Then x is a non-cut point for K.
The following lemma is proved in [10].
Lemma 2
[10, Lemma 2.12]
-
1.
Let K be a Cook continuum and S be a non-degenerate subcontinuum of K. Then S is also a Cook continuum.
-
2.
If two Cook continua \(K_1\) and \(K_2\) are homeomorphic, then they are uniquely homeomorphic, i.e., there exists a unique homeomorphism \(\varphi : K_1 \rightarrow K_2\). Moreover, if \(\psi : K_1 \rightarrow K_2\) is a continuous surjection, then \(\psi = \varphi \).
We also use the following two propositions.
Proposition 1
Let K be any Cook continuum and let S be any non-degenerate subcontinuum of K, such that \(S\ne K\). If \(f:K\rightarrow S \) is a continuous function, then f is a constant function.
Proof
Let \(g:S\rightarrow K\) be a continuous function such that \(g(x)=x\) for each \(x\in S\). Then \(g\circ f:K\rightarrow K\) is a continuous function. Since K is a Cook continuum, then \(g\circ f\) is either \(1_K\) or a constant function.
Since \(g(x)=x\) for each \(x\in S\), then \(g(f(x))=f(x)\) for each \(x\in K\). Let \(y\in K{\setminus } S\). Then \(g(f(y))=f(y)\ne y\), therefore \(g\circ f\) is a constant function. It follows that \(g(f(x))=f(x)=f(y)\) for each \(x\in K\). Consequently, f is a constant function. \(\square \)
The following proposition follows directly from Definition 6.
Proposition 2
Let K be any Cook continuum and let S be any non-degenerate subcontinuum of K, such that \(S\ne K\). Then there does not exist a continuous surjective function from S to K.
The following corollary follows from Propositions 1 and 2.
Corollary 1
Let K be a Cook continuum and let \((K_n)_{n=1}^\infty \) be a sequence of continua satisfying \(K_1=K\) and \(K_{n+1}\) is a proper subcontinuum of \(K_n\) for each positive integer n. Then for any positive integers m and n, \(m\ne n\), it holds that there does not exist a continuous surjective function \(f:K_m\rightarrow K_n\).
Proof
Let m and n be positive integers.
If \(n<m\), then \(K_m\subseteq K_n\) and \(K_n\ne K_m\), therefore, by Proposition 1, there does not exist a continuous surjective function \(f:K_m\rightarrow K_n\).
If \(m<n\), then \(K_n\subseteq K_m\) and \(K_n\ne K_m\), therefore, by Proposition 2, there does not exist a continuous surjective function \(f:K_m\rightarrow K_n\). \(\square \)
3 A Construction of Simple Fans of Cook Continua
In Construction 1, simple fans of Cook continua are constructed using any Cook continuum K. Each simple fan of Cook continua will be obtained from special sequence \((K_n)\) of non-degenerate subcontinua of K. The existence of such a sequence will be guaranteed by the Boundary Bumping Theorem (its formulation and its proof may be found in [9]).
Construction 1
Let \((A_n)_{n=1}^\infty \) be a sequence of subsets of positive integers such that
-
1.
\(\bigcup _{n=1}^\infty A_n\) is equal to the set of all positive integers,
-
2.
for all positive integers m and n it holds that: \(m\ne n\) if and only if \(A_m\cap A_n=\emptyset \), and
-
3.
the set \(A_n\) is infinite for each positive integer n.
Moreover, each \(A_n\) we split into n sets \(A_n^1,A_n^2,\ldots ,A_n^n\) such that
-
1.
\(\bigcup _{p=1}^n A_n^p=A_n\),
-
2.
for all positive integers p and q it holds that: \(p\ne q\Leftrightarrow A_n^p\cap A_n^q=\emptyset \), and
-
3.
the set \(A_n^p\) is infinite for each positive integer p.
Now, for each positive integer n and each \(p\in \{1,2,\ldots ,n\}\), let \(Q_n^p\subseteq \prod _{n=1}^\infty [0,1]\) such that
for each positive integer k.
Let K be a Cook continuum and let \((K_n)\) be a sequence of non-degenerate continua, such that
-
\(K_1=K\),
-
\(K_{n+1}\) is a proper subcontinuum of \(K_n\) for each positive integer n, and
-
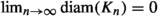 .
.
By Lemma 2, \(K_n\) is a Cook continuum for each positive integer n. The existence of such a sequence of continua follows from Boundary Bumping Theorem.
Now, let \(\{t_0\}= \bigcap _{n=1}^\infty K_n\).
For each positive integer n and for each \(p\in \{1,2,\ldots ,n\}\), let \(H_n^p:K_n\rightarrow Q_n^p\) be an embedding such that \(H_n^p(t_0)=(0,0,\ldots )\). Such embeddings do exist since \( \prod _{n=1}^\infty [0,1]\) is a homogeneous continuum.
Let \(X= \bigcup _{n=1}^\infty \bigcup _{p=1}^n H_n^p(K_n)\). Then X is called a simple fan of Cook continua.
To simplify the study of simple fans of Cook continua, we introduce the following notation, which we use throughout the paper.
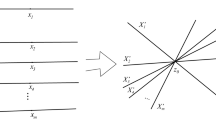
Notation: Let X be a simple fan of Cook continua. We denote
-
1.
\(K_n^p=H_n^p(K_n)\),
-
2.
\(S_n= \bigcup _{q=1}^n K_n^q\),
-
3.
\(h_n^p\) is the homeomorphism from \(K_n\) to \(K_n^p\) (note that there is precisely one such homeomorphism), and
-
4.
\(x_0=(0,0,\ldots )\),
for each positive integer n and for each \(p\in \{1,2,\ldots ,n\}\). The continuum \(S_n\) is also called a star of continua \(K_n^1,K_n^2,\ldots ,K_n^n\) (Fig. 1).
Lemma 3
Let X be a simple fan of Cook continua. Then

Proof
Since for each positive integer n and for each \(p\in \{1,2,\ldots ,n\}\) it holds \(S_n\subseteq \bigcup _{q=1}^n Q_n^q\),  , and \(x_0 \in \bigcap _{q=1}^n Q_n^q\), therefore
, and \(x_0 \in \bigcap _{q=1}^n Q_n^q\), therefore  . \(\square \)
. \(\square \)
The following observation follows directly from Construction 1 and Lemma 3.
Observation 2
Let X be a simple fan of Cook continua. Then X is a continuum.
Observation 3
Let X be an arbitrary simple fan of Cook continua. Then \(x_0\) is the only cut point for X.
The following corollary follows directly from Corollary 1 and Construction 1.
Corollary 2
Let \(K_m^p\) and \(K_n^r\) be continua from Construction 1 for some positive integers m and n such that \(m\ne n\), and for some \(p\in \{1,2,3,\ldots ,m\}\) and \(r\in \{1,2,3,\ldots ,n\}\). Then there does not exist a continuous surjection from \(K_m^p\) to \(K_n^r\).
4 Properties of Simple Fan of Cook Continua
In this section, we partially answer Problem 1. We start with some results that are needed to prove the main results, Theorem 2 and Corollary 5.
Lemma 4
Let X be any simple fan of Cook continua and let \(f:X\rightarrow X\) be any continuous surjection. Then
Proof
Suppose \(f(x_0)\ne x_0\). Let n be a positive integer and \(p\in \{1,2,\ldots , n\}\) such that \(f(x_0)\in K_n^p\). Let \(\varepsilon =\frac{d(x_0,f(x_0))}{3}\). Since f is a continuous function, there exists \(0<\delta <\frac{d(x_0,f(x_0))}{3}\) such that \(f(B_X(x_0,\delta ))\subseteq B_X(f(x_0),\varepsilon )\), where \(B_X(x_0,\delta )\) and \(B_X(f(x_0),\varepsilon )\) are open balls in X.
Let \(m_0\) be a positive integer such that for each positive integer \(m \ge m_0\), it holds that  . By Construction 1,
. By Construction 1,  for each \(p \in \{1,2,\ldots ,m\}\). Moreover, by Construction 1 and since f is continuous, the following holds:
for each \(p \in \{1,2,\ldots ,m\}\). Moreover, by Construction 1 and since f is continuous, the following holds:
-
\(n<m_0\),
-
\(K_{m}\subseteq K_n\),
-
\(h_n^p(K_{m})\subseteq K_n^p\),
-
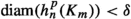 , and
, and -
\(f(h_n^p(K_{m}))\subseteq B_X(f(x_0),\varepsilon )\),
for each positive integer \(m\ge m_0\).
For each positive integer t and for each \(s\in \{1,2,\ldots ,t\}\), we define a function \(\varphi _t^s:X\rightarrow K_t^s\) by
for each \(x\in X\). Obviously, \(\varphi _t^s\) is a continuous function. Then \(\varphi _t^s\circ f|_{K_t^s}:K_t^s\rightarrow K_t^s\) is a continuous function from a Cook continuum to itself. Therefore, \(\varphi _t^s\circ f|_{K_t^s}\) is a constant function or an identity function on \(K_t^s\). We consider the following three cases for t.
Case 1: \(t\le n\). Let \(s\in \{1,2,\ldots ,t\}\). Since \((\varphi _t^s\circ f|_{K_t^s})(x_0)=(h_t^s\circ (h_n^p)^{-1})(f(x_0))\ne x_0\), it follows that \(\varphi _t^s\circ f|_{K_t^s}\) is a constant function and
for each \(x\in K_t^s\). Since \(K_t^s\) is a connected space and f is a continuous function, the image \(f(K_t^s)\) is also a connected space. Therefore,
Case 2: \(n<t<m_0\). Let \(s\in \{1,2,\ldots ,t\}\) and let \(y\in K_t^s\) such that \(d(x_0, y)<\delta \) and \(y\ne x_0\). Then \(f(y)\in B_X(f(x_0),\varepsilon )\subseteq K_n^p\). Therefore, \((\varphi _t^s\circ f|_{K_t^s})(y)=x_0\) and it follows that, \(\varphi _t^s\circ f|_{K_t^s}\) is a constant function. Therefore,
Case 3: \(t\ge m_0\). Let \(s\in \{1,2,\ldots ,t\}\). Since \(K_t^s\subseteq B_X(x_0,\delta )\), it holds that
It follows from the above cases that
which is a contradiction, since f is a surjective function.
\(\square \)
Proposition 3
Let X be any simple fan of Cook continua and let \(f:X\rightarrow X\) be any continuous surjective function. Suppose S is a subcontinuum of \(K_n^p\) for some positive integer n and some \(p\in \{1,2,\ldots ,n\}\), such that \(x_0\notin S\). If \(x_0\notin f(S)\), then there exist exactly one positive integer m and exactly one \(r\in \{1,2,\ldots , m\}\) such that \(f(S)\subseteq K_m^r\).
Proof
Since S is a continuum, f is a continuous function, and \(x_0\) is a cut-point of X, the proposition follows. \(\square \)
Lemma 5
Let X be any simple fan of Cook continua and let \(f:X\rightarrow X\) be any continuous surjective function. Then for each positive integer n and for each \(p\in \{1,2,\ldots ,n\}\), it holds that
Proof
By Lemma 4, \(f(x_0)=x_0\) and we use this fact until the end of this proof. We prove the lemma inductively.
First, we prove that \(f(K_1^1)\subseteq S_1=K_1^1\). Suppose, \(f(K_1^1)\not \subseteq S_1\). Then there exists \(y\in K_1^1{\setminus }\{x_0\}\) such that \(f(y)\notin S_1\). We define a function \(\varphi _1^1:X\rightarrow K_1^1\), where for each positive integer m, for each \(r\in \{1,2,\ldots , m\}\), and for each \(x\in K_m^r\),
It is easy to see that \(\varphi _1^1\) is a continuous function. Therefore, \(\varphi _1^1\circ f|_{K_1^1}:K_1^1\rightarrow K_1^1\) is also a continuous function, and since it maps from a Cook continuum to itself, it is a constant function or an identity function on \(K_1^1\).
Obviously, \((\varphi _1^1\circ f|_{K_1^1})(x_0)=x_0\).
Let \(s\in h_1^1(K_1\setminus K_2)\setminus \{y\}\) be any point. We distinguish two cases for f(s).
Case 1: \(f(s)=s\). Note that by Lemma 1, \(x_0\) is a non-cut point for \(K_1^1\), and by Observation 3, \(x_0\) is a cut point for X. Since \(K_1^1\setminus \{x_0\}\) is connected and f continuous, \(f(K_1^1\setminus \{x_0\})\) is also connected. Consequently, there is \(z\in K_1^1{\setminus }\{x_0,s,y\}\) such that \(f(z)=x_0\).
Then \((\varphi _1^1\circ f|_{K_1^1})(z)=x_0\ne z\), and therefore, \(\varphi _1^1\circ f|_{K_1^1}\) is a constant function with the image \(\{x_0\}\). On the other hand, \((\varphi _1^1\circ f|_{K_1^1})(s)=s\ne x_0\), a contradiction.
Case 2: \(f(s)\ne s\). From Construction 1 and the definition of \(\varphi _1^1\), it follows that \((\varphi _1^1\circ f|_{K_1^1})(s)\ne s\). Therefore, \(\varphi _1^1\circ f|_{K_1^1}\) is a constant function. Consequently, \((\varphi _1^1\circ f|_{K_1^1})(K_1^1)=\{x_0\}\) and
Let n be a positive integer and suppose \(f(K_m^r)\subseteq S_m\) for each positive integer \(m\le n\) and each \(r\in \{1,2,\ldots ,m\}\). Now we prove that \(f(K_{n+1}^p)\subseteq S_{n+1}\) for each \(p\in \{1,2,\ldots ,n+1\}\).
Let \(p\in \{1,2,\ldots ,n+1\}\) be arbitrarily chosen. Suppose, \(f(K_{n+1}^p)\not \subseteq S_{n+1}\). Then there exists \(y\in K_{n+1}^p{\setminus }\{x_0\}\) such that \(f(y)\notin S_{n+1}\). For each \(q\in \{1,2,\ldots ,n+1\}\), we define the function \(\varphi _{n+1}^q:X\rightarrow K_{n+1}^q\) by
for each \(x\in X\). Obviously, \(\varphi _{n+1}^q\) is a continuous function for each \(q\in \{1,2,\ldots ,n+1\}\). Thus, \(\varphi _{n+1}^p\circ f|_{K_{n+1}^p}:K_{n+1}^p\rightarrow K_{n+1}^p\) is a continuous function and it maps from a Cook continuum to itself. Therefore it is a constant function or an identity function on \(K_{n+1}^p\). Since \((\varphi _{n+1}^p\circ f|_{K_{n+1}^p})(y)=x_0\), it follows that \(\varphi _{n+1}^p\circ f|_{K_{n+1}^p}\) is a constant function.
Let \(a\in h_{n+1}^p(K_{n+1}\setminus K_{n+2})\setminus \{y\}\). Since f is surjective, there is \(b\in X\) such that \(f(b)=a\). From the induction assumption, it follows that \(b\notin \displaystyle \bigcup \nolimits _{m=1}^n S_m\). We distinguish the remaining cases for b.
Case A: There is a positive integer \(\ell >n+1\) and \(q\in \{1,2,\ldots ,\ell \}\) such that \(b\in K_\ell ^q\).
Let \(g:K_{\ell } \rightarrow K_{n+1}\) be the function defined by
Obviously, g is a continuous function. Moreover, \(g(t_0) = t_0\), \(g((h_{\ell }^q)^{-1}(b)) = (h_{n+1}^p)^{-1}(a) \ne t_0\), and \(g((h_{\ell }^q)^{-1}(b)) = (h_{n+1}^p)^{-1}(a) \in K_{n+1} {\setminus } K_{\ell }\), a contradiction, since \(K_{\ell } \subseteq K_{n+1}\), \(K_{n+1}\) is a Cook continuum, and g is a continuous function.
Case B: There is a positive integer \(q_1\in \{1,2,\ldots ,n+1\}\) such that \(b\in K_{n+1}^{q_1}\). Denote \(b_1 = b\). Note that \(\varphi _{n+1}^{q_1} \circ f|_{K_{n+1}^{q_1}}: K_{n+1}^{q_1} \rightarrow K_{n+1}^{q_1}\) is a continuous function and \((\varphi _{n+1}^{q_1} \circ f|_{K_{n+1}^{q_1}})(x_0) = x_0\). Moreover, \((\varphi _{n+1}^{q_1} \circ f|_{K_{n+1}^{q_1}})(b_1) = \varphi _{n+1}^{q_1} (a) = (h_{n+1}^{q_1}\circ (h_{n+1}^p)^{-1})(a) \ne x_0\), therefore \(\varphi _{n+1}^{q_1} \circ f|_{K_{n+1}^{q_1}}\) is the identity function. Thus, \((\varphi _{n+1}^{q_1} \circ f|_{K_{n+1}^{q_1}})(b_1)=(h_{n+1}^{q_1}\circ (h_{n+1}^p)^{-1})(a) = b_1\).
Since f is surjective, there is \(b_2 \in X\) such that \(f(b_2) = b_1\). From the induction assumption and Case A it follows that \(b_2 \in K_{n+1}^{q_2} \subseteq S_{n+1}\), for some \(q_2 \in \{1,2,\ldots , n+1\}\), and \((h_{n+1}^{q_2}\circ (h_{n+1}^{q_1})^{-1})(b_1) = b_2\).
Now we construct a finitely many elements \(b_3,\ldots ,b_{n} \in S_{n+1}\) such that
-
1.
\(f(b_i)=b_{i-1}\),
-
2.
\(b_i \in K_{n+1}^{q_i}\), for some \(q_i \in \{1,2,\ldots ,n+1\}\),
-
3.
\((h_{n+1}^{q_i}\circ (h_{n+1}^{q_{i-1}})^{-1})(b_{i-1}) = b_i\),
for each \(i \in \{3,\ldots ,n\}\).
We denote \(b_0=a\) and \(q_0=p\). First, if there is \(i \in \{1,2,\ldots ,n\}\) such that \(b_i = a\), then \(f(a)=b_{i-1}\) and consequently, \(f(a)\in S_{n+1}\). Otherwise, for each \(i \in \{1,2,\ldots ,n\}\) it holds that \(b_i\ne a\). It is easy to see that \(b_i\ne b_j\) for each \(i,j \in \{0,1,\ldots ,n\}\) such that \(i\ne j\). Since f is surjective, there is \(b_{n+1}\in X\) such that \(f(b_{n+1})=b_n\). From the induction assumption and Case A it follows that \(b_{n+1}\notin S_k\) for each positive integer \(k\ne n+1\). Then there exists \(q_{n+1} \in \{1,2,\ldots ,n+1\}\) satisfying \(b_{n+1} \in K_{n+1}^{q_{n+1}}\), and \((h_{n+1}^{q_{n+1}}\circ (h_{n+1}^{q_{n}})^{-1})(b_{n}) = b_{n+1}\). Clearly, there is \(j\in \{0,1,2,\ldots ,n\}\) such that \(q_{n+1}=q_j\). Since
and \((h_{n+1}^{q_{n}}\circ (h_{n+1}^{q_{n+1}})^{-1})(b_{n+1}) = b_{n}\), it follows that \(b_j=b_{n+1}\).
If \(j=0\), then \(f(a)=f(b_0)=f(b_{n+1})=b_n\in S_{n+1}\). Otherwise, if \(j\ne 0\), then \(f(b_{n+1})=b_n\) and \(f(b_{n+1})=f(b_j)=b_{j-1}\), a contradiction, since f is a function and \(b_{j-1}\ne b_n\).
From the above, we conclude that there exists \(j\in \{0,1,2,\ldots ,n\}\) such that \(f(a)=(h_{n+1}^{q_j}\circ (h_{n+1}^p)^{-1})(a)=b_j\).
Recall that, \(\varphi _{n+1}^p\circ f|_{K_{n+1}^p}\) is a constant function. On the other hand,
which is a contradiction since \(a\ne x_0\).
Thus, \(f(y)\in S_{n+1}\) and consequently, \(f(K_{n+1}^p)\subseteq S_{n+1}\).
\(\square \)
The following corollary follows directly from Lemma 5.
Corollary 3
Let X be any simple fan of Cook continua and let \(f:X\rightarrow X\) be any continuous surjective function. Then for each positive integer n,
Theorem 1
Let X be any simple fan of Cook continua and let \(f:X\rightarrow X\) be any continuous surjective function. Then for each positive integer n and for each \(p\in \{1,2,\ldots ,n\}\), there exists \(r\in \{1,2,\ldots ,n\}\) such that
Moreover, \(f(x)=(h_{n}^r\circ (h_{n}^p)^{-1})(x)\) for each \(x\in K_{n}^p\).
Proof
The theorem follows directly from Construction 1, Corollary 3, and [2, Theorem 3.7]. \(\square \)
Corollary 4
Let X be any simple fan of Cook continua and let \(f:X\rightarrow X\) be any continuous surjective function. Then f is a homeomorphism.
Proof
By Theorem 1, it holds that for each positive integer n and for each \(p\in \{1,2,\ldots ,n\}\) there exists \(r\in \{1,2,\ldots ,n\}\) such that \(f(x)=(h_{n}^r\circ (h_{n}^p)^{-1})(x)\) for each \(x\in K_{n}^p\). Consequently, f is a homeomorphism. \(\square \)
Theorem 2
Let X be any simple fan of Cook continua. Then \(\varprojlim \{X,f_n\}\) is homeomorphic to X for any sequence \((f_n)_{n=1}^\infty \) of continuous surjective functions.
Proof
Let \((f_n)_{n=1}^\infty \) be an arbitrarily chosen sequence of continuous surjective functions. By Corollary 4, \(f_n\) is a homeomorphism for each positive integer n. Therefore, \(\varprojlim \{X,f_n\}\) is homeomorphic to X. \(\square \)
Theorem 3
Let X be any simple fan of Cook continua. Then

Proof
We prove that X is not \(\frac{1}{n}\)-rigid for each positive integer n.
Let n be any positive integer. We define a function \(f:X\rightarrow X\) in the following way:

Obviously, f is a continuous surjective function. We prove that \(f^n\ne 1_X\).
Let \(x\in K_{n+1}^1\setminus \{x_0\}\).
Therefore, \(f^n(x)\in K_{n+1}^{n+1}\) and \(f^n(x)\notin K_{n+1}^{1}\). Consequently, \(f^n(x)\ne x\) and \(f^n\ne 1_X\).
We proved that X is not \(\frac{1}{n}\)-rigid for each positive integer n. Thus,  . \(\square \)
. \(\square \)
Corollary 5
There exists an uncountable family \({\mathcal {F}}\) of pairwise non-homeomorphic continua such that for each \(X\in {\mathcal {F}}\) it holds
-
1.
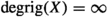 ,
, -
2.
\(\varprojlim \{X,f_n\}\) is homeomorphic to X for any sequence \((f_n)\) of continuous surjections \(f_n:X\rightarrow X\).
Proof
It is known that there are uncountably many pairwise non-homeomorphic Cook continua. Let K and \({\widetilde{K}}\) be any non-homeomorphic Cook continua. Let X be a simple fan of Cook continua obtained from K and let \({\widetilde{X}}\) be a simple fan of Cook continua obtained from \({\widetilde{K}}\).
With \(\sim \) we denote the corresponding homeomorphisms, Cook continua, and \({\widetilde{x}}_0\) for \({\widetilde{X}}\). We prove that X and \({\widetilde{X}}\) are non-homeomorphic.
Suppose X and \({\widetilde{X}}\) are homeomorphic and let \(F:X\rightarrow {\widetilde{X}}\) be a homeomorphism. First we show, that \(F(x_0)={\widetilde{x}}_0\).
If \(F(x_0)\ne {\widetilde{x}}_0\), then there exists \(z_0\in X{\setminus } \{x_0\}\) such that \(F(z_0)={\widetilde{x}}_0\). Since \(z_0\) is non-cut point in X and F is a homeomorphism, then \(F(X\setminus \{z_0\})\) is connected and \(F(X{\setminus }\{z_0\})={\widetilde{X}}{\setminus } \{{\widetilde{x}}_0\}\), a contradiction. Thus, \(F(x_0)={\widetilde{x}}_0\). Moreover, from this it also follows that for each positive integer n and for each \(p\in \{1,2,\ldots ,n\}\), there are positive integers m and \(r\in \{1,2,\ldots ,m\}\) such that \(F(K_n^p)\subseteq {\widetilde{K}}_m^r\).
Suppose n and m are positive integers, \(p\in \{1,2,\ldots ,n\}\), and \(r\in \{1,2,\ldots ,m\}\) such that \(F(K_1^1)\subseteq {\widetilde{K}}_n^p\) and \(F^{-1}({\widetilde{K}}_1^1)\subseteq K_m^r\). Now, we define \(\alpha =({\widetilde{h}}_n^p)^{-1}\circ F\circ h_1^1:K_1\rightarrow {\widetilde{K}}_1\) and \(\beta =({h}_m^r)^{-1}\circ F^{-1}\circ {\widetilde{h}}_1^1:{\widetilde{K}}_1\rightarrow K_1\). Obviously, \(\alpha \) and \(\beta \) are continuous injective functions, and therefore, \(\alpha \circ \beta \) and \(\beta \circ \alpha \) are also continuous injective functions. Since \(K_1\) and \({\widetilde{K}}_1\) are Cook continua, it follows that \(\alpha \circ \beta =1_{{\widetilde{K}}_1}\) and \(\beta \circ \alpha =1_{{K}_1}\).
Note that if \(\alpha \) was surjective, then \(\alpha \) would be a homeomorphism. Since \(K_1=K\), \({\widetilde{K}}_1={\widetilde{K}}\), K and \({\widetilde{K}}\) are not homeomorphic, it follows that \(\alpha \) is not surjective. Therefore, there is \(y\in {\widetilde{K}}\) such that for each \(x\in K\) it holds that \(\alpha (x)\ne y\). Moreover, \((\alpha \circ \beta )(y)\ne y\), a contradiction, since \(\alpha \circ \beta =1_{{\widetilde{K}}_1}\).
By Theorems 2 and 3, each simple fan of Cook continua X satisfies
-
1.
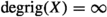 ,
, -
2.
\(\varprojlim \{X,f_n\}\) is homeomorphic to X for any sequence \((f_n)\) of continuous surjections \(f_n:X\rightarrow X\),
and the corollary is proven. \(\square \)
References
Ancel, F.D., Singh, S.: Rigid finite dimensional compacta whose squares are manifolds. Proc. Am. Math. Soc. 887, 342–346 (1983)
Banič, I., Kac, T.: Mapping theorems for rigid continua and their inverse limits. Qual. Theory Dyn. Syst. 21, 117–146 (2022)
Cook, H.: Continua which admit only the identity mapping onto non-degenerate subcontinua. Fund. Math. 60, 241–249 (1967)
Hernandez-Gutierrez, R., Martinez-de-la-Vega, V.: Rigidity of symmetric products. Topol. Appl. 160, 1577–1587 (2013)
Hernandez-Gutierez, R., Illanes, A., Martinez-de-la-Vega, V.: Rigidity of Hiperspaces. Rocky Mountain J. Math. 45, 213–236 (2015)
Kennedy, J.: Infinite product of Cook continua. Topol. Proc. 14, 89–111 (1989)
Kennedy, J.: Positive entropy homeomorphisms on the pseudoarc. Mich. Math. J. 36, 181–191 (1989)
Maćkowiak, T.: Singular arc-like continua. Diss. Math. 257, 1–40 (1986)
Nadler, S.B.: Continuum theory. An introduction, Marcel Dekker Inc, New York (1992)
Snoha, L., Ye, X., Zhang, R.: Topology and topological sequence entropy. Sci. China Math. 63, 205–296 (2020)
Terasawa, J.: Rigid continua with many embeddings. Canad. Math. Bull. 35, 557–559 (1992)
van Mill, J.: A rigid space \(X\) for which \(X \times X\) is homogeneous; an application of infinite-dimensional topology. Proc. Am. Math. Soc. 83, 597–600 (1981)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Author Contributions
All authors wrote and reviewed the manuscript.
Funding
Funders for this research are Javna agencija za Raziskovalno dejavnost RS, P1-0403, and Javna agencija za Raziskovalno dejavnost RS, J1-4632.
Data Availability
Not applicable.
Conflict of interest
The authors have no competing interests as defined by Springer, or other interests that might be perceived to influence the results and/or discussion reported in this paper.
Ethical Approval
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work is supported in part by the Slovenian Research Agency (research programs P1-0403 and J1-4632).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Črepnjak, M., Kac, T. Uncountable Family of 0-Rigid Continua that are Homeomorphic to Their Inverse Limits. Qual. Theory Dyn. Syst. 22, 80 (2023). https://doi.org/10.1007/s12346-023-00777-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12346-023-00777-0
Keywords
- Continua
- Cook continua
- Rigid continua
- Degree of rigidity
- Stars of continua
- Simple fan of Cook continua
- Inverse limits



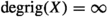 ,
,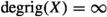 (or, equivalently, X is 0-rigid), and
(or, equivalently, X is 0-rigid), and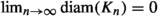 .
.
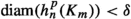 , and
, and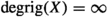 ,
,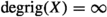 ,
,