Internal Model-Based Robust Path-Following Control for Autonomous Vehicles

Abstract

The paper presents a new internal model control (IMC) based control technique for lateral trajectory tracking of autonomous vehicles. The controller’s proposed structure employs a robust, fault-tolerant nonlinear internal servo control with optimal reference generation concerning vehicle yaw stability and physical limitations. The presented inscription of the reference generation creates a convex optimization task that can be used in real-time applications. Improvements in yaw-rate stability of vehicle motion control are first shown through simulation results performed in a Simulink environment. The controller structure was also implemented in a real-time model and was examined in a Mercedes C-Class vehicle. In this article, the simulation results and the real-time measurements are presented. The results show that the proposed controller has high efficiency in disturbance rejection and lower sensitivity towards parameter changes compared to a model predictive control (MPC) structure.

1 Introduction

One of the main reasons for developing autonomous vehicles is that these vehicles can increase safety in transportation. The safety of autonomous vehicles should be measured in handling a wide range of vehicle operating conditions (load, speed, tire friction) and disturbances. As the first step towards autonomy, driving assistant systems were developed to support inexperienced drivers and increase safety and stability. For longitudinal and lateral control, PID and LQR control is used to increase the stability of human-driven vehicles (Tavan et al., 2015). The linear matrix inequality (LMI) method is used for a robust driver assistant control improving chassis stability (Dahmani et al., 2015).

The recent emerging technologies have several challenges concerning autonomous technology (Paden et al., 2016). The algorithms should provide a real-time solution that can be evaluated on the test platform to gain reliability. The convexity of the problem space has to be provided to ensure unicity, and the parameters making these algorithms intuitive and scenario-specific should be eliminated.

An improved structure of the pure pursuit method adjusts the look-ahead point and solves the cutting-edge problem (Ahn et al., 2021). This method is good in handling the question of the distance of the look-ahead point, but the vehicle dynamics and limitations are not considered. A comprehensive list of trajectory tracking controllers that are not using optimization and have short runtime can be found in the literature (Calzolari et al., 2017). Still, these methods cannot handle nonlinearities such as tire saturation or actuator limitations. A sliding-mode controller is presented for the lateral control (Tagne et al., 2013). This method is robust in handling nonlinearities. However, it has many intuitive parameters in the control rule and in solving the chattering problem.

Model predictive control (MPC) is an effective structure for longitudinal-lateral control, but in the most cases, it uses a linear model (Lin et al., 2019). A lane change controller with a linear model for a straight and curved road is developed using the LMI method (Mammar & Arioui, 2018). A linear-quadratic integral and regulator control uses particle swarm optimization for parameter setting, but this structure assumes known road friction parameters (Omar et al., 2018).

Internal Model Control (IMC) is a well-known technique for robust control in various control engineering fields. Several usages of this method for vehicle control: There is an example of successfully using direct yaw control and active front steering with a modified internal model control structure for a robust driver assistant system (Wu et al., 2015). However, it has quite quickly changing control signals that cause a bad passenger experience. An IMC system with an ${H}_{\infty }$-based feedback loop sacrifices the performance to enhance stability (Canale et al., 2008). Two degrees of freedom IMC structure is developed, but its linear model is unable to control the vehicle at the limits of handling (Wu et al., 2016). A special controller uses an external active stabilizer to improve yaw stability (Wang & Chen, 2018), which is an effective way, but its cost is high concerning the vehicle’s transport capacity.

However, there are several solutions for lane following; these are mostly focusing strictly on trajectory tracking without thinking globally, such as performing maneuvers. Trajectory planning and tracking can be combined to improve safety (Guo et al., 2014). The maneuver-based approach allows the construction of the control signal to minimize the control effort and increase robustness to provide acceptable performance even if there are changes in the vehicle’s parameters or the environment.

In safety-critical systems such as automotive solutions, it is a need to have diverse redundant solutions for the same problem. This paper’s novel contribution is based on the new approach concerning a previewed maneuver-based optimization to gain robustness for a nonlinear system. Yaw-rate trajectory optimization aims to gain stability satisfying physical constraints. Robustness is granted by the application of the internal model control structure. The problem formulation ensures that the proposed method uses just a few parameters, having physical meaning, minimizing intuitively tuned weights and scaling factors.

The paper is organized as follows: In “Model Description” section, the vehicle and tire modeling aspects are discussed for dynamic analysis. The two main parts of the controller structure are presented in detail in “Controller Structure”. In “Simulation Results” section, the environment for simulation is explained, and the results are presented. A reference controller is presented in “MPC Controller for Comparison” section with the comparison of measurements performed in simulation, illustrating the proposed controller’s efficiency and robustness. Finally, in “Experimental Results” section, the experimental results of the real-time test are presented.

2 Model Description

Due to system complexity and computational limitations, it is common to decouple the longitudinal and lateral control and use just the second one for trajectory tracking (Rajamani, 2012). The dynamic bicycle model describes the vehicle’s lateral dynamics and different tire models explained in this section. Nonlinear vehicle and tire models have to be used to reach the purpose of this article. Constant longitudinal speed ($u$) can be assumed for lateral dynamics in the previewed maneuver (Lin et al., 2019), so longitudinal dynamics are omitted in the modeling part.

2.1 Tire Models

Linear and nonlinear tire models are used to describe the tires of the vehicle (Rajamani, 2012). The linear tire model contains only one parameter, the cornering stiffness ($C$), the steepness of the line describing the tire forces. This model cannot handle tire saturation. The nonlinear tire model is based on the well-known Pacejka magic formula (Pacejka, 2005). It describes the forces with an experimental function based on measurements, approximated by trigonometric functions. The lateral force in the tire is a function of vertical force, road friction, and tire sideslip:

$$Fy = Fz\upmu \cdot sin\left({c}_{lat}atan\left({b}_{lat}\left(-\alpha \right)\right)\right),$$

(1)

where $\alpha$ is the tire sideslip, ${F}_{z}$ is the vertical force, $\mu$ is the vehicle-road friction coefficient. Parameters ${c}_{lat}$ (the shape factor) and ${b}_{lat}$ (the stiffness factor) are derived from the Delft tire model implemented in the simulation environment.

2.2 Vehicle Model

As soon as the linear vehicle model is inaccurate in high dynamics situations, the vehicle is modeled with a nonlinear single-track bicycle model (Bobier-Tiu et al., 2019). This model describes the vehicle’s planar behavior with the following assumptions: wheels on the front axle and the rear axle are lumped, and only the front tire is steered. The vehicle is on a flat road, and longitudinal acceleration is low and ignored compared to lateral acceleration.

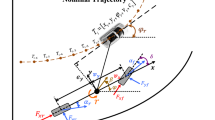
The diagram of the bicycle model can be seen in Fig. 1. This model uses a two-dimensional body-fixed coordinate system; the x-axis points to the longitudinal and the y-axis to the lateral direction.

Fig. 1

Single-track bicycle model of the vehicle for nonlinear and dynamic analysis

The differential equations of the model are written for the state variables in terms of force and moment balance in the $y$ and $z$ directions, respectively (Bobier-Tiu et al., 2019). System of Eq. (2) describes the relations between the state variables: the lateral speed and the yaw-rate of the vehicle, ${u}_{y}$ and $r$, respectively. The $m$ is the mass of the vehicle, and ${I}_{z}$ is the yaw moment of inertia for the vehicle, $a$ and $b$ are the distances of the front and the rear tires from the center of gravity (COG), as can be seen in Fig. 1. $\beta$ can also be used as a state variable and calculated from ${u}_{y}$ as follows: $\beta ={\text{arctan}}\left(\frac{{u}_{y}}{{u}_{x}}\right)$. The front and the rear tires have different parameters in the model, noted by subindex $F$ (front tire) and $R$ (rear tire).

$$\begin{aligned}{\dot{u}}_{y}&=\frac{{F}_{yF}{\text{cos}}\left(\delta \right)+{F}_{yR}}{m}-r{u}_{x}\\ \dot{r}&=\frac{a{F}_{yF}{\text{cos}}\left(\delta \right)-b{F}_{yR}}{{I}_{z}}.\end{aligned}$$

(2)

The front and rear tire slip angles noted as ${\alpha }_{F}$ and ${\alpha }_{R}$ in Fig. 1 can be calculated as follows:

$$\begin{aligned}{\alpha }_{F}&={{\text{tan}}}^{-1}\left(\frac{{u}_{y}+ar}{{u}_{x}}\right)-\delta \\ {\alpha }_{R}&={{\text{tan}}}^{-1}\left(\frac{{u}_{y}-br}{{u}_{x}}\right),\end{aligned}$$

(3)

where $\delta$ is the steering angle.

The behavior of the vehicle in the two-dimensional coordinate system is described by position and orientation ($x(t), y(t),$ and $\psi (t)$, respectively). These states can be derived from $r(t)$ and $\beta (t)$ as follows:

$$\begin{aligned}\psi \left(t\right)&={\psi }_{0}+{\int }_{0}^{t}r\left(\tau \right)d\tau \\ y\left(t\right)&=y\left(0\right)+{\int }_{0}^{t}u {\text{sin}}(\psi \left(\tau \right)+\beta (\tau )) d\tau \\ x\left(t\right)&=x\left(0\right)+{\int }_{0}^{t}u{\text{cos}}\left(\psi \left(\tau \right)+\beta \left( \tau \right)\right)d\tau. \end{aligned}$$

(4)

3 Controller Structure

The classical trajectory tracking approach needs to be reviewed to gain stability and robustness: the importance of lateral and orientational deviation is decreased in the benefit of having more reserve for the control. The main idea is based on the adaptive look-ahead design (Lee et al., 2019): the controller is analogous to the driver’s intention, who plans forward on the road and wants to drive the vehicle to a required state within a prescribed time or distance traveled. As the driver constructs the maneuver, the presented controller calculates the control signal minimizing a cost function considering yaw stability and control effort.

Based on this idea, the presented controller has two main parts, as it is shown in Fig. 2. The first part consists of the optimizer that calculates a yaw-rate reference signal prescribing the dynamic behavior of the vehicle. The second part realizes a robust yaw-rate controller with an IMC structure. Both parts are running on the same control frequency.

Fig. 2

Structure of the controller: the yaw rate reference generator and the internal model control with the filter and the physical limitations

3.1 Steady-State Analysis

Internal model control requires the inverse of the model to provide a transfer function of unity in the forward branch in the steady-state. The steady-state inverse based on linear analysis is sufficient for this purpose concerning time constants (Canale et al., 2007). The steady-state analysis investigates how the model behaves for constant input and how it converts between states. A static map ($L$) can be constructed in steady-state to describe the connection between the output yaw-rate and the constant input, the steering angle, for a specified longitudinal speed, $u$: $r,\beta = L(\delta ,u)$. The map was created using $\mu =1$ as a nominal value. The map values are stored in a look-up table, and the function values are calculated by linear interpolation. For changing speed, a two-dimensional map has to be constructed. Within the range of speed, the controller is used, the relation between yaw-rate and $\beta$ of the steady-state vehicle can be approximated with a speed-dependent constant: $\beta = c(u) \cdot r$. The map ($L$) also contains information about tire saturation: at a specified speed, it is monotonous under a certain steering angle, where the tire saturates. The steering angle is limited to ensure the uniqueness of the mapping and prevent tire saturation.

3.2 Yaw-Rate Reference Generation

Yaw-rate analysis using second-order yaw-sideslip characteristics is a standard method to examine vehicle stability properties. The yaw-moment-based controller is efficient in providing vehicle stability. An envelope control is constructed using the phase plane approach to improve yaw-rate stability, keeping away the vehicle from unstable and uncontrollable regions (Bobier-Tiu et al., 2019).

As can be seen in Eq. (2), the yaw-rate is related to the steering angle. In steady-state cornering, the model assigns a yaw-rate value to the steering angle, which means that the derivative of the yaw-rate is related to the control signal’s change. This paper aims to handle the planar motion’s yaw-rate behavior: minimize the control effort, and gain robustness in the presence of tire saturation and against model uncertainties.

3.3 Approximations of the Yaw-Rate Reference Signal

The problem to be solved by the controller is the following: find a trajectory for the given time window ($T$) concerning the actual state so that the prescribed final states ($r(T), \psi (T)$, and$\Delta y(T)$) are fulfilled, and the control effort is minimized based on yaw-rate reference generation. The $\Delta y$ corresponds to lateral position displacement prescribed to eliminate the lateral error of the COG. For the prediction- based lateral reference generation, the longitudinal velocity is assumed to be unchanged for the time window, which is a common assumption (Jalali et al., 2017). The actual longitudinal speed, measured by sensors, was used as an external parameter (Mammar & Arioui, 2018). In order to handle this problem, the look-ahead time window is divided into $N$ equal time slots, as can be seen in Fig. 3. The length of each slice is ${T}_{s} =\frac{T}{N}$. The yaw-rate is linearized concerning these slices, so each slot has only one parameter, ${d}_{i}$, the derivative of yaw-rate. With this approximation, the $r$ and $\psi$ at each time slot can be written by the following expressions:

$${r}_{i}={r}_{0}+{T}_{s}\sum _{j=1}^{i}{d}_{j} ,$$

(5)

$${\psi }_{i}={\psi }_{0}+{T}_{s}\sum _{j=1}^{i}\frac{{r}_{j}+{r}_{j-1}}{2}={\psi }_{0}+{T}_{s}\sum _{j=1}^{i}r{m}_{j},$$

(6)

where $r{m}_{i}$ is the mean yaw-rate of a specified slice ($r{m}_{i}=\frac{{r}_{i-1 }+{r}_{i}}{2}$).

Fig. 3

Sliced trajectory for optimization

The lateral position error can be calculated based on Eq. (4), using the steady-state approximations for $\beta$ estimation described in the previous subsection. The yaw-rate expression contains second-order variables of $t$, so the formulation of lateral displacement of the ith slice ($\Delta {y}_{i}$) is quite complex, containing Fresnel integrals ($C\left(u\right)\equiv {\int }_{0}^{u}{\text{cos}}\left(\frac{1}{2}\pi {x}^{2}\right)dx$, and $S\left(u\right)\equiv {\int }_{0}^{u}{\text{sin}}\left(\frac{1}{2}\pi {x}^{2}\right)dx$) as follows:

$$\begin{aligned}\Delta {y}_{i}&=u{\int }_{0}^{{T}_{s}}{\text{sin}}\left({e}_{i}+{f}_{i}\tau +{g}_{i}{\tau}^{2}\right)d\tau \\ &=u\left[\sqrt{\frac{\pi }{2{g}_{i}} }\left({\text{sin}}\left({e}_{i}+\frac{{f}_{i}^{2}}{4{g}_{i}}\right)C\left(\frac{{f}_{i}+2{g}_{i}\tau }{\sqrt{{g}_{i}2\pi }}\right)\right.\right. \\&\left.\left.\quad +{\text{cos}}\left({e}_{i}-\frac{{f}_{i}^{2}}{4g}\right)S\left(\frac{{f}_{i}+2{g}_{i}\tau }{\sqrt{{g}_{i}2\pi }}\right)\right)\right]_{0}^{{T}_{s}},\end{aligned}$$

(7)

where ${e}_{i}={\psi }_{i-1 }+c\cdot {r}_{i-1}$, ${f}_{i}={r}_{i-1}+c\cdot {d}_{i}$ and ${g}_{i}=\frac{{d}_{i}}{2}$.

Calculation of this expression is quite expensive as soon as the Fresnel integrals can be calculated only iteratively; it requires a significant runtime since the lateral position is evaluated several times during one step of optimization. Further approximations were made using the mean yaw-rate for lateral displacement calculation. With this simplification, the following expression was derived for the lateral displacement of a slice from the integral:

$$\Delta {y}_{i}=u{T}_{s}{\text{sin}}\left({\psi }_{i-1 }+\left(c+\frac{{T}_{s}}{2}\right)r{m}_{i}\right)sinc\left(\frac{{T}_{s}r{m}_{i}}{2}\right),$$

(8)

where $sinc\left(x\right)=\frac{{\text{sin}}\left(x\right)}{x}$. With these approximations, the optimization problem can be solved in real-time.

3.4 Optimization for the Yaw-Rate Reference Generation

The expressions presented in the previous section can be used to write the problem in the following form:

$$\begin{array}{*{20}l} {{\mathop {\min }\limits_x} \,f\left( x \right) } \hfill & {subject\, to} \hfill \\ {\,} \hfill & {c\left( x \right) \le 0} \hfill \\ {\,} \hfill & {Ax \le b} \hfill \\ {\,} \hfill & {\left| x \right| \le x_{max} ,} \hfill \\ \end{array}$$

(9)

where $x$ is the vector of the ${d}_{i}$ values, $c(x)$ is the nonlinear expression of the lateral displacement described in Eq. (8), $A$ is the coefficients of the sums of Eqs. (5) and (6), and ${x}_{max}$ is derived from the static map derived from steady-state analysis. Inequality is used in the problem because the prescribed final values are handled with tolerances to suppress noise from measurements of the states that are the input variables for the optimization. The cost function determines the minimal control effort, minimizing the discrete square integral of the yaw-rate derivative values:

$$f\left(x\right)={T}_{s}\sum _{i}^{N}{d}_{i}^{2}.$$

(10)

The presented optimization problem has global solutions so that MatLab’s fmincon function can solve it, but it can possibly provide local solutions that should be handled.

The cost function is convex, so it provides an opportunity for the optimization problem to be handled as a Second-Order Cone Programming (SOCP) problem. The expression of $\Delta y(T)$ has to be linearized to make the task fit the SOCP problem. Supposing that ${T}_{s}$ is small enough, $sinc(x)$ can be approximated by $f(x)$ = 1.

It can be assumed that during the look-ahead time, the orientation of the vehicle described by the argument sin function in Eq. (8) remains within $\pm\, 1\,rad$, so the $sin(x) = x$ approximation can be used.

After linearization, in the optimization problem in Eq. (9), the nonlinear expression can be omitted, and the following linear expression can be derived for lateral displacement:

$$\begin{aligned}\Delta y\left(T\right)&=\sum _{i=1}^{N}\Delta {y}_{i}\\ &\approx u\cdot {{\text{T}}}_{{\text{s}}}\cdot \left[{\uppsi }_{0}N+\frac{{T}_{s}{r}_{0}\left(N\left(N-1\right)\right)}{2}+{r}_{0}N\left(\frac{{T}_{s}}{2}+c\right)\right.\\ & \left.\quad +{T}_{s}\sum _{i=1}^{N}{d}_{i}\left(\frac{{T}_{s}{\left(N-i\right)}^{2}}{2}+\left(-i+\frac{1}{2}\right)\cdot \left(\frac{{{\text{T}}}_{{\text{s}}}}{2}+c\right)\right) \right].\end{aligned}$$

(11)

The lsqlin solver of MatLab can solve the SOCP optimization problem. The two optimization tasks with the different solvers were compared in the simulation. The difference between the two solutions is negligible in the domain of the test cases presented in the result summary section. The SOCP problem runs four times faster than the global problem, so this algorithm was used in real-time measurements to reach the desired control frequency.

3.5 Robust Yaw-Rate Controller

Internal model control is a robust control method widely used in several applications, even for yaw-rate control (Canale et al., 2007). Yaw-rate control can be used for this approach because it is measured quite standard on-board instrumentation. The feedback control method of the basic IMC can guarantee stability in the presence of model uncertainty, disturbances and can handle saturation (Zhu et al., 1995). The robustness and effectiveness of IMC in lateral control systems are proved (Aripin et al., 2014). In this application, an internal servo controller is used for signal tracking.

The feedforward branch (the controller with the process) provides a transfer function of unity to track the input by the steady-state output. This condition is fulfilled using the results of the steady-state analysis, the mapping L. The process model presented above is connected parallel with the process, and the difference between the output of the process and the model creates the feedback branch. This feedback branch is intended to compensate for model errors and disturbances. The IMC system is stable if both the controller and the process are stable. The presented dynamic bicycle model, serially connected with the steady-state model inverse, is stable, so this controller provides robust yaw-rate control.

3.6 Physical Constraints and Filtering

The physical parameters of the actuator have to be handled by the controller. The first-order element with one parameter can model the actuator. In order to eliminate the effect of this first-order element, the yaw-rate reference provided for the IMC controller is planned ahead with τ, so at time t, from the planned yaw-rate, ${r}_{ref}(t + {T}_{s} + \tau )$ provides the reference for the IMC. The actuator performance maximizes the change of the steering angle:

$\left|\frac{d\delta \left(t\right)}{dt}\right|<D$, where $D$ is a characteristic constant of the.

actuator. Limits for ${d}_{i}$ can be introduced, transferring $D$ to the derivative of yaw-rate, using the steady-state map.

An autoregressive filter was added to the feedback line of the controller to attenuate the noise of the measurement and the error coming from the model mismatch. In discrete-time, the filter has the following expression:

$$y\left(k\right)= a \cdot x\left(k\right)+ \left(1 - a\right)\cdot y\left(k - 1\right),$$

(12)

where $x(k)$ represents the feedback value calculated from the difference between the model and the plant. Number $a$ has to be smaller than one, in our case $a= 0.2$, prescribing the averaging factor of the filter.

3.7 Control Algorithm

The control algorithm performs the following steps in each control period: After the sensor measurements and state estimation, the optimization task, detailed in Eq. (9), is defined using the lateral reference and the actual states. Then the optimization is performed, creating the yaw-rate reference for the inner loop. After, the inner loop calculates the control signal, using the steady-state model inverse map and the previous filtered signal. Finally, the control signal is actuated, and the model output is calculated for the feedback of the next iteration.

4 Simulation Results

The presented controller was implemented in MatLab & Simulink version r2018b. It was first inserted into the simulation framework and, after, into the real-time environment for validation. Test environments were developed, supported, and commonly used by ThyssenKrupp. These environments are compatible with each other using the same interface. The algorithm can be cross-validated: the parameter tuning can be done in simulation, and one can replay measurements in the simulation.

4.1 Simulation Environment

The simulation environment is implemented in Simulink and contains a 12-DOF vehicle model. Tires are modeled with the TNO Delft-Tyre (2010) model using real parameter sets that are configured by measurements. The simulator’s structure depicts the structure of the real-time environment. It contains a Kalman-filter-based state estimator with odometry and GPS, sensors with parametrizable accuracy, and a localization method that provides the reference signals for the yaw rate planner. Values of mapping $L$ were calculated via simulation performed in this environment.

The parameters of the controller during the measurement were the following: $\tau = 0.25s$ (time constant of the actuator), $\Delta {y}_{tol} = 0.1 m$, $\Delta {\psi }_{tol} = 1deg$ (lateral and orientational tolerance for path tracking in optimization). The controller ran at control frequency $f = 50\,Hz$, the length of the time window was $T = 1.5s$, and the number of slots during the optimization was $N = 6$.

4.2 Skidpad Maneuver

One of the most common tests for the controller’s ability to handle unstable situations (sliding, drifting, and unexpected lateral forces) is the skid-pad test: the vehicle goes straight and runs over an actuator that jerks the front wheels of the vehicle giving angular momentum to it. The track of the vehicle is constantly watered to reduce rubber wear during the maneuver. For this test to be performed in real-time, it needs a special environment, so only simulation measurements were performed. In the simulation, the effect of the skid-pad can be replaced by a lateral force impulse affecting the front wheels of the vehicle.

The controller’s operation during the effect of a lateral force of $4000 N$ for $0.5 s$ can be seen in Fig. 4. The vehicle’s speed was $10\frac{m}{s}$. However, it is clear that the disturbance causes $3$ meters of lateral error and a high jump in the yaw-rate; the controller can compensate effectively and aperiodically the error with minimal control effort. It should be noted that on the waveform of the yaw-rate derivative, the lateral force can be seen in action.

Fig. 4

Simulated skid-pad maneuver for testing the robustness of the controller. Subplot a represents the path of the vehicle in x–y coordinates. The other subplots represent the state variables along the path taken by the vehicle

5 MPC Controller for Comparison

MatLab’s Automated Driving toolbox has a built-in solution for lateral control using Model Predictive Control Toolbox, called Lane Keeping Assist System (LKA) (MathWorks, 2020). The LKA instantiates an adaptive model predictive controller and can easily be placed into the simulation environment described above as soon as its control law is based on a receding horizon. The MPC controller is a common and well-performing approach in lateral control, according to Paden et al. (2016). The optimization of the proposed algorithm solves a quadratic problem similar to the MPC of the LKA. The computational complexity of the controllers is identical, so the advantages of the proposed structure in handling nonlinearities can be seen in the comparison.

5.1 Structure of the MPC Controller

The LKA subsystem has road curvature, lateral deviation of the center of gravity (COG), relative yaw angle, and speed as an input, and control signal as output. The adaptive MPC controller in the LKA subsystem contributes to two main parts: state estimation and optimization. Its adaptiveness appears in the prediction model as operating conditions change, in this case, the longitudinal speed. A linear time-varying Kalman filter performs the state estimator. The estimator uses the dynamic bicycle model described above, using the same vehicle parameters. MatLab’s LKA subsystem uses a linear tire model that describes lateral force by cornering stiffness and ignoring tire saturation.

The optimization solves a quadratic programming problem minimizing a cost function containing lateral deviation, orientation, and the control signal for a prescribed prediction and control horizon. The horizons were equally chosen to be 15 steps long. The optimization can take into consideration the physical restrictions of the real system: minimum and maximum steering angle and steering rate limitations.

According to Jalali et al. (2017), latencies in the control system can be handled in MPC structures. The lane-keeping assist block contains a parameter for actuator lag to handle these as first-order elements. The measured outputs of the model predictive controller are lateral deviation and relative yaw angle. The previewed curvature of the path is given as a measured disturbance vector to make the vehicle follow the track.

The complexity of the MPC controller is given by its several parameters and weights that have a complex tuning process, as explained in Wang et al. (2019). Parameters of the reference controller were chosen by reserving the default parameters used in one of MatLab’s demos. Further tuning was executed with the updated model parameters to achieve an aperiodic setting upon disturbances in lateral position and orientation. At the end of the tuning, under nominal circumstances (no disturbances, µ = 1), the system response has similar tracking properties as the proposed controller. The tuned parameters of the MPC controller can be seen in Table 1.

Table 1 Modified parameters of the MPC controller

According to Wang et al. (2019), MPC’s optimization has an extensive calculation burden when it is executed online, so beyond performance and parameter tuning, the runtime of the MPC controller is also a critical point. The presented adaptive MPC controller can provide 50 Hz control frequency only in simulation because its computational requirements are higher than the proposed controller’s needs.

5.2 Simulation Results of the Comparison

In this subsection, two different test cases highlight the main advantages of the proposed optimization and IMC-based structure. The first case focuses on robustness against ambient parameter changes showing the advantages of using the nonlinear tire model in the IMC structure. The second case shows the benefit of yaw-rate-based control. It should be noted that none of the parts of the controllers have been modified during these tests. All tests were performed using the same controller parameters.

In Fig. 5, the comparison of the two controllers can be seen, performing lane change maneuver on low-mu. In this situation, the vehicle speed was $10\frac{m}{s}$, and the friction coefficient of the simulated model was µ = 0.12. It can be seen that the IMC controller performs better with much less control action, lateral deviation, and orientation error due to the used nonlinear tire model. The maximal diversion from the centerline for both directions using the proposed method was 0.282 m and −0.375 m, and using the MPC was 0.325 and −0.782 m, which is a significant difference.

Fig. 5

Comparison of the controllers performing lane change maneuver on low-mu

The yaw-rate-based controller has additional insight into the vehicle’s movement besides position and orientation. This way, the vehicle can react immediately to disturbances affecting the yaw-rate directly. In Fig. 6, the comparison of the two controllers can be seen for the skid-pad maneuver F = 6000 N, t = 0.2 s. Both controllers are solving the situation with two main steering movements. However, the IMC controller can react faster because it immediately perceives the disturbance that appears in yaw-rate. Its maximal lateral deviation is smaller at the end than the MPC controller’s error (−0.37 m vs. −0.63 m), which can only react to the error that appears in orientation and position.

Fig. 6

Comparison of the controllers performing skidpad maneuver

6 Experimental Results

In this section, the real-time test results are presented for the proposed controller structure. The test vehicle can be seen in Fig. 7, a Mercedes C200 limousine provided by ThyssenKrupp’s Vehicle Motion Control team. The parameters of the vehicle can be seen in Table 2.

Fig. 7

Mercedes C200 test vehicle

Table 2 Parameters of the vehicle

As it is shown in Fig. 8, the parts of the test setup are the following: DGPS provides the actual position and orientation information, and the IMU provides the values of the dynamic state variables. A real-time model runs on AutoBox with a ControlDesk interface that controls the actuator for the steering, calculates the local position and orientation based on the sensors, and communicates with the industrial PC (Nuvo-6108GC-IGN) that runs the lateral control algorithm. It took 5.127 ms to run the control algorithm on the PC. ControlDesk is also responsible for saving the measurement signals. The real-time model allows the test driver to override the control signal, so robustness against this disturbance can be tested easily. During the measurement, the test driver makes longitudinal control of the vehicle, maintaining a constant speed. Test measurements took place at Kiskunlachaza airport.

Fig. 8

Block diagram of the measurement setup: the controller runs on the Industrial PC, connected to an AutoBox that performs communication with sensors (IMU, DGPS), localization, and controls the road-wheel actuator of the vehicle

6.1 Comparing Simulation Results and Measurements

Classic straight lane following maneuver is a sterile way to examine the vehicle’s dynamic response in the measurements and the simulation. One typical test case for disturbance suppression is to examine the effects of lateral position error. In Fig. 9, the simulation and the measurements can be compared on a straight path with a $3$ meters wide step. During the maneuvers, the vehicle speed was $6.5\frac{m}{s}$. The heading sign is quite noisy due to the placement and measurement inaccuracy of the dual GPS antennas. However, the control works in a quite robust way in the presence of this noise.

Fig. 9

Comparison of the measurement and the simulation, examining the response for a lateral step disturbance

The differences between the responses are due to model mismatch of the simulation’s vehicle model and measurement noise. In general, it can be stated that the simulation and the measurement give very similar results, so the simulation can be used to test the system’s real-time operation, so the simulation results for the comparison and the skid-pad test are verified.

6.2 Control Override

The real-time environment was implemented so that the test driver could override the requested control to stop unsafe maneuvers during the testing of the autonomous system. This feature provides an opportunity to test the controller’s robustness in handling the situation when the steering angle is forced for a short time into a prescribed state, simulating unexpected disturbances.

The test was the following: during straight lane following, the test driver jerked the steering wheel for a moment, overriding the control signal requested by the controller, and then let the controller suppress the deviation.

The results can be seen in Fig. 10. During the measurement, the vehicle’s speed was $10\frac{m}{s}$. In subplot (d), the external disturbance can be detected: the override is ended when the road wheel angle starts changing in the same direction as it is requested to be changed. The delay in the requested road-wheel angle is due to the filter placed in the controller’s feedback. The controller compensated for this error with minimal effort by two steering movements: the first respond quickly and start compensating for the disturbance in the yaw-rate. The second (which is less steep) corresponds to eliminating the position and the orientation error.

Fig. 10

Experimental measurement result for control overrides compensation

7 Conclusion

In this paper, a new control framework is presented, improving robustness and yaw stability for autonomous vehicles. Vehicle lateral control is solved by a method that expands the internal model servo control with optimization- based reference generation for yaw-rate. The control rule is determined by the minimalization of the control effort to gain yaw stability. The performance of the controller was demonstrated in simulation and real-time measurements, and the results were compared with a reference controller provided by MatLab. The proposed lateral control meets the expectations set out in the objective: the controller satisfied the robustness tests performed on lo-mu, control override, and skid-pad.

Future work will expand the presented approach integrating longitudinal control to handle high longitudinal dynamics situations. Another direction is to realize the IMC structure in multi-actuator control handling steering and driving/braking torques altogether.