Abstract
We derive an extension of the Walnut–Daubechies criterion for the invertibility of frame operators. The criterion concerns general reproducing systems and Besov-type spaces. As an application, we conclude that \(L^2\) frame expansions associated with smooth and fast-decaying reproducing systems on sufficiently fine lattices extend to Besov-type spaces. This simplifies and improves recent results on the existence of atomic decompositions, which only provide a particular dual reproducing system with suitable properties. In contrast, we conclude that the \(L^2\) canonical frame expansions extend to many other function spaces, and, therefore, operations such as analyzing using the frame, thresholding the resulting coefficients, and then synthesizing using the canonical dual frame are bounded on these spaces.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Given a countable collection \((g_j)_{j \in J}\) of functions \(g_j: {\mathbb {R}}^d \rightarrow {\mathbb {C}}\) and a collection \((C_j)_{j \in J}\) of matrices \(C_j \in \mathrm {GL}(d, {\mathbb {R}})\), we consider the structured function system
and aim to represent a function or distribution f as a linear combination
In many important examples of this formalism, the functions \(g_j\) are obtained through affine transforms (in the Fourier domain) of a single function g. For instance, in dimension \(d=1\), the well-known wavelet [19] and Gabor systems [34] are obtained as
For \(d>1\), anisotropic wavelet systems provide additional important examples, see e.g., [2, 12, 47].
We are interested in the ability of (1.1) to reproduce all functions or distributions f in various function spaces by a suitably convergent series (1.2). For the Hilbert space \(L^2({\mathbb {R}}^d)\) this task is significantly easier: it amounts to establishing the frame inequalities
Indeed, the norm equivalence (1.5) means that the frame operator \(S : L^2 ({\mathbb {R}}^d) \rightarrow L^2 ({\mathbb {R}}^d)\),
is bounded and invertible on \(L^2({\mathbb {R}}^d)\), and consequently (1.2) holds with \(c_{j, \gamma } = \big \langle S^{-1} f \,\mid \, T_{\gamma } \, g_j \big \rangle \).
The validity of the frame inequalities is closely related to the covering properties of the Fourier transforms of the generating functions \(\widehat{g_j}\), which is encoded in the Calderón condition:
This connection is most apparent in the so-called painless case, in which the supports of the functions \(\widehat{g_j}\) are compact. Under this assumption, the expansion (1.2) is a local Fourier expansion
In many important cases, the functions \(g_j\) are not bandlimited, but have a well concentrated frequency profile, such as a Gaussian. Then (1.7) is an almost-local Fourier expansion, that one still expects to be governed by (1.6)—and, indeed, under mild conditions, (1.6) is necessary for (1.5) to hold [18, 30].
The formal analysis of non-painless expansions with a reproducing system (1.1) relies on a remarkable representation of the frame operator in the Fourier domain, namely
where \( t_{\alpha }(\xi )= \sum _{j \in \kappa (\alpha )} \frac{1}{|\det C_j|} \,\, \overline{{\widehat{g}}_j (\xi )} \, \widehat{g_j} (\xi + \alpha ) \); here, the translation nodes \(\Lambda \subseteq {\mathbb {R}}^d\) and indices \({\kappa (\alpha ) \subseteq J}\) are determined by the matrices \(C_j\) (see (5.2) below). For Gabor expansions, the representation (1.8) is known under the name of Walnut’s representation [63] while for wavelets it is attributed to Daubechies and Tchamitchian [19, Chapter 3]. The theory of generalized shift-invariant systems [39, 53] establishes the general form of (1.8) and exploits its many consequences. For example, tight frames—that is, systems for which equality holds in (1.5)—are characterized by a set of algebraic relations involving the functions \(t_{\alpha }\); see [39].
1.1 The Walnut–Daubechies Criterion
The multiplier \(t_0\) associated with \(\alpha =0\) in (1.8) is precisely the Calderón sum appearing in (1.6); that is,
A powerful frame criterion arises by comparing the representation of S given in (1.8) to the diagonal term \({\mathcal {F}}^{-1} (t_0 \cdot {\widehat{f}} \, )\), and by estimating the corresponding discrepancy. In the model cases of Gabor and wavelets systems, these criteria are again attached to the names of Walnut and Daubechies, and are particularly useful for studying Gaussian wave-packets, which have fast-decaying frequency tails, but do not yield tight frames. A general version of the Walnut–Daubechies criterion also holds for generalized shift-invariant systems under mild assumptions [17, 45]; this criterion is greatly useful in the construction of anisotropic time-scale decompositions—see e.g. [20].
The price to pay for the flexibility of the Walnut–Daubechies criterion is that it does not produce an explicit dual system implementing the coefficient functionals \(f \mapsto c_{j, \gamma }\) in (1.2). Rather, it only yields an \(L^2\) norm estimate which is sufficient to establish (1.5) but does not imply the convergence of (1.8) in other norms. In contrast, explicit constructions of frame pairs, that is, frames where the coefficient functionals are given by
for another reproducing system \(\{h_j: j \in J\}\), naturally extend to many other Banach spaces besides \(L^2({\mathbb {R}}^d)\). These spaces are determined by the concentration of the Fourier support of the generators \(g_j\), and are generically called Besov-type spaces [56, Chapter 2] [58]. The model case is given by (1.3), where the functions \(\widehat{g_j}\) form a so-called Littlewood-Paley decomposition.
The goal of this article is to derive a variant of the Walnut–Daubechies criterion which implies that the frame operator is invertible in such Besov-type spaces.
1.2 Besov-Type Decomposition Spaces
For the informal definition of Besov-type spaces, fix a cover \({\mathcal {Q}}= (Q_i)_{i \in I}\) of a full measure open subset in the Fourier domain \(\widehat{{\mathbb {R}}}^d\). We impose a mild admissibility condition by limiting the number of overlaps between different elements of \({\mathcal {Q}}\)—see Section 3 for the precise condition. Given a suitable partition of unity \((\varphi _i)_{i \in I}\) subordinate to \({\mathcal {Q}}\), together with a suitable (so-called \({\mathcal {Q}}\)-moderate) weight function \(w : I \rightarrow (0,\infty )\), the space \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\), for \(p, q \in [1,\infty ]\), is defined as the space of distributions f satisfying
where \({\mathcal {F}}^{-1}\) denotes the inverse Fourier transform. Provided that an adequate notion of distribution is used in the definitions, the spaces \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) form Banach spaces and are independent of the particular (sufficiently regular) partition of unity used to define them.
The construction of Besov-type spaces follows the so-called decomposition method [56, Chapter 2], [58, Section 1.2], yielding an instance of the so-called spaces defined by decomposition methods [55], or decomposition spaces [23, 57] in more abstract settings. This is why we also use the term Besov-type decomposition spaces. Uniform Besov-type spaces, associated with the cover \({\mathcal {Q}}\) consisting of integer translates of a cube, are known as modulation spaces [22], while a dyadic frequency cover yields the usual Besov spaces [27, 49] —see also [56, Section 2.2]. When the cover is generated by powers of an expansive matrix, one obtains anisotropic Besov spaces [8, 12, 13, 56]. We remark that the range of spaces defined by (1.9) does not include Triebel-Lizorkin spaces [28].
1.3 Overview of the Results
We state a simplified version of our main results for systems of the form (1.1) with generating functions \(g_j \in L^1 ({\mathbb {R}}^d) \cap L^2 ({\mathbb {R}}^d)\) with \({\widehat{g}} \in C^{\infty } (\widehat{{\mathbb {R}}}^d)\), given by
for (invertible) affine maps \(S_j = A_j (\cdot ) + b_j\) and translation matrices \(C_j = \delta A_j^{-t}\) with \(\delta > 0\). The parameter \(\delta >0\) is a resolution parameter that controls the density of the translation nodes in (1.1).
To define Besov-type spaces adapted to the frequency concentration of the system \((g_j)_{j \in J}\), we also consider an affinely generated cover \({\mathcal {Q}}= (Q_j)_{j \in J}\) of the form \(Q_j = A_j Q + b_j\). If \({\widehat{g}}\) is mostly concentrated inside the basic set Q, then (1.10) implies that \(\widehat{g_j}\) is localized around \(Q_j\). Under these assumptions, the Calderón condition reads
which means that \((\widehat{g_j})_{j \in J}\) is approximately a partition of unity adapted to \({\mathcal {Q}}\).
The following is our main result, proved in Section 7.3.
Theorem 1.1
For each affinely generated cover \({\mathcal {Q}}= (A_j Q + b_j)_{j \in J} = (S_j Q)_{j \in J}\) of an open, co-null set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\), and each \({\mathcal {Q}}\)-moderate weight \(w = (w_j)_{j \in J}\), there exists a constant \(C_{d,{\mathcal {Q}},w}\) with the following property: Suppose that \((g_j)_{j \in J}\) is compatible with \({\mathcal {Q}}\) in the sense of (1.10) and that the Calderón condition (1.11) holds. Moreover, suppose that
and that \( M_1 := \max \big \{ \sup _{i \in J} \sum _{j \in J} M_{i,j},\; \sup _{j \in J} \sum _{i \in J} M_{i,j} \big \} < \infty \), where
and \( L_{i,j} := \max \big \{ \frac{w_i}{w_j}, \frac{w_j}{w_i} \big \} \cdot \big ( \max \{ 1, \Vert A_i^{-1} A_j\Vert ^2 \} \, \max \{ 1, \Vert A_j^{-1} A_i\Vert ^3 \} \big )^{d+1} \) for \(i,j \in J\). Choose \(\delta > 0\) such that
Then the frame operator associated to \((T_{\delta A_j^{-t} k} \, g_j)_{j \in J, k \in {\mathbb {Z}}^d}\) is well-defined, bounded, and invertible on \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) for all \(p,q \in [1,\infty ]\). The value of the constant \(C_{d,{\mathcal {Q}},w}\) is given in Theorem 7.5 below.
The quantities \(M_0\) and \(M_1\) in Theorem 1.1 control the interaction between the generators \(g_j\) and the elements of the cover \({\mathcal {Q}}\). In contrast to the classical \(L^2\) Walnut–Daubechies criterion, the derivatives of \({\widehat{g}}\) are now involved. We also prove a more technical version of Theorem 1.1 in which the generators need not exactly be affine images (in the Fourier domain) of a single function, but only approximately so. This is important, for example, to describe non-homogeneous time-scale systems, which contain a low-pass and a high-pass window. We refer the reader to [62] for a detailed discussion of concrete examples and calculations that can be used also in our framework.
Although the constant \(C_{d,{\mathcal {Q}}, w}\) in Theorem 1.1 is explicit, it is too large to be used as a guide for concrete numerical implementations. We also derive a version of the criterion with more favorable constants, but which only provides expansions on \(L^2\)-based Besov-type spaces; see Sect. 5.5.
A result closely related to Theorem 1.1 was recently obtained by the third named author in [62]—see the discussion below. While our techniques are significantly different from those in [62]—and, indeed, we regard the simplicity of the present methods a main contribution—we remark that we make use of several auxiliary results obtained in [62].
Under the conditions of Theorem 1.1, the coefficient and reconstruction operators
define bounded operators between the Besov-type space \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) and suitable sequence spaces (see Sect. 4). As a consequence, the invertibility of the frame operator on the spaces \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) implies that the \(L^2\)-convergent canonical frame expansions
extend to series convergent in Besov-type norms (or weak-\(*\)-convergent for \(p=\infty \) or \(q=\infty \)). In more technical terms, the canonical Hilbert-space dual frame \(\{ S^{-1} T_{\gamma } \, g_j: j \in J, \gamma \in C_j {\mathbb {Z}}^d\}\) provides a Banach frame and an atomic decomposition for the Besov-type spaces \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\). This is a novel feature of Theorem 1.1: other results on the existence of series expansions, based on so-called oscillation estimates, show that the coefficient and reconstruction maps (1.12) are respectively left and right invertible on the Besov-type spaces, but do not yield consequences for the Hilbert space pseudo-inverses \({\mathscr {C}}^\dagger = S^{-1} {\mathscr {D}}\) and \({\mathscr {D}}^\dagger ={\mathscr {C}}S^{-1}\) [24, 33, 62]. In contrast, Theorem 1.1 concerns \({\mathscr {C}}^\dagger , {\mathscr {D}}^\dagger \)— see Corollary 7.6—and implies that operations on the canonical frame expansions (1.13) that decrease the magnitude of the coefficients, such as thresholding, are uniformly bounded in Besov-type norms. More precisely, if for each \(j \in J\) and \(\gamma \in C_j {\mathbb {Z}}^d\), we are given a function \(\Phi _{j,\gamma } : {\mathbb {C}}\rightarrow {\mathbb {C}}\) satisfying \(|\Phi _{j,\gamma } (x)| \le C \, |x|\), then the maps
and
are bounded (possibly non-linear) operators on all of the spaces \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\). In particular, frame multipliers with bounded symbols—see e.g. [7]—define bounded operators on Besov-type spaces.
1.4 Related Work
The theory of localized frames. The uniform frequency cover \(\{(-1,1)^d + k: k \in {\mathbb {Z}}^d\}\)—which gives rise to Gabor systems (1.4)—is special in that every reproducing system (1.1) satisfying the frame inequalities (1.5), and mild smoothness and decay conditions, provides also expansions for other Banach spaces (the precise range of spaces being determined by the particular smoothness and decay of the generators). Indeed, the theory of localized frames [4, 5, 35] implies that the frame operator is invertible on modulation spaces. Similar results hold for \(L^p\) spaces [6, 43]. Thus, in these cases, the classical Walnut–Daubechies criterion has consequences for Banach spaces besides \(L^2\)—without having to adjust the density \(\delta \)—and Theorem 1.1 does not add anything interesting.
The key tool of the theory of localized frames is the spectral invariance of certain matrix algebras. Such tools are not applicable to general admissible covers as considered in this article. Indeed, it is known that the frame operator associated with certain smooth and fast-decaying wavelets with several vanishing moments fails to be invertible on \(L^p\)-spaces [46, Chapter 4]. In connection to this point, we mention that the Mexican hat wavelet satisfies Daubechies criterion, but the validity of the corresponding \(L^p\) expansions was established only recently with significant ad-hoc work [15].
Almost painless generators and homogeneous covers. There is a well-developed literature related to the so-called painless expansions on decomposition spaces. The first construction of Banach frames for general decomposition spaces was given by Borup and Nielsen [11] using bandlimited generators. This construction was then complemented with a delicate perturbation argument to produce compactly supported frames [48]—see also [16, 44]. The constructions in [48] for Besov-type spaces are restricted to so-called homogeneous covers, which are generated by applying integer powers of a matrix to a given set. This restriction rules out some important examples such as inhomogeneous dyadic covers and many popular wavepacket systems.
Invertibility of the frame operator versus existence of left and right inverses. The first construction of time-scale decompositions proceeded by discretizing Calderón’s reproducing formula through Riemann-like sums [29]. A similar approach works for the voice transform associated with any integrable unitary representation and is the basis of the so-called coorbit theory [24]. To some extent, those techniques extend to any integral transform, provided that one can control its modulus of continuity [38]. Such an approach was used by the third named author to construct compactly supported Banach frames and atomic decompositions in Besov-type spaces [62]. The main result of [62] is qualitatively similar to Theorem 1.1, but only concludes the existence of left and right inverses for the coefficient and synthesis maps, acting on respective Banach spaces. In contrast, we show that the Hilbert space frame operator is simultaneously invertible on all the relevant Banach spaces. The advantage of the present approach is that we are able to show that the Hilbert spaces series—which are defined by minimizing the \(\ell ^2\) norm of the coefficients in (1.2)—extend to series convergent in Besov-type spaces, and thus many operations on the canonical frame expansion are also shown to be bounded in Besov-type spaces. On the other hand, there are situations in which there exists a left inverse for the coefficient operator (or a right inverse for the reconstruction operator), but the frame operator is not invertible. For example, a wavelet system generated by a smooth mother wavelet without vanishing moments can generate an atomic decomposition for the Besov spaces \(B^s_{p,q}({\mathbb {R}}^d)\) of strictly positive smoothness \(s > 0\) without yielding a frame [62, Proposition 8.4]. Such examples are not covered by our results.
Quasi-Banach spaces. We do not treat the quasi-Banach range \(p,q \in (0,\infty ]\), which is treated in [62]. We expect the tools developed in [62] for treating the quasi-Banach range to be also applicable to the present setting, and to yield an extension of our main results to the quasi-Banach range.
1.5 Technical Overview and Organization
Our approach is as follows: we consider the Walnut–Daubechies representation (1.8) of the frame operator and bound the discrepancy between Sf and the diagonal term \({\mathcal {F}}^{-1} \big (t_0 \cdot {\widehat{f}} \, \big )\) in a Besov-type norm. To this end, we estimate each Fourier multiplier \(t_\alpha \) with a Sobolev embedding, and control the inverse Fourier multiplier \({1}/{t_0}\) by directly bounding the terms in Faà di Bruno’s formula.
The main estimates are derived in decreasing level of generality. We first consider very general covers \({\mathcal {Q}}= (Q_i)_{i \in I}\) and an abstract notion of molecule, which models the interaction between the generators \(g_j\) of the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) and the elements \(Q_i\) of the cover \({\mathcal {Q}}\). Here, the associated index sets I and J do not need to coincide. We then provide simplified estimates for affinely generated covers. The limiting cases \(p,q = \infty \) involve delicate approximation arguments that may be of independent interest.
The paper is organized as follows: Sect. 2 introduces notation and preliminaries. Besov-type spaces are introduced in Sect. 3. Section 4 treats the boundedness of the coefficient, synthesis and frame operators on suitable spaces. Section 5 is concerned with the invertibility of the frame operator and provides estimates for the abstract Walnut–Daubechies criterion. These estimates are further simplified in Sects. 6 and 7 for affinely generated covers and suitably adapted generating functions. Several technical results are deferred to the appendices.
2 Notation and Preliminaries
2.1 General Notation
We let \({\mathbb {N}}:= \{1,2,3,\dots \}\), and \({\mathbb {N}}_0 := {\mathbb {N}}\cup \{0\}\). For \(n \in {\mathbb {N}}_0\), we write \({{\underline{n}} := \{1, ..., n\}}\); in particular, \({\underline{0}} = \emptyset \). For a multi-index \(\beta \in {\mathbb {N}}_0^d\), its length is \({|\beta | = \sum _{i = 1}^d |\beta _i|}\).
The conjugate exponent \(p'\) of \(p \in (1,\infty )\) is defined as \(p' := \frac{p}{p-1}\). We let \(1' := \infty \) and \(\infty ' := 1\).
Given two functions \(f, g : X \rightarrow [0,\infty )\), we write \(f \lesssim g\) provided that there exists a constant \(C > 0\) such that \(f(x) \le C g(x)\) for all \(x \in X\). We write \(f \asymp g\) for \(f \lesssim g\) and \(g \lesssim f\).
The dot product of \(x, y \in {\mathbb {R}}^d\) is written \(x \cdot y := \sum _{i = 1}^d x_i \, y_i\). The Euclidean norm of a vector \(x \in {\mathbb {R}}^d\) is denoted by \(|x| := \sqrt{x \cdot x}\). The open Euclidean ball, with radius \(r > 0\) and center \(x \in {\mathbb {R}}^d\), is denoted by \(B_r (x)\), and the corresponding closed ball is denoted by \(\overline{B_r}(x)\). More generally, the closure of a set \(M \subseteq {\mathbb {R}}^d\) is denoted by \({\overline{M}}\).
The cardinality of a set X will be denoted by \(|X| \in {\mathbb {N}}_0 \cup \{\infty \}\). The Lebesgue measure of a Borel measurable set \(E \subset {\mathbb {R}}^d\) will be denoted by \(\lambda (E)\). Given a subset \(M \subset X\), we define its indicator function \({\mathbb {1}}_M : X \rightarrow \{0,1\}\) by requiring \({\mathbb {1}}_M (x) = 1\) if \(x \in M\) and \({\mathbb {1}}_M (x) = 0\) otherwise.
For a matrix \(M \in {\mathbb {C}}^{I \times J}\), its Schur norm is defined as
A matrix \(M \in {\mathbb {C}}^{I \times J}\) satisfying \(\Vert M \Vert _{\mathrm {Schur}} < \infty \) is said to be of Schur-type. A Schur-type matrix \(M \in {\mathbb {C}}^{I \times J}\) induces a bounded linear operator \( \mathbf{M } : \ell ^p (J) \rightarrow \ell ^p (I), \; (c_j)_{j \in J} \mapsto \big (\sum _{j \in J} M_{i,j} c_j \big )_{i \in I} \), with \(\Vert \mathbf{M }\Vert _{\ell ^p \rightarrow \ell ^p} \le \Vert M \Vert _{\mathrm {Schur}}\) for all \(p \in [1,\infty ]\); this is called Schur’s test. For a proof of a (weighted) version of Schur’s test, cf. [37, Lemma 4].
2.2 Fourier Analysis
The translate of \(f : {\mathbb {R}}^d \rightarrow {\mathbb {C}}\) by \(y \in {\mathbb {R}}^d\) is denoted by \(T_{y} \, f (x) = f(x - y)\). We denote by \(\widehat{{\mathbb {R}}}^d\) the Fourier domain of \({\mathbb {R}}^d\). Modulation of \(f : {\mathbb {R}}^d \rightarrow {\mathbb {C}}\) by \(\xi \in \widehat{{\mathbb {R}}}^d\) is denoted by \(M_{\xi } f (x) := e^{2 \pi i \xi \cdot x} f(x) \). The Fourier transform \({\mathcal {F}}: L^1 ({\mathbb {R}}^d) \rightarrow C_0 (\widehat{{\mathbb {R}}}^d), \; f \mapsto {\widehat{f}}\) is normalized as
for \(\xi \in \widehat{{\mathbb {R}}}^d\). Similarly normalized, we define \({\mathcal {F}}: L^1 (\widehat{{\mathbb {R}}}^d) \rightarrow C_0({\mathbb {R}}^d)\). The inverse Fourier transform \({\mathcal {F}}^{-1}f := {\widehat{f}}(- \cdot ) \in C_0 ({\mathbb {R}}^d)\) of \(f \in L^1 (\widehat{{\mathbb {R}}}^d)\) will occasionally also be denoted by  . Similar notation will be used for the (unitary) Fourier-Plancherel transform \({\mathcal {F}} : L^2 ({\mathbb {R}}^d) \rightarrow L^2 (\widehat{{\mathbb {R}}}^d)\).
. Similar notation will be used for the (unitary) Fourier-Plancherel transform \({\mathcal {F}} : L^2 ({\mathbb {R}}^d) \rightarrow L^2 (\widehat{{\mathbb {R}}}^d)\).
The test space of compactly supported, smooth functions on an open set \({\mathcal {O}}\subset {\mathbb {R}}^d\) will be denoted by \(C_c^{\infty } ({\mathcal {O}})\). The topology on \(C_c^{\infty } ({\mathcal {O}})\) is taken to be the usual topology defined through the inductive limit of Fréchet spaces; see [54, Sect. 6.2] for the details. The sesquilinear dual pairing between \({\mathcal {D}}({\mathcal {O}}) := C_c^\infty ({\mathcal {O}})\) and its dual \({\mathcal {D}}'({\mathcal {O}})\) is given by \( \langle f \mid g \rangle _{{\mathcal {D}}', {\mathcal {D}}} := f ({\overline{g}}) \) for \(f \in {\mathcal {D}}'({\mathcal {O}})\) and \(g \in C_c^{\infty } ({\mathcal {O}})\).
The Schwartz space is denoted by \({\mathcal {S}}({\mathbb {R}}^d)\) and its topological dual will be denoted by \({\mathcal {S}}' ({\mathbb {R}}^d)\). The canonical extension of the Fourier transform to \({\mathcal {S}}'({\mathbb {R}}^d)\) is denoted by \({\mathcal {F}}: {\mathcal {S}}' ({\mathbb {R}}^d) \rightarrow {\mathcal {S}}' (\widehat{{\mathbb {R}}}^d)\), that is, \(\langle {\mathcal {F}}f ,\, g \rangle _{{\mathcal {S}}', {\mathcal {S}}} = \langle f ,\, {\mathcal {F}}g \rangle _{{\mathcal {S}}',{\mathcal {S}}}\) for \(f \in {\mathcal {S}}'({\mathbb {R}}^d)\) and \(g \in {\mathcal {S}}(\widehat{{\mathbb {R}}}^d)\). We denote bilinear dual pairings by \(\langle \cdot ,\cdot \rangle \), while \(\langle \cdot \mid \cdot \rangle \) denotes a sesquilinear dual pairing, which is anti-linear in the second component.
Lastly, for \(p \in [1,\infty ]\) we define \({\mathcal {F}}L^p ({\mathbb {R}}^d) := \{ {\widehat{f}} :f \in L^p ({\mathbb {R}}^d) \} \subset {\mathcal {S}}' (\widehat{{\mathbb {R}}}^d)\), equipped with the norm \({\Vert f\Vert _{{\mathcal {F}}L^p} := \Vert {\mathcal {F}}^{-1} f\Vert _{L^p}}\). Here, note that \(\Vert f \cdot g\Vert _{{\mathcal {F}}L^p} \le \Vert f\Vert _{{\mathcal {F}}L^1} \cdot \Vert g\Vert _{{\mathcal {F}}L^p}\), where the exact nature of the product \(f \cdot g\) is explained in more detail in Definition 5.5. Furthermore, for any invertible affine-linear map \(S : \widehat{{\mathbb {R}}}^d \rightarrow \widehat{{\mathbb {R}}}^d\), one has \(\Vert f \circ S\Vert _{{\mathcal {F}}L^1} = \Vert f\Vert _{{\mathcal {F}}L^1}\).
2.3 Amalgam Spaces
Let \(U \subset {\mathbb {R}}^d\) be a bounded Borel set with non-empty interior. The Amalgam space \(W_U (L^{\infty }, L^1)\) is the space of all \(f \in L^{\infty } ({\mathbb {R}}^d)\) satisfying
The (closed) subspace of \(W_U (L^{\infty } \!,\! L^1)\) consisting of continuous functions is denoted \(W_U(C_0, L^1)\).
The space \(W (L^\infty , L^1) := W_U (L^\infty , L^1)\) is independent of the choice of U, with equivalent norms for different choices. In particular, if \(A \in \mathrm {GL}({\mathbb {R}}^d)\), then
an identity that will be used repeatedly. It is readily seen that the space \(W_U (L^{\infty }, L^1)\) is an \(L^1\)-convolution module; that is, if \(f \in L^1 ({\mathbb {R}}^d)\) and \(g \in W_U (L^{\infty }, L^1)\), then the product \(f *g \in W_U (L^{\infty }, L^1)\), with \(\Vert f *g \Vert _{W_U (L^{\infty }, L^1)} \le \Vert f\Vert _{L^1} \Vert g\Vert _{W_U(L^{\infty }, L^1)}\), simply because of \(\Vert f *g\Vert _{L^\infty (U + x)} \le \big ( |f| *[y \mapsto \Vert g\Vert _{L^\infty (U + y)}] \big ) (x)\).
Lastly, there is an equivalent discrete norm on \(W(L^{\infty }, L^1)\), namely
The global component in this norm is denoted by \(\ell ^1\) rather than \(L^1\) to distinguish it from \(\Vert \cdot \Vert _{W_U (L^{\infty }, L^1)}\). The norm \(\Vert \cdot \Vert _{W(C_0, \ell ^1)}\) is simply the restriction of \(\Vert \cdot \Vert _{W(L^{\infty }, \ell ^1)}\) to \(W_U(C_0, L^1)\).
The reader is referred to [26, 40] for background on amalgam spaces and to [21] for a far-reaching generalization that includes the combination of smoothness and decay conditions.
3 Besov-Type Spaces
This section introduces decomposition spaces, and related notions such as covers, weights and bounded admissible partitions of unity (BAPUs).
3.1 Covers and BAPUs
Definition 3.1
Let \({\mathcal {O}}\ne \emptyset \) be an open subset of \(\widehat{{\mathbb {R}}}^d\). A family \({\mathcal {Q}}= (Q_i)_{i \in I}\) of subsets \(Q_i \subset {\mathcal {O}}\) is called an admissible cover of \({\mathcal {O}}\) if
-
(i)
\({\mathcal {Q}}\) is a cover of \({\mathcal {O}}\), that is, \({\mathcal {O}}= \bigcup _{i \in I} Q_i\);
-
(ii)
\(Q_i \ne \emptyset \) for all \(i \in I\);
-
(iii)
\(N_{{\mathcal {Q}}} := \sup _{i \in I} |i^*| < \infty \), where \(i^* := \{ \ell \in I \; : \; Q_{\ell } \cap Q_i \ne \emptyset \}\) for \(i \in I\).
A sequence \(w = (w_i)_{i \in I}\) in \((0,\infty )\) is called a \({\mathcal {Q}}\)-moderate weight if
For a weight \(w = (w_i)_{i \in I}\) in \((0,\infty )\) and an exponent \(q \in [1, \infty ]\), we define
The significance of a \({\mathcal {Q}}\)-moderate weight is that the associated \({\mathcal {Q}}\)-clustering map is well-defined and bounded. The precise statement is as follows; see [61, Lemma 4.13].
Lemma 3.2
Let \(q \in [1,\infty ]\). Suppose that \({\mathcal {Q}}= (Q_i)_{i \in I}\) is an admissible cover of an open subset \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) and that the weight \(w = (w_i)_{i \in I}\) is \({\mathcal {Q}}\)-moderate. Then the \({\mathcal {Q}}\)-clustering map
where \( c_i^*:= \sum _{\ell \in i^*} c_\ell \, , \) is well-defined and bounded, with \(\Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell ^q_w \rightarrow \ell ^q_w} \le C_{w,{\mathcal {Q}}} \cdot N_{{\mathcal {Q}}}\).
The next definition clarifies our assumptions regarding the partitions of unity that are suitable for defining the decomposition space norm.
Definition 3.3
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be an admissible cover of an open subset \(\emptyset \ne {\mathcal {O}} \subset \widehat{{\mathbb {R}}}^d\). A family \({\Phi = (\varphi _i )_{i \in I}}\) is called a bounded admissible partition of unity (BAPU), subordinate to \({\mathcal {Q}}\), if
-
(i)
\(\varphi _i \in C_c^{\infty } ({\mathcal {O}}) \subset {\mathcal {S}}(\widehat{{\mathbb {R}}}^d)\) for all \(i \in I\);
-
(ii)
\(\sum _{i \in I} \varphi _i (\xi ) = 1\) for all \(\xi \in {\mathcal {O}}\);
-
(iii)
\(\varphi _i (\xi ) = 0\) for all \(\xi \in {\mathcal {O}}\setminus Q_i\) and all \(i \in I\);
-
(iv)
\(C_{\Phi } := \sup _{i \in I} \Vert {\mathcal {F}}^{-1} \varphi _i \Vert _{L^1} < \infty \).
The cover \({\mathcal {Q}}\) is called a decomposition cover if there exists a BAPU subordinate to \({\mathcal {Q}}\).
Given a decomposition cover \({\mathcal {Q}}= (Q_i)_{i \in I}\) of an open set \(\emptyset \ne {\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\), it will be assumed throughout this article that a BAPU \(\Phi = (\varphi _{i})_{i \in I}\) for \({\mathcal {Q}}= (Q_i)_{i \in I}\) is fixed.
Definition 3.4
Let \({\mathcal {O}} \ne \emptyset \) be an open subset of \(\widehat{{\mathbb {R}}}^d\). A family \({\mathcal {Q}}= (Q_i)_{i \in I}\) of subsets \(Q_i \subset {\mathcal {O}}\) is called an affinely generated cover of \({\mathcal {O}}\) if, for each \(i \in I\), there are \(A_i \in \mathrm {GL}(d, {\mathbb {R}})\) and \(b_i \in \widehat{{\mathbb {R}}}^d\) and an open subset \(Q'_i \subset \widehat{{\mathbb {R}}}^d\) with \(Q_i = A_i \, (Q'_i) + b_i\) satisfying the following:
-
(i)
\({\mathcal {Q}}\) is an admissible cover of \({\mathcal {O}}\);
-
(ii)
the sets \((Q'_i)_{i \in I}\) are uniformly bounded, that is,
$$\begin{aligned} R_{{\mathcal {Q}}} := \sup _{i \in I} \sup _{\xi \in Q'_i} |\xi | < \infty \, ; \end{aligned}$$ -
(iii)
for indices \(i, \ell \in I\) with \(Q_i \cap Q_\ell \ne \emptyset \), the transformations \(A_i (\cdot ) + b_i\) and \(A_{\ell } (\cdot ) + b_{\ell }\) are uniformly compatible, that is,
$$\begin{aligned} C_{{\mathcal {Q}}} := \sup _{i \in I} \sup _{\ell \in i^*} \Vert A_i^{-1} A_{\ell } \Vert < \infty ; \end{aligned}$$
and moreover, for each \(i \in I\), there is an open set \(Q''_i \subset \widehat{{\mathbb {R}}}^d\) such that
-
(iv)
the closure \(\overline{Q''_i} \subset Q'_i\) for all \(i \in I\);
-
(v)
the family \((A_i ( Q''_i) + b_i)_{i \in I}\) covers \({\mathcal {O}}\); and
-
(vi)
the sets \(\{Q'_i \,:\,i \in I \}\) and \(\{Q''_i \,:\,i \in I\}\) are finite.
Remark 3.5
An affinely generated cover is also called an (almost) structured cover in the literature, see for instance [61] and [11] for similar notions.
In the sequel, the map \(S_i : \widehat{{\mathbb {R}}}^d \rightarrow \widehat{{\mathbb {R}}}^d\) will always denote an affine linear mapping \(\xi \mapsto A_i \, \xi + b_i\) for some \(A_i \in \mathrm {GL}(d,{\mathbb {R}})\) and \(b_i \in \widehat{{\mathbb {R}}}^d\).
Definition 3.6
Let \({\mathcal {Q}}= \big (S_i (Q_{ i}')\big )_{i \in I}\) be an affinely generated cover of \({\mathcal {O}}\), and let \(\Phi = (\varphi _i)_{i \in I}\) be a smooth partition of unity subordinate to \({\mathcal {Q}}\). For \(i \in I\), define the normalization of \(\varphi _i\) by \(\varphi ^{\flat }_i := \varphi _i \circ S_i\). The family \(\Phi = (\varphi _i)_{i \in I}\) is called a regular partition of unity, subordinate to \({\mathcal {Q}}\), if
for all multi-indices \(\alpha \in {\mathbb {N}}_0^d\).
The following result shows that every affinely generated cover is a decomposition cover.
Proposition 3.7
([60, Corollary 2.7 and Theorem 2.8]) Let \({\mathcal {Q}}= \big (S_i (Q_{ i}')\big )_{i \in I}\) be an affinely generated cover of \({\mathcal {O}}\). Then, the following hold:
-
(1)
Every regular partition of unity \(\Phi \) subordinate to \({\mathcal {Q}}\) is also a BAPU subordinate to \({\mathcal {Q}}\).
-
(2)
There exists a regular partition of unity \(\Phi = (\varphi _i)_{i \in I}\) subordinate to \({\mathcal {Q}}\).
3.2 Besov-Type Spaces
We introduce Besov-type spaces following the approach in [56], which relies on the space of Fourier distributions. Since we only treat the Besov-type scale of spaces, we allow for rather general covers. More restrictions would be necessary to include the Triebel-Lizorkin scale, because the corresponding theory relies on inequalities for maximal functions; see [55, Sect. 3.6], [56, Sect. 2.4.3], and also [47].
Definition 3.8
Let \({\mathcal {O}} \ne \emptyset \) be open in \({\widehat{{\mathbb {R}}}}^d\). The space \( Z ({\mathcal {O}}) := {\mathcal {F}}(C_c^{\infty } ({\mathcal {O}})) \) is called the Fourier test function space on \({\mathcal {O}}\). The space \(Z ({\mathcal {O}})\) is endowed with the unique topology making the Fourier transform \({\mathcal {F}}: C_c^{\infty } ({\mathcal {O}}) \rightarrow Z({\mathcal {O}})\) into a homeomorphism.
The topological dual space \((Z ({\mathcal {O}}))'\) of \(Z ({\mathcal {O}})\) is denoted by \(Z' ({\mathcal {O}})\) and is called the space of Fourier distributions. The (bilinear) dual pairing between \(Z'({\mathcal {O}})\) and \(Z({\mathcal {O}})\) will be denoted by \( \langle \phi , f \rangle _{Z', Z} := \langle \phi , f \rangle _{Z'} := \langle \phi , f \rangle := \phi (f) \) for \(\phi \in Z'({\mathcal {O}})\) and \(f \in Z({\mathcal {O}})\).
The Fourier transform \(\phi \in {\mathcal {D}}'({\mathcal {O}})\) of a Fourier distribution \(\phi \in Z'({\mathcal {O}})\) is defined by duality; i.e.,
which entails \( \langle {\mathcal {F}}\phi , f \rangle _{{\mathcal {D}}', {\mathcal {D}}} = \langle \phi , {\mathcal {F}}f \rangle _{Z', Z} \) for \( \phi \in Z'({\mathcal {O}}\)) and \(f \in C_c^{\infty } ({\mathcal {O}})\).
Using the Fourier distributions as a reservoir, a decomposition space is defined as follows:
Definition 3.9
Let \(p, q \in [1, \infty ]\). Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \(\emptyset \ne {\mathcal {O}}\subset {\widehat{{\mathbb {R}}}}^d\) with associated BAPU \((\varphi _i)_{i \in I}\). Let \(w = (w_i)_{i \in I}\) be \({\mathcal {Q}}\)-moderate. For \(f \in Z' ({\mathcal {O}})\), set
and define the associated decomposition space \({\mathcal {D}}({\mathcal {Q}},L^p,\ell ^q_w)\) as
Remark 3.10
The norm (3.2) is well-defined: If \(f \in Z'({\mathcal {O}})\), then \({\widehat{f}} \in {\mathcal {D}}'({\mathcal {O}})\), whence \(\varphi _i \cdot {\widehat{f}}\) is a (tempered) distribution with compact support. By the Paley-Wiener theorem [54, Theorem 7.23], it follows therefore that \({\mathcal {F}}^{-1}(\varphi _i \cdot {\widehat{f}} \,)\) is given by a smooth function. In addition, \({\mathcal {D}}({\mathcal {Q}}, L^p, \ell ^q_w)\) is a Banach space and independent of the choice of the BAPU \((\varphi _i)_{i \in I}\), with equivalent norms for different choices; see [61, Corollary 3.18 and Theorem 3.21].
Remark 3.11
Our presentation follows [61, 62] and relies on the original approach of [56, 58], specially in the use of Fourier distributions, which is essential for the more technical aspects of our results. More abstract versions of Besov-type spaces replace the Fourier transform by an adequate symmetric operator [57] or use a more general Banach space of functions on a locally compact space in lieu of the Fourier image of \(L^p\) [23]. This latter (far reaching) generalization is particularly useful to model signal processing applications, such as sampling.
In the sequel, we will often prove our results on the subspace \( {\mathcal {S}}_{{\mathcal {O}}} ({\mathbb {R}}^d) := {\mathcal {F}}^{-1} (C_c^\infty ({\mathcal {O}})) \subset {\mathcal {S}}({\mathbb {R}}^d) \) of the space \({\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\), and then extend to all of \({\mathcal {D}} ({\mathcal {Q}}, L^p, \ell ^q_w)\) by a suitable density argument. These density arguments rely on the following concept.
Definition 3.12
Let I be an index set, and let \(w = (w_i)_{i \in I}\) be a weight. For a sequence \(F = (F_i)_{i \in I}\) of functions \(F_i \in L^p ({\mathbb {R}}^d)\), we write \( \Vert F\Vert _{\ell _w^q(I; L^p)} := \big \Vert (\Vert F_i\Vert _{L^p})_{i \in I} \big \Vert _{\ell _w^q} \in [0,\infty ] \), and set
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) with BAPU \(\Phi = (\varphi _i)_{i \in I}\), and let \(F = (F_i)_{i \in I}\) be a family of functions \(F_i : {\mathbb {R}}^d \rightarrow [0,\infty )\). A Fourier distribution \(f \in Z'({\mathcal {O}})\) is said to be \((F,\Phi )\)-dominated if, for all \(i \in I\),
We next state our density result; its proof is postponed to Appendix B.
Proposition 3.13
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \(\emptyset \ne {\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) with BAPU \(\Phi = (\varphi _i)_{i \in I}\) and let \(w = (w_i)_{i \in I}\) be a \({\mathcal {Q}}\)-moderate weight. Then
-
(i)
The inclusion \({\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d) \subset {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\) holds for all \(p,q \in [1,\infty ]\).
-
(ii)
If \(p,q \in [1,\infty )\), then \({\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) is norm dense in \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\).
-
(iii)
If \(p,q \in [1,\infty ]\) and \(f \in {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\), then there exist \(F \in \ell _w^q (I; L^p)\) satisfying
$$\begin{aligned} \Vert F\Vert _{\ell _w^q(I; L^p)} \le C_\Phi \, \Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell _w^q \rightarrow \ell _w^q}^2 \cdot \Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)}, \end{aligned}$$and a sequence \((g_n)_{n \in {\mathbb {N}}}\) of \((F, \Phi )\)-dominated functions \(g_n \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) such that \(g_n \rightarrow f\), with convergence in \(Z' ({\mathcal {O}})\).
Remark 3.14
The inclusion \({\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d) \subset {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\subset Z'({\mathcal {O}})\) in Proposition 3.13(i) should be understood in the following sense: Clearly \({\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d) \subset {\mathcal {S}}({\mathbb {R}}^d) \hookrightarrow {\mathcal {S}}'({\mathbb {R}}^d)\), where as usual a function \(f \in {\mathcal {S}}({\mathbb {R}}^d)\) is identified with the distribution \(\phi \mapsto \int f \cdot \phi \, dx\). But since \(Z({\mathcal {O}}) \hookrightarrow {\mathcal {S}}({\mathbb {R}}^d)\), each \(f \in {\mathcal {S}}' ({\mathbb {R}}^d)\) restricts to an element of \(Z'({\mathcal {O}})\); in particular, each \(f \in {\mathcal {S}}_{{\mathcal {O}}}\) can be seen as an element of \(Z'({\mathcal {O}})\) by virtue of \(\langle f, \phi \rangle _{Z',Z} = \int f \cdot \phi \, dx\). Under this identification, the Fourier transform \({\mathcal {F}}f \in {\mathcal {D}}'({\mathcal {O}})\) is just the usual \({\widehat{f}} \in {\mathcal {S}}(\widehat{{\mathbb {R}}}^d)\), interpreted as a distribution on \({\mathcal {O}}\).
As a companion to the above density result, the following Fatou property of the decomposition spaces \({\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\) will be used. For the proof, see [31, Lemma 36].
Lemma 3.15
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \(\emptyset \ne {\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\). Let \({w = (w_i)_{i \in I}}\) be a \({\mathcal {Q}}\)-moderate weight, and let \({p,q \in [1,\infty ]}\). Suppose that \((f_n)_{n \in {\mathbb {N}}}\) is a sequence in \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) such that \({\liminf _{n\rightarrow \infty } \Vert f_n\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} < \infty }\) and \(f_n \rightarrow f \in Z'({\mathcal {O}})\), with convergence in \(Z'({\mathcal {O}})\). Then \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\), with associated norm estimate \(\Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} \le \liminf _{n \rightarrow \infty } \Vert f_n\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)}\).
3.3 The Extended Pairing
We will use the following extension of the \(L^2\)-inner product.
Definition 3.16
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \(\emptyset \ne {\mathcal {O}}\subset {\widehat{{\mathbb {R}}}}^d\). Let \(\Phi = (\varphi _i)_{i \in I}\) be a BAPU subordinate to \({\mathcal {Q}}\). For \(f \in Z'({\mathcal {O}})\) and \(g \in L^1 ({\mathbb {R}}^d)\) with \({\widehat{g}} \in C^\infty ({\widehat{{\mathbb {R}}}}^d)\), define the extended inner product between f and g as
provided that the series on the right-hand side converges absolutely.
Remark 3.17
-
(i)
For \(f \in L^2 ({\mathbb {R}}^d)\) satisfying \({\widehat{f}} \equiv 0\) almost everywhere on \(\widehat{{\mathbb {R}}}^d \setminus {\mathcal {O}}\) and for \({g \in L^1 ({\mathbb {R}}^d) \cap L^2 ({\mathbb {R}}^d)}\) with \({\widehat{g}} \in C^\infty ({\widehat{{\mathbb {R}}}}^d)\), the extended inner product defined above coincides with the standard inner product on \(L^2\). Indeed, since \(|\varphi _i (\xi )| \le \Vert \varphi _i\Vert _{{\mathcal {F}}L^1} \le C_\Phi \) and thus \(\sum _{i \in I} |\varphi _i (\xi )| \le N_{\mathcal {Q}}\, C_\Phi \), we can apply the dominated convergence theorem to see that
$$\begin{aligned} \quad \quad \langle f \mid g \rangle _{\Phi }&= \sum _{i \in I} \langle {\widehat{f}} \mid \varphi _i \cdot {\widehat{g}} \, \rangle _{{\mathcal {D}}', {\mathcal {D}}} = \sum _{i \in I} \int _{{\widehat{{\mathbb {R}}}}^d} {\widehat{f}}(\xi ) \,\, \overline{\varphi _i (\xi )} \,\, \overline{{\widehat{g}} (\xi )} \, d \xi \\&= \int _{{\widehat{{\mathbb {R}}}}^d} {\widehat{f}} (\xi ) \,\, \overline{{\widehat{g}} (\xi )} \,\, \overline{\sum _{i \in I} \varphi _i (\xi )} \, d \xi = \int _{{\mathcal {O}}} {\widehat{f}} (\xi ) \, \overline{{\widehat{g}} (\xi )} \, d \xi \\&= \langle {\widehat{f}} \mid {\widehat{g}} \, \rangle _{L^2} = \langle f \mid g \rangle _{L^2} \, . \end{aligned}$$ -
(ii)
In general, it is not clear whether the extended inner product defined above is independent of the chosen BAPU. However, as we will show in Lemma 4.4, the extended pairing is independent of this choice under suitable hypotheses.
4 Boundedness of the Frame Operator
In this section, we present conditions under which the frame operator associated with a generalized shift-invariant system is well-defined and bounded on Besov-type decomposition spaces. These conditions involve the interplay between smoothness and decay of the generators and the underlying frequency cover. See also [52, Sect. 2] and [62] for related estimates.
4.1 Generalized Shift-Invariant Systems
Definition 4.1
Let J be a countable index set. For \(j \in J\), let \(C_j \in \mathrm {GL}(d, {\mathbb {R}})\) and \(g_j \in L^2({\mathbb {R}}^d)\). A generalized shift-invariant (GSI) system, associated with \((g_j)_{j \in J}\) and \((C_j)_{j \in J}\), is defined as
Throughout the paper, we assume the following standing hypotheses on the system.
Standing hypotheses. The generators \((g_j)_{j \in J}\) of \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) will be assumed to satisfy \({g_j \in L^1 ({\mathbb {R}}^d) \cap L^2 ({\mathbb {R}}^d)}\) and \(\widehat{g_j} \in C^{\infty } (\widehat{{\mathbb {R}}}^d)\). Moreover, we will use the function \(t_0 := \sum _{j \in J} |\det C_j|^{-1} |\widehat{g_j} |^2\) for which we assume that there exist constants \(A, B >0\) such that
Remark 4.2
The assumption (4.1) is automatically satisfied for any generalized shift-invariant frame \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) for \(L^2 ({\mathbb {R}}^d)\), with frame bounds \(A, B > 0\), if it satisfies the so-called \(\alpha \)-local integrability condition (5.1) introduced below. For a proof, see [30, Theorem 3.13 and Remark 5] and [39, Proposition 4.1].
Given the GSI system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\), the associated frame operator is formally defined as
For analyzing the boundedness and well-definedness of the frame operator, the following terminology will be convenient.
Definition 4.3
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) with BAPU \((\varphi _i)_{i \in I}\). Let \(w = (w_i)_{i \in I}\) and \(v = (v_j)_{j \in J}\) be weights. The system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is said to be \((w, v, \Phi )\)-adapted if the matrix \(M \in {\mathbb {C}}^{I \times J}\) defined by

is of Schur-type.
Lemma 4.4
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover with BAPU \(\Phi \). Let \(w = (w_i)_{i \in I}\) be a \({\mathcal {Q}}\)-moderate weight and let the weight \(v = (v_j)_{j \in J}\) be arbitrary.
-
(i)
If \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w, v, \Phi )\)-adapted, then \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w, v, \Psi )\)-adapted for any BAPU \(\Psi \) subordinate to \({\mathcal {Q}}\).
-
(ii)
If \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted, then the extended inner product \(\langle f \mid T_{C_j k} \, g_j \rangle _{\Phi }\) is well-defined and independent of the choice of the BAPU \(\Phi \), for any \(p,q \in [1,\infty ]\), any \({f \in {\mathcal {D}}({\mathcal {Q}}, L^p,\ell _w^q)}\), and all \(j \in J\) and \(k \in {\mathbb {Z}}^d\).
Proof
We assume throughout that \(\Phi = (\varphi _i)_{i \in I}\) and \(\Psi = (\psi _i)_{i \in I}\) are two BAPUs subordinate to \({\mathcal {Q}}\).
We first show that if \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted, then \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is also \((w,v,\Psi )\)-adapted. For this, note that \((f *g) (C x) = |\det C| \cdot \big ( (f \circ C) *(g \circ C) \big ) (x)\) for any \(f \in L^1({\mathbb {R}}^d)\), \(g \in L^1 ({\mathbb {R}}^d) \cap L^\infty ({\mathbb {R}}^d)\), and \(C \in \mathrm {GL}(d,{\mathbb {R}})\). Using this, together with \(\psi _i = \varphi _i^{*} \, \psi _i\), yields

where \(C \ge 1\) is given by the norm equivalence \(\Vert \cdot \Vert _{W(L^\infty , \ell ^1)} \asymp \Vert \cdot \Vert _{W(L^\infty , L^1)}\).
The matrix entries \(M_{i,j}\) in (4.2) satisfy

Likewise, let us define

Using the moderateness of the weight w and the equivalence \(\ell \in i^*\Longleftrightarrow i \in \ell ^*\), we obtain that

for all \(j \in J\). Similarly,

for all \(i \in I\). In combination, these two estimates show that \(N = (N_{i,j})_{i \in I, j \in J}\) is of Schur-type.
Finally, let \(p,q \in [1,\infty ]\) and \(f \in {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\), as well as \(j \in J\) and \(k \in {\mathbb {Z}}^d\) be arbitrary; we show that the extended product \(\langle f \mid T_{C_j k} \, g_j \rangle _{\Phi }\) is well-defined and that \( \langle f \mid T_{C_j k} \, g_j \rangle _{\Phi } = \langle f \mid T_{C_j k} \, g_j \rangle _{\Psi } \). To show this, set  . Since \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted, Schur’s test shows that \( \mathbf{B } : \ell _w^q (I) \rightarrow \ell _v^q (J), (c_i)_{i \in I} \mapsto \Big ( \sum _{i \in I} B_{j,i} \, c_i \Big )_{j \in J} \) is well-defined and bounded. Define \(d_i := \Vert {\mathcal {F}}^{-1} (\varphi _i \cdot {\widehat{f}} \,)\Vert _{L^p}\) and \(c_i := \Vert {\mathcal {F}}^{-1} (\varphi _i^*\cdot {\widehat{f}} \,)\Vert _{L^p} \), and note that \(0 \le c_i \le \sum _{\ell \in i^*} d_\ell = (\Gamma _{{\mathcal {Q}}} \, d)_i\), whence \(c = (c_i)_{i \in I} \in \ell _w^q(I)\), since \(d = (d_i)_{i \in I} \in \ell _w^q(I)\) as \(f \in {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\).
. Since \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted, Schur’s test shows that \( \mathbf{B } : \ell _w^q (I) \rightarrow \ell _v^q (J), (c_i)_{i \in I} \mapsto \Big ( \sum _{i \in I} B_{j,i} \, c_i \Big )_{j \in J} \) is well-defined and bounded. Define \(d_i := \Vert {\mathcal {F}}^{-1} (\varphi _i \cdot {\widehat{f}} \,)\Vert _{L^p}\) and \(c_i := \Vert {\mathcal {F}}^{-1} (\varphi _i^*\cdot {\widehat{f}} \,)\Vert _{L^p} \), and note that \(0 \le c_i \le \sum _{\ell \in i^*} d_\ell = (\Gamma _{{\mathcal {Q}}} \, d)_i\), whence \(c = (c_i)_{i \in I} \in \ell _w^q(I)\), since \(d = (d_i)_{i \in I} \in \ell _w^q(I)\) as \(f \in {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\).
As the final setup, let \(p' \in [1,\infty ]\) denote the conjugate exponent to p, and set \(g := T_{C_j k} \, g_j\). Since \(\Vert f\Vert _{L^{p'}} \le \Vert f\Vert _{W(C_0,\ell ^1)}\) for all \(f \in W(C_0, \ell ^1)\) and since  , it follows that
, it follows that

Using that \(\varphi _i = \varphi _i^*\varphi _i\), and \({\widehat{g}} \in C^\infty (\widehat{{\mathbb {R}}}^d)\), we next see
where the right-hand side is independent of \(\ell \). Given this estimate, it follows immediately that
Therefore, we can interchange the sums in the following calculation:
This calculation implies in particular that both \(\langle f \,\mid \, g \rangle _{\Phi }\) and \(\langle f \,\mid \, g \rangle _{\Psi }\) are well-defined. \(\square \)
4.2 Sequence Spaces and Operators
The frame operator can be factored into the coefficient and the reconstruction operator. In this subsection, we investigate the boundedness of these operators on suitable sequence spaces.
Definition 4.5
Let \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) be a generalized shift-invariant system and let \(p, q \in [1,\infty ]\). For a weight \(v = (v_j)_{j \in J}\) and a sequence \(c = (c_k^{(j)})_{j \in J, k \in {\mathbb {Z}}^d} \in {\mathbb {C}}^{J \times {\mathbb {Z}}^d}\), define
Finally, define the associated coefficient space \(Y^{p,q}_v\) as
Let \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) be a decomposition space. Given a GSI system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) and an associated coefficient space \(Y_v^{p,q}\), the reconstruction or synthesis operator is formally defined as the mapping
while the coefficient or analysis operator is formally defined by
where \(\langle \cdot , \cdot \rangle _{\Phi }\) denotes the extended pairing defined in Sect. 3.3.
4.3 Boundedness of Analysis and Synthesis Operators
For proving the boundedness of the operators \({\mathscr {D}}\) and \({\mathscr {C}}\), we will invoke the following lemma.
Lemma 4.6
Let \(g \in W(C_0, \ell ^1)({\mathbb {R}}^d)\) and \(M \in \mathrm {GL}({\mathbb {R}}^d)\). Then the map
is bounded from \(\ell ^{\infty } ({\mathbb {Z}}^d)\) into \(L^{\infty } ({\mathbb {R}}^d)\), with the series converging pointwise absolutely. Furthermore, for any \(p \in [1,\infty ]\), the mapping \(D_{M,g} : \ell ^p ({\mathbb {Z}}^d) \rightarrow L^p ({\mathbb {R}}^d)\) is well-defined and bounded, with \( \Vert D_{M,g} \Vert _{\ell ^p \rightarrow L^p} \le | \det M \, |^{1/p} \cdot \Vert g\circ M \Vert _{W(L^{\infty }, \ell ^1)}. \)
Proof
For the case \(M = \mathrm {id}_{{\mathbb {R}}^d}\), this follows from [1, Lemma 2.9] —see also [14]. For the general case, simply note that \(D_{M,g} \, c (x) = \big ( D_{\mathrm {id}_{{\mathbb {R}}^d}, g \circ M} (c) \big ) (M^{-1} x)\). \(\square \)
The following technical lemma allows us to use density arguments for the full range \(p,q \in [1,\infty ]\).
Lemma 4.7
Let \(p,q \in [1,\infty ]\). Suppose the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted with matrix M as in (4.2). Then, for any \(F \in \ell _w^q (I; L^p)\), there is a sequence \(\theta = (\theta _{j,k})_{j \in J, k \in {\mathbb {Z}}^d} \in Y_v^{p,q}\) such that
and \( | \langle f \,\mid \, T_{C_j k} \, g_j \rangle _{\Phi } | \le \theta _{j,k} \) for all \(j \in J, k \in {\mathbb {Z}}^d\) and every \((F,\Phi )\text {-dominated } f \in Z'({\mathcal {O}})\).
Moreover, if \((f_n)_{n \in {\mathbb {N}}}\) is a sequence of \((F,\Phi )\)-dominated Fourier distributions \(f_n \in Z'({\mathcal {O}})\) satisfying \(f_n \rightarrow f_0 \in Z'({\mathcal {O}})\) with convergence in \(Z'({\mathcal {O}})\), then \( \langle f_n \,\mid \, T_{C_j k} \, g_j \rangle _{\Phi } \rightarrow \langle f_0 \,\mid \, T_{C_j k} \, g_j \rangle _{\Phi } \) for all \(j \in J, k \in {\mathbb {Z}}^d\).
Proof
Let \(f \in Z'({\mathcal {O}})\) be \((F,\Phi )\)-dominated. Using \(\overline{\varphi _i^*} \varphi _i = \varphi _i\) and the estimate (3.3), we see that

and thus
with \(\zeta _{i,j,k,\ell }\) and \(\theta _{j,k}\) being independent of f.
Next, define a measure \(\mu _{i,j,k}\) on \({\mathbb {R}}^d\) by  . Then
. Then

There are now two cases. If \(p = \infty \), then the estimate (4.7) and \(\Vert \cdot \Vert _{L^{\infty } (\mu _{i,j,k})} \le \Vert \cdot \Vert _{L^{\infty }}\) yield that

If \(p < \infty \), then (4.7) and Lemma 4.6 together show that

Hence,  for any \(p \in [1,\infty ]\).
for any \(p \in [1,\infty ]\).
Define \(c \in \ell _w^q(I)\) by \(c_\ell := \Vert F_\ell \Vert _{L^p}\). Then, for all \(j \in J\),

where \(M_{i,j}\) is defined as in Eq. (4.2). Next, since \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted, Schur’s test shows that \( \mathbf{M } : \ell ^q (I) \rightarrow \ell ^q(J), (d_i)_{i \in I} \mapsto \big ( \sum _{i \in I} M_{i,j} d_i \big )_{j \in J} \) is well-defined and bounded, with norm \(\Vert \mathbf{M }\Vert _{\ell ^q \rightarrow \ell ^q} \le \Vert M\Vert _{\mathrm {Schur}}\). Consequently, we obtain
But \(\Vert c\Vert _{\ell _w^q} = \Vert F\Vert _{\ell _w^q(I; L^p)}\), and thus the first part of the proof is complete.
For the proof of the second part, first note
since \(\varphi _i \cdot {\mathcal {F}}[T_{C_j k} \, g_j] \in C_c^\infty ({\mathcal {O}})\) and since \(f_n \rightarrow f_0\) in \(Z'({\mathcal {O}})\) which implies \(\widehat{f_n} \rightarrow \widehat{f_0}\) in \({\mathcal {D}}'({\mathcal {O}})\). Next, since the \(f_n\) are \((F,\Phi )\)-dominated, Eq. (4.5) shows that
while Eq. (4.8) shows that \(\sum _{i \in I} \gamma _{i,j} < \infty \). Thus,
by definition of \(\langle \cdot \mid \cdot \rangle _{\Phi }\) and by the dominated convergence theorem. \(\square \)
We now prove the boundedness of the coefficient and reconstruction operators.
Proposition 4.8
Let \({\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\) be a decomposition space and let \(Y_v^{p,q}\) be the sequence space associated to the GSI system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) as per Definition 4.5. Suppose that \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted (where \(\Phi \) is a BAPU for \({\mathcal {Q}}\)) with matrix M as in (4.2). Then
-
(i)
For all \(p, q \in [1,\infty ]\), the reconstruction map
$$\begin{aligned} {\mathscr {D}}: Y_v^{p,q} \rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q), \quad (c_k^{(j)})_{j \in J, k \in {\mathbb {Z}}^d} \mapsto \sum _{j \in J} \sum _{k \in {\mathbb {Z}}^d} c_k^{(j)} \cdot T_{C_j k} \, g_j \end{aligned}$$is well-defined and bounded with \(\Vert {\mathscr {D}}\Vert _{Y_v^{p,q} \rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} \le \Vert M\Vert _{\mathrm {Schur}}\). Furthermore, the defining double series converges unconditionally in \(Z'({\mathcal {O}})\).
-
(ii)
For all \(p,q \in [1,\infty ]\), the coefficient operator
$$\begin{aligned} {\mathscr {C}}: {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q) \rightarrow Y_v^{p,q}, \quad f \mapsto \Big ( \langle f \mid T_{C_j k} \, g_j \rangle _{\Phi } \Big )_{j \in J, k \in {\mathbb {Z}}^d} \end{aligned}$$is well-defined and bounded with \( \Vert {\mathscr {C}}\Vert _{{\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q) \rightarrow Y_v^{p,q}} \le \Vert M\Vert _{\mathrm {Schur}} \cdot \Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell _w^q \rightarrow \ell _w^q} \).
-
(iii)
If \(\Psi \) is another BAPU for \({\mathcal {Q}}\), and if \(f \in {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\), then \(\langle f \mid T_{C_j k} \, g_j \rangle _{\Psi }\) is well-defined and satisfies \( \langle f \mid T_{C_j k} \, g_j \rangle _{\Psi } = \langle f \mid T_{C_j k} \, g_j \rangle _{\Phi } \) for all \(j \in J\) and \(k \in {\mathbb {Z}}^d\).
Proof
To prove (i), let \(c = (c_k^{(j)})_{j \in J, k \in {\mathbb {Z}}^d} \in Y_v^{p,q}\) be arbitrary, and set \(c^{(j)} := (c_k^{(j)})_{k \in {\mathbb {Z}}^d}\) for \(j \in J\). Then \(c^{(j)} \in \ell ^p({\mathbb {Z}}^d)\). Moreover, if \(d = (d_j)_{j \in J}\) is defined as \(d_j := |\det C_j|^{\frac{1}{p} - \frac{1}{2}} \cdot \Vert c^{(j)} \Vert _{\ell ^p}\), then \(d \in \ell _v^q (J)\) and \(\Vert d \Vert _{\ell _v^q} = \Vert c \Vert _{Y_v^{p,q}}\). Finally, let \(|c^{(j)}| = (|c_k^{(j)}|)_{k \in {\mathbb {Z}}^d}\) for \(j \in J\).
We first prove the unconditional convergence of the double series defining \({\mathscr {D}}c\). Since the Fourier transform \({\mathcal {F}}: Z'({\mathcal {O}}) \rightarrow {\mathcal {D}}'({\mathcal {O}})\) is a linear homeomorphism, it suffices to show that the double series \(\sum _{j \in J} \sum _{k \in {\mathbb {Z}}^d} c_k^{(j)} {\mathcal {F}}[ T_{C_j k} \, g_j ]\) converges unconditionally in \({\mathcal {D}}'({\mathcal {O}})\). To prove this, let \(K \subset {\mathcal {O}}\) be compact. Since \(\sum _{i \in I} \varphi _i \equiv 1\) on \({\mathcal {O}}\), the family \(\big ( \varphi _i^{-1} ({\mathbb {C}}\setminus \{0\}) \big )_{i \in I}\) forms an open cover of \({\mathcal {O}}\supset K\). By compactness of K, there is a finite set \(I_K \subset I\) for which \( K \subset \bigcup _{i \in I_K} \varphi _i^{-1} ({\mathbb {C}}\setminus \{0\}) \subset \bigcup _{i \in I_K} Q_i \). Note that \(I_K^*:= \bigcup _{\ell \in I_K} \ell ^*\subset I\) is finite. Furthermore, for \(j \in I \setminus I_K^*\), note that \(Q_j \cap K \subset \bigcup _{i \in I_K} Q_j \cap Q_i = \emptyset \), whence \(\varphi _j \equiv 0\) on K. Thus, any \(g \in C_c^\infty ({\mathcal {O}}) \subset {\mathcal {S}}(\widehat{{\mathbb {R}}}^d)\) with \(\mathop {{\text {supp}}}g \subset K\) can be written as \(g = \sum _{i \in I} \varphi _i \, g = \sum _{i \in I_K^*} \varphi _i \, g\). A direct calculation using Lemma 4.6 therefore shows

Since \(g \mapsto \Vert {\widehat{g}}\Vert _{L^{p'}}\) is a continuous norm on \(C_c^\infty ({\mathcal {O}})\) and since \(g \in C_c^\infty ({\mathcal {O}})\) with \(\mathop {{\text {supp}}}g \subset K\) was arbitrary, the desired unconditional convergence follows.
Next, we show that \({\mathscr {D}}: Y_v^{p,q} \rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is well-defined and bounded. For \(i \in I\) and \(j \in J\), define  . The assumption that \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted yields by Schur’s test that the map \( \mathbf{B } : \ell ^q_v (J) \rightarrow \ell ^q_w (I), \; (d_j)_{j \in J} \mapsto \big ( \sum _{j \in J} B_{i,j} \cdot d_j \big )_{i \in I} \, \) is bounded with \(\Vert \mathbf{B }\Vert _{\mathrm {op}} \le \Vert M \Vert _{\mathrm {Schur}}\). The series defining \({\mathscr {D}}c\) being unconditionally convergent yields
. The assumption that \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted yields by Schur’s test that the map \( \mathbf{B } : \ell ^q_v (J) \rightarrow \ell ^q_w (I), \; (d_j)_{j \in J} \mapsto \big ( \sum _{j \in J} B_{i,j} \cdot d_j \big )_{i \in I} \, \) is bounded with \(\Vert \mathbf{B }\Vert _{\mathrm {op}} \le \Vert M \Vert _{\mathrm {Schur}}\). The series defining \({\mathscr {D}}c\) being unconditionally convergent yields

Therefore, an application of Lemma 4.6 shows

whence \( \Vert {\mathscr {D}}\, c \Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} \le \Vert \mathbf{B } \, d \Vert _{\ell _w^q} \le \Vert M \Vert _{\mathrm {Schur}} \cdot \Vert d \Vert _{\ell _v^q} = \Vert M \Vert _{\mathrm {Schur}} \cdot \Vert c \Vert _{Y_v^{p,q}} \).
To prove (ii), let \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) be arbitrary. Define \(F_i := |{\mathcal {F}}^{-1} (\varphi _i {\widehat{f}} \, )|\) for \(i \in I\). Then, \(F = (F_i)_{i \in I} \in \ell _w^q (I; L^p)\) and \(\Vert F\Vert _{\ell _w^q(I; L^p)} = \Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)}\). Clearly, f is \((F,\Phi )\)-dominated. Therefore, Lemma 4.7 yields \(\theta = (\theta _{j,k})_{j \in J, k \in {\mathbb {Z}}^d} \in Y_v^{p,q}\) satisfying the estimate \(| \langle f \mid T_{C_j k} \, g_j \rangle _{\Phi }| \le \theta _{j,k}\) for all \(j \in J\) and \(k \in {\mathbb {Z}}^d\), and furthermore \( \Vert \theta \Vert _{Y_v^{p,q}} \le \Vert M\Vert _{\mathrm {Schur}} \cdot \Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell _w^q \rightarrow \ell _w^q} \cdot \Vert F\Vert _{\ell _w^q (I; L^p)} \). Hence, \({\mathscr {C}}: {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q) \rightarrow Y_v^{p,q}\) is well-defined and bounded, with the claimed estimate for the operator norm.
Assertion (iii) is a direct consequence of Lemma 4.4. \(\square \)
Proposition 4.8 shows in particular that the reconstruction operator \({\mathscr {D}}: Y_v^{p,q} \!\rightarrow {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\) is continuous. However, in case \(\max \{ p, q \} = \infty \), the convergence in \(Y_v^{p,q}\) is a quite restrictive condition. To accommodate for this, we will often employ the following lemma.
Lemma 4.9
Under the assumptions of Proposition 4.8, the following holds:
For each \(n \in {\mathbb {N}}\), let \(c^{(n)} = (c^{(n)}_{j,k})_{j \in J, k \in {\mathbb {Z}}^d} \in Y_v^{p,q}\) be such that \(c^{(n)}_{j,k} \xrightarrow [n \rightarrow \infty ]{} c_{j,k} \in {\mathbb {C}}\) for all \(j \in J\) and \(k \in {\mathbb {Z}}^d\). Suppose there exists a sequence \(\theta = (\theta _{j,k})_{j \in J, k \in {\mathbb {Z}}^d} \in Y_v^{p,q}\) satisfying \(|c^{(n)}_{j,k}| \le \theta _{j,k}\) for all \(j \in J\), \(k \in {\mathbb {Z}}^d\), and \(n \in {\mathbb {N}}\). Then, the reconstruction operator \({\mathscr {D}}\) satisfies \({\mathscr {D}}\, c^{(n)} \xrightarrow [n \rightarrow \infty ]{Z'({\mathcal {O}})} {\mathscr {D}}\, c\).
Proof
Let \(f \in Z({\mathcal {O}})\). Then \(K := \mathop {{\text {supp}}}{\mathcal {F}}^{-1} f \subset {\mathcal {O}}\) is compact. Since \((\varphi _i^{-1} ({\mathbb {C}}\setminus \{0\}))_{i \in I}\) is an open cover of K, there is a finite set \(I_0 \subset I\) satisfying \( K \subset \bigcup _{i \in I_0} \varphi _i^{-1} ({\mathbb {C}}\setminus \{0\}) \subset \bigcup _{i \in I_0} Q_i \). This easily implies \(Q_i \cap K = \emptyset \) for \(i \in I \setminus I_f\), where \(I_f := I_0^*:= \bigcup _{\ell \in I_0} \ell ^*\subset I\) is finite. Thus, \(\varphi _i \cdot {\mathcal {F}}^{-1}f \equiv 0\) for \(i \in I \setminus I_f\), and hence \({\mathcal {F}}^{-1} f = \sum _{i \in I_f} \varphi _i \, {\mathcal {F}}^{-1} f\). Therefore,

For \(\nu = (\nu _{j,k})_{j \in J, k \in {\mathbb {Z}}^d} \in Y_v^{p,q}\), it follows, therefore, by the convergence in \(Z'({\mathcal {O}})\) of the series defining \({\mathscr {D}}\nu \) that

Next, Lemma 4.6 shows that

where we defined \(\gamma _j := \Vert (\theta _{j,k})_{k \in {\mathbb {Z}}^d} \Vert _{\ell ^p}\) in the last step.
For brevity, let \(u_j := v_j \cdot |\det C_j|^{\frac{1}{p} - \frac{1}{2}}\). Note that since \(\theta \in Y_v^{p,q}\), we have \(\gamma = (\gamma _j)_{j \in J} \in \ell _u^q \hookrightarrow \ell _u^\infty \), which yields a constant \(C_1 > 0\) such that \(u_j \, \gamma _j \le C_1\) for all \(j \in J\). Using this, we see

Finally, since \(|c^{(n)}_{j,k}| \le \theta _{j,k}\) for all \(j \in J\), \(k \in {\mathbb {Z}}^d\), and \(n \in {\mathbb {N}}\), and since \(c^{(n)}_{j,k} \xrightarrow [n \rightarrow \infty ]{} c_{j,k}\), applying the dominated convergence theorem in Eq. (4.10) shows that
as desired. \(\square \)
Corollary 4.10
Under the assumptions of Proposition 4.8, the following holds: The frame operator \(S := {\mathscr {D}}\circ {\mathscr {C}}: {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q) \rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is well-defined and bounded.
Furthermore, if \((f_n)_{n \in {\mathbb {N}}} \subset {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is a sequence satisfying \(f_n \rightarrow f \in Z'({\mathcal {O}})\), with convergence in \(Z'({\mathcal {O}})\), and for which there exists \(F \in \ell _w^q (I; L^p)\) such that all \(f_n\) are \((F, \Phi )\)-dominated, then \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) and \(S f_n \rightarrow S f\) with convergence in \(Z'({\mathcal {O}})\).
Proof
S is well-defined, bounded by Proposition 4.8. Since \( \Vert f_n\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} \le \Vert F\Vert _{\ell _w^q (I; L^p)} \) for all \(n \in {\mathbb {N}}\), Lemma 3.15 yields \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\), where \(c := {\mathscr {C}}\, f \in Y_v^{p,q}\). Next, Lemma 4.7 shows that there is a sequence \(\theta = (\theta _{j,k})_{j \in J, k \in {\mathbb {Z}}^d} \in Y_v^{p,q}\) such that if we set \(c^{(n)} := {\mathscr {C}}f_n\), then \(| c^{(n)}_{j,k} | \le \theta _{j,k}\) for all \((n,j,k) \in {\mathbb {N}}\times J \times {\mathbb {Z}}^d\). The same lemma also shows that \(c^{(n)}_{j,k} \rightarrow c_{j,k}\) for all \(j \in J\) and \(k \in {\mathbb {Z}}^d\). Therefore, Lemma 4.9 shows that \(S f_n = {\mathscr {D}}\, c^{(n)} \rightarrow {\mathscr {D}}\, c = S f\) with convergence in \(Z'({\mathcal {O}})\). \(\square \)
5 Invertibility of the Frame Operator
5.1 Representation of the Frame Operator
The frame properties of generalized shift-invariant systems are usually studied under a compatibility condition that controls the interaction between the generating functions and the translation lattices of the system. Specifically, we will use the so-called local integrability conditions [39, 41, 59].
Definition 5.1
For an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) of full measure, let
A generalized shift-invariant system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is said to satisfy the \(\alpha \)-local integrability condition (\(\alpha \)-LIC), relative to \({\mathcal {O}}^c\), if, for all \(f \in {\mathcal {B}}_{{\mathcal {O}}} ({\mathbb {R}}^d)\),
Given \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\), we set \(\Lambda := \bigcup _{j \in J} C_j^{-t} {\mathbb {Z}}^d\) and \(\kappa (\alpha ) := \{ j \in J \; : \; \alpha \in C_j^{-t} {\mathbb {Z}}^d\}\) for \(\alpha \in \Lambda \). For \(\alpha \in \Lambda \), we define the functions
Note that \(t_{\alpha } \in L^{\infty } (\widehat{{\mathbb {R}}}^d)\) for all \(\alpha \in \Lambda \) by (4.1). Furthermore, \(t_\alpha (\xi - \alpha ) = \overline{t_{-\alpha } (\xi )}\).
Under the \(\alpha \)-local integrability condition, the following (weak-sense) representation of the frame operator can be obtained; this follows by polarization from the proofs of [39, Proposition 2.4] and [41, Theorem 3.4].
Proposition 5.2
Suppose \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) satisfies the \(\alpha \)-local integrability condition (5.1), relative to \({\mathcal {O}}^c\). Then, for all \(f_1, f_2 \in {\mathcal {B}}_{{\mathcal {O}}} ({\mathbb {R}}^d)\),
where the series converges absolutely; in fact,
Proposition 5.2 yields an analogous representation of the frame operator on \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\), at least on the subspace \({\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\).
Corollary 5.3
Under the assumptions of Proposition 5.2, the series \(\sum _{\alpha \in \Lambda _0} {\mathcal {F}}^{-1} [T_{\alpha } \, (t_\alpha \, {\widehat{f}} \, )]\) converges unconditionally in \(Z'({\mathcal {O}})\) for any subset \(\Lambda _0 \subset \Lambda \), and any \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\).
Furthermore, if \({\mathcal {Q}}\) is a decomposition cover of \({\mathcal {O}}\), with subordinate BAPU \(\Phi \), if w is \({\mathcal {Q}}\)-moderate, and if \(v = (v_j)_{j \in J}\) is a weight such that \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted, then the frame operator \(S : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) fulfills for each \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) the identity
Proof
Since \(t_\alpha \in L^\infty (\widehat{{\mathbb {R}}}^d)\) and \({\widehat{f}} \in {\mathcal {S}}(\widehat{{\mathbb {R}}}^d)\), we have \( T_{\alpha } \, (t_\alpha \, {\widehat{f}}) \in L^1 (\widehat{{\mathbb {R}}}^d) \hookrightarrow {\mathcal {S}}'(\widehat{{\mathbb {R}}}^d) \hookrightarrow {\mathcal {D}}'({\mathcal {O}}) \), and hence \({\mathcal {F}}^{-1} [T_{\alpha } \, (t_\alpha \, {\widehat{f}} \, )] \in Z'({\mathcal {O}})\). The Fourier transform \({\mathcal {F}}: Z'({\mathcal {O}}) \rightarrow {\mathcal {D}}'({\mathcal {O}})\) is a linear homeomorphism; hence, it suffices to prove that the series \(\sum _{\alpha \in \Lambda _0} T_{\alpha } \, (t_\alpha \, {\widehat{f}} \, )\) converges unconditionally in \({\mathcal {D}}'({\mathcal {O}})\). To see this, let \(K \subset {\mathcal {O}}\) be compact. Define \(f_1 := f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d) \subset {\mathcal {B}}_{{\mathcal {O}}} ({\mathbb {R}}^d)\), and set \(f_2 := {\mathcal {F}}^{-1} {\mathbb {1}}_K \in {\mathcal {B}}_{{\mathcal {O}}} ({\mathbb {R}}^d)\). By Eq. (5.4), the constant \( C_K := \sum _{\alpha \in \Lambda } \int _{\widehat{{\mathbb {R}}}^d} |{\widehat{f}} (\xi )| \, {\mathbb {1}}_K (\xi + \alpha ) \, |t_\alpha (\xi )| \, d \xi \) is finite. Now, let \(\psi \in C_c^\infty ({\mathcal {O}})\) be arbitrary with \(\mathop {{\text {supp}}}\psi \subset K\). Then
Since \(\Vert \cdot \Vert _{L^\infty }\) is continuous with respect to the topology on \(C_c^\infty ({\mathcal {O}})\), and since \(\psi \in C_c^\infty ({\mathcal {O}})\) with \(\mathop {{\text {supp}}}\psi \subset K\) was arbitrary, the estimate (5.6) simultaneously yields that \(\sum _{\alpha \in \Lambda _0} T_{\alpha } \, (t_\alpha \, {\widehat{f}} \, ) \in {\mathcal {D}}'({\mathcal {O}})\), cf. [54, Theorem 6.6], as well as the unconditional convergence of the series in \({\mathcal {D}}'({\mathcal {O}})\).
For the remaining part, note if \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\), then \( \langle f \mid T_{C_j k} \, g_j \rangle _{\Phi } = \langle f \mid T_{C_j k} \, g_j \rangle _{L^2} \) by Remark 3.17. This proves everything but the last equality in Eq. (5.5). To prove this, let \(g \in Z({\mathcal {O}})\). Then \(\widehat{{\overline{g}}} = \overline{{\mathcal {F}}^{-1} g} \in C_c^\infty ({\mathcal {O}})\), and hence \({\overline{g}} \in {\mathcal {B}}_{{\mathcal {O}}} ({\mathbb {R}}^d)\). This, together with Eq. (5.3), shows
and hence (5.5) follows. \(\square \)
5.2 Towards Invertibility
According to Corollary 5.3, on the set \({\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\), the frame operator can be represented as
with
and
for \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\). In the following, we estimate the norms of \(T_0^{-1}\) and R as operators on the decomposition space \({\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\). This will be used, together with the following elementary result, to provide conditions ensuring that the frame operator is invertible.
Lemma 5.4
Let X be a Banach space, and let \(S : X \rightarrow X\) be a linear operator that can be written as \(S = T_0 + R\), where \(T_0 , R\) are bounded linear operators on X. Finally, assume that \(T_0\) is boundedly invertible and that
Then, \(S : X \rightarrow X\) is also boundedly invertible.
Proof
We have \(S = T_0 + R = T_0 \big ( \mathrm {id}_X - (- T_0^{-1} R) \big )\). But \(\Vert - T_0^{-1} R\Vert _{X \rightarrow X} \le \Vert T_0^{-1}\Vert _{X \rightarrow X} \cdot \Vert R \Vert _{X \rightarrow X} < 1\), so that \(\mathrm {id}_X - (- T_0^{-1} R)\) is boundedly invertible by a Neumann series argument. This implies that S is boundedly invertible as a composition of boundedly invertible operators. \(\square \)
5.3 Estimates for Fourier Multipliers
The operator \(T_0\) is a Fourier multiplier, and we aim to estimate its inverse. As a first step, we prove a general result concerning the boundedness of Fourier multipliers on Besov-type spaces; see Proposition 5.7 below. More qualitative versions of that proposition can be found in [56, Sect. 2.4.3], [58, Sect. 2.3] and [23, Theorem 2.11]. Corresponding results for Triebel-Lizorkin spaces hold under more stringent assumptions on the decomposition cover; see [56, Sects. 2.4.2 and 2.5.4] and [55].
In contrast to [56, Sect. 2.4.3], we consider Fourier symbols with limited regularity. This entails certain technical difficulties because of our choice of the reservoir \(Z'({\mathcal {O}})\), where \(Z({\mathcal {O}}) = {\mathcal {F}}(C_c^\infty ({\mathcal {O}}))\). More precisely, if \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q) \subset Z'({\mathcal {O}})\), then \({\widehat{f}} \in {\mathcal {D}}'({\mathcal {O}})\) is a distribution, and can be multiplied by a function \(h \in C^\infty ({\mathcal {O}})\). We need, however, to make sense of the product with more general functions h, by fully exploiting the fact that \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\). To this end, we introduce the following notion:
Definition 5.5
Let \(p \in [1,\infty ]\). For \(f \in {\mathcal {F}}L^1({\mathbb {R}}^d)\) and \(g \in {\mathcal {F}}L^p ({\mathbb {R}}^d)\), we define the generalized product of f and g as
Remark 5.6
The definition makes sense because of Young’s inequality: \(({\mathcal {F}}^{-1} f) *({\mathcal {F}}^{-1} g) \in L^p({\mathbb {R}}^d)\). Furthermore, our definition indeed generalizes the usual product: if \(f \in {\mathcal {S}}({\mathbb {R}}^d)\) and \({g \in {\mathcal {S}}'({\mathbb {R}}^d)}\), then \(f \cdot g = {\mathcal {F}}[({\mathcal {F}}^{-1} f) *({\mathcal {F}}^{-1} g)]\) —see, for instance [54, Theorem 7.19].
We can now derive an estimate for Fourier multipliers on decomposition spaces. The proof is deferred to Appendix C.
Proposition 5.7
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \(\emptyset \ne {\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\), and let \((\varphi _i)_{i \in I}\) be a BAPU subordinate to \({\mathcal {Q}}\). A continuous function \(h \in C({\mathcal {O}})\) is called tame if
If h is tame and if \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) for certain \(p,q \in [1,\infty ]\) and a \({\mathcal {Q}}\)-moderate weight w, then the series
converges unconditionally in \(Z'({\mathcal {O}})\). Furthermore, the operator \(\Phi _h\) satisfies the following properties:
-
(i)
\(\Phi _h \!:\! {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q) \!\rightarrow \! {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is bounded, with \( \Vert \Phi _h\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q) \rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} \le N_{\mathcal {Q}}^2 C_{\Phi } C_h \) for arbitrary \(p,q \in [1,\infty ]\) and any \({\mathcal {Q}}\)-moderate weight w.
-
(ii)
If \((f_n)_{n \in {\mathbb {N}}} \subset Z'({\mathcal {O}})\) is \((F,\Phi )\)-dominated for some \(F \in \ell _w^q(I; L^p)\) and if \(f_n \rightarrow f\) with convergence in \(Z'({\mathcal {O}})\), then also \(\Phi _h f_n \rightarrow \Phi _h f\) with convergence in \(Z'({\mathcal {O}})\). In addition, there is \(G \in \ell _w^q(I; L^p)\) such that \(\Phi _h f_n\) is \((G,\Phi )\)-dominated for all \(n \in {\mathbb {N}}\) and such that \(\Vert G\Vert _{\ell _w^q(I;L^p)} \le N_{\mathcal {Q}}^2 C_{\Phi } C_h \cdot \Vert F_\ell \Vert _{\ell _w^q(I;L^p)}\).
-
(iii)
If \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) and \({\widehat{f}} \in C_c ({\mathcal {O}})\), then \(\Phi _h f = {\mathcal {F}}^{-1} (h \cdot {\widehat{f}} \,)\).
-
(iv)
If
 are tame, then so is \(g \cdot h\), and we have \(\Phi _h \Phi _g = \Phi _{g h}\).
are tame, then so is \(g \cdot h\), and we have \(\Phi _h \Phi _g = \Phi _{g h}\).
Remark
One can show that if \(C_h\) is finite for one BAPU \((\varphi _i)_{i \in I}\), then the same holds for any other BAPU. Still, the precise value of the constant \(C_h\) depends on the choice of the BAPU.
5.4 Estimates for the Remainder Term R
The following proposition provides a general condition under which R defines a bounded operator on \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\). Simplified versions of these are derived in Sect. 6.
Proposition 5.8
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) of full measure, with associated BAPU \(\Phi = (\varphi _i)_{i \in I}\). Let \(w = (w_i)_{i \in I}\) be \({\mathcal {Q}}\)-moderate. Suppose the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) satisfies the \(\alpha \)-local integrability condition (5.1), with respect to \({\mathcal {O}}^c\). Moreover, suppose that, for all \(i, \ell \in I\),
and that the matrix \(N = (N_{i,\ell })_{i,\ell \in I} \in {\mathbb {C}}^{I \times I}\) is of Schur-type. Then, for all \(p, q \in [1,\infty ]\), the “remainder operator R” defined in (5.9) satisfies
Proof
The assumptions yield, by Schur’s test, that the operator
is bounded, with \(\Vert \mathbf{N } \Vert _{\ell _w^q (I) \rightarrow \ell _w^q(I)} \le \Vert N \Vert _{\mathrm {Schur}}\).
Let \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) be arbitrary. For any \(\ell \in I\), define \(c_\ell := \Vert \varphi _\ell ^*\cdot {\widehat{f}}\Vert _{{\mathcal {F}}L^p}\) and \(\theta _\ell := \Vert \varphi _\ell \cdot {\widehat{f}} \Vert _{{\mathcal {F}}L^p}\), where \(\varphi _\ell ^*:= \sum _{i \in \ell ^*} \varphi _i\). Let \(c = (c_i)_{i \in I}\) and \(\theta = (\theta _i)_{i \in I}\). Then \(0 \le c_\ell \le \sum _{i \in \ell ^*} \theta _i = (\Gamma _{\mathcal {Q}}\, \theta )_\ell \), and hence \( \Vert c\Vert _{\ell _w^q} \le \Vert \Gamma _{\mathcal {Q}}\Vert _{\ell _w^q \rightarrow \ell _w^q} \cdot \Vert \theta \Vert _{\ell _w^q} = \Vert \Gamma _{\mathcal {Q}}\Vert _{\ell _w^q \rightarrow \ell _w^q} \cdot \Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} < \infty \).
Since \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\), we have \({\widehat{f}} \in C_c^\infty ({\mathcal {O}})\), and hence \( {\widehat{f}} = \sum _{\ell \in I} \varphi _\ell \cdot {\widehat{f}} = \sum _{\ell \in I} \varphi _\ell \, \varphi _\ell ^*\, {\widehat{f}} \), where only finitely many terms of the series do not vanish. Therefore, by the unconditional convergence of the series defining Rf (see Corollary 5.3), we see
Hence, for all \(i \in I\),
and thus
as claimed. \(\square \)
Corollary 5.9
Assume that the hypotheses of Proposition 5.8 are satisfied. Furthermore, assume that the function \(t_0\) defined in (5.2) is continuous on \({\mathcal {O}}\) and tame (see Proposition 5.7), so that the operator \(\Phi _{t_0} : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is well-defined and bounded. Finally, assume that \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted for some weight \(v = (v_j)_{j \in J}\).
Define \(T_0 := \Phi _{t_0}\). Then the frame operator \(S : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q) \rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is well-defined and bounded and satisfies \(S = T_0 + R_0\) with a bounded linear operator \(R_0 : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q) \rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) satisfying
where \(N \in {\mathbb {C}}^{I \times I}\) is as in (5.12), and \(C_{p,q} := 1\) if \(\max \{p,q\} < \infty \) and \(C_{p,q} := C_\Phi \, \Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell _w^q \rightarrow \ell _w^q}^2\) otherwise.
Proof
Corollary 4.10 shows that the frame operator \(S : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is well-defined and bounded, and hence so is \(R_0 := S - T_0\). Note for \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) that \(T_0 f = {\mathcal {F}}^{-1}(t_0 \cdot {\widehat{f}})\) by Proposition 5.7(iii). Therefore, Corollary 5.3 shows for \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) that \(R_0 f = R f\) with Rf as in Eq. (5.9). Thus, if \(\max \{p,q\} < \infty \), the density of \({\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) in \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) (Proposition 3.13), combined with Proposition 5.8, shows the claim.
Now, suppose that \(\max \{p,q\} = \infty \), and let \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) be arbitrary. Then, Proposition 3.13 yields a sequence \((g_n)_{n \in {\mathbb {N}}} \subset {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) and some \(F \in \ell _w^q (I; L^p)\) such that \(g_n \rightarrow f\) with convergence in \(Z'({\mathcal {O}})\), and such that each \(g_n\) is \((F,\Phi )\)-dominated, where \(\Vert F\Vert _{\ell _w^q(I; L^p)} \le C_{p,q} \cdot \Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)}\) with \(C_{p,q}\) as in the statement of the current corollary. By Proposition 5.7(ii), we get \({T_0 g_n \rightarrow T_0 f}\) with convergence in \(Z'({\mathcal {O}})\). In addition, Corollary 4.10 shows that \(S \, g_n \rightarrow S \, f\) in \(Z'({\mathcal {O}})\). Therefore, \(R \, g_n = R_0 \, g_n = (S - T_0) g_n \rightarrow (S - T_0) f = R_0 f\), while Proposition 5.8 shows
Lemma 3.15 yields \( \Vert R_0 f\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} \le C_{p,q} \Vert N\Vert _{\mathrm {Schur}} \Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell _w^q \rightarrow \ell _w^q} \Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} \). \(\square \)
In many cases, instead of verifying that the matrix N defined in Eq. (5.12) is of Schur-type, it is easier to consider the matrix \({\widetilde{N}}\) defined next.
Corollary 5.10
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) of full measure with BAPU \(\Phi = (\varphi _i)_{i \in I}\), and let \(w = (w_i)_{i \in I}\) be \({\mathcal {Q}}\)-moderate. Let \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) be a generalized shift-invariant system. Suppose that the matrix \({\widetilde{N}} = ({\widetilde{N}}_{i,\ell })_{i,\ell \in I}\) given by
is of Schur-type. Then \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) satisfies the \(\alpha \)-local integrability condition relative to \({\mathcal {O}}^c\), and \(\Vert N\Vert _{\mathrm {Schur}} \le \Vert {\widetilde{N}} \Vert _{\mathrm {Schur}}\), where N is as defined in Eq. (5.12).
Proof
By assumption, \(\Vert {\widetilde{N}} \Vert _{\mathrm {Schur}} < \infty \). We first show that
To show this, first note that since \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) is of full measure, so is
since \({\mathcal {O}}_0^c = \bigcup _{j \in J} \bigcup _{\alpha \in C_j^{-t} {\mathbb {Z}}^d} ({\mathcal {O}}^c - \alpha )\) is a countable union of null-sets. If \(\xi \in {\mathcal {O}}_0\) and \(j \in J\), \(\alpha \in C_j^{-t} {\mathbb {Z}}^d\) are arbitrary, then \(\xi + \alpha \in {\mathcal {O}}\) and hence \(\sum _{i \in I} \varphi _i(\xi +\alpha ) = 1\), whence \(1 \le \sum _{i \in I} |\varphi _i(\xi +\alpha )|\). Now, let \(\xi \in {\mathcal {O}}_0 \subset {\mathcal {O}}\) be arbitrary and choose \(i_0 \in I\) such that \(\xi \in Q_{i_0}\). Then, \(\sum _{\ell \in i_0^*} \varphi _{\ell } (\xi ) = 1\). Thus, using the estimate \(\Vert f\Vert _{\sup } \le \Vert {\mathcal {F}}^{-1} f\Vert _{L^1}\), we see that
In combination with our standing assumption (4.1), this proves (5.14).
Now, the monotone convergence theorem and (5.14) show for arbitrary \(f \in {\mathcal {B}}_{{\mathcal {O}}} ({\mathbb {R}}^d)\) that
since \({\widehat{f}} \in L^\infty (\widehat{{\mathbb {R}}}^d)\) and \(\mathop {{\text {supp}}}{\widehat{f}} \subset {\mathcal {O}}\) is compact. This shows that \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) satisfies the \(\alpha \)-LIC.
Finally, recall that \( t_\alpha (\xi ) = \sum _{j \in \kappa (\alpha )} |\det C_j|^{-1} \, \overline{\widehat{g_j}(\xi )} \, \widehat{g_j}(\xi + \alpha ), \) where \(\kappa (\alpha ) = \{ j \in J :\alpha \in C_j^{-t} {\mathbb {Z}}^d \}\). Therefore, the matrix entries \(N_{i,\ell }\) defined in (5.12) satisfy
Thus, \(\Vert N\Vert _{\mathrm {Schur}} \le \Vert {\widetilde{N}} \Vert _{\mathrm {Schur}}\), as claimed. \(\square \)
5.5 Invertibility in the Case \((p,q) = (2,2)\)
In this subsection, we focus on the special case \((p,q) = (2,2)\), where the following identification holds; see [61, Lemma 6.10].
Lemma 5.11
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \(\emptyset \ne {\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\), and let \({w = (w_i)_{i \in I}}\) be a \({\mathcal {Q}}\)-moderate weight. Then there is a measurable weight \(v : {\mathcal {O}}\rightarrow (0,\infty )\) with \(v (\xi ) \asymp w_i\) for all \(\xi \in Q_i\) and \(i \in I\). Furthermore, \( {\mathcal {D}}({\mathcal {Q}}, L^2, \ell _w^2) = {\mathcal {F}}^{-1}( L^2_v ({\mathcal {O}})) \) with equivalent norms, where the norm \( \Vert f\Vert _{{\mathcal {F}}^{-1} (L_v^2 ({\mathcal {O}}))} := \Vert {\widehat{f}}\Vert _{L_v^2 ({\mathcal {O}})} \) is used on \( {\mathcal {F}}^{-1} (L_v^2 ({\mathcal {O}})) = \big \{ f \in Z'({\mathcal {O}}) \,:\, {\widehat{f}} \in L_v^2 ({\mathcal {O}}) \big \} \).
We will also make use of the following two lemmata.
Lemma 5.12
Let \(\emptyset \ne {\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) be an open set, let \(v : {\mathcal {O}}\rightarrow (0,\infty )\) be a weight function, and let \(t_0\) be as in Eq. (5.2). Then, the Fourier multipliers \( T_0 : {\mathcal {F}}^{-1} (L^2_v ({\mathcal {O}})) \rightarrow {\mathcal {F}}^{-1} (L_v^2 ({\mathcal {O}})), f \mapsto {\mathcal {F}}^{-1} (t_0 \, {\widehat{f}} \,) \) and
are well-defined and bounded, with \(\Vert T_0^{-1} \Vert _{\mathrm {op}} \le A^{-1}\) and \(\Vert T_0\Vert _{\mathrm {op}} \le B\), where \(A,B > 0\) are as in (4.1).
Proof
If \(f \in {\mathcal {F}}^{-1}(L_v^2 ({\mathcal {O}}))\), then
The argument for \(T_0\) is similar. \(\square \)
Lemma 5.13
Let \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) be an open set of full measure and let \(v : \widehat{{\mathbb {R}}}^d \rightarrow (0,\infty )\) be \(v_0\)-moderate for some symmetric weight \(v_0 : \widehat{{\mathbb {R}}}^d \rightarrow (0,\infty )\); that is, \(v(\xi +\eta ) \le C_v \cdot v (\xi ) \cdot v_0(\eta )\) for all \(\xi ,\eta \in \widehat{{\mathbb {R}}}^d\) and some \(C_v > 0\). Then the operator R defined in Eq. (5.9) satisfies
Proof
Since \({\mathcal {O}}\) is of full measure, we have \({\mathcal {F}}^{-1} (L_v^2 ({\mathcal {O}})) = {\mathcal {F}}^{-1} (L_v^2 (\widehat{{\mathbb {R}}}^d))\), up to canonical identifications. Let \(g \in L^2 (\widehat{{\mathbb {R}}}^d)\) and \(f \in {\mathcal {F}}^{-1}(L_v^2 ({\mathcal {O}}))\) be such that \(\Vert g\Vert _{L^2} \le 1\) and \(\Vert f\Vert _{{\mathcal {F}}^{-1}(L_v^2 ({\mathcal {O}}))} \le 1\). Using the estimates \(v(\xi ) \le C_v \cdot v(\xi - \alpha ) \cdot v_0 (\alpha )\) and \(|a b| \le \frac{1}{2} \big ( |a|^2 + |b|^2 \big )\) and the identity \(t_\alpha (\xi - \alpha ) = \overline{t_{-\alpha } (\xi )}\), it follows that
Since this holds for all \(g \in L^2(\widehat{{\mathbb {R}}}^d)\) with \(\Vert g\Vert _{L^2} \le 1\), the series
is almost everywhere absolutely convergent, and
for all \(f \in {\mathcal {F}}^{-1} (L_v^2 ({\mathcal {O}}))\) with \(\Vert f\Vert _{{\mathcal {F}}^{-1}(L_v^2 ({\mathcal {O}}))} \le 1\). This proves the claim. \(\square \)
Using the previous lemmata, the following result follows easily. See [45, Theorem 3.3] for a similar result in \(L^2\).
Proposition 5.14
Let \({\mathcal {Q}}= (Q_i)_{i \in I}\) be a decomposition cover of an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) of full measure, and let \(w = (w_i)_{i \in I}\) be \({\mathcal {Q}}\)-moderate. Suppose \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) satisfies the \(\alpha \)-local integrability condition (5.1) relative to \({\mathcal {O}}^c\). Finally, assume that
where \(A > 0\) is as in (4.1), where \(v : \widehat{{\mathbb {R}}}^d \rightarrow (0,\infty )\) is a measurable weight that satisfies \(v(\xi ) \asymp w_i\) for all \(\xi \in Q_i\) and \(i \in I\), and where \(v_0 : \widehat{{\mathbb {R}}}^d \rightarrow (0,\infty )\) is assumed to be a symmetric weight satisfying \(v(\xi + \eta ) \le C_v \cdot v(\xi ) \cdot v_0 (\eta )\) for all \(\xi , \eta \in \widehat{{\mathbb {R}}}^d\).
Then, the frame operator \(S : {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d) \rightarrow L^2({\mathbb {R}}^d)\) associated to \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) uniquely extends to a bounded linear operator \(S_0 : {\mathcal {D}}({\mathcal {Q}},L^2,\ell _w^2) \rightarrow {\mathcal {D}}({\mathcal {Q}},L^2,\ell _w^2)\). This extended operator is boundedly invertible.
Proof
Lemmas 5.12 and 5.13 show, respectively, that the operators \(T_0\) and R defined in these lemmas yield bounded operators on \({\mathcal {F}}^{-1}(L_v^2({\mathcal {O}}))\), so that \(S_0 := T_0 + R : {\mathcal {F}}^{-1} (L_v^2({\mathcal {O}})) \rightarrow {\mathcal {F}}^{-1} (L_v^2({\mathcal {O}}))\) is well-defined and bounded. As seen in Proposition 5.2, we have \(S_0 f = S f\) for all \({f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d) \subset {\mathcal {B}}_{{\mathcal {O}}}({\mathbb {R}}^d)}\). Furthermore, \({\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d) \subset {\mathcal {D}}({\mathcal {Q}},L^2,\ell _w^2) = {\mathcal {F}}^{-1}(L_v^2({\mathcal {O}}))\) is dense (see Proposition 3.13 and Lemma 5.11); therefore, \(S_0\) is the unique bounded extension of S.
Finally, conditions (4.1) and (5.16) together with Lemma 5.12 and Lemma 5.13 yield that
Hence, \(S_0 = T_0 + R\) is boundedly invertible on \({\mathcal {F}}^{-1}(L_v^2({\mathcal {O}}))\) by Lemma 5.4. Using the norm equivalence \( \Vert \cdot \Vert _{{\mathcal {F}}^{-1} (L^2_v ({\mathcal {O}}))} \asymp \Vert \cdot \Vert _{{\mathcal {D}} ({\mathcal {Q}}, L^2, \ell ^2_w)} \) provided by Lemma 5.11, it follows therefore that also \(S_0 : {\mathcal {D}}({\mathcal {Q}}, L^2, \ell ^2_w) \rightarrow {\mathcal {D}}({\mathcal {Q}}, L^2, \ell ^2_w)\) is boundedly invertible. \(\square \)
Remark 5.15
The formulation of Proposition 5.14 is rather technical, because, under those assumptions, the formula defining the frame operator might not make sense for \(f \in {\mathcal {D}}({\mathcal {Q}},L^2,\ell _w^2)\). Indeed, the hypothesis are satisfied for every tight frame, even if \(g_j \notin {\mathcal {D}}({\mathcal {Q}},L^2,\ell _w^2)\). If, in addition, \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is assumed to be \((w,v,\Phi )\)-adapted for some weight v, then Proposition 4.8 applies and we can conclude unambiguously that \(S : {\mathcal {D}}({\mathcal {Q}},L^2,\ell _w^2) \rightarrow {\mathcal {D}}({\mathcal {Q}},L^2,\ell _w^2)\) is well-defined, bounded and boundedly invertible on \({\mathcal {D}}({\mathcal {Q}},L^2,\ell _w^2)\).
Remark 5.16
If \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is a tight frame for \(L^2 ({\mathbb {R}}^d)\) with lower frame bound \(A > 0\), which furthermore satisfies the \(\alpha \)-local integrability condition, then the multipliers \(t_{\alpha } \in L^{\infty } (\widehat{{\mathbb {R}}}^d)\) satisfy \(t_{\alpha } (\xi ) = A \, \delta _{\alpha , 0}\) for a.e. \(\xi \in \widehat{{\mathbb {R}}}^d\) and all \(\alpha \in \Lambda \), cf. [41, Theorem 3.4]. The condition (5.16) is then obviously satisfied. The placement of the absolute value sign outside of the series defining the multipliers \(t_{\alpha }\) allows for cancellations, which can be very important [45].
6 Concrete Estimates for Affinely Generated Covers
In this section, we simplify the results of Sect. 5 for the case that the decomposition cover \({\mathcal {Q}}\) is affinely generated. The results obtained here will be further simplified in Sect. 7.
In the sequel, we will repeatedly use \({\mathcal {Q}}\)-localized versions of the generating functions \(g_j\) of the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\). Precisely, given a family \((g_j)_{j \in J}\) of generating functions \({g_j \in L^1 ({\mathbb {R}}^d) \cap L^2 ({\mathbb {R}}^d)}\) and a family \((S_i)_{i \in I}\) of invertible affine-linear maps \(S_i = A_i (\cdot ) + b_i\), we let
so that \({\mathcal {F}}g^{\natural }_{i,j} = \widehat{g_j} \circ S_i\).
6.1 Boundedness of the Frame Operator
As a first step, we provide a sufficient condition for a system to be adapted (see Definition 4.3). The proof makes use of the following self-improving property of amalgam spaces, which is taken from [62, Theorem 2.17].
Lemma 6.1
Let \(f \in {\mathcal {S}}'({\mathbb {R}}^d)\) with \(\mathop {{\text {supp}}}{\widehat{f}} \subset A [-R, R]^d + \xi _0\) for some \(A \in \mathrm {GL}(d, {\mathbb {R}})\), \(\xi _0 \in \widehat{{\mathbb {R}}}^d\), and \(R > 0\). Then, there exists a constant \(C = C(d) > 0\) which only depends on \(d \in {\mathbb {N}}\) such that
Proposition 6.2
Let \({\mathcal {Q}}= \big ( A_i (Q_i') + b_i \big )_{i \in I}\) be an affinely generated cover of \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\), and let \(\Phi = (\varphi _i)_{i \in I}\) be a regular partition of unity subordinate to \({\mathcal {Q}}\). Let \(w = (w_i)_{i \in I}\) be \({\mathcal {Q}}\)-moderate, and let \(v = (v_j)_{j \in J}\) be a weight. Suppose that the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) satisfies, for \((i,j) \in I \times J\),
and that \(G = (G_{i,j})_{i \in I, j \in J} \in {\mathbb {C}}^{I \times J}\) is of Schur-type. Then, \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted. Consequently, the frame operator \(S : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is well-defined and bounded.
Proof
We will estimate  for \((i,j) \in I \times J\). Choose \(r > 1\) such that \(\overline{Q_i '} \subset [-r, r]^d\) for all \(i \in I\). The norm equivalence \(\Vert \cdot \Vert _{W(C_0,\ell ^1)} \asymp \Vert \cdot \Vert _{W_{[-1,1]^d} (C_0,L^1)}\) yields an absolute constant \(K_1 = K_1 (d) > 0\) satisfying
for \((i,j) \in I \times J\). Choose \(r > 1\) such that \(\overline{Q_i '} \subset [-r, r]^d\) for all \(i \in I\). The norm equivalence \(\Vert \cdot \Vert _{W(C_0,\ell ^1)} \asymp \Vert \cdot \Vert _{W_{[-1,1]^d} (C_0,L^1)}\) yields an absolute constant \(K_1 = K_1 (d) > 0\) satisfying

for \(i \in I\) and \(j \in J\). Here, we used Eq. (2.1) in the last step. Define \(P_{i,j} := r \cdot \Vert C_j^t A_i \Vert _{\ell ^\infty \rightarrow \ell ^\infty }\). Since \(\mathop {{\text {supp}}}\varphi _i \subset A_i(\overline{Q_i '}) + b_i\), it follows that

Therefore, Lemma 6.1 yields a constant \(K_2 = K_2 (d) > 0\) such that

Next, recalling the notion of the normalized version \(\varphi _i^{\flat } = \varphi _i \circ S_i\) of \(\varphi _i\) (Definition 3.6), we see
whence Lemma A.2 shows that
Now, since \(\varphi ^{\flat }_i\) vanishes outside of \(Q_i '\), it follows that  for all \(\xi \in \widehat{{\mathbb {R}}}^d\) and any \(\alpha \in {\mathbb {N}}_0^d\) with \(|\alpha | \le d + 1\), where \( K_3 := \max _{|\alpha | \le d+1} \sup _{i \in I} \Vert \partial ^\alpha \varphi _i^{\flat } \Vert _{L^\infty } \). An application of the Leibniz rule therefore yields
for all \(\xi \in \widehat{{\mathbb {R}}}^d\) and any \(\alpha \in {\mathbb {N}}_0^d\) with \(|\alpha | \le d + 1\), where \( K_3 := \max _{|\alpha | \le d+1} \sup _{i \in I} \Vert \partial ^\alpha \varphi _i^{\flat } \Vert _{L^\infty } \). An application of the Leibniz rule therefore yields

for any \(\theta \in {\mathbb {N}}_0^d\) with \(|\theta | \le d+1\). Integrating this last inequality and combining it with (6.2) yields

for a constant \(K = K({\mathcal {Q}}, d, \Phi ) > 0\). Therefore, the matrix entries \(M_{i,j}\) defined in Eq. (4.2) satisfy

This implies \(\Vert M\Vert _{\mathrm {Schur}} \le K \cdot \Vert G\Vert _{\mathrm {Schur}} < \infty \), so that \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted. \(\square \)
6.2 The Main Term
In this section, we provide a simplified bound for the operator norm of \(T_0^{-1} : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\).
Proposition 6.3
Let \({\mathcal {Q}}= (S_i (Q_i '))_{i \in I}\) be an affinely generated cover of an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) of full measure. Let \(\Phi = (\varphi _i)_{i \in I}\) be a regular partition of unity subordinate to \({\mathcal {Q}}\). Suppose the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) satisfies
Then, the function \(t_0\) defined in Eq. (5.2) is continuous on \({\mathcal {O}}\) and tame, and Eq. (4.1) holds for all \(\xi \in {\mathcal {O}}\). Furthermore, for all \(p,q \in [1,\infty ]\) and any \({\mathcal {Q}}\)-moderate weight \(w = (w_i)_{i \in I}\), the operator
with \(\Phi _{t_0}\) as in Proposition 5.7 is well-defined, bounded, and boundedly invertible, with
where \(A > 0\) is as in (4.1) and
Proof
We divide the proof into four steps.
Step 1. We show that the series defining \(t_0\) converges locally uniformly on \({\mathcal {O}}\), that Eq. (4.1) holds pointwise on \({\mathcal {O}}\), and that \(t_0\) is tame.
To see this, set \(\gamma _j := |\widehat{g_j}|^2 / |\det C_j|\), and note \(t_0 = \sum _{j \in J} \gamma _j\) and that \(\gamma _j \in C^\infty (\widehat{{\mathbb {R}}}^d)\) thanks to our standing assumptions regarding the \(g_j\). Now, for arbitrary \(i \in I\), recall that \(\varphi _i^{\flat } = \varphi _i \circ S_i\) vanishes outside \(Q_i '\), so that the Leibniz rule shows
for \(c_0 := 2^{d+1} \, \max _{|\nu | \le d+1} C_{{\mathcal {Q}},\Phi ,\nu }\) and arbitrary \(\alpha \in {\mathbb {N}}_0^d\) with \(|\alpha | \le d+1\).
Therefore, using the notation \({\mathbb {I}} := \{0\} \cup \{ (d+1) \, e_\ell :\ell \in \underline{d} \}\) (where \((e_1,\dots ,e_d)\) denotes the standard basis of \({\mathbb {R}}^d\)), Lemma A.2 shows because of \( \Vert \varphi _i \cdot \gamma _j\Vert _{{\mathcal {F}}L^1} = \Vert \varphi _i^{\flat } \cdot (\gamma _j \circ S_i)\Vert _{{\mathcal {F}}L^1} \) and \(\tfrac{d+1}{\pi ^d} \le 1\) that
where \(c_1 = c_1({\mathcal {Q}}, d) > 0\) is a constant satisfying \(\Vert \cdot \Vert _{L^1 (Q_i ')} \le c_1 \cdot \Vert \cdot \Vert _{L^{d+1} (Q_i ')}\) for all \(i \in I\), which exists since the \((Q'_i)_{i \in I}\) are uniformly bounded. Estimate (6.6) implies that
where M is as in (6.3). This guarantees the locally uniform convergence on \({\mathcal {O}}\) of the series \({t_0 = \sum _{j \in J} \gamma _j}\). Indeed, if \(\xi \in {\mathcal {O}}\) is arbitrary, then \(\xi \in Q_i\) for some \(i \in I\) where \(Q_i\) is open; furthermore, \(\sum _{\ell \in i^*} \varphi _\ell \equiv 1\) on \(Q_i\) and hence \( \sum _{j \in J} \Vert \gamma _j\Vert _{L^\infty (Q_i)} \le \sum _{j \in J} \sum _{\ell \in i^*} \Vert \varphi _\ell \cdot \gamma _j\Vert _{\sup } < \infty \), which shows that the series \(t_0 = \sum _{j \in J} \gamma _j\) converges uniformly on \(Q_i\). By locally uniform convergence, we see that \(t_0\) is continuous on \({\mathcal {O}}\). Eq. (4.1) shows that \(A \le t_0 \le B\) almost everywhere on \({\mathcal {O}}\); since \({\mathcal {O}}\) is open and \(t_0\) continuous, this estimate necessarily holds pointwise on \({\mathcal {O}}\).
Finally, since \(\mathop {{\text {supp}}}\varphi _i \subset {\mathcal {O}}\) is compact, we see \(\varphi _i \, t_0 = \sum _{j \in J} \varphi _i \gamma _j\) with uniform convergence of the series, and hence with convergence in \(L^1(\widehat{{\mathbb {R}}}^d)\), since all summands have support in the fixed compact set \(\overline{Q_i} \subset {\mathcal {O}}\). Thus, \({\mathcal {F}}^{-1} (\varphi _i \, t_0) = \sum _{j \in J} {\mathcal {F}}^{-1} (\varphi _i \, \gamma _j)\), which leads to the estimate \( \sup _{i \in I} \Vert {\mathcal {F}}^{-1} (\varphi _i \, t_0)\Vert _{L^1} \le \sup _{i \in I} \sum _{j \in J} \Vert \varphi _i \cdot \gamma _j\Vert _{{\mathcal {F}}L^1} \le c_0 \, c_1 \cdot M < \infty \). Thus, \(t_0\) is tame, so that Proposition 5.7 shows that \(T_0 = \Phi _{t_0} : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is well-defined and bounded.
Step 2. In this step, we prepare for applying Lemma A.4; we cannot apply it directly, since \(t_0\) might not be \(C^{d+1}\). Thus, we will construct a sequence \((g_N)_{N \in {\mathbb {N}}}\) of smooth functions approximating \(t_0\). We will then apply Lemma A.4 to the \(g_N\) in Step 3.
For the construction of the \((g_N)_{N \in {\mathbb {N}}}\), first note that J is infinite; indeed, we have \(\widehat{g_j} \in C_0 (\widehat{{\mathbb {R}}}^d)\) for all \(j \in J\) since \(g_j \in L^1({\mathbb {R}}^d)\); thus, (4.1) can only hold if J is infinite. Since J is countable, we thus have \(J = \{ j_n :n \in {\mathbb {N}}\}\) for certain pairwise distinct \(j_n \in J\). With this, define \(g_N := \sum _{n=1}^N \gamma _{j_n} \in C^\infty (\widehat{{\mathbb {R}}}^d)\). As seen in Step 1, \(g_N \rightarrow t_0\) locally uniformly on \({\mathcal {O}}\). Since \(0 < A \le t_0 \le B\) on \({\mathcal {O}}\), this easily implies \(G_{N} \rightarrow \tfrac{1}{t_0}\) locally uniformly on \({\mathcal {O}}\), where we defined
Thus, \(\varphi _i \cdot G_N \rightarrow \varphi _i \cdot t_0^{-1}\) in \(L^1(\widehat{{\mathbb {R}}}^d)\), and hence \({\mathcal {F}}^{-1} (\varphi _i \, G_N) \rightarrow {\mathcal {F}}^{-1} (\varphi _i \cdot t_0^{-1})\) uniformly as \(N \rightarrow \infty \). Therefore, Fatou’s lemma shows that
Step 3. We next estimate \(\liminf _{N \rightarrow \infty } \Vert \varphi _i^{\flat } \cdot (G_N \circ S_i) \Vert _{{\mathcal {F}}L^1}\). Define
Let \(V_i \subset {\mathcal {O}}\) be open and bounded with \(\overline{Q_i} \subset V_i \subset \overline{V_i} \subset {\mathcal {O}}\) and let \(\varepsilon \in (0,1)\). Since \(g_N \rightarrow t_0\) uniformly on \(V_i\) and \(t_0 \ge A > 0\) on \({\mathcal {O}}\supset V_i\), there is \(N_0 = N_0 (i,\varepsilon ) \in {\mathbb {N}}\) such that \(g_N \ge (1-\varepsilon ) \, A =: A_\varepsilon \) on \(V_i\) for all \(N \ge N_0\). Note that \(K_i^{(N)} (\xi ) \ge \sum _{n=1}^N \gamma _{j_n} (S_i \xi ) = g_N (S_i \xi ) \ge A_\varepsilon \) for \(\xi \in S_i^{-1}(V_i)\) and \(N \ge N_0\).
Define \(U_i := S_i^{-1} (V_i)\), fix \(\xi ^{(0)} \in U_i\) and \(\ell \in \underline{d}\), set
and, for \(N \ge N_0\), let \( f_N : U \rightarrow [A_\varepsilon , \infty ), \xi \mapsto (g_N \circ S_i) ( \xi _1^{(0)}, \dots , \xi _{\ell -1}^{(0)}, \xi , \xi _{\ell +1}^{(0)}, \dots , \xi _d^{(0)} ), \) noting that \(\big | f_N^{(m)} (\xi _\ell ^{(0)}) \big | \le K_i^{(N)} (\xi ^{(0)})\) for all \(m \in \underline{d+1}\). Hence, Lemma A.4 shows for all \(m \in \underline{d+1}\) that
where \(C_{d+1}\) is as in Lemma A.4.
Since \(\xi ^{(0)} \in U_i\) was arbitrary, we have thus shown, for all \(\xi \in U_i\) and \(N \ge N_0\),
Finally, since \(\varphi _i^{\flat } = \varphi _i \circ S_i\) vanishes outside of \(Q_i' = S_i^{-1} (Q_i) \subset S_i^{-1} (V_i) = U_i\), the Leibniz rule shows
for all \(\xi \in \widehat{{\mathbb {R}}}^d\), \(\ell \in \underline{d}\), \(0 \le m \le d+1\), and \(N \ge N_0\). Thus, Lemma A.2 shows
Since this holds for all \(N \ge N_0 = N_0(i,\varepsilon )\), and since \(A_\varepsilon = (1-\varepsilon ) A\) where \(\varepsilon \in (0,1)\) is arbitrary, we thus see by virtue of Eq. (6.7) that
for all \(i \in I\). Hence, \(t_0^{-1}\) is tame, and Proposition 5.7 shows that \(\Phi _{t_0^{-1}} : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is well-defined and bounded, with operator norm bounded by the right-hand side of Eq. (6.4).
Step 4. Proposition 5.7(iv) shows \(\Phi _{t_0^{-1}} \Phi _{t_0} = \Phi _{\mathbf{1 }} = \Phi _{t_0} \Phi _{t_0^{-1}}\), where \(\mathbf{1 } : {\mathcal {O}}\rightarrow {\mathbb {R}}, \xi \mapsto 1\). Directly from the definition of \(\Phi _{\mathbf{1 }}\) in Proposition 5.7, we see \(\Phi _{\mathbf{1 }} f = f\) for all \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\). Hence, \(T_0 : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is boundedly invertible with \(T_0^{-1} = \Phi _{t_0^{-1}}\). \(\square \)
6.3 The Remainder Term
The next (technical) result provides an estimate of the operator norm of the remainder term \(R_0 : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) considered in Corollary 5.9. Here, we make use of a normalized version \(g_j^{\diamond }\) of the generators \((g_j)_{j \in J}\) of \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\), namely
for invertible affine-linear maps \(U_j = B_j (\cdot ) + c_j\); note that \(\widehat{\, g_j^{\diamond } \,} = |\det B_j|^{1/2} \cdot \widehat{g_j} \circ U_j\).
Lemma 6.4
Let \({\mathcal {Q}}= (S_i (Q_i '))_{i \in I} = (A_i \, (Q_i ') + b_i)_{i \in I}\) be an affinely generated cover of an open set \({{\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d}\) of full measure. Let \(\Phi = (\varphi _i)_{i \in I}\) be a regular partition of unity subordinate to \({\mathcal {Q}}\), and let \(w = (w_i)_{i \in I}\) be a \({\mathcal {Q}}\)-moderate weight. Let \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) be a generalized shift-invariant system. Furthermore, assume that \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,v,\Phi )\)-adapted for some weight \(v = (v_j)_{j \in J}\), and assume that the function \(t_0\) introduced in Eq. (5.2) is tame.
Suppose that there is a family \((U_j)_{j \in J}\) of invertible affine-linear maps \(U_j = B_j (\cdot ) + c_j \) and a weight \(v = (v_j)_{j \in J}\) such that the Fourier transform of \(g_j^{\diamond } = |\det B_j|^{-1/2} \cdot (M_{-c_j} \, g_j)\circ B_j^{-t}\) can be factorized as \({\mathcal {F}}g_j^{\diamond } = h_{j,1} \cdot h_{j,2}\) with \(h_{j,1}, h_{j,2} \in C^{d+1}(\widehat{{\mathbb {R}}}^d)\) satisfying
Moreover, suppose that \(Y = (a_{i,j} X_{i,j})_{i \in I, j \in J} \) and \(Z = (b_{i,j} X_{i,j})_{i \in I, j \in J}\) are of Schur-type, where
and
and
Then, for all \(p,q \in [1,\infty ]\), the operator \(R_0 : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) of Corollary 5.9 is bounded, with \( \Vert R_0\Vert _{\mathrm {op}} \le C_0 C_{p,q} \Vert \Gamma _{{\mathcal {Q}}} \Vert _{\ell ^q_w \rightarrow \ell ^q_w} \cdot (C')^2 \cdot \Vert Y\Vert _{\mathrm {Schur}} \Vert Z\Vert _{\mathrm {Schur}} \), where
with \(R_{{\mathcal {Q}}} := \max _{i \in I} \sup _{\xi \in Q_i '} |\xi |\) and \(C_{p,q} := 1\) if \(\max \{p,q\} < \infty \) and \(C_{p,q} := C_{\Phi } \cdot \Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell _w^q \rightarrow \ell _w^q}^2\) otherwise.
Proof
For brevity, set \(\nu (x) := \max \{1, x\}\) for \(x \in [0,\infty )\), and note \(\nu (xy) \le \nu (x) \, \nu (y)\). This implies \(\nu (w_i / w_\ell ) \le \nu (w_i/v_j) \cdot \nu (v_j/w_\ell )\), an estimate that we will employ frequently.
According to Proposition 5.8 and Corollary 5.10, it suffices to estimate
where \( K_{i,\ell ,j,k} := |\det C_j|^{-1} \cdot \big \Vert \overline{\widehat{g_j}} \cdot \widehat{g_j}(\cdot - C_j^{-t}k) \cdot \varphi _i (\cdot - C_j^{-t}k) \cdot \varphi _\ell \big \Vert _{{\mathcal {F}}L^1} \). In order to do so, note that \( \widehat{g_j} = |\det B_j|^{-1/2} \cdot ({\mathcal {F}}g_j^{\diamond }) \circ U_j^{-1} \). Hence, since \({\mathcal {F}}g_j^{\diamond } = h_{j,1} \cdot h_{j,2}\) by assumption, the term \(K_{i,\ell ,j,k}\) can be estimated as follows:

Using the preceding estimate, one can bound \(L_1\) from Eq. (6.10) as follows:
A similar calculation gives
The remainder of the proof is divided into four steps:
Step 1. Estimates for \(K_{i,j,k}^{(1)}\) and \(K_{\ell ,j,k}^{(2)}\). For \(j \in J\) and \(k \in {\mathbb {Z}}^d\), set \( H_{j,k} := \overline{h_{j,1}} \cdot T_{B_j^{-1} C_j^{-t} k} \, h_{j,2}. \) Since \(T_{\xi } \, (g \circ U_j^{-1}) = (T_{B_j^{-1} \xi } \, g) \circ U_j^{-1}\) for any \(\xi \in \widehat{{\mathbb {R}}}^d\) and \(g : \widehat{{\mathbb {R}}}^d \rightarrow {\mathbb {C}}\), it follows that

Using the normalization \(\varphi _i^{\flat } = \varphi _i \circ S_i\) of \(\varphi _i\), a direct calculation shows

Now, define \( \zeta _j : \widehat{{\mathbb {R}}}^d \rightarrow [0,\infty ), \; \xi \mapsto \max _{|\alpha | \le d+1} |\partial ^\alpha h_{j,1} (\xi )| \, . \) By applying Leibniz’ rule, combined with the assumption \( \max _{|\alpha | \le d+1} |\partial ^\alpha h_{j,2} (\xi )| \le C' \cdot (1 + |\xi |)^{-(d+1)}\) and the identity \(\sum _{\beta \le \alpha } \left( {\begin{array}{c}\alpha \\ \beta \end{array}}\right) = 2^{|\alpha |}\), we see
for all \(\alpha \in {\mathbb {N}}_0^d\) with \(|\alpha | \le d+1\) and all \(\xi \in \widehat{{\mathbb {R}}}^d\). This, together with Lemma A.3, yields that, for all \(n \in {\underline{d}}\) and \(m \in \{0,\dots ,d+1\}\),

Since \(\Phi \) is a regular partition of unity, we have \( |\partial ^\alpha \varphi _i^{\flat } (\xi )| \le C_{{\mathcal {Q}},\Phi ,\alpha } \cdot {\mathbb {1}}_{Q_i '} (\xi ) \) for all \(\xi \in \widehat{{\mathbb {R}}}^d\) and \(\alpha \in {\mathbb {N}}_0^d\). Thus, setting \(C_1 := (4d)^{d+1} C' \cdot \max _{|\alpha | \le d+1} C_{{\mathcal {Q}},\Phi ,\alpha }\) and invoking Leibniz’s rule once more, we see that

Clearly, the same overall estimate also holds for  itself instead of its derivative
itself instead of its derivative  . Thus, setting
. Thus, setting
we can apply Lemma A.2 and Eq. (6.13) to conclude

where \({\mathbb {I}} := \{0\} \cup \{(d+1) \cdot e_n \,:\, n \in {\underline{d}} \}\). By similar arguments as for \(K_{i,j,k}^{(1)}\), one obtains
Step 2. Estimating the supremum over \(k \in {\mathbb {Z}}^d \setminus \{0\}\). Note that \(|\xi | \le \Vert A^{-1}\Vert \cdot |A \xi |\), and thus \(|A \xi | \ge \Vert A^{-1}\Vert ^{-1} \cdot |\xi |\) for any \(\xi \in \widehat{{\mathbb {R}}}^d\) and \(A \in \mathrm {GL}({\mathbb {R}}^d)\). Hence,
This implies for arbitrary \(i \in I\), \(\xi \in Q_i '\), \(k \in {\mathbb {Z}}^d \setminus \{0\}\), and \(j \in J\) that
Setting \(C_3 := 3^{d+1} \cdot \max \big \{1, R_{{\mathcal {Q}}}^{d+1} \big \}\), the preceding estimate implies
for all \(i \in I\), \(\xi \in Q_i '\), and \(j \in J\). Using this, and the estimates for \(K_{i,j,k}^{(n)}\) that we derived in Step 1, we see that
for \(n \in \{1,2\}\), \(i \in I\), and \(j \in J\).
Step 3. Estimating the sum over \(k \in {\mathbb {Z}}^d \setminus \{0\}\). Estimate (6.15) implies
By combining this estimate with Corollary D.2, we see for any \(\xi \in Q_i '\) that
Here, we used in the last step that \(|\xi | \le R_{\mathcal {Q}}\) since \(\xi \in Q_i '\).
By combining this estimate with the estimate for \(K_{i,j,k}^{(n)}\) from Step 1, we see for \(n \in \{1,2\}\) and arbitrary \(i \in I\) and \(j \in J\) that
where we defined \(C_4 := (d+1) \cdot 2^{3 + 4d} \cdot (2 + R_{\mathcal {Q}}) \cdot C_2\).
Step 4. Completing the proof. Combining the two estimates (6.11) and (6.12) with the estimates obtained in Equations (6.17) and (6.16), we conclude that
The estimate \(L_2 \le C_0 \cdot (C')^2 \cdot \Vert Y \Vert _{\mathrm {Schur}} \, \Vert Z \Vert _{\mathrm {Schur}}\) is obtained similarly. Hence, an application of Corollaries 5.9 and 5.10 gives \( \Vert R_0 \Vert _{\mathrm {op}} \le C_0 C_{p,q} \Vert \Gamma _{{\mathcal {Q}}} \Vert _{\ell ^q_w \rightarrow \ell ^q_w} \cdot (C')^2 \cdot \Vert Y \Vert _{\mathrm {Schur}} \Vert Z\Vert _{\mathrm {Schur}} \), as desired. \(\square \)
7 Results for Structured Systems
In this section, we provide further simplified conditions for the boundedness and invertibility of the frame operator. For this, we will assume throughout this section that the family \((g_j)_{j \in J}\) of functions \(g_j \in L^1({\mathbb {R}}^d) \cap L^2 ({\mathbb {R}}^d)\) defining the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) possess the form
for certain \(A_j \in \mathrm {GL}(d, {\mathbb {R}})\) and \(b_j \in \widehat{{\mathbb {R}}}^d\) and a fixed \(g \in L^1({\mathbb {R}}^d) \cap L^2({\mathbb {R}}^d)\) satisfying \({\widehat{g}} \in C^\infty (\widehat{{\mathbb {R}}}^d)\).
Observe that (7.1) can be written as \(g_j = |\det A_j|^{-1/2} \cdot {\mathcal {F}}^{-1} ({\widehat{g}} \circ S_j^{-1})\), where \(S_j = A_j (\cdot ) + b_j\).
7.1 Simplified Criteria for Invertibility of the Frame Operator
In this subsection, we give simplified versions of the estimates for the operator norms of \(T_0^{-1}\) and \(R_0\), under the assumption that the generators \((g_j)_{j \in J}\) of the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) have the form (7.1) and that the lattices \(C_j {\mathbb {Z}}^d\) are given by \(C_j = \delta A_{j}^{-t}\) for a suitable \(\delta > 0\). We begin with a simplified version of Proposition 6.3.
Proposition 7.1
Let \({\mathcal {Q}}= \big (S_j (Q_j ')\big )_{j \in J} = \big (A_j (Q_j ') + b_j)_{j \in J}\) be an affinely generated cover of an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) of full measure. Let \(\Phi = (\varphi _j)_{j \in J}\) be a regular partition of unity subordinate to \({\mathcal {Q}}\). Let \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) be such that \(C_j := \delta \cdot A_j^{-t}\) for some \(\delta > 0\) and \(g_j := |\det A_j|^{1/2} \cdot M_{b_j} [g \circ A_j^t]\) for some \(g \in L^1({\mathbb {R}}^d) \cap L^2({\mathbb {R}}^d)\) with \({\widehat{g}} \in C^\infty (\widehat{{\mathbb {R}}}^d)\). Suppose that there is some \(A' > 0\) satisfying \(A' \le \sum _{j \in J} |{\widehat{g}} (S_j^{-1} \xi )|^2\) for almost all \(\xi \in {\mathcal {O}}\), and that
Then the function \(t_0\) defined in Eq. (5.2) is continuous on \({\mathcal {O}}\) and tame, and the estimate \({A' \le \sum _{j \in J} |{\widehat{g}} (S_j^{-1} \xi )|^2}\) holds for all \(\xi \in {\mathcal {O}}\). Furthermore, for any \(p,q \in [1,\infty ]\) and any \({\mathcal {Q}}\)-moderate weight \(w = (w_j)_{j \in J}\), the operator
with \(\Phi _{t_0}\) as defined in Proposition 5.7 is well-defined, bounded, and boundedly invertible, with
where \(C'_d = C_d \cdot (2d)^{(d+1)^2}\) with \(C_d\) as in Eq. (6.5).
Proof
We apply Proposition 6.3. For this, note that since \(C_j = \delta \cdot A_j^{-t}\) and \(\widehat{g_j} = |\det A_j|^{-1/2} \cdot {\widehat{g}} \circ S_j^{-1}\), the \({\mathcal {Q}}\)-localized version \(g_{i,j}^{\natural }\) of \(g_j\) defined in (6.1) satisfies \( {\mathcal {F}}g_{i,j}^{\natural } = \widehat{g_j} \circ S_i = |\det A_j|^{-1/2} \cdot {\widehat{g}} \circ S_j^{-1} \circ S_i \) and, moreover, \( |\det C_j|^{-1} \cdot |{\mathcal {F}}g_{i,j}^{\natural }|^2 = \delta ^{-d} \cdot |{\widehat{g}}|^2 \circ S_j^{-1} \circ S_i . \) Leibniz rule entails the pointwise estimate

for any \(\alpha \in {\mathbb {N}}_0^d\) with \(|\alpha | \le d+1\). Since \(S_j^{-1} S_i = A_j^{-1} A_i (\cdot ) + \, A_j^{-1} (b_i - b_j)\), it follows by the chain rule as in Lemma A.3 that, for any \(\nu \in {\mathbb {N}}_0^d\) with \(|\nu | \le d+1\),
for \(\xi \in \widehat{{\mathbb {R}}}^d\). Using this, we can estimate the constant M from Proposition 6.3 as follows:
with \(M_0\) as defined in the statement of the current proposition.
By assumption, we have \(A' \le \sum _{j \in J} |{\widehat{g}} (S_j^{-1} \xi )|^2\), and thus
for almost all \(\xi \in {\mathcal {O}}\) and hence for almost all \(\xi \in \widehat{{\mathbb {R}}}^d\). Therefore, Proposition 6.3 shows that \(t_0\) is continuous on \({\mathcal {O}}\) and tame, that the preceding estimate holds pointwise on \({\mathcal {O}}\), and that the operator \(T_0 : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) is well-defined, bounded, and boundedly invertible with
This completes the proof. \(\square \)
Our next aim is to present a simplified version of the technical Lemma 6.4. For this, we will use the following result whose proof we postpone to Appendix D.2.
Lemma 7.2
Let \(g \in C^{d+1}(\widehat{{\mathbb {R}}}^d)\) be such that there exists a function \(\varrho : \widehat{{\mathbb {R}}}^d \rightarrow [0,\infty )\) satisfying \( |\partial ^\alpha g (\xi )| \le \varrho (\xi ) \cdot (1 + |\xi |)^{-(d+1)} \) for all \(\xi \in \widehat{{\mathbb {R}}}^d\) and \(\alpha \in {\mathbb {N}}_0^d\) with \(|\alpha | \le d+1\). Then, setting
we have \(g = h_1 \cdot h_2\) on \(\widehat{{\mathbb {R}}}^d\). Furthermore, \(h_1,h_2 \in C^{d+1}(\widehat{{\mathbb {R}}}^d)\) satisfy the estimates
for all \(\xi \in \widehat{{\mathbb {R}}}^d\), where \(C' := \big ( 12 \cdot (d+1)^2 \big )^{d+1}\).
Proposition 7.3
Let \({\mathcal {Q}}= \big (S_j (Q_j ')\big )_{j \in J} = \big (A_j (Q_j ') + b_j)_{j \in J}\) be an affinely generated cover of an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) of full measure. Let \(\Phi = (\varphi _j)_{j \in J}\) be a regular partition of unity subordinate to \({\mathcal {Q}}\), and let \(w = (w_j)_{j \in J}\) be \({\mathcal {Q}}\)-moderate. Let \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) be such that \(C_j := \delta \cdot A_j^{-t}\) for some \(\delta \in (0,1]\) and \(g_j := |\det A_j|^{1/2} \cdot M_{b_j} [g \circ A_j^t]\) for some \(g \in L^1({\mathbb {R}}^d) \cap L^2({\mathbb {R}}^d)\) satisfying \({\widehat{g}} \in C^\infty (\widehat{{\mathbb {R}}}^d)\). Assume that the function \(t_0\) defined in Eq. (5.2) is tame. Assume that \({\widetilde{Y}} = ({\widetilde{Y}}_{i,j} )_{i, j \in J}\) is of Schur-type, where
with
Then the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,w,\Phi )\)-adapted. Furthermore, for any \(p,q \in [1,\infty ]\), the operator \(R_0 : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\) defined in Corollary 5.9 is well-defined and bounded, with
with \(C_0\) as in (6.9), \(C'\) as in Lemma 7.2 and \(C_{p,q} := 1\) if \(\max \{p,q\} < \infty \) and \(C_{p,q} := C_{\Phi } \Vert \Gamma _{{\mathcal {Q}}} \Vert ^2_{\ell ^q_w \rightarrow \ell ^q_w}\), otherwise.
Proof
To show that \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,w,\Phi )\)-adapted, we use Proposition 6.2. Let us set \({v_j := w_j}\) for \(j \in J\). Note that \( {\mathcal {F}}g_{i,j}^{\natural } = \widehat{g_j} \circ S_i = |\det A_j|^{-1/2} \cdot {\widehat{g}} \circ S_j^{-1} \circ S_i \). An application of the chain rule as in Lemma A.3 shows, for any \(\alpha \in {\mathbb {N}}_0^d\) with \(|\alpha | \le d+1\), that
and hence \( \int _{Q_i'} \max _{|\alpha | \le d+1} |\partial ^\alpha [{\mathcal {F}}g_{i,j}^{\natural }] (\xi )| \, d \xi \le |\det A_j|^{-1/2} \cdot d^{d+1} \, \max \{ 1, \Vert A_j^{-1} A_i\Vert ^{d+1} \} \cdot {\widetilde{Y}}_{i,j} K_{i,j}^{-1} \). Thus, the matrix entries \(G_{i,j}\) introduced in Proposition 6.2 satisfy
for a suitable constant \(C_{d,\delta } > 0\) which is independent of \(i,j \in J\). Thus \(\Vert G\Vert _{\mathrm {Schur}} < \infty \).
To finish the proof, we will show the claimed bound on \(\Vert R_0\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)}\). For this, we will apply Lemma 6.4 with the choices \(I = J\), \(B_j = A_j\), \(c_j = b_j\) and \(v_j = w_j\). In this setting, we have \({g_j^{\diamond } = g}\) for all \(j \in J\). By defining \( \varrho : \widehat{{\mathbb {R}}}^d \rightarrow [0,\infty ), \; \xi \mapsto (1+|\xi |)^{d+1} \max _{|\alpha | \le d+1} | \partial ^{\alpha } {\widehat{g}}(\xi )| \), we clearly have \(|\partial ^{\alpha } {\widehat{g}}(\xi ) | \le \varrho (\xi ) \cdot (1 + |\xi | )^{-(d+1)}\) for all \(\xi \in \widehat{{\mathbb {R}}}^d\) and \(\alpha \in {\mathbb {N}}_0^d\) with \(|\alpha | \le d+1\). Hence, by Lemma 7.2, we can factorize \({\widehat{g}} = h_1 \cdot h_2\) with \(h_1, h_2 \in C^{d+1} (\widehat{{\mathbb {R}}}^d)\) satisfying (7.2). This shows that the first hypothesis in Lemma 6.4 is satisfied, and it remains to show that the matrices \({Y = (Y_{i,j})_{i,j \in J}}\) and \({Z = (Z_{i,j})_{i,j \in J}}\) of Lemma 6.4 are of Schur-type. For this, note that \(|\det (B_j^t C_j)|^{-1} = |\det (A_j^t \delta A_j^{-t})|^{-1} = \delta ^{-d}\) and \(\Vert C_j^t A_i\Vert = \delta \, \Vert A_j^{-1} A_i\Vert \le \Vert A_j^{-1} A_i\Vert \), since \(\delta \le 1\). Therefore,
for all \(i,j \in I\). It is now readily verified that \(Y_{i,j} \le C' \cdot \delta \cdot {\widetilde{Y}}_{i,j}\) and \(Z_{i,j} \le C' \cdot \delta \cdot {\widetilde{Y}}_{i,j}\) for \(i,j \in J\), where \(C'\) is as in Lemma 7.2. Hence, \( \Vert Y \Vert _{\mathrm {Schur}} \Vert Z \Vert _{\mathrm {Schur}} \le (C')^2 \cdot \delta ^2 \cdot \Vert {\widetilde{Y}} \Vert _{\mathrm {Schur}}^2 \). Therefore, applying Lemma 6.4 completes the proof. \(\square \)
The factor \(\max \{1, |A_i^{-1} (b_i - b_j)|\}\) that appears in defining \(K_{i,j}\) in Proposition 7.3 can be inconvenient. In particular, it does not appear in [62], which makes it difficult to translate existing concrete examples from [62] readily to the present setting. For this reason, we supply the following.
Lemma 7.4
The matrix entries \({\widetilde{Y}}_{i,j}\) introduced in Proposition 7.3 satisfy \(0 \le {\widetilde{Y}}_{i,j} \le (1 + R_{\mathcal {Q}})^{d+1} \cdot {\widehat{Y}}_{i,j}\), where
and \( L_{i,j} := \max \big \{ \frac{w_i}{w_j}, \frac{w_j}{w_i} \big \} \big ( \max \{ 1, \Vert A_i^{-1} A_j\Vert ^2 \} \, \max \{ 1, \Vert A_j^{-1} A_i\Vert ^3 \} \big )^{d+1} \) for \(i,j \in J\).
Proof
Since \( S_j^{-1} (S_i \xi ) = A_j^{-1} (A_i \xi + b_i - b_j) \) for all \(\xi \in \widehat{{\mathbb {R}}}^d\), it follows that
for \(\xi \in Q_i'\). Using this, the estimate \({\widetilde{Y}}_{i,j} \le (1 + R_{\mathcal {Q}})^{d+1} \cdot {\widehat{Y}}_{i,j}\) follows directly from the definitions. \(\square \)
7.2 Invertibility of the Frame Operator
The next result summarizes our criteria for the invertibility of the frame operator obtained in this section.
Theorem 7.5
Let \({\mathcal {Q}}= \big (S_j (Q_j ')\big )_{j \in J} = \big (A_j (Q_j ') + b_j)_{j \in J}\) be an affinely generated cover of an open set \({\mathcal {O}}\subset \widehat{{\mathbb {R}}}^d\) of full measure. Let \(\Phi = (\varphi _j)_{j \in J}\) be a regular partition of unity subordinate to \({\mathcal {Q}}\), and let \(w = (w_j)_{j \in J}\) be \({\mathcal {Q}}\)-moderate. Suppose that
-
(i)
The system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is such that \(g_j := |\det A_j|^{1/2} \cdot M_{b_j} [g \circ A_j^t]\) and \(C_j := \delta \cdot A_j^{-t}\) for some \(\delta > 0\) and some \(g \in L^1({\mathbb {R}}^d) \cap L^\infty ({\mathbb {R}}^d)\) with \({\widehat{g}} \in C^\infty (\widehat{{\mathbb {R}}}^d)\);
-
(ii)
There is an \(A' > 0\) such that \(A' \le \sum _{j \in J} |{\widehat{g}}(S_j^{-1} \xi )|^2\) for almost all \(\xi \in {\mathcal {O}}\);
-
(iii)
The matrix \({\widehat{Y}} = ({\widehat{Y}}_{i,j})_{i,j \in J}\) is of Schur-type, where \({\widehat{Y}}_{i,j}\) as in Lemma 7.4;
-
(iv)
The term \(M_0\) defined in Proposition 7.1 is finite.
Then the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,w,\Phi )\)-adapted, and for \(p,q \in [1,\infty ]\), the frame operator \({S : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q) \rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)}\) associated to \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is well-defined and bounded.
Finally, for given \(p,q \in [1,\infty ]\), let \( C_{d,{\mathcal {Q}},w} := \max \big \{ [ \sup _{j \in J} \lambda (Q_j ') ]^{-\frac{3}{d+2}} , [\kappa _d K_{{\mathcal {Q}},w}]^{1/(d+2)} \big \} \), where
and \( K_{{\mathcal {Q}},w} := \Vert \Gamma _{\mathcal {Q}}\Vert _{\ell _w^q \rightarrow \ell _w^q}^3 N_{{\mathcal {Q}}}^2 \max \{1, C_\Phi ^2 \} (1 + R_{\mathcal {Q}})^{3d + 4} \max _{|\alpha | \le d+1} C_{{\mathcal {Q}},\Phi ,\alpha }^3 . \) Then, if \(\delta > 0\) is chosen such that
then the frame operator is also boundedly invertible as an operator on \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\).
Proof
We proceed in two steps.
Step 1. Suppose that \(\delta \le 1\). Since \(A' \le \sum _{j \in J} |{\widehat{g}}(S_j^{-1} \xi )|^2\) for almost all \(\xi \in {\mathcal {O}}\), and since \(M_0\) is finite, an application of Proposition 7.1 shows that \(t_0\) is continuous on \({\mathcal {O}}\) and tame and that \( T_0 := \Phi _{t_0} : {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q) \rightarrow {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q), \) with \(\Phi _{t_0}\) as defined in Proposition 5.7, is well-defined, bounded, and boundedly invertible, with
for arbitrary \(p,q \in [1,\infty ]\). Here, \( C^{(1)} := (2d)^{(d+1)^2} \, C_{d} \, N_{{\mathcal {Q}}}^2 C_\Phi \cdot \max _{|\alpha | \le d+1} C_{{\mathcal {Q}},\Phi ,\alpha } \), with \(C_d\) as in Eq. (6.5).
Lemma 7.4 shows that \(\Vert {\widetilde{Y}}\Vert _{\mathrm {Schur}} \le (1 + R_{\mathcal {Q}})^{d+1} \, \Vert {\widehat{Y}}\Vert _{\mathrm {Schur}} < \infty \), with \({\widetilde{Y}}\) as in Proposition 7.3. Therefore, Proposition 7.3 shows that the system \((T_{\gamma } \, g_j)_{j\in J,\gamma \in C_j{\mathbb {Z}}^d}\) is \((w,w,\Phi )\)-adapted, and hence the frame operator \(S : {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q) \rightarrow {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\) is well-defined and bounded for all \(p,q \in [1,\infty ]\) by Corollary 4.10.
Lastly, it follows by Proposition 7.3 and Corollary 5.9 that the frame operator S can be written as \(S = T_0 + R_0\), where
where \(C^{(2)} := C_0 C_{p,q} (C')^4 \Vert \Gamma _{\mathcal {Q}}\Vert _{\ell _w^q \rightarrow \ell _w^q}\), with \(C_0\) as in (6.9) and \(C'\) as in Lemma 7.2, and with \({C_{p,q} := \max \{1, C_\Phi \} \cdot \Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell _w^q \rightarrow \ell _w^q}^2}\). Here, we used the easily verifiable estimate \(\Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell _w^q \rightarrow \ell _w^q} \ge 1\).
Therefore, for arbitrary \(p,q \in [1,\infty ]\), a combination of the above estimates gives
Therefore, Lemma 5.4 implies that the frame operator \(S = T_0 + R_0 : {\mathcal {D}}({\mathcal {Q}}, L^p, \ell ^q_w) \rightarrow {\mathcal {D}}({\mathcal {Q}}, L^p, \ell ^q_w)\) is boundedly invertible, as claimed.
Step 2. In this step it will be shown that (7.3) already entails \(\delta \le 1\). To this end, first note that \( A' \le \sum _{j \in J} |{\widehat{g}}(S_j^{-1} \eta )|^2 \le \big ( \sum _{j \in J} |{\widehat{g}}(S_j^{-1} \eta )| \big )^2 \), and hence \(\sum _{j \in J} |{\widehat{g}}(S_j^{-1} \eta )| \ge \sqrt{A'}\) for almost every \(\eta \in {\mathcal {O}}.\) Thus, for any fixed \(i \in J\),
Next, by applying Jensen’s inequality, we see that the constant \(M_0\) introduced in Proposition 7.1 satisfies, for each \(i \in J\), the estimate
Overall, we see that
and hence \(C_{d,{\mathcal {Q}},w} \cdot \kappa \cdot \frac{\delta }{A'} \ge \delta \). Thus, if \(\delta \) satisfies Eq. (7.3), then \(\delta < 1\). \(\square \)
7.3 Proof of Theorem 1.1
Theorem 1.1, announced in the introduction, is just a reformulation of Theorem 7.5, with the following identifications of notation: \(\mathrm {A}=A'\); \(\mathrm {B}=B'\); \(M_1 = \Vert {\widehat{Y}}\Vert _{\mathrm {Schur}}\). \(\square \)
7.4 Banach Frames and Atomic Decompositions
We now remark that, under the assumptions of Theorem 7.5, the system \((T_{\delta A_j^{-t}k} \, g_j)_{j \in J, k \in {\mathbb {Z}}^d}\) forms a Banach frame and an atomic decomposition ([33]) for the Besov-type spaces \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\), and, moreover, the corresponding dual family is given by the canonical dual frame.
Corollary 7.6
Suppose that the assumptions of Theorem 7.5 are satisfied, including the assumption (7.3). Then the system \((T_{\delta A_j^{-t} k} \, g_j)_{j \in J, k \in {\mathbb {Z}}^d}\) forms a Banach frame and an atomic decomposition for all of the spaces \({\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\), \(p,q \in [1,\infty ]\), with associated coefficient space \(Y_w^{p,q}\) as in Definition 4.5. Precisely, the analysis and synthesis maps
are well-defined and bounded, and satisfy
Proof
Theorem 7.5 shows that \((T_{\delta A_j^{-t} k} \, g_j)_{j \in J, k \in {\mathbb {Z}}^d}\) is \((w,w,\Phi )\)-adapted. Thus, the boundedness of \({\mathscr {C}}, {\mathscr {D}}\) follows from Proposition 4.8. The remaining statements follow from the invertibility of \({S = {\mathscr {D}}\circ {\mathscr {C}}}\) proven in Theorem 7.5. \(\square \)
7.5 An Example
We conclude with an example verifying the hypotheses of Theorem 7.5 for Besov-type spaces associated with covers that have a geometry which is in a certain sense intermediate between the geometry of the uniform and the dyadic covers. These covers are an instance of the non-homogeneous isotropic covers from [56, Sect. 2.5] and [58, Sect. 2.1]; the corresponding spaces are also known as \(\alpha \)-modulation spaces [32]. For similar calculations of other concrete examples, we refer to [62].
For fixed \(\alpha \in [0,1)\), the \(\alpha \)-modulation space with parameters \(p,q \in [1,\infty ]\) and \(s \in {\mathbb {R}}\) is defined as \(M_{p,q}^{s,\alpha } ({\mathbb {R}}^d) := {\mathcal {D}}({\mathcal {Q}}^{(\alpha )}, L^p, \ell _{w^{(s,\alpha )}}^q)\), where the cover \({\mathcal {Q}}^{(\alpha )}\) of \(\widehat{{\mathbb {R}}}^d\) is given by
where \( A_j^{(\alpha )} := |j|^{\alpha _0} \, \mathrm {id}_{{\mathbb {R}}^d}, \; b_j^{(\alpha )} := |j|^{\alpha _0} \, j, \) and\( Q = B_r (0) , \) with \(\alpha _0 := \tfrac{\alpha }{1-\alpha }\) and \(r \ge r_0 = r_0 (d,\alpha )\). Under this assumption on r, one can show that \({\mathcal {Q}}^{(\alpha )}\) is indeed an affinely generated cover of \(\widehat{{\mathbb {R}}}^d\); see [10, Theorem 2.6] and [62, Lemma 7.3]. Finally, the weight \(w^{(s,\alpha )}\) is given by \( w^{(s,\alpha )}_j = |j|^{s / (1 - \alpha )} \) for \(j \in {\mathbb {Z}}^d \setminus \{0\}\). In the following, we will simply write \({\mathcal {Q}}\), \(A_j\), and \(b_j\) for \({\mathcal {Q}}^{(\alpha )}\), \(A_j^{(\alpha )}\), and \(b_j^{(\alpha )}\) and fix some \(r \ge r_0(d,\alpha )\).
Fix \(s_0 \ge 0\). In the following, we will only consider “smoothness parameters” \(s \in [-s_0, s_0]\). Take \({g \in L^1({\mathbb {R}}^d) \cap L^2({\mathbb {R}}^d)}\) such that \({\widehat{g}} \in C^\infty (\widehat{{\mathbb {R}}}^d)\), and assume that there are \(c,C > 0\) and \(N > 0\) such that
We will determine conditions on N (depending on \(d, \alpha , s_0\)) which ensure that the prerequisites of Theorem 7.5 are satisfied. In fact, it will turn out that it is enough if \(N > 4d + 3 + \tau \) where \(\tau := \frac{4 \alpha d + 3 \alpha + s_0}{1-\alpha } \in [0,\infty )\).
To show this, note because of \(Q_i ' = B_r (0)\) for all \(i \in {\mathbb {Z}}^d \setminus \{0\}\) that
Thus, applying the change of variables \(\eta = S_j^{-1} (S_i \xi )\), combined with the estimate (7.4), yields
A similar computation shows
Using the notations
for \(i,j \in {\mathbb {Z}}^d \setminus \{0\}\) and \(k, M \in {\mathbb {R}}\), \(\tau \in (0,\infty )\), we have thus shown
This is useful, since [62, Eq. (7.13)] shows for \(M \ge d + 1\) that
where \(C' = C'(\alpha , d, M, r, \tau , |k|)\).
Now, using that \(w_{j}^{(s,\alpha )} = |j|^{s / (1 - \alpha )}\) and \(A_j = |j|^{\alpha _0} \, \mathrm {id}\), a straightforward computation shows that the quantity \(L_{i,j}\) introduced in Lemma 7.4 satisfies
where we introduced \(\sigma := \frac{3 \alpha (d + 1) + s_0}{1-\alpha } \in [0,\infty )\). In combination with Equations (7.5) and (7.6), we thus see that the matrix elements \({\widehat{Y}}_{i,j}\) introduced in Lemma 7.4 satisfy
where \(C_1 = C_1 (d, \alpha , N, r, s_0)\). From this, it is easy to see that \(\Vert {\widehat{Y}}\Vert _{\mathrm {Schur}} \le C \cdot C_2 < \infty \), provided that \(N > 4d + 3 + \sigma + d \alpha _0 = 4d + 3 + \tau \), where \(C_2 = C_2 (d,\alpha ,N,r,s_0)\). We have thus verified condition (iii) of Theorem 7.5.
Next, we show that \(M_0 < \infty \) for \(M_0\) as defined in Proposition 7.1. The same arguments as for estimating \({\widehat{Y}}_{i,j}\) give
where \(C_3 = C_3(\alpha , d, N, r)\). From this, we see that the constant \(M_0\) introduced in Proposition 7.1 satisfies \(M_0 = \Vert V\Vert _{\mathrm {Schur}} \le C^2 C_4 < \infty \) for a constant \(C_4 = C_4(\alpha , d, N, r)\), as soon as \(N > \frac{1 + d}{2} (1 + \alpha _0)\), which is implied by \(N > 4d + 3 + \sigma + d \alpha _0\). Thus, condition (iv) of Theorem 7.5 is satisfied.
Lastly, we verify condition (ii) of Theorem 7.5, that is, \(\sum _{j \in {\mathbb {Z}}^d \setminus \{0\}} |{\widehat{g}} (S_j^{-1} \xi )|^2 \ge A'\) for all \(\xi \in \widehat{{\mathbb {R}}}^d\), where \(A' := c^2\), with \(c > 0\) as in Eq. (7.4). To see this, note that Eq. (7.4) implies \(|{\widehat{g}}|^2 \ge c^2 \, {\mathbb {1}}_{Q}\), where we recall \(Q = B_r (0)\). Hence, \(|{\widehat{g}}(S_j^{-1} \xi )|^2 \ge c^2 {\mathbb {1}}_{Q_j}\), since \(Q_j = S_j Q\). Finally, since \({\mathcal {Q}}^{(\alpha )} = (Q_j)_{j \in {\mathbb {Z}}^d \setminus \{0\}}\) is a cover of \(\widehat{{\mathbb {R}}}^d\), we see \(\sum _{j \in {\mathbb {Z}}^d \setminus \{0\}} |{\widehat{g}}(S_j^{-1} \xi )|^2 \ge c^2 = A'\), as claimed.
Notes
Here, we use that if \(\xi _0 \in {\mathcal {O}}\) is arbitrary, then \(\xi _0 \in Q_\ell \) for some \(\ell \in I\) and hence \(\varphi _\ell ^*(\xi _0) = 1\). Thus, \({U := \{ \xi \in {\mathcal {O}}:|\varphi _\ell ^*(\xi )| > 1/2 \}} \subset Q_\ell ^*\) is an open neighborhood of \(\xi _0\); finally, if \(U \cap \overline{Q_i} \ne \emptyset \), then also \(U \cap Q_i \ne \emptyset \) and hence \(i \in \ell ^{**} = \bigcup _{j \in \ell ^*} j^*\), proving that the family \(( \, \overline{Q_i} \, )_{i \in I}\) is locally finite on \({\mathcal {O}}\).
References
Aldroubi, A., Gröchenig, K.: Nonuniform sampling and reconstruction in shift-invariant spaces. SIAM Rev. 43(4), 585–620 (2001)
Aldroubi, A., Cabrelli, C., Molter, U.M.: Wavelets on irregular grids with arbitrary dilation matrices and frame atoms for \(L^2({{\mathbb{R}}}^d)\). Appl. Comput. Harmon. Anal. 17(2), 119–140 (2004)
Alt, H.: Linear Functional Analysis. Springer, London (2016)
Balan, R., Casazza, P.G., Heil, C., Landau, Z.: Density, overcompleteness, and localization of frames. I. Theory. J. Fourier Anal. Appl. 12(2), 105–143 (2006)
Balan, R., Casazza, P.G., Heil, C., Landau, Z.: Density, overcompleteness, and localization of frames. II. Gabor systems. J. Fourier Anal. Appl. 12(3), 309–344 (2006)
Balan, R., Christensen, J.G., Krishtal, I.A., Okoudjou, K.A., Romero, J.L.: Multi-window Gabor frames in amalgam spaces. Math. Res. Lett. 21(1), 55–69 (2014)
Balazs, P.: Basic definition and properties of Bessel multipliers. J. Math. Anal. Appl. 325(1), 571–585 (2007)
Barrios, B., Betancor, J.J.: Characterizations of anisotropic Besov spaces. Math. Nachr. 284(14–15), 1796–1819 (2011)
Berend, D., Tassa, T.: Improved bounds on Bell numbers and on moments of sums of random variables. Probab. Math. Stat. 30(2), 185–205 (2010)
Borup, L., Nielsen, M.: Banach frames for multivariate \(\alpha \)-modulation spaces. J. Math. Anal. Appl. 321(2), 880–895 (2006)
Borup, L., Nielsen, M.: Frame decomposition of decomposition spaces. J. Fourier Anal. Appl. 13(1), 39–70 (2007)
Bownik, M.: Anisotropic Hardy spaces and wavelets. Mem. Am. Math. Soc. 164(781), vi+122 (2003)
Bownik, M.: Atomic and molecular decompositions of anisotropic Besov spaces. Math. Z. 250(3), 539–571 (2005)
Bui, H.-Q., Laugesen, R.S.: Affine synthesis onto Lebesgue and Hardy spaces. Indiana Univ. Math. J. 57(5), 2203–2233 (2008)
Bui, H.-Q., Laugesen, R.S.: Wavelet frame bijectivity on Lebesgue and Hardy spaces. J. Fourier Anal. Appl. 19(2), 376–409 (2013)
Cabrelli, C., Molter, U., Romero, J.L.: Non-uniform painless decompositions for anisotropic Besov and Triebel-Lizorkin spaces. Adv. Math. 232, 98–120 (2013)
Christensen, O., Rahimi, A.: Frame properties of wave packet systems in \(L^2({\mathbb{R}}^d)\). Adv. Comput. Math. 29(2), 101–111 (2008)
Christensen, O., Hasannasab, M., Lemvig, J.: Explicit constructions and properties of generalized shift-invariant systems in \(L^2({\mathbb{R}})\). Adv. Comput. Math. 43(2), 443–472 (2017)
Daubechies, I.: Ten lectures on wavelets, volume 61 of CBMS-NSF Regional Conference Series in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA (1992)
de Hoop, M.V., Gröchenig, K., Romero, J.L.: Exact and approximate expansions with pure Gaussian wave packets. SIAM J. Math. Anal. 46(3), 2229–2253 (2014)
Feichtinger, H.G.: Banach convolution algebras of Wiener type. In: Functions, series, operators, Vol. I, II (Budapest, 1980). Colloq. Math. Soc. János Bolyai, vol. 35, pages 509–524. North-Holland, Amsterdam (1983)
Feichtinger, H.G.: Atomic characterizations of modulation spaces through Gabor-type representations. Rocky Mountain J. Math. 19(1), 113–125 (1989)
Feichtinger, H.G., Gröbner, P.: Banach spaces of distributions defined by decomposition methods. I. Math. Nachr. 123, 97–120 (1985)
Feichtinger, H.G., Gröchenig, K.H.: Banach spaces related to integrable group representations and their atomic decompositions. I. J. Funct. Anal. 86(2), 307–340 (1989)
Folland, G.: Real Analysis: Modern Techniques and Their Applications. Pure and Applied Mathematics, vol. 2. Wiley, New York (1999)
Fournier, J.J.F., Stewart, J.: Amalgams of \(L^p\) and \(l^q\). Bull. Am. Math. Soc. (N.S.) 13(1), 1–21 (1985)
Frazier, M., Jawerth, B.: Decomposition of Besov spaces. Indiana Univ. Math. J. 34(4), 777–799 (1985)
Frazier, M., Jawerth, B.: A discrete transform and decompositions of distribution spaces. J. Funct. Anal. 93(1), 34–170 (1990)
Frazier, M., Jawerth, B., Weiss, G.: Littlewood-Paley theory and the study of function spaces. In: CBMS Regional Conference Series in Mathematics, vol. 79. Published for the Conference Board of the Mathematical Sciences, Washington (1991)
Führ, H., Lemvig, J.: System bandwidth and the existence of generalized shift-invariant frames. J. Funct. Anal. 276(2), 563–601 (2019)
Führ, H., Voigtlaender, F.: Wavelet coorbit spaces viewed as decomposition spaces. J. Funct. Anal. 269, 80–154 (2015)
Gröbner, P.: Banachräume glatter Funktionen und Zerlegungsmethoden. PhD thesis, University of Vienna (1992)
Gröchenig, K.: Describing functions: atomic decompositions versus frames. Monatsh. Math. 112(1), 1–42 (1991)
Gröchenig, K.: Foundations of Time-Frequency Analysis. Applied and Numerical Harmonic Analysis. Birkhäuser, Boston (2001)
Gröchenig, K.: Localization of frames, Banach frames, and the invertibility of the frame operator. J. Fourier Anal. Appl. 10(2), 105–132 (2004)
Gröchenig, K., Klotz, A.: Norm-controlled inversion in smooth Banach algebras. II. Math. Nachr. 287(8–9), 917–937 (2014)
Gröchenig, K., Samarah, S.: Nonlinear approximation with local Fourier bases. Constr. Approx. 16(3), 317–331 (2000)
Heil, C.E., Walnut, D.F.: Continuous and discrete wavelet transforms. SIAM Rev. 31(4), 628–666 (1989)
Hernández, E., Labate, D., Weiss, G.: A unified characterization of reproducing systems generated by a finite family. II. J. Geom. Anal. 12(4), 615–662 (2002)
Holland, F.: Harmonic analysis on amalgams of \(L^{p}\) and \(l^{q}\). J. Lond. Math. Soc. 2(10), 295–305 (1975)
Jakobsen, M., Lemvig, J.: Reproducing formulas for generalized translation invariant systems on locally compact abelian groups. Trans. Am. Math. Soc. 368, 8447–8480 (2016)
Johnson, W.P.: The curious history of Faà di Bruno’s formula. Am. Math. Mon. 109(3), 217–234 (2002)
Krishtal, I.A., Okoudjou, K.A.: Invertibility of the Gabor frame operator on the Wiener amalgam space. J. Approx. Theory 153(2), 212–224 (2008)
Kyriazis, G., Petrushev, P.: New bases for Triebel-Lizorkin and Besov spaces. Trans. Am. Math. Soc. 354(2), 749–776 (2002)
Lemvig, J., Van Velthoven, J.T.: Criteria for generalized translation-invariant frames. Stud. Math. 251(1), 31–63 (2020)
Meyer, Y.: Wavelets and operators. Cambridge Studies in Advanced Mathematics, vol. 37. Cambridge University Press, Cambridge (1992)
Nielsen, M.: Frames for decomposition spaces generated by a single function. Collect. Math. 65(2), 183–201 (2014)
Nielsen, M., Rasmussen, K.N.: Compactly supported frames for decomposition spaces. J. Fourier Anal. Appl. 18(1), 87–117 (2012)
Peetre, J.: New Thoughts on Besov Spaces. Duke University Mathematics Series, Mathematics Dept, Duke University, Durham (1976)
Robbins, H.: A remark on Stirling’s formula. Am. Math. Mon. 62, 26–29 (1955)
Romero, J.L.: Explicit localization estimates for spline-type spaces. Sampl. Theory Signal Image Process. 8(3), 249–259 (2009)
Romero, J.L.: Surgery of spline-type and molecular frames. J. Fourier Anal. Appl. 17(1), 135–174 (2011)
Ron, A., Shen, Z.: Generalized shift-invariant systems. Constr. Approx. 22(1), 1–45 (2005)
Rudin, W.: Functional Analysis. McGraw-Hill Education, New York (1973)
Stöckert, B., Triebel, H.: Decomposition methods for function spaces of \(B^{s}_{p, q}\) type and \(F^{s}_{p, q}\) type. Math. Nachr. 89, 247–267 (1979)
Triebel, H.: Fourier Analysis and Function Spaces (selected topics). Teubner Verlagsgesellschaft, Leipzig (1977)
Triebel, H.: General function spaces. I. Decomposition methods. Math. Nachr. 79, 167–179 (1977)
Triebel, H.: Spaces of Besov-Hardy-Sobolev type. BSB B. G. Teubner Verlagsgesellschaft, Leipzig (1978)
van Velthoven, J.T.: On the local integrability condition for generalised translation-invariant systems. Collect. Math. 70(3), 407–429 (2019)
Voigtlaender, F.: Embeddings of decomposition spaces into Sobolev and BV spaces (2016). arxiv:abs/1601.02201
Voigtlaender, F.: Embeddings of decomposition spaces. Mem. Am. Math. Soc. arxiv:1605.09705
Voigtlaender, F.: Structured, compactly supported Banach frame decompositions of decomposition spaces. Diss. Math. arxiv:1612.08772
Walnut, D.F.: Continuity properties of the Gabor frame operator. J. Math. Anal. Appl. 165(2), 479–504 (1992)
Acknowledgements
J. L. R. gratefully acknowledges support from the Austrian Science Fund (FWF): Y 1199 and P 29462-N35, and from the WWTF grant INSIGHT (MA16-053). J. v. V. acknowledges support from the Austrian Science Fund (FWF): P 29462-N35. J. v. V. is grateful for the hospitality and support of the Katholische Universität Eichstätt-Ingolstadt during his visit.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Estimation of the \({\mathcal {F}}L^1\) norm
1.1 A.1: Sobolev Embeddings
In this appendix we give an explicit bound for the constant implied in the estimate \(\Vert {\mathcal {F}}^{-1} f\Vert _{L^1} \lesssim \max _{|\alpha | \le d+1} \Vert \partial ^\alpha f\Vert _{L^1}\). Similar, but more qualitative results in the non-commutative context can be found in [36, 51].
Lemma A.1
Let \(d \in {\mathbb {N}}\) and \(\alpha , c > 0\). Define \( g : {\mathbb {R}}^d \rightarrow (0,\infty ), x \mapsto \big ( \max \{c, \Vert x\Vert _{\ell ^\infty } \} \big )^{-\alpha }. \) Then \(\int _{{\mathbb {R}}^d} g(x) \, dx < \infty \) if and only if \(\alpha > d\), and in this case
Proof
Let \(\mu \) denote the Lebesgue measure on \({\mathbb {R}}^d\). We will use [25, Proposition 6.24], which shows for measurable \(f : {\mathbb {R}}^d \rightarrow {\mathbb {C}}\) that
where \( \lambda _f (\beta ) := \mu \big ( \{x \in {\mathbb {R}}^d \,:\, | f(x) | > \beta \} \big ) \, . \) To compute the distribution function \(\lambda _g\), first note that \(g(x) \le c^{-\alpha }\) for all \(x \in {\mathbb {R}}^d\), and thus \(\lambda _g(\beta ) = 0\) for \(\beta \ge c^{-\alpha }\). For \(0< \beta < c^{-\alpha }\), note that \(g(x) > \beta \) is equivalent to \(\Vert x \Vert _{\ell ^{\infty }} < \beta ^{-1/\alpha }\), whence to \(x \in B^{\Vert \cdot \Vert ^{\ell ^{\infty }}}_{\beta ^{-1/\alpha }} (0)\). Therefore, for any \(\beta \in (0, c^{-\alpha })\), we compute \( \lambda _g (\beta ) = \mu \big ( B_{\beta ^{-1/\alpha }}^{\Vert \cdot \Vert _{\ell ^\infty }} (0) \big ) = (2 \cdot \beta ^{-1/\alpha })^d \, , \) and thus
which is finite if and only if \(d/\alpha < 1\). In the latter case, a direct calculation shows that
yielding the desired result. \(\square \)
The following result provides the announced estimate. For this, we use the usual Sobolev space
with norm \(\Vert f\Vert _{W^{k,1}} := \sum _{|\alpha | \le k} \Vert \partial ^\alpha f \Vert _{L^1}\).
Lemma A.2
Suppose \(f \in W^{d+1,1}(\widehat{{\mathbb {R}}}^d)\). Then \({\mathcal {F}}^{-1} f \in L^1({\mathbb {R}}^d)\) with
where \({\mathbb {I}} := \{0\}\cup \{(d+1) e_\ell \,:\,\ell \in {\underline{d}} \} \subset {\mathbb {N}}_0^d\), with \((e_k)_{k =1}^d\) denoting the standard basis of \({\mathbb {R}}^d\).
Proof
Since \({\mathcal {S}}(\widehat{{\mathbb {R}}}^d) \subset W^{d+1,1}(\widehat{{\mathbb {R}}}^d)\) is dense (see e.g. [3, E10.8]), and since \({{\mathcal {F}}^{-1} f_n \rightarrow {\mathcal {F}}^{-1} f}\) uniformly if \(f_n \rightarrow f\) in \(W^{d+1,1}(\widehat{{\mathbb {R}}}^d) \hookrightarrow L^1(\widehat{{\mathbb {R}}}^d)\), it suffices—in view of Fatou’s lemma—to prove the estimate for \({f \in {\mathcal {S}}(\widehat{{\mathbb {R}}}^d)}\). In this case, elementary properties of the Fourier transform yield for all \(\alpha \in {\mathbb {N}}_0^d\) and \( x \in {\mathbb {R}}^d\) the estimate
Next, using the auxiliary function \( g : {\mathbb {R}}^d \rightarrow (0,\infty ), \; x \mapsto (\max \{(2\pi )^{-1}, \Vert x\Vert _{\ell ^\infty } \})^{-(d+1)} \), it follows that
Hence, it remains to compute the integral \(\int _{{\mathbb {R}}^d} g(x) \, dx\). For this, note that an application of Lemma A.1 (with \(c = (2 \pi )^{-1}\) and \(\alpha = d+1\)) gives \( \int g(x) \, dx = \frac{2^d}{1 - \alpha ^{-1} d} \cdot c^{d - \alpha } = 2^{d+1}\pi \cdot (d+1) \), and thus
which completes the proof. \(\square \)
1.2 A.2: The Chain Rule
Lemma A.2 allows to estimate the \({\mathcal {F}}L^1\) norm of f in terms of the \(L^1\) norms of certain derivatives of f. In many cases, we will have \(f = g \circ A\), where we have good control over the derivatives of g. In such cases, the following lemma will be helpful.
Lemma A.3
([60, Lemma 2.6])
Let \(d,k \in {\mathbb {N}}\), \(A \in {\mathbb {R}}^{d \times d}\), and \(f \in C^k({\mathbb {R}}^d)\) be arbitrary. Let \((e_1,\dots ,e_d)\) denote the standard basis of \({\mathbb {R}}^d\), let \(i_1,\dots ,i_k \in {\underline{d}}\), and define \(\alpha := \sum _{m=1}^k e_{i_m} \in {\mathbb {N}}_0^d\).
Then \(|\alpha | = k\), and
1.3 A.3: The Norm of a Reciprocal
Lemma A.4
Let \(m \in {\mathbb {N}}\) and let \(U \subset {\mathbb {R}}\) be open. Suppose that \(f \in C^m (U)\) never vanishes on U. Let \(A > 0\), \(K \ge 0\), and \(x_0 \in U\) be such that
Then the reciprocal \(F := 1 / f\) of f satisfies
for all \(1 \le \ell \le m\), where the constant \(C_m\) satisfies, for all \(1 \le \ell \le m\),
Proof
Setting \(g : {\mathbb {R}}\setminus \{0\} \rightarrow {\mathbb {R}}, t \mapsto t^{-1}\), we have \(F = g \circ f\). Therefore, the “set partition version” of Faa di Bruno’s formula, see for instance [42, p. 219], shows for \(1 \le \ell \le m\) that
where \(P_\ell \subset 2^{2^{{\underline{\ell }}}}\) denotes the sets of all partitions of the set \({\underline{\ell }} := \{1,\dots ,\ell \}\). Phrased differently, the set \(P_\ell \) contains exactly those subsets \(\pi \subset 2^{{\underline{\ell }}}\) of the power set \(2^{{\underline{\ell }}}\) for which \({\underline{\ell }} = \biguplus \pi \) and \(B \ne \emptyset \) for all \(B \in \pi \). For each \(\pi \in P_\ell \), we denote by \(|\pi |\) the number of blocks of the partition determined by \(\pi \); that is, \(|\pi |\) is the number of elements of \(\pi \). Likewise, for a block \(B \in \pi \), we denote by |B| the size of the block, that is, the number of elements of B.
An induction argument shows that \(g^{(k)}(t) = (-1)^k \cdot k! \cdot t^{-(k+1)}\) for all \(k \in {\mathbb {N}}_0\). Therefore, for arbitrary \(\pi \in P_\ell \), it follows that \(|g^{(|\pi |)} (f(x_0))| = |\pi |! \cdot |f(x_0)|^{-(1 + |\pi |)} \le \ell ! \cdot A^{1 + |\pi |}\), since any \(\pi \in P_\ell \) satisfies \(\ell = \sum _{B \in \pi } |B| \ge \sum _{B \in \pi } 1 = |\pi |\). Similarly, it follows that
for all \(\pi \in P_\ell \). Combining these observations shows that
where we used again that \(1 \le |\pi | \le \ell \) for \(\pi \in P_\ell \). Since \(\ell ! \le m!\) and \(|P_\ell | \le |P_m|\) for \(\ell \le m\), it suffices to show that \(C_m := m! \cdot |P_m|\) satisfies the bound stated in the lemma. Here, the cardinalities \(|P_m|\) are the so-called Bell numbers. For these, [9, Theorem 2.1] provides the bound \(|P_m| \le \big (\frac{0.8 \cdot m}{\ln (1+m)}\big )^m\). Furthermore, the version of Stirling’s formula derived in [50] shows that
Combining these estimates gives the desired result. \(\square \)
Appendix B: Proof of Proposition 3.13
(i) Let \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) and set \(K := \mathop {{\text {supp}}}{\widehat{f}} \subset {\mathcal {O}}\). For \(i \in I\), the set \({U_i := \varphi _i^{-1}({\mathbb {C}}\setminus \{0\}) }\) is open. Moreover, since \(\sum _{i \in I} \varphi _i \equiv 1\) on \({\mathcal {O}}\), it follows that \({\mathcal {O}}= \bigcup _{i \in I} U_i\). By compactness of K, there exists a finite subset \(I_K \subset I\) satisfying \(K \subset \bigcup _{\ell \in I_K} U_\ell \subset \bigcup _{\ell \in I_K} Q_\ell \). Therefore, for any \(i \in I\) satisfying \(Q_i \cap K \ne \emptyset \), necessarily \(\emptyset \ne Q_i \cap K \subset Q_i \cap \bigcup _{\ell \in I_K} Q_\ell \), and hence \(i \in I_K^*:= \bigcup _{\ell \in I_K} \ell ^*\), which is a finite subset of I. By contraposition, we have \(Q_i \cap K = \emptyset \), and hence \(\varphi _i \cdot {\widehat{f}} \equiv 0\), for all \(i \in I \setminus I_K^*\).
Next, for each \(i \in I_K^*\), clearly \(\varphi _i \cdot {\widehat{f}} \in C_c^\infty ({\mathcal {O}}) \), and thus \(\Vert {\mathcal {F}}^{-1} (\varphi _i \cdot {\widehat{f}}\, ) \Vert _{L^p} < \infty \). Therefore, setting \( M := \max _{i \in I_K^*} \Vert {\mathcal {F}}^{-1} (\varphi _i \cdot {\widehat{f}} \, ) \Vert _{L^p} < \infty \) gives
which shows that \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\).
(ii) Let \(p, q \in [1,\infty )\). Recall the notation \(C_\Phi = \sup _{i \in I} \Vert {\mathcal {F}}^{-1} \varphi _i\Vert _{L^1}\) from Definition 3.3. Let \(f \in {\mathcal {D}}({\mathcal {Q}}, L^p, \ell _w^q)\) and \(\varepsilon > 0\) be arbitrary. Note \({c = (c_i)_{i \in I} \in \ell ^q_w (I)}\), where \(c_i := \Vert {\mathcal {F}}^{-1} (\varphi _i \cdot {\widehat{f}} \,)\Vert _{L^p}\) for \(i \in I\). Since \(\Vert c\Vert _{\ell _w^q} = \Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} < \infty \) and since \(q < \infty \), there exists a finite set \(I_0 = I_0 (\varepsilon ,f) \subset I\) such that the sequence \({\widetilde{c}} := c \cdot {\mathbb {1}}_{I \setminus I_0}\) satisfies
For each \(i \in I_0^*:= \bigcup _{\ell \in I_0} \ell ^*\), let \(c_i^*:= (\Gamma _{\mathcal {Q}}\, c)_i = \sum _{\ell \in i^*} c_\ell \) and choose some \(h_i \in {\mathcal {S}}({\mathbb {R}}^d)\) such that \( \big \Vert {\mathcal {F}}^{-1} (\varphi _i^*\cdot {\widehat{f}} \, ) - h_i \big \Vert _{L^p} \le \delta \cdot c_i^*, \) where \(\delta := (\varepsilon / 2) \cdot \big ( C_{\Phi } \cdot \Vert \Gamma _{{\mathcal {Q}}} \Vert _{\ell _w^q \rightarrow \ell _w^q} \big )^{-2} \cdot (1+\Vert c\Vert _{\ell ^q_w})^{-1}\). This is possible since we have \(p < \infty \), and since if \(c_i^*= 0\), then \( \Vert {\mathcal {F}}^{-1} (\varphi _i^*\cdot {\widehat{f}} \, )\Vert _{L^p} \le \sum _{\ell \in i^*} \Vert {\mathcal {F}}^{-1} (\varphi _\ell {\widehat{f}} \,) \Vert _{L^p} = c_i^*= 0 \).
Define \(g_i := \widehat{h_i} \in {\mathcal {S}}(\widehat{{\mathbb {R}}}^d)\) for \(i \in I_0^*\), and \(g_i := 0\) for \(i \in I \setminus I_0^*\). We claim that
for all \(i \in I\). To show this, distinguish the two cases \(i \in I_0^*\) and \(i \in I \setminus I_0^*\). In the first case,
by choice of \(h_i\). Since, furthermore, \((\Gamma _{\mathcal {Q}}\, {\widetilde{c}} \, )_i \ge 0\), the estimate (B.1) holds in the first case. For the second case, we have \(g_i = 0\). Furthermore, \(i \notin I_0^*\) and thus \(\ell \notin I_0\) for all \(\ell \in i^*\). Therefore,
As in the first case, we thus see that estimate (B.1) holds.
Define \(g := {\mathcal {F}}^{-1} \big ( \sum _{i \in I} \varphi _i \cdot g_i \big )\). Then \(g \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d) \) since \(g_i = 0\) for all but finitely many \(i \in I\). Next, note that \(\varphi _i \, \varphi _i^*= \varphi _i\), and hence
Using Young’s inequality, we thus get
where the last inequality follows by (B.1). This finally implies
which completes the proof of (ii).
(iii) Since \({\mathcal {Q}}\) is a decomposition cover, the index set I is countably infinite. Indeed, the sets \(\big ( \varphi _i^{-1} ({\mathbb {C}}\setminus \{0\}) \big )_{i \in I}\) form an open cover of \({\mathcal {O}}\). Since \({\mathcal {O}}\) is second countable, there is a countable \(I_0 \subset I\) such that \( {\mathcal {O}}\subset \bigcup _{i \in I_0} \varphi _i^{-1} ({\mathbb {C}}\setminus \{0\}) \subset \bigcup _{i \in I_0} Q_i \). Finally, for \(i \in I\), we have \( \emptyset \ne Q_i \subset {\mathcal {O}}\subset \bigcup _{\ell \in I_0} Q_\ell \), and hence \(i \in \ell ^*\) for some \(\ell \in I_0\). In other words, \(I \subset \bigcup _{\ell \in I_0} \ell ^*\) is countable as a countable union of finite sets. Finally, if I was finite, then \(\sum _{i \in I} \varphi _i \in C_c ({\mathcal {O}})\), in contradiction to \({\mathcal {O}}\) being open and to \(\sum _{i \in I} \varphi _i \equiv 1\) on \({\mathcal {O}}\). Thus, we can write \(I = \{i_n :n \in {\mathbb {N}}\}\) for pairwise distinct \((i_n)_{n \in {\mathbb {N}}}\).
For each \(i \in I\), we have \(f_i := {\mathcal {F}}^{-1} (\varphi _i \, {\widehat{f}} \,) \in L^p ({\mathbb {R}}^d)\) with \(\mathop {{\text {supp}}}\widehat{f_i} \subset \mathop {{\text {supp}}}\varphi _i \subset U_i\) for the open set \(U_i := (\varphi _i^*)^{-1} ({\mathbb {C}}\setminus \{0\}) \subset Q_i^*\subset {\mathcal {O}}\), since \(\varphi _i^*\varphi _i = \varphi _i\). Now, for each fixed \(i \in I\), [61, Lemma 3.2] yields a sequence \((f_i^{(n)})_{n \in {\mathbb {N}}}\) of Schwartz functions such that \(|f_i^{(n)}| \le |f_i|\) and \(f_i^{(n)} \xrightarrow [n\rightarrow \infty ]{} f_i\) pointwise, and such that \(\mathop {{\text {supp}}}\widehat{f_i^{(n)}} \subset B_{1/n} (\mathop {{\text {supp}}}\varphi _i)\), where \(B_{1/n}(\mathop {{\text {supp}}}\varphi _i) := \{\xi \in \widehat{{\mathbb {R}}}^d : \text {dist}(\xi , \mathop {{\text {supp}}}\varphi _i) \le n^{-1} \}\). By choosing \(N_i \in {\mathbb {N}}\) with \(B_{1/N_i} (\mathop {{\text {supp}}}\varphi _i) \subset U_i\), and by replacing \(f_i^{(1)}, \dots , f_i^{(N_i)}\) by \(f_i^{(N_i)}\), we get \(\mathop {{\text {supp}}}\widehat{f_i^{(n)}} \subset U_i \subset Q_i^*\subset {\mathcal {O}}\) for all \(i \in I\) and \(n \in {\mathbb {N}}\).
Note that we have \(f_i^{(n)} \xrightarrow [n \rightarrow \infty ]{{\mathcal {S}}'({\mathbb {R}}^d)} f_i\). Indeed, if \(p < \infty \), then this follows from \(f_i^{(n)} \xrightarrow [n\rightarrow \infty ]{L^p} f_i\), which is a consequence of the dominated convergence theorem since \(|f_i^{(n)}| \le |f_i| \in L^p\) and \(f_i^{(n)} \rightarrow f_i\) pointwise. If \(p = \infty \) and \(h \in {\mathcal {S}}({\mathbb {R}}^d)\), then \(f_i^{(n)} \cdot h \rightarrow f_i \cdot h\) pointwise, and we have the estimate \(|f_i^{(n)} \cdot h| \le |f_i \cdot h| \le \Vert f_i\Vert _{L^\infty } \cdot |h| \in L^1\), whence \( \langle f_i^{(n)}, h \rangle _{{\mathcal {S}}', {\mathcal {S}}} \rightarrow \langle f_i, h \rangle _{{\mathcal {S}}',{\mathcal {S}}} \) by dominated convergence.
Now, define \(g_N := \sum _{n=1}^N f_{i_n}^{(N)} \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\). We first verify that \(g_N \rightarrow f\) with convergence in \(Z' ({\mathcal {O}})\). To see this, let \(\psi \in Z({\mathcal {O}})\) be arbitrary. Then \({\mathcal {F}}^{-1} \psi \in C_c^\infty ({\mathcal {O}})\), so that \(K := \mathop {{\text {supp}}}{\mathcal {F}}^{-1} \psi \subset {\mathcal {O}}\) is compact. Precisely as in the proof of Part (i), we thus see that there is a finite set \(I_K \subset I\) such that \(Q_i \cap K = \emptyset \) for all \(i \in I \setminus I_K\). Therefore, \(U_i \cap K \subset Q_i^*\cap K = \emptyset \), and hence \(\widehat{f_i^{(n)}} \cdot {\mathcal {F}}^{-1} \psi \equiv 0\), for all \(i \in I \setminus I_K^*\). Now, choose \(N_0 = N_0 (K) \in {\mathbb {N}}\) such that \(I_K^*\subset \{ i_1,\dots ,i_{N_0} \}\). If \(N \ge N_0\), we then have
where the last equality follows since \(\{i_1,\dots ,i_N\} \supset I_K^*\) and \(\widehat{f_i^{(N)}} \cdot {\mathcal {F}}^{-1} \psi \equiv 0\) for \(i \in I \setminus I_K^*\). Next, using that \(f_i^{(N)} \rightarrow f_i \) in \({\mathcal {S}}'\) and noting that \( {\mathcal {F}}^{-1} \psi = \sum _{i \in I} \varphi _i \, {\mathcal {F}}^{-1} \psi = \sum _{i \in I_K^*} \varphi _i \, {\mathcal {F}}^{-1} \psi \), we see that
Thus, \(g_N \xrightarrow [N\rightarrow \infty ]{} f\) with convergence in \(Z'({\mathcal {O}})\).
Finally, we construct a sequence \(F = (F_i)_{i \in I} \in \ell _w^q (I; L^p)\) such that each \(g_N\) is \((F,\Phi )\)-dominated. To this end, set  , where \(f_\ell := {\mathcal {F}}^{-1} (\varphi _\ell \cdot {\widehat{f}})\). Note because of \(\mathop {{\text {supp}}}\widehat{f_{i_n}^{(N)}} \subset Q_{i_n}^*\) that \(\varphi _i \cdot \widehat{f_{i_n}^{(N)}} \not \equiv 0\) can only hold for \(i_n \in i^{**}\). Therefore, since \(|f_i^{(m)}| \le |f_i|\), we get
, where \(f_\ell := {\mathcal {F}}^{-1} (\varphi _\ell \cdot {\widehat{f}})\). Note because of \(\mathop {{\text {supp}}}\widehat{f_{i_n}^{(N)}} \subset Q_{i_n}^*\) that \(\varphi _i \cdot \widehat{f_{i_n}^{(N)}} \not \equiv 0\) can only hold for \(i_n \in i^{**}\). Therefore, since \(|f_i^{(m)}| \le |f_i|\), we get

Finally, setting \(c = (c_i)_{i \in I}\) with \(c_i := \Vert {\mathcal {F}}^{-1} (\varphi _i \, {\widehat{f}} \, )\Vert _{L^p}\), we see because of \(i^{**} = \bigcup _{j \in i^*} j^*\) that
Thus, \(F \in \ell _w^q(I; L^p)\) with \(\Vert F\Vert _{\ell _w^q (I; L^p)} \le C_\Phi \, \Vert \Gamma _{{\mathcal {Q}}}\Vert _{\ell _w^q \rightarrow \ell _w^q}^2 \cdot \Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)}\), since \(\Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} = \Vert c\Vert _{\ell _w^q}\). \(\square \)
Appendix C: Proof of Proposition 5.7
Before proving Proposition 5.7, we first collect a few properties of the “generalized multiplication operation” \(\odot \) introduced in Definition 5.5.
Lemma C.1
Let \(p \in [1,\infty ]\). For \(f,g \in {\mathcal {F}}L^1({\mathbb {R}}^d)\) and \(h \in {\mathcal {F}}L^p({\mathbb {R}}^d)\), the following properties hold:
-
(i)
\(f \odot (g \odot h) = (f \odot g) \odot h\).
-
(ii)
If \(f \in {\mathcal {S}}(\widehat{{\mathbb {R}}}^d)\), then \(f \odot h = f \cdot h\).
-
(iii)
If \(p \in [1,2]\), then \(f \odot h = f \cdot h\).
-
(iv)
We have \(\mathop {{\text {supp}}}(f \odot h) \subset \mathop {{\text {supp}}}f \cap \mathop {{\text {supp}}}h\), where the support is understood in the sense of tempered distributions.
Proof
(i) Note that  and
and  . Thus, Young’s inequality shows for almost all \(x \in {\mathbb {R}}^d\) that
. Thus, Young’s inequality shows for almost all \(x \in {\mathbb {R}}^d\) that  . For each such x, a standard calculation using Fubini’s theorem shows
. For each such x, a standard calculation using Fubini’s theorem shows  . Hence, both sides are identical as tempered distributions. Thus, \((f \odot g) \odot h = f \odot (g \odot h)\).
. Hence, both sides are identical as tempered distributions. Thus, \((f \odot g) \odot h = f \odot (g \odot h)\).
(ii) This was already observed in Remark 5.6.
(iii) It is well-known that if \(p \in [1,2]\), then \(\widehat{\varphi *\psi } = {\widehat{\varphi }} \cdot {\widehat{\psi }}\) for \(\varphi \in L^1({\mathbb {R}}^d)\) and \(\psi \in L^p({\mathbb {R}}^d)\). Indeed, for \(\varphi ,\psi \in {\mathcal {S}}({\mathbb {R}}^d)\), the identity is clear; furthermore, it follows from the Hausdorff-Young inequality that as elements of \(L^{p'}({\mathbb {R}}^d)\), both sides of the identity depend continuously on \(\varphi \in L^1({\mathbb {R}}^d)\) and \(\psi \in L^p({\mathbb {R}}^d)\). Therefore,  .
.
(iv) Let \(\varphi \in C_c^\infty (\widehat{{\mathbb {R}}}^d)\) with \(\mathop {{\text {supp}}}\varphi \subset \widehat{{\mathbb {R}}}^d \setminus \mathop {{\text {supp}}}f\). There is \(\psi \in C_c^\infty (\widehat{{\mathbb {R}}}^d)\) with \(\varphi = \varphi \cdot \psi \) and \(\mathop {{\text {supp}}}\psi \subset \widehat{{\mathbb {R}}}^d \setminus \mathop {{\text {supp}}}f\). Furthermore, by combining Properties (i) and (ii), we see that
Because of \(\varphi = \psi \cdot \varphi \), this entails \( \langle f \odot h, \varphi \rangle _{{\mathcal {S}}',{\mathcal {S}}} = \langle \psi \cdot (f \odot h) , \varphi \rangle _{{\mathcal {S}}',{\mathcal {S}}} = 0 \). Since this holds for every \(\varphi \in C_c^\infty (\widehat{{\mathbb {R}}}^d)\) with \(\mathop {{\text {supp}}}\varphi \subset \widehat{{\mathbb {R}}}^d \setminus \mathop {{\text {supp}}}f\), we see \(\mathop {{\text {supp}}}(f \odot h) \subset \mathop {{\text {supp}}}f\). The argument for \(\mathop {{\text {supp}}}(f \odot h) \subset \mathop {{\text {supp}}}h\) is similar. \(\square \)
With this preparation, we can now provide the proof of Proposition 5.7.
Proof of Proposition 5.7
Before proving the claims, we show that \(\Phi _h\) is well-defined, with unconditional convergence in \(Z'({\mathcal {O}})\) of the defining series. For brevity, let \(\psi _i := {\mathcal {F}}^{-1}[(\varphi _i^*h) \odot (\varphi _i {\widehat{f}})] \in {\mathcal {S}}'({\mathbb {R}}^d)\). This is well-defined since (5.10) implies \(\varphi _i \, h \in {\mathcal {F}}L^1\), and \(\varphi _i^*\, h = \sum _{\ell \in i^*} \varphi _\ell \, h \in {\mathcal {F}}L^1({\mathbb {R}}^d)\).
Since \({\mathcal {F}}: Z'({\mathcal {O}}) \rightarrow {\mathcal {D}}'({\mathcal {O}})\) is an isomorphism, it is enough to show that the series \(\sum _{i \in I} {\mathcal {F}}\psi _i\) converges unconditionally in \({\mathcal {D}}'({\mathcal {O}})\). To see this, note that \(\mathop {{\text {supp}}}\widehat{\psi _i} \subset \mathop {{\text {supp}}}\varphi _i \subset \overline{Q_i}\) for all \(i \in I\), by Property (iv) of Lemma C.1. Therefore, \(\sum _{i \in I} {\mathcal {F}}\psi _i\) converges unconditionally in \({\mathcal {D}}'({\mathcal {O}})\) as a locally finiteFootnote 1 sum of (tempered) distributions.
(ii) As above, let \(\psi _i^{(n)} := {\mathcal {F}}^{-1}[(\varphi _i^*h) \odot (\varphi _i \widehat{f_n})]\). Note that \(\widehat{f_n} \rightarrow {\widehat{f}}\) in \({\mathcal {D}}'({\mathcal {O}})\), since \(f_n \rightarrow f\) in \(Z'({\mathcal {O}})\). Thus, setting \(e_x : \widehat{{\mathbb {R}}}^d \rightarrow {\mathbb {C}}, \xi \mapsto e^{2 \pi i \langle x,\xi \rangle }\) for \(x \in {\mathbb {R}}^d\), an application of [54, Theorem 7.23] shows that
for all \(i \in I \text { and } x \in {\mathbb {R}}^d\). Therefore, using that \( \langle F *G, \varphi \rangle _{{\mathcal {S}}',{\mathcal {S}}} = \int _{{\mathbb {R}}^d} G(x) \cdot (\varphi *{\widetilde{F}})(x) \, dx \) with \({\widetilde{F}}(x) = F(-x)\) for \( F \in L^1, G \in L^p\), and the estimate \(|{\mathcal {F}}^{-1}(\varphi _i \widehat{f_n})| \le F_i \in L^p ({\mathbb {R}}^d)\), we get by the dominated convergence theorem
for all \(\varphi \in {\mathcal {S}}({\mathbb {R}}^d)\) and \(i \in I\). Here, we used that \(\varphi *\widehat{\varphi _i^*h} \in L^1({\mathbb {R}}^d) \cap L^\infty ({\mathbb {R}}^d) \subset L^{p'} ({\mathbb {R}}^d)\).
Now, let \(\varphi \in Z({\mathcal {O}})\) be arbitrary, so that \({\mathcal {F}}^{-1} \varphi \in C_c^\infty ({\mathcal {O}})\). Then there is a finite set \(I_\varphi \subset I\) such that \(\mathop {{\text {supp}}}{\mathcal {F}}^{-1} \varphi \subset \overline{Q_i}^c\) for all \(i \in I \setminus I_\varphi \). Since \(\mathop {{\text {supp}}}{\mathcal {F}}\psi _i \subset \overline{Q_i}\) and \(\mathop {{\text {supp}}}{\mathcal {F}}\psi _i^{(n)} \subset \overline{Q_i}\), this implies \( \langle \psi _i , \varphi \rangle _{Z',Z} = \langle {\mathcal {F}}\psi _i, {\mathcal {F}}^{-1} \varphi \rangle _{{\mathcal {D}}', C_c^\infty } = 0 \) for all \(i \in I \setminus I_\varphi \). The same holds for \(\psi _i\) replaced by \(\psi _i^{(n)}\). Thus,
This shows that \(\Phi _h f_n \rightarrow \Phi _h f\) with convergence in \(Z'({\mathcal {O}})\).
Finally, we see for \(\ell \in I\) directly by definition of \(\psi _i^{(n)}\) and by definition of the “extended multiplication” \(\odot \) that
This shows that \( {\mathcal {F}}^{-1} (\varphi _\ell \, \widehat{\psi _i^{(n)}}) = {\mathcal {F}}^{-1}(\varphi _i^*\, h) *{\mathcal {F}}^{-1}(\varphi _i \, \varphi _\ell \, \widehat{f_n}) = 0 \) if \(\ell \in I \setminus i^*\), since then \(\varphi _i \, \varphi _\ell \equiv 0\). Therefore, since \(|{\mathcal {F}}^{-1}(\varphi _\ell \, \widehat{f_n} \,)| \le F_\ell \), we see
In view of Young’s inequality, we see
and hence \(\Vert G\Vert _{\ell _w^q(I;L^p)} \le N_{\mathcal {Q}}^2 C_{\Phi } C_h \cdot \Vert F\Vert _{\ell _w^q(I;L^p)} < \infty \), so that indeed each \(\Phi _h f_n\) is \((G,\Phi )\)-dominated.
(i) By applying Property (ii) to the constant sequence given by \(f_n = f\) for all \(n \in {\mathbb {N}}\) and with \(F_i := |{\mathcal {F}}^{-1}(\varphi _i {\widehat{f}})|\), we see that \(\Phi _h f\) is \((G,\Phi )\)-dominated for a function \(G \in \ell _w^q(I;L^p)\) satisfying \( \Vert G\Vert _{\ell _w^q(I;L^p)} \le N_{\mathcal {Q}}^2 C_{\Phi } C_h \cdot \Vert F\Vert _{\ell _w^q(I;L^p)} = N_{\mathcal {Q}}^2 C_{\Phi } C_h \cdot \Vert f\Vert _{{\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)} \). This proves the claim.
(iii) If \({\widehat{f}} \in C_c({\mathcal {O}})\), then \(\varphi _i \, {\widehat{f}} \in C_c({\mathcal {O}}) \subset L^2(\widehat{{\mathbb {R}}}^d)\), so that \( (\varphi _i^*h) \odot (\varphi _i {\widehat{f}}) = (\varphi _i^*h) \cdot (\varphi _i {\widehat{f}}) = \varphi _i \cdot h {\widehat{f}} \); see Lemma C.1(iii). Since \(h {\widehat{f}} \in C_c({\mathcal {O}})\), it follows \( h {\widehat{f}} = \sum _{i \in I} [ \varphi _i \cdot h {\widehat{f}} ] \), where only finitely many terms do not vanish. Hence, by definition of \(\Phi _h f\),
(iv) We have
so that \(g \cdot h\) is tame. Part (iii) shows for \(f \in {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) that \(\Phi _g f = {\mathcal {F}}^{-1}(g {\widehat{f}})\), which in particular implies \({\mathcal {F}}[\Phi _g f] \in C_c ({\mathcal {O}})\). Thus, by Part (iii) again, \( \Phi _h \Phi _g f = {\mathcal {F}}^{-1} [h \cdot {\mathcal {F}}[\Phi _g f]] = {\mathcal {F}}^{-1} (h g {\widehat{f}}) = \Phi _{g h} f \). Finally, for arbitrary \(f \in {\mathcal {D}}({\mathcal {Q}},L^p,\ell _w^q)\), Proposition 3.13 yields a sequence \((f_n)_{n \in {\mathbb {N}}} \subset {\mathcal {S}}_{{\mathcal {O}}}({\mathbb {R}}^d)\) which is \((F,\Phi )\)-dominated for some \(F \in \ell _w^q (I;L^p)\) and such that \(f_n \rightarrow f\) in \(Z'({\mathcal {O}})\). By Part (ii), this implies \(\Phi _{g h} f_n \rightarrow \Phi _{g h} f\) and \(\Phi _g f_n \rightarrow \Phi _g f\) in \(Z'({\mathcal {O}})\). Furthermore, there is \(G \in \ell _w^q(I; L^p)\) such that each \(\Phi _{g} f_n\) is \((G,\Phi )\)-dominated. Thus, a final application of Part (ii) implies
which completes the proof. \(\square \)
Appendix D: Other Auxiliary Results
1.1 D.1: An Estimate for the series \(\sum _{k \in {\mathbb {Z}}^d} (1 + |\eta + A k|)^{-(d+1)}\)
Lemma D.1
For \(\eta \in {\mathbb {R}}^d\) and \(A \in \mathrm {GL}(d, {\mathbb {R}})\),
Proof
First, note that the function \( \Theta : {\mathbb {R}}^d \rightarrow [0,\infty ], \; x \mapsto \sum _{k \in {\mathbb {Z}}^d} (1 + |x+k|)^{-(d+1)} \) is \({\mathbb {Z}}^d\)-periodic, and hence \(\Vert \Theta \Vert _{\sup } = \Vert \Theta |_{[0,1)^d}\Vert _{\sup }\). For \(x \in [0,1)^d\), we have \( \Vert k\Vert _{\infty } \le 1 + \Vert x+k\Vert _{\infty } \le 1 + |x+k| \, , \) and thus \(1 + \Vert k\Vert _{\infty } \le 2 (1 + |x+k|)\). Therefore, \(\Theta (x) \le 2^{d+1} \cdot \sum _{k \in {\mathbb {Z}}^d} (1 + \Vert k\Vert _{\infty })^{-(d+1)}\). In order to estimate this last term, we rewrite it using [25, Proposition 6.24] as
Let \(f : {\mathbb {Z}}^d \rightarrow (0,1] , k \mapsto (1 + \Vert k\Vert _{\infty })^{-(d+1)}\). For \(\lambda \ge 1\), clearly \(\{k \in {\mathbb {Z}}^d \,:\, f(k) > \lambda \} = \emptyset \). In contrast, for \(\lambda \in (0,1)\),
and thus \( |\{k \in {\mathbb {Z}}^d \,:\, f(k) > \lambda \}| \le \big ( 1 + 2 \lfloor \lambda ^{-1/(d+1)} - 1 \rfloor \big )^d \le 2^d \cdot \lambda ^{-d/(d+1)} \), which implies
for all \(x \in [0,1)^d\), whence \(\Theta (x) \le (d+1) \cdot 2^{1 + 2d}\) for all \(x \in {\mathbb {R}}^d\).
Now, let \(A \in \mathrm {GL}(d,{\mathbb {R}})\) be arbitrary. Then
and hence \(\big ( 1 + |\eta + Ak| \big )^{-(d+1)} = \big ( 1 + |A(k + A^{-1} \eta )| \big )^{-(d+1)} \le \max \big \{ 1 , \Vert A^{-1}\Vert ^{d+1} \} \cdot \big ( 1 + |k + A^{-1} \eta | \big )^{-(d+1)}\). Overall, we see for arbitrary \(\eta \in {\mathbb {R}}^d\) and \(A \in \mathrm {GL}(d, {\mathbb {R}})\) that
finishing the proof. \(\square \)
As a corollary, we get the following estimate for the series where we sum over \(k \in {\mathbb {Z}}^d \setminus \{0\}\) instead of \(k \in {\mathbb {Z}}^d\).
Corollary D.2
For \(\eta \in {\mathbb {R}}^d\) and \(A \in \mathrm {GL}(d,{\mathbb {R}})\), we have
Proof
We distinguish two cases.
First, suppose \(|A^{-1} \eta | \le \tfrac{1}{3}\). Then, noting that \(|k| \ge 1\) for all \(k \in {\mathbb {Z}}^d \setminus \{0\}\), we get the estimate \( |k + A^{-1} \eta | \ge |k| - |A^{-1} \eta | \ge \tfrac{|k|}{2} + \tfrac{1}{2} - |A^{-1} \eta | \ge \tfrac{|k|}{2} \ge \tfrac{1 + |k|}{4}. \) Next, note that \(|x| = |A^{-1} A x| \le \Vert A^{-1}\Vert \, |A x|\), and hence \(|A x| \ge \Vert A^{-1}\Vert ^{-1} \, |x|\) for all \(x \in {\mathbb {R}}^d\). This implies
Now, Lemma D.1 shows that
For the other case, suppose \(|A^{-1} \eta | > \tfrac{1}{3}\). Then \((1 + |\eta |) \, \Vert A^{-1}\Vert \ge \Vert A^{-1}\Vert \cdot |\eta | \ge |A^{-1} \eta | > \tfrac{1}{3}\), and
Now, an application of Lemma D.1 shows that
Together with the first case, this shows that the claimed estimate always holds. \(\square \)
1.2 D.2: Proof of Lemma 7.2
For brevity, set \(\langle \!\langle \xi \rangle \!\rangle := 1 + |\xi |^2\) for \(\xi \in \widehat{{\mathbb {R}}}^d\). With this notation, [62, Lemma 6.8] shows for arbitrary \(\theta \in {\mathbb {R}}\) and \(\alpha \in {\mathbb {N}}_0^d\) that there is a polynomial \(P_{\theta ,\alpha } \in {\mathbb {R}}[\xi _1,\dots ,\xi _d]\) such that, for all \(\xi \in \widehat{{\mathbb {R}}}^d\),
where \(C_{\theta ,\alpha } = |\alpha |! \cdot [2 (1 + d + |\theta |)]^{|\alpha |}\). Since \((1 + |\xi |)^k \le 2^k \cdot \langle \!\langle \xi \rangle \!\rangle ^{k/2}\) for all \(k \ge 0\), it follows that
for all \(\xi \in \widehat{{\mathbb {R}}}^d\), \(\theta \in {\mathbb {R}}\) and \(\alpha \in {\mathbb {N}}_0^d\). Next, for \(\theta = -\frac{1}{2}(d+1)\) and any \(\alpha \in {\mathbb {N}}_0^d\) with \(|\alpha | \le d+1\),
Combining Equations (D.2) and (D.3) with the elementary estimate \(1 + |\xi | \le 2 \langle \!\langle \xi \rangle \!\rangle ^{1/2}\), we see that
For the estimate concerning \(h_1\), note that since \(C_{\theta ,\alpha } = C_{-\theta ,\alpha }\), we also have \(C_{(d+1)/2, \beta } \le \big (3 \cdot (d+1)^2 \big )^{d+1}\) for all \(\beta \in {\mathbb {N}}_0^d\) with \(|\beta | \le d+1\). Hence, using the Leibniz rule and Equations (D.2) and (D.3), it follows for arbitrary \(\xi \in \widehat{{\mathbb {R}}}^d\) that
which completes the proof. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Romero, J.L., van Velthoven, J.T. & Voigtlaender, F. Invertibility of Frame Operators on Besov-Type Decomposition Spaces. J Geom Anal 32, 149 (2022). https://doi.org/10.1007/s12220-022-00887-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12220-022-00887-2
Keywords
- Atomic decompositions
- Banach frames
- Besov-type decomposition space
- Canonical dual frame
- Walnut–Daubechies representation
- Frame operator
- Generalized shift-invariant systems




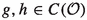 are tame, then so is
are tame, then so is