Shadowing is Generic on Various One-Dimensional Continua with a Special Geometric Structure

Abstract

In the paper we use a special geometric structure of selected one-dimensional continua to prove that some stronger versions of the shadowing property are generic (or at least dense) for continuous maps acting on these spaces. Specifically, we prove that (i) the periodic $\mathscr {T}_{S}$-bi-shadowing property, where $\mathscr {T}_{S}$ means some class of continuous methods, is generic as well as the s-limit shadowing property is dense in the space of all continuous maps (and all continuous surjective maps) of any topological graph; (ii) the $\mathscr {T}_{S}$-bi-shadowing property is generic as well as the s-limit shadowing property is dense in the space of all continuous maps of any dendrite; (iii) the $\mathscr {T}_{S}$-bi-shadowing property is generic in the space of all continuous maps of chainable continuum that can by approximated by arcs from the inside. The results of the paper extend ones obtained over the last few decades by various authors (see, e.g., Kościelniak in J Math Anal Appl 310:188–196, 2005; Kościelniak and Mazur in J Differ Equ Appl 16:667–674, 2010; Kościelniak et al. in Discret Contin Dyn Syst 34:3591–3609, 2014; Mazur and Oprocha in J Math Anal Appl 408:465–475, 2013; Mizera in Generic Properties of One-Dimensional Dynamical Systems, Ergodic Theory and Related Topics, III, Springer, Berlin, 1992; Odani in Proc Am Math Soc 110:281–284, 1990; Pilyugin and Plamenevskaya in Topol Appl 97:253–266, 1999; and Yano in J Fac Sci Univ Tokyo Sect IA Math 34:51–55, 1987) for both homeomorphisms and continuous maps of compact manifolds, including (in particular) an interval and a circle, which are the simplest examples of one-dimensional continua. Moreover, from a technical point of view our considerations are a continuation of those carried out in the earlier work by Mazur and Oprocha in J. Math. Anal. Appl. 408:465–475, 2013.

1 Introduction

When we perform numerical simulations, it is not completely certain whether sequences generated on the computer screen reflect real dynamical behavior. Moreover, we may also feel unsure when it comes to whether or not every trajectory can be revealed in these simulations. This was the motivation to investigate in the literature the notions of shadowing and inverse-shadowing properties.

The concept of shadowing was introduced independently in the works of Anosov [2] and Bowen [5]. Over the years, many various types of shadowing have been defined. The most important of them include periodic shadowing (tracing periodic pseudo-orbits by periodic orbits), inverse shadowing (tracing real orbits by pseudo-orbits produced by methods from a given class of methods), bi-shadowing (combination of shadowing and inverse shadowing) and s-limit shadowing (tracing pseudo-orbits by real orbits with an additional assumption stating that we also properly approximate limit sets by pseudo-orbits with increasing accuracy). In this article, we consider all the kinds of shadowing mentioned above. For the detailed approach to various concepts of shadowing we refer the reader to the monographs [24, 26] and (more recent one) [29].

It is quite challenging and often investigated problem to verify whether a given property is generic in a space of maps under consideration, equipped, at least, with the $\mathscr {C}^0$-topology; we recall that a property of elements of a topological space S is said to be generic, if it is satisfied on some residual subset of S, i.e., on a set that includes a countable intersection of open and dense subsets of S. In particular, many scientific works were devoted to genericity of the (usual) shadowing property and its other variants. For example, Yano in [32] proved that shadowing is generic in the space of homeomorphisms of the unit circle and Odani in [22] extended this result to the case of all smooth manifolds of the dimension at most 3. Further outcome was presented in [28], where Pilyugin and Plamenevskaya proved genericity of shadowing for homeomorphisms on any smooth compact manifold without boundary. It has been also showed in [11] and [12] that both shadowing and periodic shadowing are generic in the space of homeomorphisms on a compact smooth manifold, with or without boundary. The same conclusion was confirmed in [13] for some kind of the inverse shadowing property. For an accessible survey of various results of this type, the reader is referred to [27] (see also [1]).

When it comes to the case of non-invertible dynamical systems, one of the first theorem appeared in [18] for continuous maps on an interval. Genericity theorems for shadowing, periodic shadowing and inverse shadowing (with respect to some classes of continuous methods), in the space of all continuous (surjective) functions of a compact topological manifold that admits a decomposition, were proved in [14]. The next results were obtained in [16], where it was showed that shadowing is generic, as well as s-limit shadowing is dense in the space of continuous (surjective) maps of any compact topological manifold. At this point it is also worth to mention the results for continuous functions on a Cantor set, showing that in this case there is a residual set of maps which are conjugate with each other and have the shadowing property (see [4] and references therein). It is clear that a special geometric structure of the Cantor set was crucial for such results. Indeed, when proving genericity, geometric structure of the space was one of the most important tools; it is enough to mention a novel idea from [28], where the authors used decompositions for the first time, or from [15], where the utility of retractions was demonstrated.

In the first section of the paper we prove that the periodic $\mathscr {T}_{S}$-bi-shadowing property, where $\mathscr {T}_{S}$ means some class of continuous methods, is generic as well as the s-limit shadowing property is dense in the space of all continuous maps (and all continuous surjective maps) of any topological graph. To prove these results we elaborate on a kind of one-dimensional covering relations. In fact, slight modifications of this method are the main tools throughout the paper.

In the second section we prove that $\mathscr {T}_{S}$-bi-shadowing property is generic as well as the s-limit shadowing property is dense in the class of all continuous functions defined on any dendrite. Let us mention here that genericity of the (usual) shadowing property on dendrites was recently proved in [6]. In our proof we use a slightly different argument, motivated mainly by the methodology developed for graphs.

In the last section of our work we consider chainable continua that can be well approximated by arcs from the inside. We prove that $\mathscr {T}_{S}$-bi-shadowing property is generic in the class of maps defined on any chainable continuum that is retractable to an arc contained in it. The examples of continua with this property include the $\sin (1/x)$-curve and the Knaster bucket handle continuum (see Fig. 1 for a sketch of this continuum).

Fig. 1

The Knaster bucket handle

At the end we would like to emphasize that most techniques presented in proofs can be considered (up to some extent) as implementation of Zgliczyński’s and Gidea’s method of covering relations [34] in its simplest (one-dimensional) form (see also [33]).

2 Preliminaries

In this section we present some basic notation that is used throughout the paper. We also recall some basic notions related to the shadowing property and its other variants. Additional (more specific) definitions appear successfully in the paper as they are needed.

2.1 Basic Notation

The set of all positive integer numbers we denote by $\mathbb {N}$. For any subset A of a given metric space X and any $\varepsilon >0$, by $B_\varepsilon (A)$ we mean the $\varepsilon$-envelope of A, which contains all the points with the distance from A less than $\varepsilon$. If $R:X\rightarrow Y$, where Y is a subspace of X, is a continuous map satisfying $R(x)=x$ for any $x\in Y$, then we call R a retraction onto Y.

Let X be a (non-degenerate) continuum, i.e., a compact and connected metric space, possessing more than one point. By a curve in X we mean the image of a continuous map $\gamma$ from the closed unit interval [0, 1] into X. Then we call $\gamma$ a parametrization of the curve $\gamma ([0,1])$.

A curve $J=\gamma ([0,1])$ is an arc, if the map $\gamma$ is injective. In this case we call $\gamma (0)$ and $\gamma (1)$ the endpoints of J as well as we denote by ${{\,\mathrm{End}\,}}(J)$ the set $\{\gamma (0),\gamma (1)\}$.

If J is a curve with a parametrization $\gamma$ such that $\gamma |_{(0,1)}$ is injective and $\gamma (0)=\gamma (1)$, then J is called a simple loop or a simple closed curve. Note that, equivalently, a simple loop is the image of a continuous injective map from the unit circle into X.

2.2 Shadowing

Let (X, d) be a compact metric space. Denote by C(X) the collection of all continuous maps on X endowed with the metric $\rho (f,g)=\sup _{x\in X} d(f(x),g(x))$ for $f,g\in C(X)$. It is well known that $\rho$ is complete and if we denote by S(X) the subset of C(X) consisting of all surjective maps, then $\rho$ restricted to S(X) remains a complete metric. The topology induced by $\rho$ on C(X) (or on S(X)) is called the $\mathscr {C}^0$-topology.

If $f \in C(X)$, then the pair (X, f) is a dynamical system. The orbit of a point $x \in X$ is the sequence $\{x_n\}_{n=0}^\infty \subset X$ defined in the following way: $x_0=x$ and $x_{n+1}=f(x_n)$ for all integer $n \ge 0$.

Let $f \in C(X)$ and $\delta > 0$. A sequence $\{x_n\}_{n=0}^\infty \subset X$ is a $\delta$-pseudo-orbit of f if $d(f(x_n),x_{n+1})< \delta$ for every integer $n\ge 0$. If, additionally, the sequence $\{x_n\}$ is periodic, i.e., there exists $T>0$ such that $x_{n+T}=x_n$ for all integer $n\ge 0$, then it is a periodic$\delta$-pseudo-orbit; in this case we call T a period of $\{x_n\}$ and we also say that $\{x_n\}$ is T-periodic. If a $\delta$-pseudo-orbit $\{x_n\}$ satisfies the condition

$$\begin{aligned} \lim _{n \rightarrow \infty } d(f(x_n),x_{n+1})=0, \end{aligned}$$

then it is a limit$\delta$-pseudo-orbit. Clearly, each orbit of f is a (limit) $\delta$-pseudo-orbit of f for any $\delta >0$.

Now, we are ready to present the concepts of shadowing, periodic shadowing and s-limit shadowing, which are the main properties studied in this paper.

Definition 1

A map $f\in C(X)$ has the shadowing property if for every $\varepsilon >0$ there exists $\delta >0$ satisfying the following condition: any $\delta$-pseudo-orbit $\{y_n\}$ of f is $\varepsilon$-traced by some orbit $\{x_n\}$ of f, i.e., $d(x_n,y_n)< \varepsilon$ for every integer $n\ge 0$. If, in addition, each periodic $\delta$-pseudo-orbit $\{y_n\}$ (or each limit $\delta$-pseudo-orbit $\{y_n\}$, respectively) is $\varepsilon$-traced by a periodic orbit $\{x_n\}$ with the same period (or is $\varepsilon$-traced by an orbit $\{x_n\}$ and $d(x_n,y_n)\rightarrow 0$ as $n\rightarrow \infty$, respectively), then we say that f has the periodic shadowing property (or the s-limit shadowing property, respectively).

In the next definition $X^{\mathbb {N}}$ denotes the space of all one-sided sequences $\{x_n\}_{n=0}^\infty \subset X$, endowed with the Tikhonov product topology which makes $X^{\mathbb {N}}$ a compact metrizable space.

Definition 2

Let $f \in C(X)$ and $\delta > 0$. By a $\delta$-method for f we mean a map $\chi :X \rightarrow X^{\mathbb {N}}$ such that for every $x \in X$ the sequence $\chi (x)$ is a $\delta$-pseudo-orbit of f with $\chi (x)_0 =x$ (then we call $\chi (x)$ a $\delta$-pseudo-orbit produced by$\chi$).

We say that a family $\mathscr {T}=\{\mathscr {T}_{f,\delta } :\delta >0 \}$, consisting of classes $\mathscr {T}_{f,\delta }$ of selected $\delta$-methods for f, is complete, if $\mathscr {T}_{f,\delta } \ne \emptyset$ for every $\delta >0$.

In the definition below we present a few other concepts of shadowing: the so-called (periodic)$\mathscr {T}$-inverse shadowing and (periodic)$\mathscr {T}$-bi-shadowing.

Definition 3

Let $f \in C(X)$ and $\mathscr {T}=\{\mathscr {T}_{f,\delta } :\delta >0 \}$ be a complete family of classes $\mathscr {T}_{f,\delta }$ of $\delta$-methods for f. We say that f has the $\mathscr {T}$-inverse-shadowing property (or $\mathscr {T}$-bi-shadowing property, respectively) if for every $\varepsilon >0$ there exists $\delta >0$ such that for every $\delta$-method $\chi \in \mathscr {T}_{f,\delta }$ the following condition holds: any orbit of f (or any $\delta$-pseudo-orbit of f, respectively) is $\varepsilon$-traced by some $\delta$-pseudo-orbit that is produced by $\chi$ (or is $\varepsilon$-traced by some orbit of f as well as by some $\delta$-pseudo-orbit that is produced by $\chi$). If, additionally, each periodic orbit of f (or each periodic $\delta$-pseudo-orbit of f, respectively) with a period $T>0$ is $\varepsilon$-traced by a T-periodic $\delta$-pseudo-orbit that is produced by $\chi$ (or is $\varepsilon$-traced by a T-periodic orbit of f as well as by a T-periodic $\delta$-pseudo-orbit that is produced by $\chi$, respectively), then we say that f has the periodic$\mathscr {T}$-inverse-shadowing property (or the periodic$\mathscr {T}$-bi-shadowing property, respectively).

It is easily seen that a continuous map has the $\mathscr {T}$-bi-shadowing property if and only if it has both the shadowing and the $\mathscr {T}$-inverse-shadowing properties.

For further considerations we will use a complete family of classes of continuous $\delta$-methods that was introduced in [25] (for homeomorphisms) and investigated in [16] (for continuous maps). It is presented in the following Remark.

Remark 4

Let $f\in C(X)$ and $\delta >0$. Denote by $\mathscr {T}_{A,f,\delta }$ the class of all possible $\delta$-methods for f. We define the following class of continuous $\delta$-methods for f:

$$\begin{aligned} \begin{aligned} \mathscr {T}_{S,f, \delta }= \{\chi \in \mathscr {T}_{A,f,\delta }: \text {there exists a sequence of maps} \; \psi _n \in C(X) \text { satisfying } \\ \rho (\psi _n ,f) <\delta \; \text {such that} \; \chi (x)_{n+1}= \psi _{n} (\chi (x)_{n})\; \text {for} \; x \in X \; \text {and integer} \; n\ge 0\}. \end{aligned} \end{aligned}$$

By definition, the family $\mathscr {T}_{S}=\{\mathscr {T}_{S,f, \delta }: \delta >0 \}$ is complete.

3 Various Shadowing Properties on Topological Graphs

3.1 Preliminary Definitions and Facts

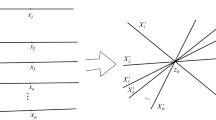
A topological graph (a graph for short) is a continuum G such that there is a one-dimensional simplicial complex K whose geometric carrier is homeomorphic to G. This way we can view each topological graph as a continuum embedded in $\mathbb {R}^3$ (see, e.g., [19]), and hence we can always consider G to be equipped with a geodesic metric d that is induced from the Euclidean structure in $\mathbb {R}^3$ onto an associated simplicial complex K. In other words, the distance between two points is equal to the length of the shortest path connecting them. By the definition, each graph G can be represented as the union of a family $\mathscr {I}=\{I_i\}_{i=1}^n$, where each set $I_i$ is an arc (in practice, a line segment in $\mathbb {R}^3$) and $|I_j\cap I_k|\le 1$ for $j\ne k$, assuming that non-empty intersection is allowed only in the endpoints of the arcs $I_i$ for $i\in \{1,\ldots ,n\}$.

Let us establish above-described representation for a moment. A point $x\in G$ is called a vertex of G if it is an endpoint of some arc $I_i$.

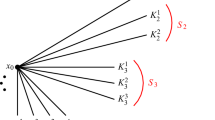
By the star of a vertex $x\in G$ we mean the set $S(x)=\bigcup \{I_i\in \mathscr {I}: x\in I_i\}$. For any point $x\in G$ define the valence of x, denoted by ${{\,\mathrm{val}\,}}(x)$, in the following way: if x is a vertex of G then ${{\,\mathrm{val}\,}}(x)$ is equal to the number of connected components of the set $S(x)\setminus \{x\}$, and ${{\,\mathrm{val}\,}}(x)=2$ otherwise. If ${{\,\mathrm{val}\,}}(x)=1$ (or ${{\,\mathrm{val}\,}}(x)>2$, respectively), then we call x an endpoint of G (or a branch point of G, respectively). The sets of all endpoints and all branch points of G are denoted by ${{\,\mathrm{End}\,}}(G)$ and ${{\,\mathrm{Br}\,}}(G)$, respectively. It is not hard to see that these definitions are independent of the choice of a representation of G.

All of the above concepts are illustrated in the example shown in Fig. 2.

Before proving the main theorems of this section, we need some technical lemmas. The first two will be helpful in proving the bi-shadowing property and its periodic version. Their proofs are, in fact, easy exercises, which we leave to the reader.

Fig. 2

Sample representation of a graph

Lemma 5

Let G be a graph and $f \in C(G)$. If $S,V\subset G\setminus {{\,\mathrm{Br}\,}}(G)$ are arcs such that $V \subset f(S)$ and f(S) does not contain a simple loop, then there exists an arc $S^{*}\subset S$ such that $f(S^{*})=V$.

Lemma 6

Let G be a graph and $f \in C(G)$. If $S_0,\ldots S_{T-1}\subset G\setminus {{\,\mathrm{Br}\,}}(G)$ are arcs such that each set $f(S_i)$ has no simple loop as well as $S_{i+1} \subset f(S_i)$ for all $i\in \{0,\ldots ,T-2\}$ and $S_0 \subset f(S_{T-1})$, then there exists a point $x \in S_0$ such that $f^{T}(x)=x$ and $f^{i}(x)\in S_i$ for all $i\in \{0,\ldots ,T-1\}$.

In order to formulate the next lemma, which gives some sufficient tools for proving the main results of this section, let us denote by $\alpha _G$ the minimal distance between two different points of the set ${{\,\mathrm{End}\,}}(G)\cup {{\,\mathrm{Br}\,}}(G)$, i.e.,

$$\begin{aligned} \alpha _G=\min \{d(a,b): a,b\in {{\,\mathrm{End}\,}}(G)\cup Br(G), a\ne b\}. \end{aligned}$$

If there is a simple loop in G, then we define

$$\begin{aligned} \beta _G=\min \{{{\,\mathrm{diam}\,}}C : C\subset G \text { is a simple loop}\}, \end{aligned}$$

and we put $\beta _G={{\,\mathrm{diam}\,}}G$ otherwise. Finally, we define

$$\begin{aligned} \Gamma (G)=\min \{\alpha _G,\beta _G\}. \end{aligned}$$

Lemma 7

Let G be a graph, $f\in C(G)$ and $\varepsilon >0$. Let $\left\{ U_i\right\} _{i=1}^n$ be a cover of G consisting of pairwise distinct arcs satisfying

$$\begin{aligned} \max \{{{\,\mathrm{diam}\,}}{U_i}, {{\,\mathrm{diam}\,}}{f(U_i)}\}<\min \{\varepsilon , \Gamma (G)/3\}, \end{aligned}$$

(3.1)

for which the following implication holds:

$$\begin{aligned} U_i \cap U_j \ne \emptyset \implies {{\,\mathrm{Int}\,}}U_i \cap {{\,\mathrm{Int}\,}}U_j \ne \emptyset . \end{aligned}$$

(3.2)

Denote by $\left\{ V_{i,j}\right\} _{j=1}^{k(i)}$ for $i\in \{1,\ldots ,n\}$ the maximal (in the sense of the number of elements) subfamilies of $\left\{ U_s\right\} _{s=1}^n$ such that

$$\begin{aligned} f(U_i)\subset {\mathrm {Int}}\, \bigcup _{j=1}^{k(i)}V_{i,j}\; \text { and } \; f(U_i)\cap {{\,\mathrm{Int}\,}}V_{i,j}\ne \emptyset \end{aligned}$$

for each $i\in \{1,\ldots , n\}$, $j\in \{1,\ldots , k(i)\}$. Under the above assumptions, there exist pairwise disjoint arcs $S_{i,1},\ldots , S_{i,k(i)}, \; i\in \{1,\ldots , n\},$ such that $S_{i,j}\subset {\mathrm {Int}}\, U_i$ (hence each set $S_{i,j}$ has no branch points), a constant $\xi >0$ and a map $g\in C(G)$ with $\rho (f,g)<\varepsilon$, such that for every $i\in \{1,\ldots , n\}$ the following conditions are satisfied:

• (i) the map $g|_{S_{i,j}}$ is injective for every $j\in \{1,\ldots , k(i)\}$,

• (ii) $g(U_i)=\bigcup _{j=1}^{k(i)} g(S_{i,j})$,

• (iii) $B_\xi (\bigcup _{l=1}^{k(\psi (i,j))}{S_{\psi (i,j),l}}) \subset g(S_{i,j})$ for $j\in \{1,\ldots , k(i)\}$ and each set $\overline{B_\xi (S_{\psi (i,j),l})}$ is an arc containing no branch points,

• (iv) $B_\xi (g(U_i))\subset \bigcup _{j=1}^{k(i)}V_{i,j},$

where $\psi (i,j)$ is the unique index such that $V_{i,j}=U_{\psi (i,j)}$.

Proof

Fix any cover $\{U_i\}_{i=1}^n$ of G satisfying required properties and note that intersection of its two different members is an arc, when non-empty.

At first, we claim that for every $i\in \{1,\ldots , n\}$ and $j\in \{1,\ldots k(i)\}$ there exists an arc $W_{i,j} \subset {\mathrm {Int}}\, V_{i,j}\cup ({{\,\mathrm{Br}\,}}(G)\cap V_{i,j})\subset V_{i,j}$ satisfying the following conditions:

$$\begin{aligned} f(U_i)\subset {\mathrm {Int}}\,\bigcup _{j=1}^{k(i)}W_{i,j}, \;\; f(U_i)\cap {\mathrm {Int}}\, W_{i,j}\ne \emptyset , \;\; \psi (i,j)=\psi (k,l) \Rightarrow W_{i,j}=W_{k,l}. \end{aligned}$$

(3.3)

Indeed, for any $i\in \{1,\ldots ,n\}$ take

$$\begin{aligned} \alpha _i=\min \{{{\,\mathrm{diam}\,}}(V_{i,j}\cap V_{i,k})\;:\; V_{i,j}\cap V_{i,k} \ne \emptyset \}, \end{aligned}$$

which, by (3.2), is a positive constant. We also know that $\bigcup _{j=1}^{k(i)}V_{i,j}$ is a subgraph of G containing, by (3.1), at most one point form the set ${{\,\mathrm{End}\,}}(G)\cup {{\,\mathrm{Br}\,}}(G)$. Define

$$\begin{aligned} \beta _i=\min \left\{ {\mathrm {dist}} (f(U_i),z)\;:\; z \in {{\,\mathrm{End}\,}}\left( \bigcup _{j=1}^{k(i)}V_{i,j}\right) \setminus {{\,\mathrm{End}\,}}(G) \right\} \end{aligned}$$

and note that by compactness of $f(U_i)$ we have $\beta _i>0$. Now choose a collection of points $x_{i,j}$ for $i\in \{1,\ldots , n\}$ and $j\in \{1,\ldots , k(i)\}$, such that $x_{i,j}\in f(U_i)\cap {{\,\mathrm{Int}\,}}V_{i,j}$. Put

$$\begin{aligned} \gamma =\min _{i,j}\{\text{ dist }(x_{i,j},{{\,\mathrm{End}\,}}({V_{i,j}})\setminus {{\,\mathrm{End}\,}}(G))\}>0 \end{aligned}$$

and

$$\begin{aligned} \eta =\min _i\{\min \{\alpha _i/3,\beta _i/3,\gamma /3\}\}>0. \end{aligned}$$

Then for each $i\in \{1,\ldots , n\}$ and $j\in \{1,\ldots , k(i)\}$ take an arc $W_{i,j}\subset {\mathrm {Int}}\, V_{i,j}\cup ({{\,\mathrm{Br}\,}}(G)\cap V_{i,j})\subset V_{i,j}$ such that ${{\,\mathrm{End}\,}}(G)\cap V_{i,j}={{\,\mathrm{End}\,}}(G)\cap W_{i,j}$ and all connected components of the set $V_{i,j}\setminus W_{i,j}$ have diameters equal to $\eta$.

Consequently, one can easily check that

$$\begin{aligned} x_{i,j}\in f(U_i)\cap {\mathrm {Int}}\, W_{i,j}\ne \emptyset \; \text { and } \; f(U_i)\subset {\mathrm {Int}}\,\bigcup _{j=1}^{k(i)}W_{i,j}. \end{aligned}$$

(3.4)

By the choice of $\eta$, if $V_{i,j}=V_{k,l}$ then $W_{i,j}=W_{k,l}$. Summing up, the condition (3.3) holds.

Since the sets $W_{i,j}$ depend only on $\eta$ and their supersets $U_{\psi (i,j)}=V_{i,j}$, we obtain a collection of arcs $\{R_s\}_{s=1}^n$ such that $R_{\psi (i,j)}=W_{i,j}\subset U_{\psi (i,j)}$. Observe that if we decrease $\eta$ then we, in fact, decrease ${{\,\mathrm{diam}\,}}(V_{i,j}\setminus W_{i,j})$, so doing this, if necessary, we easily ensure also that the following implication holds:

$$\begin{aligned} f(U_i)\cap {{\,\mathrm{Int}\,}}V_{i,j}\ne \emptyset \Longrightarrow f(R_i)\cap {{\,\mathrm{Int}\,}}W_{i,j}\ne \emptyset . \end{aligned}$$

Hence we can find pairwise distinct points $z_{i,j}\in {\mathrm {Int}}\, R_i$ for $j\in \{1,\ldots , k(i)\}$ such that $f(z_{i,j})\in {{\,\mathrm{Int}\,}}W_{i,j}$. In particular, we can construct arcs

$$\begin{aligned} S_{i,1},\ldots , S_{i,k(i)}, \; S^*_{i,1},\ldots , S^*_{i,k(i)} \; \text { for } \; i\in \{1,\ldots , n\}, \end{aligned}$$

such that

$$\begin{aligned} S_{i,j}\subset & {} {\mathrm {Int}}\, S^*_{i,j}\subset S^*_{i,j}\subset {{\,\mathrm{Int}\,}}R_i \setminus {{\,\mathrm{End}\,}}(G)\subset U_i \quad \text {and}\nonumber \\ f( S^*_{i,j})\subset & {} {\mathrm {Int}}\, W_{i,j} \subset U_{\psi (i,j)}. \end{aligned}$$

(3.5)

Note that each set ${{\,\mathrm{Int}\,}}R_i$ does not contain branch points of G, so each set $S^*_{i,j}$ does not contain them as well. Clearly, we may also assume that all the arcs $S^*_{i,j}$ are pairwise disjoint. Put

$$\begin{aligned} \xi {:}{=}1/2\cdot \min _{i,j}\left\{ \text{ dist }(S^*_{i,j},{{\,\mathrm{End}\,}}(R_{i})\cup ({{\,\mathrm{Br}\,}}(G)\cap R_i)\right\} >0, \end{aligned}$$

and note that all the sets $\overline{B_\xi (S^*_{i,j})}$ are arcs with no branch points. We can define a map $g\in C(G)$ by putting on each set $S_{i,j}$ an affine map with the image equal to $W_{i,j}$ and taking

$$\begin{aligned} g(x)=f(x)\; \text { for any } \; x \in G\setminus \bigcup _{i=1}^{n}\bigcup _{j=1}^{k(i)} {\mathrm {Int}}\, S^*_{i,j}. \end{aligned}$$

By (3.5) we can define g on connected components of the sets ${\mathrm {Int}} \, S^*_{i,j}\setminus S_{i,j}$ in such a way that g is continuous, and the following conditions are satisfied:

$$\begin{aligned} g(S_{i,j})=g(S^*_{i,j})=W_{i,j}=R_{\psi (i,j)}\subset V_{i,j}=U_{\psi (i,j)}\; \text { and }\; g|_{S_{i,j}}\; \text { is injective} \end{aligned}$$

(3.6)

for $i\in \{1,\ldots , n\}$ and $j\in \{1,\ldots , k(i)\}$. Since the diameter of each $U_i$ is less than $\varepsilon$, we conclude that $\rho (f,g)<\varepsilon$, and hence the condition (i) holds.

Recall that $f(S^*_{s,t})\subset {\mathrm {Int}}\, W_{s,t} \subset V_{s,t}$ by (3.5), and therefore if $U_i\cap S^*_{s,t}\ne \emptyset$ then $f(U_i)\cap V_{s,t}\ne \emptyset$ and hence, by (3.3), there exists $1\le j \le k(i)$ such that $W_{s,t}=W_{i,j}$. Taking into account the definition of g, (3.2), (3.3) and (3.6), this immediately implies that

$$\begin{aligned} g(U_i)\subset & {} f(U_i)\cup \bigcup _{s=1}^{n}\bigcup _{t=1}^{k(s)} g(U_i\cap S^*_{s,t}) \subset {\mathrm {Int}}\, \bigcup _{j=1}^{k(i)} W_{i,j} \cup \bigcup _{j=1}^{k(i)} W_{i,j} \\\subset & {} \bigcup _{j=1}^{k(i)} W_{i,j}\subset \bigcup _{j=1}^{k(i)}{\mathrm {Int}}\, V_{i,j}\cup {{\,\mathrm{Br}\,}}(V_{i,j})\subset {\mathrm {Int}}\,\bigcup _{j=1}^{k(i)}V_{i,j}. \end{aligned}$$

Hence, decreasing $\xi$ if necessary, we see that the condition (iv) holds. Additionally, by (3.6) we have

$$\begin{aligned} \bigcup _{j=1}^{k(i)} W_{i,j}=\bigcup _{j=1}^{k(i)}g(S_{i,j})\subset g(U_i), \end{aligned}$$

(3.7)

so the condition (ii) is satisfied.

Finally, note that each set $\overline{B_\xi (S_{i,j})}$ is an arc containing no branch points of G. Furthermore, by the definition of $\xi$ and (3.6) we obtain that

$$\begin{aligned} B_\xi \left( \bigcup _{l=1}^{k(\psi (i,j))}S_{\psi (i,j),l}\right) \subset R_{\psi (i,j)}= g(S_{i,j}), \end{aligned}$$

which gives the condition (iii), and hence completes the proof. $\square$

Remark 8

Denote $S_i{:}{=}\bigcup _{j=1}^{k(i)} S_{i,j}$. From the statement of Lemma 7 it follows that for each $i\in \{1,\ldots ,n\}$ we have

$$\begin{aligned} g(U_i)=g(S_i)\supset \bigcup _{j=1}^{k(i)}B_{\xi }(S_{\psi (i,j)})\supset \bigcup _{j=1}^{k(i)} S_{\psi (i,j)} \end{aligned}$$

and $S_i\subset {{\mathrm {Int}}}\,U_i$. It is also clear that if $f\in S(G)$ then also $g\in S(G)$, because, by (3.4) and (3.7), we have $f(U_i)\subset g(U_i)$ for every $i\in \{1,\ldots ,n\}$.

Example 9

Fix any graph G, any map $f\in C(G)$ and any constant $\varepsilon >0$. We can construct a cover satisfying the assumptions of Lemma 7 as follows. At first fix a positive constant $\gamma <\min \{\varepsilon ,\Gamma (G)/3\}$ such that the following implication holds for any points $x,y\in G$:

$$\begin{aligned} d(x,y)<\gamma \implies d(f(x),f(y))<\min \{\varepsilon ,\Gamma (G)/3\}. \end{aligned}$$

If $x\in {{\,\mathrm{Br}\,}}(G)$ then, obviously, $\overline{B_{\gamma /2}(x)}$ is an n-star ($n\ge 3$) and thus the set $\overline{B_{\gamma /2}(x)}\setminus \{x\}$ has n connected components $C_1,\ldots , C_n$, such that each set $\overline{C_i}$ is an arc containing x as one of its endpoints. So we include into the cover the following $n-1$ arcs:

$$\begin{aligned} \overline{C_i}\cup \overline{C_n}\;\; {\mathrm { for }} \;\; i\in \{1,\ldots , n-1\}, \end{aligned}$$

which clearly satisfy the condition (3.2). Next, for each $x\in {{\,\mathrm{End}\,}}(G)$ the set $\overline{B_{\gamma }(x)}$ is an arc and thus we also consider it as a member of the cover. Finally, each connected component of the set

$$\begin{aligned} G\setminus \cup _{x\in {{\,\mathrm{End}\,}}(G)\cup {{\,\mathrm{Br}\,}}(G)}B_{\gamma /4}(x) \end{aligned}$$

is an arc, so it can be easily covered by finite number of arcs with diameters bounded by $\varepsilon$, in such a way that if two arcs intersect, then so do their interiors. Now, it is clear that taking all these sets together we obtain a cover of G satisfying the assumptions of Lemma 7.

The concept of the procedure described in Example 9 is presented in Fig. 3.

Fig. 3

An illustration of the procedure described in Example 9 in a neighborhood of a vertex, a branch point and an endpoint

3.2 $\pmb {{\mathscr {T}}}_{S}$-bi-Shadowing is $\pmb {{\mathscr {C}}}^0$-Generic on Graphs

Now, we are ready to prove the first result regarding genericity of shadowing on graphs.

Theorem 10

Let G be a graph. Then for every $\varepsilon >0$ and every map $f \in C(G)$ there exists $\delta >0$ and a map $g \in C(G)$ with $\rho (f,g)<\varepsilon$, such that for every $h\in C(G)$ with $\rho (g,h)<\delta$ and every $\delta$-method $\chi \in \mathscr {T}_{S,h,\delta }$, each (periodic) $\delta$-pseudo-orbit of h is $\varepsilon$-traced by some (periodic) orbit of h as well as by some (periodic) $\delta$-pseudo-orbit of h that is produced by $\chi$. Additionally, if $f \in S(G)$ then also $g \in S(G).$

Proof

Fix any $\varepsilon >0$ and any $f\in C(G)$. Let $\left\{ U_i\right\} _{i=1}^n$ be a cover of G satisfying assumptions of Lemma 7. By definition, for all $i\in \{1,\ldots ,n\}$ the set $\bigcup _{j=1}^{k(i)}V_{i,j}$ contains no simple loop. We apply Lemma 7 to this cover and the map f obtaining a map $g\in C(G)$, a constant $\xi >0$ and a collection of arcs $\{S_{i,j}\}$. Recall that $g\in S(G)$ if $f\in S(G)$ (see Remark 8 for more details). Take any positive number $\delta <\xi /2$, any map $h \in C(G)$ with $\rho (h,g)<\delta$ and any $\delta$-method $\chi \in \mathscr {T}_{S,h,\delta }$ for h, together with the respective functions $\psi _t\in C(G)$ with $\rho (h,\psi _t)<\delta$, such that $\chi (x)_{t+1} = \psi _{t}(\chi (x)_{t})$ for all $x \in G$ and all $t \ge 0$. Note that then $\rho (g,\psi _t)<2 \delta <\xi$ and $h(S_{i,j})$ does not contain a simple loop for any choice of $i\in \{1,\ldots ,n\}$ and $j\in \{1,\ldots ,k(i)\}$.

Fix a $\delta$-pseudo-orbit $\{x_t\}_{t=0}^{\infty }$ of h. Directly from Lemma 7 (iv) we obtain that for every integer $t\ge 0$, if $x_t \in U_i$ then $x_{t+1} \in \bigcup _{j=1}^{k(i)} V_{i,j}$. Additionally, we can construct sequences $\{\eta (t)\}_{t=0}^{\infty }\subset \{1,\ldots ,n\}$ and $\{\xi (t)\}_{t=0}^{\infty } \subset \mathbb {N}$ such that for every integer $t \ge 0$ the following conditions are satisfied:

$$\begin{aligned} x_{t} \in U_{\eta (t)},\qquad x_{t+1}\in U_{\eta (t+1)} \in \{ V_{\eta (t),j} \}_{j=1}^{k(\eta (t))}, \end{aligned}$$

and $\psi (\eta (t),\xi (t))=\eta (t+1)$. Such selection is possible, because by Lemma 7 (iv) we have

$$\begin{aligned} x_{t+1}\in B_\delta (h(x_t))\subset B_{2\delta }(g(x_t))\subset B_\xi (g(U_{\eta (t)}))\subset \bigcup _{j=1}^{k(\eta (t))} V_{\eta (t),j}. \end{aligned}$$

Then, by the definition of the sets $S_{i,j}$, we have $S_{\eta (t),\xi (t)}\subset U_{\eta (t)}$ and, by Lemma 7 (iii), we additionally obtain

$$\begin{aligned} B_\xi (S_{\eta (t+1),\xi (t+1)})&=B_\xi (S_{\psi (\eta (t),\xi (t)),\xi (t+1)})\subset B_\xi \left( \bigcup _{l=1}^{k(\psi (\eta (t),\xi (t)))}S_{\psi (\eta (t),\xi (t)),l}\right) \nonumber \\&\quad \subset g(S_{\eta (t),\xi (t)}). \end{aligned}$$

(3.8)

Therefore,

$$\begin{aligned} S_{\eta (t+1),\xi (t+1)} \subset h(S_{\eta (t),\xi (t)})\quad \text {and} \quad S_{\eta (t+1),\xi (t+1)} \subset \psi _t(S_{\eta (t),\xi (t)}). \end{aligned}$$

By the above,

$$\begin{aligned} \bigcap _{t=0}^\infty h^{-t}(S_{\eta (t),\xi (t)})\ne \emptyset \;\; \text {and} \;\; S_{\eta (0),\xi (0)}\cap \bigcap _{t=1}^\infty (\psi _{t-1}\circ \dots \circ \psi _0)^{-1}(S_{\eta (t),\xi (t)})\ne \emptyset , \end{aligned}$$

which implies that there exist points $y,z\in S_{\eta (0),\xi (0)}$ such that for each $t \ge 0$ we have $h^t(y),\chi (z)_t\in S_{\eta (t),\xi (t)} \subset U_{\eta (t)}$. In particular,

$$\begin{aligned} d(h^t(y),x_t)\le {{\,\mathrm{diam}\,}}(U_{\eta (t)})<\varepsilon \;\; \text {and} \;\; d(\chi (z)_t,x_t)\le {{\,\mathrm{diam}\,}}(U_{\eta (t)})<\varepsilon \end{aligned}$$

for every integer $t\ge 0$.

Now, assume that $\{x_t\}_{t=0}^{\infty }$ is a periodic $\delta$-pseudo-orbit of h, i.e., $x_{t+T}=x_t$ for some integer $T>0$ and all $t\ge 0$. It is easy to see that we can then put $\eta (t)=\eta (t+T)$ and setting $\xi (t+T)=\xi (t)$ we obtain

$$\begin{aligned} \eta (t+T+1)=\eta (t+1)=\psi (\eta (t),\xi (t))=\psi (\eta (t+T),\xi (t+T)), \end{aligned}$$

so all the previous calculations hold and, consequently, this sequence is good for proving tracing. But then, in particular, we have $S_{\eta (0),\xi (0)}= S_{\eta (T),\xi (T)}$, and hence by Lemma 6 we conclude that there are points $y,z\in S_{\eta (0),\xi (0)}$, such that the orbit of y and the $\delta$-pseudo-orbit $\chi (z)$ are periodic (with a period T) and both $\varepsilon$-trace $\{x_t\}_{t=0}^{\infty }$. The proof is completed. $\square$

Theorem 11

For any graph G, the set of continuous maps possessing the periodic $\mathscr {T}_S$-bi-shadowing property is residual in C(G) and in S(G).

Proof

Let $\mathscr {X}=C(G)$ or $\mathscr {X}=S(G)$, depending on the case we are proving.

For each $n\in \mathbb {N}$ denote by $A_n \subset \mathscr {X}$ the set consisting of maps $g \in \mathscr {X}$ for which there are constants $\delta >0$ such that if $h\in \mathscr {X}$ satisfies $\rho (g,h)<\delta$ and $\chi \in \mathscr {T}_{{S,h,\delta }}$, then every (periodic) $\delta$-pseudo-orbit of h is 1/n-traced by some (periodic) orbit of h and by some (periodic) $\delta$-pseudo-orbit of h that is produced by $\chi$.

We are going to show that each set $A_n$ is open in $\mathscr {X}$. Indeed, fix $n\in \mathbb {N}$, $g \in A_n$ and take a respective constant $\delta >0$. We claim that $B_{\delta }(g)\subset A_n$. Indeed, for a given $h\in B_{\delta } (g)$ there exists $\eta >0$ such that $B_{\eta }(h)\subset B_{\delta }(g)$. Hence, if $\tilde{h} \in \mathscr {X}$ satisfies $\rho (h,\tilde{h})<\eta$ then $\tilde{h} \in B_{\delta }(g)$, which implies that if we establish $\chi \in \mathscr {T}_{S,\tilde{h},\eta }\subset \mathscr {T}_{S,\tilde{h},\delta }$, then every (periodic) $\eta$-pseudo-orbit of $\tilde{h}$, being at the same time a (periodic) $\delta$-pseudo-orbit of $\tilde{h}$, is 1/n-traced by some orbit of $\tilde{h}$ and by some (periodic) $\eta$-pseudo-orbit of $\tilde{h}$ that is produced by $\chi$. So indeed $h\in A_n$, which completes the proof of the openness of $A_n$.

On the other hand, by Theorem 10, the set $A_n$ is also dense in $\mathscr {X}$ and therefore $\bigcap _n A_n$ is a residual subset of $\mathscr {X}$. To finish the proof it is enough to note that, by definition, every map in the set $\bigcap _n A_n$ has the periodic $\mathscr {T}_{S}$-bi-shadowing property. $\square$

3.3 S-Limit Shadowing is $\pmb {{\mathscr {C}}}^0$-Dense on Graphs

For the proof of the second result of this section we need the following lemma, which gives a tool that allows us to deal with tracing limit $\delta$-pseudo-orbits with increasing accuracy.

Lemma 12

Let G be a graph, $f\in C(G)$ and $\varepsilon >0$. Let $\left\{ U_i\right\} _{i=1}^n$ be a cover of G consisting of pairwise distinct arcs, such that the conditions (3.1) and (3.2) are satisfied. Furthermore, assume that the arcs $\left\{ S_{i,j}\right\} _{j=1}^{k(i)}$, $i\in \{1,\ldots ,n\}$, and a continuous map $g\in C(G)$ are provided by Lemma 7 for the above setting.

Then for any $\gamma >0$ there exists a refinement $\left\{ W_s\right\} _{s=1}^m$ of $\left\{ U_i\right\} _{i=1}^n$ (i.e., each $W_s$ is a subset of some $U_i$), consisting of arcs satisfying the condition (3.2), such that

$$\begin{aligned} \max \{{\mathrm {diam}}\,(W_s),{\mathrm {diam}}\,(g(W_s))\}<\min \{\gamma ,\Gamma (G)/3\} \; \text { for each } s\in \{1,\ldots , m\} \end{aligned}$$

and the following conditions hold:

• (1) for each $i\in \{1,\ldots ,n\}$ we have

  $$\begin{aligned} \bigcup \left\{ W\in \left\{ W_s\right\} _{s=1}^m\mid W\subset U_{i}\right\} =U_i, \end{aligned}$$

• (2) for each $i\in \{1,\ldots ,n\}$ and each $j\in \{1,\ldots ,k(i)\}$ we have

  $$\begin{aligned} \bigcup \left\{ W\in \left\{ W_s\right\} _{s=1}^m\mid W\subset S_{i,j}\right\} =S_{i,j}. \end{aligned}$$

Proof

It is an easy exercise. We leave details to the reader. $\square$

The proof of the following theorem, which is our last result for continuous maps on graphs, follows similar lines to the proof of Theorem 2 in [16], with the main difference that we need to use Lemma 7 to overcome technical difficulties of the considered setting.

Theorem 13

For any graph G, the set of continuous maps with the s-limit shadowing property is dense in C(G) and in S(G).

Proof

Let $\mathscr {X}=C(G)$ or $\mathscr {X}=S(G)$, depending on the case we are proving.

Let $f\in \mathscr {X}$ and $\varepsilon >0$. Put $\varepsilon _1{:}{=}\varepsilon$ and $g_0=f$. Take $g_1\in \mathscr {X}$ and $\xi _1>0$ with $\rho (g_0,g_1)<\varepsilon _1$, as well as a collection of sets $\left\{ S_{i,j}^1\right\}$ provided by Lemma 7 for some cover $\{U^1_i\}$, consisting of sets with sufficiently small diameters, satisfying the conditions (3.1) and (3.2). Take a refinement $\left\{ U^2_i\right\}$ of the cover $\{U^1_i\}$ provided by Lemma 12 with $\gamma =\varepsilon _2/16$, where $\varepsilon _2{:}{=}\min \{\xi _1/2,\varepsilon _{1}-\rho (g_0,g_{1}), \varepsilon _1/2\}$. Take $g_2\in \mathscr {X}$ with $\rho (g_1,g_2)<\varepsilon _2$, a constant $\xi _2<\xi _1$ and a collection of sets $\left\{ S_{i,j}^2\right\}$ by Lemma 7 for the cover $\{U^2_i\}$.

Proceeding inductively in this way we obtain sequences $\{\varepsilon _m\}$, $\{\xi _m\}$, $\{U^m_i\}$, $\{S^m_{i,j}\}$, $\{g_m\}$ such that

$$\begin{aligned} \rho (g_{m-1},g_m)<\varepsilon _m= \min \{\xi _{m-1}/2,\varepsilon _{m-1}-\rho (g_{m-2},g_{m-1}),\varepsilon _{m-1}/2\}\le \varepsilon /2^{m-1}. \end{aligned}$$

All the properties of the collections of sets $\left\{ U_i^{m-1}\right\}$,$\left\{ U_i^{m}\right\}$, $\left\{ S_{i,j}^{m-1}\right\}$ and $\left\{ S_{i,j}^{m}\right\}$ mentioned above apply accordingly.

Since $\mathscr {X}$ is a complete metric space and $\{g_m\}$ is a Cauchy sequence, we have $g_m\rightarrow g\in \mathscr {X}$ when $m\rightarrow \infty$. Observe that

$$\begin{aligned} \rho (g_0,g)\le & {} \sum _{n=1}^\infty \rho (g_{n-1},g_n)\le \varepsilon \sum _{n=1}^\infty \frac{1}{2^{n-1}}=2\varepsilon ,\\ \rho (g_m,g)\le & {} \sum _{n=m}^\infty \rho (g_{n},g_{n+1}). \end{aligned}$$

To estimate the upper bound in the above formula, observe that for every $k>0$ we have

$$\begin{aligned} \sum _{n=m}^{m+k}\rho (g_{n},g_{n+1})= & {} \sum _{n=m}^{m+k-2}\rho (g_{n},g_{n+1}) + \rho (g_{m+k-1},g_{m+k})+\rho (g_{m+k},g_{m+k+1})\\\le & {} \sum _{n=m}^{m+k-2}\rho (g_{n},g_{n+1})+ \varepsilon _{m+k}\\\le & {} \sum _{n=m}^{m+k-2}\rho (g_{n},g_{n+1})+ \varepsilon _{m+k-1}-\rho (g_{m+k-2},g_{m+k-1})\\= & {} \sum _{n=m}^{m+k-3}\rho (g_{n},g_{n+1})+ \varepsilon _{m+k-1}\le \dots \le \rho (g_{m},g_{m+1})+\varepsilon _{m+2}\\\le & {} \rho (g_{m},g_{m+1})+\varepsilon _{m+1}-\rho (g_{m},g_{m+1}) =\varepsilon _{m+1}\le \xi _m/2, \end{aligned}$$

and therefore

$$\begin{aligned} \rho (g_m,g)\le \xi _m/2. \end{aligned}$$

To show that g has the s-limit shadowing property take $\tau >0$ and establish $N>0$ such that $\varepsilon _N<\tau$. Take any $\xi _N/2$-limit-pseudo-orbit $\{x_t\}_{t=0}^\infty$ of g. Then there exists an increasing sequence $\{t_m\}_{m\ge N}$ ($t_N{:}{=}0$) such that $\{x_t\}_{t\ge t_m}$ is a $\xi _m/2$-pseudo-orbit of g. Since $\rho (g_m,g)\le \xi _m/2$ for $m\ge N$, our construction (by Lemma 7 and Lemma 12) ensures that there are sequences

$$\begin{aligned} \{U^m_{\eta ^m(t_m)},U^m_{\eta ^m(t_m+1)},\ldots , U^m_{\eta ^m(t_{m+1}-1)}, U^m_{\eta ^m(t_{m+1})}\}, \; m\ge N, \end{aligned}$$

satisfying

$$\begin{aligned}&U^{m+1}_{\eta ^{m+1}(t_{m+1})}\subset U^{m}_{\eta ^{m}(t_{m+1})},\\&\quad x_t\in U^m_{\eta ^m(t)}\; \text { for } t\in \{t_m,t_m+1,\ldots , t_{m+1}\} \end{aligned}$$

and

$$\begin{aligned} U^m_{\eta ^m(t+1)}\in \{V^m_{\eta ^m(t),j}\}_{j=1}^{k^m(\eta ^m(t))}\; \text { for } t\in \{t_m,t_m+1,\ldots , t_{m+1}-1\}. \end{aligned}$$

It is possible, because to define $U^{m+1}_{\eta ^{m+1}(t_{m+1})}$ we can take any set $U^{m+1}_i\subset U^{m}_{\eta ^{m}(t_{m+1})}$ of the refining cover, which satisfies $x_{t_{m+1}}\in U^{m+1}_i$ (by Lemma 12 there is at least one such set).

By the above construction we obtain that

$$\begin{aligned} g_{m-1}(U^{m}_{\eta ^{m}(t)})\cap {\mathrm {Int}}\, U^m_{\eta ^m(t+1)}\ne \emptyset \; \text { for } t\in \{t_m,t_m+1,\ldots , t_{m+1}-1\}. \end{aligned}$$

(3.9)

Note that for $t\in \{t_m,t_m+1,\ldots , t_{m+1}-1\}$ we have

$$\begin{aligned} d(g_m(x_t),x_{t+1})\le d(g_m(x_t),g(x_t))+d(g(x_t),x_{t+1})\le \xi _m, \end{aligned}$$

and hence directly by Remark 8 we obtain that

$$\begin{aligned} S^m_{\eta ^m(t+1)} \subset \bigcup _{j=1}^{k^m(\eta ^m(t))} S^m_{\psi ^m(\eta ^m(t),j)}\subset g(S^m_{\eta ^m(t)}) \quad \text { for } t=t_m,t_m+1,\ldots , t_{m+1}-1. \end{aligned}$$

(3.10)

To finish the construction we are going to show that there is a point $y\in S^N_{\eta ^N(0)}$ such that $d(f^j(y),x_j)\rightarrow 0$ if $j\rightarrow \infty$. As the first step, let us verify that

$$\begin{aligned} S^{m+1}_{\eta ^{m+1}(t_{m+1}+1)}\subset g(S^m_{\eta ^m(t_{m+1})})\; \text { for } m\ge N. \end{aligned}$$

Indeed, note that

$$\begin{aligned} g_m(U^{m+1}_{\eta ^{m+1}(t_{m+1})})\subset g_m(U^{m}_{\eta ^{m}(t_{m+1})})= g_m(S^{m}_{\eta ^{m}(t_{m+1})}) \end{aligned}$$

and by (3.9) we also have

$$\begin{aligned} g_{m}(U^{m+1}_{\eta ^{m+1}(t_{m+1})})\cap {\mathrm {Int}}\, U^{m+1}_{\eta ^{m+1}(t_{m+1}+1)}\ne \emptyset , \end{aligned}$$

and hence

$$\begin{aligned} g_m(S^{m}_{\eta ^{m}(t_{m+1})})\cap {\mathrm {Int}}\,U^{m+1}_{\eta ^{m+1}(t_{m+1}+1)}\ne \emptyset . \end{aligned}$$

By Lemma 12, which was used to define consecutive refinements, there is some $U^{m+1}_q\subset S^{m}_{\eta ^{m}(t_{m+1})}$ from the cover $\{U^{m+1}_i\}$, such that

$$\begin{aligned} g_m(U^{m+1}_q)\cap {\mathrm {Int}}\, U^{m+1}_{\eta ^{m+1}(t_{m+1}+1)}\ne \emptyset , \end{aligned}$$

which means that

$$\begin{aligned} U^{m+1}_{\eta ^{m+1}(t_{m+1}+1)}\in \{V^{m+1}_{q,j}\}_{j=1}^{k^{m+1}(q)}. \end{aligned}$$

Then, since $\rho (g,g_{m+1})<\xi _{m+1}/2$ we obtain (by Remark 8) that

$$\begin{aligned} S^{m+1}_{\eta ^{m+1}(t_{m+1}+1)}\subset g(S^{m+1}_q)\subset g(U^{m+1}_q)\subset g(S^{m}_{\eta ^{m}(t_{m+1})}). \end{aligned}$$

(3.11)

Hence by (3.10) and (3.11) we see that (recall that $t_N=0$)

$$\begin{aligned} S_{\eta ^{N}(0)}^{N} \cap \bigcap _{m=N}^\infty \bigcap _{j=t_m+1}^{t_{m+1}} g^{-j}(S^m_{\eta ^m(j)})\ne \emptyset , \end{aligned}$$

which implies that there exists a point $y\in S^N_{\eta ^N(0)}$ such that

$$\begin{aligned} g^j(y)\in S^m_{\eta ^m(j)}\subset U^m_{\eta ^m(j)}, \end{aligned}$$

and, as a consequence, we conclude that, if $t_m< j \le t_{m+1}$ then

$$\begin{aligned} d(x_j,g^j(y))\le {\mathrm {dist}}\,(x_j, S^m_{\eta ^m(j)})\le {\mathrm {diam}}\,(U^m_{\eta ^m(j)})< \varepsilon _m. \end{aligned}$$

The proof is completed. $\square$

4 Various Shadowing Properties on Dendrites

4.1 Preliminary Definitions and Facts

A continuum D is a (non-degenerate) dendrite, if D is a locally connected set containing no simple loop. It is known (by the results due to Ważewski and Manger, see, e.g., [30]), that D can be embedded in $\mathbb {R}^2$, which allows us, as in the case of graphs, to consider a geodesic metric d on D that is induced by the Euclidean structure in $\mathbb {R}^2$.

A point $x\in D$ is called an endpoint of D, if the set $D\setminus \{x\}$ is connected, as well as is called a branch point of D, if the set $D\setminus \{x\}$ has at least three connected components. Similarly as in the case of graphs, we denote by ${{\,\mathrm{End}\,}}(D)$ and ${{\,\mathrm{Br}\,}}(D)$ the sets of endpoints and branch points of D, respectively.

The following lemma summarizes a few useful properties of dendrites (see Chapter X in [20] for proofs of these facts).

Lemma 14

Let D be a dendrite and let $Y\subset D$ be a continuum. Then we have the following conclusions.

• (1) The set of branch points of D is countable.

• (2) An intersection of two connected subsets of D is either empty or connected.

• (3) The continuum Y is a dendrite itself, in particular Y is uniquely arcwise connected, i.e., for any two different points $x,y\in D$ there is a unique arc $Z_{x,y}$ joining x with y.

• (4) For any $x\in X\setminus Y$ there exists a unique point $R(x)\in Y$ such that R(x) belongs to any arc between x and a point $y\in Y$.

• (5) If a map $R:X\rightarrow Y$ is a map obtained by extending the above definition by putting $R(x)=x$ for $x\in Y$, then R is continuous (we call it the first point map for Y).

• (6) There exists an increasing sequence of sets $Y_1\subset Y_2\subset \ldots \subset D$ such that

  • (i) each set $Y_i$ is a tree (i.e., a graph which does not contain a simple loop) and $\lim _{i\rightarrow \infty }Y_i=D$ in the Hausdorff distance,

  • (ii) $Y_1=\{p_1\}$ and for each $i\in \mathbb {N}$ the set $\overline{Y_{i+1}\setminus Y_i}$ is an arc with an endpoint $p_{i}$ such that $\overline{Y_{i+1}\setminus Y_i}\cap Y_i=\{p_i\}$,

  • (iii) the sequence of the first point maps $R_i:X\rightarrow Y_i$ converges uniformly to the identity map.

We refer the readers not familiar with the theory of dendrites to the monograph [20], where an accessible presentation of this topic can be found.

The following lemma is the main tool for proving the results of this section.

Lemma 15

Let D be a dendrite, $f\in C(D)$, $\varepsilon >0$ and $\gamma <\varepsilon /8$ be a positive constant such that if $d(x,y)<\gamma$ then $d(f(x),f(y))<\varepsilon /8$. Let $T\subset D$ be a tree such that $\rho (R,id)<\gamma$, where R denotes the first point map for T. Let $\left\{ {\tilde{U}}_i\right\} _{i=1}^n$ be a cover of T meeting the assumptions of Lemma 7 for the map $R\circ f|_T\in C(T)$ and the constant $\varepsilon /4$. Take respective families of sets $\{\tilde{V}_{i,j}\}$ and $\{S_{i,j}\}$ for $i\in \{1,\ldots , n\}$, $j\in \{1,\ldots , k(i)\}$, provided by Lemma 7, and put $U_i=R^{-1}(\tilde{U}_i)$ (consequently, $V_{i,j}=R^{-1}(\tilde{V}_{i,j})$).

Then $\{U_i\}_{i=1}^n$ is a cover of D consisting of connected sets with diameters less than $\varepsilon /2$ as well as there exist a constant $\eta >0$ and a map $g\in C(D)$ with $\rho (f,g)<\varepsilon /2$, such that for any map $h\in C(D)$, with $\rho (g,h)<\eta$, the following conditions are satisfied for every $i\in \{1,\ldots ,n\}$:

• (i) $B_{\eta }(h(U_i))\subset \bigcup _{j=1}^{k(i)}V_{i,j}$,

• (ii) $\bigcup _{l=1}^{k(\psi (i,j))}S_{\psi (i,j),l}\subset h(S_{i,j})$ for $j\in \{1,\ldots , k(i)\}$,

where $\psi (i,j)$ is the unique index such that $V_{i,j}=U_{\psi (i,j)}$.

Proof

At first observe that if $R:X\rightarrow Z\subset X$ is a continuous map such that $\rho (R,id)<\zeta$, then for every set $A\subset Z$ we have

$$\begin{aligned} {{\,\mathrm{diam}\,}}(R^{-1}(A))\le {{\,\mathrm{diam}\,}}(A)+2\zeta . \end{aligned}$$

(4.1)

Take a constant $\xi >0$ and a map $\tilde{g}\in C(T)$ with $\rho (R\circ f|_T,\tilde{g})<\varepsilon /4$, provided by Lemma 7 for the map $R\circ f|_T\in C(T)$, the constant $\varepsilon /4$ and the cover $\left\{ {\tilde{U}}_i\right\} _{i=1}^n$ of T. Put $g=\tilde{g}\circ R$. Observe that by (4.1) we have

$$\begin{aligned} {{\,\mathrm{diam}\,}}(R^{-1}(\tilde{U}_i))\le {{\,\mathrm{diam}\,}}(\tilde{U}_i)+2\gamma <\frac{\varepsilon }{4}+\frac{\varepsilon }{4}=\frac{\varepsilon }{2} \end{aligned}$$

and, consequently,

$$\begin{aligned} d(f(x),g(x))\le & {} d(f(x),f(R(x)))\\&+\,d(f(R(x)),R(f(R(x))))+d(R(f(R(x))),\tilde{g}(R(x)))\\< & {} \frac{\varepsilon }{8} +\gamma +\frac{\varepsilon }{4}<\frac{\varepsilon }{2}, \end{aligned}$$

which implies that $\max \{{\mathrm {diam}}\,( U_i)\}<\varepsilon /2$ and $\rho (f,g)<\varepsilon /2$. It is easily seen that $\{U_i\}_{i=1}^n$ is a cover of D consisting of connected sets. Note that we also have $R(U_i)=U_i\cap T=\tilde{U}_i$.

Since $g|_T=\tilde{g}$, by Lemma 7 (iii) we have that

$$\begin{aligned} B^T_\xi \left( \bigcup _{l=1}^{k(\psi (i,j))}S_{\psi (i,j),l}\right) \subset g(S_{i,j}) \end{aligned}$$

(4.2)

for $j\in \{1,\ldots , k(i)\}$, where $\psi (i,j)$ is the unique index such that $\tilde{V}_{i,j}=\tilde{U}_{\psi (i,j)}$ (hence $V_{i,j}=U_{\psi (i,j)}$) and $B^T_\xi (\cdot )$ is a $\xi$-envelope in T, i.e., $B^T_\xi (\cdot )=T\cap B_\xi (\cdot )$. By Lemma 7 (iv) we also obtain that $B^T_\xi (\tilde{g}(\tilde{U}_i))\subset \bigcup _{j=1}^{k(i)}\tilde{V}_{i,j},$ which leads to the following sequence of inclusions:

$$\begin{aligned} B_\xi (g(U_i))\subset R^{-1}(B^T_\xi (\tilde{g}(\tilde{U}_i)))\subset \bigcup _{j=1}^{k(i)}R^{-1}(\tilde{V}_{i,j})= \bigcup _{j=1}^{k(i)}V_{i,j}. \end{aligned}$$

(4.3)

Indeed, it is enough to note that if $W\subset D$ is a connected set (hence also arcwise connected) such that $W\cap T\ne \emptyset$, then $R(W)=W\cap T.$

Take sufficiently small $\eta <\xi /2$, so that if $d(x,y)<\eta$ then $d(R(x),R(y))<\xi /2$. Fix any map $h\in C(D)$ such that $\rho (h,g)<\eta$. By (4.3) we obtain

$$\begin{aligned} B_{\eta }(h(U_i))\subset B_{\xi }(g(U_i))\subset \bigcup _{j=1}^{k(i)}V_{i,j}. \end{aligned}$$

By Lemma 7 (iii) each set $\overline{B^T_\xi (S_{\psi (i,j),l})}$ is an arc, and therefore, by (4.2), there are points $a,b\in S_{i,j}$ such that

$$\begin{aligned} B^T_\xi (S_{\psi (i,j),l}) = Z_{g(a),g(b)}\subset T. \end{aligned}$$

Indeed, it is enough to take any points a and b, which are mapped by g onto different endpoints of the arc $\overline{B^T_\xi (S_{\psi (i,j),l})}$. Note also that the arc $\overline{B^T_\xi (S_{\psi (i,j),l})\setminus S_{\psi (i,j),l}}\subset T$ has two connected components, both of them being arcs having diameters equal to $\xi$. By the definition of $\eta$, since $d(g(a),h(a))<\eta$ and $d(g(b),h(b))<\eta$ we have $d(g(a),R(h(a)))<\xi /2$ and $d(g(b),R(h(b)))<\xi /2$. This implies that the unique arc $Z_{h(a),h(b)}$ joining h(a) with h(b) have to pass through both connected components of $\overline{B^T_\xi (S_{\psi (i,j),l})}\setminus B^T_{\xi /2}(S_{\psi (i,j),l})$ and therefore

$$\begin{aligned} S_{\psi (i,j),l}\subset Z_{h(a),h(b)}\subset h(S_{i,j}). \end{aligned}$$

The proof is completed. $\square$

Remark 16

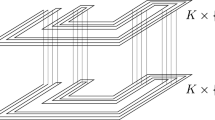
Let us consider a dendrite D shown in Fig. 4. We take a tree $T\subset D$ consisting of the only horizontal segment $T_1$ of D as well as the first two (counting from the right) vertical ones $T_2$ and $T_3$. The figure presents a concept of construction of covers $\{\tilde{U}_i\}$ and $\{U_i\}$ satisfying the assumptions of Lemma 15.

Fig. 4

The idea of a construction of covers satisfying the assumptions of Lemma 15

Remark 17

From the statement of Lemma 15 it follows that for each $i\in \{1,\ldots ,n\}$ and every map $h\in C(D)$ such that $\rho (g,h)<\eta$ we have

$$\begin{aligned} h(S_i)\supset \bigcup _{j=1}^{k(i)} S_{\psi (i,j)} \end{aligned}$$

and $S_i\subset U_i$, where $S_i{:}{=}\bigcup _{j=1}^{k(i)} S_{i,j}$.

4.2 $\pmb {{\mathscr {T}}}_S$-bi-Shadowing is $\pmb {{\mathscr {C}}}^0$-Generic on Dendrites

One of the aims of this section is to prove a result similar to Theorem 11. Unfortunately, we do not have as good covering property as in the case of graphs. Because of that difficulty, we are not able to prove (using this method) periodic version of the bi-shadowing property in the case of dendrites. Additionally, proposed approach does not cover the case of surjective mappings.

Theorem 18

Let D be a dendrite. Then for every $\varepsilon >0$ and every map $f \in C(D)$ there is $\delta >0$ and a map $g \in C(D)$ with $\rho (f,g)<\varepsilon$, such that for every $h\in C(D)$ with $\rho (g,h)<\delta$ and every $\delta$-method $\chi \in \mathscr {T}_{S,h,\delta }$, each $\delta$-pseudo-orbit of h is $\varepsilon$-traced by some orbit of h as well as by some $\delta$-pseudo-orbit of h that is produced by $\chi$.

Proof

Fix any $\varepsilon >0$ and any $f\in C(D)$. Take a cover $\left\{ U_i\right\} _{i=1}^n$ of D, consisting of pairwise distinct connected sets with diameters less than $\varepsilon /2$, a map $g\in C(D)$ with $\rho (f,g)<\varepsilon /2$ and a constant $\eta >0$, provided by Lemma 15 for properly chosen tree $T\subset D$ and a cover $\{\tilde{U}_i\}_{i=1}^n$ of T. Put $\delta =\eta /2$. Fix any $h \in C(D)$ with $\rho (h,g)<\delta$ and any $\delta$-method $\chi \in \mathscr {T}_{S,h,\delta }$ for h, together with respective functions $\psi _t\in C(D)$ with $\rho (h,\psi _t)<\delta$ such that $\chi (x)_{t+1} = \psi _{t}(\chi (x)_{t})$ for all $x \in D$ and all integer $t \ge 0$. Note that then $\rho (\psi _t,g)<\eta$.

Fix any $\delta$-pseudo-orbit $\{x_t\}_{t=0}^{\infty }$ of h. Directly from Lemma 15 we obtain that for all $t\ge 0$, if $x_t \in U_i$ then $x_{t+1} \in \bigcup _{j=1}^{k(i)} V_{i,j}$. Moreover, using arguments similar to those used in the proof of Theorem 10, we select sequences $\{\eta (t)\}_{t=0}^{\infty }\subset \{1,\ldots ,n\}$ and $\{\zeta (t)\}_{t=0}^{\infty } \subset \mathbb {N}$ such that for every $t \ge 0$ the following conditions are satisfied:

$$\begin{aligned} x_{t} \in U_{\eta (t)},\qquad x_{t+1}\in U_{\eta (t+1)} \in \{ V_{\eta (t),j} \}_{j=1}^{k(\eta (t)}, \end{aligned}$$

and

$$\begin{aligned} S_{\eta (t+1),\xi (t+1)} \subset h(S_{\eta (t),\xi (t)}), \qquad S_{\eta (t+1),\xi (t+1)} \subset \psi _t(S_{\eta (t),\xi (t)}). \end{aligned}$$

By the above, there exist points

$$\begin{aligned} y \in \bigcap _{t=0}^\infty h^{-t}(S_{\eta (t),\xi (t)}),\qquad z \in S_{\eta (0),\xi (0)}\cap \bigcap _{t=1}^\infty (\psi _{t-1}\circ \dots \circ \psi _0)^{-1}(S_{\eta (t),\xi (t)}), \end{aligned}$$

which implies that for each $t \ge 0$ we have $h^t(y),\chi (z)_t\in S_{\eta (t),\xi (t)} \subset U_{\eta (t)}$. In particular,

$$\begin{aligned} d(h^t(y),x_t)\le {{\,\mathrm{diam}\,}}(U_{\eta (t)})<\varepsilon \;\; \text {and} \;\; d(\chi (z)_t,x_t)\le {{\,\mathrm{diam}\,}}(U_{\eta (t)})<\varepsilon \end{aligned}$$

for every integer $t\ge 0$, which ends the proof. $\square$

Theorem 19

For any dendrite D, the set of continuous maps with the $\mathscr {T}_S$-bi-shadowing property is residual in C(D).

Proof

The proof generally follows the same steps as the proof of Theorem 11, with the main difference that instead of Theorem 10 we apply Theorem 18. We leave the details to the reader. $\square$

4.3 S-Limit Shadowing is $\pmb {{\mathscr {C}}}^0$-Dense on Dendrites

We finish this section by proving the results regarding density of s-limit shadowing for continuous maps on dendrites. We start with the following auxiliary lemma.

Lemma 20

Let D be a dendrite, $f\in C(D)$ and $\gamma <\varepsilon /8$ be a positive constant such that if $d(x,y)<\gamma$ then $d(f(x),f(y))<\varepsilon /8$. Let $T\subset D$ be a tree such that $\rho (R,id)<\gamma$, where R denotes the first point map for T. Let $\left\{ {\tilde{U}}_i\right\} _{i=1}^n$ be a cover of T meeting the assumptions of Lemma 7 for the map $R\circ f|_T\in C(T)$ and the constant $\varepsilon /4$. Put $U_i=R^{-1}(\tilde{U}_i)$ and take a respective family of sets $\{S_{i,j}\}$ for $i\in \{1,\ldots , n\}$, $j\in \{1,\ldots , k(i)\}$, provided by Lemma 7 as well as a map $g\in C(D)$ provided by Lemma 15 for the above setting.

Then for any tree Y such that $T\subset Y \subset D$ and any $\eta >0$ there exists a cover $\{W_s\}_{s=1}^m$ of Y consisting of pairwise distinct arcs satisfying (3.2), such that

$$\begin{aligned} \max \{{\mathrm {diam}}\,(W_s),{\mathrm {diam}}\,(g(W_s))\}<\min \{\eta ,\Gamma (Y)/3\} \;\; \text { for each } \; s\in \{1,\ldots , m\}, \end{aligned}$$

and the following conditions hold:

• (1) for each $s\in \{1,\ldots , m\}$ there is $i\in \{1,\ldots ,n\}$ such that

  $$\begin{aligned} R(W_s)\subset \tilde{U}_i, \end{aligned}$$

• (2) for each $i\in \{1,\ldots ,n\}$ we have

  $$\begin{aligned} \bigcup \left\{ W\in \left\{ W_s\right\} _{s=1}^m\mid W\subset U_{i}\right\} =U_i, \end{aligned}$$

• (3) for each $i\in \{1,\ldots ,n\}$ and each $j\in \{1,\ldots ,k(i)\}$ we have

  $$\begin{aligned} \bigcup \left\{ W\in \left\{ W_s\right\} _{s=1}^m\mid W\subset S_{i,j}\right\} =S_{i,j}. \end{aligned}$$

Proof

The proof is left to the reader as an easy exercise. $\square$

Remark 21

Under the assumptions of Lemma 20, if $Q:D\rightarrow Y$ is the first point map then $R=R|_Y\circ Q=R\circ Q$. In particular, the family $\{Q^{-1}(W_s)\}$ is a cover of D that refines $\{U_i\}$.

Now, we are ready to prove our last result for continuous maps on dendrites.

Theorem 22

For any dendrite D, the set of continuous maps with the s-limit shadowing property is $\mathscr {C}^0$-dense in C(D).

Proof

The proof is analogous to the proof of Theorem 13. Specifically, we apply Lemma 15 for some cover $\{\tilde{U_i^1}\}$ of appropriately chosen tree $T^1\subset D$ and so we obtain a cover $\{U_i\}{:}{=}\{U^1_i\}$ of D, consisting of sets with sufficiently small diameters. Then we take a larger tree $T^2\supset T^1$ provided by Lemma 14, together with its suitable cover $\{\tilde{U_i^2}\}$ that allows us to apply Lemma 20 and Remark 21 in order to construct an appropriate refinement $\left\{ U^2_i\right\}$ of the cover $\{U^1_i\}$. This way we proceed inductively, adjusting steps from the proof of Theorem 13 accordingly. $\square$

5 Shadowing is $\mathscr {C}^0$-Generic on Chainable Continua Retractable to Arcs

Let (X, d) be a continuum. A chain in X is a finite, non-empty, indexed collection $\mathscr {C}=\left\{ U_1,\ldots ,U_n\right\}$ of open subsets of X such that $U_i\cap U_j\ne \emptyset$ if and only if $|i-j|\le 1$. If, additionally, ${{\,\mathrm{diam}\,}}(U_i)<\varepsilon$ for some $\varepsilon >0$ and every $i\in \{1,\ldots ,n\}$, then we say that $\mathscr {C}$ is an $\varepsilon$-chain in X. A chain $\mathscr {C}$ (or an $\varepsilon$-chain $\mathscr {C}$, respectively) which is also a cover of X is called a chain cover of X (or an $\varepsilon$-chain cover of X, respectively).

We say that X is a chainable continuum, if for every $\varepsilon >0$ there exists an $\varepsilon$-chain cover of X. It is well known (see, e.g., [20, Lemma 12.10]) that if a continuum X is chainable, then for every $\varepsilon >0$ there is an $\varepsilon$-chain cover $\mathscr {C}=\left\{ U_1,\ldots ,U_n\right\}$ of X such that $\overline{U_i}\cap \overline{U_j}=\emptyset$, provided that $|i-j|\ge 2$. Additionally, without loss of generality we may also assume that $\mathscr {C}\setminus \left\{ U_i\right\}$ is not a cover of X for every $i\in \{1,\ldots ,n\}$, which is equivalent to saying that $U_1\setminus U_2\ne \emptyset$ and $U_n\setminus U_{n-1}\ne \emptyset$. Any cover $\mathscr {C}$ satisfying the above two properties is called a taut cover of X. It is also not hard to verify that if $\left\{ U_1,\ldots ,U_n\right\}$ is a chain cover of X and $C\subset X$ is a continuum such that $C\cap U_s\ne \emptyset$ and $C\cap U_t\ne \emptyset$ for some $s<t$, then $C\cap U_l\ne \emptyset$ for every $s\le l \le t$. The reader not familiar with the continuum theory is referred to the monograph [20].

The aim of this section is to prove the following theorem, which is one of the main results of this paper.

Theorem 23

Let X be a chainable continuum and assume that for every $\gamma >0$ there are an arc $Y\subset X$ and a retraction $R:X\rightarrow Y$, such that $\rho (R,id)<\gamma$. Then the set of continuous maps with the $\mathscr {T}_S$-bi-shadowing property is residual in C(X).

Proof

Fix $f\in C(X)$ and $\varepsilon >0$. Let $\eta <\varepsilon /9$ be a positive constant such that if $d(x,y)<3\eta$ then $d(f(x),f(y))<\varepsilon /9$. Let $\mathscr {C}=\left\{ U_1,\ldots ,U_n\right\}$ be a taut $\eta$-chain cover of X. Note that then

$$\begin{aligned} {{\,\mathrm{diam}\,}}(f(U_{i-1}\cup U_i\cup U_{i+1}))<\varepsilon /9 \;\text { for } i\in \{2,\ldots ,n-1\}. \end{aligned}$$

(5.1)

Take a positive constant $\alpha$ such that $\alpha < \min \{\text {dist}(\overline{U_i},\overline{U_j}): |i-j|\ge 2\}$ and let $\beta >0$ be a Lebesgue number of the cover $\mathscr {C}$. Fix any $\gamma >0$ such that

$$\begin{aligned} \gamma< \min \{\alpha /3,\beta /3\}<\beta \le \max \{{{\,\mathrm{diam}\,}}(U_i) \}<\varepsilon /9. \end{aligned}$$

(5.2)

By the assumptions there are an arc $Y \subset X$ and a retraction $R:X \rightarrow Y$ with $\rho (R,id)<\gamma$. Furthermore, if $a,b\in X$ with $d(a,b)>\alpha$ then $d(R(a), R(b))>\alpha -2\gamma >0$, which shows that $\overline{R(U_i)}\cap \overline{R(U_j)}=\emptyset$ if and only if $|i-j|\ge 2$.

Take any taut $\gamma$-chain cover $\mathscr {C^*}=\left\{ W^*_1,\ldots , W^*_k\right\}$ of Y consisting of connected sets (it, consequently, means that each set $\overline{W^*_j}$ is an arc). Then there exists $\omega >0$ such that for every $i\in \{1,\ldots ,k\}$ there is a point $q_i\in Y$ satisfying conditions

$$\begin{aligned} B_\omega (q_i)\cap Y\subset W^*_i\setminus \bigcup _{j\ne i}\overline{W^*_j} \end{aligned}$$

(5.3)

and

$$\begin{aligned} \omega < \min \{ \text {dist}(\overline{W^*_i},\overline{W^*_j}): |i-j|\ge 2 \}. \end{aligned}$$

(5.4)

Put $W_i=R^{-1}(W^*_i)$ for all $i\in \{1,\ldots ,k\}$ and observe that $W^*_i=R(W_i)=W_i\cap Y$. Then, by (4.1), $\mathscr {D}=\left\{ W_1,\ldots ,W_k\right\}$ is $3\gamma$-chain cover of X and, additionally, $\mathscr {D}$ refines $\mathscr {C}$ because $3\gamma <\beta$. In particular, for each $i\in \{1,\ldots ,k\}$ there is s(i) such that $W_i\subset U_{s(i)}$.

Define $F=R \circ f \circ R :X \rightarrow Y$ and for every $i\in \{1,\ldots ,k\}$ put

$$\begin{aligned} r(i)=\min \{j\;:\; F(\overline{W_i})\cap W^*_{j}\ne \emptyset \}, \;\;\; t(i)=\max \{j\;:\; F(\overline{W_i})\cap W^*_{j}\ne \emptyset \}. \end{aligned}$$

Then, obviously, $r(i)\le t(i)$ and

$$\begin{aligned} F(\overline{W_i})\subset W^*_{r(i)}\cup W^*_{r(i)+1}\cup \ldots \cup W^*_{t(i)}\subset W_{r(i)}\cup W_{r(i)+1}\cup \ldots \cup W_{t(i)}. \end{aligned}$$

(5.5)

Moreover, since $F(\overline{W_i})=R(f(\overline{W^*_i}))$ is a continuum, $F(\overline{W_i})\cap W^*_j\ne \emptyset$ for all $r(i)\le j\le t(i)$. Hence, by (5.1), for any $i\in \{1,\ldots ,k\}$ we have

$$\begin{aligned} {{\,\mathrm{diam}\,}}(F(\overline{W_i}))\le & {} {{\,\mathrm{diam}\,}}(R(f(B_{\alpha /3}(\overline{U_{s(i)}}))))\le {{\,\mathrm{diam}\,}}\left( R\left( f\left( \bigcup _{|j-s(i)|\le 1}U_{j}\right) \right) \right) \\\le & {} \varepsilon /9+2\gamma , \end{aligned}$$

which implies that

$$\begin{aligned} {{\,\mathrm{diam}\,}}(W_{r(i)}\cup \ldots \cup W_{t(i)})\le & {} {{\,\mathrm{diam}\,}}(F(\overline{W_i}))+2\max _j {{\,\mathrm{diam}\,}}(W_j)\nonumber \\\le & {} \varepsilon /9+2\gamma + 2\varepsilon /9\le \varepsilon /3+2\gamma . \end{aligned}$$

(5.6)

Take a positive constant $\mu <\min \{\delta _{W^*},\omega /7 \}$, where $\delta _{W^*}$ is a Lebesgue number of the cover $\mathscr {C}^*$. Take any taut $\mu$-chain cover $\{V^*_1,\ldots ,V^*_m\}$ of Y consisting of connected sets (it, consequently, means that each set $\overline{V^*_j}$ is an arc). By (5.3), for every $i\in \{1,\ldots ,k\}$ there is p(i) such that $q_i\in V^*_{p(i)}$. Reversing indexing of sets $V_i$, if required, we may assume that $p(1)<p(k)$. Now, if we put $j(1)=p(1)$ and $j(k)=p(k)-4$, then for $i=1$ and $i=k$ the following condition is satisfied:

$$\begin{aligned} V^*_{j(i)+l}\subset B_{\omega }(q_i)\subset W^*_i \setminus \bigcup _{j\ne i}\overline{W^*_j} \end{aligned}$$

(5.7)

for $l\in \{0,\ldots ,4\}$. For $i\in \{2,\ldots ,k-1\}$ take inductively as j(i) the smallest integer $j(i)>j(i-1)$ such that $V^*_{j(i)+5}\cap \overline{W^*_{i+1}}\ne \emptyset$. Since $V^*_{j(i-1)}\subset W^*_{i-1}$ we see that $V^*_{j(i)+l}\subset \bigcup _{j\le i}W^*_j$ for $l\in \{0,\ldots ,4\}$, which obviously implies that (5.7) holds for that particular i. It is also clear that each j(i) constructed this way satisfies condition $j(i)<j(k)$ and therefore

$$\begin{aligned} i_1<i_2 \implies j(i_1)<j(i_2). \end{aligned}$$

(5.8)

Define $V_i=R^{-1}(V^*_i)$ for all $i\in \{1,\ldots , k\}$ and observe that $V^*_i=R(V_i)=V_i\cap Y$. Directly by definition, $\{V_1,\ldots ,V_m\}$ is a chain cover of X that refines $\{W_1,\ldots ,W_k\}$ and for all $i\in \{1,\ldots ,k\}$ we have

$$\begin{aligned} V_{j(i)+l}\subset W_i \setminus \bigcup _{j\ne i}\overline{W_j}. \end{aligned}$$

Since the closure of the set $W^*_{r(i)}\cup W^*_{r(i)+1}\cup \ldots \cup W^*_{t(i)}$ is an arc, we easily construct (by “stretching” the arcs $\overline{ V^*_{j(i)}},\overline{V^*_{j(i)+2}}$ and $\overline{V^*_{j(i)+4}}$ inside $W^*_{r(i)}\cup W^*_{r(i)+1}\cup \ldots \cup W^*_{t(i)}$) a continuous map $G:Y\rightarrow Y$ such that for all $i\in \{1,\ldots k\}$ we have

$$\begin{aligned} G(x)= & {} F(x) \;\; \text{ for } \text{ all } \;\; x \in Y\setminus \bigcup _i \bigcup _{l=0}^4 \overline{V^*_{j(i)+l}},\nonumber \\&G(\overline{W^*_i})\subset W^*_{r(i)}\cup W^*_{r(i)+1}\cup \ldots \cup W^*_{t(i)}\subset W_{r(i)}\cup W_{r(i)+1}\cup \ldots \cup W_{t(i)}\nonumber \\ \end{aligned}$$

(5.9)

and

$$\begin{aligned} G(\overline{V^*_{j(i)+1}})\subset V^*_{j(r(i))}\subset V_{j(r(i))},\;\; G(\overline{ V^*_{j(i)+3}})\subset V^*_{j(t(i))+4}\subset V_{j(t(i))+4}. \end{aligned}$$

(5.10)

Put $g=G\circ R$ and observe that, by (5.10), we obtain

$$\begin{aligned} g(\overline{V_{j(i)+1}})\subset W_{r(i)} \;\;\;\text{ and } \;\;\; g(\overline{V_{j(i)+3}})\subset W_{t(i)}. \end{aligned}$$

Now note that for any $x\in X$ there is $i\in \{1,\ldots ,k\}$ such that $x\in W_i$ and so (5.5), (5.6) and (5.9) give the following sequence of estimates:

$$\begin{aligned} d(F(x),G\circ R(x))\le {{\,\mathrm{diam}\,}}(W_{r(i)}\cup \ldots \cup W_{t(i)}) \le \varepsilon /3+2\gamma . \end{aligned}$$

Similarly, by the definition of $\gamma$ and R we obtain

$$\begin{aligned} d(f(x),F(x))\le d(f(x), f(R(x))+d(f(R(x)),R(f(R(x)))\le \frac{\varepsilon }{9}+\gamma . \end{aligned}$$

Summing up the above, we conclude that

$$\begin{aligned} \rho (f,g)\le \rho (f,F)+\rho (F,g) \le \frac{\varepsilon }{9}+\gamma +\frac{\varepsilon }{3}+2\gamma <\varepsilon . \end{aligned}$$

Clearly, by (5.9) and (5.10) there is a constant $\delta >0$ such that

$$\begin{aligned} B_{3\delta }(g(\overline{V_{j(i)+1}}))\subset V_{j(r(i))}, \;\;\; B_{3\delta }(g(\overline{V_{j(i)+3}}))\subset V_{j(t(i))+4} \end{aligned}$$

(5.11)

and

$$\begin{aligned} B_{3\delta } (g(\overline{W_i}))\subset \bigcup _{j=r(i)}^{t(i)} W_j. \end{aligned}$$

(5.12)

Assume additionally that $2\delta$ is a Lebesgue number for the cover $\{W_1, \dots ,W_k\}$.

Let $h\in C(X)$ be a map satisfying $\rho (h,g)<\delta$ and let $\left\{ x_s\right\} _{s=0}^\infty$ be a $\delta$-pseudo-orbit of h. Take any sequence of continuous maps $\{h_s\}_{s=1}^\infty$ with $\rho (h_s,h)<\delta$ and note that, by (5.12) and the fact that 2$\delta$ is a Lebesgue number of $\{W_1, \dots ,W_k\}$ there exists a sequence of indices $\{n(s)\}_{s=0}^\infty$ such that for every s we have $x_{s}\in W_{n(s)}$, $h(x_s)\in W_{n(s+1)}$, $h_s(x_s)\in W_{n(s+1)}$ and $r(n(s))\le n(s+1)\le t(n(s))$.

Let $I_0$ be any arc in Y with endpoints in $V^*_{j(n(0))+1}$ and $V^*_{j(n(0))+3}$. Obviously, $I_0\subset V^*_{j(n(0))+1}\cup V^*_{j(n(0))+2}\cup V^*_{j(n(0))+3}\subset W_{n(0)}$, because each set $\overline{V^*_i}$ is an arc.

Now suppose that for some $s\ge 0$ we have already constructed an arc $I_s\subset Y$ such that

$$\begin{aligned} (h_s\circ \dots \circ h_0)(I_s)\cap V_{j(n(s))+1}\ne \emptyset ,\;\;\; (h_s\circ \dots \circ h_0)(I_s)\cap V_{j(n(s))+3}\ne \emptyset \end{aligned}$$

and

$$\begin{aligned} (h_s\circ \dots \circ h_0)(I_s)\subset V_{j(n(s))+1}\cup V_{j(n(s))+2}\cup V_{j(n(s))+3}\subset W_{n(s)}, \end{aligned}$$

where for technical reasons we put here $h_0=\text {id}$. Then $(h_{s+1}\circ h_s\circ \dots \circ h_1)(I_s)\cap h_{s+1}( V_{j(n(s))+1})\ne \emptyset$ and, using (5.11), we obtain

$$\begin{aligned} (h_{s+1}\circ \dots \circ h_1)(I_s)\cap V_{j(r(n(s)))}\ne \emptyset . \end{aligned}$$

In the same way we obtain

$$\begin{aligned} (h_{s+1}\circ \dots \circ h_1)(I_s)\cap V_{j(t(n(s)))+4}\ne \emptyset . \end{aligned}$$

But the sets $V_i$ form a chain cover of X and the set $(h_{s+1}\circ \dots \circ h_1)(I_s)$ is a continuum, so, using (5.8), we obtain

$$\begin{aligned}&(h_{s+1}\circ \dots \circ h_1)(I_s)\cap V_{j(n(s+1))+1}\ne \emptyset \;\;\;\text{ and } \;\;\;\\&(h_{s+1}\circ \dots \circ h_1)(I_s)\cap V_{j(n(s+1))+3}\ne \emptyset . \end{aligned}$$

Fix any two points $a,b\in I_s$ such that

$$\begin{aligned} (h_{s+1}\circ \dots \circ h_1)(a)\in V_{j(n(s+1))+1} \;\;\; \text{ and } \;\;\; (h_{s+1}\circ \dots \circ h_1)(b)\in V_{j(n(s+1))+3}. \end{aligned}$$

Take a subarc of $I_s$ with the endpoints a and b, together with its parametrization $\tau :[0,1]\rightarrow Y$ satisfying $\tau (0)=a$ and $\tau (1)=b$. Put

$$\begin{aligned} t_1= & {} \sup \left\{ t\in (0,1) : (h_{s+1}\circ \dots \circ h_1)(\tau (t))\in V_{j(n(s+1))+1}\right\} ,\\ t_2= & {} \inf \left\{ t\in (t_1,1) : (h_{s+1}\circ \dots \circ h_1)(\tau (t))\in V_{j(n(s+1))+3}\right\} . \end{aligned}$$

Clearly,

$$\begin{aligned} (h_{s+1}\circ \dots \circ h_1)(\tau (t_1))\in \overline{V_{j(n(s+1))+1}}, \;\;\; (h_{s+1}\circ \dots \circ h_1)(\tau (t_2))\in \overline{V_{j(n(s+1))+3}}, \end{aligned}$$

and so we can find sufficiently small $\zeta >0$ such that the arc $I_{s+1}=\tau ([t_1-\zeta ,t_2+\zeta ])\subset I_s$ satisfies

$$\begin{aligned}&(h_{s+1}\circ \dots \circ h_0)(I_{s+1})\cap V_{j(n(s+1))+1}\ne \emptyset , \;\;\; \\&(h_{s+1}\circ \dots \circ h_0)(I_{s+1})\cap V_{j(n(s+1))+3}\ne \emptyset \end{aligned}$$

and

$$\begin{aligned} (h_{s+1}\circ \dots \circ h_0)(I_{s+1})\subset V_{j(n(s+1))+1}\cup V_{j(n(s+1))+2}\cup V_{j(n(s+1))+3}\subset W_{n(s+1)}. \end{aligned}$$

Using the induction, we obtain a nested sequence of arcs

$$\begin{aligned} I_0\supset I_1\supset I_2\supset \ldots , \end{aligned}$$

such that $(h_{s}\circ \dots \circ h_0)(I_s)\subset W_{n(s)}$ for all $s\ge 0$. Hence there exists $z\in \bigcap _{s=0}^\infty I_s$, which by the construction satisfies

$$\begin{aligned} d( (h_{s}\circ \dots \circ h_0)(z),x_s)\le {{\,\mathrm{diam}\,}}(W_{n(s)})< \varepsilon /9<\varepsilon . \end{aligned}$$

(5.13)

Take any $\delta$-method $\chi \in \mathscr {T}_{S,h,\delta }$ for h, together with respective functions $\psi _t\in C(X)$ such that $\rho (h,\psi _t)<\delta$ and $\chi (x)_{t+1} = \psi _{t}(\chi (x)_{t})$ for each $x\in X$ and all integers $t\ge 0$. Additionally, for technical reasons, put $\psi _{-1}=\text {id}$. Following the preceding arguments, it is not hard to show that the $\delta$-pseudo-orbit $\left\{ x_s\right\}$ is $\varepsilon$-traced by some orbit of h as well as by some $\delta$-pseudo-orbit of h that is produced by $\chi$. Indeed, it is enough to apply the above reasoning for the following sequences of continuous maps: $\{h\}_{s=1}^\infty$ and $\{\psi _{s-1}\}_{s=1}^\infty$, and then $\varepsilon$-tracing of $\{x_s\}$ is guaranteed in the first case by the orbit $\{h^s(z)\}_{s=0}^\infty$ and in the second case by the $\delta$-pseudo-orbit $\chi (z)=\{(\psi _{s-1}\circ \dots \circ \psi _{-1})(z)\}_{s=0}^\infty$. Hence we conclude that for any $n\in \mathbb {N}$ taking the set $A_n$ consisting of continuous maps f for which there is $\delta >0$ such that, having established a $\delta$-method $\chi \in \mathscr {T}_{S,f,\delta }$ for f, any $\delta$-pseudo-orbit of f is 1/n-traced by some orbit of f as well as by some $\delta$-pseudo-orbit of f that is produced by $\chi$, we obtain that $A_n$ contains a subset that is open and dense in C(X). But then the set $A=\bigcap _{n=1}^\infty A_n$ is residual in C(X), while all its elements have the $\mathscr {T}_S$-bi-shadowing property. This completes the proof. $\square$

Remark 24

An example of a continuum satisfying the assumptions of Theorem 23 is the closure of $\sin (1/x)$-curve on any interval (0, a], where $a>0$. In this case, the concept of a construction of consecutive taut chain covers (as in the above proof) is presented in Fig. 5.

Fig. 5

The idea of a construction of chain covers from the proof of Theorem 23

Remark 25

In [7] it was proved that many tent maps have the shadowing property. The inverse limit of each of these maps, restricted to the core, defines a Knaster continuum (the Knaster bucket handle continuum is obtained using then map with slope 2), and it is not hard to see that each of these continua satisfies assumptions of Theorem 23. On the other hand, shift homeomorphism defined by associated tent map has the shadowing property if and only if the tent map has it, too. Therefore, some of these homeomorphism have, and some other does not have, the shadowing property. But by Theorem 23 on each of these continua shadowing is generic, which, in particular, means that close to any shift homeomorphism there is a continuous map with the shadowing property.