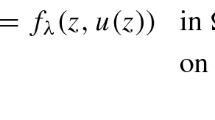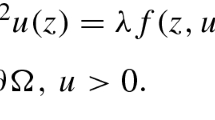Positive solutions for a class of nonlinear parametric Robin problems

Abstract

We consider a nonlinear Robin problem driven by the p-Laplacian and a parametric concave-convex reaction with the parameter multiplying the convex (superlinear) term. We prove a multiplicity result for positive solutions which is global in the parameter $\lambda >0$ (bifurcation-type theorem). We also show the existence of a minimal positive solution $u_{\lambda }^*$ and determine the monotonicity and continuity properties of the map $\lambda \longmapsto u_{\lambda }^*$

1 Introduction

Let $\Omega \subseteq \mathbb {R}^N$ be a bounded domain with a $C^2$-boundary $\partial \Omega$. We study the following parametric Robin problem

By $\Delta _p$ we denote the p-Laplacian differential operator defined by

$$\begin{aligned} \Delta _p u=\textrm{div}\,(|Du|^{p-2}Du)\quad \forall u\in W^{1,p}(\Omega ). \end{aligned}$$

There is also a potential term $\xi (z)u^{p-1}$ with $\xi \in L^{\infty }(\Omega )$, $\xi (z)\geqslant 0$ for almost all $z\in \Omega$. In the reaction we have the combined effects of two nonlinearities g(z, x) and $\lambda f(z,x)$ with $\lambda >0$ being a parameter. Both functions are Carathéodory. We assume that $g(z,\cdot )$ is strictly $(p-1)$-sublinear as $x\rightarrow +\infty$, while $f(z,\cdot )$ is $(p-1)$-superlinear as $x\rightarrow +\infty$, but need not satisfy the usual in such cases Ambrosetti-Rabinowitz condition. So, in the reaction we have the combined effect of concave and convex terms. However, in our case this parameter multiplies the convex (superlinear) term, while in the classical “concave-convex problem”, the parameter multiplies the concave (sublinear) term. This changes the structure of the equation and consequently the approach is different.

In the Robin boundary condition $\frac{\partial u}{\partial n_p}$ denotes the conormal derivative of u corresponding to the p-Laplacian and if $u\in C^1(\overline{\Omega })$, then

$$\begin{aligned} \frac{\partial u}{\partial n_p}=|Du|^{p-1}(Du,n)_{\mathbb {R}^N}=|Du|^{p-2}\frac{\partial u}{\partial n}, \end{aligned}$$

with n being the outward unit normal on $\partial \Omega$. For general u, the boundary condition is understood using the nonlinear Green’s identity (see Papageorgiou-Rădulescu-Repovš [19, p. 35]). The boundary coefficient $\beta$ is nonnegative.

Our aim is to prove a multiplicity theorem for the positive solutions of $(P_{\lambda })$ which is global with respect to the parameter $\lambda >0$, that is, our result gives a precise description of the changes in the set of positive solutions as the parameter $\lambda$ varies in $(0,+\infty )$ (bifurcation-type theorem). So, our main result in the paper (Theorem 3.8) establishes the existence of a critical parameter value $\lambda ^*>0$ such that

$\bullet$ for all $\lambda \in (0,\lambda ^*)$ problem $(P_{\lambda })$ has at least two distinct positive solutions;

$\bullet$ for $\lambda =\lambda ^*$ problem $(P_{\lambda })$ has at least one positive solutions;

$\bullet$ for $\lambda >\lambda ^*$ problem $(P_{\lambda })$ has no positive solutions.

This global multiplicity result reveals an interesting discontinuity property for the “spectrum” of $(P_{\lambda })$. This is better illustrated when we consider the standard “concave-convex” reaction

$$\begin{aligned} x\longmapsto x^{q-1}+\lambda x^{r-1}, \end{aligned}$$

with $1<q<p<r<p^*$, where

$$\begin{aligned} p^*= \left\{ \begin{array}{lll} \frac{Np}{N-p} &{} \text {if} &{} p<N,\\ +\infty &{} \text {if} &{} N\leqslant p. \end{array} \right. \end{aligned}$$

According to our global multiplicity result described above, for all $\lambda >0$ small problem $(P_{\lambda })$ has at least two positive solutions. On the other hand in the limit case $\lambda =0$, the problem becomes

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta _p u(z) +\xi (z)u(z)^{p-1} = u^{q-1}\quad \text {in}\ \Omega ,\\ \frac{\partial u}{\partial n_p}+\beta (z)u^{p-1}=0\quad \text {on}\ \partial \Omega ,\ u\geqslant 0,\ \lambda >0. \end{array} \right. \end{aligned}$$

This problem has a unique positive solution (see Proposition 2.6 in Sect. 2). For the other case where the parameter $\lambda >0$ multiplies the concave term, the limit problem (that is for $\lambda =0$) always has a positive solution which is not unique (see Papageorgiou-Rădulescu [14]). This illustrates the different structure of the two concave-convex problems. We mention also the recent works of Papageorgiou-Rădulescu-Repovš [16] and Papageorgiou-Vetro-Vetro [20], where the reader can find instances of such discontinuities in the “spectrum” of parametric problems.

In the past most the works on concave-convex problems, focused on Dirichlet problems with the parameter multiplying the concave (sublinear) term. Everything started with the paper of Ambrosetti-Brézis-Cerami [2], which deals with semilinear equations driven by the Laplacian. Their work was extended to nonlinear Dirichlet problems driven by the p-Laplacian by García Azorero-Manfredi-Peral Alonso [5] and Guo-Zhang [9]. All the aforementioned works deal with problems having the classical concave-convex reaction

$$\begin{aligned} u\longmapsto \lambda u^{q-1}+u^{r-1}, \end{aligned}$$

with $1<q<p<r<p^*$. More general differential operators and/or reactions can be found in the works of Papageorgiou-Rădulescu-Repovš [15], Rădulescu-Repovš [23] (semilinear equations) and El Manouni-Papageorgiou-Winkert [3], Papageorgiou-Rădulescu-Repovš [18], Papageorgiou-Vetro-Vetro [21], Winkert [24] (nonlinear equations). We also mention the recent work of Papageorgiou-Zhang [22], where the “concave” contribution comes from the boundary condition. The only “concave-convex” work with the parameter multiplying the convex (superlinear) term, is that of Marano-Marino-Papageorgiou [12]. There the problem is a Dirichlet (p, q)-equation, with the concave contribution being of the power form ($g(z,u)=u^{q-1}$) and the condition on $f(z,\cdot )$ are more restrictive (see hypotheses $(h_1)$–$(h_4)$ in [12]).

2 Mathematical background: hypotheses

The main spaces in the study of $(P_{\lambda })$ are the Sobolev space $W^{1,p}(\Omega )$, the Banach space $C^1(\overline{\Omega })$ and the “boundary” Lebesgue space $L^s(\partial \Omega )$ ($1\leqslant s<+\infty$).

By $\Vert \cdot \Vert$ we denote the norm of $W^{1,p}(\Omega )$ defined by

$$\begin{aligned} \Vert u\Vert =\big (\Vert u\Vert _p^p+\Vert Du\Vert _p^p\big )^{\frac{1}{p}}\quad \forall u\in W^{1,p}(\Omega ). \end{aligned}$$

The Banach space $C^1(\overline{\Omega })$ is ordered with positive (order) cone

$$\begin{aligned} C_+=\{u\in C^1(\overline{\Omega }):\ u(z)\geqslant 0\ \text {for all}\ z\in \overline{\Omega }\}. \end{aligned}$$

This cone has a nonempty interior given by

$$\begin{aligned} \textrm{int}C_+=\{u\in C_+:\ u(z)>0\ \text {for all}\ z\in \overline{\Omega }\}. \end{aligned}$$

We will also use another open cone in $C^1(\overline{\Omega })$ which is defined by

$$\begin{aligned} D_+=\left\{ u\in C^1(\overline{\Omega }):\ u(z)>0\ \text {for all}\ z\in \Omega ,\ \frac{\partial u}{\partial n}|_{\partial \Omega \cap u^{-1}(0)}<0\right\} . \end{aligned}$$

On $\partial \Omega$ we consider the $(N-1)$-dimensional Hausdorff (surface) measure $\sigma$. Using this measure we can define in the usual way the boundary Lebesgue space $L^s(\partial \Omega )$ $(1\leqslant s\leqslant +\infty )$. From the theory of Sobolev spaces, we know that there exists a unique continuous linear operator $\widehat{\gamma }_0:W^{1,p}(\Omega )\longrightarrow L^p(\partial \Omega )$ known as the “trace operator” such that

$$\begin{aligned} \widehat{\gamma }_0(u)=u|_{\partial \Omega }\quad \forall u\in W^{1,p}(\Omega )\cap C(\overline{\Omega }). \end{aligned}$$

So, the trace operator extends the notion of “boundary values” to all Sobolev functions. In the sequel for the sake of notational simplicity, we drop the use of the trace operator $\widehat{\gamma }_0$. All restrictions of Sobolev functions on $\partial \Omega$ are understood in the sense of traces. We mention that using the trace operator, we have that $W^{1,p}(\Omega )\subseteq L^s(\partial \Omega )$ continuously for all $1\leqslant s\leqslant \frac{(N-1)p}{N-p}$ if $p<N$ and for all $1\leqslant s<+\infty$ if $N\leqslant p$. Also $W^{1,p}(\Omega )\subseteq L^s(\partial \Omega )$ compactly for all $1\leqslant s<\frac{(N-1)p}{N-p}$ if $p<N$ and for all $1\leqslant s<+\infty$ if $N\leqslant p$.

If $u:\Omega \longrightarrow \mathbb {R}$ is a measurable function, we define

$$\begin{aligned} u^{\pm }(z)=\max \{\pm u(z),0\}\quad \forall z\in \Omega . \end{aligned}$$

If $u\in W^{1,p}(\Omega )$, then $u^{\pm }\in W^{1,p}(\Omega )$ and we have $u=u^+-u^-$, $|u|=u^++u^-$. Also, given two measurable functions $u,v:\Omega \longrightarrow \mathbb {R}$ such that $u(z)\leqslant v(z)$ for all $z\in \Omega$, we define

$$\begin{aligned} \begin{array}{rcl} [u,v] &{} = &{} \{h\in W^{1,p}(\Omega ):\ u(z)\leqslant h(z)\leqslant v(z)\ \text {for a.a.}\ z\in \Omega \},\\ {[}u{)} &{} = &{} \{h\in W^{1,p}(\Omega ): u(z)\leqslant h(z)\ \text {for a.a.}\ z\in \Omega \}. \end{array} \end{aligned}$$

We introduce the hypotheses on the potential function $\xi$ and on the boundary coefficient $\beta$.

$\underline{H_0}:$ $\xi \in L^{\infty }(\Omega )$, $\xi (z)\geqslant 0$ for almost $z\in \Omega$, $\beta \in C^{0,\alpha }(\partial \Omega )$ with $0<\alpha <1$, $\beta (z)\geqslant 0$ for all $z\in \partial \Omega$ and $\xi \not \equiv 0$ or $\beta \not \equiv 0$.

Remark 2.1

With this hypotheses, we cover also the case of Neumann problem, which corresponds to the case $\beta \equiv 0$.

Let $\gamma _p:W^{1,p}(\Omega )\longrightarrow \mathbb {R}$ be defined by

$$\begin{aligned} \gamma _p(u)=\Vert Du\Vert _p^p+\int _{\Omega }\xi (z)|u|^p\,dz+\int _{\partial \Omega } \beta (z)|u|^p\,d\sigma \quad \forall u\in W^{1,p}(\Omega ). \end{aligned}$$

Hypotheses $H_0$ together with Lemma 4.11 of Mugnai-Papageorgiou [13] and Proposition 2.4 of Gasiński-Papageorgiou [8], imply that there exists $c_0>0$ such that

$$\begin{aligned} c_0\Vert u\Vert ^p\leqslant \gamma _p(u)\quad \forall u\in W^{1,p}(\Omega ) \end{aligned}$$

(2.1)

(that is, $\gamma _p(\cdot )$ is equivalent norm on $W^{1,p}(\Omega )$).

Let $\widehat{\lambda }_1$ be the first eigenvalue of

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta _p u+\xi (u)|u|^{p-2}u=\widehat{\lambda }|u|^{p-2}u\quad \text {in}\ \Omega ,\\ \frac{\partial u}{\partial n_p}+\beta (z)|u|^{p-2}u=0. \end{array} \right. \end{aligned}$$

On account of (2.1), we have $\widehat{\lambda }_1>0$. We know that

$$\begin{aligned} \widehat{\lambda }_1=\inf _{u\in W^{1,p}(\Omega )\setminus \{0\}}\frac{\gamma _p(u)}{\Vert u\Vert _p^p}. \end{aligned}$$

This infimum is realized on the corresponding eigenspace, the elements of which have fixed sign. Let $\widehat{u}_1$ be the positive, $L^p$-normalized (that is, $\Vert \widehat{u}_1\Vert _p=1$) eigenfunction for $\widehat{\lambda }_1$. We know that $\widehat{u}_1\in \textrm{int}C_+$. Note that $\widehat{\lambda }_1$ is the only eigenvalue with eigenfunctions of constant sign (see Fragnelli-Mugnai-Papageorgiou [4]).

Let $A:W^{1,p}(\Omega )\longrightarrow W^{1,p}(\Omega )^*$ be defined by

$$\begin{aligned} \langle A(u),h\rangle =\int _{\Omega }|Du|^{p-2}(Du,Dh)_{\mathbb {R}^N}\,dz\quad \forall u,h\in W^{1,p}(\Omega ). \end{aligned}$$

From Gasiński-Papageorgiou [7, p. 279], we have the following property.

Proposition 2.2

If hypotheses $H_0$ hold, then A is continuous, monotone (thus maximal monotone too) and of type $(S)_+$, that is “if $u_n{\mathop {\longrightarrow }\limits ^{w}}u$ in $W^{1,p}(\Omega )$ and

$$\begin{aligned} \limsup \limits _{n\rightarrow +\infty }\langle A(u_n),u_n-u\rangle \leqslant 0, \end{aligned}$$

then $u_n\longrightarrow u$ in $W^{1,p}(\Omega )$.”

Next we introduce the hypotheses on the two functions involved in the reaction (right hand side of $(P_{\lambda })$).

$\underline{H_1}:$ $g:\Omega \times \mathbb {R}\longrightarrow \mathbb {R}$ is a Carathéodory function such that $g(z,0)=0$ for almost all $z\in \Omega$ and

• (i) for every $\varrho >0$, there exists $a_{\varrho }\in L^{\infty }(\Omega )$ such that

  $$\begin{aligned} |g(z,x)|\leqslant a_{\varrho }(z)\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ 0\leqslant x\leqslant \varrho ; \end{aligned}$$

• (ii) $\displaystyle \lim _{x\rightarrow +\infty }\frac{g(z,x)}{x^{p-1}}=0$ uniformly for almost all $z\in \Omega$;

• (iii) there exist $q\in (1,p)$ and $\delta >0$, $\widehat{c}>0$ such that

  $$\begin{aligned} \widehat{c}x^{q-1}\leqslant g(z,x)\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ 0\leqslant x\leqslant \delta . \end{aligned}$$

Remark 2.3

Since we are interested on positive solutions and the above hypotheses concern the positive semiaxis $\mathbb {R}_+=[0,+\infty )$, without any loss of generality we may assume that $g(z,x)=0$ for almost all $z\in \Omega$, all $x\leqslant 0$. Hypothesis $H_1(ii)$ implies that $g(z,\cdot )$ is strictly $(p-1)$-sublinear as $x\rightarrow +\infty$ (“concave” nonlinearity). Hypothesis $H_1(iii)$ implies that $g(z,\cdot )$ is $(p-1)$-sublinear as $x\rightarrow 0^+$. We point out that we do not assume that $g\geqslant 0$. It can change sign. The following functions satisfy hypotheses $H_1$ (for the sake of simplicity we drop the z-dependence):

$$\begin{aligned} g_1(x)= & {} (x^+)^{q-1},\\ g_2(x)= & {} (x^+)^{q-1}-2(x^+)^{\tau -1}, \end{aligned}$$

with $1<q<\tau <p$. Note that $g_2$ is sign changing.

$\underline{H_2}$: $f:\Omega \times \mathbb {R}\longrightarrow \mathbb {R}$ is a Carathéodory function such that $f(z,0)=0$ for almost all $z\in \Omega$ and

• (i) $f(z,x)\leqslant a(z)(1+x^{r-1})$ for almost all $z\in \Omega$, all $x\geqslant 0$, with $a\in L^{\infty }(\Omega )$, $p<r<p^*$;

• (ii) if $F(z,x)=\int _0^x f(z,s)\,ds$, then $\lim \limits _{x\rightarrow +\infty }\frac{F(z,x)}{x^p}=+\infty$ uniformly for almost all $z\in \Omega$;

• (iii) if $G(z,x)=\int _0^x g(z,s)\,ds$ and

  $$\begin{aligned} e_{\lambda }(z,x)=\big (g(z,x)+\lambda f(z,x)\big )-p\big (G(z,x)+\lambda F(z,x)\big ),\quad \lambda >0, \end{aligned}$$

  then there exists $\widetilde{\vartheta }_{\lambda }\in L^!(\Omega )$ such that

  $$\begin{aligned} e_{\lambda }(z,x)\leqslant e_{\lambda }(z,y)+\widetilde{\vartheta }_{\lambda }(z)\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ 0\leqslant x\leqslant y; \end{aligned}$$

• (iv) $\displaystyle \lim _{x\rightarrow 0^+}\frac{f(z,x)}{x^{p-1}}=0$ uniformly for almost all $z\in \Omega$ and for every $s>0$, there exists $\eta _s>0$ such that $\eta _s\leqslant f(z,x)$ for almost all $z\in \Omega$, all $x\geqslant s$.

Remark 2.4

Again we assume that $f(z,x)=0$ for almost all $z\in \Omega$, all $x\leqslant 0$. Evidently in hypothesis $H_2(iii)$ we can assume that $\lambda \rightarrow \Vert \widetilde{\vartheta }_{\lambda }\Vert _1$ is increasing. Also, if in $H_2(iii)$ we let $x=0$ and use hypotheses $H_1(ii)$ and $H_2(ii)$, we see that

$$\begin{aligned} \lim _{x\rightarrow +\infty }\frac{f(z,x)}{x^{p-1}}=+\infty \quad \text {uniformly for a.a.}\ z\in \Omega . \end{aligned}$$

Therefore $f(z,\cdot )$ is $(p-1)$-superlinear (“convex” nonlinearity). Usually problems with superlinear reaction are treated using the so-called Ambrosetti-Rabinowith condition. We recall that this condition (unilateral version since $g(z,x)=f(z,x)=0$ for almost all $z\in \Omega$, all $x\leqslant 0$), says that there exist $\eta >p$ and $M>0$ such that

$$\begin{aligned} \left\{ \begin{array}{l} 0<\eta F(z,x)\leqslant f(z,x)x\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant M,\\ 0<\mathop {\text {ess inf}}\limits _{\Omega } F(\cdot ,M). \end{array} \right. \end{aligned}$$

Integrating, we obtain the weaker requirement that

$$\begin{aligned} c_1 x^{\eta }\leqslant F(z,x)\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant M, \end{aligned}$$

for some $c_1>0$, thus

$$\begin{aligned} c_2 x^{\eta -1}\leqslant f(z,x)\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant M, \end{aligned}$$

for some $c_2>0$. So, we see that the Ambrosetti-Rabinowitz condition imposes at least $(\eta -1)$-polynomial growth on $f(z,\cdot )$. This way we exclude superlinear functions with slower growth as $x\rightarrow +\infty$. Consider the functions (as before we drop the z-dependence):

$$\begin{aligned} f_1(x)= & {} (x^+)^{\eta -1},\\ f_2(x)= & {} (x^+)^{p-1}\ln (1+x^+), \end{aligned}$$

with $1<p<\eta <p^*.$ Then these two functions combined with any of $g_1$ or $g_2$ satisfy hypothesis $H_2(iii)$. Note that $f_2$ does not satisfy the Ambrosetti-Rabinowitz condition.

$\underline{H_3}$: For every $\varrho >0$ and every $J\subseteq (0,+\infty )$ finite, there exists $\widehat{\xi }_{\varrho }^J>0$ such that for almost all $z\in \Omega$, all $\lambda \in J$, the function

$$\begin{aligned} x\longmapsto g(z,x)+\lambda f(z,x)+\widehat{\xi }_{\varrho }^Jx^{p-1} \end{aligned}$$

is nondecreasing on $[0,\varrho ]$.

Remark 2.5

Any pair of functions g, f formed by the collections $\{g_1,g_2\}$ and $\{f_1,f_2\}$ satisfies $H_3$. In general, if $g(z,\cdot )$ and $f(z,\cdot )$ are differentiable and for every $J\subseteq (0,+\infty )$ finite, we have

$$\begin{aligned} \big (g_x'(z,x)+\lambda f_x'(z,x)\big )x\geqslant -\widehat{\xi }_{\varrho }^J x^{p-1} \end{aligned}$$

for almost all $z\in \Omega$, all $0\leqslant x\leqslant \varrho$, all $\lambda \in J$, with $\widehat{\xi }_{\varrho }^J>0$, then hypothesis $H_3$ is satisfied.

We introduce the following sets related to problem $(P_{\lambda })$:

$$\begin{aligned} \mathcal {L}= & {} \{\lambda >0:\ \text {problem} (P_{\lambda }) \text {has a positive solution}\},\\ S_{\lambda }= & {} \{ u:\ u \text {is a positive solutions of} (P_{\lambda })\}. \end{aligned}$$

Also we set

$$\begin{aligned} \lambda ^*=\sup \mathcal {L}. \end{aligned}$$

Note that on account of hypotheses $H_1(i),(ii)$, we have

$$\begin{aligned} |g(z,x)|\leqslant c_3 (1+x^{p-1})\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant 0, \end{aligned}$$

(2.2)

for some $c_3>0$. Also hypothesis $H_1(iii)$ and the fact that $f\geqslant 0$ imply that for all $\lambda >0$, we have

$$\begin{aligned} g(z,x)+\lambda f(z,x)\geqslant \widehat{c}x^{q-1}\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ 0\leqslant x\leqslant \delta . \end{aligned}$$

(2.3)

This unilateral growth restriction on the reaction, leads to the following auxiliary Robin problem

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta _p u(z) +\xi (z)u(z)^{p-1} = \widehat{c} u(z)^{q-1}\quad \text {in}\ \Omega ,\\ \frac{\partial u}{\partial n_p}+\beta (z)u^{p-1}=0\quad \text {on}\ \partial \Omega ,\ u\geqslant 0. \end{array} \right. \end{aligned}$$

(2.4)

Proposition 2.6

If hypotheses $H_0$ hold, then problem (2.4) admits a unique positive solution $\widetilde{u}\in \textrm{int}C_+$.

Proof

First we show the existence of a positive solution. To this end, let $\psi _0:W^{1,p}_0(\Omega )\longrightarrow \mathbb {R}$ be the $C^1$-functional defined by

$$\begin{aligned} \psi _0(u) = \frac{1}{p}\gamma _p(u)-\frac{\widehat{c}}{q}\Vert u^+\Vert _q^q \geqslant \frac{c_0}{p}\Vert u\Vert ^p-c_4\Vert u\Vert ^q, \end{aligned}$$

for some $c_4>0$ (see (2.1) and recall that the embedding $W^{1,p}(\Omega )\subseteq L^q(\Omega )$ is continuous). So $\psi _0$ is coercive (recall that $q<p$).

Also from the Sobolev embedding theorem and the compactness of the trace operator, we infer that $\psi _0$ is sequentially weakly lower semicontinuous. So, by the Weierstrass-Tonelli theorem, we can find $\widetilde{u}\in W^{1,p}(\Omega )$ such that

$$\begin{aligned} \psi _0(\widetilde{u})=\inf _{u\in W^{1,p}(\Omega )}\psi _0(u). \end{aligned}$$

(2.5)

Recall that $\widehat{u}_1\in \textrm{int}C_+$ and let $t>0$. Then

$$\begin{aligned} \psi _0(t\widehat{u}_1)=\frac{t^p}{p}\widehat{\lambda }_1-\frac{\widehat{c}t^q}{q}\Vert \widehat{u}_1\Vert _q^q. \end{aligned}$$

Since $1<q<p$, choosing $t\in (0,1)$ small, we have

$$\begin{aligned} \psi _0(t\widehat{u}_1)<0, \end{aligned}$$

so

$$\begin{aligned} \psi _0(\widetilde{u})<0=\psi _0(0) \end{aligned}$$

(see (2.5)) and thus $\widetilde{u}\ne 0$. From (2.5) we have

$$\begin{aligned} \psi _0'(\widetilde{u})=0, \end{aligned}$$

so

$$\begin{aligned}{} & {} \langle A(\widetilde{u}),h\rangle +\int _{\Omega }\xi (z)|\widetilde{u}|^{p-2}\widetilde{u}h\,dz +\int _{\partial \Omega }\beta (z)|\widetilde{u}|^{p-2}\widetilde{u}h\,d\sigma \nonumber \\{} & {} \quad = \int _{\Omega }\widehat{c}(\widetilde{u})^{q-1}h\,dz\quad \forall h\in W^{1,p}(\Omega ). \end{aligned}$$

(2.6)

In (2.6) we choose $h=-\widetilde{u}^-\in W^{1,p}(\Omega )$ and obtain

$$\begin{aligned} \gamma (\widetilde{u}^-)=0, \end{aligned}$$

so

$$\begin{aligned} \widetilde{u}\geqslant 0,\quad \widetilde{u}\ne 0 \end{aligned}$$

(2.7)

(see (2.1)). Then from (2.6) and (2.7) we have

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta _p \widetilde{u}(z) +\xi (z)\widetilde{u}(z)^{p-1} = \widehat{c}\widetilde{u}^{q-1}\quad \text {in}\ \Omega ,\\ \frac{\partial \widetilde{u}}{\partial n_p}+\beta (z)\widetilde{u}^{p-1}=0\quad \text {on}\ \partial \Omega . \end{array} \right. \end{aligned}$$

(2.8)

From (2.8) and Proposition 2.10 of Papageorgiou-Rădulescu [14], we have that

$$\begin{aligned} \widetilde{u}\in L^{\infty }(\Omega ). \end{aligned}$$

Applying Theorem 2 of Lieberman [11], we infer that

$$\begin{aligned} \widetilde{u}\in C_+\setminus \{0\}. \end{aligned}$$

From (2.8) we have that

$$\begin{aligned} \Delta _p \widetilde{u}\leqslant \Vert \xi \Vert _{\infty }\widetilde{u}^{p-1}\quad \text {in}\ \Omega , \end{aligned}$$

so $\widetilde{u}\in \textrm{int}C_+$ (see Gasiński-Papageorgiou [6]).

Now we show the uniqueness of this positive solution of (2.4). So, suppose that $\widetilde{v}$ is another positive solution of (2.4). Again we have $\widetilde{v}\in \textrm{int}C_+$. Consider the function

$$\begin{aligned} R(\widetilde{u},\widetilde{v})=|D\widetilde{u}|^p-|D\widetilde{v}|^{p-2}\bigg (D\widetilde{v}, D\bigg (\frac{\widetilde{u}^p}{\widetilde{v}^{p-1}}\bigg )\bigg )_{\mathbb {R}^N}. \end{aligned}$$

Using the nonlinear Picone’s identity of Allegretto-Huang [1], we have

$$\begin{aligned} 0\leqslant & {} \int _{\Omega }R(\widetilde{u},\widetilde{v})\\= & {} \Vert D\widetilde{u}\Vert _p^p -\int _{\Omega }(-\Delta _p\widetilde{v})\frac{\widetilde{u}^p}{\widetilde{v}^{p-1}}\,dz +\int _{\partial \Omega }\beta (z)\widetilde{u}^p\,d\sigma \\= & {} \gamma _p(\widetilde{u})-\widehat{c}\int _{\Omega }\frac{\widetilde{u}}{\widetilde{v}^{p-q}}\,dz\\= & {} \int _{\Omega }\widehat{c}\frac{\widetilde{u}^q}{\widetilde{v}^{p-q}}\big (\widetilde{v}^{p-q}-\widetilde{u}^{p-q}\big )\,dz \end{aligned}$$

(2.9)

(using the nonlinear Green’s identity; see Gasiński-Papageorgiou [6, p. 211]). Interchanging the roles of $\widetilde{u}$ and $\widetilde{v}$ in the above argument we also have

$$\begin{aligned} 0\leqslant \int _{\Omega }\widehat{c}\frac{\widetilde{v}^q}{\widetilde{u}^{p-q}}\big (\widetilde{u}^{p-q}-\widetilde{v}^{p-q}\big )\,dz. \end{aligned}$$

(2.10)

Adding (2.9) and (2.10) we have

$$\begin{aligned} 0\leqslant & {} \int _{\Omega }\widehat{c}\bigg (\frac{\widetilde{v}^q}{\widetilde{u}^{p-q}}-\frac{\widetilde{u}^q}{\widetilde{v}^{p-q}}\bigg )\big (\widetilde{u}^{p-q} -\widetilde{v}^{p-q}\big )\,dz\\= & {} \int _{\Omega }\frac{\widehat{c}}{\widetilde{u}^{p-q}\widetilde{v}^{p-q}}\big (\widetilde{v}^p-\widetilde{u}^p\big )(\widetilde{u}^{p-q}-\widetilde{v}^{p-q}\big )\,dz\leqslant 0, \end{aligned}$$

so $\widetilde{u}=\widetilde{v}$ (recall that $1<q<p$).

This proves the uniqueness of the positive solution $\widetilde{u}\in \textrm{int}C_+$ of problem (2.4). $\square$

Since $\widetilde{u}\in \textrm{int}C_+$, we can find $t\in (0,1)$ small such that

$$\begin{aligned} \overline{u}(z)= t\widetilde{u}(z)\in (0,\delta ]\quad \forall z\in \overline{\Omega }, \end{aligned}$$

with $\delta >0$ as in the hypothesis $H_1(iii)$. Then $\overline{u}\in \textrm{int}C_+$ and

$$\begin{aligned} -\Delta _p \overline{u}+\xi (z)\overline{u}^{p-1}= & {} t^{p-1}\big (-\Delta _p \widetilde{u}+\xi (z)\widetilde{u}^{p-1}\big )\\= & {} t^{p-1}\widehat{c}\widetilde{u}^{q-1} \leqslant \widehat{c}\overline{u}^{q-1}\quad \text {in}\ \Omega \end{aligned}$$

(2.11)

(since $t\in (0,1)$ and $1<q<p$).

3 Positive solutions

First we show the nonemptiness of $\mathcal {L}$ and determine the regularity of the elements of the solution set $S_{\lambda }$.

Proposition 3.1

If hypotheses $H_0$, $H_1$, $H_2$ and $H_3$ hold, then $\mathcal {L}\ne \emptyset$ and for every $\lambda >0$ we have $S_{\lambda }\subseteq \textrm{int}C_+$.

Proof

Let $\overline{u}\in \textrm{int}C_+$ be as above. For $\lambda >0$ we consider the Carathéodory function $k_{\lambda }:\Omega \times \mathbb {R}\longrightarrow \mathbb {R}$ defined by

$$\begin{aligned} k_{\lambda }(z,x) = \left\{ \begin{array}{lll} g(z,\overline{u}(z))+\lambda f(z,\overline{u}(z)) &{} \text {if} &{} x\leqslant \overline{u}(z),\\ g(z,x)+\lambda f(z,x) &{} \text {if} &{} \overline{u}(z)<x. \end{array} \right. \end{aligned}$$

(3.1)

We set

$$\begin{aligned} K_{\lambda }(z,x)=\int _0^x k_{\lambda }(z,s)\,ds \end{aligned}$$

and consider the $C^1$-functional $\widehat{\varphi }_{\lambda }:W^{1,p}(\Omega )\longrightarrow \mathbb {R}$ defined by

$$\begin{aligned} \widehat{\varphi }_{\lambda }(u)=\frac{1}{p}\gamma _p(u)-\int _{\Omega }K_{\lambda }(z,u)\,dz\quad \forall u\in W^{1,p}(\Omega ). \end{aligned}$$

Let $u\in \textrm{int}C_+$ and choose $t\in (0,1)$ small so that $tu\leqslant \overline{u}$ (recall that $\overline{u}\in \textrm{int}C_+$). We have

$$\begin{aligned} \widehat{\varphi }_{\lambda }(tu)\leqslant \frac{t^p}{p}\gamma _p(u)-t\int _{\Omega }\big (g(z,\overline{u})+\lambda f(z,\overline{u})\big )u\,dz \end{aligned}$$

(see (3.1)). Since $t\in (0,1)$ and $p>1$, choosing $t\in (0,1)$ even smaller if necessary, we have

$$\begin{aligned} \widehat{\varphi }_{\lambda }(tu)<0\quad \forall t\in (0,1)\ \text {small}. \end{aligned}$$

(3.2)

On account of hypotheses $H_1$, given $\varepsilon >0$, we can find $c_5=c_5(\varepsilon )>0$ such that

$$\begin{aligned} g(z,x)\leqslant \varepsilon x^{p-1}+c_5 x^{q-1}\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant 0, \end{aligned}$$

so

$$\begin{aligned} G(z,x)\leqslant \frac{\varepsilon }{p} x^p+\frac{c_5}{q} x^q\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant 0. \end{aligned}$$

(3.3)

Then for $u\in W^{1,p}(\Omega )$ we have

$$\begin{aligned} \widehat{\varphi }_{\lambda }(u)= & {} \frac{1}{p}\gamma _p(u) -\int _{\{u\leqslant \overline{u}\}}\big (g(z,\overline{u})+\lambda f(z,\overline{u})\big )u\,dz\\{} & {} -\int _{\{\overline{u}<v\}}\big (G(z,u)-G(z,\overline{u})+\lambda (F(z,u)-F(z,\overline{u}))\big )\,dz\\\geqslant & {} \frac{1}{p}\gamma _p(u) -\int _{\Omega }\big (g(z,\overline{u})+\lambda f(z,\overline{u})\big )u^+\,dz\\= & {} -\int _{\Omega }G(z,u)\,dz-\lambda \int _{\{\overline{u}\leqslant u\}}F(z,u)\,dz\\\geqslant & {} \frac{1}{p}\big (\gamma _p(u)-\varepsilon \Vert u\Vert ^p\big ) -c_6\big (\Vert u\Vert ^q+\Vert u\Vert \big ) -\lambda c_7\big (\Vert u\Vert +\Vert u\Vert ^r\big )\\\geqslant & {} c_8\Vert u\Vert ^p-c_6\big (\Vert u\Vert ^q+\Vert u\Vert \big ) -\lambda c_7\big (\Vert u\Vert +\Vert u\Vert ^r\big ) \end{aligned}$$

(3.4)

for some $c_6,c_7,c_8>0$ (see hypothesis $H_1(ii)$, (3.3), hypothesis $H_1(i)$ and recall that $\overline{u}(z)\leqslant \delta$ for all $z\in \overline{\Omega }$). Choose $\varrho _0>0$ such that

$$\begin{aligned} \xi _0=c_6\varrho _0^p-c_6 (\varrho _0^q+\varrho _0)>0. \end{aligned}$$

Having fixed $\varrho _0>0$ as above, choose $\lambda _0>0$ small so that

$$\begin{aligned} \xi _0>\lambda c_7 (\varrho _0+\varrho _0^r)\quad \forall \lambda \in (0,\lambda _0). \end{aligned}$$

Returning to (3.4), we have

$$\begin{aligned} \widehat{\varphi }_{\lambda }(u)>0\quad \forall \Vert u\Vert =\varrho _0,\ 0<\lambda <\lambda _0. \end{aligned}$$

(3.5)

Let $\overline{B}_0=\overline{B}_{\varrho _0}=\{u\in W^{1,p}(\Omega ):\ \Vert u\Vert \leqslant \varrho _0\}$. The functional $\widehat{\varphi }_{\lambda }$ is sequentially weakly lower semicontinuous and $\overline{B}_0$ is sequentially weakly compact (from the reflexivity of $W^{1,p}(\Omega )$ and the Eberlein-Smulian theorem). So, we can find $u_{\lambda }\in W^{1,p}(\Omega )$ such that

$$\begin{aligned} \widehat{\varphi }_{\lambda }(u_{\lambda })=\inf _{u\in \overline{B}_0}\widehat{\varphi }_{\lambda }(u), \end{aligned}$$

(3.6)

so

$$\begin{aligned} 0<\Vert u_{\lambda }\Vert<\varrho _0\quad \forall 0<\lambda <\lambda _0 \end{aligned}$$

(3.7)

(see (3.2) and (3.5)). From (3.6) and (3.7) it follows that

$$\begin{aligned} \widehat{\varphi }_{\lambda }'(u_{\lambda })=0, \end{aligned}$$

so

$$\begin{aligned}{} & {} \langle A(u_{\lambda },h) +\int _{\Omega }\xi (z)|u_{\lambda }|^{p-2}u_{\lambda }h\,dz +\int _{\partial \Omega }\beta (z)|u_{\lambda }|^{p-2}u_{\lambda }h\,d\sigma \\= & {} \int _{\Omega }k_{\lambda }(z,u_{\lambda })h\,dz\quad \forall h\in W^{1,p}(\Omega ). \end{aligned}$$

(3.8)

In (3.8) we choose $h=(\overline{u}-u_{\lambda })^+\in W^{1,p}(\Omega )$. Then

$$\begin{aligned}{} & {} \langle A(u_{\lambda }),(\overline{u}-u_{\lambda })^+\rangle +\int _{\Omega }\xi (z)|u_{\lambda }|^{p-2}u_{\lambda }(\overline{u}-u_{\lambda })^+\,dz\\{} & {} +\int _{\partial \Omega }\beta (z)|u_{\lambda }|^{p-2}u_{\lambda }(\overline{u}-u_{\lambda })^+\,d\sigma \\= & {} \int _{\Omega }\big (g(z,\overline{u})+\lambda f(z,\overline{u})\big )(\overline{u}-u_{\lambda })^+\,dz\\\geqslant & {} \int _{\Omega }g(z,\overline{u})(\overline{u}-u_{\lambda })^+\,dz\\\geqslant & {} \int _{\Omega }\widehat{c}\overline{u}^{q-1}(\overline{u}-u_{\lambda })^+\,dz\\\geqslant & {} \langle A(\overline{u}),(\overline{u}-u_{\lambda })^+\rangle +\int _{\Omega }\xi (z)\overline{u}^{p-1}(\overline{u}-u_{\lambda })^+\,dz +\int _{\partial \Omega }\beta (z)\overline{u}^{p-1}(\overline{u}-u_{\lambda })\,d\sigma \end{aligned}$$

(see (3.1), (2.11) use hypothesis $H_1(iii)$ and recall that $f\geqslant 0$ and $\overline{u}(z)\leqslant \delta$ for all $z\in \overline{\Omega }$), so

$$\begin{aligned} \overline{u}\leqslant u_{\lambda }. \end{aligned}$$

(3.9)

Then on account of (3.1), (3.9) and (3.8), we obtain

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta _p u_{\lambda }(z) +\xi (z)u_{\lambda }(z)^{p-1} = g(z,u_{\lambda })+\lambda f(z,u_{\lambda })\quad \text {in}\ \Omega ,\\ \frac{\partial u_{\lambda }}{\partial n_p}+\beta (z)u_{\lambda }^{p-1}=0\quad \text {on}\ \partial \Omega . \end{array} \right. \end{aligned}$$

(3.10)

As before the nonlinear regularity theorem (see Lieberman [11] and Papageorgiou-Rădulescu [14]) implies that $u_{\lambda }\in C_+{\setminus } \{0\}$. Let $\varrho =\Vert u_{\lambda }\Vert _{\infty }$ and with $J=\{\lambda \}$, let $\widehat{\xi }_{\varrho }^{J}>0$ be as postulated by hypothesis $H_3$. Then from (3.10) we have

$$\begin{aligned} \Delta _p u_{\lambda }\leqslant \big (\Vert \xi \Vert _{\infty }+\widehat{\xi }_{\varrho }^{J}\big )u_{\lambda }^{p-1}\quad \text {in}\ \Omega , \end{aligned}$$

so $u_{\lambda }\in \textrm{int}C_+$ (see Gasiński-Papageorgiou [6, p. 738]). Therefore we have proved that

$$\begin{aligned} (0,\lambda _0)\subseteq \mathcal {L}\ne \emptyset \end{aligned}$$

and

$$\begin{aligned} S_{\lambda }\subseteq \textrm{int}C_+\quad \forall \lambda >0. \end{aligned}$$

$\square$

Next we show that $\mathcal {L}$ is an interval (connected).

Proposition 3.2

If hypotheses $H_0$, $H_1$, $H_2$ and $H_3$ hold, $\lambda \in \mathcal {L}$ and $0<\mu <\lambda$, then $\mu \in \mathcal {L}$.

Proof

Since $\lambda \in \mathcal {L}$ we can find $u_{\lambda }\in S_{\lambda }\subseteq \textrm{int}C_+$. We consider the following truncation of the reaction for the problem $(P_{\mu })$:

$$\begin{aligned} d_{\mu }(z,x)=\left\{ \begin{array}{lll} g(z,x^+)+\mu f(z,x^+) &{} \text {if} &{} x\leqslant u_{\lambda }(z)\\ g(z,u_{\lambda }(z))+\mu f(z,u_{\lambda }(z)) &{} \text {if} &{} u_{\lambda }(z)<x. \end{array} \right. \end{aligned}$$

(3.11)

This is a Carathéodory function. We set

$$\begin{aligned} D_{\mu }(z,x)=\int _0^x d_{\mu }(z,s)\,ds \end{aligned}$$

and consider the $C^1$-functional $\widehat{\psi }_{\mu }:W^{1,p}(\Omega )\longrightarrow \mathbb {R}$ defined by

$$\begin{aligned} \widehat{\psi }_{\mu }(u)=\frac{1}{p}\gamma _p(u)-\int _{\Omega }D_{\mu }(z,u)\,dz\quad \forall u\in W^{1,p}(\Omega ). \end{aligned}$$

From (3.11) and (2.1) it is clear that $\widehat{\psi }_{\mu }$ is coercive. Also using the Sobolev embedding theorem and the compactness of the trace map, we see that $\widehat{\psi }_{\mu }$ is sequentially weakly lower semicontinuous. So, we can find $u_{\mu }\in W^{1,p}(\Omega )$ such that

$$\begin{aligned} \widehat{\psi }_{\mu }(u_{\mu })=\inf _{u\in W^{1,p}(\Omega )}\widehat{\psi }_{\mu }(u). \end{aligned}$$

(3.12)

We choose $t\in (0,1)$ small so that

$$\begin{aligned} t\widehat{u}_1\leqslant u_{\lambda }\quad \text {and}\quad t\widehat{u}_1(z)\in (0,\delta ]\quad \forall z\in \overline{\Omega }. \end{aligned}$$

Since $\widehat{u}_1,u_{\lambda }\in \textrm{int}C_+$ such a $t\in (0,1)$ exists. We have

$$\begin{aligned} \widehat{\psi }_{\mu }(t\widehat{u}_1)\leqslant \frac{\widehat{t}^p}{p}\widehat{\lambda }_1-t^q\frac{\widehat{c}}{q}\Vert \widehat{u}_1\Vert _q^q \end{aligned}$$

(see hypothesis $H_1(iii)$ and recall that $\Vert \widehat{u}_1\Vert _p=1$). Since $1<q<p$, by choosing $t\in (0,1)$ even smaller if necessary, we have that

$$\begin{aligned} \widehat{\psi }_{\mu }(t\widehat{u}_1)<0, \end{aligned}$$

so

$$\begin{aligned} \widehat{\psi }_{\mu }(u_{\mu }) <0 = \widehat{\psi }_{\mu }(0) \end{aligned}$$

(see (3.12)) and thus $u_{\mu }\ne 0$.

From (3.12) we have

$$\begin{aligned} \widehat{\psi }_{\mu }'(u_{\mu })=0, \end{aligned}$$

so

$$\begin{aligned}{} & {} \langle A(u_{\mu }),h\rangle +\int _{\Omega }\xi (z)|u_{\mu }|^{p-2}u_{\mu }h\,dz +\int _{\partial \Omega }\beta (z)|u_{\mu }|^{p-2}u_{\mu }h\,d\sigma \\= & {} \int _{\Omega }d_{\mu }(z,u_{\mu })h\,dz\quad \forall h\in W^{1,p}(\Omega ). \end{aligned}$$

(3.13)

In (3.13) we first choose $h=-u_{\mu }^-\in W^{1,p}(\Omega )$. Then

$$\begin{aligned} \gamma _p(u_{\mu }^-)=0 \end{aligned}$$

(see (3.11)), so

$$\begin{aligned} u_{\mu }\geqslant 0,\quad u_{\mu }\ne 0 \end{aligned}$$

(see (2.1)). Nest in (3.13) we choose $(u_{\mu }-u_{\lambda })^+\in W^{1,p}(\Omega )$. Then, using (3.10) and since $0<\mu <\lambda$ and $f\geqslant 0$, we have

$$\begin{aligned}{} & {} \langle A(u_{\mu }),(u_{\mu }-u_{\lambda })^+\rangle +\int _{\Omega }\xi (z)u_{\mu }^{p-1}(u_{\mu }-u_{\lambda })^+\,dz \\{} & {} \qquad +\int _{\partial \Omega }\beta (z)u_{\mu }^{p-1}(u_{\mu }-u_{\lambda })^+\,d\sigma \\{} & {} \quad = \int _{\Omega }\big (g(z,u_{\lambda })+\mu f(z,u_{\lambda })\big )(u_{\mu }-u_{\lambda })^+\,dz \\{} & {} \quad \leqslant \int _{\Omega }\big (g(z,u_{\lambda })+\lambda f(z,u_{\lambda })\big )(u_{\mu }-u_{\lambda })^+\,dz\\{} & {} \quad = \langle A(u_{\lambda }),(u_{\mu }-u_{\lambda })^+ +\int _{\Omega }\xi (z)u_{\lambda }^{p-1}(u_{\mu }-u_{\lambda })^+\,dz\\{} & {} \qquad +\int _{\partial \Omega }\beta (z)u_{\lambda }^{p-1}(u_{\mu }-u_{\lambda })^+\,d\sigma , \end{aligned}$$

so $u_{\mu }\leqslant u_{\lambda }$ (see Proposition 2.2). So, we have proved that

$$\begin{aligned} u_{\mu }\in [0,u_{\lambda }],\quad u_{\mu }\ne 0. \end{aligned}$$

(3.14)

Then (3.14), (3.11) and (3.13) imply that

$$\begin{aligned} u_{\mu }\in S_{\mu }\subseteq \textrm{int}C_+, \end{aligned}$$

and so $\mu \in \mathcal {L}$. $\square$

Embedded in the above proof, is the following “monotonicity” property for $S_{\lambda }$ as a function of the parameter $\lambda >0$.

Corollary 3.3

If hypotheses $H_0$, $H_1$, $H_2$ and $H_3$ hold, $\lambda \in \mathcal {L}$, $u_{\lambda }\in S_{\lambda }\subseteq \textrm{int}C_+$ and $0<\mu <\lambda$, then $\mu \in \mathcal {L}$ and we can find $u_{\mu }\in S_{\mu }\subseteq \textrm{int}C_+$ such that

$$\begin{aligned} u_{\mu }\leqslant u_{\lambda }. \end{aligned}$$

We can improve the conclusion of this corollary.

Proposition 3.4

If hypotheses $H_0$, $H_1$, $H_2$ and $H_3$ hold, $\lambda \in \mathcal {L}$, $u_{\lambda }\in S_{\lambda }\subseteq \textrm{int}C_+$ and $0<\mu <\lambda$, then $\mu \in \mathcal {L}$ and there exists $u_{\mu }\in S_{\mu }\subseteq C_+$ such that

$$\begin{aligned} u_{\lambda }-u_{\mu }\in D_+. \end{aligned}$$

Proof

From Corollary 3.3 we already know that $\mu \in \mathcal {L}$ and that we can find $u_{\mu }\in S_{\mu }\subseteq \textrm{int}C_+$ such that

$$\begin{aligned} 0< u_{\mu }\leqslant u_{\lambda }. \end{aligned}$$

(3.15)

Let $\varrho =\Vert u_{\lambda }\Vert _{\infty }$, $J=\{\lambda ,\mu \}$ and consider $\widehat{\xi }_{\varrho }^J>0$ as postulated by hypothesis $H_3$, We have

$$\begin{aligned}{} & {} -\Delta _p u_{\mu }+\big (\xi (z)+\widehat{\xi }_{\varrho }^J\big )u_{\mu }^{p-1}\\= & {} g(z,u_{\mu })+\mu f(z,u_{\mu })+\xi _{\varrho }^Ju_{\mu }^{p-1}\\= & {} g(z,u_{\mu })+\lambda f(z,u_{\mu })-(\lambda -\mu )f(z,u_{\mu })+\widehat{\xi }_{\varrho }^Ju_{\mu }^{p-1}\\\leqslant & {} g(z,u_{\lambda })+\lambda f(z,u_{\lambda })+\widehat{\xi }_{\varrho }^Ju_{\lambda }^{p-1}\\= & {} -\Delta _p u_{\lambda }\big (\xi (z)+\widehat{\xi }_{\varrho }^J\big )u_{\lambda }^{p-1} \end{aligned}$$

(3.16)

(see (3.15) and hypothesis $H_3$), with $0<m_{\mu }=\min \limits _{\overline{\Omega }}u_{\mu }$ ($u_{\mu }\in \textrm{int}C_+$) and $\eta _{m_{\mu }}$ as in $H_2(iv)$.

From (3.16) and using Proposition 2.10 of Papageorgiou-Rădulescu-Repovš [17], we obtain that

$$\begin{aligned} u_{\lambda }-u_{\mu }\in D_+. \end{aligned}$$

$\square$

Recall that $\lambda ^*=\sup \mathcal {L}$. Next we show that $\lambda ^*<+\infty$.

Proposition 3.5

If hypotheses $H_0$, $H_1$, $H_2$ and $H_3$ hold, then $\lambda ^*<+\infty$.

Proof

Let $\eta >\widehat{\lambda }_1$. Hypotheses $H_1(iii)$ and $H_2(ii),(iv)$ imply that we can find $\widetilde{\lambda }>0$ big such that

$$\begin{aligned} g(z,x)+\widetilde{\lambda } f(z,x)\geqslant \eta x^{p-1}\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant 0. \end{aligned}$$

(3.17)

Let $\lambda >\widetilde{\lambda }$ and suppose that $\lambda \in \mathcal {L}$. We can find $u_{\lambda }\in S_{\lambda }\subseteq \textrm{int}C_+$. We introduce the Carathéodory function $\vartheta _{\lambda }(z,x)$ defined by

$$\begin{aligned} \vartheta _{\lambda }(z,x)=\left\{ \begin{array}{lll} \eta (x^+)^{p-1} &{} \text {if} &{} x\leqslant u_{\lambda }(z),\\ \eta u_{\lambda }(z)^{p-1} &{} \text {if} &{} u_{\lambda }(z)<x. \end{array} \right. \end{aligned}$$

(3.18)

We set

$$\begin{aligned} \Theta _{\lambda }(z,x)=\int _0^x \vartheta _{\lambda }(z,s)\,ds \end{aligned}$$

and consider the $C^1$-functional $\tau _{\lambda }:W^{1,p}(\Omega )\longrightarrow \mathbb {R}$ defined by

$$\begin{aligned} \tau _{\lambda }(u)=\frac{1}{p}\gamma _p(u)-\int _{\Omega }\Theta _{\lambda }(z,u)\,dz\quad \forall u\in W^{1,p}(\Omega ). \end{aligned}$$

From (3.18) and (2.1) we see that $\tau _{\lambda }$ is coercive. Also it is sequentially weakly lower semicontinuous. So, we can find $\widehat{u}_*\in W^{1,p}(\Omega )$ such that

$$\begin{aligned} \tau _{\lambda }(\widehat{u}_*)=\inf _{u\in W^{1,p}(\Omega )}\tau _{\lambda }(u). \end{aligned}$$

(3.19)

As before we choose $t\in (0,1)$ small so that

$$\begin{aligned} 0<t\widehat{u}_1\leqslant u_{\lambda }. \end{aligned}$$

Then we have

$$\begin{aligned} \tau _{\lambda }(t\widehat{u}_1)=\frac{t^p}{p}(\widehat{\lambda }_1-\eta )<0 \end{aligned}$$

(recall that $\Vert \widehat{u}_1\Vert _p=1$), so

$$\begin{aligned} \tau _{\lambda }(\widehat{u}_*)<0=\tau _{\lambda }(0) \end{aligned}$$

(see (3.19)), thus

$$\begin{aligned} \widehat{u}_*\ne 0. \end{aligned}$$

From (3.19) we have

$$\begin{aligned} \tau _{\lambda }'(\widehat{u}_*)=0, \end{aligned}$$

so

$$\begin{aligned}{} & {} \langle A(\widehat{u}_*),h\rangle +\int _{\Omega }\xi (z)|\widehat{u}_*|^{p-2}\widehat{u}_* h\,dz +\int _{\partial \Omega }\beta (z)|\widehat{u}_*|^{p-2}\widehat{u}_* h\,d\sigma \\= & {} \int _{\Omega }\vartheta _{\lambda }(z,\widehat{u}_*)h\,dz \quad \forall h\in W^{1,p}(\Omega ). \end{aligned}$$

(3.20)

In (3.20) first we choose $h=-\widehat{u}_*^-\in W^{1,p}(\Omega )$ and obtain

$$\begin{aligned} \gamma _p(\widehat{u}_*^-)=0 \end{aligned}$$

(see (3.18)), so

$$\begin{aligned} \widehat{u}_*\geqslant 0,\quad \widehat{u}_*\ne 0 \end{aligned}$$

(see (2.1)).

Next in (3.20) we choose $h=(\widehat{u}_*-u_{\lambda })^+\in W^{1,p}(\Omega )$. Then

$$\begin{aligned}{} & {} \langle A(\widehat{u}_*),(\widehat{u}_*-u_{\lambda })^+\rangle +\int _{\Omega }\xi (z)\widehat{u}_*^{p-1}(\widehat{u}_*-u_{\lambda })^+\,dz+\int _{\partial \Omega }\beta (z)\widehat{u}_*^{p-1}(\widehat{u}_*-u_{\lambda })^+\,d\sigma \\{} & {} \quad = \int _{\Omega }\eta u_{\lambda }^{p-1}(\widehat{u}_*-u_{\lambda })^+\,dz\\{} & {} \quad \leqslant \int _{\Omega }\big (g(z,u_{\lambda })+\lambda f(z,u_{\lambda })\big )(\widehat{u}_*-u_{\lambda })^+\,dz\\{} & {} \quad = \langle A(u_{\lambda }),(\widehat{u}_*-u_{\lambda })^+\rangle +\int _{\Omega }\xi (z)u_{\lambda }^{p-1}(\widehat{u}_*-u_{\lambda })^+\,dz\\{} & {} \qquad +\int _{\partial \Omega }\beta (z)u_{\lambda }^{p-1}(\widehat{u}_*-u_{\lambda })^+\,d\sigma \end{aligned}$$

(see (3.18), (3.17) and recall that $\lambda >\widetilde{\lambda }$ and $u_{\lambda }\in S_{\lambda }$), so

$$\begin{aligned} \widehat{u}_*\leqslant u_{\lambda }. \end{aligned}$$

So, we have proved that

$$\begin{aligned} \widehat{u}_*\in [0,u_{\lambda }],\quad \widehat{u}_*\ne 0. \end{aligned}$$

(3.21)

From (3.21), (3.18) and (3.20), we infer that

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta _p \widehat{u}_*+\xi (z)\widehat{u}_*^{p-1}=\eta u_*^{p-1}\quad \text {in}\ \Omega ,\\ \frac{\partial \widehat{u}_*}{\partial n_p}+\beta (z)\widehat{u}_*^{p-1}0\quad \text {on}\ \partial \Omega . \end{array} \right. \end{aligned}$$

Since $\widehat{u}_*\geqslant 0$, $\widehat{u}_*\ne 0$ and $\eta >\widehat{\lambda }_1$, we have a contradiction. Therefore $\lambda \in \mathcal {L}$ and so $\lambda ^*\leqslant \widetilde{\lambda }<+\infty$. $\square$

We show that the critical parameter $\lambda ^*$ is admissible (that is, $\lambda ^*\in \mathcal {L}$).

Proposition 3.6

If hypotheses $H_0$, $H_1$, $H_2$ and $H_3$ hold, then $\lambda ^*\in \mathcal {L}$.

Proof

In what follows for every $\lambda >0$ by $\varphi _{\lambda }:W^{1,p}(\Omega )\longrightarrow \mathbb {R}$ we denote the energy functional for problem $(P_{\lambda })$ defined by

$$\begin{aligned} \varphi _{\lambda }(u)=\frac{1}{p}\gamma _p(u)-\int _{\Omega }\big (G(z,u)+\lambda F(z,u)\big )\,dz \quad \forall u\in W^{1,p}(\Omega ). \end{aligned}$$

We know that $\varphi _{\lambda }\in C^1(W^{1,p}(\Omega ))$.

Let $\{\lambda _n\}_{n\in \mathbb {N}}\subseteq \mathcal {L}$ be such that $\lambda _n\nearrow \lambda ^*$ and $u_n\in S_{\lambda _n}\subseteq \textrm{int}C_+$, $n\in \mathbb {N}$. According to Proposition 3.2 and its proof, we can have

$$\begin{aligned} \varphi _{\lambda _n}(u_n)<0\quad \forall n\in \mathbb {N}, \end{aligned}$$

so

$$\begin{aligned} \gamma _p(u_n)-\int _{\Omega }p\big (G(z,u_n)+\lambda _n F(z,u_n)\big )\,dz<0\quad \forall n\in \mathbb {N}. \end{aligned}$$

(3.22)

Also we have

$$\begin{aligned}{} & {} \langle A(u_n),h\rangle +\int _{\Omega }\xi (z)u_n^{p-1}h\,dz +\int _{\partial \Omega }\beta (z) u_n^{p-1}h\,d\sigma \\= & {} \int _{\Omega }\big (g(z,u_n)+\lambda _n f(z,u_n)\big )h\,dz\quad \forall h\in W^{1,p}(\Omega ),\ n\in \mathbb {N}. \end{aligned}$$

We choose $h=u_n\in W^{1,p}(\Omega )$. Then

$$\begin{aligned} -\gamma _p(u_n)+\int _{\Omega }\big (g(z,u_n)+\lambda f(z,u_n)\big )u_n\,dz=0\quad \forall n\in \mathbb {N}. \end{aligned}$$

(3.23)

We add (3.22) and (3.23) and obtain

$$\begin{aligned} \int _{\Omega }e_{\lambda _n}(z,u_n)\,dz<0\quad \forall n\in \mathbb {N}. \end{aligned}$$

(3.24)

Claim. The sequence $\{u_n\}_{n\in \mathbb {N}}\subseteq W^{1,p}(\Omega )$ is bounded.

We argue by contradiction. So, suppose that at least for a subsequence, we have

$$\begin{aligned} \Vert u_n\Vert \longrightarrow +\infty \quad \text {as}\ n\rightarrow +\infty . \end{aligned}$$

Let $y_n=\frac{u_n}{\Vert u_n\Vert }$ for $n\in \mathbb {N}$. Then $\Vert y_n\Vert =1$, $y_n\geqslant 0$ for all $n\in \mathbb {N}$ and so we may assume that

$$\begin{aligned} y_n{\mathop {\longrightarrow }\limits ^{w}}y\quad \text {in}\ W^{1,p}(\Omega )\quad \text {and}\quad y_n\longrightarrow y\quad \text {in}\ L^r(\Omega )\ \text {and in}\ L^p(\partial \Omega ), \end{aligned}$$

(3.25)

with $y\geqslant 0$.

First assume that $y\ne 0$. Let $\Omega _+=\{z\in \Omega :\ y(z)>0\}$. If by $|\cdot |_N$ we denote the Lebesgue measure on $\mathbb {R}^N$, then $|\Omega _+|_N>0$ (recall that $y\geqslant 0$; see (3.25)) and we have

$$\begin{aligned} u_n(z)\longrightarrow +\infty \quad \text {for a.a.}\ z\in \Omega _+, \end{aligned}$$

so

$$\begin{aligned} \frac{F(z,u_n(z))}{u_n(z)^p}\longrightarrow +\infty \quad \text {for a.a.}\ z\in \Omega _+ \end{aligned}$$

(see hypothesis $H_1(ii)$), thus

$$\begin{aligned} \frac{F(z,u_n(z))}{\Vert u_n\Vert ^p} = \frac{F(z,u_n(z))}{u_n(z)^p}y_n(z)^p \longrightarrow +\infty \quad \text {for a.a.}\ z\in \Omega _+. \end{aligned}$$

Then hypothesis $H_2(ii)$ and Fatou’s lemma imply that

$$\begin{aligned} \frac{1}{\Vert u_n\Vert ^p}\int _{\Omega _+}F(z,u_n)\,dz\longrightarrow +\infty . \end{aligned}$$

(3.26)

Note that

$$\begin{aligned} \frac{1}{\Vert u_n\Vert ^p}\int _{\Omega }F(z,u_n)\,dz= & {} \frac{1}{\Vert u_n\Vert ^p}\int _{\Omega _+}F(z,u_n)\,dz +\frac{1}{\Vert u_n\Vert ^p}\int _{\Omega \setminus \Omega _+}F(z,u_n)\,dz\\\geqslant & {} \frac{1}{\Vert u_n\Vert ^p}\int _{\Omega _+}F(z,u_n)\,dz \end{aligned}$$

(since $F\geqslant 0$), so

$$\begin{aligned} \frac{1}{\Vert u_n\Vert ^p}\int _{\Omega }F(z,u_n)\,dz\longrightarrow +\infty \end{aligned}$$

(3.27)

(see (3.26)).

On the other hand from hypotheses $H_1(i),(ii)$ we see that given $\varepsilon >0$, we can find $c_8=c_8(\varepsilon )>0$ such that

$$\begin{aligned} |G(z,x)|\leqslant \varepsilon x^p+c_8\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant 0. \end{aligned}$$

Therefore we have

$$\begin{aligned} \lim _{n\rightarrow +\infty }\frac{1}{\Vert u_n\Vert ^p}\int _{\Omega }|G(z,u_n)|\,dz\leqslant \varepsilon . \end{aligned}$$

Since $\varepsilon >0$ is arbitrary, we conclude that

$$\begin{aligned} \frac{1}{\Vert u_n\Vert ^p}\int _{\Omega }G(z,u_n)\,dz\longrightarrow 0\quad \text {as}\ n\rightarrow +\infty . \end{aligned}$$

(3.28)

From (3.27) and (3.28), we have

$$\begin{aligned} \frac{1}{\Vert u_n\Vert ^p}\int _{\Omega }\big ( G(z,u_n)+\lambda _n F(z,u_n) \big ) \,dz\longrightarrow +\infty \quad \text {as}\ n\rightarrow +\infty . \end{aligned}$$

(3.29)

Hypothesis $H_2(iii)$ implies that for all $\lambda >0$ we have

$$\begin{aligned} 0\leqslant e_{\lambda }(z,x)+\widehat{\vartheta }_{\lambda }(z)\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant 0, \end{aligned}$$

so

$$\begin{aligned} p\big (G(z,x)+\lambda F(z,x)\big ) \leqslant \big (g(z,x)+\lambda f(z,x)\big )+\widehat{\vartheta }_{\lambda }(z)\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ x\geqslant 0.\nonumber \\ \end{aligned}$$

(3.30)

Therefore

$$\begin{aligned}{} & {} \int _{\Omega }p\big (G(z,u_n)+\lambda _n F(z,u_n)\big )\,dz\\\leqslant & {} \int _{\Omega }\big (g(z,u_n)+\lambda _n f(z,u_n)\big )u_n\,dz+\Vert \vartheta _{\lambda _n}\Vert _1\\\leqslant & {} \gamma _p(u_n)+\Vert \vartheta _{\lambda ^*}\Vert _1 \end{aligned}$$

(see (3.30), (3.23)), so

$$\begin{aligned} \frac{1}{\Vert u_n\Vert ^p}\int _{\Omega }p\big (G(z,u_n)+\lambda F(z,u_n)\big )\,dz \leqslant \gamma _p(y_n)+\frac{\Vert \vartheta _{\lambda ^*}\Vert _1}{\Vert u_n\Vert ^p}\leqslant c_9\quad \forall n\in \mathbb {N}, \end{aligned}$$

(3.31)

for some $c_9<0$. Comparing (3.29) and (3.31), we have a contradiction.

Next we assume that $y\equiv 0$. Let $\eta >0$ and define

$$\begin{aligned} v_n=(p\eta )^{\frac{1}{p}}y_n\in W^{1,p}(\Omega )\quad \forall n\in \mathbb {N}. \end{aligned}$$

We have

$$\begin{aligned} v_n\longrightarrow 0\quad \text {in}\ L^r(\Omega ) \end{aligned}$$

(see (3.25) and recall that $y=0$), so

$$\begin{aligned} \int _{\Omega }\big (G(z,u_n)+\lambda _n F(z,u_n)\big )\,dz\longrightarrow 0 \end{aligned}$$

(3.32)

(see (2.2) and hypothesis $H_2(i)$).

Since $\Vert u_n\Vert \longrightarrow +\infty$, we can find $n_0\in \mathbb {N}$ such that

$$\begin{aligned} (p\eta )^{\frac{1}{p}}\frac{1}{\Vert u_n\Vert }\leqslant 1\quad \forall n\geqslant n_0. \end{aligned}$$

(3.33)

Let $t_n\in [0,1]$ be such that

$$\begin{aligned} \varphi _{\lambda _n}(t_n u_n)=\max _{0\leqslant t\leqslant 1}\varphi _{\lambda _n}(t u_n). \end{aligned}$$

(3.34)

We have

$$\begin{aligned} \varphi _{\lambda _n}(t_n u_n)\geqslant & {} \varphi _{\lambda _n}(v_n)\\= & {} \frac{1}{p}\gamma _p(v_n)-\int _{\Omega }\big (G(z,v_n)+\lambda _n F(z,v_n)\big )\,dz\\\geqslant & {} \eta \gamma _p(y_n)-\int _{\Omega }\big (G(z,v_n)+\lambda _n F(z,v_n)\big )\,dz\\\geqslant & {} \eta \widehat{c}-\int _{\Omega }\big (G(z,v_n)+\lambda _n F(z,v_n)\big )\,dz \end{aligned}$$

(see (3.33), (3.34), (2.1) and recall that $\Vert y_n\Vert =1$), so

$$\begin{aligned} \varphi _{\lambda _n}(u_n)\geqslant \frac{\eta \widehat{c}}{2}\quad \forall n\geqslant n_1\geqslant n_0 \end{aligned}$$

(see (3.32)). Since $\eta >0$ is arbitrary, we conclude that

$$\begin{aligned} \varphi _{\lambda _n}(t_b u_n)\longrightarrow +\infty \quad \text {as}\ n\rightarrow +\infty . \end{aligned}$$

(3.35)

We know that

$$\begin{aligned} \varphi _{\lambda _n}(0)=0\quad \text {and}\quad \varphi _{\lambda _n}(u_n)<0\quad \forall n\in \mathbb {N}. \end{aligned}$$

(3.36)

From (3.35) and (3.36) it follows that

$$\begin{aligned} t_n\in (0,1)\quad \forall n\geqslant n_2, \end{aligned}$$

so

$$\begin{aligned} \frac{d}{dt}\varphi _{\lambda _n}(tu_n)\big |_{t=t_n}=0\quad \forall n\geqslant n_2 \end{aligned}$$

(see (3.34)) and thus

$$\begin{aligned} \langle \varphi _{\lambda _n}'(t_n u_n),u_n\rangle =0\quad \forall n\geqslant n_2 \end{aligned}$$

(by the chain rule). Hence for $n\geqslant n_2$ we have

$$\begin{aligned} \gamma _p(t_n u_n)-\int _{\Omega }\big ( g(z,t_n u_n)+\lambda _n f(z,t_n u_n)\big ) (t_n u_n)\,dz=0, \end{aligned}$$

so

$$\begin{aligned} \gamma _p(t_n u_n)= & {} \int _{\Omega }e_{\lambda _n}(z, t_n u_n)\,dz +\int _{\Omega }p\big (G(z,t_n u_n)+\lambda _n F(z,t_n u_n)\big )\,dz\\\leqslant & {} \int _{\Omega }e_{\lambda _n}(z,u_n)\,dz +\Vert \vartheta _{\lambda ^*}\Vert _1 +\int _{\Omega }p\big (G(z,t_n u_n)+\lambda _n F(z,t_n u_n)\big )\,dz \end{aligned}$$

and thus

$$\begin{aligned} p\varphi _{\lambda _n}(t_n u_n)\leqslant \Vert \vartheta _{\lambda ^*}\Vert _1\quad \forall n\geqslant n_2 \end{aligned}$$

(3.37)

(see (3.24)). Comparing (3.37) and (3.34) we have a contradiction. Therefore the sequence $\{u_n\}_{n\in \mathbb {N}}\subseteq W^{1,p}(\Omega )$ is bounded. This proves the Claim.

On account of the Claim we may assume that

$$\begin{aligned} u_n{\mathop {\longrightarrow }\limits ^{w}}u_*\quad \text {in}\ W^{1,p}(\Omega )\quad \text {and}\quad u_n\longrightarrow u_*\quad \text {in}\ L^r(\Omega )\ \text {and in}\ L^p(\partial \Omega ). \end{aligned}$$

(3.38)

We have

$$\begin{aligned}{} & {} \langle A(u_n),u_n-u_*\rangle +\int _{\Omega }\xi (z)u_n^{p-1}(u_n-u_*)\,dz +\int _{\partial \Omega }\beta (z)u_n^{p-1}(u_n-u_*)\,d\sigma \\= & {} \int _{\Omega }\big (g(z,u_n)+\lambda _n f(z,u_n)\big )(u_n-u_*)\,dz\quad \forall n\in \mathbb {N}, \end{aligned}$$

so

$$\begin{aligned} \lim _{n\rightarrow +\infty }\langle A(u_n),u_n-u_*\rangle =0 \end{aligned}$$

(see (3.38)) and thus

$$\begin{aligned} u_n\longrightarrow u_*\quad \text {in}\ W^{1,p}(\Omega ) \end{aligned}$$

(3.39)

(see Proposition 2.2), with $u\geqslant 0$.

Using (3.39) in the limit as $n\rightarrow +\infty$, we have

$$\begin{aligned}{} & {} \langle A(u_*),h\rangle +\int _{\Omega }\xi (z)u_*^{p-1}h\,dz +\int _{\partial \Omega }\beta (z)u_*^{p-1}h\,d\sigma \\= & {} \int _{\Omega }\big (g(z,u_*)+\lambda ^* f(f,u_*)\big )h\,dz\quad \forall h\in W^{1,p}(\Omega ). \end{aligned}$$

If we show that $u_*\ne 0$, then $u_*\in S_{\lambda ^*}\subseteq \textrm{int}C_+$ and so $\lambda ^*\in \mathcal {L}$. Arguing by contradiction, suppose that $u_*=0$. Then from (3.40), Proposition 2.10 of Papageorgiou-Rădulescu [14], Theorem 2 of Lieberman [11] and exploiting the compactness of the embedding $C^{1,\vartheta }(\overline{\Omega })\subseteq C^1(\overline{\Omega })$ (with $0<\vartheta <1$), we have that

$$\begin{aligned} u_n\longrightarrow u_*\quad \text {in}\ C^1(\overline{\Omega }), \end{aligned}$$

so

$$\begin{aligned} u_n(z)\in (0,\delta ]\quad \forall z\in \overline{\Omega },\ n\geqslant \widehat{n} \end{aligned}$$

(where $\delta >0$ is as in hypothesis $H_1(iii)$), so

$$\begin{aligned} g(z,u_n(z))+\lambda ^* f(z,u_n(z))\geqslant \widehat{c} u_n(z)^{q-1}\quad \text {for a.a.}\ z\in \Omega ,\ \text {all}\ n\geqslant \widehat{n} \end{aligned}$$

(see (3.20)). Then for $n\geqslant \widehat{n}$ we consider the Carathéodory function

$$\begin{aligned} l_n(z,x)= \left\{ \begin{array}{lll} \widehat{c}(x^+)^{q-1} &{} \text {if} &{} x\leqslant u_n(z),\\ \widehat{c}u_n(z)^{q-1} &{} \text {if} &{} u_n(z)<x. \end{array} \right. \end{aligned}$$

(3.40)

We set

$$\begin{aligned} L_n(z,x)=\int _0^x l(z,s)\,ds \end{aligned}$$

and consider the $C^1$-functional $\zeta _n:W^{1,p}(\Omega )\longrightarrow \mathbb {R}$ defined by

$$\begin{aligned} \zeta _n(u)=\frac{1}{p}\gamma _p(u)-\int _{\Omega }L_n(z,u)\,dz\quad \forall u\in W^{1,p}(\Omega ). \end{aligned}$$

Using the direct method od the calculus of variation and the fact that $q<p$, we can find $\widetilde{u}_*\in W^{1,p}(\Omega )$ such that

$$\begin{aligned} \zeta _n(\widetilde{u}_*)=\inf _{u\in W^{1,p}(\Omega )}\zeta _n(u)<0=\zeta _n(0), \end{aligned}$$

so $\widetilde{u}_*\ne 0$. Then using (3.40) we show that

$$\begin{aligned} \widetilde{u}_*\in [0,u_n],\quad \widetilde{u}_*\ne 0, \end{aligned}$$

so

$$\begin{aligned} \widetilde{u}_*=\widetilde{u}\in \textrm{int}C_+ \end{aligned}$$

(see Proposition 2.6), thus

$$\begin{aligned} \widetilde{u}\leqslant u_n\quad \forall n\geqslant \widehat{n}, \end{aligned}$$

and finally

$$\begin{aligned} \widetilde{u}\leqslant u_*, \end{aligned}$$

a contradiction. Therefore $u_*\ne 0$ and so $u_*\in S_{\lambda ^*}\subseteq \textrm{int}C_+$ and so $\lambda ^*\in \mathcal {L}$. $\square$

So, we have proved that

$$\begin{aligned} \mathcal {L}=(0,\lambda ^*]. \end{aligned}$$

Finally we show that for $0<\lambda <\lambda ^*$ we have multiplicity of positive solutions.

Proposition 3.7

If hypotheses $H_0$, $H_1$, $H_2$ and $H_3$ hold and $0<\lambda <\lambda ^*$, then problem $(P_{\lambda })$ has at least two positive solutions $u_0,\widehat{u}\in \textrm{int}C_+$, $u_0\ne \widehat{u}$.

Proof

Let $0<\mu<\lambda<\eta <\lambda ^*$. According to Corollary 3.3, we can find $u_{\eta }\in S_{\eta }\subseteq \textrm{int}C_+$, $u_{\lambda }\in S_{\lambda }\subseteq \textrm{int}C_+$, $u_{\mu }\in S_{\mu }\subseteq \textrm{int}C_+$ such that

$$\begin{aligned} u_{\eta }-u_{\lambda }\in D_+ \quad \text {and}\quad u_{\lambda }-u_{\mu }\in D_+, \end{aligned}$$

so

$$\begin{aligned} u_{\lambda }\in \textrm{int}_{C^1(\overline{\Omega })}[u_{\mu },u_{\eta }] \end{aligned}$$

(3.41)

(by $\textrm{int}_{C^1(\overline{\Omega })}[u_{\mu },u_{\eta }]$ we denote the interior in $C^1(\overline{\Omega })$ of $[u_{\mu },u_{\eta }]\cap C^1(\overline{\Omega })$). We consider the following truncation of the reaction in problem $(P_{\lambda })$

$$\begin{aligned} \widetilde{\tau }_{\lambda }(z,x) = \left\{ \begin{array}{lll} g(z,u_{\mu }(z))+\lambda f(z,u_{\mu }(z)) &{} \text {if} &{} x< u_{\mu }(z),\\ g(z,x)+\lambda f(z,x) &{} \text {if} &{} u_{\mu }(z)\leqslant x\leqslant u_{\eta }(z),\\ g(z,u_{\eta }(z))+\lambda f(z,u_{\eta }(z)) &{} \text {if} &{} u_{\eta }(z)<x. \end{array} \right. \end{aligned}$$

(3.42)

This is a Carathéodory function. We set

$$\begin{aligned} \widetilde{T}_{\lambda }(z,x)=\int _0^x \widetilde{\tau }_{\lambda }(z,s)\,ds \end{aligned}$$

and consider the $C^1$-functional $\widetilde{\psi }_{\lambda }:W^{1,p}(\Omega )\longrightarrow \mathbb {R}$ defined by

$$\begin{aligned} \widetilde{\psi }_{\lambda }(u)=\frac{1}{p}\gamma _p(u)-\int _{\Omega }\widetilde{T}_{\lambda }(z,u)\,dz\quad \forall u\in W^{1,p}(\Omega ) \end{aligned}$$

Let

$$\begin{aligned} K_{\widetilde{\psi }_{\lambda }}=\{u\in W^{1,p}(\Omega ):\ \widetilde{\psi }_{\lambda }'(u)=0\} \end{aligned}$$

(the critical set of $\widetilde{\psi }_{\lambda }$).

Claim 1: $K_{\widetilde{\psi }_{\lambda }}\subseteq [u_{\mu },u_{\eta }]\cap \textrm{int}C_+$.

Let $u\in K_{\widetilde{\psi }_{\lambda }}$. We have

$$\begin{aligned} \widetilde{\psi }_{\lambda }'(u)=0, \end{aligned}$$

so

$$\begin{aligned}{} & {} \langle A(u),h\rangle +\int _{\Omega }\xi (z)|u|^{p-2}u h \,dz +\int _{\partial \Omega }\beta (z)|u|^{p-2}u h\,d\sigma \\= & {} \int _{\Omega }\widetilde{\tau }_{\lambda }(z,u)h\,dz\quad \forall h\in W^{1,p}(\Omega ). \end{aligned}$$

(3.43)

In (3.43) first we choose $h=(u_{\mu }-u)^+\in W^{1,p}(\Omega )$. Then, using (3.42) and the facts that $\lambda >\mu$, $f\geqslant 0$ and $u_{\mu }\in S_{\mu }$, we have

$$\begin{aligned}{} & {} \langle A(u),(u_{\mu }-u)^+\rangle +\int _{\Omega }\xi (z)|u|^{p-2}u(u_{\mu }-u)^+\,dz\\{} & {} \qquad +\int _{\partial \Omega }\beta (z)|u|^{p-2}u(u_{\mu }-u)^+\,d\sigma \\{} & {} \quad = \int _{\Omega }\big ( g(z,u_{\mu })+\lambda f(z,u_{\mu })\big )(u_{\mu }-u)^+\,dz\\{} & {} \quad \geqslant \int _{\Omega }\big ( g(z,u_{\mu })+\mu f(z,u_{\mu })\big )(u_{\mu }-u)^+\,dz\\{} & {} \quad = \langle A(u_{\mu }),(u_{\mu }-u)^+\rangle +\int _{\Omega }\xi (z)|u_{\mu }|^{[-2}u_{\mu }(u_{\mu }-u)^+\,dz\\{} & {} \qquad +\int _{\partial \Omega }\beta (z)|u_{\mu }|^{p-2}u_{\mu }(u_{\mu }-u)^+\,d\sigma , \end{aligned}$$

so

$$\begin{aligned} u_{\mu }\leqslant u. \end{aligned}$$

Similarly if in (3.43) we choose $h=(u-u_{\eta })^+\in W^{1,p}(\Omega )$, we show that

$$\begin{aligned} u\leqslant u_{\eta }, \end{aligned}$$

so

$$\begin{aligned} u\in [u_{\mu },u_{\eta }]. \end{aligned}$$

Moreover, the nonlinear regularity theory (see Lieberman [11]) implies that $u\in C^1(\overline{\Omega })$. Therefore

$$\begin{aligned} K_{\widetilde{\psi }_{\lambda }}\subseteq [u_{\mu },u_{\eta }]\cap \textrm{int}C_+. \end{aligned}$$

This proves Claim 1.

Evidently $u_{\lambda }\in K_{\widetilde{\psi }_{\lambda }}$ (see (3.42)). We may assume that

$$\begin{aligned} K_{\widetilde{\psi }_{\lambda }}=\{u_{\lambda }\}. \end{aligned}$$

(3.44)

Otherwise on account of Claim 1 and (3.42), we see that we already have a second positive solution of problem $(P_{\lambda })$ and so we are done.

From (2.1) and (3.42), we see that $\widetilde{\psi }_{\lambda }$ is coercive. Also it is sequentially weakly lower semicontinuous. So, we can find $\widetilde{u}_{\lambda }\in W^{1,p}(\Omega )$ such that

$$\begin{aligned} \widetilde{\psi }_{\lambda }(\widetilde{u}_{\lambda })=\inf _{u\in W^{1,p}(\Omega )}\widetilde{\psi }_{\lambda }(u), \end{aligned}$$

so

$$\begin{aligned} \widetilde{u}_{\lambda }\in K_{\widetilde{\psi }_{\lambda }} \end{aligned}$$

and thus

$$\begin{aligned} \widetilde{u}_{\lambda }=u_{\lambda }\in \textrm{int}_{C^1(\overline{\Omega })}[u_{\mu },u_{\eta }] \end{aligned}$$

(3.45)

(see (3.44) and (3.41)). We introduce the Carathéodory function $\widetilde{k}_{\lambda }(z,x)$ defined by

$$\begin{aligned} \widetilde{k}_{\lambda }(z,x)= \left\{ \begin{array}{lll} g(z,u_{\mu }(z))+\lambda f(z,u_{\mu }(z)) &{} \text {if} &{} x\leqslant u_{\mu }(z),\\ g(z,x)+\lambda f(z,x) &{} \text {if} &{} u_{\mu }(z)<x. \end{array} \right. \end{aligned}$$

(3.46)

We set

$$\begin{aligned} \widetilde{K}_{\lambda }(z,x)=\int _0^x \widetilde{k}_{\lambda }(z,s)\,ds \end{aligned}$$

and consider the $C^1$-functional $\widetilde{\varphi }_{\lambda }:W^{1,p}(\Omega )\longrightarrow \mathbb {R}$ defined by

$$\begin{aligned} \widetilde{\varphi }_{\lambda }(u)=\frac{1}{p}\gamma _p(u)-\int _{\Omega }\widetilde{K}_{\lambda }(z,u)\,dz\quad \forall u\in W^{1,p}(\Omega ). \end{aligned}$$

If

$$\begin{aligned} K_{\widetilde{\varphi }_{\lambda }} =\{u\in W^{1,p}(\Omega ):\ \widetilde{\varphi }_{\lambda }'(u)=0\}, \end{aligned}$$

then using (3.46) we can check that

$$\begin{aligned} K_{\widetilde{\varphi }_{\lambda }}\subseteq [u_{\mu })\cap \textrm{int}C_+. \end{aligned}$$

(3.47)

Moreover, from (3.42) and (3.46) it is clear that

$$\begin{aligned} \widetilde{\varphi }_{\lambda }|_{[u_{\mu },u_{\eta }]}=\widetilde{\psi }_{\lambda }|_{[u_{\mu },u_{\eta }]}. \end{aligned}$$

(3.48)

From (3.45) and (3.48) it follows that

$$\begin{aligned} u_{\lambda }\text { is a local }C^1(\overline{\Omega })\text {-minimizer of }\widetilde{\varphi }_{\lambda }, \end{aligned}$$

so also

$$\begin{aligned} u_{\lambda }\text { is a local }W^{1,p}(\Omega )\text {-minimizer of }\widetilde{\varphi }_{\lambda } \end{aligned}$$

(3.49)

(see Papageorgiou-Rădulescu [14]).

On account of (3.47) we may assume that $K_{\widetilde{\varphi }_{\lambda }}$ is finite (otherwise we already have an infinity of positive smooth solutions of $(P_{\lambda })$ and so we are done). Then (3.49) and Theorem 5.7.6 of Papageorgiou-Rădulescu-Repovš [19, p. 449], imply that we can find $\varrho \in (0,1)$ small such that

$$\begin{aligned} \widetilde{\varphi }_{\lambda }(u_{\lambda })<\inf _{\Vert u-u_{\lambda }\Vert =\varrho }\widetilde{\varphi }_{\lambda }(u)=\widetilde{m}_{\lambda }. \end{aligned}$$

(3.50)

Also, because of hypothesis $H_2(ii)$ we have

$$\begin{aligned} \widetilde{\varphi }_{\lambda }(t\widehat{u}_1)\longrightarrow -\infty \quad \text {as}\ t\rightarrow +\infty . \end{aligned}$$

(3.51)

Claim 2. $\widetilde{\varphi }_{\lambda }$ satisfies the Cerami condition (see Papageorgiou-Rădulescu-Repovš [19, p. 366]).

We consider a sequence $\{u_n\}_{n\in \mathbb {N}}\subseteq W^{1,p}(\Omega )$ such that

$$\begin{aligned} |\widetilde{\varphi }_{\lambda }(u_n)|\leqslant c_9\quad \forall n\in \mathbb {N}, \end{aligned}$$

(3.52)

for some $c_9>0$, and

$$\begin{aligned} (1+\Vert u_n\Vert )\widetilde{\varphi }_{\lambda }'(u_n)\longrightarrow 0\quad \text {in}\ W^{1,p}(\Omega )^*\quad \text {as}\ n\rightarrow +\infty . \end{aligned}$$

(3.53)

From (3.53) we have

$$\begin{aligned}{} & {} \bigg |\langle A(u_n),h\rangle +\int _{\Omega }\xi (z)|u_n|^{p-2}u_n h\,dz\\{} & {} \int _{\partial \Omega }\beta (z)|u_n|^{p-2}u_n h\,d\sigma -\int _{\Omega }\widetilde{k}_{\lambda }(z,u_n)h\,dz\bigg |\\\leqslant & {} \frac{\varepsilon _n \Vert h\Vert }{1+\Vert u_n\Vert } \quad \forall h\in W^{1,p}(\Omega ), \end{aligned}$$

(3.54)

with $\varepsilon _n\rightarrow 0^+$. In (3.54) we choose $h=-u_n^-\in W^{1,p}(\Omega )$. Then

$$\begin{aligned} \gamma _p(u_n^-)\leqslant c_{10}\quad \forall n\in \mathbb {N}, \end{aligned}$$

for some $c_{10}>0$ (see (3.46)), so

$$\begin{aligned} \{u_n^-\}_{n\in \mathbb {N}}\subseteq W^{1,p}(\Omega )\text { is bounded} \end{aligned}$$

(3.55)

(see (2.1)). From (3.52) and (3.55) we have

$$\begin{aligned} |\widetilde{\varphi }_{\lambda }(u_n^+)|\leqslant c_{11}\quad \forall n\in \mathbb {N}, \end{aligned}$$

(3.56)

for some $c_{11}>0$, so

$$\begin{aligned} \gamma _p(u_n^+)-\int _{\Omega }p\big (G(z,u_n^+)+\lambda F(z,u_n^+)\big )\,dz\leqslant c_{12}\quad \forall n\in \mathbb {N}, \end{aligned}$$

(3.57)

for some $c_{12}>0$ (see (3.46)). In (3.54), we choose $h=u_n^+\in W^{1,p}(\Omega )$ and obtain

$$\begin{aligned} -\gamma _p(u_n^+)+\int _{\Omega }\big (g(z,u_n^+)+\lambda f(z,u_n^+) u_n^+\,dz\leqslant c_{13}\quad \forall n\in \mathbb {N}, \end{aligned}$$

(3.58)

for some $c_{13}>0$ (see (3.46)).

Adding (3.57) and (3.58) we obtain

$$\begin{aligned} \int _{\Omega }e_{\lambda }(z,u_n^+)\,dz\leqslant c_{14}\quad \forall n\in \mathbb {N}, \end{aligned}$$

(3.59)

for some $c_{14}>0$. Using (3.59) and arguing as in the Claim of the proof of Proposition 3.6, we show that the sequence $\{u_n^+\}_{n\in \mathbb {N}}\subseteq W^{1,p}(\Omega )$ is bounded and so

$$\begin{aligned} \{u_n\}_{n\in \mathbb {N}}\subseteq W^{1,p}(\Omega )\quad \text {is bounded} \end{aligned}$$

(3.60)

(see (3.55)). Then from (3.60) as in the proof of Proposition 3.6, using the $(S)_+$-property of A (see Proposition 2.2), we show that at least for a subsequence, we have

$$\begin{aligned} u_n\longrightarrow u\quad \text {in}\ W^{1,p}(\Omega ), \end{aligned}$$

so $\widetilde{\varphi }_{\lambda }$ satisfied the Cerami condition. This proves Claim 2.

Then (3.50), (3.51) and Claim 2 permit the use of the mountain pass theorem. So, we can find $\widehat{u}_{\lambda }\subseteq W^{1,p}(\Omega )$ such that

$$\begin{aligned} \widehat{u}_{\lambda }\subseteq K_{\widetilde{\varphi }_{\lambda }}\subseteq [u_{\lambda })\cap \textrm{int}C_+ \end{aligned}$$

(see (3.47)), so

$$\begin{aligned} \widetilde{\varphi }_{\lambda }(u_{\lambda })<\widetilde{m}_{\lambda }\leqslant \widetilde{\varphi }_{\lambda }(\widehat{u}_{\lambda }) \end{aligned}$$

(see (3.50)). We conclude that

$$\begin{aligned} \widehat{u}_{\lambda }\ne u_{\lambda }\quad \text {and}\quad \widehat{u}_{\lambda }\subseteq S_{\lambda }\subseteq \textrm{int}C_+ \end{aligned}$$

(see (3.46)). $\square$

So, summarizing we can have the following multiplicity theorem for problem $(P_{\lambda })$ which is global with respect to the parameter $\lambda >0$ (bifurcation-type theorem).

Theorem 3.8

If hypotheses $H_0,H_1,H_2,H_3$ hold, then there exists $\lambda ^*>0$ such that

(a) for all $\lambda \in (0,\lambda ^*)$ problem $(P_{\lambda })$ has at least two positive solutions $u_{\lambda },\widehat{u}_{\lambda }\subseteq \textrm{int}C_+$, $u_{\lambda }\ne \widehat{u}_{\lambda }$;

(b) for $\lambda =\lambda ^*$ problem $(P_{\lambda })$ has at least one positive solution $u_*\in \textrm{int}C_+$;

(c) for all $\lambda >\lambda ^*$ problem $(P_{\lambda })$ has no positive solutions.

4 Minimal positive solution

In this section we show that for every admissible parameter $\lambda \in \mathcal {L}=(0,\lambda ^*]$, problem $(P_{\lambda })$ has a smallest positive solution $u_{\lambda }^*\in \textrm{int}C_+$ (that is, $u_{\lambda }^*\leqslant u$ for all $u\in S_{\lambda }$) and study the monotonicity and continuity properties of the map $\lambda \longmapsto u_{\lambda }^*$.

From Papageorgiou-Rădulescu-Repovš [15] (see the proof of Proposition 3.5), we know that the set $S_{\lambda }$ is downward directed (that is, if $u_1,u_2\in S_{\lambda }$, then we can find $u\in S_{\lambda }$ such that $u\leqslant u_1$, $u\leqslant u_2$).

Proposition 4.1

If hypotheses $H_0$, $H_1$, $H_2$ and $H_3$ hold and $\lambda \in \mathcal {L}=(0,\lambda ^*]$, then problem $(P_{\lambda })$ has a smallest positive solution $u_{\lambda }^*\in \textrm{int}C_+$.

Proof

Since $S_{\lambda }$ is downward directed, using Lemma 3.10 of [10, p. 178], we can find a decreasing sequence $\{u_n\}_{n\in \mathbb {N}}\subseteq S_{\lambda }$ such that

$$\begin{aligned} \inf _{n\in \mathbb {N}}u_n=\inf S_{\lambda }. \end{aligned}$$

We have

$$\begin{aligned}{} & {} \langle A(u_n),h\rangle +\int _{\Omega }\xi (z)u_n^{p-1}h\,dz +\int _{\partial \Omega }\beta (z)u_n^{p-1}h\,d\sigma \\= & {} \int _{\Omega }\big (g(z,u_n)+\lambda f(z,u_n)\big )h,\,dz \quad \forall h\in W^{1,p}(\Omega ). \end{aligned}$$

(4.1)

Since $0\leqslant u_n\leqslant u_1$ for all $n\in \mathbb {N}$, choosing $h=u_n\in W^{1,p}(\Omega )$ and using hypotheses $H_1(i)$ and $H_2(ii)$, we obtain that

$$\begin{aligned} \gamma _p(u_n)\leqslant c_{15}\quad \forall n\in \mathbb {N}, \end{aligned}$$

for some $c_{15}>0$, so

$$\begin{aligned} \{u_n\}_{n\in \mathbb {N}}\subseteq W^{1,p}(\Omega )\quad \text {is bounded} \end{aligned}$$

(4.2)

(see (2.1)). From (4.1), we have

$$\begin{aligned} \left\{ \begin{array}{l} -\Delta _p u_n(z) +\xi (z)u(z)_n^{p-1} = g(z,u_n)+\lambda f(z,u_n)\quad \text {in}\ \Omega ,\\ \frac{\partial u_n}{\partial n_p}+\beta (z)u_n^{p-1}=0\quad \text {on}\ \partial \Omega . \end{array} \right. \end{aligned}$$

(4.3)

Then from (4.2), (4.3) and Proposition 2.10 of [14], we can find $c_{16}>0$ such that

$$\begin{aligned} \Vert u_n\Vert _{\infty }\leqslant c_{16}\quad \forall n\in \mathbb {N}. \end{aligned}$$

Invoking Theorem 2 of Lieberman [11], we can find $\alpha \in (0,1)$ and $c_{17}>0$ such that

$$\begin{aligned} u_n\in C^{1,\alpha }(\overline{\Omega }) \quad \text {and}\quad \Vert u_n\Vert _{C^{1,\alpha }(\overline{\Omega })}\leqslant c_{17}\quad \forall n\in \mathbb {N}. \end{aligned}$$

(4.4)

Exploiting the compactness of the embedding $C^{1,\alpha }(\overline{\Omega })\subseteq C^1(\overline{\Omega })$, we see that at least for a subsequence, we have

$$\begin{aligned} u_n\longrightarrow u_{\lambda }^*\quad \text {in}\ C^1(\overline{\Omega }). \end{aligned}$$

(4.5)

As in the proof of Proposition 3.6, using hypothesis $H_1(iii)$ and Proposition 2.6, we show that $u_{\lambda }^*\ne 0$.

Passing to the limit as $n\rightarrow +\infty$ in (4.1) and using (4.5), we conclude that

$$\begin{aligned} u_{\lambda }^*\in S_{\lambda }\subseteq \textrm{int}C_+\quad \text {and}\quad u_{\lambda }^*=\inf S_{\lambda }. \end{aligned}$$

$\square$

We consider the minimal solution map $\widehat{m}:\mathcal {L}=(0,\lambda ^*]\longrightarrow S_{\lambda }\subseteq \textrm{int}C_+$ defined by

$$\begin{aligned} \widehat{m}(\lambda )=u_{\lambda }^*. \end{aligned}$$

We say that $\widehat{m}$ is “strictly increasing”, if

$$\begin{aligned} 0<\mu <\lambda \leqslant \lambda ^*\ \Longrightarrow \ \widehat{m}(\lambda )-\widehat{m}(\mu )\in D_+. \end{aligned}$$

Proposition 4.2

If hypotheses $H_0$, $H_1$, $H_2$ and $H_3$ hold, then

(a) $\widehat{m}$ is strictly increasing;

(b) $\widehat{m}$ is right continuous.

Proof

(a) Let $0<\mu <\lambda \leqslant \lambda ^*$. According to Corollary 3.3, we can find $u_{\mu }\in S_{\mu }\subseteq \textrm{int}C_+$, such that

$$\begin{aligned} u_{\lambda }^*-u_{\mu }\in D_+, \end{aligned}$$

so

$$\begin{aligned} u_{\lambda }^*-u_{\mu }^*\in D_+ \end{aligned}$$

(since $u_{\mu }^*\leqslant u_{\mu }$) and thus $\widehat{m}$ is strictly increasing.

(b) Let $\{\lambda _n\}_{n\in \mathbb {N}}\subseteq \mathcal {L}$ and suppose that $\lambda _n\nearrow \lambda$ ($\lambda \in \mathcal {L}$). As before (see the proof of Proposition 4.1), from the nonlinear regularity theory (see Lieberman [11]), we know that we can find $\lambda \in (0,1)$ and $c_{18}>0$ such that

$$\begin{aligned} u_{\lambda _n}^*\in C^{1,\alpha }(\overline{\Omega })\quad \text {and}\quad \Vert u_{\lambda _n}^*\Vert _{C^{1,\alpha }(\overline{\Omega })}\leqslant c_{18}\quad \forall n\in \mathbb {N}. \end{aligned}$$

The compactness of the embedding $C^{1,\alpha }(\overline{\Omega })\subseteq C^1(\overline{\Omega })$ and part (a) imply that

$$\begin{aligned} u_{\lambda _n}^*\longrightarrow \widetilde{u}^*\quad \text {in}\ C^1(\overline{\Omega }). \end{aligned}$$

(4.6)

We claim that $\widetilde{u}^*=u_{\lambda }^*$. If this is not true, then we can find $z_0\in \overline{\Omega }$ such that

$$\begin{aligned} u_{\lambda }^*(z_0)<\widetilde{u}^*(z_0), \end{aligned}$$

so

$$\begin{aligned} u_{\lambda }^*(z_0)<u_{\lambda _n}^*(z_0)\quad \forall n\geqslant n_0 \end{aligned}$$

(see (4.6)), which contradicts (a) (recall $\lambda _n<\lambda$ for all $n\in \mathbb {N}$). Therefore $\widehat{m}$ is right continuous. $\square$