1 Introduction

The main aim of the present note is to provide some explicit constraints on weak combinatorics for a certain class of conic arrangements in the complex projective plane. This topic has recently been revived and has attracted the attention of researchers, both combinatorialists and algebraic geometers, see for example [1, 2, 9, 10]. As we know, in the case of line arrangements in the plane, the most important results devoted to weak combinatorics are Hirzebruch-type inequalities, which encode information about the set of singular points of a given topological type. Our main goal is to investigate natural combinatorial constants on the weak combinatorics of arrangements consisting of smooth conics with prescribed topological type of singularities. Our note is mostly inspired by a recent paper by Dimca, Janasz and Pokora [1], where the authors study arrangements of conics with only nodes and tacnodes as singularities. One of their main results tells us that if \(\mathcal {C} \subset \mathbb {P}^{2}_{\mathbb {C}}\) is an arrangement of \(k\ge 6\) conics with nodes and tacnodes, then

$$\begin{aligned} \#\textrm{tacnodes} \le \frac{1}{3}k^{2} + 3k \end{aligned}$$

and, as it turns out, this result provides sharper upper bound on the number of tacnodes compared with the classical result due to Miyaoka [7] provided that \(k\ge 16\).

Our aim here is to follow this path by exploring possible tight upper bounds on certain quasi-homogeneous singularities of complex plane conic arrangements. Here is our set-up.

Let \(\mathcal {C} = \{C_{1}, \ldots , C_{k}\} \subset \mathbb {P}^{2}_{\mathbb {C}}\) be an arrangement of \(k\ge 2\) smooth conics. Assume that our arrangements \(\mathcal {C}\) have only \(n_{2}\) nodes, \(t_{2}\) tacnodes, \(n_{3}\) ordinary triple points, \(t_{5}\) singular points of type \(A_{5}\), and \(t_{7}\) singular points of type \(A_{7}\)—it means that a given \(\mathcal {C}\) has only \(\textrm{ADE}\) singularities.

Now we can define the weak combinatorics for a given \(\mathcal {C}\), i.e., this is a vector of the form

$$\begin{aligned} (k;n_{2},t_{2},n_{3},t_{5},t_{7}) \in \mathbb {Z}^{6}_{\ge 0}. \end{aligned}$$

As we can see, this vector only informs us about the numerics associated with \(\mathcal {C}\), so it provides weaker information than the intersection poset of \(\mathcal {C}\). For our purposes, however, it is sufficient to provide combinatorial constraints on \(\mathcal {C}\). We start with the following count, which comes from Bézout.

$$\begin{aligned} 4\cdot \left( {\begin{array}{c}k\\ 2\end{array}}\right) = n_{2} + 2t_{2} + 3n_{3} + 3t_{5} + 4t_{7}. \end{aligned}$$
(1)

Proof

The left-hand side follows from the fact that we have \(\left( {\begin{array}{c}k\\ 2\end{array}}\right) \) pairs of conics that intersect. The right hand side is based on the count of the intersection indices. Indeed, each node has the intersection index equal to 1, each tacnode has the intersection index equal to 2, and for ordinary triple we have the intersection index equal to 3, and finally for \(A_{5}\) and \(A_{7}\) singular points we have 3 and 4, respectively, which completes our justification. \(\square \)

In principle, the above combinatorial count gives a rough estimate of the weak combinatorics of conic arrangements, and it is a rather weak tool. Our main aim is to provide a more precise result, inspired by the results presented in [1, 9].

Here is the main result of our note.

Theorem 1.1

Let \(\mathcal {C}\) be an arrangement of \(k\ge 3\) smooth conics admitting nodes, tacnodes, ordinary triple, \(A_{5}\) and \(A_{7}\) singular points. Then the following inequality holds

$$\begin{aligned} 560 k + 100 n_2 + 75 n_3 \ge 608 t_7 + 404 t_5 + 184 t_2. \end{aligned}$$
(2)

Based on the above count, we are able to provide upper bounds on the number of \(A_{5}\) and \(A_{7}\) singularities for such conic arrangements, and this path was recently indicated by considerations in [4]. This result is inspired by similar work devoted to bounds on the number of tacnodes \(t_{2}\), and to the best of our knowledge the bounds on \(A_{5}\) and \(A_{7}\) are the first of their kind explicitly presented in the literature.

Corollary 1.2

Let \(\mathcal {C}\) be an arrangement of \(k\ge 3\) smooth conics in the plane admitting \(A_{5}\) and \(A_{7}\) singularities. Then we have the following bounds:

$$\begin{aligned} t_{5} \le \frac{25}{88}k^{2}+\frac{45}{88}k, \\ t_{7} \le \frac{25}{126}k^{2}+\frac{5}{14}k. \end{aligned}$$

Here is the structure of our paper. In Sect. 2 we present tools that allow us to prove Theorem 1.1, namely the orbifold Bogomolov-Miyaoka-Yau inequality for pairs, which comes from [6]. In Sect. 3 we give our proof of Theorem 1.1 and explain how to obtain upper bounds on \(t_{5}\) and \(t_{7}\).

2 Technicalities

Our main technical tool is an orbifold version of the classical Bogomolov-Miyaoka-Yau inequality proved by Langer [6]. His result applies to complex normal surfaces X with boundary divisors D. Here we focus on a special case when \(X = \mathbb {P}^{2}_{\mathbb {C}}\) and D is a \(\mathbb {Q}\)-divisor whose support consists of smooth conics in \(\mathbb {P}^{2}_{\mathbb {C}}\). The following result is the technical core of the note that we will exploit.

Theorem 2.1

(Langer) Let \(C \subset \mathbb {P}^{2}_{\mathbb {C}}\) be a reduced curve of degree d and assume that \((\mathbb {P}^{2}_{\mathbb {C}},\alpha C)\) is a an effective log canonical pair for a suitably chosen \(\alpha \in [0,1]\), then one has

$$\begin{aligned} \sum _{p \in \textrm{Sing}(C)} 3\bigg (\alpha (\mu _{p}-1)+1-e_{orb}(p,\mathbb {P}^{2}_{\mathbb {C}},\alpha C)\bigg )\le (3\alpha - \alpha ^{2})d^{2}-3\alpha d, \end{aligned}$$

where \(\textrm{Sing}(C)\) denotes the set of all singular points, \(\mu _{p}\) is the Milnor number of a singular point p, and \(e_{orb}\) denotes the local orbifold Euler number of p.

We refer to [6] for details, especially for the definition of local orbifold Euler numbers. Instead of presenting the technicalities devoted to these orbifold Euler numbers, we briefly present their values for the singularities we are going to study, and these numbers depend on a choice of a parameter \(\alpha \in [0,1]\). For the sake of completeness, we add information about the Milnor numbers of the singular points of our conic arrangements.

Singularity Type

\(\mu _{p}\)

\(e_{orb}(p,\mathbb {P}^{2}_{\mathbb {C}},\alpha C)\)

\(\alpha \)

\(A_{1}\)

1

\((1-\alpha )^{2}\)

\(0 < \alpha \le 1\)

\(A_{3}\)

3

\(\frac{(3-4\alpha )^{2}}{8}\)

\(1/4 \le \alpha \le 3/4\)

\(D_{4}\)

4

\(\frac{(2-3\alpha )^{2}}{4}\)

\(0<\alpha \le 2/3\)

\(A_{5}\)

5

\(\frac{(4-6\alpha )^{2}}{12}\)

\(1/3 \le \alpha \le 2/3\)

\(A_{7}\)

7

\(\frac{(5-8\alpha )^{2}}{16}\)

\(3/8 \le \alpha \le 5/8\)

We will study the pair \((\mathbb {P}^{2}_{\mathbb {C}},\alpha C)\), where C is the boundary divisor \(C=C_{1} + \cdots +C_{k}\) associated with \( \mathbb{c} = \{ C_{1} , \ldots ,C_{k} \} \) being an arrangement of k smooth conics having singularities prescribed as above, and \(\alpha \) will be indicated in the next section.

3 Results

Now we are in a position to present our proof of Theorem 1.1.

Proof

Let \( \mathbb{c} = \{ C_{1} , \ldots ,C_{k} \} \subset {\mathbb{P}}_{\mathbb{C}}^{2} \) be an arrangement admitting only singularities as in the assumption, and denote by \(C = C_{1} + \cdots + C_{k}\) the associated divisor. In order to apply Theorem 2.1, we need to have \((\mathbb {P}^{2}_{\mathbb {C}},\alpha C)\) being an effective and log-canonical pair, so we need to find a suitable \(\alpha \). First constraint is that our pair is effective, which translates into the condition that \(\alpha \ge \frac{3}{2k}\). On the other hand, based on the table above, we should have \(\alpha \in [3/8, \, 5/8]\). Combining that we arrive at

$$\begin{aligned} \alpha \in \bigg [\textrm{max}\{3/2k, \, 3/8\}, 5/8 \bigg ], \end{aligned}$$

and this condition is non-empty provided that \(k \ge 3\). From now on we pick

$$\begin{aligned} \alpha = \frac{5}{8}, \end{aligned}$$

and we apply directly the inequality in Theorem 2.1. We start with the left-hand side, and we obtain:

$$\begin{aligned} 3n_2 \bigg (\frac{5}{8}(1-1)+1-\frac{9}{64}\bigg ) + 3t_2 \bigg (\frac{5}{8}(3-1)+1-\frac{1}{32}\bigg ) + 3n_3 \bigg (\frac{5}{8}(4-1)+1-\frac{1}{256}\bigg ) + \\ 3t_5 \bigg (\frac{5}{8}(5-1)+1-\frac{1}{192}\bigg ) + 3t_7 \bigg (\frac{5}{8}(7-1)+1-0\bigg ) \\ =\frac{165}{64}n_2 + \frac{213}{32}t_2 + \frac{2205}{256}n_3 + \frac{671}{64}t_5 + \frac{57}{4}t_7 . \end{aligned}$$

Based on that we get the following inequality:

$$\begin{aligned} \frac{165}{64} n_2 + \frac{213}{32} t_2 + \frac{2205}{256}n_3 + \frac{671}{64}t_5 + \frac{57}{4}t_7 \le \bigg (3 \cdot \frac{5}{8} - \Big (\frac{5}{8}\Big )^2\bigg ) d^2 - 3 \cdot \frac{5}{8}d = \frac{95}{64}d^2 - \frac{15}{8}d \end{aligned}$$

Since we have \( d = 2k \), we can write:

$$\begin{aligned} \frac{165}{64}n_2 + \frac{213}{32}t_2 + \frac{2205}{256}n_3 + \frac{671}{64}t_5 + \frac{57}{4}t_7 \le \frac{95}{32} (2k^2) - \frac{15}{4}k \end{aligned}$$

Now we are going to apply the combinatorial count. Since

$$\begin{aligned} 2k^2 = n_{2} + 2t_{2} + 3n_{3} + 3t_{5} + 4t_{7} + 2k, \end{aligned}$$

we get

$$\begin{aligned}\frac{165}{64}n_2 + \frac{213}{32}t_2 + \frac{2205}{256}n_3 + \frac{671}{64}t_5 + \frac{57}{4}t_7 \le \frac{95}{32}\bigg ( n_{2} + 2t_{2} + 3n_{3} + 3t_{5} + 4t_{7}+ 2k \bigg ) - \frac{15}{4}k. \end{aligned}$$

After simple manipulations, we finally obtain

$$\begin{aligned} 560 k + 100 n_2 + 75 n_3 \ge 608 t_7 + 404 t_5 + 184 t_2 , \end{aligned}$$

which completes the proof. \(\square \)

Now we can present our justification for Corollary 1.2.

Proof

We start with our upper bound on \(t_{5}\). Based on the combinatiorial count (1), we have

$$\begin{aligned} 2k^{2} - 2k \ge n_{2} + 3n_{3} + 3t_{5} \ge n_{2} + \frac{3}{4}n_{3} + 3t_{5}, \end{aligned}$$

we obtain that

$$\begin{aligned} 560k + 100(2k^{2}-2k - 3t_{5}) \ge 560k + 100\bigg (n_{2} + \frac{3}{4}n_{3}\bigg ) \ge 404t_{5}, \end{aligned}$$

so we get

$$\begin{aligned} t_{5} \le \frac{200}{704}k^{2} + \frac{360}{704}k = \frac{25}{88}k^{2} + \frac{45}{88}k. \end{aligned}$$

which completes our justification for \(A_{5}\) singularities. In a similar vein, we find an upper bound on \(t_{7}\). Based on the combinatorial count (1), we obtain that

$$\begin{aligned} 2k^{2}-2k \ge n_{2} + \frac{3}{4}n_{3}+4t_{7}, \end{aligned}$$

so we finally get

$$\begin{aligned} t_{7} \le \frac{200}{1008}k^{2} + \frac{360}{1008}k = \frac{25}{126}k^{2} + \frac{5}{14}k. \end{aligned}$$

\(\square \)

4 Examples

In this short section we will discuss examples of conic arrangements with \(A_{5}\) and \(A_{7}\) singularities. These examples are important in the context of the so-called freeness and the nearly-freeness of curve arrangements, but we are not going to discuss that matter here and we will come back to this problem in a forthcoming paper.

4.1 Arrangements with \(A_{7}\) singularities

Recall that by the naive combinatorial count we have the following upper bound on the number of \(A_{7}\) singularities:

$$\begin{aligned} t_{7} \le \left( {\begin{array}{c}k\\ 2\end{array}}\right) =\frac{k^{2}-k}{2}. \end{aligned}$$

Note that our upper bound for the number of \(A_{7}\) singularities, obtained in Corollary 1.2, is better than the naive one when \(k\ge 3\), and here we present the very first example maximizing the number of \(A_{7}\) singularities for \(k=3\) conics.

First of all, observe that for \(k=3\) we have that \(t_{7}\le \frac{20}{7}\) which means that we want to find an arrangement with 3 conics and 2 singular points of type \(A_{7}\).

Consider the following arrangement of conics \(\mathbb{c} = \{C_{1}, C_{2}, C_{3}\} \subset \mathbb {P}^{2}_{\mathbb {C}}\) with the defining equation

$$\begin{aligned} Q(x,y,z) = (x^{2}+y^{2}-z^{2})(2x^2 + y^2 +2xz)(2x^2 + y^2 - 2xz) =0. \end{aligned}$$

This arrangement is well-known in the literature and it is called Persson’s triconical arrangement [8]. Due to the visible symmetries, it has the following weak combinatorics:

$$\begin{aligned} t_{2} = 2, \quad t_{3}=1, \quad t_{7}=2. \end{aligned}$$

Based on the above discussion, Persson’s example maximizes the number of \(A_{7}\) singularities when \(k=3\). It would be very interesting to construct new examples of arrangements with \(k=4,5\) conics that are maximizing the number of \(A_{7}\) singularities—we are not aware of such examples.

4.2 Arrangements with \(A_{5}\) singularities

Recall that by the naive combinatorial count we have the following upper bound on the number of \(A_{5}\)-singularties:

$$\begin{aligned} t_{5} \le \frac{2k(k-1)}{3}. \end{aligned}$$

Similar to the case with \(A_{7}\)-singularities, the above naive bound is weak compared to the one given in Corollary 1.2 when \(k\ge 4\) and for \(k=3\) gives the same bound as the naive one. Based on our result, there is room for an arrangement of 3 conics such that \(t_{5}=4\). Let us recall that by a result due to du Plessis and Wall [5], if \(C\subset \mathbb {P}^{2}_{\mathbb {C}}\) is a reduced plane sextic with only \(\textrm{ADE}\) singularities, then the maximal Milnor number of a curve C, i.e,

$$\begin{aligned} \mu (C):=\sum _{p \in \textrm{Sing}(C)}\mu _{p}, \end{aligned}$$

is bounded from above by 19. This is because the total Milnor number is equal the total Tjurina number for curves with only \(\textrm{ADE}\) singularities. By [3, Proposition 2.3], we have

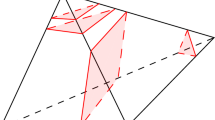
$$\begin{aligned} \mu (C)\le 3k(k-1)+1, \end{aligned}$$

so for \(k=3\) we obtain \(\mu (C)\le 19.\) When \(\mu (C)=19\), then such a curve is called maximizing. Details of the maximizing curves can be found, for example, in [3]. Since the Milnor number of the \(A_5\) singularity is 5, so for \(t_5=4\) and \(k=3\) the maximal Milnor number of a curve would be greater than 19. Thus there is no reduced plane sextic with \(\textrm{ADE}\) singularities which has exactly 4 singularities of type \(A_{5}\) which complete the first part of our discussion. Moreover, we can find an arrangement of 3 conics with exactly 3 singularities of type \(A_{5}\) and 3 nodes, which is shown below - we avoid presenting the defining equation of the arrangement due to unpleasant equations (Fig. 1).

Fig. 1
figure 1

An arrangement of 3 conics with 3 singularities of type \(A_{5}\)

Full size image