Skip to main content
SpringerLink
Log in

LSTM-based deep learning approach for remaining useful life prediction of rolling bearing using proposed C-MMPE feature

  • Original Article
  • Published:
Journal of Mechanical Science and Technology Aims and scope Submit manuscript

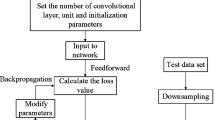
Abstract

Prognostic health management (PHM) is essential for the predictive maintenance of industrial systems, aiming to predict the remaining useful life (RUL) of system to ensure safe, reliable, and cost-effective operation of the machinery. This work proposes an innovative method for RUL prediction of bearings, by combining a health indicator (HI) proposed from the absolute cumulative modified multiscale permutation entropy (C-MMPE) feature with a deep learning long short-term memory (LSTM) model. The work also introduces a virtual health degree for bearings, using an exponential degradation pattern as the target function for the LSTM model output. Experimental validation showcases the effectiveness of proposed approach, achieving a high score value of 0.81 and demonstrating a lower mean absolute error value of 7.38 in RUL prediction for test bearings compared to conventional features and regression labeling functions. This highlights the superior RUL prediction capability of the proposed methodology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

The data and material supporting this study’s findings are openly available and provided by the FEMTO-ST Institute in PHM 2012 data repository.

Abbreviations

X i :

Original time series

p(π):

Relative frequency for each permutation ‘π’

M :

Embedding dimension

T :

Time lag

H PE :

Permutation entropy

H NPE :

Normalized permutation entropy

y sj :

New time series sequence

f :

Original feature

T :

Time index

\({\bar f}\) :

Smoothing processing of the original feature

CI :

Comprehensive indicator

t n :

Whole life duration of bearing

t i :

Current time

t j :

Initial degradation time of bearing

f t :

Forget gate

i t :

Input gate

o t :

Output gate

\({{\bar C}_t}\) :

Cell state

C t :

Update cell state

H t :

Output

ER% :

Error percentage

\(\overline {ER\% } \) :

Mean error percentage

\(\left| {\overline {ER\% } } \right|\) :

Mean absolute error percentage

A i :

Score for the ith test bearing

CG :

Coarse graining

C-Prefix :

Cumulative effect of features

HI :

Health indicator

MAG :

Moving average graining

MMPE :

Modified multiscale permutation entropy

MSPE :

Multi-scale permutation entropy

LSTM :

Long short-term memory

PE :

Permutation entropy

PHM :

Prognostic health management

RMS :

Root mean square

RUL:

Remaining useful life

References

  1. Z. Liu and L. Zhang, A review of failure modes, condition monitoring and fault diagnosis methods for large-scale wind turbine bearings, Measurement, 149 (2020) 107002.

    Article  Google Scholar 

  2. A. Kumar, C. P. Gandhi, Y. Zhou, R. Kumar and J. Xiang, Improved deep convolution neural network (CNN) for the identification of defects in the centrifugal pump using acoustic images, Applied Acoustics, 167 (2020) 107399.

    Article  Google Scholar 

  3. X. Zhang, S. Wan, Y. He, X. Wang and L. Dou, Teager energy spectral kurtosis of wavelet packet transform and its application in locating the sound source of fault bearing of belt conveyor, Measurement, 173 (2021) 108367.

    Article  Google Scholar 

  4. Y. Wei, Y. Li, M. Xu and W. Huang, A review of early fault diagnosis approaches and their applications in rotating machinery, Entropy, 21(4) (2019) 409.

    Article  Google Scholar 

  5. X. Kong and J. Yang, Remaining useful life prediction of rolling bearings based on RMS-MAVE and dynamic exponential regression model, IEEE Access, 7 (2019) 169705–169714.

    Article  Google Scholar 

  6. V. Atamuradov, K. Medjaher, P. Dersin, B. Lamoureux and N. Zerhouni, Prognostics and health management for maintenance practitioners-review, implementation and tools evaluation, Int. J. Progn. Health Manag., 8(3) (2017) 1–31.

    Google Scholar 

  7. R. Llasag Rosero, C. Silva and B. Ribeiro, Remaining useful life estimation of cooling units via time-frequency health indicators with machine learning, Aerospace, 9(6) (2022) 309.

    Article  Google Scholar 

  8. P. K. Sahu, R. N. Rai and T. C. A. Kumar, Grease contamination detection in the rolling element bearing using deep learning technique, International Journal of Mechanical Engineering and Robotics Research, 11(4) (2022) 275–280.

    Article  Google Scholar 

  9. A. V Dube, L. S. Dhamande and P. G. Kulkarni, Vibration based condition assessment of rolling element bearings with localized defects, Int. J. Sci. Technol. Res., 2(4) (2013) 149–155.

    Google Scholar 

  10. P. Arun, S. A. Lincon and N. Prabhakaran, Detection and characterization of bearing faults from the frequency domain features of vibration, IETE J. Res., 64(5) (2018) 634–647.

    Article  Google Scholar 

  11. X. Zhang, Y. Liang and J. Zhou, A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM, Measurement, 69 (2015) 164–179.

    Article  Google Scholar 

  12. P. K. Sahu and R. N. Rai, Fault diagnosis of rolling bearing based on an improved denoising technique using complete ensemble empirical mode decomposition and adaptive thresholding method, Journal of Vibration Engineering & Technologies, 11 (2023) 513–535.

    Article  Google Scholar 

  13. Y. Li, X. Wang, Z. Liu, X. Liang and S. Si, The entropy algorithm and its variants in the fault diagnosis of rotating machinery: A review, IEEE Access, 6 (2018) 66723–66741.

    Article  Google Scholar 

  14. C. E. Shannon, A mathematical theory of communication, The Bell System Technical Journal, 27(3) (1948) 379–423.

    Article  MathSciNet  Google Scholar 

  15. S. Pincus, Approximate entropy (ApEn) as a complexity measure, Chaos: An Interdisciplinary Journal of Nonlinear Science, 5(1) (1995) 110–117.

    Article  MathSciNet  Google Scholar 

  16. J. S. Richman and J. R. Moorman, Physiological time-series analysis using approximate entropy and sample entropy, American Journal of Physiology-Heart and Circulatory Physiology, 278(6) (2000) H2039–H2049.

    Article  Google Scholar 

  17. C. Bandt and B. Pompe, Permutation entropy: A natural complexity measure for time series, Phys. Rev. Lett., 88(17) (2002) 174102.

    Article  Google Scholar 

  18. R. Yan, Y. Liu and R. X. Gao, Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines, Mech. Syst. Signal Process, 29 (2012) 474–484.

    Article  Google Scholar 

  19. D.-Y. Lee and Y.-S. Choi, Multiscale distribution entropy analysis of short-term heart rate variability, Entropy, 20(12) (2018) 952.

    Article  Google Scholar 

  20. Q. Xue et al., Feature extraction using hierarchical dispersion entropy for rolling bearing fault diagnosis, IEEE Trans. Instrum. Meas., 70 (2021) 1–11.

    Google Scholar 

  21. J. Jiao, J. Yue and D. Pei, Feature enhancement method of rolling bearing based on K-adaptive VMD and RBF-fuzzy entropy, Entropy, 24(2) (2022) 197.

    Article  MathSciNet  Google Scholar 

  22. H. Zhang and S. He, Analysis and comparison of permutation entropy, approximate entropy and sample entropy, 2018 International Symposium on Computer, Consumer and Control (IS3C), Taichung, Taiwan (2018) 209–212.

  23. M. Costa, A. L. Goldberger and C.-K. Peng, Multiscale entropy analysis of complex physiologic time series, Phys. Rev. Lett., 89(6) (2002) 068102.

    Article  Google Scholar 

  24. H. Ren, W. Liu, M. Shan and X. Wang, A new wind turbine health condition monitoring method based on VMD-MPE and feature-based transfer learning, Measurement, 148 (2019) 106906.

    Article  Google Scholar 

  25. Y. Li, M. Xu, Y. Wei and W. Huang, A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree, Measurement, 77 (2016) 80–94.

    Article  Google Scholar 

  26. S.-D. Wu, C.-W. Wu, K.-Y. Lee and S.-G. Lin, Modified multiscale entropy for short-term time series analysis, Physica A: Statistical Mechanics and its Applications, 392(23) (2013) 5865–5873.

    Article  Google Scholar 

  27. C. Su, Z. Liang, X. Li, D. Li, Y. Li and M. Ursino, A comparison of multiscale permutation entropy measures in on-line depth of anesthesia monitoring, PLoS One, 11(10) (2016) e0164104.

    Article  Google Scholar 

  28. B. Zhang, L. Zhang and J. Xu, Degradation feature selection for remaining useful life prediction of rolling element bearings, Qual. Reliab. Eng. Int., 32(2) (2016) 547–554.

    Article  Google Scholar 

  29. L. Duan, F. Zhao, J. Wang, N. Wang and J. Zhang, An integrated cumulative transformation and feature fusion approach for bearing degradation prognostics, Shock and Vibration, 2018 (2018) 9067184.

    Article  Google Scholar 

  30. P. K. Sahu and R. N. Rai, Degradation monitoring and RUL prediction of rolling element bearing using proposed C-MMPE feature, 2022 11th International Conference on Power Science and Engineering (ICPSE), Eskisehir, Turkey (2022) 54–60.

  31. D. Chen, Y. Qin, Y. Wang and J. Zhou, Health indicator construction by quadratic function-based deep convolutional autoencoder and its application into bearing RUL prediction, ISA Trans., 114 (2021) 44–56.

    Article  Google Scholar 

  32. C. Wang, W. Jiang, X. Yang and S. Zhang, RUL prediction of rolling bearings based on a DCAE and CNN, Applied Sciences, 11(23) (2021) 11516.

    Article  Google Scholar 

  33. X.-S. Si, W. Wang, C.-H. Hu and D.-H. Zhou, Remaining useful life estimation–a review on the statistical data driven approaches, Eur. J. Oper. Res., 213(1) (2011) 1–14.

    Article  MathSciNet  Google Scholar 

  34. J. Zhu, N. Chen and W. Peng, Estimation of bearing remaining useful life based on multiscale convolutional neural network, IEEE Transactions on Industrial Electronics, 66(4) (2018) 3208–3216.

    Article  Google Scholar 

  35. R. Liu, B. Yang and A. G. Hauptmann, Simultaneous bearing fault recognition and remaining useful life prediction using joint-loss convolutional neural network, IEEE Trans. Industr. Inform., 16(1) (2019) 87–96.

    Article  Google Scholar 

  36. C. Sun, M. Ma, Z. Zhao, S. Tian, R. Yan and X. Chen, Deep transfer learning based on sparse autoencoder for remaining useful life prediction of tool in manufacturing, IEEE Trans. Industr. Inform., 15(4) (2018) 2416–2425.

    Article  Google Scholar 

  37. J. Deutsch and D. He, Using deep learning-based approach to predict remaining useful life of rotating components, IEEE Trans. Syst. Man. Cybern. Syst., 48(1) (2017) 11–20.

    Article  Google Scholar 

  38. J. Lei, C. Liu and D. Jiang, Fault diagnosis of wind turbine based on long short-term memory networks, Renew. Energy, 133 (2019) 422–432.

    Article  Google Scholar 

  39. S. Zheng, K. Ristovski, A. Farahat and C. Gupta, Long short-term memory network for remaining useful life estimation, 2017 IEEE International Conference on Prognostics and Health Management (ICPHM), Dallas, TX, USA (2017) 88–95.

  40. C.-S. Hsu and J.-R. Jiang, Remaining useful life estimation using long short-term memory deep learning, 2018 IEEE International Conference on Applied System Invention (ICASI), Chiha, Japan (2018) 58–61.

  41. J. Xia, Y. Feng, C. Lu, C. Fei and X. Xue, LSTM-based multilayer self-attention method for remaining useful life estimation of mechanical systems, Eng. Fail. Anal., 125 (2021) 105385.

    Article  Google Scholar 

  42. W. Mao, J. He, J. Tang and Y. Li, Predicting remaining useful life of rolling bearings based on deep feature representation and long short-term memory neural network, Advances in Mechanical Engineering, 10 (12) (2018).

  43. M. S. Rathore and S. P. Harsha, Rolling bearing prognostic analysis for domain adaptation under different operating conditions, Eng. Fail Anal., 139 (2022) 106414.

    Article  Google Scholar 

  44. M. Rostaghi and H. Azami, Dispersion entropy: A measure for time-series analysis, IEEE Signal Process Lett., 23(5) (2016) 610–614.

    Article  Google Scholar 

  45. W. Chen, Z. Wang, H. Xie and W. Yu, Characterization of surface EMG signal based on fuzzy entropy, IEEE Transactions on Neural Systems and Rehabilitation Engineering, 15(2) (2007) 266–272.

    Article  Google Scholar 

  46. K. Javed, R. Gouriveau, N. Zerhouni and P. Nectoux, Enabling health monitoring approach based on vibration data for accurate prognostics, IEEE Transactions on Industrial Electronics, 62(1) (2014) 647–656.

    Article  Google Scholar 

  47. Y. Yu, X. Si, C. Hu and J. Zhang, A review of recurrent neural networks: LSTM cells and network architectures, Neural Comput., 31(7) (2019) 1235–1270.

    Article  MathSciNet  Google Scholar 

  48. F. A. Gers, J. Schmidhuber and F. Cummins, Learning to forget: continual prediction with LSTM, Neural Comput., 12(10) (2000) 2451–2471.

    Article  Google Scholar 

  49. J. Bae and Z. Xi, Learning of physical health timestep using the LSTM network for remaining useful life estimation, Reliab. Eng. Syst. Saf., 226 (2022) 108717.

    Article  Google Scholar 

  50. P. Nectoux et al., PRONOSTIA: An experimental platform for bearings accelerated degradation tests, IEEE International Conference on Prognostics and Health Management, Denver, USA (2012) 1–8.

  51. A. Z. Hinchi and M. Tkiouat, Rolling element bearing remaining useful life estimation based on a convolutional long-short-term memory network, Procedia Comput. Sci., 127 (2018) 123–132.

    Article  Google Scholar 

  52. Y. Chen, G. Peng, Z. Zhu and S. Li, A novel deep learning method based on attention mechanism for bearing remaining useful life prediction, Appl. Soft Comput., 86 (2020) 105919.

    Article  Google Scholar 

  53. G. Zhang, W. Liang, B. She and F. Tian, Rotating machinery remaining useful life prediction scheme using deep-learning-based health indicator and a new rvm, Shock and Vibration, 2021 (2021) doi: https://doi.org/10.1155/2021/8815241.

  54. B. Wang, Y. Lei, N. Li and N. Li, A hybrid prognostics approach for estimating remaining useful life of rolling element bearings, IEEE Trans. Reliab., 69(1) (2018) 401–412.

    Article  Google Scholar 

  55. W. Xu, Q. Jiang, Y. Shen, F. Xu and Q. Zhu, RUL prediction for rolling bearings based on convolutional autoencoder and status degradation model, Appl. Soft. Comput., 130 (2022) 109686.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Subir Chowdhury School of Quality and Reliability, Indian Institute of Technology, Kharagpur, India

    Prashant Kumar Sahu & Rajiv Nandan Rai

Authors
  1. Prashant Kumar Sahu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rajiv Nandan Rai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Prashant Kumar Sahu.

Additional information

Prashant Kumar Sahu is presently working as a Research Scholar under the guidance of Dr. Rajiv Nandan Rai at Subir Chowdhury School of Quality and Reliability, Indian Institute of Technology Kharagpur, West Bengal, India. He received his B.E degree in Mechanical Engineering from Sathyabama University, Chennai in 2014 and MTech in Maintenance Engineering and Tribology from IIT (ISM) Dhanbad in 2017. His research interests include prognostic health management for rotating machinery.

Rajiv Nandan Rai, a Ph.D. in Mechanical Engineering from IIT Delhi, and presently a faculty at IIT Kharagpur, is an accomplished engineer with over 29 years of experience in the field of Reliability, Quality and Maintenance Engineering. He has authored more than 30 publications (SCI and Scopus indexed) including 02 book and 05 book chapters. He has also completed a number of sponsored Projects. His research interests include Reliability analysis of repairable systems, maintenance engineering, quality management and engineering, machine diagnostics and prognostics.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sahu, P.K., Rai, R.N. LSTM-based deep learning approach for remaining useful life prediction of rolling bearing using proposed C-MMPE feature. J Mech Sci Technol 38, 2197–2209 (2024). https://doi.org/10.1007/s12206-024-0402-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12206-024-0402-8

Keywords

Search

Navigation