1 Introduction

The generalized inverse of an integral operator was introduced by Fredholm [1]. The generalized inverse of a matrix was described by Moore who proposed a unique generalized inverse by means of projectors of matrices [2]. Until mid-1950s, there was few research on this subject. Later on, the use of matrix inverses in the solution of the linear equation systems began to increase the interest in this topic. In particular, R. Penrose proposed a generalization of the inverse of a non-singular matrix, as the unique solution of a certain set of equations in 1955 [3]. This work inspired new studies on generalized inverses and began to attract the attention of many researchers. This inverse is called the Moore–Penrose inverse in honor of the works of E. H. Moore and R. Penrose.

Let \(\mathscr {C}^{m \times n}\) be the set of \(m \times n\) complex matrices. For every \(A \in \mathscr {C}^{m \times n}\), the Moore–Penrose inverse of matrix A is the unique \(n \times m\) matrix \(A^{\dagger }\) with the following properties:

$$\begin{aligned} A A^{\dagger } A=A, \quad A^{\dagger } A A^{\dagger }=A^{\dagger }, \quad \left( A A^{\dagger }\right) ^{*}=A A^{\dagger }, \quad \left( A^{\dagger } A\right) ^{*}=A^{\dagger } A, \end{aligned}$$
(1)

where \(A^{*}\) denotes the conjugate transpose of A.

The Moore–Penrose inverse appears in many fields such as applied mathematics, statistics, neural networks, machine learning, applied physics, control system analysis, curve fitting, digital image restoration, numerical analysis, tensor computations and the solution of system of equations (see [4, 5]). Up until now, there have been several studies in different areas related to the Moore–Penrose inverse and its applications (see [1, 6,7,8,9,10,11,12,13,14]). For example, Courrieu developed an algorithm based on a full rank Cholesky factorization which allows for fast computation of Moore–Penrose inverse of the matrices and fast solving of large least square systems, possibly with rank deficient matrices [8]. Baksalary et al. examined some problems with the Moore–Penrose inverse of the sum of two matrices, by combining various facts known in the literature and using some properties of matrix inverses [7]. Sun et al. introduced the Moore–Penrose inverse of tensors with the Einstein product, and the authors found explicit formulas of the Moore–Penrose inverse of some block tensors [13]. Ma et al. examined the perturbation theory for the Moore–Penrose inverse of tensor via Einstein product by using derived representations of some tensor expressions involving the Moore-Penrose inverse [14]. Radičić studied the Moore–Penrose inverse and the group inverse of the k-circulant matrices whose elements are the binomial coefficients [11]. Zhang et al. proposed the Zhang neural networks (ZNN) models for online time-varying full-rank matrix Moore–Penrose inversion [12]. The authors presented the feasibility and effectiveness of ZNN models for online time-varying full-rank matrix Moore–Penrose inversion with the help of computer simulation results and application to inverse kinematic control of redundant robot arms.

In recent years, there has been a huge interest of modern science in the application of the Golden Section and Fibonacci numbers. The Fibonacci numbers, \(\left\{ F_n \right\} _{n=0}^{\infty }\), are the terms of the sequence \(\left\{ 0, 1, 1, 2, 3, 5, \ldots \right\} \) wherein each term is the sum of two consecutive terms, starting with the initial conditions \(F_0 = 0\) and \(F_1 = 1\). As \(n \rightarrow \infty \), the ratio between successive Fibonacci numbers is called as golden ratio, \(\tau = \frac{1 + \sqrt{5}}{2} = 1.618\ldots \), which plays an important role in arts, architecture, engineering, geometry, music, electrostatics, poetry, stock market trading and trigonometry [15]. Up until now, many researchers have studied the applications, generalizations and relations with other disciplines of the Fibonacci and related integer sequences [16,17,18,19,20,21,22,23,24,25,26,27]. For example, Falcón and Plaza proposed the k-Fibonacci numbers, \(\left\{ F_{k,n} \right\} _{n=0}^{\infty }\), by studying the recursive application of two geometrical transformations used in the well-known 4-triangle longest-edge (4TLE) partition [16]. Yazlik and Taskara defined the generalized k-Horadam sequence, \(\left\{ H_{k,n} \right\} _{n=0}^{\infty }\), and they obtained several identities by using determinant [18]. With a different perspective, Edson and Yayenie introduced the notable generalization of the Fibonacci sequence, biperiodic Fibonacci sequence, which is generated by the recurrence relation \(q_n=a q_{n-1}+q_{n-2}\) (when n is even) or \(q_n=b q_{n-1}+q_{n-2}\) (when n is odd), where a and b are nonzero real numbers [19]. Moreover, the authors derived the extended Binet’s formula, generating function and several identities of \(\left\{ q_n\right\} _{n=0}^{\infty }\). In a similar way, Bilgici presented the biperiodic Lucas numbers which is generated by the recurrence relation \(l_n = b l_{n-1} + l_{n-2}\) (when n is even) or \(l_n = a q_{n-1} + q_{n-2}\) (when n is odd), where a and b are nonzero real numbers [21]. Moreover, he gave generating functions, the Binet formulas and some special identities of \(\left\{ l_n \right\} _{n=0}^{\infty }\). Yazlık et al. illustrated a new generalization of the Fibonacci and Lucas p-numbers, biperiodic Fibonacci and Lucas p-numbers [20]. The authors built up the tree diagrams for the biperiodic Fibonacci and Lucas p-sequences, and they derived the recurrence relations of these sequences by using these diagrams. Moreover they obtained the Binet formulas of the biperiodic Fibonacci and Lucas p-sequences by using Vandermonde matrices. Edson et al. defined a further generalization of the Fibonacci sequence, k-periodic Fibonacci sequence, which is defined using a non-linear recurrence relation that depends on k real parameters, and is an extension of the biperiodic Fibonacci sequence [24]. By analogy to the studies [19, 21, 23] Tan and Leung proposed the generalized biperiodic Horadam sequence and investigated some congruence properties of the generalized Horadam sequence [22]. Throughout this paper, we call the generalized biperiodic Horadam sequence as generalized conditional sequence.

Up to the present, several researchers have studied the Moore–Penrose inverse of some matrices whose elements are the classical special number sequences (see [10, 28,29,30]). For example, Miladinovic and Stanimirovic studied the pseudoinverse of the generalized singular Fibonacci matrix and they derived some combinatorial identities by using generalized singular Fibonacci matrices [10]. Shen and He proposed the Moore–Penrose inverse of the matrix whose nonzero entries are the classical Horadam numbers [28]. As a generalization of the studies [10, 28], Shen et al. studied the Moore–Penrose inverse of the strictly lower triangular Toeplitz matrix and they derived a convolution formula containing the Horadam numbers. Moreover, the authors derived various combinatorial identities by using convolution formula [29].

In this paper, drawing inspiration from the previous works on the Moore–Penrose inverse, we focus on the following topics in order to obtain novel results:

  1. 1.

    Constructing a singular matrix with generalized conditional sequences,

  2. 2.

    Establishing a new convolution formula with the help of generalized conditional sequences,

  3. 3.

    Proving auxiliary identities in order to use the convolution formula effectively,

  4. 4.

    Obtaining the Moore–Penrose inverse of a singular matrix explicitly by using convolution formula,

  5. 5.

    Expressing the Moore–Penrose inverse of a singular matrix in the form of block matrices,

  6. 6.

    Providing more general results for different values of the initial conditions and the coefficients of the generalized conditional sequence.

2 Preliminaries and main results

In this section, we introduce some definitions and preliminary facts which are used in this paper.

Definition 1

[22] For any arbitrary numbers s and t and nonzero real numbers a, b and c, the generalized conditional sequence is defined by the recurrence relation

$$\begin{aligned} W_{n}^{(s,t)} = {\left\{ \begin{array}{ll} a W_{n-1}^{(s,t)} + c W_{n-2}^{(s,t)}, &{} \textit{if n is even} \\ b W_{n-1}^{(s,t)} + c W_{n-2}^{(s,t)}, &{} \textit{if n is odd} \\ \end{array}\right. }, ~~ W_0^{(s,t)} = s , ~~ W_1^{(s,t)} = t, \quad n \geqslant 2. \end{aligned}$$
(2)

It’s not difficult to see from the following table that the generalized conditional sequence can be reduced infinite special number sequences for the special cases of a, b, c, s and t.

a

b

c

s

t

Generalized conditional sequence

a

b

c

0

1

Generalized conditional Fibonacci sequence

a

b

c

2

b

Generalized conditional Lucas sequence

a

b

1

0

1

Biperiodic Fibonacci sequence

a

b

1

2

a

Biperiodic Lucas sequence

a

b

2

0

1

Biperiodic Jacobsthal sequence

a

b

2

2

a

Biperiodic Jacobsthal–Lucas sequence

k

k

1

0

1

k-Fibonacci sequence

k

k

1

2

k

k-Lucas sequence

k

k

2

0

1

k-Jacobsthal sequence

k

k

2

2

k

k-Jacobsthal–Lucas sequence

2

2

k

0

1

k-Pell sequence

2

2

k

2

2

k-Pell–Lucas sequence

2

2

1

0

1

Pell sequence

2

2

1

2

1

Pell–Lucas sequence

1

1

1

0

1

Fibonacci sequence

1

1

1

2

1

Lucas sequence

1

1

2

0

1

Jacobsthal sequence

1

1

2

2

1

Jacobsthal–Lucas sequence

\(\vdots \)

\(\vdots \)

\(\vdots \)

\(\vdots \)

\(\vdots \)

\(\vdots \)

The French mathematician Jacques–Marie Binet found an explicit formula of the Fibonacci sequence in 1843 and it was called as Binet’s formula after this discovery. The next definition explains generalized Binet formula of the sequence \(\left\{ W_{n}^{(s,t)} \right\} _{n=0}^{\infty }\).

Definition 2

[22] The Binet formula of the generalized conditional sequence is

$$\begin{aligned} W_{n}^{(s,t)} = \frac{a^{\xi (n+1)}}{(a b)^{\left\lfloor \frac{n}{2}\right\rfloor }}\left( D \alpha ^{n} - E \beta ^{n}\right) , \end{aligned}$$
(3)

where \(D=\frac{W_{1}^{(s,t)} - \frac{\beta }{a} W_{0}^{(s,t)}}{\alpha -\beta }\), \(E=\frac{W_{1}^{(s,t)}-\frac{\alpha }{a} W_{0}^{(s,t)}}{\alpha -\beta }\), \(\alpha \) and \(\beta \) are the zeros of the polynomial \(x^{2}-a b x-a b c\), that is, \(\alpha =\frac{a b+\sqrt{a^{2} b^{2}+4 a b c}}{2}\) and \(\beta =\frac{a b-\sqrt{a^{2} b^{2}+4 a b c}}{2}\). Moreover, \(\xi (n)=n-2\left\lfloor \frac{n}{2}\right\rfloor \) is the parity function, i.e., \(\xi (n)=0\) when n is even and \(\xi (n)=1\) when n is odd. Let assume \(\Delta =a^{2} b^{2}+4 a b c \ne 0\). Also we have \(\alpha +\beta =a b, \alpha -\beta =\sqrt{a^{2} b^{2}+4 a b c}\) and \(\alpha \beta =-a b c\).

The following definition explains a lower triangular and strictly lower triangular matrix \(\mathscr {W}_n^{(r, k)}\), whose nonzero elements are the generalized conditional sequence satisfying \(W_{k+1}^{(s,t)} \ne 0\). The non-positive integer r indicates the number of the zero diagonals including the main diagonal and below.

Definition 3

For any integers r and k satisfying \(r < 0\) and \(k \geqslant 0\), and the generalized conditional sequence \(\left\{ W_{n}^{(s,t)}\right\} _{n \in N}\) with \(W_{k+1}^{(s,t)} \ne 0\), the \(n \times n\) matrix \(\mathscr {W}_n^{(r, k)}=\left[ \omega _{i, j}^{(r, k)}\right] \) is defined by

$$\begin{aligned} \omega _{i, j}^{(r, k)}= {\left\{ \begin{array}{ll} \left( \frac{b}{a}\right) ^{\frac{\xi (i-j+k+r)}{2} } W_{i-j+r+k+1}^{(s, t)}, &{}\quad {\text {if }} i-j+r \geqslant 0 \\ 0, &{} \quad {\text {if }} i-j+r<0\end{array}\right. }. \end{aligned}$$
(4)

Due to the the specific structure of the matrix \(\mathscr {W}_n^{(r, k)}\), we can express it by the following block matrix form

(5)

where \(\mathscr {O}_{p \times q}\) denotes the \(p \times q\) zero matrix.

Example 1

The \(5 \times 5\) generalized conditional matrix for \((r,k) = (-2,2)\) is equal to

$$\begin{aligned}&\mathscr {W}_5^{(-2, 2)}=\left[ \begin{array}{c|c} \mathscr {O}_{2 \times 3} &{} \mathscr {O}_{2 \times 2} \\ \hline \mathscr {W}_{3}^{(2)} &{} \mathscr {O}_{3 \times 2} \end{array}\right] \\&\quad = \left[ \begin{array}{ccc|cc} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \hline a b t+b c s+c t &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{\sqrt{b} (c s (a b+c)+a t (a b+2 c))}{\sqrt{a}} &{} a b t+b c s+c t &{} 0 &{} 0 &{} 0 \\ a^2 b^2 t+a b c (b s+3 t)+c^2 (2 b s+t) &{} \frac{\sqrt{b} (c s (a b+c)+a t (a b+2 c))}{\sqrt{a}} &{} a b t+b c s+c t &{} 0 &{} 0 \\ \end{array}\right] . \end{aligned}$$

The underlying idea in convolution is to combine a kernel list with consecutive sublists of a list of data. Next definition explains the convolution formula.

Definition 4

[31] For any two arrays \(x=\left\{ x_1, x_2, \dots , x_n \right\} \) and \(y=\left\{ y_1, y_2, \dots , y_n \right\} \), the convolution of x and y is defined by

$$\begin{aligned} x \star y = \sum _{i=1}^{n} x_i y_{n-i+1}. \end{aligned}$$
(6)

The next theorem describes a convolution formula which involves the generalized conditional sequences with corresponding powers of \(\left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} } \right) \), where \(m\geqslant 0\) and \(W_{m+1}^{(s, t)} \ne 0\).

Throughout this paper, for the sake of simplicity, we will use the following notation

$$\begin{aligned} Con(r,m)&= \left\{ \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} , \dots , \left( \frac{b}{a}\right) ^{\frac{\xi (m+r-2)}{2} } W_{m+r-1}^{(s,t)} \right\} \\&\qquad \times \left\{ 1, \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} }, \dots , \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} } \right) ^{r-2} \right\} . \end{aligned}$$

Theorem 1

Let m, r be two integers with \(m\geqslant 0\) and \(r \geqslant 2\). If \(c\ne 0 \), \(W_{m+1}^{(s,t)} \ne 0\) and \(\alpha , \beta \ne \frac{-c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} }\), then we have

$$\begin{aligned} Con(r,m) = \frac{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \times \left( \begin{aligned}&\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m+r-1)}{2} } W_{m+r}^{(s,t)} \\&- \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m+r)}{2} } W_{m+r-1}^{(s,t)} \end{aligned} \right) }{\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m+1)}{2} } W_{m+2}^{(s,t)} - \left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^2}. \end{aligned}$$
(7)

Proof

In a clear way, Eq. (7) hold for \(W_{m}^{(s,t)} = 0\). Hence, we take into account the case \(W_{m}^{(s,t)} \ne 0\). By virtue of the Binet formula (3) and doing simple transformations, we obtain

$$\begin{aligned} Con(r,m)&= \sum _{l=0}^{r-2} \left( \frac{b}{a}\right) ^{\frac{\xi (l+m)}{2} } W_{l+m+1}^{(s,t)} \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} } \right) ^{r-l-2} \\&= \sum _{l=0}^{r-2} \left( \frac{b}{a}\right) ^{\frac{\xi (l+m)}{2} } \frac{a^{\xi (l+m+2)}}{(ab)^{\lfloor \frac{l+m+1}{2}\rfloor }} \left( D \alpha ^{l+m+1} - E \beta ^{l+m+1}\right) \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} } \right) ^{r-l-2} \\&= \sum _{l=0}^{r-2} \frac{1}{\left( ab \right) ^{\frac{l+m}{2}}} \left( D \alpha ^{l+m+1} - E \beta ^{l+m+1}\right) \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} } \right) ^{r-l-2} \\&= \frac{D \alpha ^{m+1}}{(ab)^{\frac{m}{2}}} \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} } \right) ^{r-2} \sum _{l=0}^{r-2} \left( \frac{- \alpha \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} }{c \sqrt{ab}\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} } \right) ^{l} \\&- \frac{E \beta ^{m+1}}{(ab)^{\frac{m}{2}}} \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} } \right) ^{r-2} \sum _{l=0}^{r-2} \left( \frac{- \beta \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} }{c \sqrt{ab}\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} } \right) ^{l} \\&= \frac{D \alpha ^{m+1}}{(ab)^{\frac{m}{2}}} \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} } \right) ^{r-2} \left( \frac{1 - \left( \frac{- \alpha \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} }{c \sqrt{ab}\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} } \right) ^{r-1} }{1 + \frac{ \alpha \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} }{c \sqrt{ab}\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} } } \right) \\&- \frac{E \beta ^{m+1}}{(ab)^{\frac{m}{2}}} \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} } \right) ^{r-2} \left( \frac{1 - \left( \frac{- \beta \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} }{c \sqrt{ab}\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} } \right) ^{r-1} }{1 + \frac{ \beta \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} }{c \sqrt{ab}\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} } } \right) \\&= \frac{\left( \begin{aligned}&\frac{(-1)^{r-2} D \alpha ^{m+1} \sqrt{ab}}{(ab)^{\frac{m}{2}}} \frac{\left( c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \right) ^{r-1}}{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^{r-2}} \\&+ \frac{D \alpha ^{m+r} \sqrt{ab}}{(ab)^{\frac{m}{2}} \left( \sqrt{ab} \right) ^{r-1} } \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \end{aligned} \right) \times \left( \begin{aligned}&c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \\&+ \beta \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \end{aligned} \right) }{\left( \begin{aligned}&\left( c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} + \alpha \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) \\&\quad \times \left( c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} + \beta \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) \end{aligned} \right) } \\&- \frac{\left( \begin{aligned}&\frac{(-1)^{r-2} E \beta ^{m+1} \sqrt{ab}}{(ab)^{\frac{m}{2}}} \frac{\left( c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \right) ^{r-1}}{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^{r-2}} \\&+ \frac{E \beta ^{m+r} \sqrt{ab}}{(ab)^{\frac{m}{2}} \left( \sqrt{ab} \right) ^{r-1} } \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \end{aligned} \right) \times \left( \begin{aligned}&c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \\&+ \alpha \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \end{aligned} \right) }{\left( \begin{aligned}&\left( c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} + \alpha \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) \\&\quad \times \left( c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} + \beta \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) \end{aligned} \right) }. \end{aligned}$$

By using identities \(\alpha \beta = -abc\) and \( \alpha + \beta = ab \), we obtain denumerator of Con(r, m) as

$$\begin{aligned} Denum(Con(r,m))&= \left( c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} + \alpha \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) \\&\qquad \times \left( c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} + \beta \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) \\&= abc \left( \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m+1)}{2} } W_{m+2}^{(s,t)} - \left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^{2} \right) . \end{aligned}$$

After some algebraic operations, the numerator of Con(r, m) can be transformed into the following form:

$$\begin{aligned} Num\left( Con(r,m)\right)&= \frac{(-1)^{r-2} ab \left( D \alpha ^{m+1} - E \beta ^{m+1} \right) }{\left( ab\right) ^{\frac{m}{2}}} \frac{ \left( c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \right) ^{r}}{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^{r-2}} \\&\quad + \frac{1}{(ab)^{\frac{m+r-1}{2}}}\left( D \alpha ^{m+r} - E \beta ^{m+r} \right) \left( abc \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) \\&\quad + \frac{(-1)^{r-2} (-abc) \left( D \alpha ^{m} - E \beta ^{m} \right) }{\left( ab\right) ^{\frac{m-1}{2}}} \frac{ \left( c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \right) ^{r-1}}{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^{r-3}} \\&\quad + \frac{(-abc)}{\left( ab\right) ^{\frac{m+r-2}{2}}} \left( D \alpha ^{m+r-1} - E \beta ^{m+r-1}\right) \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} . \end{aligned}$$

Taking into account the Binet formula (3), \(Num\left( Con(r,m)\right) \) and \(Denum\left( Con(r,m)\right) \), we get

$$\begin{aligned} Con(r,m)&= \frac{\left( \begin{aligned}&(-1)^{r-2} ab \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \frac{ \left( c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \right) ^{r}}{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^{r-2}} \\&\quad + (-1)^{r-2} (-abc) \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \frac{ \left( c \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \right) ^{r-1}}{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^{r-3}}\\&\quad + abc \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m+r-1)}{2} } W_{m+r}^{(s,t)} \\&\quad -abc \left( \frac{b}{a}\right) ^{\frac{\xi (m+r-2)}{2} } W_{m+r-1}^{(s,t)} \left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^2 \end{aligned}\right) }{abc \left( \left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m+1)}{2} } W_{m+2}^{(s,t)} - \left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^{2} \right) }. \end{aligned}$$

By simplifying the above equation, we obtain

$$\begin{aligned} Con(r,m) = \frac{\left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \times \left( \begin{aligned}&\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m+r-1)}{2} } W_{m+r}^{(s,t)} \\&\quad - \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m+r)}{2} } W_{m+r-1}^{(s,t)} \end{aligned} \right) }{\left( \frac{b}{a}\right) ^{\frac{\xi (m-1)}{2} } W_{m}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (m+1)}{2} } W_{m+2}^{(s,t)} - \left( \left( \frac{b}{a}\right) ^{\frac{\xi (m)}{2} } W_{m+1}^{(s,t)} \right) ^2}. \end{aligned}$$

Therefore, the proof is completed. \(\square \)

Lemma 1

Let r be an arbitrary positive integer and \(W_{k+1}^{(s,t)} \ne 0\). If \(\alpha = \frac{-c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} }\) or \(\beta = \frac{-c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} }\), then we get

$$\begin{aligned} \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r)}{2} } W_{k+r+1}^{(s,t)} - \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} = 0. \end{aligned}$$
(8)

Proof

Clearly, equality (8) is valid for \(c=0\). So, we consider the case \(c\ne 0\). If \(\alpha = \frac{-c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} }\), then we get

$$\begin{aligned} \frac{a b+\sqrt{a^{2} b^{2}+4 a b c}}{2} = \frac{-c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} }. \end{aligned}$$

After some algebraic operations, we have

$$\begin{aligned} 1&= \frac{\left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} \left( c \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} + \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2} \\&= \frac{\left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2}. \end{aligned}$$

Thus, we obtain \(\left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} = \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2\). On the other hand, by virtue of the Binet formula (3), we have

$$\begin{aligned} \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} - \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2 \nonumber \\= \frac{\left( -c\right) ^k \left( -a t^2 + b s (a t+c s) \right) }{a}. \end{aligned}$$
(9)

Furthermore, with the help of (9), we obtain

$$\begin{aligned}&\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r)}{2} } W_{k+r+1}^{(s,t)} - \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} \\&\qquad = \frac{D E \left( -c\right) ^k abc \left( \alpha - \beta \right) \left( \alpha ^{r-1} - \beta ^{r-1} \right) }{\left( ab \right) ^{\frac{r}{2}}} \\&\qquad = \frac{\left( -c\right) ^{k+1} \left( -at^2+bs\left( cs+at \right) \right) }{\sqrt{a^2b^2+4abc}} \frac{\alpha ^{r-1} - \beta ^{r-1}}{\left( ab \right) ^{\frac{r}{2}}} = 0. \end{aligned}$$

In a similar way, we can verify that the equality (8) is valid for \(\beta = \frac{-c \sqrt{ab} \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} }\). Hence, the proof is completed. \(\square \)

Lemma 2

Let \(\left\{ W_{n}^{(s,t)} \right\} _{n=0}^{\infty }\) be the generalized conditional sequence satisfying \(W_{k+1}^{(s,t)} \ne 0\). Then the inverse of the matrix \(\mathscr {W}_{n}^{(k)}\), \(\Phi _{n} = \left[ \phi _{ij} \right] _{n \times n}\), is defined by

$$\begin{aligned} \phi _{i, j} = \left\{ \begin{array}{ll} \frac{(-1)^k c^{k+1} \left( -a t^2 + b s (a t+c s) \right) }{a \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^{3}} \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} }{ \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} } \right) ^{i-j-2}, &{}\quad i>j+1, \\ - \frac{ \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} }{ \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^{2} }, &{}\quad i=j+1, \\ \frac{1}{ \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} }, &{}\quad i=j \\ 0, &{} \quad \text {otherwise } \end{array}\right. , \end{aligned}$$
(10)

where k is an arbitrary integer satisfying \(0 \leqslant k < n\).

Proof

Let us denote the matrices \(\mathscr {W}_{n}^{(k)} = \left[ \omega _{ij} \right] _{n \times n}\) and \(\mathscr {X}_{n} = \left[ x_{ij} \right] _{n \times n} = \mathscr {W}_{n}^{(k)} \Phi _{n} \). Due to the structure of the matrices, we can observe that \(x_{i,j} = 0\) for \(i < j\).

For \(i = j\), we obtain

$$\begin{aligned} x_{i,j} = \omega _{i,i} \phi _{i, i} = \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \frac{1}{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} } = 1. \end{aligned}$$

\(\square \)

For \(i = j+1\), we obtain

$$\begin{aligned}&x_{i,j} {=} \omega _{j+1, j} \phi _{j, j} + \omega _{j+1, j+1} \phi _{j+1, j} \\&\quad {=} \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} \frac{1}{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} } - \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \left( \frac{\left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2} \right) {=} 0. \end{aligned}$$

For the last case, \(i > j\), we obtain

$$\begin{aligned} x_{i,j}&= \omega _{i, j} \phi _{j, j} + \omega _{i, j+1} \phi _{j+1, j} + \sum _{l=2}^{i-j} \omega _{i, i-l+2} \phi _{i-l+2, j} \\&= \frac{\omega _{i, j}}{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} } - \frac{\left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2}\omega _{i, j+1} \\&\quad + \frac{(-1)^k c^{k+1} \left( -a t^2 + b s (a t+c s) \right) }{a \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^{3}} \\&\quad \left[ \sum _{l=2}^{i-j} \omega _{i, i-l+2} \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} } \right) ^{i-j-l} \right] . \end{aligned}$$

By taking \(r=i-j\), we can obtain \(\omega _{i, j} = \left( \frac{b}{a}\right) ^{\frac{\xi (k+r)}{2} } W_{k+r+1}^{(s,t)} \) and \(\omega _{i, j+1} = \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} \). Therefore, we get

$$\begin{aligned} x_{i,j} =&\frac{\left( \frac{b}{a}\right) ^{\frac{\xi (k+r)}{2} } W_{k+r+1}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} } - \frac{\left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2}\left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} \\&\quad + \frac{(-1)^k c^{k+1} \left( -a t^2 + b s (a t+c s) \right) }{a \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^{3}}\\ {}&\quad \left[ \sum _{l=2}^{r} \left( \frac{b}{a}\right) ^{\frac{\xi (l+k-2)}{2} } W_{l+k-1}^{(s,t)} \left( \frac{-c \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} }{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} } \right) ^{r-l} \right] \\&= \frac{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r)}{2} } W_{k+r+1}^{(s,t)} - \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2} \\&\quad + \frac{(-1)^k c^{k+1} \left( -a t^2 + b s (a t+c s) \right) }{a \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^{3}} Con(r,k). \end{aligned}$$

By virtue of Theorem 1, we obtain

$$\begin{aligned} x_{i,j} =&\frac{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r)}{2} } W_{k+r+1}^{(s,t)} - \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2} \\&\quad + \frac{(-1)^k c^{k+1} \left( -a t^2 + b s (a t+c s) \right) }{a \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^{3}} \\&\qquad \times \left( \frac{ \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \times \left( \begin{aligned}&\left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} \\&\quad - \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r)}{2} } W_{k+r-1}^{(s,t)} \end{aligned} \right) }{\left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} - \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2} \right) \\&= \frac{\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r)}{2} } W_{k+r+1}^{(s,t)} - \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } W_{k+2}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2} \\&\quad + \frac{c \left( \left( \frac{b}{a}\right) ^{\frac{\xi (k-1)}{2} } W_{k}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} - \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-2)}{2} } W_{k+r-1}^{(s,t)} \right) }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2}\\&= \frac{ \begin{aligned}&\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \left( \left( \frac{b}{a} \right) ^{\frac{\xi (k+r)}{2}} \left( W_{k+r+1}^{(s,t)} - cW_{k+r-1}^{(s,t)} \right) \right) \\&\qquad - \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } W_{k+r}^{(s,t)} \left( \left( \frac{b}{a} \right) ^{\frac{\xi (k+1)}{2}} \left( W_{k+2}^{(s,t)} - cW_{k}^{(s,t)} \right) \right) \end{aligned} }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2} \\&= \frac{ \begin{aligned}&\left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } \left( \frac{b}{a}\right) ^{\frac{\xi (k+r)}{2} } \left( \frac{b}{a}\right) ^{\xi (k+r+1)} a W_{k+1}^{(s,t)} W_{k+r}^{(s,t)} \\&\qquad - \left( \frac{b}{a}\right) ^{\xi (k)} \left( \frac{b}{a}\right) ^{\frac{\xi (k+r-1)}{2} } \left( \frac{b}{a}\right) ^{\frac{\xi (k+1)}{2} } a W_{k+1}^{(s,t)} W_{k+r}^{(s,t)} \end{aligned} }{\left( \left( \frac{b}{a}\right) ^{\frac{\xi (k)}{2} } W_{k+1}^{(s,t)} \right) ^2} \\&= 0. \end{aligned}$$

Therefore, we prove that \(\mathscr {X}_{n}\) is the \(n \times n\) identity matrix. In a similar way, we can verify that \(\Phi _{n} \mathscr {W}_{n}^{(k)} = \mathscr {X}_{n}\). So, the proof is completed.

Example 2

For \(n=5\) and \(k=0\), we get

$$\begin{aligned} \mathscr {W}_{5}^{(0)}\Phi _{5}&= \left( \begin{array}{ccccc} t &{} 0 &{} 0 &{} 0 &{} 0 \\ \frac{\sqrt{b} (a t+c s)}{\sqrt{a}} &{} t &{} 0 &{} 0 &{} 0 \\ a b t+b c s+c t &{} \frac{\sqrt{b} (a t+c s)}{\sqrt{a}} &{} t &{} 0 &{} 0 \\ \frac{\sqrt{b} (c s (a b+c)+a t (a b+2 c))}{\sqrt{a}} &{} a b t+b c s+c t &{} \frac{\sqrt{b} (a t+c s)}{\sqrt{a}} &{} t &{} 0 \\ a^2 b^2 t+a b c (b s+3 t)+c^2 (2 b s+t) &{} \frac{\sqrt{b} (c s (a b+c)+a t (a b+2 c))}{\sqrt{a}} &{} a b t+b c s+c t &{} \frac{\sqrt{b} (a t+c s)}{\sqrt{a}} &{} t \\ \end{array} \right) \\&\quad \times \left( \begin{array}{ccccc} \frac{1}{t} &{} 0 &{} 0 &{} 0 &{} 0 \\ -\frac{\sqrt{b} (a t+c s)}{\sqrt{a} t^2} &{} \frac{1}{t} &{} 0 &{} 0 &{} 0 \\ \frac{c \left( b s (a t+c s)-a t^2\right) }{a t^3} &{} -\frac{\sqrt{b} (a t+c s)}{\sqrt{a} t^2} &{} \frac{1}{t} &{} 0 &{} 0 \\ -\frac{\sqrt{b} c^2 s \left( b s (a t+c s)-a t^2\right) }{a^{3/2} t^4} &{} \frac{c \left( b s (a t+c s)-a t^2\right) }{a t^3} &{} -\frac{\sqrt{b} (a t+c s)}{\sqrt{a} t^2} &{} \frac{1}{t} &{} 0 \\ \frac{b c^3 s^2 \left( b s (a t+c s)-a t^2\right) }{a^2 t^5} &{} -\frac{\sqrt{b} c^2 s \left( b s (a t+c s)-a t^2\right) }{a^{3/2} t^4} &{} \frac{c \left( b s (a t+c s)-a t^2\right) }{a t^3} &{} -\frac{\sqrt{b} (a t+c s)}{\sqrt{a} t^2} &{} \frac{1}{t} \\ \end{array} \right) \\&= \left( \begin{array}{ccccc} 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ \end{array} \right) = \mathscr {X}_{5}. \end{aligned}$$

If we take \(a=b=A\), \(c=B\), \(s=a\) and \(t=b\) in Lemma 2, we obtain the inverse of the matrix \(\mathscr {U}_{n}^{(k)}\) whose elements are the classical Horadam numbers.

Corollary 1

[29] Let \(\left\{ U_n^{(a, b)}\right\} _{n \in N}\) be the Horadam sequence satisfying \(U_{k+1}^{(a, b)} \ne 0\). Then the inverse of the matrix \(\mathscr {U}_n^{(k)}\) is the matrix \(\mathscr {R}_n=\left[ r_{i, j}\right] _{n \times n}\) defined by

$$\begin{aligned} r_{i, j}= {\left\{ \begin{array}{ll}\frac{(-1)^k B^{k+1}\left( a^2 B+a b A-b^2\right) }{\left( U_{k+1}^{(a, b)}\right) ^3}\left( \frac{-B U_k^{(a, b)}}{U_{k+1}^{(a, b)}}\right) ^{i-j-2}, &{}\quad {\text {if }} i>j+1, \\ -\frac{U_{k+2}^{(a, b)}}{\left( U_{k+1}^{(a, b)}\right) ^2}, &{} \quad {\text {if }} i=j+1, \\ \frac{1}{U_{k+1}^{(a, b)},} &{} \quad {\text {if }} i=j, \\ 0, &{}\quad {\text {otherwise}},\end{array}\right. } \end{aligned}$$

where k is an arbitrary integer satisfying \(0 \leqslant k<n\).

Theorem 2

For any integers r and k satisfying \(r < 0\) and \(k \geqslant 0\), and the generalized conditional sequence \(\left\{ W_{n}^{(s,t)}\right\} _{n \in N}\) with \(W_{k+1}^{(s,t)} \ne 0\), the Moore–Penrose inverse of the matrix \(\mathscr {W}_n^{(r, k)}\) is given by the following block matrix form

$$\begin{aligned} \left( \mathscr {W}_n^{(r, k)} \right) ^{\dagger }&= \left[ \begin{array}{c|c} \mathscr {O}_{(n+r) \times (-r)} &{} \left( \mathscr {W}_{n+r}^{(k)}\right) ^{-1}\\ \hline \mathscr {O}_{(-r) \times (-r)} &{} \mathscr {O}_{(-r) \times (n+r)} \end{array}\right] . \end{aligned}$$

Proof

As the blocks are null or invertible, by virtue of the Lemma 2, the proof is obvious so we omit it. \(\square \)

Example 3

The Moore–Penrose inverse of the \(5 \times 5\) generalized conditional matrix for \((r,k) = (-2,2)\) is equal to

$$\begin{aligned} \left( \mathscr {W}_5^{(-2, 2)}\right) ^{\dagger }&= \left[ \begin{array}{c|c} \mathscr {O}_{3 \times 2} &{} \left( \mathscr {W}_{3}^{(2)} \right) ^{-1} \\ \hline \mathscr {O}_{2 \times 2} &{} \mathscr {O}_{2 \times 3} \end{array}\right] \\&= \left[ \begin{array}{cc|ccc} 0 &{} 0 &{} \frac{1}{a b t+b c s+c t} &{} 0 &{} 0 \\ 0 &{} 0 &{} -\frac{\sqrt{b} (c s (a b+c)+a t (a b+2 c))}{\sqrt{a} (a b t+b c s+c t)^2} &{} \frac{1}{a b t+b c s+c t} &{} 0 \\ 0 &{} 0 &{} \frac{c^3 \left( b s (a t+c s)-a t^2\right) }{a (a b t+b c s+c t)^3} &{} -\frac{\sqrt{b} (c s (a b+c)+a t (a b+2 c))}{\sqrt{a} (a b t+b c s+c t)^2} &{} \frac{1}{a b t+b c s+c t} \\ \hline 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ \end{array}\right] . \end{aligned}$$

If we take \(a=b=A\), \(c=B\), \(s=a\) and \(t=b\) in Theorem 2, we obtain the Moore–Penrose inverse of the matrix \(\mathscr {U}_{n}^{(s,k)}\) whose elements are the classical Horadam numbers.

Corollary 2

[29] Let \(s<0, k \geqslant 0\) be arbitrary integers, and \(\left\{ U_n^{(a, b)}\right\} _{n \in N}\) be the Horadam sequence satisfying \(U_{k+1}^{(a, b)} \ne 0\). Then the Moore–Penrose inverse of the matrix \(\mathscr {U}_n^{(s, k)}\) is the \(n \times n\) block matrix \(\mathscr {Q}_n\) given by

$$\begin{aligned} \mathscr {Q}_n=\left( \begin{array}{cc} \mathscr {O}_{(n+s) \times (-s)} &{}\quad \mathscr {R}_{n+s} \\ \mathscr {O}_{(-s) \times (-s)} &{}\quad \mathscr {O}_{(-s) \times (n+s)} \end{array}\right) , \end{aligned}$$

where \(\mathscr {R}_{n+s}=\left[ r_{i, j}\right] \) is an \((n+s) \times (n+s)\) matrix given by

$$\begin{aligned} r_{i, j}= {\left\{ \begin{array}{ll}\frac{(-1)^k B^{k+1}\left( a^2 B+a b A-b^2\right) }{\left( U_{k+1}^{(a, b)}\right) ^3}\left( \frac{-B U_k^{(a, b)}}{U_{k+1}^{(a, b)}}\right) ^{i-j-2} &{}\quad {\text {if }} i>j+1, \\ -\frac{U_{k+2}^{(a, b)}}{\left( U_{k+1}^{(a, b)}\right) ^2}, &{} \quad {\text {if }} i=j+1, \\ \frac{1}{U_{k+1}^{(a,b)},} &{}\quad {\text {if }} i=j, \\ 0, &{} {\text {otherwise.}}\end{array}\right. } \end{aligned}$$

3 Conclusion and discussions

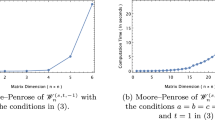
The topic of generalized inverses has become one of the most important and the most interesting research fields of applied and computational mathematics in recent years. One of the most important inversion method is the Moore–Penrose inverse, which has been actively studied by researchers for years [4, 5, 7, 8, 10, 11, 13, 14, 28, 29, 31]. Although there are many methods for calculating the Moore–Penrose inverse, it is commonly used for Singular Value Decomposition (SVD) when performing computations. Despite this method is robust, it cannot compute the results faster when the matrix size is large. In this paper, we obtain the Moore–Penrose inverse of a singular matrix whose elements are the generalized conditional sequence by using convolution formula. Since the results are obtained with analytical methods, it reduces the computational costs compared to other methods. Moreover, we give some important identities in order to find the Moore–Penrose inverse of the matrix \(\mathscr {W}_n^{(r, k)}\). For special values of a, b, c, s and t, our results can be reduced into the works [29, 31]. Thus we provide more general results compared to the previous studies. To sum up, the results we have presented have eliminated the difficulties in computation of the Moore–Penrose inverse of the singular matrices.