Skip to main content

Advertisement

SpringerLink
Log in

Fractional optimal control of an HIV/AIDS epidemic model with random testing and contact tracing

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

Abstract

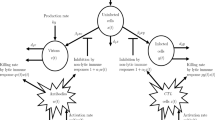
In this paper, we present a fractional model for transmission dynamics of HIV/AIDS with random testing and contact tracing and incorporate into the model the control parameters of condom use and antiretroviral therapy (ART) aimed at controlling the spread of HIV/AIDS epidemic. The stability of equilibria of the model is discussed using the stability theorem and using the fractional La-Salle invariance principle for fractional differential equations. The effect of the fractional derivative order \(\alpha \) (\( 0.6\le \alpha <1 \)) on the HIV/AIDS epidemic model is investigated. The numerical results show that the derivative order \(\alpha \) can play the role of precautionary measures against infection transmission, treatment of infection and delay in accepting HIV test. We give a general formulation for a fractional optimal control problem, in which the state and co-state equations are given in terms of the left fractional derivatives. We develop the Forward–Backward sweep method using the Adams-type predictor–corrector method to solve the fractional optimal control of the model. The results show that implementing the ART treatment control of diagnosed HIV-infected people together with contact tracing results in a significant decrease in the number of undiagnosed HIV-infected population and AIDS people. Also, implementing all the control efforts decreases significantly the number of diagnosed and undiagnosed HIV-infected population and AIDS people. In addition, the values of the controls are reduced when the fractional derivative order \(\alpha \) limits to 1 (\( 0< \alpha < 1\)).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Anderson, R.M., Medly, G.F., May, R.M., Johnson, A.M.: A preliminary study of the transmission dynamics of the human immunodeficiency virus (HIV), the causative agent of AIDS. IMA J. Math. Appl. Med. Biol. 3, 229–263 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  2. Egonmwan, A.O., Okuonghae, D.: Analysis of a mathematical model for tuberculosis with diagnosis. J. Appl. Math. Comput. (2018). https://doi.org/10.1007/s12190-018-1172-1

  3. Pitchaimani, M., Monica, C.: Global stability analysis of HIV-1 infection model with three time delays. J. Appl. Math. Comput. 48(1–2), 293–319 (2015). https://doi.org/10.1007/s12190-014-0803-4

    Article  MathSciNet  MATH  Google Scholar 

  4. Guihua, L., Zhen, J.: Global stability of a SEIR epidemic model with infectious force in latent, infected and immune period. Chaos Soliton Fractals 25(5), 1177–1184 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  5. Tripathi, A., Naresh, R., Sharma, D.: Modelling the effect of screening of unaware infectives on the spread of HIV infection. Appl. Math. Comput. 184, 1053–1068 (2007)

    MathSciNet  MATH  Google Scholar 

  6. Mukandavire, Z., Gumel, A.B., Garira, W., Tchuenche, J.M.: Mathematical analysis of a model for HIV-malaria co-infection. Math. Biosci. Eng. 6, 333–362 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  7. Hernandez-Vargasa, E.A., Middleton, R.H.: Modeling the three stages in HIV infection. J. Theor. Biol. 320, 33–40 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Mastroberardino, A., Cheng, Y., Abdelrazec, A., Liu, H.: Mathematical modeling of the HIV/AIDS epidemic in Cuba. Int. J. Biomath. 08, 1550047 (2015). https://doi.org/10.1142/S1793524515500473

    Article  MathSciNet  MATH  Google Scholar 

  9. Jabbari, A., kheiri, H., Jodayree Akbarfam, A., Bekir, A.: Dynamical analysis of the avian–human influenza epidemic model using multistage analytical method. Int. J. Biomath. 09, 1650090 (2016). https://doi.org/10.1142/S179352451650090X

    Article  MathSciNet  MATH  Google Scholar 

  10. Mojaver, A., Kheiri, H.: Dynamical analysis of a class of hepatitis C virus infection models with application of optimal control. Int. J. Biomath. 09, 1650038 (2016). https://doi.org/10.1142/S1793524516500388

    Article  MathSciNet  MATH  Google Scholar 

  11. Karrakchou, J., Rachik, M., Gourari, S.: Optimal control and infectiology: application to an HIV/AIDS model. Appl. Math. Comput. 177, 807–818 (2006)

    MathSciNet  MATH  Google Scholar 

  12. Adams, B.M., Banks, H.T., Kwon Hee-Dae, T.T., Hien, T.: Dynamic multidrug therapies for HIV: optimal and STI control approaches. Math. Biosci. Eng. 1, 223–241 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Das, A., Pal, M.: A mathematical study of an imprecise SIR epidemic model with treatment control. J. Appl. Math. Comput. 56(1–2), 477–500 (2018). https://doi.org/10.1007/s12190-017-1083-6

    Article  MathSciNet  MATH  Google Scholar 

  14. Mukandavire, Z., Garira, W., Tchuenche, J.M.: Modelling effects of public health educational campaigns on HIV/AIDS transmission dynamics. Appl. Math. Model. 33, 2084–2095 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  15. Yang, J.Y., Chen, Y., Zhang, F.Q.: Stability analysis and optimal control of a hand-foot-mouth disease (HFMD) model. J. Appl. Math. Comput. 41(1–2), 99–117 (2013). https://doi.org/10.1007/s12190-012-0597-1

    Article  MathSciNet  MATH  Google Scholar 

  16. Okosun, K.O., Makinde, O.D., Takaidza, I.: Impact of optimal control on the treatment of HIV/AIDS and screening of unaware infectives. Appl. Math. Model. 37, 3802–3820 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  17. Mwanga, G.G., Aly, S., Haario, H., Nannyonga, B.K.: Optimal control of malaria model with drug resistance in presence of parameter uncertainty. App. Math. Sci. 8, 2701–2730 (2014)

    Google Scholar 

  18. Choi, S., Jung, E., Lee, S.M.: Optimal intervention strategy for prevention tuberculosis using a smoking tuberculosis model. J. Theor. Biol. 380, 256–270 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  19. Okyere, E., Oduro, F.T., Amponsah, S.K., Dontwi, I.K.: Fractional order optimal control model for malaria infection (2016). arXiv preprint arXiv:1607.01612

  20. Vitanov, N.K., Ausloos, M.R.: Knowledge epidemics and population dynamics models for describing idea diffusion. In: Scharnhorst, A., Boerner, K., van den Besselaar, P. (eds.) Models of Science Dynamics: Encounters Between Complexity Theory and Information Sciences, pp. 69–125. Springer, Berlin (2012). (Ch. 3)

    Chapter  Google Scholar 

  21. Saeedian, M., Khalighi, M., Azimi Tafreshi, N., Jafari, G.R., Ausloos, M.: Memory effects on epidemic evolution: the susceptible infected recovered epidemic model. Phys. Rev. E 95(2), 022409 (2017)

    Article  MathSciNet  Google Scholar 

  22. Okyere, E., Oduro, F.T., Amponsah, S.K., Dontwi, I.K., Frempong, N.K.: Fractional order SIR model with constant population. Br. J. Math. Comput. Sci. 14(2), 1–12 (2016)

    Article  Google Scholar 

  23. Sun, H.G., Chen, W., Wei, H., chen, Y.Q.: A comparative study of constant-order and variable-order fractional models in characterizing memory property of systems. Eur. Phys. J. Spec. Top. 193(1), 185–192 (2011)

    Article  Google Scholar 

  24. Petras, I.: Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation. Springer, Berlin (2011)

    Book  MATH  Google Scholar 

  25. Podlubny, I.: Fractional Differential Equations, Mathematics in Science and Engineering. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  26. Rihan, F.A.: Numerical modeling of fractional-order biological systems. Abstr. Appl. Anal. 2013, Article ID 816803 (2013)

  27. Sun, H.G., chen, Y.Q., Chen, W.: Random-order fractional differential equation models. Signal Process. 91(3), 525–530 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  28. Chen, W., Liang, Y.: New methodologies in fractional and fractal derivatives modeling. Chaos Solitons Fractals 102, 72–77 (2017)

    Article  MathSciNet  Google Scholar 

  29. Pinto, C.M.A., Carvalho, A.R.M.: New findings on the dynamics of hiv and tb coinfection modelsl. Appl. Math. Comput. 242, 36–46 (2014)

    MathSciNet  MATH  Google Scholar 

  30. Ahmed, E., El-Saka, H.A.: On fractional order models for hepatitis C. Nonlinear Biomed. Phys. 4, 1–3 (2010)

    Article  Google Scholar 

  31. Ding, Y., Ye, H.: A fractional-order differential equation model of HIV infection of CD4+ T-cells. Math. Comput. Model. 50, 386–392 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  32. Kheiri, H., Jafari, M.: Stability analysis of a fractional order model for the HIV/AIDS epidemic in a patchy environment. J. Comput. Appl. Math. 346, 323–339 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  33. Singh, J., Kumar, D., Hammouch, Z., Atangana, A.: A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 316, 504–515 (2018)

    MathSciNet  MATH  Google Scholar 

  34. Singh, J., Kumar, D., Baleanu, D., Rathore, S.: An efficient numerical algorithm for the fractional Drinfeld–Sokolov–Wilson equation. Appl. Math. Comput. 335, 12–24 (2018)

    MathSciNet  Google Scholar 

  35. Singh, J., Kumar, D., Baleanu, D.: A new analysis of Fornberg-Whitham equation pertaining to a fractional derivative with Mittag–Leffler type kernel. Eur. Phys. J. Plus 133, 70 (2018). https://doi.org/10.1140/epjp/i2018-11934-y

    Article  Google Scholar 

  36. Singh, J., Kumar, D., Baleanu, D.: On the analysis of chemical kinetics system pertaining to a fractional derivative with Mittag–Leffler-type kernel. Chaos 27, 103113 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  37. He, s, Banerjee, S.: Epidemic outbreaks and its control using a fractional order model with seasonality and stochastic infection. Physica A 501, 408–417 (2018)

    Article  MathSciNet  Google Scholar 

  38. Hsieh, Y.H., de Arazoza, H., Lounes, R., Joanes, J.: A class of methods for HIV contact tracing in Cuba: implications for intervention and treatment. Determ. Stoch. Models AIDS Epidemics HIV Infect. Interv. (2005). https://doi.org/10.1142/9789812569264-0004

  39. Agrawal, O.P.: A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 38, 323–337 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  40. Agrawal, O.P.: A quadratic numerical scheme for fractional optimal control problems. J. Dyn. Syst. Meas. Control 130, 011010-1–011010-6 (2008)

    Article  Google Scholar 

  41. Basir, F.A., Elaiw, A.M., Kesh, D., Roy, P.K.: Optimal control of a fractional-order enzyme kinetic model. Control Cybern. 44, 1–18 (2015)

    MathSciNet  MATH  Google Scholar 

  42. Sweilam, N.H., Al-Mekhla, S.M.: On the optimal control for fractional multi-strain TB model. Optim. Control Appl. Methods (2016). https://doi.org/10.1002/oca.2247

  43. Ding, Y., Wang, Z., Ye, H.: Optimal control of a fractional-order HIV-immune system with memory. IEEE Trans. Control Syst. Technol. 13, 763–769 (2012)

    Article  Google Scholar 

  44. Lenhart, S., Workman, T.: Optimal Control Applied to Biological Models. Chapman and Hall, New York (2007)

    MATH  Google Scholar 

  45. McAsey, M., Mou, L., Han, H.: Convergence of the forward–backward sweep method in optimal control. Comput. Optim. Appl. 53, 207–226 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  46. Diethelm, K., Ford, N.J., Freed, A.D.: A predictor–corrector approach for the numerical solution differential equations. Nonlinear Dyn. 29, 3–22 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  47. Diethelm, K., Ford, N.J., Freed, A.D.: Detailed error analysis for a fractional Adams method. Nonlinear Dyn. 35, 31–52 (2004)

    MathSciNet  MATH  Google Scholar 

  48. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Application of Fractional Differential Equations. Elsevier, New York (2006)

    MATH  Google Scholar 

  49. Samko, S.G., Kilbas, A.A., Marichev, O.I.: Fractional Integrals and Derivatives-Theory and Applications. Gordon and Breach, Linghorne (1993)

    MATH  Google Scholar 

  50. Diethelm, K.: The Analysis of Fractional Differential Equations, An Application-Oriented Exposition Using Operators of Caputo Type. Springer, Berlin (2004)

    MATH  Google Scholar 

  51. Gorry, C.: Cuba’s HIV/AIDS Strategy: An Integrated, Rights-Based Approach. Oxfam International, Havana (2008)

    Google Scholar 

  52. Odibat, Z.M., Shawagfeh, N.T.: Generalized Taylors formula. Appl. Math. Comput. 186, 286–293 (2007)

    MathSciNet  MATH  Google Scholar 

  53. Lin, W.: Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 332, 709–726 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  54. van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshhold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180, 29–48 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  55. Li, C., Ma, Y.: Fractional dynamical systemand its linearization theorem. Nonlinear Dyn. 71, 621–633 (2013)

    Article  MATH  Google Scholar 

  56. Mishina, A.M., Proskuryako, I.V.: Higher Algebra. Nauka, Moscow (1965)

    Google Scholar 

  57. Huo, J., Zhao, H., Zhu, L.: The effect of vaccines on backward bifurcation in a fractional order HIV model. Nonlinear Anal. RWA 26, 289–305 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  58. Aguila-Camacho, N., Duarte-Mermoud, M.A., Gallegos, J.A.: Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 19(9), 2951–2957 (2014)

    Article  MathSciNet  Google Scholar 

  59. Agrawal, O.P.: General formulation for the numerical solution of optimal control problems. Int. J. Control 50, 627–638 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  60. Meiberg, A.E., Bos, A.E.R., Onya, H.E., Schaalma, H.P.: Fear of stigmatization as barrier to voluntary HIV counselling and testing in South Africa. East Afr. J. Public Health 5(2), 49–54 (2008)

    Google Scholar 

  61. Rapatski, B., Klepac, P., Duecks, S., Liu, M., Weiss, L.I.: Mathematical epidemiology of HIV/AIDS in Cuba during the period 1986–2000. Math. Biosci. Eng. 3, 545–556 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  62. Mastroberardino, T.: Mathematical Modeling of the HIV/AIDS Epidemic in Cuba. AMS Eastern Sectional Meeting University of Maryland, Baltimore County (2014)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Mathematical Sciences, University of Tabriz, Tabriz, Iran

    H. Kheiri & M. Jafari

Authors
  1. H. Kheiri
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Jafari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. Kheiri.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kheiri, H., Jafari, M. Fractional optimal control of an HIV/AIDS epidemic model with random testing and contact tracing. J. Appl. Math. Comput. 60, 387–411 (2019). https://doi.org/10.1007/s12190-018-01219-w

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-018-01219-w

Keywords

Mathematics Subject Classification

Search

Navigation