1 Introduction

Unconventional oil and gas resources, such as tight gas, tight oil and shale oil, have been successfully developed commercially in the USA, Canada, Australia and some other countries. The production of tight oil soared from 30 million tons in 2011 to 96.9 million tons in 2012 in the USA by using new unconventional technologies (Du et al. 2014). In China, the Ordos Basin, the Junggar Basin, the Songliao Basin, the Sichuan Basin, the Qaidam Basin, etc., have abundant tight-oil resources with an output of 97 million tons, accounting for 22% of the nationwide total oil output (Jia et al. 2014). In the Ordos Basin, the tight-oil reservoirs in the Triassic Yanchang Formation have become a major target of petroleum exploration and development in recent years (e.g., Guo et al. 2012; Yao et al. 2013).

Since tight-oil reservoirs in the Ordos Basin are of low-permeability (<2 × 10−3 μm2) and low-porosity (<10%) overall, fracturing is crucial for the reservoir reconstruction, even though the reservoirs are formed with complicated mechanisms (e.g., Yao et al. 2013; Ezulike and Dehghanpour 2014). Therefore, it is important to predict the natural fracture distribution in reservoirs, including their orientation and density, for future exploration and development (e.g., Smart et al. 2009). Previous studies have focused on the geometrical or kinematic models, such as analyses of seismic techniques or of the layer curvature (e.g., Zahm et al. 2010; Pearce et al. 2011; Tong and Yin 2011), and fracture prediction in the Ordos Basin has also been involved in some papers (e.g., Ju et al. 2014a). However, since earlier fracture prediction was mainly carried out through layer curvature or two-dimensional (2D) models, which cannot meet the demands for the tight-oil study and exploration, it is necessary to build three-dimensional (3D) mechanical models in order to achieve the accuracy needed for further research on the unconventional petroleum.

Various factors, such as the proximity of faults, the curvature of folds, the layer thickness and the lithology, are deemed to control the fracture development in tight reservoirs (e.g., Ju et al. 2013), and the anisotropy or heterogeneity should also be considered in the modeling (e.g., Glukhmanchuk and Vasilevskiy 2013). However, it is difficult for 2D geomechanical models to fully consider all these factors, and the modeling results cannot be used successfully for exploration and production. Therefore, 3D models will be utilized in this paper, which take the lithology, the thickness and the stress fields into consideration.

The study area in this paper, namely the Longdong area, is located in the southern Ordos Basin, where research on structural fractures in the tight reservoirs is still deficient (e.g., Ren et al. 2014; Li et al. 2015). The structural fractures in the Longdong area were mainly formed after the Late Triassic, as a result of multiple-stage tectonic events in the Late Mesozoic and the Cenozoic. These extensively developed fractures are mostly unfilled and effective, which noticeably improve the permeability of tight reservoirs in the Ordos Basin.

2 Geological background

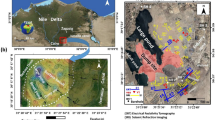
The Ordos Basin, covering an area of 2.6 × 105 km2, is a large N–S trending basin in the western North China Craton, which is located between the Siberian Craton and the South China Craton (Hou et al. 2010) (Fig. 1). Three orogenic belts have been developed along different boundaries of the stable basin, including the Yinshan Mountain in the north, the Qinling Orogen in the south and the Liupanshan Mountain in the southwest (e.g., Nutman et al. 2011) (Fig. 2). The basement of the basin is composed of Archean rocks with Proterozoic sedimentary cover. Although the margin underwent multiple tectonic activities, the central part is still stable and is covered by shallow Paleozoic marine carbonate sediment (Kusky and Li 2009). Some small-scale paleo-faults exist, but no large faults have been found within the basin (Wan and Zeng 2002; Yang et al. 2013).

Fig. 1
figure 1

A geological summary of the Ordos Basin. a Tectonic framework of the major cratonic blocks in China (after Kusky 2011 and Santosh et al. 2012); b generalized geological and tectonic map of the North China Craton (after Zhao et al. 2005). TC Tarim Craton, NCC North China Craton, SCC South China Craton, YB Yangtze Block, CB Cathaysia Block, WB Western Block, EB Eastern Block

Full size image
Fig. 2
figure 2

Tectonic framework of the Ordos Basin. The orange area denotes the Ordos Basin, and the light yellow ones denote the adjacent blocks. The light gray areas represent the graben system along the margins, and the dark gray ones represent the orogenic belts around the basin. The black frame denotes the study area (the Longdong area) (after Darby and Ritts 2002) (1 Boundary of orogenic belt, 2 Fault, 3 Normal fault, 4 Reversed fault, 5 Strike-slip fault, 6 Fold, 7 River, 8 City)

Full size image

Contrary to the evolution of the eastern North China Craton including thickening, thinning and destruction, the Ordos Basin has evolved from three Mesoproterozoic aulacogens to a Paleozoic–Mesozoic cratonic basin since the Middle Proterozoic (Menzies et al. 2007; Yang et al. 2013; Wang et al. 2014b). The interior part of the basin is characterized by horizontal or gently dipping strata (<3°), especially for the Mesozoic and Cenozoic strata, whereas the strata along the margins have been subjected to significant folding and faulting since the Late Triassic.

Two distinct tectonic events took place from the Late Mesozoic to the Cenozoic, resulting in two different stress fields in these periods. In the Late Mesozoic, namely from the Early Jurassic to the Late Cretaceous, the long-distance effect of subduction of the Izanagi Plate turned from north-northwestward to northwestward when the force arrived at the Ordos Basin, resulting in the WNW-trending stress fields and the structural fractures in NW–EW trends (e.g., Wan 1994; Hou et al. 2010; Sun et al. 2014; Zhao et al. 2016); while in the Cenozoic, the predominant tectonic event became the northeastward collision between the Indian and the Eurasian Plate, which led to the NE-trending stress fields and the structural fractures in NNE–ENE trends (e.g., Yuan et al. 2007; Wang et al. 2014b). Two episodes of fractures are developed under distinct tectonic events, so the stress fields of different periods should be taken into consideration during the fracture prediction.

3 Fracture measurement

The parameters of fracture characteristics are important in the exploration and development of fractured tight reservoirs. The fracture density is one of the significant indicators to reflect the failure degree of rocks, which can be divided into three types, including the linear density, the surface density and the bulk density of fractures. In this paper, the surface density is utilized to describe the fracture distribution in the Ordos Basin. The surface density is defined as the ratio between the cumulative fracture length and the cross-sectional area of the matrix, which can better reflect the degrees of fracture development and be measured more effectively than others (Golf-Racht 1982). The fracture density from core observations can be calculated as:

$$f = \frac{{\sum {l_{i} } }}{S} = \frac{{\sum {l_{i} } }}{{2\pi r^{2} + 2\pi r \times L}}$$
(1)

where f is the fracture surface density, l i is the length of each structural fracture, S is the surface area of the observed core, r is the radius and L is the length of the core.

In this paper, the Longdong area was selected as the study area to carry out fracture measurements (Fig. 2). Sixty-six wells were chosen to study the distribution of structural fractures in the Chang 71 and 72 members (Fig. 3). As shown in Fig. 4, the fracture density in the tight-sandstone cores is relatively low (smaller than 0.5 m−1), representing the general condition in the Longdong area. The fracture density of the Chang 72 member is more concentrative than that of Chang 71 member, even though their average densities are similar in general (0.071 m−1 for the Chang 71 member and 0.081 m−1 for the Chang 72 member). The difference of fracture distribution between the Chang 71 and 72 members is obvious: The highest fracture density in the Chang 71 member lies in the Laocheng and Qingyang areas, while that in the Chang 72 member lies in the Laocheng, the Qingyang and the Zhengning areas (Fig. 4).

Fig. 3
figure 3

Synthetical stratigraphic column and depositional environment of the Upper Triassic—Middle Jurassic in the Ordos Basin (after Duan et al. 2008)

Full size image
Fig. 4
figure 4

Distribution of the measured fracture density and the sandstone thickness in a the Chang 71 and b Chang 72 members in the Longdong area. The black solid dots denote the observed wells, while the hollow dots denote the cities. Measured fracture densities in the Chang 71 and 72 members are marked with red cylinders, and the contours represent the sandstone thickness in the study area

Full size image

4 Modeling approach

Methods such as geological analysis, physical modeling and numerical simulation including the finite element method (FEM) can be applied in the study of stress fields, which is the foundation of fracture prediction. In this study, the finite element software ANSYS is used to calculate the stress field and predict the fracture distribution (Velázquez et al. 2009; Jarosinski et al. 2011). The basic concept of FEM is that a geological body can be discretized into finite continuous elements connected by nodes. The geometrical and mechanical parameters allocated on each element are consistent with the properties of real rocks. The continuous field function of the geological area is first transformed into linear functions at every node that contain displacement, stress and strain variables resulting from the applied forces (Jiu et al. 2013), and then all these elements are used to obtain the stress distribution over the entire area.

4.1 Geometrical model

The Ordos Basin is a near-rectangular basin in the western part of the North China Craton (Li and Li 2008; Tang et al. 2012) (Fig. 2). Although the Ordos Basin underwent multi-stage tectonic movements in the Late Mesozoic–Cenozoic eras, the deformation was confined to the western margin and no significant tectonic events occurred in the central part. Therefore, the outline of the basin remained unchanged in these periods (Sun et al. 2014) (Fig. 5a). Since no large faults or folds have been recorded inside the Ordos Basin, the sedimentary facies, the lithology and the distribution of sand bodies are the key factors to determine the fracture development.

Fig. 5
figure 5

Simplified geometrical model of the Longdong area (b) and its nested model (a) in the Ordos Basin

Full size image

In this paper, the Chang 71 and 72 members in the Triassic Yanchang Formation, the major tight-oil members in the Ordos Basin, are selected as the study strata, and the Longdong area is chosen to discuss the stress fields and the fracture distribution (Figs. 2, 3, 5). Since the Yanchang Formation is characterized by strong heterogeneity with facies change, the simplified model with only one rock mechanical property is no longer suitable for the complex interior of the Ordos Basin (Yang and Deng 2013). Based on the sandstone-mudstone ratio, it is assumed that the ratios between the sandstone and mudstone layers are 0.43–4.26 (average 1.27) in the Chang 71 member and 0.54–9.00 (average 1.70) in the Chang 72 member (e.g., Guo et al. 2012; Li et al. 2015), and multiple-layer constructions (four sandstone layers in Chang 71 member and three sandstone layers in Chang 72 member) are applied in the geometrical model to simulate the sandstone-mudstone interlayers (Fig. 5). To avoid the boundary effect, forces in the models are set on the boundaries of the Ordos Basin, and the study area is nested inside the basin (Fig. 5). The sandstone layers, which are also the main layers in fracture development, in the middle of each member, are selected to display the modeling results in the following text, representing the general situation of fracture development in the Chang 71 and 72 members.

4.2 Boundary conditions and modeling

In order to predict the fracture distribution of the Ordos Basin, it is assumed that the upper crustal thickness of the basin in the Late Mesozoic–Cenozoic era is 25 km (e.g., Liu et al. 2006). The top of the model is set as a free surface, and the entire model is subjected to gravity load. The average density of the upper crust, which mainly consists of sedimentary cover, greenschist and granite, is 2750 kg/m3 (Hou et al. 2010; Wang et al. 2014b). Based on the velocities of P and S waves, the calculated average Poisson’s ratio is 0.20 and the average Young’s modulus is 80 GPa for the whole basin (Liu et al. 2006).

To subtly depict the distribution of structural fractures in the Longdong area, four more kinds of material elements are involved in the 3D geometrical model, including the sandstones/mudstones of the Chang 71 member and the sandstones/mudstones of the Chang 72 member. Tri-axial rock mechanical experiments were carried out by the Institute of Acoustics, Chinese Academy of Sciences, on 62 core samples collected from observed wells in the Longdong area (Fig. 4). In order to simulate the real conditions underground, in these experiments, confining pressures corresponding to the original depth of the Yanchang Formation are applied in the radial directions, and vertical pressures are applied in the axial directions of all samples. Through statistical analysis and geological classification, five sets of rock mechanical properties, the average density, Young’s modulus, Poisson’s ratio, internal friction angle and cohesion, are listed in Table 1 by layer and lithology.

Table 1 Rock mechanical parameters for the numerical modeling of the Chang 71 and 72 members in the Longdong area
Full size table

Because the stress fields in the Late Mesozoic and the Cenozoic are strikingly different and both of them had a significant effect on the fracture development in the Ordos Basin, the boundary conditions during these two episodes along the basin need to be defined (Zhao et al. 2016).

As a result of intense compression from the Early Jurassic to the Middle Cretaceous, the Yinshan Orogen Belt was developed as thrust faults with dextral shearing features in the Late Mesozoic (Darby and Ritts 2002; Zhang et al. 2007; Faure et al. 2012). A uniform direction and a constant magnitude of a 40 MPa normal component with a 10 MPa dextral shearing component are applied along the northern side of the Ordos Basin (L1) (Fig. 6a). The east-dipping thrusts, the NWW-dipping back-thrusts and the associated folds developed along the Lüliang Mountain in the Jurassic show that the stress regime in the eastern margin was related to the long-distance effect of the push from the northwestward subduction of the Izanagi Plate in the Late Mesozoic (Zhang et al. 2007; Hou and Hari 2014). Hence, it is a compressive boundary with a sinistral shearing component along the eastern edge of the basin. A deviatoric stress of an approximately 150 MPa normal component with a 45 MPa shearing component is set along the eastern boundary (L2) (Fig. 6a). Based on the paleo-magnetic constraints, geological evidence and 40Ar/39Ar and U–Pb dating, it can be assumed that in the southern part of the Ordos Basin, the Qinling Ocean finally closed during the Late Jurassic-Early Cretaceous period. This indicates that the collision between the North China Craton and the South China Craton continued up to the Cretaceous period (Huang et al. 2005; Liu et al. 2015). And due to this collision, thrust faults with sinistral strike-slip features were developed along the northern margin of the Qinling Orogen Belt (Malaspina et al. 2006; Yuan et al. 2007). Therefore, a constant magnitude of normal stress (60 MPa) with sinistral shearing stress (30 MPa) is applied along the southern margin of the basin (L3) (Fig. 6a). In the western and southern margins, the long-distance effect of collision from the Qiangtang Massif affected the Ordos Basin (Zhang et al. 2007; Li and Li 2008), so a compressive traction with a uniform direction and a constant magnitude of deviatoric stress of 30 MPa on the southwestern boundary (L4) and 75 MPa on the western boundary (L5) are applied along the basin (Fig. 6a). On the basis of SHRIMP zircon U–Pb ages and other geochronological data, it can be presumed that the closure of the Paleo-Asian Ocean finally took place after the Early Permian. Due to this episode of closure, the northward movement of the Alashan Block (Fig. 2) was arrested by the Siberian Craton in the Late Mesozoic (e.g., Zheng et al. 2014). The final closure of the Qilian Ocean took place at the end of the Ordovician, and after that, the Qaidam Block, which was adjacent to the Alashan Block, restricted the southward movement of the Alashan Block (Song et al. 2013). The nonidentical apparent polar wandering paths of the Tarim Block and the Alashan Block up to the Jurassic period clearly indicates that the amalgamation of these two blocks might have occurred during the Jurassic (Gilder et al. 2008). As a result of amalgamation in the Jurassic, the wedge-shaped Alashan Block was trapped between the Siberian Plate, the Qaidam Block, the Tarim Block and the Ordos Block (Zhang et al. 2007). Therefore, the northwestern boundary (L6) is kept fixed as the Alashan Block was locked by the adjacent blocks in the Late Mesozoic (Fig. 6a).

Fig. 6
figure 6

Boundary conditions of the Ordos Basin in a the Late Mesozoic and b the Cenozoic eras. Arrows indicate the tectonic forces and the length represents the stress magnitude. The crosses represent the fixed boundaries in different models

Full size image

The stress field in the Cenozoic era, which is regarded as a consequence of the Indo-Asian collision, is strikingly different from that in the Late Mesozoic era (e.g., Darby and Ritts 2002; Bao et al. 2013) (Fig. 6b). During the Cenozoic, the extension along the margins of the Ordos Basin triggered the formation of the Hetao, the Weibei and the Yinchuan Grabens, which in turn transposed reverse faults to normal faults in the Helan Mountain and the Qinling Mountain (Rao et al. 2014). Therefore, a tensile traction with a uniform direction and a constant magnitude of 5 MPa is applied on the northern, the southern and the northwestern margins, respectively (L7, L9 and L12) (Fig. 6b). The subduction of northwestern Pacific Plate restricted the further eastward movement of the Ordos Basin (Fournier et al. 2004; Schellart and Lister 2005). The current GPS horizontal velocity field map shows that the eastward velocity of the Shanxi Block (Fig. 2) is relatively smaller than that of the Ordos Basin (e.g., Zhu and Shi 2011; Wang et al. 2014c). The velocity differences between the Shanxi Block and the Ordos Basin suggest that the northeastward motion of the Ordos Basin, which was pushed by the Tibet Plateau, was restricted by the Shanxi Block due to the westward subduction of the Pacific Plate in the Cenozoic (Hou et al. 2010). Accordingly, the eastern edge of the basin is kept fixed for the Cenozoic era (L8) (Fig. 6b). On the basis of massive fault-striation data, it can be interpreted that the southern margin, namely the Weihe Graben, turned into a sinistral shearing tensile boundary (e.g., Mercier et al. 2013; Rao et al. 2014), and hence, a constant left-lateral shearing stress of 30 MPa is set on the southeastern border of the basin (L9) (Fig. 6b).

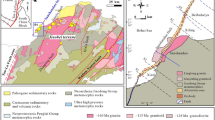
Due to the impact of collision between the Indian Plate and the Eurasian Plate, the Liupanshan Thrust-Fold Belt (namely the Liupan Mountain in Fig. 2) was developed along the southwestern margin of the Ordos Basin, which resulted in the transformation of the west-southwestern margin into a strongly compressive boundary during the Cenozoic era (Yuan et al. 2007; Li and Li 2008). When the western boundary of the basin is taken into consideration, as the shortening rate of the northern section (Tianshuibao Profile: 30.4%–50.6%) is greater than that of the southern one (Pengyang Profile: 12.9%–17.9%) (Feng et al. 2013) (Table 2; Fig. 7), a compressive traction with a uniform direction and a gradient magnitude from 80 to 55 MPa is applied on the western boundary (L11), whereas a compressive traction with a constant magnitude of 80 MPa is applied on the southwestern margin (L10) (Fig. 6b).

Table 2 Shortening rates of different profiles in the mid-south section of the western margin (L11) in the Ordos Basin
Full size table
Fig. 7
figure 7

Maps of tectonic units, two relevant profiles and their corresponding balanced sections in the mid-south section along the western margin (L11) of the Ordos Basin (1 Western Liupanshan Fault, 2 Eastern Liupanshan Fault, 3 Haiyuan Fault, 4 Qingshuihe Fault, 5 Yantongshan-Yaoshan Fault, 6 Qingtongxia-Guyuan Fault, 7 Hui’anbao-Shajingzi Fault) (modified after Feng et al. 2013). Area: I Tianhuan Depression, II Thrust Belt of Western Margin, III Qilianshan Orogen, IV Alashan Block. Age: O Ordovician, C Carboniferous, P Permian, T Triassic, J Jurassic, K Cretaceous

Full size image

4.3 Theory of fracture prediction

Lagrangian formulations are used in ANSYS to simulate the three-dimensional, plane strain deformation, applying 8-node isotropic elements to represent each lithological layer. The mechanical behavior in the elastic domain is dominated by the generalized Hook’s law. As the Yanchang Formation is generally less than 3000 m in depth where the plastic deformation is not obvious and the structural fractures in the Chang 71 and 72 members are chiefly shearing fractures based on field measurements and core observations (Fig. 8), the mechanical behavior follows the elastic model, which is described by the generalized Hook’s law.

Fig. 8
figure 8

Photographs of structural fractures in outcrops and cores of the Ordos Basin. a Conjugate fractures indicate the maximum principal compressive stress of WNW orientation in the Late Mesozoic; b conjugate fractures indicate the maximum principal compressive stress of NE orientation in the Cenozoic; c near-vertical fracture plane in a core from the Longdong area; and d moderate-dipping fracture plane in a core from the Longdong area

Full size image

Various methods for fracture prediction have been proposed in previous literature, such as the conventional logging method, the stress field method, the principle curvature method, the geostatistical method, etc. (e.g., Savage et al. 2010; Zahm et al. 2010; Jiu et al. 2013). The two-factor method, involving the rupture value and the strain energy density, is used in this paper to predict the distribution of structural fractures in the Ordos Basin (Ding et al. 1998).

4.3.1 Rupture value

Tensile fractures and shearing fractures conform to different criteria. Griffith’s criterion, which is derived from the micro-mechanism, is an effective criterion to predict the development and the distribution of tensile fractures; however, this criterion, which in nature is equivalent with the theory of maximum tensional stress, is only suitable for the tensile fractures (Griffith 1920). Although tensile fractures are found in some areas of the Ordos Basin, they are limited to the contact surfaces of sandstone and mudstone layers, and more than 95% of structural fractures in the Longdong area are shearing fractures, whose rupture is controlled by the Mohr–Coulomb failure criterion (Xie et al. 2008). Therefore, only Mohr–Coulomb failure criterion is taken into consideration in this study, which follows the equation (Coulomb 1776):

$$\left[ \tau \right] = C + \sigma_{n} \times \tan \varphi$$
(2)

where [τ] represents the critical shearing stress, C represents the cohesion, σ n represents the stress normal to the shearing fractures and φ represents the internal friction angle (Table 1). Shearing fracture is triggered once the shearing stress exceeds the critical shearing stress ([τ]) in Eq. (2). σ n can be obtained via the maximum principal stress (σ 1) and the minimum principal stress (σ 3) according to Wang et al. (2004):

$$\sigma_{n} = \left( {\sigma_{1} + \sigma_{3} } \right)/2 - \left( {\sigma_{1} - \sigma_{3} } \right) \times \sin \varphi /2$$
(3)

The shearing stress (τ n ) can also be obtained via the two principal stresses according to Wang et al. (2004):

$$\tau_{n} = \left( {\sigma_{1} - \sigma_{3} } \right) \times \cos \varphi /2$$
(4)

Following the Mohr–Coulomb failure criterion, the rock will break when the shearing stress is equal or greater than the critical shearing stress in Eq. (2), so the rupture value (I) is introduced in order to measure the probability of rock’s rupture according to Ding et al. (1998):

$$I = \tau_{n} /\left[ \tau \right]$$
(5)

The possibility of rock’s failure is very small when the rupture value (I) is far smaller than 1, whereas the possibility is relatively larger when the rupture value (I) exceeds 1. The fracture density (f) and the rupture value (I) may have a positive correlation, so the rupture value (I) is an effective index for fracture prediction through empirical formulas established between them.

4.3.2 Strain energy density

It is generally accepted that the rocks with relatively high strain energy density are more likely to develop structural fractures than those with a lower one. The strain energy density, namely the strain energy per unit volume, is described as follows (Prince and Rhodes 1966):

$$\begin{aligned} U =& \left[ {\sigma_{X}^{2} + \sigma_{Y}^{2} + \sigma_{Z}^{2} - 2v\left( {\sigma_{X} \sigma_{Y} + \sigma_{Y} \sigma_{Z} + \sigma_{Z} \sigma_{X} } \right) }\right. \\&+\left.{ 2\left( {1 + v} \right)\left( {\tau_{XY}^{2} + \tau_{YZ}^{2} + \tau_{ZX}^{2} } \right)} \right]/2E \end{aligned}$$
(6)

where U is the strain energy density, v is Poisson’s ratio, σ X , σ Y and σ Z are the normal stress components in x, y and z directions, respectively, and τ XY , τ YZ and τ ZX are the shearing stress components in the corresponding directions. Strain energy density (U) could be utilized to indicate the fracture distribution.

Rupture value (I) stands for the possibility of rock failure, whereas the strain energy density (U) stands for the developing ability of structural fractures. In this study, syntheses of the rupture value and the strain energy density, namely the two-factor method, are applied, in order to build finite element models for fracture prediction in the Ordos Basin (Ding et al. 1998).

5 Results and analyses

Because the orientation and the distribution of structural fractures are the key elements in fracture prediction, the fracture orientation and the estimated density have been calculated with the finite element modeling and will be compared with the observed data in outcrops and cores. With the two-factor method, modeling results, including the principal compressive stress orientations, the rupture values, the strain energy density and the fracture density, are presented as maps, which can imply the relative degrees of fracture development in the Longdong area.

5.1 Validity of models

Since reliable numerical models are the basis of further study on the fracture prediction in the Longdong area, it is necessary to verify the correctness of the two models proposed in this paper, including the Late Mesozoic and the Cenozoic ones, by comparing the results of finite element modeling with earlier published data.

The calculated displacement directions reveal that the relative rotation directions in these periods are (1) anticlockwise from the Early Jurassic to the Cretaceous and (2) clockwise in the Cenozoic era (Fig. 9). These results are in good agreement with earlier findings (e.g., Pei et al. 2011; Li et al. 2014; Yang et al. 2014).

Fig. 9
figure 9

Displacement fields of the two models for the Ordos Basin in the Late Mesozoic and the Cenozoic eras. Thin black arrows indicate the calculated displacement directions and their lengths indicate the magnitude of displacement. Thick black arrows outside the basin denote the rotation of the basin during these periods. Black crosses represent the fixed boundaries in different models

Full size image

Acoustic Emission (AE) is an important technique in rock mechanics and experimental seismology, which can offer rock mechanical parameters, such as the maximum principal stress magnitudes generated in the geological history. The maximum principal stress magnitudes of the Late Mesozoic era after pore-pressure correction range from 40.0 to 103.9 MPa in the Yanhewan, the Dingbian, the Dongsheng areas, etc. (Fig. 10a). The Cenozoic stress magnitudes remain in a limited range of 22.3–58.5 MPa within the Wuqi-Yanhewan, the Zhenyuan, the Wushengqi areas, etc. (Zhou et al. 2009a, b; Wang et al. 2014a; Zhang et al. 2014) (Fig. 10b). The calculated maximum principal stress magnitudes in the Late Mesozoic and the Cenozoic are in agreement with the range of stress magnitudes measured by AE technology (Fig. 10). The above-mentioned evidence strengthens the validity of our calculated results in the models.

Fig. 10
figure 10

Maximum principal stress distribution of the two models in a the Late Mesozoic and b the Cenozoic eras. Red frames denote the areas where the calculated stress magnitudes match well with the Acoustic Emission paleo-stress magnitudes in earlier literature (Zhou et al. 2009a, b; Wang et al. 2014a; Zhang et al. 2014)

Full size image

In addition, earlier published stress orientation data (Wan 1994; Hou et al. 2010; Sun et al. 2014) are also used as evidence to substantiate our models (Fig. 11a). These stress orientation data suggest that the dominant orientation of maximum principal compressive stress in the Late Mesozoic is WNW. Current stress field data can also be utilized to interpret the Cenozoic stress fields because the basin has been stable during this period (Wang et al. 2008; Xie et al. 2011; Sun et al. 2014; Yang et al. 2014). Based on the borehole collapse and multiple strain analyses in the Yanhewan area, it can be inferred that the dominant orientation of maximum principle compressive stress in the Cenozoic is NE (Zhou et al. 2009a). All these orientations are presented in the stereonets (Fig. 11). The differences between the calculated orientations of maximum compressive stress and the measured ones, including the stress orientations in previous literature (e.g., Wan 1994; Hou et al. 2010; Sun et al. 2014) and the measured data in the present study, are in general less than 5°, proving the reliability of the Late Mesozoic and Cenozoic models (Fig. 11).

Fig. 11
figure 11

Maximum principal compressive stress trajectory maps of the two models for the Ordos Basin in the a Late Mesozoic and b Cenozoic eras. Green and red arrows represent the two major orientations of horizontal maximum principal stress (S Hmax) through conjugate joint measurements. Short black bars indicate the calculated S Hmax, and bars in other colors represent the observed S Hmax in previous literature. 1 Late Mesozoic S Hmax from Wan (1994), 2 Late Mesozoic S Hmax from Hou et al. (2010), 3 Late Mesozoic S Hmax from Sun et al. (2014), 4 Late Mesozoic S Hmax from Zhou et al. (2009b), 5 Late Mesozoic S Hmax deduced from conjugate joints in our field measurements, 6 Cenozoic S Hmax from Wang et al. (2008), 7 Cenozoic S Hmax from Xie et al. (2011), 8 Cenozoic S Hmax from Sun et al. (2014), 9 Cenozoic S Hmax from Yang et al. (2014), 10 Cenozoic S Hmax from Zhou et al. (2009a), 11 Cenozoic S Hmax deduced from conjugate joints in our field measurements, 12 City

Full size image

Evidence including the rotation directions, the measured maximum principal stress magnitudes and the previous stress data is gathered to prove the authenticity of the two stress fields in the Late Mesozoic–Cenozoic models, and it is found that the calculated results are reliable. Despite slight differences between the calculated and observed maximum principal compressive stress, the modeling results of the Late Mesozoic stress fields indicate that the orientation of the maximum principal compressive stress in the Ordos Basin is WNW, whereas in the Cenozoic model, the orientation is NE. Based on the above-mentioned proofs, the validity of the two models in the Late Mesozoic and the Cenozoic can be corroborated.

5.2 Maximum principal stress orientations

Tectonic events of different episodes have distinct effects on the principal stress orientations in the Ordos Basin. Since there is little difference between the Chang 71 and 72 members except for lithology and layer thickness, the pattern of principal stress orientation during the same period is similar in each layer of the Longdong area. Thus, the Chang 71 member is taken as an example to demonstrate the distribution of maximum principal compressive stress in the study area (Fig. 12).

Fig. 12
figure 12

Calculated maximum principal compressive stress orientations in a the Late Mesozoic and b the Cenozoic within the Longdong area are compared with the observed fracture orientations in 19 wells. The observed orientations are obtained from imaging logging (FMI technology) data, which are shown as rose diagrams in the figures. The green rose diagrams denote the structural fractures in NW–EW trends, whereas the red ones denote those in NNE–ENE trends

Full size image

On the basis of paleo-magnetic evidence in earlier studies, although the Ordos Basin experienced rotation in different directions from the Late Mesozoic to the Cenozoic, the rotation angle of the basin is less than 5° in the Late Mesozoic–Cenozoic eras (e.g., Huang et al. 2005). Therefore, the present stress data, including fracture trends and Formation Microscanner Image (FMI) data, can also be utilized to indicate the stress orientations in the Late Mesozoic–Cenozoic. From numerical modeling, the orientations of calculated maximum compressive stress in the Late Mesozoic are mainly WNW, while those in the Cenozoic are mainly NE (Zhao et al. 2013, 2016) (Fig. 12). In outcrops and cores, the observed fractures developed in the Late Mesozoic are chiefly in NW–EW trends and those in the Cenozoic are chiefly in NNE–ENE trends (Fig. 8). Our field measurements also corroborate that the ENE-trending structural fractures developed later than the NW-trending ones. Therefore, it can be concluded that the NW to EW fractures were developed in a Late Mesozoic stress field, whereas the NNE to ENE ones were developed in a Cenozoic stress field. Despite tiny differences between the calculated and the observed data, in general, modeling results fit well with the dominant orientations of observed fractures which are obtained from the FMI technology (Fig. 12).

Structural fractures in the Ordos Basin were developed in multiple orientations under different stress fields, primarily in the Late Mesozoic and the Cenozoic episodes, and this intersection pattern will contribute to wider opening and better connectivity of the fractures. The formed fracture networks provide a path for fluid transmission and enhance the permeability, which will have notably improved the fractured tight-oil reservoirs in the Ordos Basin (e.g., Izadi and Elsworth 2014).

5.3 Rupture values

Since the rupture value is an important parameter to indicate the fracture development in the study area, comparison between the calculated rupture values and the observed core fracture density is informative to help analyze the reliability of the models (Figs. 13, 14).

Fig. 13
figure 13

Distribution of rupture value of the Late Mesozoic and the Cenozoic in the Chang 71 and 72 members within the Longdong area. a Rupture values of the Late Mesozoic in the Chang 71 member, b rupture values of the Cenozoic in the Chang 71 member, c rupture values of the Late Mesozoic in the Chang 72 member and d rupture values of the Cenozoic in the Chang 72 member

Full size image
Fig. 14
figure 14

Distribution of strain energy density (104 J/m3) of the Late Mesozoic and the Cenozoic in Chang 71 and 72 members within the Longdong area. a Strain energy density of the Late Mesozoic in the Chang 71 member, b strain energy density of the Cenozoic in the Chang 71 member, c strain energy density of the Late Mesozoic in the Chang 72 member and d strain energy density of the Cenozoic in the Chang 72 member

Full size image

In the maps of rupture values in the Chang 71 member during the Late Mesozoic–Cenozoic era, the highest rupture values are situated in the east and center of the study area, mainly concentrated in the Qingyang, the Laocheng and the Zhengning areas (Fig. 13a, b), while the highest rupture values in the Chang 72 member are chiefly situated in the mid-southern area, particularly in the Qingyang-Heshui and the Ningxian areas (Fig. 13c, d). The distribution of sand bodies and the thickness of sandstone layers have a distinct impact on the distribution of rupture values within the Longdong area. Both in the Chang 71 and 72 members, the rupture values are relatively higher where sand bodies are developed and the thickness of sandstone layers is relatively larger, due to the brittleness of sandstones (Fig. 4). The regional stress fields during different periods also influence the rupture values, resulting in the Cenozoic rupture values being smaller than the Late Mesozoic ones. However, the influence of regional stress fields is not as remarkable as that of lithology, because regional stress fields determine only the magnitudes, not the distribution of rupture values in the Chang 71 and 72 members within the study area (Fig. 13).

5.4 Strain energy density

Because rocks with higher strain energy density are more likely to form structural fractures than those with a lower one, the strain energy density can be used as another parameter to predict the fracture density.

Similar to the rupture value, there is obvious positive correlation between the strain energy density and the thickness of sandstone layers. The strain energy density is higher where the sand bodies are developed as a whole (Figs. 4, 14). Although the Cenozoic stress field of the Ordos Basin is strikingly different from the Late Mesozoic one, the impact of regional stress is mainly limited to the magnitudes, not the distribution of strain energy density in the Longdong area. The distribution of strain energy density in the Late Mesozoic and the Cenozoic periods is similar, but the Late Mesozoic strain energy density is larger than the Cenozoic one both in the Chang 71 and 72 members, implying that the strain energy density is more influenced by the movement in the Late Mesozoic than that in the Cenozoic (Fig. 14).

5.5 Predicted fracture distribution

In order to predict the fracture distribution in the Yanchang Formation within the Longdong area, connection between the calculated and the measured fracture density in cores must be established to study their relationship. In this paper, the two-factor method is utilized to compare the calculated data (including the rupture value and the strain energy density) and the measured fracture density (Ding et al. 1998). Since structural fractures in the Ordos Basin were chiefly developed during two stages of stress fields, namely the Late Mesozoic and the Cenozoic ones, two episodes of fractures should be fitted separately and then be added up by weight.

By multiple regression analyses, bi-quadratic relationships between the rupture values, the strain energy density and the measured fracture density in the Chang 71 and 72 members of different episodes have been built and the empirical formulas are shown in Table 3. Correlation coefficients in all curve-fitting relationships are larger than 0.87, which means that there is a significant correlation between the calculated and the measured data.

Table 3 Curve-fitting relationships of the measured fracture densities, the calculated rupture values and the strain energy densities of Chang 71 and 72 members in the Longdong area
Full size table

To further illustrate the reliability of our models, error analyses are carried out as follows. Both the absolute error and the relative error were applied to reflect the accuracy of fracture prediction. Absolute error is calculated by:

$$\Delta = \left| {D_{\text{p}} - D_{\text{m}} } \right|$$
(7)

And relative error can be described as follows:

$$\varepsilon = \frac{{\left| {D_{\text{p}} - D_{\text{m}} } \right|}}{{D_{\text{m}} }} \times 100\%$$
(8)

Δ denotes the absolute error and ε denotes the relative error. D P and D M represent the predicted and the measured fracture densities, respectively. Generally, when ε is less than 50%, we can consider that the predicted data match the measured ones and the modeling results are reliable to a certain extent.

The differences between the measured and the predicted fracture densities are shown in Tables 4 and 5. For most of the wells in the Chang 71 member, the predicted and the measured data match quite well. In the 54 measured wells, only 2 wells exceed 0.05 m−1 in absolute errors and 3 wells exceed 50% in relative errors (Table 4). The differences between them may be caused by the stress concentration in some areas, such as Well Z47 and Z78, where numerous fractures are found. As for the Chang 72 member, predicted data of only 8 wells in the 39 measured wells are more than 0.05 m−1 in absolute errors, and data of only 5 wells are more than 50% in relative errors (Table 5). Most of these wells are with extraordinarily high fracture density, which results in large errors between the predicted and the measured fracture densities. Some large errors may be caused by non-structural factors, such as various sedimentary phenomena. Cross bedding and lenticular bedding appeared widely in Well Ze77, etc., which may lead to the difference between the predicted and measured data. Despite these differences, the tendency of predicted fracture distribution is still in accordance with the measured one. In short, the errors between the predicted and the measured fracture densities are within acceptable limits, implying that the modeling results are suitable for the fracture prediction in the Yanchang Formation of the Ordos Basin.

Table 4 Overview of predicted and measured fracture densities in the Chang 71 member in the Longdong area
Full size table
Table 5 Overview of predicted and measured fracture densities in the Chang 72 member in the Longdong area
Full size table

6 Discussion

As is shown in the maps of maximum principal compressive stress orientations in the Chang 71 and 72 members in the Longdong area, the dominant orientations of the Late Mesozoic fractures are NW–EW (Fig. 12a) and those of the Cenozoic ones are NNE–ENE (Fig. 12b) which are consistent with the regional stress fields of the Ordos Basin in the corresponding periods (e.g., Zhang et al. 2003). In the maps of predicted fracture density in different periods, the average density of the Cenozoic fractures is larger than that of the Late Mesozoic ones (Fig. 15). By comparison between the distribution maps of predicted total fracture densities in the Chang 71 and 72 members within the study area (Fig. 16), the predicted fracture density in each member is alike as a whole; however, their fracture distributions are significantly distinct. In the Chang 71 member, the maximum fracture density is located in the center and the east of the Longdong area (Fig. 16a), while in the Chang 72 member, the maximum density is situated in the southern-central section of the study area (Fig. 16b).

Fig. 15
figure 15

Distribution of predicted fracture density (m−1) of the Late Mesozoic and the Cenozoic in the Chang 71 and 72 members within the Longdong area. a Predicted fracture density of the Late Mesozoic in the Chang 71 member, b predicted fracture density of the Cenozoic in the Chang 71 member, c predicted fracture density of the Late Mesozoic in the Chang 72 member and d predicted fracture density of the Cenozoic in the Chang 72 member

Full size image
Fig. 16
figure 16

Distribution of predicted total fracture density (m−1) in a the Chang 71 and b Chang 72 members within the Longdong area. Black solid dots represent the measured wells in the study area

Full size image

In addition, by comparing the predicted fracture density with the distribution of sand bodies, their similarity reveals that the lithology is a key factor in controlling the fracture distribution in the Ordos Basin. Structural fractures are more likely to be developed in the sandstones rather than in the mudstones. Where thicker sandstone layers are developed, the fracture density is relatively higher than other areas (Figs. 4, 16). However, there is still a difference between the predicted fracture distribution and the outline of sand bodies, indicating that the regional stress field also plays a role in the fracture development, even though its influence is limited compared with the lithology and the layer thickness.

In brief, the stress fields determine the overall fracture orientations, and the lithology distribution and the thickness of sandstone layers in the study area play a predominant role in the distribution of predicted fracture density. Some potential factors which are not covered in these numerical models may restrict the accuracy of predicted results, including:

  1. 1.

    The complicated heterogeneity of each layer;

  2. 2.

    The extreme stress in some areas;

  3. 3.

    The interaction between the two episodes of structural fractures; and

  4. 4.

    The influence of deep paleo-faults.

Since the modeling is on a relatively large-scale while the outline of sand bodies is depicted in considerable detail, the modeling results, including the rupture values and the strain energy density, can still be used to guide further exploration in spite of the four above-mentioned restrictions. Meanwhile, the qualitative fracture prediction obtained from the numerical modeling may also be applicable. These results act as a reference for future regional-scale petroleum exploration, while the method of fracture prediction, including the two-factor method and the empirical formulas can be used at well scale. Structural fractures play an important role in reconstructing the tight clastic reservoirs, especially in their permeability (Réda 2013).

The controlling factors of fracture development are complex owing to the complicated geological background. Fault systems can be a vital factor in developing fractures where tectonic movements are strong such as the Kuqa Depression of the northern Tarim Basin in the northwestern China (Ju et al. 2014b) and the Upper Rhine Graben in France and Germany (Johanna et al. 2015); flow may notably promote fracture development where fluid flow or lava flow appears (e.g., Agosta et al. 2010). However, in the Ordos Basin, where the tectonic events are rather weak and the dips of the Mesozoic–Cenozoic strata are less than 3°, the lithology and the layer thickness are the dominant factors in governing the distribution of fracture density. The relationship between the lithology and the fracture density is still obscure, but it may be related to the difference of rock physical parameters (Table 1) according to previous study (e.g., Zeng et al. 2008). The different grain sizes in various clastic rocks may be the micro-mechanism that causes the distribution of fracture density in the Ordos Basin (Zhao et al. 2013; Ju et al. 2015).

7 Conclusions

The predicted fracture distribution provides a clear view of the fracture concentration and fracture development. Several primary conclusions can be drawn from the modeling results:

  1. 1.

    A finite element modeling technique, applying the two-factor method, is suitable for the fracture prediction of the Ordos Basin, based on comparison between the calculated and the measured fracture densities of the Chang 71 and 72 members in the Longdong area.

  2. 2.

    Two episodes of structural fractures have been developed since the Late Triassic: The dominant orientations of the Late Mesozoic fractures in the Yanchang Formation are NW–EW, whereas those of the Cenozoic fractures are NNE–ENE, both of which are in agreement with the modeling results.

  3. 3.

    Structural fractures in the Ordos Basin are controlled by the regional stress fields, and the lithology and the layer thickness have a significant impact on the distribution of structural fractures, because the stress distribution will be affected by the inhomogeneity of lithology and layer thickness. This conclusion is shown in the similarity between the maps of predicted fracture density and observed sand bodies in the Yanchang Formation within the study area.

  4. 4.

    The average fracture density is close in the Chang 71 and 72 members, but there are obvious differences in their fracture distributions. In the Chang 71 member, the maximum fracture density is concentrated in the center and the east of the Longdong area, particularly in the Qingyang, the Laocheng and the Zhengning areas (up to 1.5 m−1), while in the Chang 72 member, the maximum value is located in the central and southern part of the area.

  5. 5.

    The modeling results and the predicted fracture density can be utilized to guide future regional exploration, and the method of fracture prediction, namely the two-factor method, can be referred for further study of the tight-sand reservoirs.