1 Introduction

Upscaling is the process of reducing a large number of the fine-scale grid blocks to a smaller number of coarse-scale grid blocks. This is required because it is often impractical to perform simulation at finest scale of the reservoir. Therefore, upscaling is one of the most important components of reservoir simulation. The last few decades have seen significant advancements in upscaling which include development of single-phase and multiphase upscaling as well as upscaling in the near wellbore and away from wellbore regions. Single-phase upscaling involves the upscaling of permeability distribution only. The technique is simple and can be used for structurally complex reservoirs but it neglects the multiphase flow effects (Durlofsky 1991; Ringrose 2007). In multiphase flow upscaling, relative permeability curves are also upscaled in addition to absolute permeability upscaling. This approach is computationally expensive and as such its use is limited to simple reservoir models (Ekrann and Dale 1992; Ringrose 2007).

One method of upscaling involves averaging the parameters and imputing the averaged values directly into the simulation flow grid. Most of the averaging techniques (arithmetic, harmonic, geometric, power law, pressure solver) are only appropriate under the circumstances of perfectly layered or heterogeneous distributions that are perfectly random and seldom observed in realistic reservoir descriptions. Another method of upscaling is an averaging technique that first computes the lower and upper bounds of the effective properties, based on geology, and then uses a new correlation and scaling technique to estimate the effective properties for the upscaled grid (Li et al. 2001). Purely local upscaling methods consider only those fine-scale grids that are combined in the target coarse-scale grid (Durlofsky 1991; King and Mansfield 1999). The hydraulic conductivity upscaling method (Wen and Gómez-Hernández 1996) involves upscaling of hydraulic conductivities at the scale of measurements to a coarser grid of block conductivity tensors. The extended local procedure includes few of the adjacent grids in the local problems (Gómez-Hernández and Journel 1994; Wu et al. 2002). In global upscaling methods, the flow solution utilized to calculate the upscaled parameters is performed over the entire domain (White and Horne 1987; Pickup et al. 1992; Holden and Nielson 2000). This technique can provide high level of accuracy, but it has a disadvantage of requiring global fine-scale solutions.

An adaptive local–global procedure has also been proposed for multiphase near-well problems (Nakashima 2009). Adaptive means that the actual boundary conditions are applied for global coarse-scale simulations rather than the generic set of boundary conditions. The adaptive local–global upscaling technique involves global coarse-scale simulation with initial estimates for wellblock parameters which provides the coarse-block pressure and saturations. The resultant pressure and saturation distributions are then interpolated onto the local well model to obtain boundary conditions for the near-well upscaling computations.

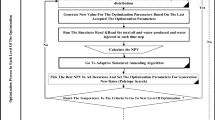
History matching has long been used to estimate reservoir parameters from dynamic production history data. However, a limitation of this procedure is that it is often the case that the information content of the production histories is not enough to resolve the model parameters at the finest scale. Thus, different methods of model space reduction have been proposed in the literature to reduce the number of model parameters to be estimated from the production history, thereby reducing the non-uniqueness associated with the inverse modeling. One such model reduction method is the wavelet multiscale inverse analysis (Lu and Horne 2000; Sahni and Horne 2005, 2006a, b; Awotunde and Horne 2011a, b, 2012, 2013). The various methods of model space reduction often automatically produce some level of smoothening (homogenization) of the reservoir model parameters such as grid block permeabilities. This smoothening creates a scenario in which several adjacent grid blocks have the same permeability values. However, during such history matching procedures, forward simulation runs are still performed at the finest scale (Lu and Horne 2000; Sahni and Horne 2005; Awotunde and Horne 2012, 2013). In this way, a huge amount of time is spent on forward simulations. Another permeability upscaling procedure using the fast marching method was implemented by Sharifi and Kelkar (2014). The purpose of this work is to utilize the pattern of smoothening in the permeability field created by the model space reduction during history matching, to upscale the forward simulation model with an ultimate goal of reducing the total time required for history matching.

We propose and evaluate an upscaling procedure based on wavelet sensitivity thresholding. Sensitivity-based thresholding has been reported in the literature to reduce model parameter space during history matching (Sahni and Horne 2006a, b; Awotunde and Horne 2012). Sensitivity computation is required for computing the Hessian matrix in the Gauss–Newton and LM algorithms (Gill et al. 1981; Nocedal and Wright 2006; Griva et al. 2009). In addition, a sensitivity matrix has been used to reduce the model space. One of the features of such model reduction is the emergence of several neighboring grids with similar values of the reservoir model parameter. For example, in the 2Dwp–wk approach presented in Awotunde and Horne (2013), the thresholding of wavelet sensitivity matrix computed in early iterations of the nonlinear regression is used to determine the reduced model space.

The back-transformation of the model space coefficients into the real permeability field would identify the regions of homogeneity in the upscaled reservoir model. Combining the grid blocks based on the pattern obtained from the model reduction would result in a coarse-scale unstructured grid system. The method is expected to be more consistent as it predetermines the areas of the reservoir with homogeneous permeability distribution based on sensitivity analysis. To improve the accuracy of simulation results, grid blocks having wells completed in them were not combined with any neighboring grid blocks. Further, two scenarios were tested; one in which all neighboring grid blocks with equal permeabilities but without any well were combined, and the second in which wellblocks and their neighbors were not combined. The second scenario was done to improve the accuracy of the variables obtained from the wells. If the neighbors of a wellblock are much larger in size than the wellblock, the accuracy of variables such as wellbore pressure and water cut may be compromised.

To properly investigate the effectiveness of the sensitivity-based upscaling approach, the methodology was applied to history match data from two synthetic reservoir models. The reliability of the technique was evaluated by comparing the results of history matching performed using coarse-scale forward simulations to those obtained from history matching performed using a fine-scale forward simulation model. In both, the history matching was used to obtain a reduced model parameter space.

2 Reservoir parameter estimation

The process of determining the spatial distribution of reservoir properties, particularly porosity and permeability, is known as reservoir characterization. History matching is the process of modifying the reservoir model by fitting simulation results to actual field data. Originally, history matching was done manually, then progress was made and the industry shifted to automated history matching. Automated history matching often relies on nonlinear regression of the observed dataset. Nonlinear regression comprises the class of inverse analysis techniques used in minimizing the l 2—norm of errors between modeled data and the measured data. In a nonlinear regression, the objective function is often given by

$$\varPhi \left( {\vec{\alpha }} \right) = \frac{1}{2\xi }\left\| {\vec{d}_{\text{cal}} - \vec{d}_{\text{meas}} } \right\|_{2}^{2} ,$$
(1)

where \(\vec{\alpha }\) is the vector of the unknown parameters (to be estimated by optimization or nonlinear regression), \(\vec{d}_{\text{cal}}\) is the vector of modeled pressure data, \(\vec{d}_{\text{meas}}\) is the vector of measured data and ξ is a scaling factor. Most nonlinear regression algorithms follow the Newton–Raphson approach in which the parameters of the model are iteratively estimated by repeatedly finding an optimum direction (first-order optimality) and step-length with which to move the current iterate. This is achieved by computing the gradient \(\vec{g}\) and the Hessian H (or its approximation) at each iteration of the nonlinear regression. The optimum direction of descent \(\delta \vec{\alpha }\), in the minimization algorithm, is then computed from

$$H\delta \vec{\alpha } = - \vec{g}$$
(2)

and the subsequent iterate is

$$\vec{\alpha }^{\kappa + 1} = \vec{\alpha }^{\kappa } + \delta \vec{\alpha }^{\kappa } ,$$
(3)

where κ represents the iteration index. In the standard Newton–Raphson approach, the exact Hessian is computed and used to calculate the direction of descent. Although the Newton method gives fast convergence (fewer number of iterations) relative to other gradient-based methods, the computation of the Hessian matrix can be time-consuming when the problem dimension is large. Also, a simple analytic expression for the first and/or second derivative of the objective function may not be obtainable. Thus, an approximation to the Hessian is often used and this forms the basis of the different nonlinear regression algorithms such as the steepest descent, the conjugate gradient, the quasi-Newton methods, the Gauss–Newton approach, and the Levenberg–Marquardt (LM) method (Levenberg 1944; Marquardt 1963). For small- and medium-sized problems, the LM approach is often the nonlinear regression technique of choice. Thus, we use the LM approach to estimate the parameters of the well test problems considered and compare its results to the results from the global optimization techniques. In the LM approach, the Hessian matrix is approximated by

$$H = S^{\text{T}} S + \dot{\lambda }I,$$
(4)

where S is the sensitivity matrix computed from

$$S = \frac{{\partial \vec{d}_{\text{cal}} }}{{\partial \vec{\alpha }}},$$
(5)

and \(\dot{\lambda }\) is a small positive number that ensures the algorithm remains stable.

3 Reservoir simulator

The reservoir model is usually solved by a numerical approach due to its complex nature. The fine-scale simulator used in this work is a three-dimensional, oil–water, black oil, finite-difference reservoir simulator. The upscaling simulator is also purposely built for this work using the same governing equations for the reservoir model. Both simulators have a built-in functionality of computing sensitivity of data to reservoir parameters using the Adjoint-State approach.

3.1 Fine-scale simulator

A three-dimensional reservoir system with a total number of M grid blocks is considered with the total number of wells to be N well. The general residual equation can be given as

$$\vec{f}^{n + 1} \left( {\vec{u}^{n + 1} ,\;\vec{u}^{n} ,\;\vec{v},\;\Delta t;\;\vec{\alpha }} \right) = \vec{0},$$
(6)

where \(\vec{f}\) represents the vector of residual for flow equations; \(\vec{\alpha }\) is the reservoir parameters; vector \(\vec{v}\) consists of known reservoir properties and vector \(\vec{u}\) contains state variables and can be written as

$$\vec{u} = [p_{{{\text{o}},1}} ,\;S_{{{\text{w}},1}} ,\; \ldots ,p_{\text{o,M}} ,\;S_{\text{w,M}} ,\;p_{\text{wf,1}} ,\; \ldots ,\;p_{{{\text{wf}},N_{\text{well}} }} ]^{\text{T}} ,$$
(7)

where p o is the pressure of the oil phase, S w is the water saturation, p wf is the wellbore pressure \(\vec{f}_{\text{blk}}^{n + 1}\) contains the residual due to flow in and out of reservoir grid blocks and is given as

$$\vec{f}_{\text{blk}}^{n + 1} = \left[ {f_{{{\text{w,}}1}}^{n + 1} ,\;f_{{{\text{o}},1}}^{n + 1} ,\;f_{{{\text{w}},2}}^{n + 1} ,\;f_{{{\text{o}},2}}^{n + 1} ,\; \ldots ,\;f_{\text{w,M}}^{n + 1} ,\,f_{\text{o,M}}^{n + 1} } \right]^{\text{T}}$$
(8)

whereas \(\vec{f}_{\text{well}}^{n + 1}\) represents the residual due to flow into or out of the wells in the reservoir and can be presented as

$$\vec{f}_{\text{well}}^{n + 1} = \left[ {f_{{{\text{well}},1}}^{n + 1} ,\;f_{{{\text{well}},2}}^{n + 1} ,\; \ldots ,\;f_{{{\text{well}},N_{\text{well}} }}^{n + 1} } \right]^{\text{T}} .$$
(9)

\(\vec{f}_{\text{blk}}^{n + 1}\) and \(\vec{f}_{\text{well}}^{n + 1}\) both combine to form \(\vec{f}^{n + 1}\) as

$$\vec{f}^{n + 1} = \left[ \begin{aligned} \vec{f}_{\text{blk}}^{n + 1} \hfill \\ \vec{f}_{\text{well}}^{n + 1} \hfill \\ \end{aligned} \right],$$
(10)

Now, Eq. (8) indicates that \(\vec{f}_{\text{blk}}^{n + 1}\) comprises the residuals of the two phases existing in the reservoir system which can be given as

$$\vec{f}_{\text{w}} \left( {\vec{p}_{\text{o}}^{n + 1} ,\;S_{\text{w}}^{n + 1} ,\;\vec{p}_{\text{wf}}^{n + 1} ,\;\vec{p}_{\text{o}}^{n} ,\;S_{\text{w}}^{n} ,\;\vec{\phi }_{\text{ini}} ,\;\Delta t;\;\vec{k}} \right) = \vec{0},$$
(11)

and

$$\vec{f}_{\text{o}}^{n + 1} \left( {\vec{p}_{\text{o}}^{n + 1} ,\;S_{\text{w}}^{n + 1} ,\;\vec{p}_{\text{wf}}^{n + 1} ,\;\vec{p}_{\text{o}}^{n} ,\;S_{\text{w}}^{n} ,\;\vec{\phi }_{\text{ini}} ,\;\Delta t;\;\vec{k}} \right) = \vec{0}.$$
(12)

whereas the well residual for \(\vec{f}_{\text{well}}^{n + 1}\) of Eq. (9) can be written as

$$\vec{f}_{\text{well}}^{n + 1} \left( {\vec{p}_{\text{o}}^{n + 1} ,\;S_{\text{w}}^{n + 1} ,\;\vec{p}_{\text{wf}}^{n + 1} ,\;\vec{p}_{\text{o}}^{n} ,\;S_{\text{w}}^{n} ,\;\vec{\phi }_{\text{ini}} ,\;\Delta t;\;\vec{k}} \right) = \vec{0},$$
(13)

where \(\vec{\phi }_{\text{ini}}\) represents initial porosity distribution and \(\vec{k}\) represents the permeability distribution in the reservoir in all the residual equation presented above.

Consider the constraint of the total production rate,

$$f_{{{\text{well}},i}}^{n + 1} = \sum\limits_{\text{ph = o,w}}^{{}} {\sum\limits_{j}^{{N{\text{comp}}}} {q_{{{\text{ph}},j}}^{\text{well}} } } - q_{\text{t},i} = 0.$$
(14)

In Eq. (14), q wellph,j represents the flow rate of the phases (oil or water, denoted by ph) at the jth completion and it can be defined as

$$q_{{{\text{ph}},j}}^{\text{well}} = \lambda_{{{\text{ph}},j}}^{n + 1} WI_{j} \left( {p_{{{\text{ph}},j}}^{n + 1} - p_{\text{wf}}^{n + 1} - \gamma_{{{\text{ph}},j}}^{n + 1} \Delta z_{j} } \right)$$
(15)

There is no p c (capillary pressure) in Eq. (15) because p ph represents both p o and p w, so the capillary pressure will be incorporated in p w in the case of the water phase.

The mobility ratio and specific gravity of any phase ph at the completion j are represented by λ n+1ph,j and γ n+1ph,j , respectively, while WI j denotes the well index at the jth completion. The Newton–Raphson iterative method is used in order to solve the nonlinear system of equations at every iteration; so we have at any iteration κ,

$$J^{n + 1,\kappa } \delta \vec{u}^{n + 1,\kappa } = - \vec{f}^{n + 1,\kappa } ,$$
(16)

where J n+1,κ is known as the Jacobian matrix and can be written as

$$J^{n + 1,\kappa } = \frac{{\partial \vec{f}^{n + 1,\kappa } }}{{\partial \vec{u}^{n + 1,\kappa } }}.$$
(17)

the solution is then updated as

$$\vec{u}^{n + 1,\kappa + 1} = \vec{u}^{n + 1,\kappa } + \delta \vec{u}^{n + 1,\kappa } .$$
(18)

3.2 Upscaled simulator

The basic governing equations in the upscaled simulator are the same as those used in the fine-scale simulator. The principal difference is in the manner of calculating the transmissibility between the upscaled grid blocks. The central idea in this work involves the upscaling of the reservoir grid blocks based on homogenization of the system parameters. This would result in upscaled grid blocks that have different structures. Also, the neighboring grid blocks will not be structured as in the rectangular grid system. Thus, we need to find an appropriate way of computing the transmissibility between the interacting grid blocks. The detailed description of the upscaling procedure and its calculations is presented in Sect. 4.

4 Upscaling based on homogenization of reservoir model during history matching

This work involves upscaling of the reservoir system based on the sensitivity of production data to model parameters. Sensitivity computation is a part of some inverse analysis methods such as the Gauss–Newton and the LM algorithms. Sensitivities provide us information on the grid block parameters that have similar effects on calculated production data. During history matching and at any particular nonlinear iteration to estimate the unknown reservoir parameters (e.g., in the LM approach), adjacent grid blocks that exhibit almost similar values of sensitivities are considered as a homogenous patch and may then be combined to form an upscaled grid block. The pattern of upscaling is thus based on the pattern of homogenous patches obtained through sensitivity analysis during history matching. The adjacent grid blocks whose parameters (ln k) have almost similar effects on the production data are expected to have similar permeability trends and are merged to form an upscaled grid block. The combination of fine-scale grid blocks into larger ones, based on permeability distribution, ultimately reduces the number of grid blocks for simulation and this in turn reduces the required computational resources. The upscaling of grid blocks with similar permeability values is performed subject to one of two different constraints. The first constraint involves ensuring that grid blocks having wells in them (wellblocks) are not combined with any other grid. The second constraint involves ensuring that any wellblock and the grid blocks adjacent to it are not combined with one another or with any other block in their neighborhood.

Figure 1 illustrates an example of a 6 × 6 reservoir system with the implementation of the second constraint. The figure shows that fine-scale grid blocks are combined based on homogeneity of the system. The grid blocks having the same color have the same permeability value; therefore, these fine-scale grid blocks would be combined to form the upscaled system. The transformation from fine-scale to upscale grid blocks is explained using Table 1.

Fig. 1
figure 1

A reservoir system with some homogeneous patches

Full size image
Table 1 Combination of fine-scale grid blocks in the upscaled system
Full size table

Table 1 shows the fine-scale grid blocks in the 6 × 6 reservoir system that are combined due to homogeneity to form the upscaled system. Figure 1 and Table 1 also illustrate that the grid block having a well in it (i.e., Grid block 21) and the grids adjacent to this wellblock (Grid blocks 15, 20, 22, and 27) are not combined with any other grid block. However, because we combine the grid blocks based on permeability distribution, the resulting upscaled grid blocks do not necessarily form well-defined shapes, resulting often in unstructured gridding systems. This is observed in Fig. 1. This poses a challenge in the calculation of transmissibilities between any pairs of grid blocks. The transmissibility is performed by first locating the centroid of each upscaled grid block. Thus, the algorithm, used to upscale the fine-scale system, based on the presence of homogeneous patches is described below:

  1. (1)

    The fine-scale grid blocks are combined to form the upscaled grid blocks based on the presence of homogenous patches in the permeability distribution.

  2. (2)

    The centroid of each upscaled grid block is calculated.

  3. (3)

    All adjacent grids to every upscaled grid block are assembled and stored; to be used in transmissibility calculations.

  4. (4)

    At each simulation time step, the Newton–Raphson iteration is performed.

  5. (5)

    During each Newton-iteration of each simulation time-step, the transmissibility between pairs of upscaled grid blocks is calculated based on their centroids.

  6. (6)

    The procedure is repeated in each iteration, and each time step.

5 Transmissibility and centroid calculations for the upscaled system

Transmissibility is the property calculated at the interface of the grid blocks. However, the properties used in its calculation are known at the grid center. In a structured gridding system in rectangular coordinates, the size of a grid block and its center are appropriately defined. However, in the type of upscaled system shown in Fig. 1, the shape of the resulting upscaled grid blocks may not be regular, and for calculating transmissibility we need to define the centers of these grids. Thus, the centroids of the upscaled grid blocks are evaluated and used for transmissibility computation. In a two-dimensional system, the faces of the resulting upscaled grid blocks are polygons. Figure 2 shows one of such grid blocks. In order to calculate the centroid of any object, its vertices should be arranged in either the clockwise or counter-clockwise direction. The first step is to define the vertices of the new grid block. An algorithm is developed that finds the vertices of an upscaled grid from all the vertices of fine-scale grids contained in it. This is better understood from Fig. 2 in which vertices A, B, C, D, E, and F are the vertices of an upscaled grid, and the algorithm developed in this work finds these vertices. Vertices P1, P2, etc. of the fine-scale grids are excluded as these are not vertices of the upscaled grid. Once these vertices have been found, they are arranged in a clockwise or counter-clockwise order.

Fig. 2
figure 2

Example of an upscaled grid block

Full size image

A separate algorithm is written to arrange the vertices. This algorithm is based on the structure of x- and y- coordinates and it arranges the vertices in counter-clockwise order. Subsequently, the arranged points are used to determine the centroid using the following equations:

$$C_{x} = \frac{1}{6A}\sum\limits_{i = 0}^{n - 1} {(x_{i} + x_{i + 1} )(x_{i} y_{i + 1} - x_{i + 1} y_{i} )}$$
(19)
$$C_{y} = \frac{1}{6A}\sum\limits_{i = 0}^{n - 1} {(y_{i} + y_{i + 1} )(x_{i} y_{i + 1} - x_{i + 1} y_{i} )}$$
(20)

where C x is the x-coordinate of the centroid; C y is the y-coordinate of the centroid; A is the area of the polygon and is given as

$$A = \frac{1}{2}\sum\limits_{i = 0}^{n - 1} {(x_{i} y_{i + 1} - x_{i + 1} y_{i} )}$$
(21)

6 Usefulness and limitations of the sensitivity-based upscaling

The method proposed in this work can be performed only when there is a sensitivity matrix to indicate the response of the well data to changes in grid block parameters. Thus, the method is useful during history matching only if the method of history matching used involves the computation of a sensitivity matrix at each iteration. For instance, if the conjugate gradient method or the quasi-Newton method is used, sensitivities are not computed and such sensitivity-based upscaling of grid blocks is not possible. Also, we observed that the method has a severe limitation in the acceptable pattern of homogeneous patches. The problem that arises here is that sensitivity-based upscaling often results in unstructured grid blocks. In the case of such unstructured gridding, the centroid of all grid blocks in the new system must be located. To compute the centroid of a block, all the vertices of the block must form a continuous connection. That is, there must not be a void inside the block. However, in certain cases of unstructured gridding, cases arise in which one large grid block entirely envelopes a smaller grid block so that the large grid block has an opening within it and thus its centroid cannot be computed. A scenario of this type is illustrated in Fig. 3. In this figure, a large-grid formed by combining smaller blocks 14, 15, 16, 19, 20, 22, 25, 26, 27, and 28 (all shown in pink color) envelops a smaller grid, block 21 (shown in green color). In this case, the centroid of the larger grid cannot be computed. This situation is more likely to occur when the reduction in the model size is large. As a result, the model reduction that was achieved in this work is limited by this problem.

Fig. 3
figure 3

An unstructured grid system showing a large grid enveloping a small grid

Full size image

7 Comparison of fine-scale and upscale forward simulation

First, we considered a 32 × 32 reservoir model with such permeability distributions that result in some homogenous regions in the reservoir. This reservoir (Fig. 4) has three producers and three injectors. The reservoir was upscaled based on the homogeneous patches indicated by its inherent permeability distribution. Then a flow simulation was performed on both the fine-scale and the upscaled reservoir model. In upscaling the reservoir sample, the two constraints were imposed. The constraints are that all neighboring grid blocks having equal permeability values are allowed to be merged during upscaling except

Fig. 4
figure 4

Log permeability distribution and well locations for the 32 × 32 reservoir model

Full size image
  1. (1)

    those having wells; and

  2. (2)

    those having wells and their respective adjacent grid blocks.

The fine-scale and upscaled simulators were run to obtain bottom-hole pressure and water cut data, and the match between the results from the upscaled reservoir model and those from the fine-scale model was used to determine which constraint produced better results. Figure 5 shows the bottom-hole pressure and water cut matches with Constraint 1, while Fig. 6 shows the matches obtained with Constraint 2. We obtained very good matches of the bottom-hole pressure with both constraints, but the water cut match was not good with any of the constraints. However, the results from Constraint 2 were better than those from Constraint 1. Therefore, we chose only Constraint 2 for the history matching.

Fig. 5
figure 5

Production data from the fine-scale and upscale reservoir models for the 32 × 32 system. a Bottom-hole pressures. b Water cut (Constraint 1)

Full size image
Fig. 6
figure 6

Production data from the fine-scale and upscale reservoir models for the 32 × 32 system. a Bottom-hole pressures. b Water cut (Constraint 2)

Full size image

8 Example application of sensitivity-based upscaling to inverse analysis

In this section, we present history matching results for a reservoir model discretized into 64 × 64 grid blocks. The 64 × 64 reservoir has 16 producers and 16 injectors. Three thresholding values were used separately to select the wavelets that make up the model space. The upscaling procedure used in the forward simulations was based on the homogeneity-pattern created by thresholding the model space using the wavelet sensitivity matrix. Furthermore, history matching was performed for the upscaled model (this work) and the fine-scale model (Awotunde 2010; Awotunde and Horne 2012, 2013) and the results from both systems were compared. We transformed the model space into wavelets and then perform thresholding to reduce the number of model parameters used for describing the system. This is done to reduce the computation time and also the non-uniqueness associated with the estimated results. The three fractions used in thresholding the model space are 0.60, 0.40, and 0.25. Each of these fractions determines the number of wavelets of the parameters we retain for history matching. The wavelet fraction of 0.60 indicates that the problem dimension is reduced to 60 % of its original size. That is 60 % of the total number of wavelets (of reservoir parameters) are selected. Upon inversion, the selected wavelets result in heterogeneous permeability distribution with some homogeneous patches. These number and size of homogenous patches tend to increase as we reduce the wavelet fraction.

8.1 Fine-scale inverse analysis

Fine-scale history matching was performed for the three wavelet fractions as mentioned above. The match of bottom-hole pressure (producers and injectors) for all the fraction of wavelets considered are shown in Figs. 7, 8, and 9, respectively. The matches to the water cut for fractions 0.60, 0.40, and 0.25 are presented in Fig. 10.

Fig. 7
figure 7

Match of production data for the 64 × 64 reservoir system (wavelet fraction 0.60, no upscaling performed during history matching). a Bottom-hole pressures in producers. b Bottom-hole pressures in injectors

Full size image
Fig. 8
figure 8

Match of production data for the 64 × 64 reservoir system (wavelet fraction 0.40, no upscaling performed during history matching). a Bottom-hole pressures in producers. b Bottom-hole pressures in injectors

Full size image
Fig. 9
figure 9

Match of production data for the 64 × 64 reservoir system (wavelet fraction 0.25, no upscaling performed during history matching). a Bottom-hole pressures in producers. b Bottom-hole pressures in injectors

Full size image
Fig. 10
figure 10

Match to water cut in all producers for the 64 × 64 reservoir system with no upscaling performed during history matching. a Wavelet fraction 0.60. b Wavelet fraction 0.40. c Wavelet fraction 0.25

Full size image

Good matches are obtained to all pressure and water cut histories, in all the cases considered. The trend of the number of wavelet coefficients selected using each fraction of 0.60, 0.40, and 0.25 is shown in Fig. 11. The figure shows that the number of wavelet coefficients increases in the early iterations and reaches the maximum preset number of wavelets (based on wavelet fraction used). Figure 12 shows the reduction of error as the iteration proceeds. The true permeability distribution, initial guess, and the final distribution obtained for the three scenarios are shown in Fig. 13. None of the estimates in Fig. 13c–e is close enough to the true permeability map (Fig. 13b). However, the estimate obtained from the fraction 0.60 gives a better representation of the heterogeneity than the other estimates.

Fig. 11
figure 11

Trend of wavelet coefficients for the 64 × 64 reservoir system (all fractions, no upscaling performed during history matching)

Full size image
Fig. 12
figure 12

Data residual for the 64 × 64 reservoir system (all fractions, no upscaling performed during history matching)

Full size image
Fig. 13
figure 13

Log permeability distribution for the 64 × 64 reservoir system. a True. b Initial guess. c Estimate of wavelet fraction 0.60. d Estimate of wavelet fraction 0.40. e Estimate of wavelet fraction 0.25 (no upscaling performed during history matching)

Full size image

8.2 Upscaled inverse analysis

In this case, simulation models are upscaled based on the analysis of sensitivity matrix at each iteration of the LM algorithm. The matches obtained to measured pressure data (producers and injectors), for the three fractions considered, are presented in Figs. 14, 15, and 16 while the matches to the water cut data are presented in Fig. 17. We observe that the pressure histories are adequately matched. However, matches obtained with data fractions of 0.60 and 0.40 are better than those obtained with 0.25. Similarly, the matches to the water cut data for all fractions are acceptable. The selection of wavelet coefficients for each fraction is shown in Fig. 18 while the reductions in the mismatch error for all the fractions are presented in Fig. 19. All the fractions exhibit similar performances. Figure 20 shows the true permeability, the initial guess, and the permeability maps estimated from the three fractions. We observe that a better estimate of the permeability map is obtained when a 0.60 fraction of all the model wavelets is used.

Fig. 14
figure 14

Match of production data for the 64 × 64 reservoir system (wavelet fraction 0.60, upscaling performed during history matching). a Bottom-hole pressures in producers. b Bottom-hole pressures in injectors

Full size image
Fig. 15
figure 15

Match of production data for the 64 × 64 reservoir system (wavelet fraction 0.40, upscaling performed during history matching). a Bottom-hole pressures in producers. b Bottom-hole pressures in injectors

Full size image
Fig. 16
figure 16

Match of production data for the 64 × 64 reservoir system (wavelet fraction 0.25, upscaling performed during history matching). a Bottom-hole pressures in producers. b Bottom-hole pressures in injectors

Full size image
Fig. 17
figure 17

Match to water cut in all producers for the 64 × 64 reservoir system with upscaling of grid blocks during history matching. a Wavelet fraction 0.60. b Wavelet fraction 0.40. c Wavelet fraction 0.25

Full size image
Fig. 18
figure 18

Trend of wavelet coefficients for the 64 × 64 reservoir system (all fractions, upscaling performed during history matching)

Full size image
Fig. 19
figure 19

Data residual for the 64 × 64 reservoir system (all fractions, upscaling performed during history matching)

Full size image
Fig. 20
figure 20

Log permeability distribution for the 64 × 64 reservoir system. a True. b Initial guess. c Estimate of wavelet fraction 0.60. d Estimate of wavelet fraction 0.40. e Estimate of wavelet fraction 0.25 (upscaling performed during history matching)

Full size image

A summary of performance information from all the cases is presented in Table 2. It represents that we have total of 6144 production data points (pressure and water cut), out of which only 496 have been selected for history matching which gives a compression ratio of 12.92. It is a 64 × 64 grid system that results in 4096 reservoir parameter (permeability) values. As discussed earlier that as the wavelet fraction is reduced the number of parameters considered is also reduced. Thus, a fraction of 0.60 has maximum parameters of 2545 which reduce to 1144 in the case of fraction 0.25. The parameters considered are almost the same in both fine-scale and upscale history matching.

Table 2 Important statistics for history matched 64 × 64 reservoir system
Full size table

9 Conclusions

The following conclusions can be drawn from the results obtained during this work:

  1. (1)

    A good match is obtained for all the fine-scale history matching cases, as it was established in earlier work (Awotunde 2010; Awotunde and Horne 2012, 2013).

  2. (2)

    During upscaling, combining the grid blocks that are adjacent to the well grid blocks does not provide good results. This is evident from the fact the Constraint 2 provides better results than Constraint 1. The upscaling of grid blocks can be achieved by analyzing the transformed sensitivity matrix and implemented during the iterations of the LM algorithm.

  3. (3)

    Sensitivity-based upscaling during history matching provides reasonable results with a sufficient reduction in computation time as compared to the fine-scale inverse analysis.

  4. (4)

    It is observed that the results from all three fractions (0.60, 0.40, and 0.25) are reasonably good. However, results from 0.25 are beginning to show some slight deviation from the true results, indicating that further reduction may lead to larger deterioration in the performance of the algorithms.

  5. (5)

    The reduction of the simulation model size due to sensitivity-based upscaling can be limited by the emergence of an upscaled grid block that envelopes a smaller grid block.