1 Introduction

With the development of petroleum exploration, seismic surveys have gradually extended into areas with complex geological conditions, such as regions with continental faulted basins and offshore salt deposits. This situation presents new challenges for seismic imaging, which compel us to explore a more efficient, accurate, and robust migration method than the existing ones.

Over the past decades, dramatical progress has been achieved in the field of prestack depth imaging. Ray-based Kirchhoff migration has been developed from 2D to 3D (Hubral et al. 1996; Epili and McMechan 1996; Sun et al. 2000), from single-arrival migration (including first arrival, most energy arrival etc.) to multi-arrival migration (Brandsberg-Dahl et al. 2001; Xu et al. 2001) and from kinematic migration to true-amplitude migration (Schleicher et al. 1993; Albertin et al. 1999; Xu and Lambaré 2006). Due to its high efficiency and flexibility, Kirchhoff migration is still the workhorse in practical applications, especially for land seismic data. On the other hand, one-way wave equation migration accuracy has also been improved significantly using different numerical algorithms, such as split-step Fourier, Fourier finite difference, and generalized screen propagator (Stoffa et al. 1990; Ristow and Rühl 1994; Chen and Ma 2006; Li et al. 2008; Kaplan et al. 2010; Huang and Fehler 2000; Liu and Yin 2007; Zhu et al. 2009; De Hoop et al. 2000; Wu et al. 2001; Le Rousseau and De Hoop 2003; Liu et al. 2012). Reverse time migration based on two-way wave equations has become more and more practical in actual projects as computer technology develops (Baysal et al. 1983), and many geophysicists have provided lots of constructive suggestions about the problems of time-consuming defects and low frequency imaging noise (Fletcher et al. 2006; Symes 2007; Chattopadhyay and McMechan 2008; Abdelkhalek et al. 2009; Li et al. 2010).

Gaussian beam migration (GBM) is an elegant and effective depth imaging method, which not only retains the advantage of ray-based migration, such as flexibility and efficiency, but also has an imaging accuracy comparable with wave equation migration. Ever since the basic framework of GBM was presented by Hill (1990, 2001), it has been extended to irregular topographic conditions (Gray 2005; Yue et al. 2012; Yang et al. 2014) and true-amplitude migration (Gray and Bleistein 2009). In addition, many new seismic beam imaging methods have been developed, such as fast beam migration (Gao et al. 2006, 2007), focused beam migration (Nowack 2008), and laser beam migration (Xiao et al. 2014), which expand the members of the beam migration family. Most of them, however, are based on the GBM framework and use a constant initial beam parameter, which makes a seismic beam focused either at the initial position or at a certain depth. Thus, the imaging accuracy varies along the central ray, highest at the focus point and decreasing as moving away from the focus point.

Aiming at this problem, Nowack (2009) has provided a dynamically focused beam method, which improves the deep imaging quality to some extent. Because this method is achieved using a unified beam width for all the subsurface imaging points and performing many local slant stacks and quadratic phase corrections for each beam, it does not consider the effects of velocity variation on the beam width and is very time-consuming. Hu and Stoffa (2009) have implemented a modified GBM for low-fold seismic data acquired sparsely, utilizing the instantaneous slowness of the local plane wave. Derived from the Maslov wave equation solution, Zhu (2009) also proposed a complex-ray beam method for exploration areas with complex topography. All methods mentioned above use the Fresnel zone information to limit the seismic beam energy and improve the imaging quality, which provides new options for beam migration.

In this paper, we have proposed another way to optimize the beam propagation shape and implemented an adaptive focused beam migration method for common-shot data, which could improve the shallow and deep imaging quality simultaneously. Using the information of the input smoothed velocity field, we derived an adaptive focused parameter that makes a seismic beam focused at the whole central ray, and then use it to construct a Green function in the acoustic medium and to solve the seismic migration problem. Unlike the dynamically focused beam method proposed by Nowack, our method uses the single input-trace imaging approach of classic Kirchhoff migration to avoid repeating local slant stacks for a beam at different imaging points, which is helpful to speed up the migration process. However, compared with Hill’s GBM, there is a tradeoff in computational efficiency, as now the number of emergent beams increases. In addition, using the amplitude-preserved extrapolation formula and deconvolution imaging condition, we have included the concept of amplitude-preserved imaging in our method. Typical numerical examples and the field data processing results demonstrate the feasibility and validity of the proposed method.

2 Theory

2.1 Adaptive focused beam

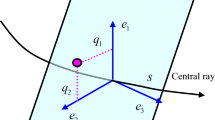
Considering a Gaussian beam from \( Q(s_{0} ,0) \) to \( P(s,0) \) in a 2D acoustic medium, its ray propagation matrix can be written as

$$ \pi (s;s_{0} ) = \left[ {\begin{array}{*{20}l} {q_{1} (s)} \hfill & {q_{2} (s)} \hfill \\ {p_{1} (s)} \hfill & {p_{2} (s)} \hfill \\ \end{array} } \right], $$
(1)

where \( (s,n) \) are ray-centered coordinates as shown in Fig. 1, \( (p_{1} (s),q_{1} (s)) \) and \( (p_{2} (s),q_{2} (s)) \) are two fundamental solutions of dynamic ray tracing equation system (Červený et al. 1982).

Fig. 1
figure 1

Ray-centered coordinate system

Full size image

If the beam focused at P and its beam width equals \( l(s) \), then the complex dynamic parameter at the initial position can be calculated by

$$ \left[ {\begin{array}{*{20}l} {q(s_{0} )} \hfill \\ {p(s_{0} )} \hfill \\ \end{array} } \right] = \pi (s;s_{0} )^{ - 1} \left[ {\begin{array}{*{20}l} { - i\omega_{\text{ref}} l^{2} (s)} \hfill \\ 1 \hfill \\ \end{array} } \right], $$
(2)

here \( \omega_{\text{ref}} \) denotes the referenced frequency, \( i = \sqrt { - 1} \) and \( l(s) \) takes the following form

$$ l(s) = 2\pi v(s)/\omega_{\text{ref}} , $$
(3)

where \( v(s) \) is the velocity of central ray.

Further, using the relation

$$ \varepsilon = q(s_{0} )/p(s_{0} ), $$
(4)

We obtain a new initial beam parameter

$$ \varepsilon (s) = \frac{{ - q_{2} (s) - i\omega_{\text{ref}} l^{2} (s)p_{2} (s)}}{{q_{1} (s) + i\omega_{\text{ref}} l^{2} (s)p_{1} (s)}}. $$
(5)

Unlike the Gaussian beam and focused beam, the initial parameter in Eq. (5) is no longer a constant, but a function of ray arc length. This choice makes the main energy of the beams focus in the range of a wavelength along the whole ray. For the convenience of discussion, we define the beam determined by \( \varepsilon (s) \) in Eq. (5) as the adaptive focused beam.

Now we analyze the propagation property of the adaptive focused beam briefly. Considering an inhomogeneous medium as shown in Fig. 2a, which includes a high-speed layer and a low-speed layer in a constant-gradient velocity background, the adaptive focused beam keeps a narrow beam width and plane wave-front along the whole central ray (see Fig. 2b). Besides, it has a small beam width at the low-speed layer and large beam width at the high-speed layer marked by the blue ellipses in Fig. 2b, which is helpful to resolve the steep-dip reflectors and velocity abnormal bodies in seismic imaging. For a Gaussian beam, however, the beam width increases quickly and the wave-front diffuses rapidly (see Fig. 2c), which result in inaccurate travel-time and amplitude extrapolated from central ray at deep parts, especially in a medium with strong lateral velocity variation.

Fig. 2
figure 2

The propagation of different seismic beams. a Velocity model, b adaptive focused beam, c Gaussian beam

Full size image

2.2 Green function represented with the adaptive focused beam integral

With the initial parameter \( \varepsilon (s) \) in Eq. (5), we can write the expression of the adaptive focused beam in the frequency domain as

$$U(s,n,\omega ) = \sqrt {\frac{{\varepsilon (s_{0} )v(s)}}{{\left[ {\varepsilon (s)q_{1} (s) + q_{2} (s)} \right]v(s_{0} )}}} \times \exp \left[ {i\omega \left( {\tau (s) + \frac{1}{2}\frac{{\varepsilon (s)p_{1} (s) + p_{2} (s)}}{{\varepsilon (s)q_{1} (s) + q_{2} (s)}}n^{2} } \right)} \right].$$
(6)

where \( \omega \) denotes the circular frequency, \( \tau \) is the travel-time of central ray.

According to Müller (1984), Green’s function at point M shown in Fig. 3 can be approximately represented with an integral over all the rays of beams, i.e.,

$$ G(M,\omega ) = \int\limits_{{\phi_{0} - \pi /2}}^{{\phi_{0} + \pi /2}} {\varPhi (\phi ,s)} U_{\phi } (s,n,\omega ){\text{d}}\phi , $$
(7)

where \( \varPhi (\phi ,s) \) is an integral weight coefficient for the adaptive focused beam with emergence angle \( \phi \).

Fig. 3
figure 3

Green’s function constructed with adaptive focused beam summation (referenced to Červený et al. 1982)

Full size image

If the weight coefficient \( \varPhi (\phi ,s) \) was known, Eq. (7) could be used to calculate the seismic wave-field at any point of the medium. Now we determine the function \( \varPhi (\phi ,s) \) in a homogenous medium with constant velocity \( v_{0} \). Denoting

$$ \begin{aligned} F(\phi ) = \varPhi (\phi ,s)\sqrt {\frac{{\varepsilon (\phi ,s_{0} )v(s)}}{{\left[ {\varepsilon (\phi ,s)q_{1} (s) + q_{2} (s)} \right]v(s_{0} )}}} \hfill \\ f(\phi ) = - i\left[ {\tau (s) + \frac{1}{2}\frac{{\varepsilon (\phi ,s)p_{1} (s) + p_{2} (s)}}{{\varepsilon (\phi ,s)q_{1} (s) + q_{2} (s)}}n^{2} } \right]. \hfill \\ \end{aligned} $$
(8)

Equation (7) can be rewritten as

$$G(M,\omega ) = \int\limits_{{\phi_{0} - \pi /2}}^{{\phi_{0} + \pi /2}} {F(\phi )} \exp \left[ { - \omega f(\phi )} \right]{\text{d}}\phi .$$
(9)

In a homogeneous medium, we have (see Fig. 3)

$$ \begin{aligned} \tau (s) = r \cos (\phi - \phi_{0} )/v_{0} , \, n = r \sin (\phi - \phi_{0} ) \hfill \\ q_{1} = p_{2} = 1, \, p_{1} = 0, \, q_{2} = v_{0} r \cos (\phi - \phi_{0} ). \hfill \\ \end{aligned} $$
(10)

Inserting the latter expression in the Eq. (8), we obtain

$$ \begin{aligned} F(\phi ) = \varPhi (\phi ,s)\sqrt {\frac{{\varepsilon (\phi ,s_{0} )}}{{\varepsilon (\phi ,s) + v_{0} r \cos (\phi - \phi_{0} )}}} \hfill \\ f(\phi ) = - i\left[ {r \cos (\phi - \phi_{0} )/v_{0} + \frac{1}{2}\frac{{r^{2} \sin^{2} (\phi - \phi_{0} )}}{{\varepsilon (\phi ,s) + v_{0} r \cos (\phi - \phi_{0} )}}} \right]. \hfill \\ \end{aligned} $$
(11)

In a smoothed medium, \( \varepsilon_{\phi} \,(\phi ,s) \) can be expanded with Taylor’s formula as follows

$$ \varepsilon (\phi ,s) = \varepsilon (\phi_{0} ,s) + \varepsilon_{\phi } (\phi_{0} ,s)(\phi - \phi_{0} ), $$
(12)

where \(\varepsilon_{\phi}(\phi_{0} ,s)\) denotes the partial derivative of \( \varepsilon (\phi_{0} ,s) \) with respect to \( \phi \).

It is easy to see from Eq. (11) that the saddle point of Eq. (9), defined by \( f_{\phi } (\phi ) = 0 \), is \( \phi = \phi_{0} \). So we assume that in the vicinity of \( \phi_{0} \), which contributes most to Eq. (9), \( \varPhi (\phi ,s) \) can be replaced by \( \varPhi (\phi_{0} ,s) \). Then, the corresponding approximation of \( F(\phi ) \) and \( f(\phi ) \) takes the form

$$ \begin{aligned} F(\phi ) = \varPhi (\phi_{0} ,s)\sqrt {\frac{{\varepsilon (\phi_{0} ,s_{0} ) + \varepsilon_{\phi } (\phi_{0} ,s_{0} )(\phi - \phi_{0} )}}{{\varepsilon (\phi_{0} ,s) + \varepsilon_{\phi } (\phi_{0} ,s)(\phi - \phi_{0} ) + v_{0} r}}} \hfill \\ f(\phi ) = \frac{ - ir}{{v_{0} }} + \frac{ir}{{2v_{0} }}\left\{ {\frac{{\varepsilon (\phi_{0} ,s)(\phi - \phi_{0} )^{2} }}{{\varepsilon (\phi_{0} ,s) + v_{0} r}} + \frac{{v_{0} r\varepsilon_{\phi } (\phi_{0} ,s)(\phi - \phi_{0} )^{3} }}{{\left[ {\varepsilon (\phi_{0} ,s) + v_{0} r} \right]^{2} }}} \right\}. \hfill \\ \end{aligned} $$
(13)

Under the far-field condition, the latter expressions can be further reduced to

$$ \begin{aligned} F(\phi ) = \varPhi (\phi_{0} ,s)\sqrt {\frac{{\varepsilon (\phi_{0} ,s_{0} ) + \varepsilon_{\phi } (\phi_{0} ,s_{0} )(\phi - \phi_{0} )}}{{v_{0} r}}} \hfill \\ f(\phi ) = \frac{ - ir}{{v_{0} }} + \frac{i}{{2v_{0}^{2} }}\left[ {\varepsilon (\phi_{0} ,s)(\phi - \phi_{0} )^{2} + \varepsilon_{\phi } (\phi_{0} ,s)(\phi - \phi_{0} )^{3} } \right]. \hfill \\ \end{aligned} $$
(14)

Therefore, we obtain the approximate expression of Green’s function represented by the adaptive focused beam integral as

$$ G(r,\phi_{0} ) \approx \varPhi (\phi_{0} ,s)\frac{{\exp (i\omega r/v_{0} )}}{{\sqrt {v_{0} r} }}\varTheta , $$
(15)

where

$$ \varTheta = \int\limits_{{\phi_{0} - \pi /2}}^{{\phi_{0} + \pi /2}} {{\text{d}}\phi \left[ {\varepsilon (\phi_{0} ,s) + \varepsilon_{\phi } (\phi_{0} ,s)(\phi - \phi_{0} )} \right]^{1/2} } \exp \left\{ {\frac{i\omega }{{2v_{0}^{2} }}\left[ {\varepsilon (\phi_{0} ,s)(\phi - \phi_{0} )^{2} + \varepsilon_{\phi } (\phi_{0} ,s)(\phi - \phi_{0} )^{3} } \right]} \right\}. $$
(16)

Comparing Eq. (15) with the leading term in the expansion of Green’s function obtained by asymptotic ray theory (ART):

$$ G \approx \frac{{\exp \left[ {i\omega r/v_{0} + i\text{sgn} (\omega )\pi /4} \right]}}{{2\sqrt {2\pi \left| \omega \right|r/v} }}, $$
(17)

we obtain

$$ \varPhi (\phi_{0} ,s) = \frac{{v_{0} \exp (i\text{sgn} (\omega )\pi /4)}}{{2\sqrt {2\pi \left| \omega \right|} \varTheta }}. $$
(18)

In order to simplify the integral of Eq. (16), here we consider two extreme cases:

  1. Case 1

    \( \varepsilon_{\phi } (\phi_{0} ,s) = 0, \, \varepsilon (\phi_{0} ,s) \ne 0 \)

    $$ \varTheta = v_{0} \sqrt {\frac{2\pi }{i\omega }} , \, \varPhi (\phi_{0} ,s) = \frac{i}{4\pi } $$
    (19)
  2. Case 2

    \( \varepsilon _{\phi } (\phi _{0} ,s) \ne 0,{\text{ }}\varepsilon (\phi _{0} ,s) = 0, \)

    $$ \varTheta = \frac{2}{3}v_{0} \sqrt {\frac{2\pi }{i\omega }} , \, \varPhi (\phi_{0} ,s) = \frac{i}{6\pi } $$
    (20)

Case (1) means there is no variation of \( \varepsilon (\phi ,s) \) in the neighborhood of \( \phi_{0} \), and the corresponding integral coefficient is consistent with that proposed by Červený et al. (1982). Case (2) means there is strong variation of \( \varepsilon (\phi ,s) \) around \( \phi_{0} \), but the integral coefficient in this case is only the 2/3 times of that of case (1), which means \( \varPhi (\phi_{0} ,s) \) has only a relatively mild dependence on the beam parameter \( \varepsilon (\phi ,s) \). Thus, it appears reasonable to use the results of case (1), and we obtain the expression of Green’s function represented by the adaptive focused beam integral

$$ G(M,\omega ) = \frac{i}{4\pi }\int\limits_{{\phi_{0} - \pi /2}}^{{\phi_{0} + \pi /2}} {U_{\phi } (s,n,\omega ){\rm d}\phi } . $$
(21)

In order to demonstrate the validity of Eq. (21), we compare it with the analytic Green’s function calculated with ART in a homogeneous medium, where the velocity is 2000 m/s and the reference frequency and the data frequency are all 10 Hz. The results are shown in Fig. 4. It is easy to see that both the real and imaginary parts of the Green’s function calculated with the two methods are similar for most distances, except the real part in the shallow zone marked by the green arrow. One possible explanation is that an adaptive focused beam appears a plane wave at the initial point and its beam width is about a wavelength, which is not consistent with the point source wave-field calculated with Eq. (17). But the near-source error can be neglected in practical seismic modeling and imaging applications.

Fig. 4
figure 4

Real (a) and imaginary (b) parts of Green’s function calculated with ART and adaptive focused beam methods

Full size image

2.3 Adaptive focused beam migration formula

Nowack (2009) has used many local slant stacks and quadratic phase corrections for every beam in the dynamically focused beam migration, which is time-consuming and complex in designing the implementation algorithm. Here we adopt the single input-trace imaging approach of classical Kirchhoff migration to implement the adaptive focused migration. As a result, our method is more computer intensive than Hill’s method, but it is more efficient than Nowack’s method and can be accepted given the current level of computer power for an accurate depth image of subsurface geological structures.

The main point of our method is replacing the Green’s function by its approximate form in terms of the adaptive focused beam integral. From the latter section, we know the Green’s function from \({{\mathbf{x}}^{\prime}}\) to \( {\mathbf{x}} \) can be written as

$$ G({\mathbf{x}};{\mathbf{x}}';\omega ) = \frac{i}{4\pi }\int {{\text{d}}\phi } A({\mathbf{x}};{\mathbf{x}}')\exp \left[ {i\omega T({\mathbf{x}};{\mathbf{x}}')} \right]. $$
(22)

Here \( A({\mathbf{x}};{\mathbf{x}}') \) and \( T({\mathbf{x}};{\mathbf{x}}') \) are the complex amplitude and travel-time of the adaptive focused beam respectively, and they have the following form

$$ \begin{aligned} A({\mathbf{x}};{\mathbf{x}}') = \sqrt {\frac{{\varepsilon ({\mathbf{x}}')v({\mathbf{x}})}}{{\left[ {\varepsilon ({\mathbf{x}})q_{1} ({\mathbf{x}}) + q_{2} ({\mathbf{x}})} \right]v({\mathbf{x}}')}}} \hfill \\ T({\mathbf{x}};{\mathbf{x}}') = \tau ({\mathbf{x}};{\mathbf{x}}'){ + }\frac{1}{ 2}\frac{{\varepsilon ({\mathbf{x}})p_{1} ({\mathbf{x}}) + p_{2} ({\mathbf{x}})}}{{\varepsilon ({\mathbf{x}})q_{1} ({\mathbf{x}}) + q_{2} ({\mathbf{x}})}}n_{{\mathbf{x}}}^{2} , \hfill \\ \end{aligned} $$
(23)

where \( \varepsilon ({\mathbf{x}}) \) is the adaptive focused beam parameter defined in Eq. (5).

According to the true-amplitude GBM formula presented by Gray and Bleistein (2009), the up-going and down-going wave-fields can be written as

$$ \begin{aligned} P_{U} ({\mathbf{x}}^{\text{P}} ;{\mathbf{x}}^{\text{S}} ;\omega ) = - 2i\omega \int {\text{d}} r\frac{{\cos \phi^{\text{R}} }}{{v^{\text{R}} }}G^{*} ({\mathbf{x}}^{\text{P}} ;{\mathbf{x}}^{\text{R}} ;\omega )P_{U} ({\mathbf{x}}^{\text{R}} ;{\mathbf{x}}^{\text{S}} ;\omega ) \hfill \\ P_{D} ({\mathbf{x}}^{\text{P}} ;{\mathbf{x}}^{\text{S}} ;\omega ) = - 2i\omega \frac{{\cos \phi^{\text{S}} }}{{v^{\text{S}} }}G({\mathbf{x}}^{\text{P}} ;{\mathbf{x}}^{\text{S}} ;\omega ), \hfill \\ \end{aligned} $$
(24)

where \( {\mathbf{x}}^{\text{S}} \), \( {\mathbf{x}}^{\text{R}}, \) and \( {\mathbf{x}}^{\text{P}} \) are the Cartesian coordinates of source, receiver, and imaging point, respectively, \( \phi^{\text{S}} \) and \( \phi^{\text{R}} \) are the ray emergence angles from surface at source and receiver (see Fig. 5), \( P_{U} ({\mathbf{x}}^{\text{R}} ;{\mathbf{x}}^{\text{S}} ;\omega ) \) is the recorded wave-field, \( v^{\text{S}} \) and \( v^{\text{R}} \) are the velocity at source and receiver separately, “*” denotes the complex conjugate.

Fig. 5
figure 5

Scheme of adaptive focused beam migration

Full size image

Inserting Eq. (22) into Eq. (24) and using the deconvolution imaging condition

$$R({\mathbf{x}}^{P} ,{\mathbf{x}}^{\text{S} } ) = \frac{1}{2\pi }\frac{{\cos \phi^{\text{S} } }}{{v^{\text{S} } }}\int {{\text{d}}\omega } i\omega \frac{{P_{U} ({\mathbf{x}}^{P} ;{\mathbf{x}}^{\text{S}} ;\omega )P_{D}^{*} ({\mathbf{x}}^{P} ;{\mathbf{x}}^{\text{S} } ;\omega )}}{{P_{D} ({\mathbf{x}}^{P} ;{\mathbf{x}}^{\text{S} } ;\omega )P_{D}^{*} ({\mathbf{x}}^{P} ;{\mathbf{x}}^{\text{S} } ;\omega )}}.$$
(25)

We obtain the shot-domain adaptive focused beam migration formula

$$ \begin{aligned} R({\mathbf{x}}^{P} ,{\mathbf{x}}^{\text{S} } ) = \frac{ - 1}{{8\pi^{3} }}\frac{{\cos \phi^{\text{S} } }}{{v^{\text{S} } }}\int {{\text{d}}\omega } \int {{\text{d}}r} \frac{{i\omega^{3} }}{{P_{D} P_{D}^{*} }}\iint {{\text{d}}\phi^{\text{S} } {\text{d}}\phi^{\text{R}} } \hfill \\ \times \frac{{\cos \phi^{\text{S} } }}{{v^{\text{S} } }}\frac{{\cos \phi^{\text{R}} }}{{v^{\text{R}} }}A_{\text{S}}^{*} A_{\text{R}}^{*} \exp \left( { - i\omega T^{*} } \right)P_{U} ({\mathbf{x}}^{\text{R}} ,{\mathbf{x}}^{\text{S}} ,\omega ). \hfill \\ \end{aligned} $$
(26)

To reduce the computational cost, Gray and Bleistein (2009) used the stationary-phase approximation to simplify the double integral about the emergence angles of source and receiver. Here we adopt this accelerating strategy. Denoting

$$ \begin{aligned} \phi^{m} = \phi^{\text{S}} + \phi^{\text{R}} \hfill \\ \phi^{h} = \phi^{\text{R}} - \phi^{\text{S}}, \hfill \\ \end{aligned}$$
(27)

Equation (26) can be rewritten as

$$ \begin{aligned} R({\mathbf{x}}^{P} ,{\mathbf{x}}^{\text{S} } ) = \frac{ - 1}{{16\pi^{3} }}\frac{{\cos \phi^{\text{S} } }}{{v^{\text{S} } }}\int {{\text{d}}\omega } \int {{\text{d}}r} \frac{{i\omega^{3} }}{{P_{D} P_{D}^{*} }}\iint {{\text{d}}\phi^{m} {\text{d}}\phi^{h} } \hfill \\ \times \frac{{\cos \phi^{\text{S} } }}{{v^{\text{S} } }}\frac{{\cos \phi^{\text{R}} }}{{v^{\text{R}} }}A_{\text{S}}^{*} A_{\text{R}}^{*} \exp \left( { - i\omega T^{*} } \right)P_{U} ({\mathbf{x}}^{\text{R}} ,{\mathbf{x}}^{\text{S}} ,\omega ). \hfill \\ \end{aligned} $$
(28)

Further, using the stationary-phase approximation to calculate the inner integral with respect to \( \phi^{h} \) and the term of source illumination \( P_{D} P_{D}^{*} \), we obtain the final adaptive focused beam migration formula

$$\begin{aligned} R({\mathbf{x}}^{\text{P}} , {\mathbf{ x}}^{\text{S}} ) = \frac{ - 1}{{4\pi \sqrt {2\pi } }}\int {{\text{d}}\omega } \int {{\text{d}}r} \sqrt {i\omega }\omega \int {{\text{d}}\phi^{m} } \exp \left( { - i\omega T^{*} } \right) \hfill \\ \times \left( {\frac{{\cos \phi^{\text{S}} }}{{v^{\text{S}} }}} \right)^{2} \frac{{\cos \phi^{\text{R}} }}{{v^{\text{R}} }}\frac{{A_{\text{S}}^{*} A_{\text{R}}^{*} }}{{\left| {A_{\text{S}} } \right|^{2} }}\frac{{\left| {T_{\text{S}}^{{\prime \prime }} (\phi_{0}^{\text{S}} )} \right|}}{{\sqrt {T^{{*{\prime \prime }}} (\phi_{0}^{h} )} }}P_{U} ({\mathbf{x}}^{\text{R}} ,{\mathbf{x}}^{\text{S}} ,\omega ), \hfill \\ \end{aligned}$$
(29)

where

$$\begin{aligned} T = T({\mathbf{x}}^{\text{P}} ;{\mathbf{x}}^{\text{S}} ) + T({\mathbf{x}}^{\text{P}} ;{\mathbf{x}}^{\text{R}} ) \hfill \\ T_{\text{S}}^{{{\prime \prime }}} (\phi_{0}^{\text{S}} ) = \left[ {\frac{{q({\mathbf{x}}^{\text{S}} )q_{2} ({\mathbf{x}}^{\text{P}} )}}{{q({\mathbf{x}}^{\text{P}} )v^{2} ({\mathbf{x}}^{\text{S}} )}}} \right] \hfill \\ T^{{*{\prime \prime }}} (\phi_{0}^{h} ) = \left[ {\frac{{q({\mathbf{x}}^{\text{S}} )q_{2} ({\mathbf{x}}^{\text{P}} )}}{{q({\mathbf{x}}^{\text{P}} )v^{2} ({\mathbf{x}}^{\text{S}} )}} + \frac{{q({\mathbf{x}}^{\text{R}} )q_{2} ({\mathbf{x}}^{\text{P}} )}}{{q({\mathbf{x}}^{\text{P}} )v^{2} ({\mathbf{x}}^{\text{R}} )}}} \right]^{*} , \hfill \\ \end{aligned}$$
(30)

\( \phi_{0}^{h} \) is the stationary value, i.e., when \( \phi^{m} \) is fixed, \( \phi_{0}^{h} \) minimizes the imaginary part of the total time T. \( \phi_{0}^{\text{S}} \) and \( \phi_{0}^{\text{R}} \) are the corresponding emergence angles of source and receiver determined by Eq. (27).

3 Numerical examples

We present a hierarchy of numerical examples in this section. First, we use a simple horizontal layered model to test the amplitude-preserved property of the proposed method. Then, we carry out two applications of this method to the Marmousi dataset and the field data of a survey in East China, respectively.

To show how the adaptive focused beam migration works, we first apply it to a layered model in a medium with constant velocity of 2000 m/s, which simulates reflections from density contrasts as shown in Fig. 6a. Three horizontal reflectors with identical reflection coefficients are placed at depths of 2000, 3000, and 4000 m. A common-shot record shown in Fig. 6b, with a recording aperture of 3750 m on either side of the source, is migrated with our method, and the result is displayed in Fig. 6c. The normalized migration amplitude of reflectors and distances is shown in Fig. 7. Half-opening angles were limited to 50° in the migration.

Fig. 6
figure 6

Layered model and its migration result. a Density model, b single-shot record, c depth image migrated with the proposed method

Full size image
Fig. 7
figure 7

Normalized amplitude along reflectors (a) and at different distances (b) in Fig. 6c

Full size image

It is easy to see that the proposed method has eliminated the influences of offset and images the reflectors accurately (see Fig. 6c). On the other hand, the amplitude-preserved extrapolation formula and deconvolution imaging conditions have eliminated the reflection amplitude difference caused by the different incident angles (see Fig. 7a) and compensated the deep energy loss caused by geometric spreading (see Fig. 7b), leading to the migration amplitude being proportional to the vertical reflection coefficients in effective aperture. Migration aperture truncation artifacts marked by red arrows in Fig. 7a begin to interfere with the amplitudes at the distance corresponding to half-opening angles approaching 50°.

The second example is a synthetic dataset from the 2D Marmousi model as shown in Fig. 8a. The model is about 9.2 km long and 3 km deep, and is characterized by strong lateral velocity variations that cause complicated multipathing of the seismic energy. Because the smoothed velocity is required in ray-based migration for numerical stability in ray tracing, here we use a damped least squares algorithm to smooth the velocity (see Fig. 8b), which permits us to specify the degree of smoothing of the first- and second-order derivatives of the velocity (Popov et al. 2010). The depth images migrated with the Kirchhoff method and GBM with different initial widths l 0, one-way wave equation migration and the proposed method are shown in Fig. 9, where the migration aperture is about 5 km and frequency range is from 5 to 60 Hz.

Fig. 8
figure 8

Marmousi model: a the velocity used for simulation, b the smoothed velocity used for migration

Full size image
Fig. 9
figure 9

Depth images migrated from the Marmousi dataset: a Kirchhoff migration, b GBM with \( l_{0} = 0.25\lambda_{\text{avg}} \), c GBM with \( l_{0} = \lambda_{\text{avg}} \), d GBM with \( l_{0} = 2\lambda_{\text{avg}} \), e one-way wave equation migration, f adaptive focused beam migration. \( \lambda_{\text{avg}} \) denotes the average wavelength of the input velocity field and the reference frequency for GBM and our method is 10 Hz

Full size image

In general, all four methods have imaged the three main faults, pinch-outs, and the anticline at the bottom of the model. The Kirchhoff result shows lots of swing noise in the central deep parts with large lateral velocity variation, which blurs the steep-dip fault boundaries and the anticline (marked by blue arrows and green rectangle in Fig. 9a). Figure 9b–d shows the effects of the initial width on the imaging quality of GBM. It is noticed that both the shallow and the deep structures are blurred and destroyed in the image with initial width l 0 = 2λ avg (see the blue arrows and green rectangle in Fig. 9b). The reason is that the large initial width of the Gaussian beam makes its travel-time and amplitude extrapolation inaccurate in the vicinity of the whole ray. The migrated result with initial width l 0 = λ avg (the parameter proposed by Hill) appears relatively cleaner at depth, but small-scale geological structures in the shallow part are not defined well (see the blue arrows in Fig. 9c). That is because the Gaussian window width used in plane wave decomposition, which is calculated by the initial beam width, is still larger than the scale of shallow structures. Figure 9d shows good resolution in the shallow zone with initial width l 0 = 0.25λ avg (marked by the blue arrows in Fig. 9d), but low imaging accuracy at depth (see the green rectangle in Fig. 9d), which is caused by the beam width increasing rapidly when using a small initial width and becoming excessively large at deeper parts of the beam. The wave equation migration resolves the simple structures well, but it is unable to image the steep-dip faults accurately due to its one-way approximation (see the blue arrows in Fig. 9e). Adaptive focused beam migration, on the other hand, produces little migration noise (see the green rectangle in Fig. 9c), and defines the steep-dip structures clearly (see blue arrows in Fig. 9c). The reason is that adaptive focused beam is narrow and stable in propagation along the whole central ray, which is critical for imaging the structures with strong lateral velocity variations. It is worthy to note that our method also resolves the shallow part small-scale structures accurately (see the red ellipse in Fig. 9f). One possible explanation is that without slant stack, it reduces the beam spacing to trace spacing, which has the potential to improve the shallow resolution. As shown in Fig. 10, the proposed method has compensated the deep energy loss and makes the peak amplitude of the events basically consistent with the main reflection coefficient.

Fig. 10
figure 10

Comparison of the vertical reflection coefficient (the green line) with migration result produced with our method (the blue line) for the Marmousi model

Full size image

The computer run time of our method is about four times of that of GBM, which is caused by the increased beam number and the removal of local slant stack. Under the current computer power levels, however, it is acceptable for an accurate depth image.

The final example is from a 2D seismic survey in east China, which covers a basin edge with complex geological structures. As shown in Fig. 11a, the grid size of the velocity model is 809 × 1525 with a CDP spacing of 12.5 m and a depth sample of 4 m. A single-shot record of the field dataset processed with muting, traces-killing, and band-pass filtering is shown in Fig. 11b. The data were migrated using Kirchhoff migration, GBM, and our method, and the migrated results are shown in Fig. 12. Compared with Kirchhoff and GBM sections, the image migrated with our method is in general cleaner and the events are more continuous and better defined as indicated by the red arrows both at the shallow and the deep parts, which makes it more convenient for subsequent interpretation.

Fig. 11
figure 11

A seismic survey in east China: a velocity model, b a single-shot record

Full size image
Fig. 12
figure 12

Depth images of a 2D seismic survey in east China: a Kirchhoff method, b Gaussian beam method, c adaptive focused beam method. The images’ frequency is from 5 to 50 Hz, the migration aperture is about 5500 m, the initial width of GBM equals the average wavelength of the velocity model and the reference frequency of GBM and our method is also 10 Hz

Full size image

4 Conclusions

Using the information of the input velocity field to control the beams shape, we have developed an amplitude-preserved adaptive focused beam method for shot-domain prestack depth migration. This method represents an improvement over GBM while still retaining its advantages over Kirchhoff and wave equation migration, and is more robust in imaging geologically complex structures. The example with the constant-velocity model shows that our method can eliminate the effects of geometric spreading and incident angles on the migrated amplitude, producing a depth section with correct kinematic and dynamic information. The second example demonstrates that the adaptive focused beam method is superior to Kirchhoff and Gaussian beam methods in imaging steep-dip structures and producing less swing noise and fewer migration artifacts. More importantly, it shows that our method has high shallow resolution, which is helpful to define the shallow small-scale geological structures. The example of field data processing further confirms the conclusions obtained from the previous two examples and shows its potential in practical applications. Thus, adaptive focused beam migration provides a new robust and flexible tool for seismic depth imaging in geologically complex areas.