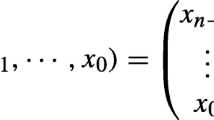A lower bound for differential uniformity by multiplicative complexity & bijective functions of multiplicative complexity 1 over finite fields

Abstract

The multiplicative complexity of an S-box over a finite field is the minimum number of multiplications needed to implement the S-box as an arithmetic circuit. In this paper we fully characterize bijective S-boxes with multiplicative complexity 1 up to affine equivalence over any finite field. We show that under affine equivalence in odd characteristic there are two classes of bijective functions and in even characteristic there are three classes of bijective functions with multiplicative complexity 1. Moreover, in (Jeon et al., Cryptogr. Commun., 14(4), 849-874 (2022)) A-boxes where introduced to lower bound the differential uniformity of an S-box over $\mathbb {F}_{2}^{n}$ via its multiplicative complexity. We generalize this concept to arbitrary finite fields. In particular, we show that the differential uniformity of a (n, m)-S-box over $\mathbb {F}_{q}$ is at least $q^{n - l}$, where $\lfloor \frac{n - 1}{2} \rfloor + l$ is the multiplicative complexity of the S-box.

1 Introduction

A natural performance measure for boolean circuits is the so-called multiplicative complexity, the minimal number of ${{\,\textrm{AND}\,}}$ gates needed to implement a circuit as ${{\,\textrm{AND}\,}}$-${{\,\textrm{XOR}\,}}$-${{\,\textrm{NOT}\,}}$ circuit. Though, for the design of boolean ciphers and hash functions the multiplicative complexity was only of minor concern in the past, because circuit implementations can be replaced by look-up tables. A prime example is the AES [1] S-box that operates on the finite field with $2^8$ elements

$$\begin{aligned} S: \mathbb {F}_{2^8}&\rightarrow \mathbb {F}_{2^8}, \\ x&\mapsto x^{2^8 - 2}, \end{aligned}$$

which can be implemented via a look-up table of size $2^8 \times 2^8$.

On the other hand, with the advancement of Zero-Knowledge (ZK) and Multi-Party Computation (MPC) multiplicative complexity became the major performance measure for cryptographic primitives that implement these protocols. First we note that ZK and MPC protocols operate on “big” finite fields $\mathbb {F}_q$ where typically $q \ge 2^{64}$ and in principle q can be a prime number instead of a power of two. If q is a prime, then the analog of the ${{\,\textrm{AND}\,}}$ gate is simply the multiplication gate which multiplies two elements, hence the name multiplicative complexity. Obviously, for fields of this size the memory requirement of look-up tables is too big, so one has to implement the circuit of a cryptographic primitive. The raison d’être for multiplicative complexity as performance measure is that for ZK protocols based on “MPC-in-the-head” the signature size increases proportionally to the number of multiplication gates in the underlying cryptographic primitive [2]. Also, for MPC protocols based on Yao’s garbled circuit [3, 4] the computational complexity depends on the number of multiplication gates in the underlying primitive.

Cryptographic primitives for efficient implementation of ZK and MPC are called Arithmetization-Oriented (AO) primitives. Examples of AO primitives are LowMC [5], MiMC [6], GMiMC [7], Hades [8], Jarvis [9], Poseidon [10], Vision and Rescue [11], Rescue-Prime [12] and Ciminion [13]. Although a lot of AO designs have already been proposed, their cryptanalysis is not well-understood yet. First, one has to generalize known cryptanalytic techniques over $\mathbb {F}_2$ or $\mathbb {F}_{2^n}$ to prime fields $\mathbb {F}_p$. Second, attack vectors that have been a minor concern in the past may become a viable threat, in particular Gröbner basis attacks [14]. Lastly, although most AO designs are very generic, so they can be instantiated over arbitrary finite fields, instantiating them over field extensions $\mathbb {F}_{2^n}$ can reduce the security compared to an instantiation over a prime field $\mathbb {F}_p$ of similar size. As example, let us take a look at MiMC whose keyed round function is defined as

$$\begin{aligned} R_{i}: \mathbb {F}_q&\times \mathbb {F}_q \rightarrow \mathbb {F}_q, \\&(x, k) \mapsto \left( x + k + c_i \right) ^{3}, \end{aligned}$$

where $c_i \in \mathbb {F}_q$ is a round constant. Note that cubing induces a permutation if and only if $\gcd \left( 3, q - 1 \right) = 1$. If we decide for $q = 2^{n}$ instead of a prime, then suddenly we have two possible models for $\texttt {MiMC}$. From the theory of finite fields it is well-known that

$$\begin{aligned} \mathbb {F}_{q^n} \cong \mathbb {F}_{q}^{n} \end{aligned}$$

as $\mathbb {F}_q$-vector spaces. So instead of the natural MiMC model over $\mathbb {F}_{2^n}$, we can also model it over $\mathbb {F}_2^n$, but over $\mathbb {F}_2$ one has an unique tool to analyze functions: the so-called algebraic normal form. Analysis of the degree growth of the algebraic normal form of MiMC yielded a slower than expected degree growth. Consequently, this property was exploited to mount a key recovery attack via a generalized higher-order differential attack on MiMC over binary fields [15].

Finally, for vectorial boolean functions

$$\begin{aligned} F: \mathbb {F}_2^n \rightarrow \mathbb {F}_2^m \end{aligned}$$

there already exists an established literature that connects multiplicative complexity with security parameters [16,17,18,19]. Therefore, the aim of this paper is to extend tools to analyze properties of functions via multiplicative complexity over binary fields to arbitrary finite fields.

1.1 Preliminaries & notation

In this paper, with $p \in \mathbb {Z}$ we always denote a prime number and with $q = p^e$ a prime power where $e \ge 1$. With $\mathbb {F}_q$ we denote the finite field with q elements, and with $\mathbb {F}_q^\times = \mathbb {F}_q \setminus \{0\}$ we denote the cyclic group of invertible elements. By ${{\,\textrm{char}\,}}\left( \mathbb {F}_q \right)$ we denote the characteristic of the field $\mathbb {F}_q$, i.e., the number of ones such that

$$\begin{aligned} 1 + \ldots + 1 = 0 \end{aligned}$$

in $\mathbb {F}_q$. If $\mathbb {F}_q$ is clear from context, then we call a function $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^m$ a (n, m)-S-box. Matrices $\textbf{M} \in \mathbb {F}_q^{n \times n}$ are denoted with bold capital letters, vectors are with lower capital letters $\textbf{v} \in \mathbb {F}_q^n$, and the matrix-vector product is denoted as $\textbf{M} \textbf{v}$. We denote the canonical basis of $\mathbb {F}_q^n$ with $\textbf{e}_1, \dots , \textbf{e}_n$, and the group of invertible $n \times n$ matrices over $\mathbb {F}_q$ is denoted as $\textrm{GL}_{n} ({\mathbb {F}_q})$. Since multiplications play a special role in this paper, we denote with $x \cdot y$ only the product of field elements $x, y \in \mathbb {F}_q$.

1.1.1 Arithmetic circuits

To properly define multiplicative complexity over arbitrary finite fields we need a proper generalization of ${{\,\textrm{AND}\,}}$-${{\,\textrm{XOR}\,}}$-${{\,\textrm{NOT}\,}}$ logic. Any function $F: \mathbb {F}_2^n \rightarrow \mathbb {F}_2$ can be constructed using only ${{\,\textrm{AND}\,}}$-${{\,\textrm{XOR}\,}}$-${{\,\textrm{NOT}\,}}$, on the other hand any function over a finite field can be expressed as polynomial. Moreover, one can express ${{\,\textrm{AND}\,}}$-${{\,\textrm{XOR}\,}}$-${{\,\textrm{NOT}\,}}$ with the following polynomials

$$\begin{aligned} {{\,\textrm{AND}\,}}\left( x, y \right) = x \cdot y, \qquad {{\,\textrm{XOR}\,}}\left( x, y \right) = x + y, \qquad {{\,\textrm{NOT}\,}}\left( x \right) = x + 1. \end{aligned}$$

Our route to generalize Boolean logic will be through polynomials. Any function $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q$ can be represented by a polynomial, moreover if we restrict the degree in each variable to be less than q, then the polynomial representing the function is unique. Therefore, we call the $\mathbb {F}_q$-algebra $\mathbb {F}_q [\textbf{X}_n] = \mathbb {F}_q [x_1, \dots , x_n] / \left( x_1^q - x_1, \dots , x_n^q - x_n \right)$ the algebra of polynomial valued functions. Moreover, we will use the terms function and polynomial synonymously throughout this paper.

Definition 1.1

Let $\mathbb {F}_q$ be a finite field. We call a polynomial in two variables $f \in \mathbb {F}_q [x, y]$ a binary gate. We call a finite subset of binary gates $\mathcal {F} \subset \mathbb {F}_q [x, y]$ a generating set, if any polynomial valued function $g \in \mathbb {F}_q [\textbf{X}_n]$, where $n \ge 1$, can be constructed using only $x_1, \dots , x_n$ and $\mathcal {F}$.

To construct any polynomial we definitely need a gate that represents multiplication, a gate that represents addition and a gate that adds a constant term, but if q is a prime power, then we need to introduce an additional gate, which will be called the cyclic gate, to construct all polynomials. The following theorem certainly is well-known, though we need it to properly define multiplicative complexity, and we need the explicit construction in the proof to generalize [16, Lemma 6].

Theorem 1.2

Let $\mathbb {F}_q$ be a finite field, and let $\alpha \in \mathbb {F}_q^\times$ be a generator. Then the gates

$$\begin{aligned} {\begin{matrix} {{\,\textrm{MUL}\,}}\left( x, y \right) &{}= x \cdot y, \\ {{\,\textrm{ADD}\,}}\left( x, y \right) &{}= x + y, \end{matrix}} \qquad \qquad {\begin{matrix} {{\,\textrm{CON}\,}}\left( x \right) &{}= x + 1, \\ {{\,\textrm{CYC}\,}}\left( x \right) &{}= \alpha \cdot x \end{matrix}} \end{aligned}$$

form a generating set.

Proof

Let $m = \beta \cdot x_1^{m_1} \cdots x_n^{m_n} \in \mathbb {F}_q [\textbf{X}_n]$ be a monomial. Note that any $x^k$ can be iteratively constructed via $x^k = {{\,\textrm{MUL}\,}}\left( x^{k - 1}, x \right)$, so we can construct the monomials $x_1^{m_1}, \dots , x_n^{m_n}$ via iterated ${{\,\textrm{MUL}\,}}$ gates and their product again via iteration of ${{\,\textrm{MUL}\,}}$ gates. For $\beta \in \mathbb {F}_{q}^{\times }$ there exists an $i \ge 0$ such that $\beta = \alpha ^i$. So after constructing $x_1^{m_1} \cdots x_n^{m_n}$ we apply ${{\,\textrm{CYC}\,}}$ i-times to arrive at m. If we have two monomials $m, n \in \mathbb {F}_q [\textbf{X}_n]$, then we can construct their sum $m + n$ via ${{\,\textrm{ADD}\,}}$. So we can construct any polynomial with constant term 0 using only ${{\,\textrm{MUL}\,}}$-${{\,\textrm{ADD}\,}}$-${{\,\textrm{CYC}\,}}$. Let $f, g \in \mathbb {F}_q [\textbf{X}_n]$ be such that $f (0) = \beta \in \mathbb {F}_{q}^{\times }$ and $g = f - \beta$. If $\beta = 1$ then $f = {{\,\textrm{CON}\,}}\left( g \right)$, so let’s assume $\beta \ne 1$. We again can find an $i, j \ge 0$ such that $\alpha ^i = \beta$ and $\alpha ^j = (1 - \beta )$. Now we apply the gates

$$\begin{aligned} {{\,\textrm{ADD}\,}}\Big ( {{\,\textrm{CYC}\,}}^{(j)} \left( g \right) , {{\,\textrm{CYC}\,}}^{(i)} \big ( {{\,\textrm{CON}\,}}\left( g \right) \big ) \Big ) = \left( 1 - \beta \right) \cdot g + \beta \cdot \left( g + 1 \right) = g + \beta , \end{aligned}$$

and the claim follows.$\square$

Remark 1.3

• 1. If q is a prime, then the gate ${{\,\textrm{CYC}\,}}$ is redundant, because for any $\beta \in \{ 0, \dots , q - 1 \}$ and any monomial $m = x_1^{m_1} \cdots x_n^{m_n}$ we can construct $\beta \cdot m$ by $(\beta - 1)$-fold application of ${{\,\textrm{ADD}\,}}$, i.e., $\beta \cdot m = {{\,\textrm{ADD}\,}}\big ( (\beta - 1) \cdot m, m \big )$.

• 2. If $q = 2$, then the gates ${{\,\textrm{MUL}\,}}$, ${{\,\textrm{ADD}\,}}$, ${{\,\textrm{CON}\,}}$ reduce to the Boolean gates ${{\,\textrm{AND}\,}}$, ${{\,\textrm{XOR}\,}}$, ${{\,\textrm{NOT}\,}}$.

Now we can define multiplicative complexity over any finite field.

Definition 1.4

Let $\mathbb {F}_q$ be a finite field, and let $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^m$ be a function. The multiplicative complexity ${{\,\textrm{MC}\,}}\left( F \right)$ of F is defined as the minimum number of ${{\,\textrm{MUL}\,}}$ gates needed to implement F in a ${{\,\textrm{ADD}\,}}$-${{\,\textrm{MUL}\,}}$-${{\,\textrm{CON}\,}}$-${{\,\textrm{CYC}\,}}$ circuit.

1.1.2 Differential uniformity

Differential cryptanalysis is one of the most important tools of modern cryptography [20] which studies how a difference in input values can effect the resulting difference in output values. The key measure to quantify whether a function is weak to differential cryptanalysis is the so-called differential uniformity.

Definition 1.5

Let $\mathbb {F}_q$ be a finite field, and let $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^m$ be a function.

• (1) The differential distribution table of F at $\textbf{a} \in \mathbb {F}_q^n$ and $\textbf{b} \in \mathbb {F}_q^m$ is defined as

  $$\begin{aligned} \delta _F (\textbf{a}, \textbf{b}) = \left| \{ \textbf{x} \in \mathbb {F}_q^n \mid F (\textbf{x} + \textbf{a}) - F (\textbf{x}) = \textbf{b} \} \right| . \end{aligned}$$

• (2) The differential uniformity of F is defined as

  $$\begin{aligned} \delta (F) = \max _{ \begin{array}{c} \textbf{a} \in \mathbb {F}_q^n \setminus \{ \textbf{0} \},\\ \textbf{b} \in \mathbb {F}_q^m \end{array} } \delta _F (\textbf{a}, \textbf{b}). \end{aligned}$$

1.1.3 Notions of equivalence

By linear functions we refer to functions that are given via matrix multiplication, and by affine functions we refer to functions that are given via matrix multiplication and addition of a non-zero constant. Throughout this paper we will characterize functions between vector spaces over finite fields with respect to the following equivalence notions.

Definition 1.6

Let $\mathbb {F}_q$ be a finite field, and let $F, G: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^m$ be two functions.

• (1) F and G are said to be linearly equivalent if there exist two linear permutations $A_1: \mathbb {F}_q^m \rightarrow \mathbb {F}_q^m$, $A_2: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ such that $A_1 \circ F = G \circ A_2$.

• (2) F and G are said to be affine equivalent if there exist two affine permutations $A_1: \mathbb {F}_q^m \rightarrow \mathbb {F}_q^m$, $A_2: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ such that $A_1 \circ F = G \circ A_2$.

• (3) F and G are said to be extended-affine equivalent if there exist two affine permutations $A_1: \mathbb {F}_q^m \rightarrow \mathbb {F}_q^m$, $A_2: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ and an affine function $A_3: \mathbb {F}_q^m \rightarrow \mathbb {F}_q^n$ such that $F (\textbf{x}) = (A_2 \circ G \circ A_1) (\textbf{x}) + A_3 (\textbf{x})$.

It is easy to see that these notions indeed define equivalence classes, moreover they preserve differential uniformity as well as multiplicative complexity.

1.2 Contributions

In the first part of this paper (Section 2) we extend the characterization of bijective functions with multiplicative complexity 1 up to affine equivalence from [16] to arbitrary finite fields. We show that in odd characteristic there are two classes of bijective functions and in even characteristic there are three classes of bijective functions up to affine equivalence.

Theorem 1.7

(Theorems 2.6 and 2.11) Let $\mathbb {F}_q$ be a finite field, let $n \ge 3$, let $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ be a bijective function with multiplicative complexity 1, and let

$$\begin{aligned}&\begin{aligned} \Lambda _n: \mathbb {F}_q^n&\rightarrow \mathbb {F}_q^n, \\ (x_1, \dots , x_n)&\mapsto (x_1 + x_{n - 1} \cdot x_n, x_2, \dots , x_n), \end{aligned} \\ \\&\begin{aligned} \Theta _n: \mathbb {F}_q^n&\rightarrow \mathbb {F}_q^n, \\ (x_1, \dots , x_n)&\mapsto (x_1 + x_2^2, x_2, \dots , x_n), \end{aligned} \\ \\&\begin{aligned} \Gamma _n: \mathbb {F}_q^n&\rightarrow \mathbb {F}_q^n, \\ (x_1, \dots , x_n)&\mapsto (x_1^2, x_2, \dots , x_n). \end{aligned} \end{aligned}$$

Then,

• (1) ([16, Theorem 1]) for $q = 2$, F is affine equivalent to $\Lambda _n$.

• (2) for $q = 2^m$ and $m \ge 2$, F is affine equivalent to either $\Lambda _n$, $\Theta _n$ or $\Gamma _n$.

• (3) for q odd, F is affine equivalent to either $\Lambda _n$ or $\Theta _n$.

If $q \ne 2$, then we obtain the following characterization in dimension 2.

Corollary 1.8

(Corollaries 2.7 and 2.12) Let $\mathbb {F}_q$ be a finite field, let $F: \mathbb {F}_q^2 \rightarrow \mathbb {F}_q^2$ be a bijective function with multiplicative complexity 1, and let

$$\begin{aligned}&\Theta _2: \mathbb {F}_q^2 \rightarrow \mathbb {F}_q^2, \qquad \qquad&\Gamma _2: \mathbb {F}_q^2&\rightarrow \mathbb {F}_q^2, \\&(x_1, x_2) \mapsto (x_1 + x_2^2, x_2), \qquad \qquad and \qquad \qquad&(x_1, x_2)&\mapsto (x_1^2, x_2). \end{aligned}$$

Then,

• (1) for $q = 2^m$ and $m \ge 2$, F is affine equivalent to either $\Theta _2$ or $\Gamma _2$.

• (2) for q odd, F is affine equivalent to $\Theta _2$.

In [19] the differential uniformity of a boolean function was lower bounded via its multiplicative complexity. In the second part of this paper (Section 3) we generalize their techniques to arbitrary finite fields. In particular, we derive the following lower bound for the differential uniformity in terms of multiplicative complexity.

Corollary 1.9

(Corollary 3.9) Let $\mathbb {F}_q$ be a finite field, and let S be a (n, m)-S-box.

• (1) If ${{\,\textrm{MC}\,}}\left( S \right) \le \left\lfloor \frac{n - 1}{2} \right\rfloor$, then $\delta (S) = q^n$.

• (2) If ${{\,\textrm{MC}\,}}\left( S \right) = \left\lfloor \frac{n - 1}{2} \right\rfloor + l$, then $\delta (S) \ge q^{n - l}$ for all $l \ge 0$.

Though, we also have to note that the number of multiplications is in general not an indicator whether also $\delta (S) < q^n$. In Example 3.7 we present an S-box over finite fields $\mathbb {F}_q$, where $q > 2$, with an arbitrary number of multiplications that always has maximal differential uniformity.

2 Bijective functions with multiplicative complexity 1

In this section we characterize bijections $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ with multiplicative complexity 1 up to affine equivalence.

2.1 Products of affine permutation polynomials

We call a polynomial $f \in \mathbb {F}_q [x_1, \dots , x_n]$ such that $f(x) = \sum _{i = 1}^{n} a_i \cdot x_i + a$, where $a_i, a \in \mathbb {F}_q$, an affine polynomial. As preparation, we need to establish that the product of two affine permutation polynomials is not a permutation polynomial.

Definition 2.1

([21, 7.34. Definition]) Let $\mathbb {F}_q$ be a finite field. A polynomial $f \in \mathbb {F}_q [x_1, \dots , x_n]$ is called a permutation polynomial in n indeterminates over $\mathbb {F}_q$ if the equation $f (x_1, \dots , x_n) = \alpha$ has $q^{n - 1}$ solutions in $\mathbb {F}_q^n$ for each $\alpha \in \mathbb {F}_q$.

Remark 2.2

In the computer science literature for characteristic 2 a function represented by a permutation polynomial is commonly called a balanced function.

Moreover, with the notion of orthogonal systems, see [21, 7.35. Definition], it is easy to see that any non-constant affine polynomial is a multivariate permutation polynomial.

That the product of two non-constant affine polynomials is not a permutation polynomial follows as corollary to two theorems of Niederreiter [22]. Two polynomials $f, g \in \mathbb {F}_q [x_1, \dots , x_n]$ are said to be equivalent if they can be transformed into each other via an affine change of variables $\textbf{x} = \textbf{A} \textbf{y} + \textbf{c}$, where $\textbf{A} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ and $\textbf{c} \in \mathbb {F}_{q}^{n}$.

Lemma 2.3

Let $\mathbb {F}_q$ be a finite field, let $p = {{\,\textrm{char}\,}}\left( \mathbb {F}_q \right)$, and let $f, g \in \mathbb {F}_q [x_1, \dots , x_n]$ be non-constant affine polynomials.

• (1) If $p = 2$ and $g \ne \alpha \cdot f$, where $\alpha \in \mathbb {F}_q^\times$, then $f \cdot g$ is not a permutation polynomial.

• (2) If $p > 2$, then $f \cdot g$ is not a permutation polynomial.

Proof

For (1), by [22, Theorem 3] a polynomial h of degree at most 2 in n variables in characteristic $p = 2$ is a permutation polynomial if and only if h is equivalent to a polynomial of the form $\hat{h} (x_1, \dots , x_{n - 1}) + x_n$ or $\hat{h} (x_1, \dots , x_{n - 1}) + x_n^2$. Let us now consider the product

$$\begin{aligned} h (\textbf{x}) = f (\textbf{x}) \cdot g (\textbf{x}) = \left( \sum _{i = 1}^{n} a_i x_i + a \right) \cdot \left( \sum _{i = 1}^{n} b_i x_i + b \right) . \end{aligned}$$

(1)

First we observe that if $g = \alpha \cdot f$, where $\alpha \in \mathbb {F}_q^\times$, then $h = \alpha \cdot f^2$. In characteristic two squaring induces a permutation, so h is a permutation polynomial. Therefore, we have to rule this case out. Now we do a case distinction on different values for the constant terms $a, b \in \mathbb {F}_q$.

Suppose $a, b = 0$, we have to make sure that for all variables $x_i$ such that $x_i^2$ is present in h at least one mixed term $x_i \cdot x_j$, $i \ne j$, is present, then the decomposition fails. Suppose there exists a variable for which all mixed terms vanish, say $x_1$, but $x_1^2$ is present in the product. Then we must have that

$$\begin{aligned} a_1 \cdot b_2 + a_2 \cdot b_1&= 0, \\ \vdots \\ a_1 \cdot b_n + a_n \cdot b_1&= 0. \end{aligned}$$

Of course, if $b_j \ne 0$, then also $a_j \ne 0$. Now we pick two indices $k, l \ge 2$ such that $a_k, b_l \ne 0$. We want to show that $a_k \cdot b_l + a_l \cdot b_l = 0$. We consider the equations

$$\begin{aligned} a_1 \cdot b_k + a_k \cdot b_1&= 0, \\ a_1 \cdot b_l + a_l \cdot b_1&= 0, \\ \Longrightarrow \\ a_1 \cdot b_k \cdot a_l + a_k \cdot b_1 \cdot a_l&= 0, \\ a_1 \cdot b_l \cdot a_k + a_l \cdot b_1 \cdot a_k&= 0, \\ \Longrightarrow \\ a_1 \cdot \left( a_k \cdot b_l + a_l \cdot b_k \right)&= 0. \end{aligned}$$

Hence, the mixed term $x_k \cdot x_l$ must also vanish. So, if all mixed terms in h that contain $x_1$ vanish but $a_1 \cdot b_1 \ne 0$, then all mixed terms in h must vanish. Consequently,

$$\begin{aligned} f (\textbf{x}) \cdot g (\textbf{x}) = \left( \sum _{i = 1}^{n} a_i \cdot b_i \cdot x_i^2 \right) = \left( \sum _{i = 1}^{n} \left( a_i \cdot b_i \right) ^{1 / 2} x_i \right) ^2, \end{aligned}$$

and therefore $g = \alpha \cdot f$, where $\alpha \in \mathbb {F}_q^\times$.

Now suppose $a \ne 0$ and $b = 0$, then any linear term of the product polynomial h must be present in a quadratic or mixed term, so the decomposition fails. By symmetry, we can conclude the same for $a = 0$ and $b \ne 0$.

For the last case $a, b \ne 0$, we rewrite

$$\begin{aligned} h (\textbf{x}) = \hat{f} (\textbf{x}) \cdot \hat{g} (\textbf{x}) + b \cdot \hat{f} (\textbf{x}) + a \cdot \hat{g} (\textbf{x}) + a \cdot b, \end{aligned}$$

where $\hat{f} = f - a$ and $\hat{g} = g - b$. Now we have to do a subcase distinction, if $b \cdot \hat{f} + a \cdot \hat{g} = 0$, then we can pass to the first case $\hat{a}, \hat{b} = 0$ to conclude that if h is a permutation polynomial, then $\hat{g} = \alpha \cdot \hat{f}$, where $\alpha \in \mathbb {F}_q^\times$. Consequently, this implies that $\alpha \cdot a + b = 0$ and that

$$\begin{aligned} g = \hat{g} + b = \alpha \cdot \hat{f} + \alpha \cdot a = \alpha \cdot f. \end{aligned}$$

On the other hand, if $b \cdot \hat{f} + a \cdot \hat{g} \ne 0$, then a decomposition of the form

$$\begin{aligned} h = \hat{h} (x_1, \dots , x_{n - 1}) + \lambda \cdot x_n, \end{aligned}$$

$\lambda \in \mathbb {F}_q^\times$, is impossible, because if the linear monomial $x_n$ is present in h, then the variable $x_n$ must also be present in at least one quadratic term of h. So, the decomposition must be of the form

$$\begin{aligned} h = \hat{h} (x_1, \dots , x_{n - 1}) + \lambda \cdot x_n^2, \end{aligned}$$

$\lambda \in \mathbb {F}_q^\times$, then we require that

$$\begin{aligned} a_n \cdot b + b_n \cdot a_n = 0. \end{aligned}$$

Thus, the product $\hat{f} \cdot \hat{g}$ may not contain any mixed terms with the variable $x_n$, but again this already implies that $\hat{g} = \alpha \cdot \hat{f}$ and also $\alpha \cdot a + b = 0$.

Finally, if $g = \alpha \cdot f$, then this property is invariant under any invertible affine coordinate change of the product polynomial $h = f \cdot g$. Further, any affine coordinate change of h will end up in one of the discussed cases. We have now established that if $h = f \cdot g$ is equivalent to a permutation polynomial, then $g = \alpha \cdot f$, where $\alpha \in \mathbb {F}_q$. By negation, if $g \ne \alpha \cdot f$, then h cannot be equivalent to a permutation polynomial.

For (2), by [22, Theorem 2] a polynomial f of degree at most 2 in n variables in characteristic $p > 2$ is a permutation polynomial if and only if f is equivalent to a polynomial of the form $g (x_1, \dots , x_{n - 1}) + x_n$. Again we do a case distinction. If $a, b = 0$, then trivially such a decomposition cannot exist.

Now suppose $a \ne 0$ and $b = 0$, then any linear term of the product must be present in a quadratic or mixed term so the decomposition fails. By symmetry, we can conclude the same for $a = 0$ and $b \ne 0$.

If $a, b \ne 0$, assume that $x_1$ is present in h. Now let us try to do the composition with $x_1$. If $a_1, b_1 \ne 0$, then $x_1^2$ must also be present in h, so the decomposition is impossible. Hence, either $a_1 \ne 0$ and $b_1 = 0$ or $a_1 = 0$ and $b_1 \ne 0$. If one of them is non-zero, then there still must be a mixed term $x_1 \cdot x_j$, $j \ne 1$, present in h since f and g are non-constant. (Also, recall that the mixed terms containing $x_1$ can only be canceled if $a_1, b_1 \ne 0$.) So the decomposition fails.

Again, under any invertible affine change of coordinates we end up in one of the three cases.$\square$

2.2 Odd characteristic

In [16, Lemma 4] a description of all bijections over $\mathbb {F}_2^n$ with multiplicative complexity 1 and constant term $\textbf{0}$ was given. Our first major step is to extend this result, though in odd characteristic we also need to account for squaring.

Lemma 2.4

Let $\mathbb {F}_q$ be a finite field with ${{\,\textrm{char}\,}}\left( \mathbb {F}_q \right) \ne 2$. Any bijective function $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ with $F (\textbf{0}) = \textbf{0}$, and multiplicative complexity 1, can be written in the form

$$\begin{aligned} F (\textbf{x}) = \textbf{M} \textbf{x} + \Big ( \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right) \Big ) \textbf{d}, \end{aligned}$$

where $\textbf{a}, \textbf{b}, \textbf{d} \in \mathbb {F}_q^n \setminus \{ \textbf{0} \}$, $\textbf{M} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$, and $\textbf{a}^\intercal \textbf{M}^{-1} \textbf{d} = \textbf{b}^\intercal \textbf{M}^{-1} \textbf{d} = 0$.

Proof

It is easy to see that any function of this form has multiplicative complexity at most 1, and that the expression covers all functions over $\mathbb {F}_q^n$ that can be realized with a single $\mathbb {F}_q$ multiplication. So it is left to show that the conditions are necessary.

For a contradiction suppose that $\textbf{M}$ is singular, and let $\textbf{u} \in \ker \left( \textbf{M} \right)$ be non-zero. For the pair $(\textbf{x}_1,\textbf{x}_2 = \textbf{x}_1 + \textbf{u})$ we have that $\textbf{M} \textbf{x}_1 = \textbf{M} \textbf{x}_2$. On the other hand, if F is a bijection, then we must have that $F (\textbf{x}_1) \ne F (\textbf{x}_2)$ or equivalently $F (\textbf{x}_1) - F (\textbf{x}_2) \ne \textbf{0}$. Therefore, we have that

$$\begin{aligned} {\begin{matrix} F (\textbf{x}_1) - F (\textbf{x}_2) = \Big ( \left( \textbf{a}^\intercal \textbf{x}_1 \right) \cdot \left( \textbf{b}^\intercal \textbf{x}_1 \right) &{}- \left( \textbf{a}^\intercal \textbf{x}_2 \right) \cdot \left( \textbf{b}^\intercal \textbf{x}_2 \right) \Big ) \textbf{d} \ne \textbf{0} \\ \Rightarrow \left( \textbf{a}^\intercal \textbf{x}_1 \right) \cdot \left( \textbf{b}^\intercal \textbf{x}_1 \right) &{}\ne \left( \textbf{a}^\intercal \textbf{x}_2 \right) \cdot \left( \textbf{b}^\intercal \textbf{x}_2 \right) . \end{matrix}} \end{aligned}$$

(2)

Let $g (\textbf{x}) = \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right)$, and suppose that g is not a permutation polynomial. Then there exists $\alpha \in \mathbb {F}_q$ such that $\left| g^{-1} (\alpha ) \right| > q^{n - 1}$. For every $\textbf{x} \in g^{-1} (\alpha )$ we define the sequence

$$\begin{aligned} \textbf{s}_\textbf{x}^{(j)} = {\left\{ \begin{array}{ll} \textbf{x}, &{} j = 0, \\ \textbf{x} + \beta ^{j - 1} \textbf{u}, &{} 1 \le j \le q - 1, \end{array}\right. } \end{aligned}$$

where $\beta \in \mathbb {F}_{q}^{\times }$ is a generator. For each $\textbf{x}$ and all $j \ne k$ the elements $\textbf{s}_\textbf{x}^{(j)}$ and $\textbf{s}_\textbf{x}^{(k)}$ are pairwise distinct but $\textbf{M} \textbf{s}_\textbf{x}^{(j)} = \textbf{M} \textbf{s}_\textbf{x}^{(k)}$. So by (2) we have that $g (\textbf{x}) \ne g \Big ( \textbf{s}_\textbf{x}^{(j)} \Big )$ for $1 \le j \le q - 1$. Suppose that for distinct $\textbf{x}_1, \textbf{x}_2 \in g^{-1} (\alpha )$ there exist $j \ne k$ such that $\textbf{s}_{\textbf{x}_1}^{(j)} = \textbf{s}_{\textbf{x}_2}^{(k)}$, then $\textbf{x}_2 = \textbf{x}_1 + \beta ^l \textbf{u}$ for some $1 \le l \le q - 1$ or $\textbf{x}_2 = \textbf{x}_1$. So either $\textbf{x}_2 \notin g^{-1} (\alpha )$ or $\textbf{x}_2 = \textbf{x}_1$, a contradiction for both cases. Therefore, for distinct $\textbf{x}_1$, $\textbf{x}_2$ the corresponding sequences are distinct. In particular, we have that

$$\begin{aligned} S= & {} \left\{ \left\{ \textbf{s}_\textbf{x}^{(j)} \right\} _{1 \le j \le q - 1} \, \vert \, \textbf{x} \in g^{-1} (\alpha ) \right\} \subset g^{-1} (\alpha )^\complement , \\ \vert S \vert= & {} (q - 1) \cdot \left| g^{-1} (\alpha ) \right| . \end{aligned}$$

Thus,

$$\begin{aligned} q^n = \left| g^{-1} (\alpha ) \right| + \left| g^{-1} (\alpha )^\complement \right| \ge \left| g^{-1} (\alpha ) \right| + \left| S \right| = q \cdot \left| g^{-1} (\alpha ) \right| > q^n. \end{aligned}$$

A contradiction, so g has to be a permutation polynomial. But this is a contradiction to Lemma 2.3 (2), so $\textbf{M}$ cannot be singular.

For another contradiction, assume that $\textbf{a}^\intercal \textbf{M}^{-1} \textbf{d} \ne 0$ or $\textbf{b}^\intercal \textbf{M}^{-1} \textbf{d} \ne 0$. Without loss of generality we can assume that $\textbf{a}^\intercal \textbf{M}^{-1} \textbf{d} = 1$ (and similar for $\textbf{b}$). By assumption F is a bijection, if we substitute $\textbf{y} = F (\textbf{x})$, then it is easy to see that $\textbf{a}^\intercal \textbf{M}^{-1} F (\textbf{x})$ is also a permutation polynomial (cf. [21, 7.39. Corollary]). Expanding the product we see that

$$\begin{aligned} \textbf{a}^\intercal \textbf{M}^{-1} F (\textbf{x})&= \textbf{a}^\intercal \textbf{M}^{-1} \textbf{M} \textbf{x} + \Big ( \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right) \Big ) \textbf{a}^\intercal \textbf{M}^{-1} \textbf{d} \\&= \textbf{a}^\intercal \textbf{x} + \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right) \\&= \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( 1 + \textbf{b}^\intercal \textbf{x} \right) . \end{aligned}$$

On the other hand, by Lemma 2.3 (2) the product of two affine polynomials cannot be a permutation polynomial.

It is left to show that every such F is indeed a bijection. Now suppose that F is not a bijection, but the conditions for $\textbf{a}$, $\textbf{b}$, $\textbf{d}$ and $\textbf{M}$ are satisfied. Let

$$\begin{aligned} G (\textbf{x}) = \textbf{M}^{-1} \textbf{x} - \Big ( \left( \textbf{a}^\intercal \textbf{M}^{-1} \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{M}^{-1} \textbf{x} \right) \Big ) \textbf{d}, \end{aligned}$$

then a simple computation, see Appendix A, yields that $(F \circ G) (\textbf{x}) = (G \circ F) (\textbf{x}) = \textbf{x}$. So F has a right and a left inverse, a contradiction. So F has to be a bijection. $\square$

The next lemma is trivial, though we state it for completeness.

Lemma 2.5

Let $\mathbb {F}_q$ be a finite field, and let $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ be a bijective function. Then F is affine equivalent to $F_\textbf{c} = F + \textbf{c}$ with $\textbf{c} \in \mathbb {F}_q^n$.

Now we are ready to prove the generalization of [16, Theorem 1] in odd characteristic.

Theorem 2.6

Let $\mathbb {F}_q$ be a finite field with ${{\,\textrm{char}\,}}\left( \mathbb {F}_q \right) \ne 2$, let $n \ge 3$, and let $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ be a bijective function with multiplicative complexity 1. Then F is affine equivalent to either

$$\begin{aligned} \Lambda _n: \mathbb {F}_q^n&\rightarrow \mathbb {F}_q^n, \\ (x_1, \dots , x_n)&\mapsto (x_1 + x_{n - 1} \cdot x_n, x_2, \dots , x_n), \\ {}&\text {or} \\ \Theta _n: \mathbb {F}_q^n&\rightarrow \mathbb {F}_q^n, \\ (x_1, \dots , x_n)&\mapsto (x_1 + x_2^2, x_2, \dots , x_n). \end{aligned}$$

Proof

By Lemma 2.5 and transitivity of affine equivalence we can restrict the proof to functions with constant term equal to zero, i.e., $F (\textbf{0}) = \textbf{0}$. Let $\textbf{e}_i \in \mathbb {F}_q^n$ have a 1 on the i-th position and else zeros. With Lemma 2.4 we can express $\Lambda _n$ as

$$\begin{aligned} \textbf{M} = \textbf{I}_{n \times n}, \quad \textbf{a} = \textbf{e}_{n - 1}, \quad \textbf{b} = \textbf{e}_n, \quad \textbf{d} = \textbf{e}_1, \end{aligned}$$

and similar for $\Theta _n$

$$\begin{aligned} \textbf{M} = \textbf{I}_{n \times n}, \quad \textbf{a} = \textbf{b} = \textbf{e}_{n - 1}, \quad \textbf{d} = \textbf{e}_1. \end{aligned}$$

For $i \ne j$ one clearly has that $\textbf{e}_i^\intercal \textbf{I}_{n \times n} \textbf{e}_j = 0$. Now we have to show that for any permissible choice of generators $\textbf{M} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$, $\textbf{a}, \textbf{b}, \textbf{d} \in \mathbb {F}_q^n \setminus \{ \textbf{0} \}$ from Lemma 2.4 we can find two invertible matrices $\textbf{A}, \textbf{B} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ such that either $F (\textbf{x}) = \textbf{B} \Lambda _n (\textbf{A} \textbf{x})$ or $F (\textbf{x}) = \textbf{B} \Theta _n (\textbf{A} \textbf{x})$. In particular, if $\textbf{a} \ne \alpha \cdot \textbf{b}$, where $\alpha \in \mathbb {F}_q^\times$, then we show equivalence to $\Lambda _n$ and if $\textbf{a} = \alpha \cdot \textbf{b}$, then we show equivalence to $\Theta _n$.

First let’s assume that $\textbf{a} \ne \alpha \cdot \textbf{b}$. Let $\textbf{A} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ be arbitrary, we denote the rows of $\textbf{A}$ by $\textbf{u}_i^\intercal = \textbf{e}_i^\intercal \textbf{A}$. Let $\textbf{B} = \textbf{M} \textbf{A}^{-1}$, then we have

$$\begin{aligned} F (\textbf{x}) = \textbf{B} \Lambda _n (\textbf{A} \textbf{x})&= \textbf{B} \textbf{A} \textbf{x} + \Big ( \left( \textbf{u}_{n - 1}^\intercal \textbf{x} \right) \cdot \left( \textbf{u}_n^\intercal \textbf{x} \right) \Big ) \textbf{B} \textbf{e}_1 \\&= \textbf{M} \textbf{x} + \Big ( \left( \textbf{u}_{n - 1}^\intercal \textbf{x} \right) \cdot \left( \textbf{u}_n^\intercal \textbf{x} \right) \Big ) \left( \textbf{M} \textbf{A}^{-1} \textbf{e}_1 \right) . \end{aligned}$$

By comparing these equations with Lemma 2.4 we must require that $\textbf{u}_{n - 1} = \textbf{a}$, $\textbf{u}_n = \textbf{b}$, and $\textbf{M} \textbf{A}^{-1} \textbf{e}_1 = \textbf{d}$. Since $\textbf{a}, \textbf{b} \ne \textbf{0}$ and $\textbf{a} \ne \alpha \cdot \textbf{b}$ we can conclude that the last two rows of $\textbf{A}$ are linearly independent. Since $\textbf{M}$ is invertible, we also have that $\textbf{A}^{-1} \textbf{e}_1 = \textbf{M}^{-1} \textbf{d}$. Now we see that

$$\begin{aligned} \textbf{u}_i^\intercal \textbf{M}^{-1} \textbf{d} = \textbf{e}_i^\intercal \textbf{A} \textbf{A}^{-1} \textbf{e}_1 = {\left\{ \begin{array}{ll} 1, &{} i = 1, \\ 0, &{} i \ne 1. \end{array}\right. } \end{aligned}$$

(3)

The conditions $\textbf{a}^\intercal \textbf{M}^{-1} \textbf{d} = \textbf{b}^\intercal \textbf{M}^{-1} \textbf{d} = \textbf{0}$ from Lemma 2.4 guarantee that these conditions hold for $\textbf{u}_{n - 1} = \textbf{a}$ and $\textbf{u}_n = \textbf{b}$. We can always choose the remaining $n - 3$ rows such that all $u_i$ are linearly independent and (3) holds. E.g., we can choose $\textbf{u}_1 = \textbf{e}_1$ and the remaining basis vectors. If we have a conflict $\textbf{u}_j \cdot \textbf{M}^{-1} \textbf{d} = \alpha \ne 0$, then we replace the vector with $\alpha ^{-1} \textbf{u}_j - \textbf{u}_1$.

For $\textbf{a} = \alpha \cdot \textbf{b}$, let us first take a look at

$$\begin{aligned} F (\textbf{x}) = \textbf{M} \textbf{x} + \alpha \cdot \left( \textbf{a}^\intercal \textbf{b} \right) ^2 \textbf{d}. \end{aligned}$$

Let $\textbf{N} = \alpha ^{-1} \cdot \textbf{1}_{n \times n}$, then we pass to $\textbf{N} F (\textbf{x})$. So without loss of generality we can assume that $\textbf{a} = \textbf{b}$, now we can in principle use the same strategy as in the first case to construct the affine equivalence to $\Theta _n$, though we have one more row of $\textbf{A}$ which can be chosen freely. $\square$

Corollary 2.7

Let $\mathbb {F}_q$ be a finite field with ${{\,\textrm{char}\,}}\left( \mathbb {F}_q \right) \ne 2$, and let $F: \mathbb {F}_q^2 \rightarrow \mathbb {F}_q^2$ be a bijective function with multiplicative complexity 1. Then F is affine equivalent to

$$\begin{aligned} {\begin{matrix} \Theta _2: \mathbb {F}_q^2 &{}\rightarrow \mathbb {F}_q^2, \\ (x_1, x_2) &{}\mapsto (x_1 + x_2^2, x_2). \end{matrix}} \end{aligned}$$

Remark 2.8

Let ${{\,\textrm{char}\,}}\left( \mathbb {F}_q \right) > 2$ and $\alpha \in \mathbb {F}_q^\times$, and suppose that for a bijective function $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ with ${{\,\textrm{MC}\,}}\left( F \right) = 1$ we have a decomposition as in Lemma 2.4. If $\textbf{a} \ne \alpha \cdot \textbf{b}$, then F is affine equivalent to $\Lambda _n$, and if $\textbf{a} = \alpha \cdot \textbf{b}$, then F is affine equivalent to $\Theta _n$.

For completeness, let us discuss that $\Lambda _n$ and $\Theta _n$ are not affine equivalent. Since only three variables are used in a non-trivial way it suffices to do the argument for $n = 3$. Assume that there exist matrices $\textbf{A}, \textbf{B} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ such that

$$\begin{aligned} \Theta _3 (\textbf{x}) = \textbf{B} \Lambda _3 (\textbf{A} \textbf{x}). \end{aligned}$$

(4)

Denote with $\textbf{a}_i \in \mathbb {F}_q^n$ the row vectors of $\textbf{A}$, then

$$\begin{aligned} \Lambda _3 (\textbf{A} \textbf{x}) = \begin{pmatrix} \textbf{a}_1 \textbf{x} + \left( \textbf{a}_2 \textbf{x} \right) \cdot \left( \textbf{a}_3 \textbf{x} \right) \\ \textbf{a}_2 \textbf{x} \\ \textbf{a}_3 \textbf{x} \end{pmatrix} . \end{aligned}$$

(5)

In the first component we must have the monomial $x_2^2$, but all other quadratic monomials must vanish since we cannot cancel them via $\textbf{B}$. Then our only possible choice is

$$\begin{aligned} \textbf{a}_2&= \left( 0, \alpha , 0 \right) , \end{aligned}$$

(6)

$$\begin{aligned} \textbf{a}_3&= \left( 0, \beta , 0 \right) , \end{aligned}$$

(7)

where $\alpha , \beta \in \mathbb {F}_q^\times$, but then $\textbf{A}$ is singular.

2.3 Even characteristic

For binary fields $\mathbb {F}_{2^n}$ with $n \ge 2$ squaring induces a proper permutation, hence for the characterization of bijections with multiplicative complexity 1 we also have to account for this case.

As preparation, we need a matrix decomposition from linear algebra. This decomposition was also used in [19, §2.2], since the authors did not provide a reference for this decomposition and we could not find it in the standard literature available to us, we provide a proof here.

Lemma 2.9

Let k be a field, and let $\textbf{M}, \textbf{N} \in k^{n \times m}$ be matrices such that $\textbf{M}$ is the reduced row echelon form of $\textbf{N}$. Then there exist matrices $\textbf{A} \in {{\,\textrm{GL}\,}}_{n} \left( k \right)$ and $\textbf{B} \in {{\,\textrm{GL}\,}}_{m} \left( k \right)$ such that $\textbf{N} = \textbf{A} \textbf{M}$ and $\textbf{N} = \textbf{M} \textbf{B}$.

Proof

Let ${{\,\textrm{rank}\,}}\left( \textbf{M} \right) = r$, any of the r row vectors of $\textbf{M}$ can be expressed as linear combinations of row vectors of $\textbf{N}$. We fill these combinations into the first r rows of $\textbf{A}$. Note that these rows have to be linearly independent, if they were not, then we could express at least one non-zero row of $\textbf{M}$ as linear combination of the other rows, a contradiction. Let $\textbf{m}_i$ and $\textbf{n}_i$ denote the row vectors of $\textbf{M}$ and $\textbf{N}$ respectively, for all $s > r$ we have that $\textbf{n}_1, \dots , \textbf{n}_s$ are linearly dependent. For every $r < s \le n$ we use such a linear dependence equation with $\alpha _s \ne 0$ and $\alpha _t = 0$, where $\alpha _s$ is the coefficient of $\textbf{n}_s$ in the combination and $s < t \le n$, and fill these coefficients into $\textbf{A}$. Clearly, we have that ${{\,\textrm{rank}\,}}\left( \textbf{A} \right) > r$, because at least the $(r + 1)$^th row is independent from the first r rows. Denote with $\textbf{a}_i = (a_{1,i}, \dots , a_{m, i})$ the row vectors of $\textbf{A}$ and suppose that ${{\,\textrm{rank}\,}}\left( \textbf{A} \right) = s < n$, then

$$\begin{aligned} \textbf{a}_{s + 1} = \sum _{i = 1}^{s} \beta _i \textbf{a}_i, \end{aligned}$$

(8)

for some $\beta _i \in k$. By construction of $\textbf{A}$ we now have that

$$\begin{aligned} \textbf{0}&= \sum _{j = 1}^{m} a_{j, s + 1} \textbf{n}_j = \sum _{j = 1}^{m} \sum _{i = 1}^{s} \beta _i a_{j, i} \textbf{n}_j = \sum _{i = 1}^{s} \beta _i \sum _{j = 1}^{m} a_{j, i} \textbf{n}_j \\&= \sum _{i = 1}^{r} \beta _i \sum _{j = 1}^{m} a_{j, i} \textbf{n}_j = \sum _{i = 1}^{r} \beta _i \textbf{m}_i. \end{aligned}$$

The second equality follows from (8), the third follows because we can always interchange finite sums, the fourth follows because for $i > s$ the $\textbf{n}_j$’s sum up to $\textbf{0}$, and the last equality follows from the construction of the first r rows of $\textbf{A}$. The $\textbf{m}_i$’s are a basis of the row space of $\textbf{N}$, therefore $\beta _i = 0$ for all i. Consequently,

$$\begin{aligned} \textbf{a}_{s + 1} = \sum _{i = r + 1}^{s} \beta _i \textbf{a}_i, \end{aligned}$$

but this is impossible because $\textbf{a}_{s + 1}$ has a non-zero component which is zero for all $\textbf{a}_i$ in the sum. A contradiction, so $\textbf{A}$ has to be of full rank.

For the second decomposition, the reduced row echelon form $\textbf{N}$ is an upper triangle matrix, therefore $\textbf{N}^\intercal$ is a lower triangle matrix which obviously has a lower triangle reduced row echelon form. Our proof of the decomposition $\textbf{N} = \textbf{A} \textbf{M}$ works equally well for a matrix $\textbf{N}'$ in lower triangle reduced row echelon form. So let $\textbf{N}'$ be the lower triangle reduced row echelon form of $\textbf{M}^\intercal$, then

$$\begin{aligned} \textbf{N} = \left( \textbf{N}' \right) ^\intercal = \left( \textbf{B}^\intercal \textbf{M}^\intercal \right) ^\intercal = \textbf{M} \textbf{B}. \end{aligned}$$

$\square$

Now we can prove the analog of Lemma 2.4 in even characteristic.

Lemma 2.10

Let $\mathbb {F}_q$ be a finite field with ${{\,\textrm{char}\,}}\left( \mathbb {F}_q \right) = 2$ and $q \ge 4$, and let $\alpha \in \mathbb {F}_q^\times$. Any bijective function $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ with $F (\textbf{0}) = \textbf{0}$, and multiplicative complexity 1, can be written in the form

$$\begin{aligned} F (\textbf{x}) = \textbf{M} \textbf{x} + \Big ( \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right) \Big ) \textbf{d}, \end{aligned}$$

where

• (1) $\textbf{a}, \textbf{b}, \textbf{d} \in \mathbb {F}_q^n \setminus \{ \textbf{0} \}$, $\textbf{a} \ne \alpha \cdot \textbf{b}$, $\textbf{M} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$, and $\textbf{a}^\intercal \textbf{M}^{-1} \textbf{d} = \textbf{b}^\intercal \textbf{M}^{-1} \textbf{d} = 0$, or

• (2) $\textbf{a}, \textbf{d} \in \mathbb {F}_q^n \setminus \{ \textbf{0} \}$, $\textbf{a} = \alpha \cdot \textbf{b}$, $\textbf{M} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$, and $\textbf{a}^\intercal \textbf{M}^{-1} \textbf{d} = 0$, or

• (3) $\textbf{a}, \textbf{d} \in \mathbb {F}_q^n \setminus \{ \textbf{0} \}$, $\textbf{a} = \alpha \cdot \textbf{b}$, $\textbf{M} \in \mathbb {F}_q^{n \times n}$ has rank $n - 1$, the matrix $\begin{pmatrix} \textbf{M} \\ \textbf{a}^\intercal \end{pmatrix}$ has rank n, and if $\textbf{A} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ is the invertible matrix such that $\textbf{N} = \textbf{A} \textbf{M}$ is the reduced row echelon form of $\textbf{M}$, then $\textbf{A} \textbf{d}$ has a non-zero entry on the zero row of $\textbf{N}$.

Proof

As in odd characteristic, it is easy to see that any function of these forms has multiplicative complexity at most 1, and that the expressions cover all functions over $\mathbb {F}_q^n$ that can be realized with a single $\mathbb {F}_q$ multiplication. The arguments for necessity when $\textbf{M} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ are identical to Lemma 2.4, though this time we apply Lemma 2.3 ().

So let $\textbf{M} \notin {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ and assume that we are given an equation

$$\begin{aligned} F (\textbf{x}) = \textbf{M} \textbf{x} + \alpha \cdot \left( \textbf{a}^\intercal \textbf{x} \right) ^2 \textbf{d} = \textbf{c}, \end{aligned}$$

(9)

with $\textbf{c} = (c_1, \dots , c_n) \in \mathbb {F}_q^n$. By Lemma 2.9 there exists a matrix $\textbf{A} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ such that $\textbf{N} = \textbf{A} \textbf{M}$ is in reduced row echelon form. Thus, we can rewrite the previous equation system as

$$\begin{aligned} \textbf{N} \textbf{x} + \left( \textbf{a}^\intercal \textbf{x} \right) ^2 \textbf{A}\textbf{d} = \textbf{A} \textbf{c}. \end{aligned}$$

(10)

For the system to admit a unique solution we need n equations, so if j is the index of a zero row of $\textbf{N}$, then we must have that $\left( \textbf{A} \textbf{d} \right) _j \ne 0$. Suppose that ${{\,\textrm{rank}\,}}\left( \textbf{M} \right) \le n - 2$, then $\textbf{N}$ has at least two zero rows, then (10) has two linearly dependent quadratic equations, i.e., the system does not admit a unique solution. Therefore, we must have that ${{\,\textrm{rank}\,}}\left( M \right) = n - 1$. Now let us explicitly write out the system of equations

$$\begin{aligned} \sum _{ \begin{array}{c} k = 1 \\ i \ne j \end{array} }^{n} N_{i, k} \cdot x_k + \hat{d}_i \cdot \left( \textbf{a}^\intercal \textbf{x} \right) ^2&= \hat{c}_i, \quad 1 \le i < n \\ \hat{d}_n \cdot \left( \textbf{a}^\intercal \textbf{x} \right) ^2&= \hat{c}_n, \end{aligned}$$

where $\hat{\textbf{d}} = \textbf{A} \textbf{d}$ and $\varvec{\hat{c}} = \textbf{A} \textbf{c}$. We can use the last equation to transform the system into $n - 1$ linear equations and one quadratic equation. Moreover, in characteristic 2 squaring induces a permutation, i.e., by raising the last equation to the power q/2 we can find a unique $\tilde{c}_j \in \mathbb {F}_q$ such that

$$\begin{aligned} \textbf{a}^\intercal \textbf{x} = \tilde{c}_j. \end{aligned}$$

So we can transform the system of equations into a linear one which admits a solution if and only if the matrix $\begin{pmatrix} \textbf{A} \textbf{M} \\ (\textbf{A} \textbf{d})_n \textbf{a}^\intercal \end{pmatrix}$ has rank n. Obviously, this is also equivalent to the matrix $\begin{pmatrix} \textbf{M} \\ \textbf{a}^\intercal \end{pmatrix}$ having full rank.

Now suppose that the conditions for one of the three cases are satisfied, but F is not a bijection. For each case we already derived a unique procedure to find a unique solution to (9). (For the first two cases again see Appendix A.) A contradiction, so F has to be a bijection. $\square$

Now we can generalize [16, Theorem 1] to field extensions of $\mathbb {F}_2$.

Theorem 2.11

Let $\mathbb {F}_q$ be a finite field with ${{\,\textrm{char}\,}}\left( \mathbb {F}_q \right) = 2$ and $q \ge 4$, let $n \ge 3$, and let $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ be a bijective function with multiplicative complexity 1. Then F is affine equivalent to either

$$\begin{aligned} \Lambda _n: \mathbb {F}_q^n&\rightarrow \mathbb {F}_q^n, \\ (x_1, \dots , x_n)&\mapsto (x_1 + x_{n - 1} \cdot x_n, x_2, \dots , x_n), \\ {}&\text {or} \\ \Theta _n: \mathbb {F}_q^n&\rightarrow \mathbb {F}_q^n, \\ (x_1, \dots , x_n)&\mapsto (x_1 + x_2^2, x_2, \dots , x_n), \\ {}&\text {or} \\ \Gamma _n: \mathbb {F}_q^n&\rightarrow \mathbb {F}_q^n, \\ (x_1, \dots , x_n)&\mapsto (x_1^2, x_2, \dots , x_n). \end{aligned}$$

Proof

In the situations () and () of Lemma 2.10 we can use the same strategy as in Theorem 2.6 to establish affine equivalence with $\Lambda _n$ and $\Theta _n$ respectively. So we only have to prove case (). Let $\textbf{a}, \textbf{b} \in \mathbb {F}_q^n \setminus \{ \textbf{0} \}$ be such that $\textbf{a} = \alpha \cdot \textbf{b}$, where $\alpha \in \mathbb {F}_q^\times$. Then

$$\begin{aligned} F (\textbf{x}) = \textbf{M} \textbf{x} + \alpha \cdot \left( \textbf{b}^\intercal \textbf{x} \right) ^2 \textbf{d}. \end{aligned}$$

Let $\textbf{N} = \alpha ^{-1} \cdot \textbf{1}_{n \times n}$, then

$$\begin{aligned} \textbf{N} \textbf{F} (\textbf{x}) = \alpha ^{-1} \cdot \textbf{M} \textbf{x} + \left( \textbf{b}^\intercal \textbf{x} \right) ^2 \textbf{d}. \end{aligned}$$

So without loss of generality we can assume that $\textbf{a} = \textbf{b}$.

Let us now construct the affine equivalence. $\Gamma _n$ can be written as

$$\begin{aligned} \Gamma _n (\textbf{x}) = \begin{pmatrix} 0 &{} 0 &{} \dots &{} 0 \\ 0 &{} 1 &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \dots &{} 1 \end{pmatrix} \textbf{x} + \left( \textbf{e}_1^\intercal \textbf{x} \right) ^2 \textbf{e}_1 \end{aligned}$$

We want to find $\textbf{A}, \textbf{B} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ such that $F (\textbf{x}) = \textbf{B} \Gamma _n (\textbf{A} \textbf{x})$. We require that $\textbf{e}_1^\intercal \textbf{A} = \textbf{a}^\intercal$ and $\textbf{B} \textbf{e}_1 = \textbf{d}$. Without loss of generality we can assume that

$$\begin{aligned} \textbf{M} = \begin{pmatrix} \textbf{M}_1 \\ \textbf{0}^\intercal \\ \textbf{M}_2 \end{pmatrix} . \end{aligned}$$

If $\textbf{M}$ is not of this form, then we apply Lemma 2.9 to find $\textbf{C} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ such that $\textbf{N} = \textbf{C} \textbf{M}$ is in row echelon form of rank $n - 1$, so it has a zero row. Since we try to find equivalence up to affine transformations we can replace $F (\textbf{x})$ by $\textbf{C} F (\textbf{x})$ and permute the components of the resulting mapping. Moreover, we must have that

$$\begin{aligned} \textbf{M} = \begin{pmatrix} \textbf{M}_1 \\ \textbf{0}^\intercal \\ \textbf{M}_2 \end{pmatrix} = \underbrace{ \begin{pmatrix} \textbf{d}&\textbf{b}_2&\dots&\textbf{b}_n \end{pmatrix} }_ {= \textbf{B}} \begin{pmatrix} 0 &{} 0 &{} \dots &{} 0 \\ 0 &{} 1 &{} \dots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \dots &{} 1 \end{pmatrix} \underbrace{ \begin{pmatrix} \textbf{a}^\intercal \\ \textbf{a}_2^\intercal \\ \vdots \\ \textbf{a}_n^\intercal \end{pmatrix} }_{= \textbf{A}} = \begin{pmatrix} \textbf{0}&\textbf{b}_2&\dots&\textbf{b}_n \end{pmatrix} \begin{pmatrix} \textbf{a}^\intercal \\ \textbf{a}_2^\intercal \\ \vdots \\ \textbf{a}_n^\intercal \end{pmatrix} . \end{aligned}$$

Let j be the index of the zero row of $\textbf{M}$, for the $\textbf{b}_i$’s we pick all canonical unit vectors $\textbf{e}_i$ except for $\textbf{e}_j$. Note that $\textbf{d}_j \ne 0$, else we would not have a permutation in Lemma 2.10, and henceforth $\textbf{B}$ has full rank. Now the last equation becomes

$$\begin{aligned} \begin{pmatrix} \textbf{M}_1 \\ \textbf{0}^\intercal \\ \textbf{M}_2 \end{pmatrix} = \begin{pmatrix} \textbf{0}&\textbf{e}_1&\dots&\textbf{e}_{j - 1}&\textbf{e}_{j + 1}&\dots&\textbf{e}_n \end{pmatrix} \begin{pmatrix} \textbf{a}^\intercal \\ \textbf{a}_2^\intercal \\ \vdots \\ \textbf{a}_n^\intercal \end{pmatrix} = \begin{pmatrix} \textbf{a}_2^\intercal \\ \vdots \\ \textbf{a}_j^\intercal \\ \textbf{0}^\intercal \\ \textbf{a}_{j + 1}^\intercal \\ \vdots \\ \textbf{a}_n^\intercal \end{pmatrix} . \end{aligned}$$

By the conditions from Lemma 2.10 the matrix on the left-hand side has rank $n - 1$, so we have a unique solution for the $\textbf{a}_i$’s. Finally, by construction

$$\begin{aligned} \textbf{A} = \textbf{D} \begin{pmatrix} \textbf{M}_1 \\ \textbf{a}^\intercal \\ \textbf{M}_2 \end{pmatrix} , \end{aligned}$$

where $\textbf{D} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ is a suitable reordering of the rows, has full rank. $\square$

Corollary 2.12

Let $\mathbb {F}_q$ be a finite field with ${{\,\textrm{char}\,}}\left( \mathbb {F}_q \right) = 2$ and $q \ge 4$, and let $F: \mathbb {F}_q^2 \rightarrow \mathbb {F}_q^2$ be a bijective function with multiplicative complexity 1. Then F is affine equivalent to either

$$\begin{aligned} {\begin{matrix} \Theta _2: \mathbb {F}_q^2 &{}\rightarrow \mathbb {F}_q^2, \\ (x_1, x_2) &{}\mapsto (x_1 + x_2^2, x_2), \end{matrix}} \quad \qquad \text {or} \quad \qquad {\begin{matrix} \Gamma _2: \mathbb {F}_q^2 &{}\rightarrow \mathbb {F}_q^2, \\ (x_1, x_2) &{}\mapsto (x_1^2, x_2). \end{matrix}} \end{aligned}$$

Remark 2.13

Let ${{\,\textrm{char}\,}}\left( \mathbb {F}_q \right) = 2$, $q \ge 4$ and $\alpha \in \mathbb {F}_q^\times$, and suppose that for a bijective function $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ with ${{\,\textrm{MC}\,}}\left( F \right) = 1$ we have a decomposition as in Lemma 2.10. If $\textbf{a} \ne \alpha \cdot \textbf{b}$, then F is affine equivalent to $\Lambda _n$, if $\textbf{a} = \alpha \cdot \textbf{b}$ and $\textbf{M} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$, then F is affine equivalent to $\Theta _n$, and if $\textbf{a} = \alpha \cdot \textbf{b}$ and $\textbf{M} \notin {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$, then F is affine equivalent to $\Gamma _n$.

For completeness, let us again discuss that $\Lambda _n$, $\Theta _n$ and $\Gamma _n$ are not affine equivalent. For $\Lambda _n$ and $\Theta _n$ the argument is identical to the one in odd characteristic, see the end of Section 2.2. For $\Theta _n$ and $\Gamma _n$ it suffices to reduce to $n = 2$, note that for all $a, b \in \mathbb {F}_q^\times$ one has

$$\begin{aligned} \left( a \cdot x_1 + b \cdot x_2 \right) ^2 = a^2 \cdot x_1^2 + b^2 \cdot x_2^2. \end{aligned}$$

(11)

Thus, any affine change of coordinates for $\Gamma _2$ is unable to produce the required polynomial $x_1 + x_2^2$. For $\Lambda _n$ and $\Gamma _n$ is suffices to reduce to $n = 3$. Let $\textbf{A} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$ and denote with $\textbf{a}_{i} \in \mathbb {F}_{q}^{n}$ its rows. Note that

$$\begin{aligned} \left( \sum _{i = 1}^{3} \textbf{a}_i \mathbf {x_i} \right) ^2 \end{aligned}$$

cannot contain any monomial $x_i \cdot x_j$, where $i \ne j$. So one can never produce the required polynomial $x_1 + x_2 \cdot x_3$.

3 M-Boxes and differential uniformity

In [19] a new tool was introduced to describe properties of a (n, m)-S-box S over $\mathbb {F}_2$: the associated A-box $S_A$. Conceptually, the A-box $S_A$ collects all ${{\,\textrm{AND}\,}}$-gates of a ${{\,\textrm{AND}\,}}$-${{\,\textrm{XOR}\,}}$-${{\,\textrm{NOT}\,}}$ circuit that implements S in a vector. Then one can construct S from $S_A$ by applying an affine function. Since we want to generalize this tool to arbitrary finite fields we will define the so-called M-box which contains all multiplications of an arithmetic circuit for an S-box.

3.1 Expansion–compression lemma

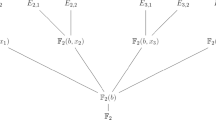
In [16, Lemma 6] a process was given to construct any function $F: \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ with multiplicative complexity ${{\,\textrm{MC}\,}}\left( F \right) \le c$ and $F (\textbf{0}) = \textbf{0}$ by extending iteratively with single multiplications to $\mathbb {F}_q^{n + c}$ and then contracting back to $\mathbb {F}_2^n$ via a linear map. The proof of [16, Lemma 6] can be applied over any finite field, for completeness we summarize the main idea of the proof. Let $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ be any function with multiplicative complexity ${{\,\textrm{MC}\,}}\left( F \right) \le c$, by Theorem 1.2 we have a circuit for F using at most c many ${{\,\textrm{MUL}\,}}$ gates. Iteratively, we compute each ${{\,\textrm{MUL}\,}}$ gate and append its output to $\textbf{x}$, this way we end up with a vector $\textbf{z} \in \mathbb {F}_q^{n + c}$ which contains all monomials that are present in the polynomial vector representation of F. Now one can apply a linear function to construct F. Moreover, with this lemma we have a well-defined procedure to extract all multiplications in an S-box into a new associated function.

Lemma 3.1

(Expansion–Compression Lemma [16, Lemma 6]) Let $\mathbb {F}_q$ be a finite field, let

$$\begin{aligned} {\begin{matrix} E_n: \mathbb {F}_q^n &{}\rightarrow \mathbb {F}_q^{n + 1}, \\ \textbf{x} &{}\mapsto \begin{pmatrix} \textbf{x}, \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right) \end{pmatrix} , \end{matrix}} \end{aligned}$$

with $\textbf{a}, \textbf{b} \in \mathbb {F}_q^n \setminus \{ \textbf{0} \}$, and let $C_{m, n}: \mathbb {F}_q^{m} \rightarrow \mathbb {F}_q^n$ be a linear map. Any function $F: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$ with $F (\textbf{0}) = \textbf{0}$, and multiplicative complexity ${{\,\textrm{MC}\,}}\left( F \right) \le c$ can be written as composition

$$\begin{aligned} F = C_{n + c, n} \circ E_{n + c - 1} \circ \cdots \circ E_{n}. \end{aligned}$$

We will refer to the $E_i$’s as expansion functions. Moreover, we denote the vectors that define the i^th expansion function by $\textbf{b}_i$ and $\textbf{b}_{i + 1}$ and refer to them as i^th partner vectors. The tuple $\left( \textbf{b}_1, \dots , \textbf{b}_{2k + 1} \right)$ will be called the partner tuple.

3.2 Definition of the M-box

With Lemma 3.1 we can decompose any (n, m)-S-box S with ${{\,\textrm{MC}\,}}\left( S \right) \le k$ into an expansion part and a compression part. (We now allow affine transformations in the compression to adjust for the constant term.) The output of the expansion part consists of two parts, n elements for the input $\textbf{x} \in \mathbb {F}_q^n$, we call this part the identity part, and k elements that are the output of ${{\,\textrm{MUL}\,}}$ gates, we call this part the multiplication part or simply ${{\,\textrm{MUL}\,}}$-part. We can interpret the ${{\,\textrm{MUL}\,}}$-part as a (n, k)-S-box, which we therefore define as an M-box. We denote the M-box associated to an S-box S by $S_M$, obviously we have also that ${{\,\textrm{MC}\,}}\left( S_M \right) \le k$. Let’s formalize the concept of M-boxes in mathematical terms.

Definition 3.2

(M-box, cf. [19, Definition 1]) Let $\mathbb {F}_q$ be a finite field, and Let $\textbf{x} \in \mathbb {F}_q^n$ and $\textbf{y} \in \mathbb {F}_q^k$ be the input and output, respectively, of a (n, k)-S-box $S_M$. For 2k vectors $\textbf{b}_1, \textbf{b}_2 \in \mathbb {F}_q^n, \dots , \textbf{b}_{2k}, \textbf{b}_{2k + 1} \in \mathbb {F}_q^{n + k}$ that satisfy the following inductive properties, $S_M$ is called a (n, k)-M-box.

• (i) $y_1 = \left( \textbf{b}_1^\intercal \textbf{x} \right) \cdot \left( \textbf{b}_2^\intercal \textbf{x} \right)$.

• (ii) For $2 \le i \le k$, $y_i = \big ( \textbf{b}_{i}^\intercal \left( \textbf{x}, y_1, \dots , y_{i - 1} \right) \big ) \cdot \big ( \textbf{b}_{i + 1}^\intercal \left( \textbf{x}, y_1, \dots , y_{i - 1} \right) \big )$.

For a (n, k)-M-box $S_M$, $\textbf{b}_{2i - 1}$ and $\textbf{b}_{2i}$ are called the i^th partner vectors for all i, and $\left( \textbf{b}_1, \dots , \textbf{b}_{2k} \right)$ is called the partner tuple of $S_M$.

Provided a circuit $\mathcal {C}_S$ for the (n, m)-S-box S such that ${{\,\textrm{MC}\,}}\left( S \right) \le k$ is given, then it is straight-forward to extract a circuit $\mathcal {C}_{S_M}$ for a corresponding (n, k)-M-box $S_M$. We build $\mathcal {C}_{S_M}$ inductively in k layers. First we collect all the multiplication gates in $\mathcal {C}_S$, then we pick one multiplication gate which can be built only with linear combinations of the input $\textbf{x} \in \mathbb {F}_q^n$. In the first layer of $\mathcal {C}_{S_M}$ we now construct the multiplication gate and denote its output by $y_1$. Next we pick a multiplication gate that only requires $\textbf{x}$ and $y_1$ as input, then we construct this gate in the second layer of $\mathcal {C}_{S_M}$ and denote its output by $y_2$. Inductively, we now run-through all remaining multiplication gates until we have constructed all multiplication gates of $\mathcal {C}_S$. This yields a circuit for $\mathcal {C}_{S_M}$. Of course from the construction of $\mathcal {C}_{S_M}$ we can also extract a set of suitable partner vectors $\textbf{b}_1, \textbf{b}_2, \dots , \textbf{b}_{2k - 1}, \textbf{b}_{2k}$.

3.3 Equivalence classes of M-boxes

For this section we fix some notation, with $T_\textbf{A}: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^m$ we will always denote a linear function $T_\textbf{A} (\textbf{x}) = \textbf{A} \textbf{x}$, where $\textbf{A} \in \mathbb {F}_q^{n \times m}$.

Using Lemma 3.1 and Definition 3.2 we can decompose a (n, m)-S-box S as

$$\begin{aligned} S (\textbf{x}) = T \Big ( \big ( \textbf{x}, S_M (\textbf{x}) \big ) \Big ) + \textbf{c}, \end{aligned}$$

(12)

for a (n, k)-M-box $S_M$, a linear function $T: \mathbb {F}_q^{m + k} \rightarrow \mathbb {F}_q^n$, and $\textbf{c} \in \mathbb {F}_q^n$. The linear function T can be further decomposed into a M-box part and an identity part, i.e., there are $T_\textbf{N}: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^m$ and $T_{\varvec{N'}}: \mathbb {F}_q^{k} \rightarrow \mathbb {F}_q^m$ such that

$$\begin{aligned} T \Big ( \big ( \textbf{x}, S_M (\textbf{x}) \big ) \Big ) = T_\textbf{N} (\textbf{x}) + T_{\varvec{N'}} \big ( S_M (\textbf{x}) \big ). \end{aligned}$$

(13)

(Note that in the last equation we considered the natural extension of $T_\textbf{N}$ and $T_{\varvec{N'}}$ to $\mathbb {F}_q^{n + k} \rightarrow \mathbb {F}_q^m$.) With Lemma 2.9 we can further rewrite (13) as

$$\begin{aligned} T \Big ( \big ( \textbf{x}, S_M (\textbf{x}) \big ) \Big ) = T_\textbf{N} (\textbf{x}) + (T_\textbf{D} \circ T_\textbf{M} \circ S_M) (\textbf{x}), \end{aligned}$$

(14)

where $\textbf{M} \in \mathbb {F}_q^{m \times k}$ is a matrix in reduced row echelon form and $\textbf{D} \in {{\,\textrm{GL}\,}}_{m} \left( \mathbb {F}_q \right)$. I.e., we have established extended-affine equivalence between S and $T_\textbf{M} \circ S_M$. We technically summarize this construction in the following theorem which generalizes [19, Theorem 1].

Theorem 3.3

Let $\mathbb {F}_q$ be a finite field. For any (n, m)-S-box S with ${{\,\textrm{MC}\,}}\left( S \right) \le k$, there exists a matrix $\textbf{M} \in \mathbb {F}_q^{m \times k}$ in reduced row echelon form and a (n, k)-M-box $S_M$ such that $T_\textbf{M} \circ S_M$ is extended-affine equivalent to S. If ${{\,\textrm{MC}\,}}\left( S \right) = k$, then $S_M$ is called suitable for S.

Now let’s characterize equivalence for M-boxes. For two linear permutations $T_\textbf{A}: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$, $T_\textbf{B}: \mathbb {F}_q^m \rightarrow \mathbb {F}_q^m$ a (n, m)-M-box $S_M$ is clearly linearly equivalent to $T_\textbf{B} \circ S_M \circ T_\textbf{A}$. Substituting this equivalence into (14) we obtain that

$$\begin{aligned} T_\textbf{D} \circ T_\textbf{M} \circ S_M = T_\textbf{D} \circ T_\textbf{M} \circ T_\textbf{B} \circ S_M \circ T_\textbf{A} = T_{\textbf{D}'} \circ T_{\textbf{M}'} \circ S_M \circ T_\textbf{A} \end{aligned}$$

(15)

for an invertible matrix $\textbf{D}' \in \mathbb {F}_q^{m \times m}$, and a matrix $\textbf{M}' \in \mathbb {F}_q^{m \times k}$ in reduced row echelon form. Therefore, we can reduce our search for equivalent M-boxes to $S_M \circ T_\textbf{A}$ which leads to the generalization of [19, Theorem 2].

Theorem 3.4

Let $\mathbb {F}_q$ be a finite field. For a (n, k)-M-box $S_M$ and a linear permutation $T_\textbf{L}: \mathbb {F}_q^n \rightarrow \mathbb {F}_q^n$, let $S_M' = S_M \circ T_\textbf{L}$, which is a M-box linearly equivalent to $S_M$. If $(\textbf{b}_1, \dots , \textbf{b}_{2k})$ is a partner tuple of $S_M$, then the following $(\textbf{b}_1', \dots , \textbf{b}_{2k + 1}')$ is a partner tuple of $S_M'$ such that

$$\begin{aligned} \begin{aligned} \textbf{b}_{2i - 1}'&= T_{\textbf{L}_i^\intercal } (\textbf{b}_{2i - 1}), \\ \textbf{b}_{2i}'&= T_{\textbf{L}_i^\intercal } (\textbf{b}_{2i}), \end{aligned} \end{aligned}$$

where $\textbf{L}_i = \begin{pmatrix} \textbf{L} &{} \textbf{0}_{n \times (i - 1)} \\ \textbf{0}_{(i - 1) \times n} &{} \textbf{I}_{(i - 1) \times (i - 1)} \end{pmatrix}$ for $1 \le i \le k$.

Proof

The proof of [19, Theorem 2] does not depend on $\mathbb {F}_2$, therefore we can apply it for any finite field. For a thorough presentation we repeat the arguments. We denote with $S_M (\textbf{x}) = \textbf{y}$ and $S_M \circ T_\textbf{L} (\textbf{x}) (\textbf{x}) = (z_1, \dots , z_k)$. Now we expand the inductive definition of the M-box to obtain

$$\begin{aligned} z_1&= \left( \textbf{b}_1^\intercal T_\textbf{L} (\textbf{x}) \right) \cdot \left( \textbf{b}_2^\intercal T_\textbf{L} (\textbf{x}) \right) \\&= \left( T_\mathbf {L^\intercal } (\textbf{b}_1)^\intercal \textbf{x} \right) \cdot \left( T_\mathbf {L^\intercal } (\textbf{b}_2)^\intercal \textbf{x} \right) . \end{aligned}$$

So $T_\mathbf {L^\intercal } (\textbf{b}_1)$ and $T_\mathbf {L^\intercal } (\textbf{b}_2)$ become new partner vectors and we denote

$$\begin{aligned} \textbf{b}_1' = T_\mathbf {L^\intercal } (\textbf{b}_1), \quad \textbf{b}_2' = T_\mathbf {L^\intercal } (\textbf{b}_2). \end{aligned}$$

Continuing,

$$\begin{aligned} z_2&= \Big ( \textbf{b}_3^\intercal \big ( T_\textbf{L} (\textbf{x}), z_1 \big ) \Big ) \cdot \Big ( \textbf{b}_4^\intercal \big ( T_\textbf{L} (\textbf{x}), z_1 \big ) \Big ) \\&= \left( \textbf{b}_3^\intercal T_{\textbf{L}_1} (\textbf{x}, z_1) \right) \cdot \left( \textbf{b}_4^\intercal T_{\textbf{L}_1} (\textbf{x}, z_1 \right) \\&= \left( T_{\mathbf {L_1^\intercal }} (\mathbf {b_3})^\intercal (\textbf{x}, z_1) \right) \cdot \left( T_{\mathbf {L_1^\intercal }} (\mathbf {b_4})^\intercal (\textbf{x}, z_1) \right) , \end{aligned}$$

where

$$\begin{aligned} \textbf{L}_2 = \begin{pmatrix} \textbf{L} &{} \textbf{0}_{n \times 1} \\ \textbf{0}_{1 \times n} &{} \textbf{1}_{1 \times 1} \end{pmatrix} . \end{aligned}$$

Again, we denote

$$\begin{aligned} \textbf{b}_3' = T_{\textbf{L}_2^\intercal } (\textbf{b}_3), \quad \textbf{b}_4' = T_{\textbf{L}_2^\intercal } (\textbf{b}_4). \end{aligned}$$

Inductively repeating this process we obtain that

$$\begin{aligned} \textbf{L}_i&= \begin{pmatrix} \textbf{L} &{} \textbf{0}_{n \times (i - 1)} \\ \textbf{0}_{(i - 1) \times n} &{} \textbf{I}_{(i - 1) \times (i - 1)} \end{pmatrix} , \\ \textbf{b}_{2i - 1}'&= T_{\textbf{L}_i^\intercal } (\textbf{b}_{2i - 1}) \\ \textbf{b}_{2i}'&= T_{\textbf{L}_i^\intercal } (\textbf{b}_{2i}) \\ z_i&= \left( \mathbf {b'_{2i - 1}}^\intercal (\textbf{x}, z_1, \dots , z_{i - 1}) \right) \cdot \left( \mathbf {b'_{2i}}^\intercal (\textbf{x}, z_1, \dots , z_{i - 1}) \right) . \end{aligned}$$

This yields a (n, k)-M-box $S_M' = S_M \circ T_\textbf{L}$. $\square$

3.4 Lower bounds of differential uniformity via multiplicative complexity

Since differential uniformity is invariant under extended-affine equivalence it suffices to consider a (n, m)-S-box $S = T_\textbf{M} \circ S_M$ with a suitable M-box $S_M$ and a matrix $\textbf{M}$ in reduced row echelon form. Moreover, differential uniformity is preserved under affine equivalence, therefore without loss of generality we can assume that the affine permutations from the extended-affine equivalence are the identity permutations and that S is constant free. I.e.,

$$\begin{aligned} S = T_\textbf{M} \circ S_M + T_\textbf{C}, \end{aligned}$$

(16)

where $T_\textbf{C}$ is a linear function. So, for any $\textbf{x}, \textbf{a} \in \mathbb {F}_q^n$ we have that

$$\begin{aligned} S (\textbf{x} + \textbf{a}) - S (\textbf{x}) = T_\textbf{M} \circ \big ( S_M (\textbf{x} + \textbf{a}) - S_M (\textbf{x}) \big ) + T_\textbf{C} (\textbf{a}). \end{aligned}$$

(17)

Consequently, for any $\textbf{b} \in \mathbb {F}_q^m$ and $\hat{\textbf{b}} = T_\textbf{M} (\textbf{b}) + T_\textbf{C} (\textbf{a})$ we have the following inclusion of sets

$$\begin{aligned}&\left\{ \textbf{x} \in \mathbb {F}_q^n \mid S_M (\textbf{x} + \textbf{a}) - S_M (\textbf{x}) = \textbf{b} \right\} \\ \subseteq&\left\{ \textbf{x} \in \mathbb {F}_q^n \mid T_\textbf{M} \circ \big ( S_M (\textbf{x} + \textbf{a}) - S_M (\textbf{x}) \big ) = T_\textbf{M} (\textbf{b}) \right\} \\ =&\left\{ \textbf{x} \in \mathbb {F}_q^n \mid T_\textbf{M} \circ \big ( S_M (\textbf{x} + \textbf{a}) - S_M (\textbf{x}) \big ) = \hat{\textbf{b}} - T_\textbf{C} (\textbf{a}) \right\} \\ =&\left\{ \textbf{x} \in \mathbb {F}_q^n \mid S (\textbf{x} + \textbf{a}) - S (\textbf{x}) = \hat{\textbf{b}} \right\} . \end{aligned}$$

Moreover, this inclusion of sets implies that

$$\begin{aligned} \delta (S)&= \delta (T_\textbf{M} \circ S_m + T_\textbf{C}) \ge \delta _S \big ( \textbf{a}, \hat{\textbf{b}} \big ) \\&\ge \delta _{S_M} \big ( \textbf{a}, T_\textbf{M} (\textbf{b}) \big ) \ge \delta _{S_M} (\textbf{a}, \textbf{b}), \end{aligned}$$

which also implies that

$$\begin{aligned} \delta (S) \ge \delta (S_M). \end{aligned}$$

(18)

Hence, to prove lower bounds on S-boxes it suffices to prove lower bounds for (suitable) M-boxes. Note that technically we never used the assumption that $S_M$ is suitable to derive Inequality (18). Though, we will see in Theorem 3.8 that with suitable M-boxes we derive the highest upper bounds.

For partner vectors $\textbf{b}_i$ of a M-box we denote with $\textbf{b}_i\vert ^{n}$ the restriction to the first n entries of $\textbf{b}_i$. The input difference vectors $\textbf{a}$ such that $\left( \textbf{b}_i \vert ^{n} \right) ^{\intercal } \textbf{a} = 0$ form a vector space which will be called complementable space. In the following lemma, which generalizes [19, Lemma 1], we collect the key properties of complementable spaces.

Lemma 3.5

Let $\mathbb {F}_q$ be a finite field, and let $S_M$ be a (n, k)-M-box. Define the set $\mathcal {C}_{S_M} \subset \mathbb {F}_q^n$ of all $\textbf{a} \in \mathbb {F}_q^n$ satisfying $\left( \textbf{b}_i\vert ^{n} \right) ^\intercal \textbf{a} = 0$ for all partner vectors $\textbf{b}_i$ to be a complementable space of $S_M$. The complementable space $\mathcal {C}_{S_M}$ has the following properties.

• (1) For $\textbf{a} \in \mathcal {C}_{S_M}$, $S_M (\textbf{a}) = \textbf{0}$.

• (2) For $\textbf{a} \in \mathcal {C}_{S_M}$ and $\textbf{x} \in \mathbb {F}_q^n$, $S_M (\textbf{x}) = S_M (\textbf{x} + \textbf{a})$.

• (3) If there is a non-zero vector in $\mathcal {C}_{S_M}$, then $\delta (S_M) = q^n$.

Proof

The proof of [19, Lemma 1] does not depend on $\mathbb {F}_2$ therefore we can apply it for any finite field. For a thorough presentation we repeat the arguments. For (1), let $\textbf{a} \in \mathcal {C}_{S_M}$ and $S_M = (f_1, \dots , f_k)$. By assumption

$$\begin{aligned} f_1 (\textbf{a}) = \left( \textbf{b}_1^\intercal \textbf{a} \right) \cdot \left( \textbf{b}_2^\intercal \textbf{a} \right) = 0, \end{aligned}$$

inductively we now continue

$$\begin{aligned} f_i (\textbf{a}) = \left( \textbf{b}_{2i - 1}^\intercal (\textbf{a}, \textbf{0}_{i - 1}) \right) \cdot \left( \textbf{b}_{2i}^\intercal (\textbf{a}, \textbf{0}_{i - 1}) \right) = 0. \end{aligned}$$

Therefore, $S_M (\textbf{a}) = \textbf{0}$.

For (2), let $S_M (\textbf{x}) = \left( y_1, \dots , y_k \right)$ and $S_M (\textbf{x} + \textbf{a}) = (y_1', \dots , y_k')$. We show per induction that $y_i = y_i'$. For $i = 1$,

$$\begin{aligned} y_1'&= \left( \textbf{b}_1^\intercal \left( \textbf{x} + \textbf{a} \right) \right) \cdot \left( \textbf{b}_2^\intercal \left( \textbf{x} + \textbf{a} \right) \right) \\&= \left( \textbf{b}_1^\intercal \textbf{x} + \textbf{b}_1^\intercal \textbf{a} \right) \cdot \left( \textbf{b}_2^\intercal \textbf{x} + \textbf{b}_2^\intercal \textbf{a} \right) \\&= \left( \textbf{b}_1^\intercal \textbf{x} \right) \cdot \left( \textbf{b}_2^\intercal \textbf{x} \right) = y_1. \end{aligned}$$

Suppose now that the claim is true for $2 \le i \le k - 1$, then

$$\begin{aligned} y_i'&= \Big ( \textbf{b}_{2i - 1}^\intercal \left( \textbf{x} + \textbf{a}, y_1', \dots , y_{i - 1}' \right) \Big ) \cdot \Big ( \textbf{b}_{2i}^\intercal \left( \textbf{x} + \textbf{a}, y_1', \dots , y_{i - 1}' \right) \Big ) \\&= \left( \textbf{b}_{2i - 1}^\intercal \left( \textbf{x} + \textbf{a}, y_1, \dots , y_{i - 1} \right) \right) \cdot \left( \textbf{b}_{2i}^\intercal \left( \textbf{x} + \textbf{a}, y_1, \dots , y_{i - 1} \right) \right) \\&= \Big ( \textbf{b}_{2i - 1}^\intercal \left( \textbf{x}, y_1, \dots , y_{i - 1} \right) + \left( \textbf{b}_{2i - 1}\vert ^n \right) ^\intercal \textbf{a} \Big ) \cdot \Big ( \textbf{b}_{2i}^\intercal \left( \textbf{x}, y_1, \dots , y_{i - 1} \right) + \left( \textbf{b}_{2i}\vert ^n \right) ^\intercal \textbf{a} \Big ) \\&= y_i. \end{aligned}$$

Lastly, (3) follows from (2) because $S_M (\textbf{x} + \textbf{a}) = S_M (\textbf{a})$ for all $\textbf{x} \in \mathbb {F}_q^n$, so $\delta (S_M) = \delta _{S_M} (\textbf{a}, \textbf{0}) = q^n$. $\square$

So, for k large enough can one ensure that $\mathcal {C}_{S_M} = \{ \textbf{0} \}$? We already mentioned that $\mathcal {C}_{S_M}$ is a linear space. We define the matrix of transposed truncated partner vectors as

$$\begin{aligned} \textbf{A} = \begin{pmatrix} \textbf{b}_1\vert ^{n}&\dots&\textbf{b}_{2k + 1}\vert ^{n} \end{pmatrix} ^\intercal , \end{aligned}$$

(19)

then by definition we can view $\mathcal {C}_{S_M}$ as the following kernel

$$\begin{aligned} \mathcal {C}_{S_M} = \ker \left( \textbf{A} \right) = \left\{ \textbf{x} \in \mathbb {F}_q^n \mid \textbf{A} \textbf{x} = \textbf{0} \right\} . \end{aligned}$$

(20)

If k is increased by one, then two more rows are appended to $\textbf{A}$. For the complementable space to be trivial we need that ${{\,\textrm{rank}\,}}\left( \textbf{A} \right) = n$. Therefore, we have the necessary condition that

$$\begin{aligned} k > \left\lfloor \frac{n - 1}{2} \right\rfloor . \end{aligned}$$

(21)

This leads to the generalization of [19, Theorem 3].

Theorem 3.6

Let $\mathbb {F}_q$ be a finite field, and let $S_M$ be a (n, k)-M-box. If $k \le \left\lfloor \frac{n - 1}{2} \right\rfloor$, then $\delta (S_M) = q^n$.

In [19, §3.1] it was established that this condition is sufficient over $\mathbb {F}_2$. Essentially, this is due to $x^2 = x$ in $\mathbb {F}_2$. Unfortunately, this condition cannot be sufficient over other finite fields as one can see from the following counterexample.

Example 3.7

Let $\mathbb {F}_q$ be a finite field. We consider the map

$$\begin{aligned} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \mapsto \begin{pmatrix} (x_1 + x_2) \cdot x_3 \\ \big ( (x_1 + x_2) \cdot x_3 \big )^2 \\ \vdots \\ \big ( (x_1 + x_2) \cdot x_3 \big )^{2k} \end{pmatrix} , \end{aligned}$$

for some $k \ge 1$. For any finite field with $q > 2$ this defines an $(3, k + 1)$-M-box. Obviously, for $k \ge 1$ we have more than $\left\lfloor \frac{3 - 1}{2} \right\rfloor = 1$ multiplications. On the other hand, for any $k \ge 1$ the matrix of the restricted partner vectors has only two non-zero vectors.

We conclude that over finite fields different from $\mathbb {F}_2$ having many multiplications does not suffice, we need sufficiently many elementary multiplications for the complementable space to be trivial. We will shortly revisit this notion in Section 3.5 and prove an efficient criterion for an S-box not having sufficiently many elementary multiplications.

On the other hand, the lower bound from [19, Theorem 4] can be generalized independently from this observation.

Theorem 3.8

Let $\mathbb {F}_q$ be a finite field, and let $S_M$ be a (n, k)-M-box. If $k = \left\lfloor \frac{n - 1}{2} \right\rfloor + l$, then $\delta (S_M) \ge q^{n - l}$ for all $l \ge 0$.

Proof

We can generalize the proof of [19, Theorem 3], though we have to account for more than two field elements. We do induction on l, for $l = 0$ we can apply Theorem 3.6. Now suppose that the theorem holds for $l > 0$, we consider a $(n, k + 1)$-M-box $S_M$, where $k = \left\lfloor \frac{n - 1}{2} \right\rfloor + l$. If we consider $S_M\vert _k$, i.e., $S_M$ without the last ${{\,\textrm{MUL}\,}}$ gate, then by our induction hypothesis $\delta (S_M\vert _k) \ge q^{n - l}$. On the other hand, we have the following equality of sets

$$\begin{aligned}&\left\{ \textbf{x} \in \mathbb {F}_q^n \mid S_M\vert _k (\textbf{x} + \textbf{a}) - S_M\vert _k (\textbf{x}) = \textbf{b} \right\} \\&= \bigcup _{\alpha \in \mathbb {F}_q} \left\{ \textbf{x} \in \mathbb {F}_q^n \mid S_M (\textbf{x} + \textbf{a}) - S_M (\textbf{x}) = (\textbf{b}, \alpha ) \right\} . \end{aligned}$$

We can now conclude from the pigeonhole principle that at least for one $\alpha \in \mathbb {F}_q$ we have that $\delta _{S_M} \big ( \textbf{a}, (\textbf{b}, \alpha ) \big ) \ge q^{n - l - 1}$. Therefore, we have that $\delta (S_M) \ge q^{n - l - 1}$.$\square$

One should keep in mind that only if the M-box has sufficiently many elementary multiplications, then the inequality could become non-trivial, else the differential uniformity is always maximal.

Combining Theorems 3.3, 3.6, 3.8 we now obtain the generalization of [19, Corollary 1].

Corollary 3.9

Let $\mathbb {F}_q$ be a finite field, and let S be a (n, m)-S-box.

• (1) If ${{\,\textrm{MC}\,}}\left( S \right) \le \left\lfloor \frac{n - 1}{2} \right\rfloor$, then $\delta (S) = q^n$.

• (2) If ${{\,\textrm{MC}\,}}\left( S \right) = \left\lfloor \frac{n - 1}{2} \right\rfloor + l$, then $\delta (S) \ge q^{n - l}$ for all $l \ge 0$.

3.5 An efficient criterion for not sufficiently many elementary multiplications

In the previous section we observed in Example 3.7 that only multiplications with linear combinations of $x_1, \dots , x_n$ have the potential to lower the differential uniformity. For practical considerations one would like to have criteria to efficiently determine whether an S-box has sufficiently many elementary multiplications or not. In the following proposition we show that at least for the latter case it can be sufficient to simply look at the monomials in the components of the S-box.

Proposition 3.10

Let $\mathbb {F}_q$ be a finite field, and let S be a (n, m)-S-box, and let $\mathcal {M} \in \mathbb {F}_q [x_1, \dots , x_n]$ be the set of all non-linear monomials that are present in the components of S. If there exists an $x_i$ which is not present in any monomial of $\mathcal {M}$, then S has maximal differential uniformity $\delta (S) = q^n$.

Proof

We implement S with the M-box $S_M$ which constructs every monomial independently. (I.e., the product $(x_1 + x_2) \cdot x_3$ is implemented via $(x_1 \cdot x_3, x_2 \cdot x_3)$.). Since $x_j$ is not present in any component of $S_M$ it is obvious that all partner vectors of $S_M$ are zero on the i^th component. So by Lemma 3.5$S_M$ has maximal differential uniformity.$\square$

We note that this criterion has a rather trivial proof too, since any such (n, m)-S-box can also be considered as $(n - 1, m)$-S-box via extended-affine equivalence and being constant in one component implies maximal differential uniformity. Though, to showcase the theory developed in this paper we proved it via the M-box.

We provide evidence that a converse positive criterion like “every variable $x_i$ divides at least one monomial in $\mathcal {M}$, then the differential uniformity is less than $q^n$” won’t be true in general as it is quite simple to find a counterexample.

Example 3.11

(cf. [23, §4.3]) Let $\mathbb {F}_q$ be finite field, and let $f \in \mathbb {F}_q [x]$ be a polynomial with $\deg (f) \ge 2$. We consider the Lai–Massey permutation

$$\begin{aligned} \mathcal {F}_\text {LM}: \begin{pmatrix} x_1 \\ x_2 \end{pmatrix} \mapsto \begin{pmatrix} x_1 + f(x_1 - x_2) \\ x_2 + f(x_1 - x_2) \end{pmatrix}. \end{aligned}$$

Clearly, we can find for both variables monomials that are divisible by them. On the other hand, the Lai–Massey permutation is affine equivalent to the Feistel permutation

$$\begin{aligned} \textbf{A} = \begin{pmatrix} 1 &{} -1 \\ 0 &{} 1 \end{pmatrix} ,\ \textbf{B} = \begin{pmatrix} 1 &{} 1 \\ 0 &{} 1 \end{pmatrix} ,\ F (x_1, x_2) = \begin{pmatrix} x_1 \\ x_2 + f (x_1) \end{pmatrix} , \end{aligned}$$

then $F_\text {LM} = T_\textbf{B} \circ F \circ T_\textbf{A}$.

4 Conclusions

In this paper, we fully characterized bijective functions with multiplicative complexity 1 over finite fields. We also extended the techniques of [19] to study differential uniformity in terms of the associated M-box. We want to mention that in [19, §4] an algorithm was described to find S-boxes over $\mathbb {F}_2^n$ which satisfy the lower bound on differential uniformity in Corollary 3.9. In principle, one could come up with a similar algorithm for arbitrary finite fields $\mathbb {F}_q$, though for large n or q this method becomes computationally infeasible.

Appendix A

1.1 A simple calculation

Let $\textbf{a}, \textbf{b}, \textbf{d} \in \mathbb {F}_q^n \setminus \{ \textbf{0} \}$, $\textbf{M} \in {{\,\textrm{GL}\,}}_{n} \left( \mathbb {F}_q \right)$, $\textbf{a}^\intercal \textbf{M}^{-1} \textbf{d} = \textbf{b}^\intercal \textbf{M}^{-1} \textbf{d} = 0$, and let

$$\begin{aligned} F (\textbf{x})&= \textbf{M} \textbf{x} + \Big ( \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right) \Big ) \textbf{d}, \\ G (\textbf{x})&= \textbf{M}^{-1} \textbf{x} - \Big ( \left( \textbf{a}^\intercal \textbf{M}^{-1} \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{M}^{-1} \textbf{x} \right) \Big ) \textbf{M}^{-1} \textbf{d}. \end{aligned}$$

We first observe that

$$\begin{aligned} \textbf{a}^\intercal G (\textbf{x}) = \textbf{a}^\intercal \textbf{M}^{-1} \textbf{x}, \qquad \qquad \textbf{a}^\intercal \textbf{M}^{-1} F (\textbf{x}) = \textbf{a}^\intercal \textbf{x}, \\ \textbf{b}^\intercal G (\textbf{x}) = \textbf{b}^\intercal \textbf{M}^{-1} \textbf{x}, \qquad \qquad \textbf{b}^\intercal \textbf{M}^{-1} F (\textbf{x}) = \textbf{b}^\intercal \textbf{x}. \end{aligned}$$

Then

$$\begin{aligned}{} & {} \left( F \circ G \right) (\textbf{x}) = \\{} & {} \qquad = \textbf{M} \left( \textbf{M}^{-1} \textbf{x} - \left( \left( \textbf{a}^\intercal \textbf{M}^{-1} \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{M}^{-1} \textbf{x} \right) \right) \textbf{M}^{-1} \textbf{d} \right) \\{} & {} \qquad \quad + \left( \left( \textbf{a}^\intercal G (\textbf{x}) \right) \cdot \left( \textbf{b}^\intercal g(\textbf{x}) \right) \right) \textbf{d} \\{} & {} \qquad = \textbf{x} - \left( \left( \textbf{a}^\intercal \textbf{M}^{-1} \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{M}^{-1} \textbf{x} \right) \right) \textbf{d} + \left( \left( \textbf{a}^\intercal \textbf{M}^{-1} \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{M}^{-1} \textbf{x} \right) \right) \textbf{d} \\{} & {} \qquad = \textbf{x}, \end{aligned}$$

and similar

$$\begin{aligned}{} & {} ( G \circ F ) (\textbf{x}) = \\{} & {} \qquad = \textbf{M}^{-1} \left( \textbf{M} \textbf{x} + \left( \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right) \right) \textbf{d} \right) \\{} & {} \qquad \quad - \left( \left( \textbf{a}^\intercal \textbf{M}^{-1} F (\textbf{x}) \right) \cdot \left( \textbf{b}^\intercal \textbf{M}^{-1} F (\textbf{x}) \right) \right) \textbf{M}^{-1} \textbf{d} \\{} & {} \qquad = \textbf{x} + \left( \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right) \right) \textbf{M}^{-1} \textbf{d} - \left( \left( \textbf{a}^\intercal \textbf{x} \right) \cdot \left( \textbf{b}^\intercal \textbf{x} \right) \right) \textbf{M}^{-1} \textbf{d} \\{} & {} \qquad = \textbf{x}. \end{aligned}$$