Introduction

Although long-distance dispersal (LDD) has been recognized as a key factor in the spread of populations, many aspects of LDD are still poorly understood (Cain et al. 2000). Long-distance dispersal can surely hasten invasions (Shigesada and Kawasaki 2002), but how else does it affect invasions? The mechanisms underlying LDD are also poorly understood (Higgins et al. 2003). Long-distance dispersal events are often attributed to multiple dispersal vectors, with infrequent but extreme vectors facilitating far-flung dispersal, but can LDD occur without so-called mixed dispersal? The terms “fat-tailed” and “heavy-tailed” dispersal are often associated with long-distance dispersal, but it is unclear exactly how these terms from probability relate to long-distance dispersal or range expansion.

Much of classical ecological theory has focused on asymptotic dynamics, yet transient dynamics have increasingly been recognized as important, especially over ecologically relevant time scales (Hastings et al. 2018). Mathematical analyses of long-distance dispersal have typically focused on the spreading speed, or asymptotic, long-time average speed of spread (Higgins and Richardson 1999; Shigesada and Kawasaki 2002; Kawasaki et al. 2006; Lutscher 2019). This focus on asymptotics leaves unaddressed many practical questions about how LDD affects invasions. How rare can LDD be while still meaningfully affecting invasions, and what possible impacts can it have? How is the range expansion, or full course of an invasion, rather than just its speed, affected?

The scattered- and coalescing-colony models of stratified diffusion by Shigesada et al. (1995) are an important exception to the focus on asymptotics in the study of LDD. Their work showed that diffusion paired with long-distance dispersal could generate range expansions of three types: linear, biphasic linear–linear, and accelerating (Shigesada et al. 1995); however, their models were spatially implicit and assumed that all short-distance dispersal occurred by diffusion. In this paper, I study a spatially explicit integrodifference equation model of spread with generalizable dispersal, and demonstrate its capacity to produce two types of biphasic range expansion.

Long-distance dispersal is hypothesized to occur in two ways (Higgins et al. 2003). First, long-distance dispersal may occur when rare dispersal vectors act on a small proportion of propagules to disperse them to extreme distances. In these cases, dispersal is governed by two or more distinct dispersal vectors. The most common vectors act at relatively short distances and account for the majority of dispersal, while atypical vectors act at great distances. Such dispersal is said to be mixed (Nathan et al. 2008). Second, typical dispersal vectors, such as wind, which most often deposit propagules close to their source, may occasionally disperse much further (Bullock et al. 2006). Long-distance dispersal of this type may be attributed to fat- or heavy-tailed dispersal, both technical terms from probability relating to probability distributions with capacities to generate extreme events with low yet non-negligible probability (Cooke et al. 2014).

There are many examples of multiple reproduction and dispersal vectors in the dispersal of plants, many of which can reproduce vegetatively but also by seed, but also in the movements of ants (Suarez et al. 2001), beetles (Shigesada and Kawasaki 1997), and birds (Kesler et al. 2010). Plants that reproduce by seed may have some proportion of their seeds transported long distances by birds and mammals (Janzen 1984). Studies that have modeled the distribution on dispersal distances of seeds or pollen often resort to mixed models to achieve good fits to data (Bullock and Clarke 2000; Streiff et al. 1999; Goto et al. 2006). Even within a movement vector, dispersal may be stratified. Horn et al. (2001) partition dispersal of tree seeds by wind according to whether the seed falls below or rise above the canopy, with the latter portion becoming candidates for long-distance dispersal; Higgins and Richardson (1999) hypothesize similarly.

“Fat-tailed” dispersal kernels have become popular for describing dispersal data (Nathan et al. 2012), and the tail of the dispersal kernel is often cited as a cause of long-distance dispersal (Katul et al. 2005) or faster-than-expected spread (Clark 1998; Caswell et al. 2003). Although the term has a formal definition in probability, it is often used beyond that scope in ecology to describe heavy-tailed or leptokurtic kernels. “Fat-tailed” kernels from ecology are often in fact heavy tailed. Fat- and heavy-tailed kernels have been found to accurately represent many sets of dispersal data, where thin-tailed kernels do not. A recent and comprehensive meta-analysis of plant dispersal data conducted by Bullock et al. (2017) compared popular thin- and heavy-tailed kernels, and found the best fitting ones to be heavy- and fat-tailed.

Dispersal is undoubtedly mixed, at least for some species, but fat-tailed kernels may still be useful models. Even if dispersal is better explained mechanistically by mixed-dispersal kernels, such kernels may be harder to deal with practically. Mixed kernels have, in general, more parameters than fat-tailed kernels, and so require more data or types of observations to properly fit (Higgins et al. 2003). Some researchers argue that, when taken together in combination, the sum total of dispersal by multiple vectors will yield a fat-tailed kernel (Nathan et al. 2008). Ultimately, the choice between mixed and fat-tailed kernels may in some cases be moderated by whether a mechanistic or phenomenological model is desired.

Integrodifference equation (IDE) models are one way by which many types of dispersal, including mixed dispersal and fat-tailed dispersal, can be incorporated into models of spread. IDE models are discrete-time, continuous-space models that describe populations whose growth and dispersal occur in distinct, non-overlapping stages. At each generation, reproduction occurs in-place, followed by dispersal according to a dispersal kernel, a probability density function that governs the likelihood of an offspring settling at any location relative to its parent.

In this paper, I analyze IDE models with two classes of dispersal kernels: mixed thin-tailed dispersal kernels and fat-tailed dispersal kernels, a particular class of heavy-tailed kernels whose tails decay according to power laws. I use a combination of known approaches, as well as new analytic techniques to analyze point-release invasions. Whereas many analyses of invasions focus on asymptotic properties of spread, I focus on their transient dynamics. I show how both mixed-dispersal and fat-tailed kernels can give rise to invasions with biphasic range expansions, which have two distinct phases of spread. For fat-tailed kernels, I introduce a way of quantifying how different parts of the kernel contribute to the rate of spread of an invasion, allowing me to more clearly define the “shoulders” of a dispersal kernel in the context of an invasion.

The remainder of this paper is organized as follows. In Model, I introduce the nonlinear and linear IDE models that I study, their components, how to measure invasion, and the key assumptions I make when using these models. I next review the relevant types and characteristics of Dispersal kernels, focusing on mixed and fat-tailed kernels. I also review thin-tailed and regularly varying probability densities for the role that they play in my analyses. I begin by analyzing Invasions with mixed thin-tailed dispersal, and show that they produce biphasic range expansions. I relate their speeds of spread to short- and long-distance dispersal. I find that a diminishing probability of LDD may or may not eliminate the effects of LDD, depending on the form of long-distance dispersal. In Fat tails: long- and short-distance dispersal, I show that fat-tailed dispersal can also generate biphasic range expansions. Fat-tailed invasions can invade at near-constant speeds for long times, so I review techniques for approximating this speed. I also introduce a technique for graphically delineating between the peak and tail of a dispersal kernel based on speed rarefaction curves. For both mixed-dispersal and fat-tailed kernels, I find the Time of phase transition, which corresponds to a transition between dynamics governed by short- and long-distance dispersal. In Discussion, I briefly summarize and interpret my results and their implications for the study of long-distance dispersal, range expansions, and invasions.

Model

Consider the discrete-time, nonlinear integrodifference equation (IDE) model

$$\begin{aligned} n_{t+1}(x)= & {} \int _{-\infty }^\infty f(n_t(y)) k(x-y) \text {d} y \nonumber \\= & {} \big ( f(n_t) * k \big )(x). \end{aligned}$$
(1)

In this model, space is continuous and time is discrete, with t corresponding to the generation number. \(n_t(x)\) is the population density at position x in generation t. Reproduction and dispersal occur in two distinct phases. First, the growth function f(n) measures the recruitment of the next generation, during the sedentary stage, as a function of the population density n at a particular point. Dispersal then occurs according to the dispersal kernel \(k(x-y)\), a probability density function that gives the probability of offspring from position y settling at location x.

I also study the linearized IDE model,

$$\begin{aligned} n_{t+1}(x)= & {} \int _{-\infty }^\infty R_0 n_t(y) k(x-y) \text {d} y \nonumber \\= & \ R_0 \cdot \big ( n_t * k \big )(x). \end{aligned}$$
(2)

Here, the nonlinear growth model \(n_{t+1} = f(n_t)\) has been replaced with linear growth, \(n_{t+1} = R_0 n_t\). The parameter \(R_0 = f'(0)\) is the net reproductive rate, which governs recruitment at low densities. The linear model is often easier to analyze than the nonlinear model, but can have different dynamics. Under certain conditions on the growth function, the rate of spread of the linear model will match the nonlinear model. Further, for certain initial conditions, a formal solution exists.

Initial condition

The initial condition, \(n_0(x)\), describes the spatial density or distribution of the population at time \(t=0\). In this paper, I restrict my attention to point-release invasions, or invasions whose populations are initially highly localized.

The most idealized point-release condition corresponds to total concentration of the initial population at a single point. This condition is represented mathematically by the Dirac-delta distribution \(\delta (x)\). This initial condition can only be used in conjunction with the linear model, for which the formal solution becomes,

$$\begin{aligned} n_t(x)= & \ R_0^t (\overbrace{k * k * \cdots * k}^\text {$t$-many})(x) \nonumber \\= & \ R_0^t k^{t*}(x). \end{aligned}$$
(3)

Here \(k^{t*}(x)\) denotes the convolution power, or convolution of k(x) with itself t-many times (Feller 1971).

In simulations, and when using the nonlinear IDE model (1), a non-idealized initial condition must be used so that the population begins at a finite density. In this paper, I use a uniform distribution as the initial condition,

$$\begin{aligned} n_0(x)&= {\left\{ \begin{array}{ll} 1 &{} |x| < \frac{1}{2} \\ \frac{1}{2} &{} |x| = \frac{1}{2} \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$
(4)

I set \(n_t(x) = 1/2\) at the discontinuities of the uniform distribution because 1/2 is the average value across each discontinuity; I have found this to improve the convergence of numerical methods.

Growth function

The growth function \(f(n)\) can take many forms, depending on how the population reproduces at various densities. Typically, zero and the population carrying capacity are fixed points of \(f(n)\); it is possible that \(f(n)\) may have other fixed points, but I will not be considering these cases in this paper. Rescaling \(n_t(x)\) so that the carrying capacity is 1, this means that \(f(0) = 0\) and \(f(1) = 1\), with \(n=0\) being an unstable and \(n=1\) a stable equilibrium of the non-spatial model, \(n_{t+1} = f(n_t)\).

A key factor in growth, especially when considering long-distance dispersal, is whether the growth function has an Allee effect, or reduced recruitment at low densities compared with recruitment at higher densities (Allee 1938). This occurs when \(f(n^*) / n^* > R_0\) for some value \(n^* > 0\). Under a weak Allee effect, \(R_0 > 1\), so that the population will grow at low densities, but at a reduced rate. A strong Allee effect corresponds to the case where \(R_0 < 1\), so that the population dies off at low densities (Wang et al. 2002). In this paper, I will assume that there is no Allee effect, so that \(f(n) / n \le R_0\) for all \(n > 0\). With no Allee effect, the speed of invasion of the linear model (2) matches that of the nonlinear model (1) (Lewis et al. 2002; Lutscher 2019).

I further restrict my attention to growth functions with no overcompensation. Overcompensation occurs when the growth function is not monotonically increasing between zero and the population carrying capacity, typically at high densities (Li et al. 2009). These assumptions result in the discrete-time IDE model behaving qualitatively very similarly to a continuous-time reaction-diffusion model, such as the Fisher–KPP model.

Throughout this paper, I will use the Beverton–Holt stock-recruitment curve (Beverton and Holt 1957) as the growth function in all simulations of the nonlinear model,

$$\begin{aligned} f(n)= & \ \frac{R_0 n}{(1 + (R_0 - 1)n)}. \end{aligned}$$
(5)

This function has no Allee effect.

Measuring invasion extent

To measure the extent of an invasion at time t, I set a detection threshold \(\overline{N} > 0\), and look for the position of the invasion front \(x_t\) such that

$$\begin{aligned} n_t(x_t) = \overline{N}. \end{aligned}$$
(6)

In general, there may be many points satisfying equation (6). These points comprise the level set of \(n_t(x)\) with level-set value \(\overline{N}\). The number of points can even change in time, if for instance two spatially separated populations coalesce or the population goes extinct.

In a point-release invasion with conditions on the growth function as I have laid out, there will ultimately be two points satisfying (6), moving outward symmetrically from the point source. For values of \(R_0 > 1\) that are close to 1, or if the kernel disperses very widely compared to the initial population distribution, the invasion front may recede, as the initially concentrated population is redistributed. In some cases, the population density may temporarily decrease below the detection threshold before ultimately increasing (Shigesada and Kawasaki 1997).

Dispersal kernels

In this section, I briefly review thin-tailed, mixed, and fat-tailed dispersal kernels.

Thin-tailed kernels

The term “thin-tailed” comes from probability, and describes probability distributions that possess moment generating functions. For example, the Gaussian or Normal distribution, with variance \(\sigma ^2\) has kernel k(x) given by

$$\begin{aligned} k(x)&= \frac{1}{\sqrt{2 \pi \sigma ^2}} \exp \left( \frac{-x^2}{2 \sigma ^2} \right) , \end{aligned}$$
(7)

and corresponding moment generating function

$$\begin{aligned} M(s)&= e^{\sigma ^2 s^2/2}. \end{aligned}$$
(8)

Another thin-tailed kernel commonly seen in modeling studies is the Laplace kernel,

$$\begin{aligned} k(x)&= \frac{1}{2a} \exp \left( \frac{-|x|}{a} \right) , \end{aligned}$$
(9)

which has moment generating function

$$\begin{aligned} M(s)&= \frac{1}{1 - a^2 s^2}, \quad |s| < \frac{1}{a}. \end{aligned}$$
(10)

Note that the domain of the moment generating function is bounded for the Laplace kernel, but unbounded for the Gaussian kernel. The bounded support of the moment generating function is not unique to the Laplace kernel. The WALD kernel, used in ecology to model dispersal by wind, also has a moment generating function with bounded support (Thompson and Katul 2008). We will see that the bounded support of the moment generating function has implications for long-distance dispersal in Invasions with mixed thin-tailed dispersal.

Invasions with thin-tailed kernels are known to approach constant speeds of invasion. An invasion starting from a point release, or any initial condition with bounded support, will approach an asymptotic speed c, known as the spreading speed. When the growth function has no Allee effect, this speed can be found in terms of the net reproductive rate \(R_0\) and the moment generating function M(s) of the kernel,

$$\begin{aligned} c&= \inf _{s > 0} \frac{\log \left( R_0 M(s) \right) }{s}. \end{aligned}$$
(11)

For a derivation of this result, see Lewis et al. (2016). Alternatively, equation (11) can be transformed into a system of parametric equations,

$$\begin{aligned} c= & \ \frac{M'(s)}{M(s)} \end{aligned}$$
(12a)
$$\begin{aligned} R_0= & \ \frac{ \exp \big [ s M'(s) / M(s) \big ] }{M(s)} \end{aligned}$$
(12b)

This latter representation was first derived by Kot et al. (1996).

Thin-tailed kernels, and in particular the Gaussian kernel, have largely fallen out of favor for representing dispersal data, as numerous studies have shown that dispersal is leptokurtic and potentially even heavy-tailed. One noteable study by Bullock et al. (2017) found that thin-tailed kernels generally performed worse than heavy-tailed kernels when fit to dispersal data. In the study, eleven common kernel forms, both thin- and heavy-tailed, were fit to dispersal data from over one hundred plant species; the Gaussian kernel was said to perform “very poorly,” and the two overall best-fitting kernels that they tested were both heavy-tailed.

Thin-tailed kernels are still popular as mechanistically derived models of dispersal. The Gaussian kernel corresponds to movement by a diffusive process for a fixed amount of time, and the Laplace kernel to diffusive movement for an exponentially distributed amount of time (Lewis et al. 2016). The thin-tailed WALD kernel was mechanistically derived to model the dispersal of seeds by wind with the goal of having parameters that can be estimated from characteristics of the environment and the dispersing species, rather than from dispersal data (Katul et al. 2005).

Mixed dispersal

A mixed-dispersal kernel is a dispersal kernel that represents dispersal through distinct vectors by combining multiple dispersal kernels. Mixed-dispersal kernels, functions, or models are also called mixtures (Higgins and Richardson 1999) or composite (Shigesada and Kawasaki 2002).

For each of m-many dispersal modes or vectors, there is a probability \(p_i \ge 0\) of a propagule dispersing according to that vector, and an associated dispersal kernel \(k_i(x)\) that governs the probability and distance of dispersal according to that vector. The probabilities sum to one, so that dispersal by one of the vectors is guaranteed. These distinct dispersal kernels are combined into a single dispersal kernel in a weighted sum,

$$\begin{aligned} k(x)&= \sum _{j=1}^m p_i k_i(x). \end{aligned}$$
(13)

In principle, mixed kernels can combine any number of dispersal vectors that may act at similar or dissimilar spatial scales.

In a mixed kernel, the heaviness of the tail is determined by the tail of the heaviest component kernel. This means that if any constituent kernel is heavy-tailed, the resulting mixed kernel will itself by heavy tailed. If all constituent kernels are thin-tailed, the resulting mix is thin-tailed.

Fat-tailed kernels

Despite their name, fat-tailed kernels are not “opposite” or complementary to thin-tailed kernels. While thin-tailed kernels possess moment generating functions, it is actually heavy-tailed kernels that are defined by their lack of moment generating functions; therefore, every symmetric dispersal kernel is either thin- or heavy-tailed. Fat-tailed kernels are a subclass of heavy-tailed kernels with a much more specific form. A kernel k(x) is fat-tailed if it has tails that decay asymptotically like a power law,

$$\begin{aligned} k(x) \sim \widetilde{c} x^{-\alpha } \quad x \rightarrow \infty , \end{aligned}$$
(14)

where \(\widetilde{c}\) is a scaling constant and \(\alpha > 1\) is the degree of tail fatness. A smaller value of \(\alpha\) indicates more slowly decaying tails, and so increases the fatness of the tails. Because fat-tailed kernels are also heavy-tailed, they lack moment generating functions. In addition, fat-tailed kernels have infinitely many divergent moments, with all moments of order \(\alpha -1\) and higher failing to converge.

Perhaps the most well-known fat-tailed kernel is the Cauchy distribution,

$$\begin{aligned} k(x)&= \frac{1}{\pi b \left[ 1 + \left( \frac{x}{b} \right) ^2 \right] }. \end{aligned}$$
(15)

Here b is a shape parameter that controls the width of the kernel. The Cauchy distribution has degree of tail fatness \(\alpha =2\); as such, it is so fat-tailed that none of its moments, including its mean, variance, and kurtosis, are defined.

Student’s t-distribution is a family of fat-tailed distributions, indexed by a parameter \(\nu\) that controls the degree of tail fatness. For \(\nu \ge 1\), the density function is given by

$$\begin{aligned} k(x)&= \frac{ \Gamma \left( \frac{\nu +1}{2} \right) }{ \Gamma \left( \frac{\nu }{2} \right) \sqrt{\nu \pi }} \left( 1 + \frac{x^2}{\nu } \right) ^{- \left( \frac{\nu +1}{2} \right) }. \end{aligned}$$
(16)

Student’s t-distribution has tail fatness of degree \(\nu +1\). For \(\nu =1\), the t-distribution reduces to the Cauchy distribution (15). In the limit as \(\nu \rightarrow \infty\), the t-distribution converges to the Gaussian distribution.

I also introduce the following fat-tailed kernel, which I term the fat-tailed Laplace kernel,

$$\begin{aligned} k(x)&= \frac{\alpha -1}{2 \alpha (1 + |x|/\alpha )^\alpha }. \end{aligned}$$
(17)

This kernel has a peaked shape at the origin, and in the limit as \(\alpha \rightarrow \infty\), k(x) converges to the Laplace distribution.

Regular variation and tail additivity

A class of distributions that has not received much attention in ecology is that of regularly varying distributions. A kernel k(x) is regularly varying with index \(\beta\) if, for all \(t > 0\),

$$\begin{aligned} \lim _{x \rightarrow \infty } \frac{k(tx)}{k(x)} = t^\beta . \end{aligned}$$
(18)

Regularly varying distributions can be thought of as a generalization of fat-tailed kernels. A fat-tailed kernel with degree of tail fatness \(\alpha\) is also necessarily regularly varying with index \(-\alpha\).

Regularly varying densities possess several useful tail additivity properties. For my purposes, the most useful theorems are those proven by Bingham et al. (2006). First, if k(x) is a regularly varying probability density, then

$$\begin{aligned} (k * k)(x) \sim 2 k(x), \qquad x \rightarrow \infty . \end{aligned}$$
(19)

This result says that the convolution, which in general has no simple closed-form expression, can be approximated in the tails as simply twice the original kernel density. A similar result holds for repeat convolutions, in which

$$\begin{aligned} (k^{t*})(x)&\sim t k(x), \qquad x \rightarrow \infty . \end{aligned}$$
(20)

This latter property is particularly useful in analyzing point-release invasions under the linear model, where the formal solution (3) involves the repeat convolution of the kernel k(x).

Comparing mixed and fat-tailed dispersal

Fig. 1
figure 1

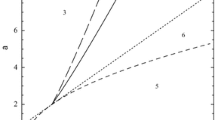
Mixed and fat-tailed dispersal kernels. Top Mixed thin-tailed dispersal kernels. The short-distance kernel \(k_S(x)\) is the Gaussian kernel with \(\sigma _S = 1\), and is shown as a black dashed curve. The long-distance kernel \(k_L(x)\) is another Gaussian kernel, but with \(\sigma _L = 20\). The plot shows the mixed kernel for \(p = 10^{-1}, 10^{-2}, \dots , 10^{-10}\), from top to bottom. Bottom Fat-tailed dispersal kernels. Each solid curve is a t-distribution (16), with \(\alpha =2,3,\dots ,11\), from top to bottom. The Gaussian kernel with \(\sigma = 1\) is shown for comparison, as a black dashed curve

Full size image

Shape

In practice, a near surefire way of distinguishing thin- and fat-tailed kernels is by viewing log-scale plots of their tails. For a fat-tailed kernel, the log of k(x) appears concave-up in the tail, rather than concave-down; see for example Fig. 1. This behavior is in direct contrast to that of the Gaussian kernel, whose tails decay rapidly to zero; its tails appear concave-down. Most heavy-tailed kernels that are used in practice have tails that are concave-up, although pathological examples can be constructed as exceptions. Near the source, a fat-tailed kernel can be either concave-up or concave-down (called convex by some authors, see for example Clark et al. 1999), examples include the fat-tailed Laplace kernel (17) and the t-distribution (16). A mixed thin-tailed kernel can be shaped similarly to a fat-tailed kernel on a limited domain; in Fig. 1, the Gaussian–Gaussian mixed kernels flare outward where the long-distance kernel meets the short-distance kernel.

Short- and long-distance dispersal

Mixed kernels clearly delineate between distinct dispersal vectors. Each vector may be clearly defined as short- or long-distance, and its corresponding component kernel can be tuned to disperse widely or narrowly. The probability of dispersal by each vector is set by a parameter, and so the total probability of dispersal by LDD vectors can be considered the probability of long-distance dispersal.

Fat-tailed dispersal kernels naturally incorporate capacities for short- and long-distance dispersal in a continuum of dispersal distances. Although the degree of tail fatness can be controlled, fat-tailed kernels do not have a parameter that directly tunes the probability of long-distance dispersal. Although short- and long-distance dispersal can be attributed to the ‘peak’ and ‘tail’ of the kernel, there is no clear or obvious delineation between these parts of the kernel. In Spreading speeds for truncated fat-tailed kernels, I introduce a method of characterizing the “shoulder” of a fat-tailed kernel as a region lying between the peak and tail.

Capacity to generate LDD

There are two commonly used criteria for classifying LDD. The first stipulates that LDD is defined proportionally, for example by the furthest 5% or even 1% of dispersing propagules. The second stipulates an absolute criterion, whereby a fixed distance, say 100 km, qualifies long-distance dispersal. Both mixed and fat-tailed kernels can generate LDD according to either of these criteria.

Heavy- and fat-tailed kernels have special capacities for generating extreme events. This capability is exemplified by the tail additivity property of regularly varying densities (also of the larger subexponential class) and can be interpreted as follows. Suppose that several random dispersal displacements are summed, and that the sum is very large. If the displacements are drawn from a thin-tailed distribution, such as the Gaussian or Laplace, then it is most likely that each individual displacement was larger than typical. If on the other hand, the displacements are from a fat-tailed distribution, then it is more likely that a single displacement was very large, or “extreme” (Cooke et al. 2014).

Invasions with mixed thin-tailed dispersal

In this section, I analyze thin-tailed mixed dispersal kernels of the form

$$\begin{aligned} k(x)&= (1-p) k_S(x) + p k_L(x). \end{aligned}$$
(21)

Here p is the probability of dispersal by the long-distance vector, with \(0< p < 1\). The kernels \(k_S(x)\) and \(k_L(x)\) are dispersal kernels associated with short- and long-distance dispersal vectors, respectively. In addition to assuming both kernels are thin-tailed, I also assume that \(k_S(x)\) is thinner-tailed than \(k_L(x)\), or that \(k_L(x)\) dominates \(k_S(x)\) in the tail. This assumption is important for guaranteeing that all long-distance dispersal is in fact due to \(k_L(x)\).

I show that invasions with mixed dispersal can have biphasic range expansions that spread at an initially slow speed before transitioning to a higher speed. The invasion speed during the first phase is governed by short-distance dispersal, whereas long-distance dispersal boosts the speed in the second phase of spread. The parameter p, governing the probability of long-distance dispersal, controls the time of occurrence of the transition between phases of spread. A lower probability of LDD delays the onset of the second phase, and extends the initial phase of spread.

The probability of LDD also influences the speed of spread during the second phase of spread, but the nature of this influence depends heavily on the long-distance dispersal kernel \(k_L(x)\). In some cases, long-distance dispersal elevates speeds of invasion even when p is made arbitrarily small, while in others, the speed smoothly reduces to that of short-distance dispersal. I explore this phenomenon in detail in Persistent effects of infinitesimal LDD.

Speeds of spread and biphasic range expansion

Fig. 2
figure 2

Spreading speed c as a function of net reproductive rate \(R_0\) for mixed-dispersal kernels. For each mixed kernel, \(k_S(x)\) and \(k_L(x)\) are Gaussian kernels with \(\sigma _S=1\) and \(\sigma _L=20\). The probability p of long-distance dispersal varies from \(p=10^{-1}, 10^{-2}, \dots , 10^{-15}\); the curves for the largest given values of p are labeled. The thick black curve corresponds to \(p=0\), or dispersal by the short-distance kernel \(k_S(x)\) only

Full size image

In a mixed kernel, the spreading speeds for both the mixed and unmixed kernels can be found.

For a mixed-dispersal kernel k(x) of the form (21), the moment generating function M(s) is given in terms of the moment generating functions of the constituent kernels. Denoting the moment generating functions of \(k_S(x)\) and \(k_L(x)\) as \(M_S(s)\) and \(M_L(s)\), respectively,

$$\begin{aligned} M(s)&= (1-p) M_S(s) + p M_L(s). \end{aligned}$$
(22)

Thus, if the moment generating functions of all of the constituent kernels are known, it is easy to find the moment generating function of a mixed kernel itself. The resulting moment generating function can be used in system (11) to find the spreading speed for a particular value of \(R_0\). Alternatively, the parametric system (12) can be used to relate spreading speed c and net reproductive value \(R_0\) as the parameter s is varied. Doing so yields a speed curve, which can be graphically interpreted to yield c as a function of \(R_0\).

Figure 2 shows speed curves for mixed-dispersal kernels, along with the speed curve for an unmixed kernel representing short-distance dispersal only. In each mixed kernel, both \(k_S(x)\) and \(k_L(x)\) are Gaussian kernels, with variances \(\sigma ^2_S = 1\) and \(\sigma ^2_L = 100\). The thick black curve indicates the spreading speed \(c_S\) associated with short-distance dispersal only. For \(p=10^{-1}\), long-distance dispersal is less common than short-distance dispersal, but still disperses one tenth of propagules. The speed of invasion is significantly increased, relative to \(c_S\), for all values of \(R_0 > 1\). As p is reduced, the speed likewise reduces, and eventually converges to \(c_S\). The speed curve for \(p=10^{-15}\), shown in yellow, is visually closest to the short-distance speed curve, and shows that c essentially coincides with \(c_S\) for values of \(R_0\) less than around 1.15. Smaller values of p are omitted for visual clarity, but further reducing p results in closer agreement for larger values of \(R_0\). Note that this behavior does not occur with all mixed kernels; Lutscher (2019) has proven when the speed of the mixed kernel converges to that of the short-distance kernel, as well as when it does not. For further information on how this latter case affects range expansion, see Persistent effects of infinitesimal LDD.

Numerical simulations

I perform numerical simulations to complement my analytic results. While the spreading speed tells us how fast an invasion will spread as time becomes large, it does not inform us about any transient behaviors that may occur. Transient dynamics can last for short or long times, and can be difficult to predict or anticipate.

In my simulations, the domain is a large interval, centered about the origin, with half-width H. The domain is represented by an evenly spaced grid of points, with grid-spacing \(\Delta x\). The population density \(n_t(x)\) is represented on this domain. In each simulation, H is chosen sufficiently large so that the invasion front position does not tend too close to the boundary of the domain. I implement point-release initial conditions by setting \(n_0(x_j) = 1\), for all gridpoints \(x_j\) where \(x_j \in (-1/2, 1/2)\), and \(n_0(x_j) = 1/2\) for \(|x_j| = 1/2\).

I perform my simulations in MATLAB. To evaluate the convolution integrals in the nonlinear IDE (1), I use a midpoint-rule integration scheme. I implement this scheme with the numerical convolution function “conv” with the “same” option. To find the invasion extent \(x_t\), I define a threshold value \(\overline{N}\), typically \(\overline{N}=0.1\), and use the “find” command to select the last grid point \(x_j\) such that \(n_t(x_j) > \overline{N}\). I then use the “interp1” command to perform cubic spline interpolation on the points \(x_{j-1}, x_j, x_{j+1}, x_{j+2}\) to compute the position \(x_t\) satisfying \(n_t(x_t) = \overline{N}\).

Fig. 3
figure 3

Invasions with short- and long-distance dispersal and \(R_0\) varied. Plots show range expansion curves for four invasions, two with mixed dispersal and two with unmixed, short-distance dispersal only. In all cases, short- and long-distance dispersal are Gaussian with \(\sigma _S = 1\) and \(\sigma _L = 20\), respectively. Growth is Beverton–Holt with \(R_0 = 1.2\) (open circles) and \(R_0 = 1.5\) (dots). For invasions with mixed dispersal (black markers), the probability of LDD is \(p=10^{-5}\); invasions with unmixed, short-distance dispersal (gray markers) have \(p=0\). The dashed lines in the plots of invasion speed indicate the spreading speed of the mixed-dispersal kernel for each value of \(R_0\). Red cross symbols indicate the approximate time and position of the phase transition as determined by the procedure in Time of phase transition. In all simulations, the grid spacing is \(\Delta x = 1/16\) and the domain half-width is \(H=1000\)

Full size image

Figure 3 shows range-expansion curves from four separate invasions, two with mixed dispersal and two with unmixed, short-distance dispersal only. Dispersal is as in Fig. 2, with \(k_S(x)\) Gaussian with \(\sigma _S = 1\), and \(k_L(x)\) Gaussian with \(\sigma _L = 10\). The probability of LDD is \(p=10^{-5}\). Only \(R_0\) is varied, taking on the values \(R_0 = 1.2, 1.5\). For each value of \(R_0\), two invasions, one with mixed dispersal (\(p=10^{-5}\)) and one with unmixed dispersal (\(p=0\)), are shown.

Perhaps the most striking feature in Fig. 3 is that each invasion with mixed dispersal has a biphasic range-expansion curve. These invasions initially spread at slow constant speeds, but later transition to faster speeds. In plots of invasion extent \(x_t\) versus time, the transition appears very rapid. Plots of the per-step invasion speed, \(v_t = x_t - x_{t-1}\), show that the velocity can grow rapidly during this transition, and can temporarily spike to very high speeds before slowing.

The spreading speed c of the mixed-dispersal kernel determines the asymptotic speed of invasion during the second, ultimate phase of spread. This speed is calculated using the parametric system (12), and is shown in Fig. 3 as black dashed lines for each mixed-dispersal invasion and associated value of \(R_0\). At the start of the second phase of spread, the per-step invasion speed \(v_t\) jumps far above the spreading speed, but soon after decays and begins oscillating around the spreading speed. These oscillations continue to dampen as the per-step invasion speed converges to c.

During the initial phase of spread, the speed does not match or approach the spreading speed. Instead, each mixed-dispersal invasion initially advances at the spreading speed \(c_S\) associated with the short-distance dispersal kernel, \(k_S(x)\). This can be seen by the close agreement of the invasions with mixed and unmixed dispersal for each value of \(R_0\); the timeseries of \(x_t\) from the two invasions are indistinguishable, and the same is true for the timeseries of \(v_t\). This indicates that the initial rate of spread of invasions with mixed dispersal is governed by short-distance dispersal. To calculate \(c_S\), I again use system (12), this time with the moment generating function \(M_S(s)\) of the short-distance kernel \(k_S(x)\).

There are a number of ways to conceptualize why LDD only affects the latter phase of an invasion. First, if we consider the mixed kernel as a perturbation of the unmixed kernel, it makes sense that the timeseries of the two invasions would initially closely agree. A second perspective comes from how steepness and speed of the invasion front are related, and how thin-tailed invasions converge to a traveling-wave profiles. As a thin-tailed invasion progresses, the tail of its population density \(n_t(x)\) converges to a decaying exponential, proportional to \(e^{-sx}\) for some \(s>0\). A smaller value of s corresponds to a shallower yet more rapidly traveling invasion front, whereas larger values of s describe steeper and more slowly moving fronts. On the other hand, after only one generation, \(n_1(x)\) closely resembles the dispersal kernel, which can be seen from the formal solution (3). Initially, the invasion front is close to the origin, well away from the tails, and the shape of the kernel in this region is governed by the short-distance kernel. The invasion-front profile produced by the mixed-distance kernel is typically much shallower in shape than the short-distance dispersal kernel, and takes time to develop; the invasion front is steep and moves slowly during this time, until the exponentially decaying tail develops and boosts the speed of invasion, after which point it is shallower and faster. For a relevant discussion of how the slope of a decaying exponential determines the speed of traveling waves in reaction-diffusion equations, see (Murray 2007, p. 442).

The parameter \(R_0\) affects mixed-dispersal range expansions in two ways. First, \(R_0\) determines the speed of spread during both phases of the invasion. This conforms with the behavior of the speed curves in Fig. 2, where all curves increase as \(R_0\) grows. Second, as \(R_0\) is increased, the duration of the initial phase of spread decreases. For \(R_0 = 1.2\), the initial phase of spread lasts for around 60–65 generations. In contrast, for \(R_0 = 1.6\), the initial phase lasts for a shorter time of around 30 generations.

Fig. 4
figure 4

Invasions with mixed dispersal and the probability p of long-distance dispersal varied. Dispersal is as in Fig. 3, growth is Beverton–Holt with \(R_0 = 1.1\), and \(p = 10^{-1}, 10^{-2}, \dots , 10^{-5}\). Dashed lines in the plot of invasion speeds indicates the spreading speed of the mixed kernel for each value of \(R_0\). The thick black curve corresponds to an invasion with short-distance dispersal only (\(p=0\)). In all simulations, the grid spacing is \(\Delta x = 1/16\); the domain half-width is \(H=1000\) for \(p=10^{-1}\), \(H=700\) for \(p=10^{-2}\), and \(H=500\) for \(p=10^{-3},10^{-4},10^{-5}\)

Full size image

To see how the probability p of LDD events affects range expansion, I perform additional simulations, this time keeping \(R_0\) constant and varying p. Figure 4 shows range expansion curves from six invasion simulations. Dispersal is as in Fig. 2; both \(k_S(x)\) and \(k_L(x)\) are Gaussian kernels, with \(\sigma _S^2 = 1\) and \(\sigma _L^2 = 100\). The only parameter varied is \(p = 10^{-1}, 10^{-2}, \dots , 10^{-5}\); the case where \(p=0\), which corresponds to dispersal by the short-distance vector only, is also shown.

The range expansions in Fig. 4 appear similar to those shown when \(R_0\) was varied, but there is an important difference in the initial phase of spread. All of the mixed-dispersal invasions have linear–linear biphasic range expansions, but the speed of spread during the initial phase is identical across simulations. This is because the net reproductive rate \(R_0\) and short-distance dispersal are kept constant, so the short-distance spreading speed \(c_S\) does not change.

The probability p of LDD affects the second phase of range expansion in two ways. First, as p is decreased, the spreading speed c of the mixed kernel decreases. We first saw this in Fig. 2, and the range expansions in Fig. 4 confirm this; the spreading speed for each value of p is shown as a dashed line, and the per-step invasion speed \(v_t\) converges to the spreading speed. Second, decreasing p delays the onset of the second phase of spread, or equivalently lengthens the initial phase of spread. The initial phase of spread lasts for around ten generations for \(p=10^{-1}\), fifty generations for \(p=10^{-3}\), and around one hundred generations for \(p=10^{-5}\).

In all of the mixed-dispersal invasions shown so far, the effects of long-distance dispersal vanished as p was reduced to zero. This is not always the case, and in fact even when p is decreased to zero, some kernels significantly impact range expansion when used as the long-distance kernel. The determining factor turns out to be the moment generating function. I next explore this phenomenon, when it happens, and how it affects range expansions.

Persistent effects of infinitesimal LDD

Vanishingly rare long-distance dispersal may or may not impact range expansions, depending on the nature of the long-distance kernel \(k_L(x)\). In this section, I analyze how range expansions respond when the probability p of long-distance dispersal is reduced to zero, and show that invasions may nevertheless invade faster and exhibit biphasic range expansions. Lutscher has previously found that the asymptotic spreading speed can be boosted in sedentary (Lutscher 2007) and dispersing populations (Lutscher 2019), and that the deciding factor is whether the moment generating function \(M_L(s)\) of \(k_L(x)\) diverges within the support of \(M_S(s)\). Here, I examine this result in the context of range expansions.

The first case occurs if \(M_L(s)\) converges on the entire support of \(M_S(s)\), as in the case of the Gaussian–Gaussian mixed kernels in the preceding section. Here, the effects of LDD vanish as p goes to zero. In the second, the moment generating function \(M_L(s)\) diverges within the support of \(M_S(s)\). This can occur, for example, in a Gaussian–Laplace or Laplace–Laplace mixed kernel. In these cases, the effects of LDD do not disappear as p is reduced to zero, and I refer to the long-distance kernel \(k_L(x)\) as persistent.

A persistent long-distance dispersal kernel affects the \(R_0\)-versus-c speed curve in the following way. Denote by \(C_0\) the \(R_0\)-versus-c speed curve of the short-distance dispersal kernel \(k_S(x)\), and by \(C_p\) the speed curve for the mixed kernel with parameter value p. As p is decreased, \(C_p\) does not converge to \(C_0\), but rather to a curve I will denote by \(C_{0^+}\). In a neighborhood of \(R_0 = 1\), the curves \(C_0\) and \(C_{0^+}\) coincide. At a transition point T, the curves \(C_0\) and \(C_{0^+}\) diverge, with \(C_{0^+}\) taking on larger values than \(C_0\) for increasing \(R_0\) (Lutscher 2019). Figure 5 shows how this behavior manifests in the speed curves for a Laplace–Laplace family of mixed kernels. Here, the transition point T occurs at roughly \(R_0 = 1.0434\) and \(c \approx 0.41667\).

Fig. 5
figure 5

Speed curves for a family of mixed kernels with a persistent long-distance component. Here \(k_S(x)\) is the Laplace kernel (9) with parameter \(a=1\) (variance \(\sigma _S^2=2\)), and \(k_L(x)\) is also a Laplace kernel but with \(a=5\) (variance \(\sigma _L^2 = 50\)). Each curve indicates the spreading speed c as a function of \(R_0\) for a mixed kernel with probability of LDD \(p=10^{-1}, 10^{-2}, \dots , 10^{-4}\). The thick black curve (label \(C_0\)) corresponds to the case where \(p=0\), and the dashed black curve (label \(C_{0^+}\) corresponds to the limiting curve as p approaches zero from above. The curves \(C_0\) and \(C_{0^+}\) meet in tangency at the point T, and overlap for smaller values of \(R_0\)

Full size image

Typically, the \(R_0\)-versus-c speed curve cannot be solved for in closed form; the parametric variable cannot in general be eliminated. In the case of a persistent LDD kernel, a portion of the \(C_{0^+}\) speed curve can be explicitly solved for. The portion of the curve lying between the point \((R_0,c) = (1,0)\) and T exactly matches that of \(C_0\), and so can be found parametrically; the point T lies on this curve, evaluated at the parametric value \(s=a\), or the point of divergence of \(M_L(s)\). Beyond T, the curve \(C_{0^+}\) has the closed form (Lutscher 2019),

$$\begin{aligned} c&= \frac{ \log (R_0) + \log (M_S(a)) }{a}, \quad R_0 \ge \frac{\exp \left[ \frac{a M_S'(a) }{ M_S(a) } \right] }{M_S(a)}. \end{aligned}$$
(23)

This function is shown in Fig. 5 as a black dashed curve.

Figure 6 shows example range expansions with mixed dispersal where \(k_L(x)\) is a persistent kernel. For nearly all values of p, the resulting range expansion is biphasic, with two distinct phases of spread. For \(p = 10^{-1}\), the duration of the initial phase is shortened, but this also coincides with the LDD vector being quite common.

Fig. 6
figure 6

Mixed-dispersal invasions with persistent long-distance dispersal. Dispersal is as in Fig. 5. Growth is Beverton–Holt with \(R_0 = 1.3\). Seven mixed-dispersal invasions are shown, corresponding to \(p = 10^{-1}, 10^{-2}, \dots , 10^{-7}\), along with an unmixed invasion (\(p=0\)). The ultimate speed of spread decreases as p is reduced, but for \(p < 10^{-3}\), the reduction in speed is negligible. The duration of the first phase of spread increases as p decreases; rarer long-distance dispersal delays the onset of the phase of spread that is dominated by LDD. In all simulations, the grid spacing is \(\Delta x = 1/16\), and the domain half-width is \(H=1000, 800, 600\) for \(p=10^{-1},10^{-2},10^{-3}\) respectively, and \(H=400\) for \(p=10^{-4},\dots ,10^{-7}\)

Full size image

Although reducing the probability of occurrence of LDD has little effect on the ultimate spreading speed, it does affect when the transition between phases occurs. As we see in Fig. 4, as p is decreased, the onset of the phase transition is delayed; thus, p plays a role similar to \(R_0\) in determining when the phase transition occurs. Further, as p decreases in orders of magnitude, this delay grows roughly linearly.

Fat tails: long- and short-distance dispersal

I now turn to invasions with true fat-tailed dispersal. In contrast with the mixed-dispersal models described in the previous section, where two distinct modes of dispersal were incorporated into a single dispersal kernel, there is no such distinction with fat-tailed dispersal. As such, there is no clear way to separate the effects of short- and long-distance dispersal. Furthermore, an invasion with true fat-tailed dispersal will continuously accelerate, and so has no asymptotic spreading speed (Kot et al. 1996).

Despite these differences, fat-tailed invasions behave qualitatively very similarly to mixed-dispersal invasions: they can express biphasic range expansions, and can initially progress at near-constant speeds for long times before ultimately accelerating. To find this speed, I review approaches for approximating the speed of spread and introduce a new method based on speed rarefaction curves (Kot and Neubert 2008). This method also enables us to measure the contribution of different parts of the dispersal kernel to the invasion speed, which defines a notion of kernel “shoulders” in the context of invasion.

Range expansions with fat-tailed dispersal

In a previous paper (Liu and Kot 2019), we detailed how the tail-additivity properties of regularly varying probability density functions can be used to approximate the tail of a point-release invasion with fat-tailed dispersal. We used these tail approximations to find that the invasion front position, \(x_t\), advances geometrically fast, with the base of geometric growth a function of net reproductive rate \(R_0\) and the degree of tail fatness \(\alpha\),

$$\begin{aligned} x_{t+1} \approx R_0^{1/\alpha } x_t, \qquad t \rightarrow \infty . \end{aligned}$$
(24)

Consequently, the per-step invasion speed \(v_t = x_t - x_{t-1}\) itself grows geometrically quickly,

$$\begin{aligned} v_{t+1} \approx R_0^{1/\alpha } v_t, \qquad t \rightarrow \infty . \end{aligned}$$
(25)

Despite asymptotically accelerating without bound, fat-tailed invasions initially spread slowly. How long an invasion spreads at a slow speed depends in part on the rate of acceleration of the invasion, but there can also be a delay before the onset of acceleration. Figure 7 shows plots of range expansions for invasions with fat-tailed dispersal. In each case, dispersal is governed by the fat-tailed Laplace kernel (16). Growth is according to the Beverton–Holt stock-recruitment function (5) with \(R_0 = 1.3, 1.5, 2.0\). These invasions have linear–accelerating biphasic range expansions: in the first phase spread is linear at a constant speed, and in the second phase they continuously accelerate.

Raising and lowering the net reproductive rate \(R_0\) affects fat-tailed invasions similarly to mixed-dispersal invasions. As \(R_0\) is increased, the speed of range expansion increases, both during the initial rate of constant-speed expansion as well as during the accelerating phase. Lowering \(R_0\) delays the onset of the accelerating phase, or extends the duration of the initial phase.

Unlike mixed dispersal kernels, fat-tailed kernels do not comprise distinct short- and long-distance dispersal vectors. As such, there is no obvious speed that can be associated to short-distance dispersal only. In the following section, I review ways of approximating this speed.

Fig. 7
figure 7

Range-expansion curves of fat-tailed invasions. Each invasion follows from a point-release, with dispersal given by the fat-tailed Laplace kernel (16) with \(\alpha = 8\), and Beverton–Holt growth with \(R_0 = 1.3\) (\(\circ\)), \(R_0=1.5\) (\(\bullet\)), and \(R_0 = 2.0\) (\(\triangleright\)). Range expansion can be biphasic linear–accelerating or continuously accelerating; for small values of \(R_0\), the initial phase of spread is at a constant speed, but for larger values this phase disappears. Each invasion eventually enters into an accelerating regime, where its rate of advance is geometric with base \(R_0^{1/\alpha }\); this can be seen in logarithmic scale (bottom panel), when the per-step invasion speed \(v_t\) tends to follow straight lines, indicating geometric growth at the expected rate (24). Red crosses in the plots of \(x_t\) indicate the approximate time \(\overline{t}\) and position \(\overline{x}\) of the phase transition between constant and accelerating phases. In the plots of \(v_t\), red crosses are plotted on the vertical axis at the value \(\overline{x} / \overline{t}\). In all simulations, the grid spacing is \(\Delta x = 1/16\) and the domain half-width is \(H=2000\)

Full size image

Spreading speeds for truncated fat-tailed kernels

Fat-tailed invasions have no finite spreading speed (Kot et al. 1996), but some techniques for finding or approximating the spreading speed can be applied or adapted. Techniques for calculating the spreading speed of thin-tailed kernels depend on the moment generating function — something that fat-tailed kernels lack — but there are approximations for the speed with milder requirements. Here I review two such approximations: the Gaussian and Kurtosis approximations. I then introduce a technique based on truncation of tails of the kernel.

To apply the Gaussian approximation, it is necessary that k(x) have finite variance. Many fat-tailed kernels have finite variance, with notable exceptions being the Cauchy distribution or any fat-tailed kernel with tail fatness \(\alpha \le 3\). Denoting \(\sigma ^2\) as the variance of k(x), the Gaussian approximation gives the approximate speed

$$\begin{aligned} c_G&= \sqrt{ 2 \sigma ^2 \log R_0 }. \end{aligned}$$
(26)

The Gaussian approximation comes from replacing the kernel k(x) with a Gaussian kernel of equal variance, and in practice under-predicts the speed of invasion. Alternatively, the Gaussian approximation can be derived from a truncation of the Taylor series expansion of the moment generating function (Lutscher 2007).

The kurtosis approximation comes from a higher-order truncation of the moment generating function (Lutscher 2007), and is given by

$$\begin{aligned} c_{\gamma _2} = c_G \left( 1 + \frac{ \gamma _2 }{12} \log R_0 \right) . \end{aligned}$$
(27)

Whereas the variance \(\sigma ^2\) is the second-order moment of k(x), the excess kurtosis \(\gamma _2\) is derived from the fourth-order moment. In order for the excess kurtosis to be defined, k(x) must have tail decay of order \(\alpha > 5\); the kurtosis is undefined for \(\alpha \le 5\). Therefore, despite being more accurate, the kurtosis approximation is more restrictive in that it cannot be applied to as many kernels as can the Gaussian approximation.

To find a better approximation for the initial constant speed of spread of a fat-tailed invasion, I return to the moment generating function, formally defined as

$$\begin{aligned} M(s)&= \int _{-\infty }^\infty e^{s x} k(x) \text {d} x. \end{aligned}$$
(28)

The key feature of heavy- and fat-tailed kernels that distinguishes them from thin-tailed kernels is their lack of moment generating functions. This means that analytic methods for characterizing thin-tailed dispersal that use the moment generating function cannot be simply extended for use with fat-tailed kernels.

The moment generating function fails to exist for fat-tailed dispersal kernels precisely because of their tails, which do not decay to zero fast enough for the integral in equation (28) to converge. Truncating these tails, even at a great distance from their peak, will cause the integral to converge. This is because a dispersal kernel with compact support, where the kernel is nonzero only over a closed and bounded interval, must be thin tailed.

I define the moment generating function of the normalized dispersal kernel with truncated support \(-H \le x \le H\), denoted \(M_H(s)\), as

$$\begin{aligned} M_H(s)&= \frac{ \int _{-H}^{H} e^{s x} k(x) \text {d} x }{ \int _{-H}^{H} k(x) \text {d} x }. \end{aligned}$$
(29)

In this definition, the integral in the numerator is modified from the moment generating function, and the integral in the denominator is a normalization constant. This normalization constant accounts for the fact that truncating the tails of the dispersal kernel results in its integral being less than one.

The truncated moment generating function (29) can be used in the parametric relations (12). Doing so yields the spreading speed of the thin-tailed kernel that is obtained from truncating and re-normalizing the fat-tailed kernel k(x) at a fixed half-width H. I denote this speed as \(c_H\), with H indicating the truncation half-width. Holding H constant and finding the spreading speed as a function of \(R_0\) yields a speed curve like those shown in Figs. 2 or 5. Alternatively, fixing \(R_0\) and varying H allows us to find the spreading speed of a truncated fat-tailed kernel as a function of the H, yielding a “speed rarefaction curve”.

Speed rarefaction curves were first introduced by Kot and Neubert (2008) in the study of range-limited or censored dispersal data. They studied thin- rather than fat-tailed kernels, for which the speed rarefaction curve approaches a finite limit: the spreading speed of the non-truncated thin-tailed kernel. They used speed rarefaction curves to determine the sampling radius required for accurate estimates of the spreading speed.

For fat-tailed kernels, the speed rarefaction curve does not approach a finite limit. Instead, as the truncation half-width increases, the speed of spread of the truncated kernel approaches infinity. Despite having no finite limit, the shape of the speed rarefaction curve is useful in indicating the importance of different parts of the kernel.

Fig. 8
figure 8

Rarefaction curves for a fat-tailed kernel. Horizontal axes on each plot both correspond to distance at the same scale. Top A fat-tailed dispersal kernel. The peak corresponds to the bulk of dispersal that occurs at a short scale, and the tail corresponds to rare long-distance dispersal. The term “shoulder” describes a part of the kernel that lies between the peak and the tail. Bottom The spreading speed associated with truncating and re-normalizing the fat-tailed kernel at various lengths. As the truncation half-width increases, the spreading speed increases. A flat part of the curve indicates a part of the kernel that contributes minimally to the spreading speed. This plateau defines the shoulder of the kernel in the context of invasion

Full size image

Rarefaction curves for the fat-tailed t-distribution for a variety of values of \(R_0\) are shown in Fig. 8. For each curve, the spreading speed increases as truncation length increases, but the rate of increase is not steady. The behavior of these rarefaction curves is most easily understood for very large and very small values of H. The spreading speed first increases rapidly near \(H=0\); for a zero-width kernel, spread does not occur. As the truncation width H approaches infinity, so does the spreading speed; this is consistent with the fact that full, non-truncated fat-tailed kernel produces continuously accelerating invasions, for which the invasion speed is unbounded and approaches infinity.

For some range of intermediate truncation widths, the rarefaction curve of a fat-tailed kernel can plateau or become nearly flat. For the curves in Fig. 8, this occurs in a range of values of approximately \(8 \le H \le 50\) for \(R_0 = 1.2\). For \(R_0 = 1.4\) the interval is shorter, around \(8 \le H \le 30\). As \(R_0\) increases, the length the interval decreases; for \(R_0 = 2.0\), the rate of increase of the curve slows near \(H \approx 12\), but does not flatten to the degree seen in the curves for lower values of \(R_0\). When the plateau is present, I denote by \(H^*\) the truncation half-width at which \(c_H\) changes most slowly, or the derivative \({dc_H}/{dH}\) is minimal. The corresponding speed \(c_{H^*}\) is the speed at which the rarefaction curve plateaus.

It is not immediately obvious that \(c_{H^*}\) should be relevant to a true fat-tailed invasion, but I have found \(c_{H^*}\) to be a good predictor of the near-constant speed of spread during fat-tailed invasions. I give the following heuristic argument for why this may be the case. Denote by \(v_t\) the per-step invasion speed of the invasion with the non-truncated, true fat-tailed dispersal kernel k(x). Consider the family of invasions by the truncated kernels \(k_H(x)\) for all H, and denote the per-step invasion speed for these invasions by \(v^H_t\). As the truncation half-width H is taken to infinity, \(v^H_t \rightarrow v_t\) for each fixed t. Furthermore, for each invasion with truncated dispersal, the per-step invasion speed will approach the spreading speed, so \(v^H_t \rightarrow c_H\) as time increases. These two facts mean that \(|v^H_t - v_t|\) becomes small as H becomes large, while \(|v^H_t - c_H|\) becomes small as t becomes large. Applying the triangle inequality gives

$$\begin{aligned} |v_t - c_H| \le |v_t - v^H_t| + |v^H_t - c_H|. \end{aligned}$$
(30)

At certain times and for certain truncation widths, the two positive quantities on the right of equation (31) are simultaneously small, and consequently so is the difference on the left. I have observed that this occurs for values of \(H \approx H^*\). Under these circumstances, the per-step speed \(v_t\) approaches or becomes very close to the spreading speed of the truncated kernel. Formalizing this heuristic argument is difficult because these limits do not concurrently hold as both t and H become infinite, and indeed the per-step speed cannot be said to converge in a typical limiting sense. I hope to expand on this argument in future work.

Figure 9 shows how the Gaussian, kurtosis, and rarefaction approaches compare with the speed of spread of a fat-tailed invasion. The invasion has Beverton–Holt growth with \(R_0 = 1.8\) and fat-tailed Laplace dispersal (17) with tail fatness \(\alpha =100\). These values were chosen to increase the differences between the three quantities \(c_G, c_{\gamma _2},\) and \(c_{H^*}\) in order to make comparison with data clearer and to delay the onset of the accelerating regime of spread. The plots show that the per-step invasion speed \(v_t\) appears to asymptotically approach a constant value up until a time around \(t=225\), after which the speed rapidly grows, corresponding to the transition between the constant-speed and accelerating phases of range expansion. The Gaussian approximation under-predicts this speed, the kurtosis approximation over-predicts but is closer, and the speed \(c_{H^*}\) from the rarefaction curve closely matches the apparent limit of \(v_t\) before the phase transition.

Fig. 9
figure 9

Speed of spread of a fat-tailed invasion. Data (black points) indicate the per-step invasion speed \(v_t\) of a simulated fat-tailed invasion; the grid spacing is \(\Delta x = 1/16\) and the domain half-width is \(H=1000\). Dispersal is governed by the fat-tailed Laplace kernel with tail fatness \(\alpha =100\). Growth is Beverton–Holt with \(R_0 = 1.8\). The invasion progresses at a steady pace for over 200 generations, and appears to approach a finite spreading speed, before rapidly accelerating. The solid, dashed, and dash-dotted lines indicate estimates of the transient speed from the rarefaction curve (\(C_{H^*}\)), the kurtosis approximation (\(c_{\gamma _2}\)), and the Gaussian approximation \(C_G\), respectively

Full size image

Time of phase transition

In this section, I find an approximation for the time at which a phase transition will occur in a biphasic range expansion of a fat-tailed invasion. To do this, I develop an approximation for the central, established portion of the invading population, and another for the tail of the population under the linear model. I then look for the time at which these approximations are simultaneously equal and match a detection threshold. At this time, the invasion front transitions from being governed by short-distance dispersal to long-distance dispersal.

I begin by developing an approximation for the central portion of the population density, \(n_t(x)\). Assume that k(x) has finite variance, denoted by \(\sigma _S^2\). All thin-tailed kernels possess a finite variance, as do fat-tailed kernels with tail fatness \(\alpha > 3\). As long as the dispersal kernel k(x) has finite variance, the central limit theorem applies. For my purposes, the related local limit theorems are more useful, as they allow approximation of probability densities rather than distribution functions. Lutscher (2007) previously detailed how local limit theorems can be applied in this context, with the key result being

$$\begin{aligned} k^{*t}(x) \rightarrow \frac{1}{\sqrt{2 \pi t \sigma _S^2}} \exp \left( \frac{-x^2}{2 t \sigma _S^2} \right) , \quad t \rightarrow \infty . \end{aligned}$$
(31)

Equation (31) can be combined with the formal solution for a point-release invasion under linear IDE model (3),

$$\begin{aligned} n_t(x)&\approx \frac{R_0^t}{\sqrt{2 \pi t \sigma _S^2}} \exp \left( \frac{-x^2}{2 t \sigma _S^2} \right) . \end{aligned}$$
(32)

Unfortunately, this approximation converges too slowly to provide a good approximation in the tails of \(n_t(x)\) at large times; this is because approximation (31) converges more slowly than the growing factor of \(R_0^t\) due to repeated growth of the population. Fortunately, I will use this approximation at the edge of the central bulk of the invasion, rather than in the tails, and restrict my attention to finite and relatively small, rather than large, times.

To approximate \(n_t(x)\) in the tails, I use the tail additivity properties of fat-tailed kernels. Assuming that k(x) is fat-tailed, it is also a regularly varying density. Due to tail additivity of the kernel (20), \(n_t(x)\) is asymptotically equal to a scaled copy of the dispersal kernel,

$$\begin{aligned} n_t(x) \sim R_0^t t k(x), \qquad x \rightarrow \infty . \end{aligned}$$
(33)

To predict when the behavior of the invasion front transitions from being dominated by short- to long-distance dispersal, I look for when these two terms are equal and match a detection threshold \(\overline{N}\). This occurs when all three quantities are equal,

$$\begin{aligned} \frac{R_0^{\overline{t}}}{\sqrt{2 \pi \overline{t} \sigma _S^2}} e^{-\overline{x}^2 / (2 \overline{t} \sigma _S^2)}= & {} \overline{N}, \end{aligned}$$
(34a)
$$\begin{aligned} R_0^{\overline{t}} \overline{t} k(\overline{x})= & {} \overline{N}. \end{aligned}$$
(34b)

Here \(\overline{x}\) and \(\overline{t}\) indicate the spatial position and time at which the regime shift occurs. Figure 10 shows how the equations are satisfied by the two approximations and the detection threshold in a fat-tailed invasion.

In general, solving for \(\overline{x}\) and \(\overline{t}\) in system (34) is not possible analytically, but can be done numerically. \(\overline{t}\) may be non-integer, in which case the largest integer that is smaller than \(\overline{t}\) will provide a more conservative estimate for the time at which the regime shift occurs. Furthermore, these approximations were derived under the linear integrodifference model (2). Assuming that the growth function f(n) has no Allee effect, the linear and nonlinear models will have the same asymptotic spreading speeds, but the two models generally have different transient dynamics. The nonlinear model typically lags behind the linear model.

Examples of this approximation are shown in Fig. 7. Red crosses indicate the time \(\overline{t}\) and position \(\overline{x}\) of the phase transition. While the transition between phases of spread is not sharp, \(\overline{t}\) precedes the onset of acceleration in all cases where a demarcation is evident.

Fig. 10
figure 10

Population densities at phase transition. The population density \(n_t(x)\) (thick gray curves) according to the linear model (2) follows a Gaussian-like profile (black dashed curves) in a central region. Top A fat-tailed invasion transitions between being dominated by short- to long-distance dispersal at time \(t=35\). The tails are approximated by equation (33) using tail additivity (solid black curve). The central and tail approximations intersect and both equal a detection threshold \(\overline{N} = 0.1\) (black dotted curve) at the position indicated by the cross. Dispersal is governed by the t-distribution with \(\nu =5\). Growth is linear with \(R_0 = 1.4\). Bottom The phase transition of a mixed-dispersal invasion. Similar to the fat-tailed invasion, approximations for the central bulk (black dashed curve) and tail (solid black curve) of the invasion meet at the detection threshold. Both short- and long-distance dispersal are Gaussian, with \(\sigma _S=1\) and \(\sigma _L = 20\). Figure shows \(n_t(x)\) at time \(t=24\)

Full size image

Although system (34) cannot be solved in general, we can make some broad inferences. First, the time \(\overline{t}\) of the phase transition increases as \(R_0\) is decreased. This is because in equation, \(R_0\) must be raised to the power of \(\overline{t}\) for the left-hand side to be of sufficient magnitude; that is, the compounding geometric growth at rate \(R_0\) must counteract the small probability \(k(\overline{x}) \ll 1\) in order to reach the threshold of detection. Second, all things being equal, larger values of \(\alpha\) indicate more rapidly decaying tails; \(\overline{t}\) correspondingly increases as \(\alpha\) is increased, at least within a parameterized family of kernels such as the t-distribution. (See Fig. 10)

Mixed dispersal

Thin-tailed mixed-dispersal kernels do not possess the asymptotic tail additivity properties of fat-tailed kernels that I used in tail approximation (34). Instead, for a mixed kernel with \(k(x) = (1-p) k_S(x) + p k_L(x)\), I derive the approximation

$$\begin{aligned} n_t(x)&\approx \frac{R_0^t}{\sqrt{2 \pi t \sigma _S^2}} \exp \left( \frac{-x^2}{2 t \sigma _S^2} \right) + R_0^t t p k_L(x). \end{aligned}$$
(35)

Details of this derivation are in appendix Approximation of point-release invasions with mixed dispersal. The key assumptions are (1) that long-distance dispersal events are rare, so \(p \ll 1\), (2) that \(k_S(x)\) has finite variance \(\sigma ^2_S\), so that the self-convolution \(k_S^{*t}(x)\) can be approximated with a Gaussian distribution, and (3) that \(k_S(x)\) disperses very narrowly compared to \(k_L(x)\), with \(\sigma ^2_S \ll \sigma ^2_L\). Under these assumptions, equation (36) provides a good approximation for \(n_t(x)\) in a spatial domain that encompasses the transition point between spread governed by short- and long-distance dispersal.

I now proceed similarly to how I found the transition time for fat-tailed kernels. The first term in equation (36) approximates the central bulk of \(n_t(x)\), while the second term is a first-order approximation of the tails of \(n_t(x)\). I equate these terms to \(\overline{N}\), and look for the time \(\overline{t}\) and position \(\overline{x}\) that solve this system,

$$\begin{aligned} \frac{R_0^{\overline{t}}}{\sqrt{2 \pi \overline{t} \sigma _S^2}} \exp \left( \frac{- \overline{x}^2}{2 \overline{t} \sigma _S^2} \right)= & {} \overline{N}, \end{aligned}$$
(36a)
$$\begin{aligned} R_0^{\overline{t}} \overline{t} p k_L(\overline{x})= & {} \overline{N}. \end{aligned}$$
(36b)

This system is nearly identical to system (34), with the major difference that \(p k_L(\overline{x})\) replaces \(k(\overline{x})\) in the second equation. Figure 10 shows how these two terms relate to and approximate the population density in a mixed-dispersal invasion.

Figure 3 shows how this approximation applies to mixed-dispersal invasions. In these invasions, dispersal is Gaussian–Gaussian mixed, with \(k_S(x)\) having variance \(\sigma _S^2 = 1\) and \(k_L(x)\) with variance \(\sigma _L^2 = 400\). Each red cross in the figure marks the time \(\overline{t}\) and position \(\overline{x}\) of the phase transition, as calculated by system (36).

System (36) is very similar to system (34), with the difference that \(k_L(x)\) is thin-tailed. This important distinction can, in some cases, result in the system having no solution. This can happen if, for example, \(k_L(x)\) is a Gaussian kernel; in this case, the approximation for the central bulk (36a) will eventually become heavier-tailed than \(k_L(x)\), and the two approximations may never intersect at a value matching the detection threshold \(\overline{N}\). This only occurs when \(k_L(x)\) is as thin-tailed or thinner tailed than a Gaussian kernel. If \(k_L(x)\) is heavier-tailed than any Gaussian distribution (e.g. a Laplace kernel) then a solution is guaranteed.

Discussion

In this paper, I analyzed two approaches for modeling spread with long-distance dispersal: mixed-dispersal kernels and fat-tailed dispersal kernels. Both approaches are commonly used in the modeling and study of dispersal data, and can be incorporated into integrodifference-equation models of spread. My results contribute to our developing understanding of two aspects of spread and invasions: long-distance dispersal and transient phenomena.

There are several common patterns that emerge from both approaches. First and foremost, range expansions with LDD can be biphasic; invasions with short- and long-distance dispersal may progress at slow constant speeds before accelerating or switching to faster speeds. For both mixed and fat-tailed dispersal, short-distance dispersal determines the speed during the initial phase, while long-distance dispersal boosts the ultimate speed. Rarity of long-distance dispersal and the net reproductive rate control the time of transition between phases of spread; rarer long-distance dispersal and a lower value of \(R_0\) increases the delay.

For mixed-dispersal invasions, both phases of spread are at constant speeds. The speed during the second phase of spread is boosted by long-distance dispersal, and the speedup can be significant. For some combinations of kernels, I found that even exceedingly rare LDD (of arbitrarily small probability) can boost the speed significantly. In these cases, reducing the probability of LDD delays the onset of the second phase of spread, and has an essentially fixed effect on the ultimate spreading speed. For this to occur, the net reproductive rate must be sufficiently large; if \(R_0\) is close to one, long-distance dispersal no longer overshadows short-distance dispersal.

Mixed dispersal has been studied as a means of producing biphasic range expansions by Ramanantoanina et al. (2014) in a similar model. In their study, dispersal ability is heritable, and the population consists of two or more distinct types of individuals with different dispersal abilities. Short-dispersing individuals disperse according to a dispersal kernel with variance smaller than that of long-dispersing individuals. With suitable initial conditions, the resulting range expansion is biphasic with two linear phases. Although these results are similar to those I have presented in Invasions with mixed thin-tailed dispersal, there are some key differences. First, in my model, every propagule is equally likely to disperse according to the long-distance dispersal kernel. Long-distance dispersal is rare, and occurs with probability p for each dispersing propagule. In contrast, the longer dispersal ability of individuals in the model of Ramanantoanina et al. (2014) is a genetic trait, and is only initially rare due to their initially small number; after a number of generations, the longer dispersing individuals are in the majority. Second, Ramanantoanina et al. (2014) found that long-dispersing individuals eventually dominate the invasion front, with short-dispersing individuals persisting only in the initial core of invaded territory. In my model, there is a single combined population, demonstrating that a bias in the spatial distribution of short- and long-distance dispersers is not necessary to produce biphasic range expansions.

Fat-tailed kernels are popular for modeling dispersal data, but are less often used in conjunction with IDE models. With new analytic techniques, a focus on their behavior over ecologically relevant timescales rather than their asymptotic dynamics, and an improved understanding of their effect on range expansion, it is possible to incorporate them in models of spread.

Invasions with fat-tailed dispersal can have biphasic range expansions similar to those of mixed-dispersal invasions; however their ultimate phase of spread consists of continuous acceleration. During the initial phase of spread, the invasion speed is nearly constant. Fat-tailed kernels have no separate mechanisms for short- and long-distance dispersal, making estimation of this initial speed difficult. I reviewed two known approaches for approximating the speed of invasion and introduced a new approach based on speed rarefaction curves (Kot and Neubert 2008) for finding the speed of spread of truncated fat-tailed kernels; I found this method best predicted the speed of spread.

Speed rarefaction curves also provide a way of delineating short- and long-distance dispersal for fat-tailed kernels. By truncating the tails of a fat-tailed kernel, it becomes thin-tailed and gains a finite spreading speed. Plotting spreading speed versus truncation distance generates an increasing curve of speed versus distance that indicates how different parts of the kernel contribute to the spreading speed. Speed rarefaction curves enable us to define a “shoulder” of a dispersal kernel as a part of the kernel between the peak and the tail that contributes minimally to the speed of spread.

Many types of range-expansion curves are now known to be possible under IDE model (1). Following the classification scheme of Shigesada et al. (1995), type 1 or linear expansion occurs under many common thin-tailed kernels, type 2 or linear biphasic emerges under certain mixed-dispersal kernels, and type 3 or continuously accelerating range-expansions can be generated from fat-tailed kernels (Liu and Kot 2019). In addition to these types, fat-tailed kernels can generate a biphasic linear–accelerating range expansion absent in the original classification; we might think of this as a type 2.5 range expansion, with behavior somewhere between the classic linear biphasic and continuously accelerating types. These results demonstrate the capability of a simple, single-population model to produce a great variety of types of range expansion, driven purely by different forms of dispersal kernel.

All of the biphasic range expansions I have shown, where spread initially follows a regime that differs from its ultimate or asymptotic dynamics, are ultimately transient phenomena. It is important to remember that these rapid shifts in speed and dynamics arise solely as a result of the dispersal kernel, rather than through a change in a parameter value or transition across a heterogeneous landscape. No outside influence or environmental change is necessary for a regime shift to occur in the case of transient dynamics Hastings et al. (2018). An invasion that has progressed at a slow pace may accelerate with little warning; its apparent steady progress may in actuality be a long, transient phase of spread. Depending on the rarity and form of long-distance dispersal, the ultimate rate of spread of an invasion may be vastly different than its initial speed.

Researchers should note the causal connection between long-distance dispersal and transient dynamics in range expansion. Specifically, the study of LDD necessitates consideration of transient timescales and use of non-asymptotic analytic techniques. As long-distance dispersal is incorporated into models of spread, transient behavior will necessarily arise. A focus on spreading speed, for instance, may be misleading, if the effects of long-distance dispersal are not felt for many generations or only beyond ecologically relevant timescales.