Broadcasting of non-locality

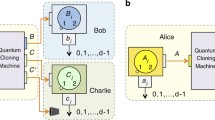
Abstract

Bell non-locality and steering are archetypal characteristics of quantum mechanics that mark a significant departure from conventional classical notions. They basically refer to the presence of quantum correlations between separated systems which violate a non-local inequality, the violation otherwise is not possible if we restrict ourselves only to classical correlations. In view of the importance of such unique correlations, one may be interested to generate more states exhibiting non-locality starting from a few, a protocol which is termed as broadcasting. However, in the present submission, we show using universal Buzek–Hillary (BH) quantum cloning machine that, if one restricts to broadcasting through local quantum cloning, then such non-locality cannot be broadcasted. Our study is done in the purview of the Bell-CHSH inequality and the CJWR [E G Cavalcanti et al, Phys. Rev. A 80, 032112 (2009)] steering inequality. It is observed that when the number of measurement settings is greater than 6, some of the output states are steerable after the application of local optimal BH cloners. We found that, under some restrictions, if the Werner and Bell diagonal states are subjected to such procedures, then the resultant state is rendered unsteerable. We extended this study to three qubit systems and found that genuine tripartite non-locality cannot be broadcasted using universal BH local quantum cloners, when the Svetlichny’s inequality was considered. For two qubit systems, we considered $10^5$ simulated general local unitaries over Werner and Bell-diagonal states and found that for none of these states, broadcasting on non-locality and 3-steerability is possible.

Appendix A. Proof of Lemma 1

Let

$$\begin{aligned}\omega _{A} = \frac{{\mathbb {I}} + \vec {x}\cdot \vec {\sigma }}{2} \in {\mathbb {C}}^{2},\end{aligned}$$

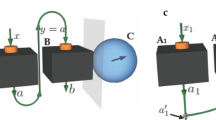
be a state of quantum system A. Also, let the blank state and the machine state be denoted as $E_{a}$ and $X_{x}$, respectively. Let $U^{\mu }_{Aax}$ be a unitary operator applied on the joint system of A, a and x, and it defines the BH cloning machine with the machine parameter $\mu$. After applying this cloning transformation to the joint system $\omega _{\textrm{A}} \otimes E_{a} \otimes X_{x}$, we get the following output states $\omega ^{\textrm{out}}_{\textrm{A}}$ and $\omega ^{\textrm{out}}_{a}$:

$$\begin{aligned} \omega ^{\textrm{out}}_{\textrm{A}}&= {\text {Tr}}_{ax}\left[ U^{\mu }_{Aax} \left( \omega _{\textrm{A}} \otimes E_{a} \otimes X_{x} \right) U^{\mu \dagger }_{Aax}\right] \nonumber \\&= \frac{{\mathbb {I}} + \mu \vec {x}\cdot \vec {\sigma }}{2}, \end{aligned}$$

(A.1)

$$\begin{aligned} \omega ^{\textrm{out}}_{a}&= {\text {Tr}}_{Ax}\left[ U^{\mu }_{Aax} \left( \omega _{\textrm{A}} \otimes E_{a} \otimes X_{x} \right) U^{\mu \dagger }_{Aax}\right] \nonumber \\&= \frac{{\mathbb {I}} + \mu \vec {x}\cdot \vec {\sigma }}{2}. \end{aligned}$$

(A.2)

Both the output states are the same as we are using a symmetric cloning machine. Intuitively, when we compare these output states with the input state $\omega$, it is very interesting to observe that the vector associated with Pauli matrices is shrunk by the factor of $\mu$. This observation is crucial for this proof.

Now, let us expand this development to the two-qubit case. As given, Alice (A) and Bob (B) share a state $\rho _{\textrm{AB}}$, which is a general two-qubit state as written in (1). Additionally, let $E_{a}$ and $E_{b}$ serve as initial blank quantum states in Alice and Bob’s lab, respectively. Let us denote the machine qubits as x and y for Alice’s and Bob’s local cloning machines, respectively. Furthermore, they apply local cloning unitaries $U_{Aax}^{\mu _{1}}\otimes U_{Bby}^{\mu _{2}}$ on their respective qubits, i.e., qubits (A, a, x) and qubits (B, b, y). Here, we assume that both the machine parameters, i.e., $\mu _{1}$ and $\mu _{2}$, need not be the same for generalising the approach. Let ${\tilde{\rho }}_{Ab}$ and ${\tilde{\rho }}_{Ba}$ be non-local output states obtained after cloning. Here, we only show for ${\tilde{\rho }}_{Ab}$ as we are using symmetric cloners, and therefore, we have ${\tilde{\rho }}_{Ab} = {\tilde{\rho }}_{Ba}$.

$$\begin{aligned}&{\tilde{\rho }}_{Ab} = {\text {Tr}}_{aBxy}\left[ U_{Aax}^{\mu _{1}}\otimes U_{Bby}^{\mu _{2}}\left( \rho _\textrm{AB}\right. \right. \nonumber \\&\qquad \left. \left. \otimes E_{a}\otimes E_{b} \otimes X_{x} \otimes X_{y} \right) U_{Aax}^{\mu _{1}\dagger }\otimes U_{Bby}^{\mu _{2}\dagger }\right] \nonumber \\&\quad \overset{(a)}{=}\ {\text {Tr}}_{aBxy}\left[ U_{Aax}^{\mu _{1}}\otimes U_{Bby}^{\mu _{2}}\left( \frac{1}{4}\Bigg [{\mathbb {I}}_A \otimes {\mathbb {I}}_B \right. \right. \nonumber \\&\qquad +\sum _{i=1}^{3}\left( x_{i}(\sigma ^{i}_{A}\otimes {\mathbb {I}}_B)+ y_{i}({\mathbb {I}}_A\otimes \sigma ^{i}_{B})\right) \nonumber \\&\qquad +\sum _{i,j=1}^{3}t_{ij}(\sigma ^{i}_{A}\otimes \sigma ^{j}_{B})\Bigg ]\nonumber \\&\qquad \left. \left. \otimes E_{a}\otimes E_{b} \otimes X_{x} \otimes X_{y} \right) U_{Aax}^{\mu _{1}\dagger }\otimes U_{Bby}^{\mu _{2}\dagger }\right] \nonumber \\&\quad \overset{(b)}{=}\ 1/4 \Bigg ({\text {Tr}}_{aBxy}\left[ U_{Aax}^{\mu _{1}}\otimes U_{Bby}^{\mu _{2}}\left( {\mathbb {I}}_A \otimes E_{a} \otimes X_{x} \right. \right. \nonumber \\&\qquad \left. \left. \otimes {\mathbb {I}}_B\otimes E_{b} \otimes X_{y} \right) U_{Aax}^{\mu _{1}\dagger }\otimes U_{Bby}^{\mu _{2}\dagger } \right] \nonumber \\&\qquad +\sum _{i=1}^{3} x_{i} {\text {Tr}}_{aBxy}\left[ U_{Aax}^{\mu _{1}}\otimes U_{Bby}^{\mu _{2}} \left( \sigma ^{i}_{A}\otimes E_{a} \otimes X_{x} \right. \right. \nonumber \\&\qquad \left. \left. \otimes {\mathbb {I}}_B \otimes E_{b} \otimes X_{y} \right) U_{Aax}^{\mu _{1}\dagger }\otimes U_{Bby}^{\mu _{2}\dagger } \right] \nonumber \\&\qquad + \sum _{i=1}^{3} y_{i} {\text {Tr}}_{aBxy}\left[ U_{Aax}^{\mu _{1}}\otimes U_{Bby}^{\mu _{2}} \left( {\mathbb {I}}_{A}\otimes E_{a} \otimes X_{x} \right. \right. \nonumber \\&\qquad \left. \left. \otimes \sigma ^{i}_B \otimes E_{b} \otimes X_{y} \right) U_{Aax}^{\mu _{1}\dagger }\otimes U_{Bby}^{\mu _{2}\dagger } \right] \nonumber \\&\qquad +\sum _{i, j=1}^{3} t_{ij} {\text {Tr}}_{aBxy}\left[ U_{Aax}^{\mu _{1}}\otimes U_{Bby}^{\mu _{2}} \left( \sigma ^{i}_{A}\otimes E_{a} \otimes X_{x} \right. \right. \nonumber \\&\qquad \left. \left. \otimes \sigma ^{j}_B \otimes E_{b} \otimes X_{y} \right) U_{Aax}^{\mu _{1}\dagger }\otimes U_{Bby}^{\mu _{2}\dagger } \right] \Bigg )\nonumber \\&\quad \overset{(c)}{=}\ 1/4 \Bigg ({\text {Tr}}_{ax}\left[ U_{Aax}^{\mu _{1}}\left( {\mathbb {I}}_A \otimes E_{a} \otimes X_{x}\right) U_{Aax}^{\mu _{1}\dagger } \right] \nonumber \\&\qquad \otimes {\text {Tr}}_{By}\left[ U_{Bby}^{\mu _{2}}\left( {\mathbb {I}}_B \otimes E_{b} \otimes X_{y}\right) U_{Bby}^{\mu _{2}\dagger } \right] \nonumber \\&\qquad +\sum _{i=1}^{3} x_{i} {\text {Tr}}_{ax}\left[ U_{Aax}^{\mu _{1}}\left( \sigma ^{i}_A \otimes E_{a} \otimes X_{x}\right) U_{Aax}^{\mu _{1}\dagger } \right] \nonumber \\&\qquad \otimes {\text {Tr}}_{By}\left[ U_{Bby}^{\mu _{2}}\left( {\mathbb {I}}_B \otimes E_{b} \otimes X_{y}\right) U_{Bby}^{\mu _{2}\dagger } \right] \nonumber \\&\qquad + \sum _{i=1}^{3} y_{i} {\text {Tr}}_{ax}\left[ U_{Aax}^{\mu _{1}}\left( {\mathbb {I}}_A \otimes E_{a} \otimes X_{x}\right) U_{Aax}^{\mu _{1}\dagger } \right] \nonumber \\&\qquad \otimes {\text {Tr}}_{By}\left[ U_{Bby}^{\mu _{2}}\left( \sigma ^{i}_B \otimes E_{b} \otimes X_{y}\right) U_{Bby}^{\mu _{2}\dagger } \right] \nonumber \\&\qquad +\sum _{i, j=1}^{3} t_{ij} {\text {Tr}}_{ax}\left[ U_{Aax}^{\mu _{1}}\left( \sigma ^{i}_A \otimes E_{a} \otimes X_{x}\right) U_{Aax}^{\mu _{1}\dagger } \right] \nonumber \\&\qquad \otimes {\text {Tr}}_{By}\left[ U_{Bby}^{\mu _{2}}\left( \sigma ^{j}_B \otimes E_{b} \otimes X_{y}\right) U_{Bby}^{\mu _{2}\dagger } \right] \Bigg )\nonumber \\&\overset{(d)}{=}\ 1/4\left( {\mathbb {I}}_{A} \otimes {\mathbb {I}}_{b} + \sum _{i=1}^{3} x_{i} \mu _{1} (\sigma ^{i}_{A} \otimes {\mathbb {I}}_{b})\right. \nonumber \\&\qquad \left. + \sum _{i=1}^{3} y_{i} \mu _{2} ({\mathbb {I}}_{A} \otimes \sigma ^{i}_{b}) + \sum _{i, j=1}^{3} t_{ij} \mu _{1} \mu _{2} (\sigma ^{i}_{A} \otimes \sigma ^{j}_{b}) \right) \nonumber \\&= \{\mu _{1} \vec {x}, \mu _{2} \vec {y}, \mu _{1} \mu _{2}{\mathbb {T}} \}. \end{aligned}$$

(A.3)

The equality (a) follows from the definition of a general two-qubit mixed state, the equalities (b) and (c) follow by expanding the expression and rearranging it for simplicity and the equality (d) follows from (A.1) and (A.2).