Introduction

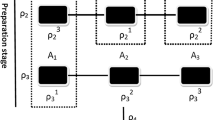
Three forms of quantum correlation occur in nature—entanglement, Bell nonlocality, and steering. The distinction between them can be viewed, from an operational perspective, as given by the level of trust and control that one has on the systems involved. Entanglement, for instance, is naturally formulated in the so-called device-dependent (DD) scenario1. There, one assumes that the system can be completely characterized by the measurement apparatus, at least in principle. Bell nonlocality, in contrast, takes place in the device-independent (DI) description2. There, measurement devices are treated as untrusted black boxes whose actual measurement process is uncharacterized or ignored, relying only on classical measurement settings (inputs) and results (outputs). Quantum steering, on the other hand, is a hybrid type of correlation—intermediate between entanglement and Bell nonlocality—that arises in semi-DI settings3,4,5. The latter involve both DD and DI parties, and an example is shown in Fig. 1a for the tripartite case of two untrusted devices and one trusted one. For all three types of correlation, the multipartite scenario is considerably richer than the bipartite one.

Fig. 1: Several hybrid (trusted-untrusted) multipartite scenarios.
figure 1

In the device-dependent (DD) case, measurement devices are well characterized (trusted), so that a specific quantum state (represented by Bloch spheres) can be attributed to the system. In the device-independent (DI) case, in contrast, the devices are uncharacterized (untrusted), so that systems are represented by black boxes. Semi-DI scenarios contain both trusted and untrusted components. There, the joint system is mathematically described by a hybrid object—intermediate between a state and a Bell behavior—called assemblage, and the type of nonlocality they can feature is called steering. In all three panels the shaded plane illustrates the bipartition of the trusted subsystem versus the untrusted ones. a An assemblage in the 2DI+1DD scenario: Alice and Bob rely on a black-box description, whereas Charlie’s system is trusted. All three subsystems are space-like separated. b Alice and Bob are no longer space-like separated: she communicates her output to him and he uses this to choose his input. This is an example of a bilocal wiring (local with respect to the bipartition AB∣C). Such operations cannot create any correlations across the bipartition, but they can expose a subtle form of multipartite quantum nonlocality that otherwise does not violate any Bell or steering inequality across the bipartition (see text). c A 4DI+1DD assemblage is mapped onto a 2DI + 1DD one by a bilocal wiring (x2 = a3, x3 = x4, and \({a}_{1}^{\prime}={a}_{1}+{a}_{2}\,{\mathrm{mod}}\,\,2\)). Such wirings can implement non-trivial resource-theoretic transformations, but not enough to enable a multi-black-box universal steering bit, i.e., an N-partite assemblage from which all bipartite ones, e.g., can be reached (see Supplementary Note E).

Full size image

Whereas entanglement is a resource for DD applications in quantum information, Bell nonlocality is the key resource for DI applications such as DI quantum key distribution6,7,8,9, DI-certified randomness10,11,12,13, DI-verifiable blind quantum computation14,15 and DI conference-key agreement16,17,18, which are typically much more experimentally demanding than the corresponding DD protocols. Steering is known to be the crucial resource for key technological applications in the semi-DI scenario, which are generally less technically difficult than their DI counterparts, while requiring less assumptions than the corresponding DD protocols. These include semi-DI entanglement certification4,5,19,20, quantum key distribution21,22, certified-randomness generation23, quantum secret sharing24,25, as well as other useful protocols in multipartite quantum networks26.

Interestingly, an operational inconsistency has arisen in the fully DI multipartite scenario27,28. It is rooted in the existence of an operation local to the AB partition that can create a Bell nonlocality across AB∣C. The issue, however, is best understood with the framework of resource theories.

Resource theories constitute formal treatments of a physical property as a resource, providing a complete toolbox for its quantification, classification, and operational manipulation (see, e.g., refs. 29,30,31). Applied and fundamental interest has motivated their formulation for entanglement1 and Bell nonlocality27,32,33,34, as well as for other relevant quantum properties34,35,36,37,38,39. Most important for our discussion is the resource theory of steering40,41. The cornerstone of any resource theory is the set of its free operations. These are unable to create the resource: they transform every resourceless state into a resourceless state. As a concrete example, free operations for quantum steering include, on the untrusted side, pre and post-processings of classical variables of the black boxes and, on the trusted side, local quantum operations and classical communication to the untrusted parties. It can be shown40 that these operations cannot create quantum steering out of unsteerable systems.

A fully DI description is cast in terms of a Bell behavior, given by a conditional probability distribution of the outputs given the inputs. Bell locality implies that there exists a local-hidden-variable model, in which correlations are explained by a (hypothetical) classical common cause (the hidden variable) within the common past light-cone of the measurement events42. Any Bell-inequality violation implies incompatibility with LHV models, i.e., Bell nonlocality. Bell-local behaviors are, naturally, the resourceless states of the resource theory of Bell nonlocality. We shall use the term bilocal to refer to being local with respect to the AB∣C bipartition. It stands to reason that operations within a given partition are free. However, a “wiring” between A and B (e.g., linking the output of one black box to the input of another as in Fig. 1b) is confined to AB but can map tripartite Bell behaviors that are local in the AB∣C partition (i.e., bilocal) into bipartite Bell behaviors that violate a Bell inequality across AB∣C. The problem, however, lied in the definition of Bell nonlocality in multipartite scenarios used previously43.

According to the traditional definition43, Bell nonlocality across a system bipartition is incompatible with any LHV model with respect to it. This includes so-called "fine-tuned” models44 with hidden signaling. These are LHV models where, for each value of the hidden variable, the subsystems on each side of the bipartition communicate, but for which the statistical mixture over all values of the hidden variable renders the observable correlations non-signaling. The problem is that the bilocal wiring can conflict with the hidden signaling in such models, giving rise to a causal loop. For instance, assume that for a particular tripartite system, there is only one LHV decomposition, which uses hidden signaling from Bob to Alice. To physically implement the wiring in Fig. 1b, which is an example of a free operation allowed within the AB partition, Bob must be in the causal future of Alice. This, in turn, is inconsistent with the direction of the hidden signaling. This explains why apparently bilocal behaviors can lead to Bell violations after a bilocal wiring. A redefinition of multipartite Bell nonlocality was then proposed27,28. This considers the correlations from conflicting bilocal models as already nonlocal across the bipartition, so that the wiring simply exposes an already-existing subtle form of Bell nonlocality. We refer to the latter form and effect as subtle Bell nonlocality and Bell-nonlocality exposure, respectively.

The redefinition fixed the inconsistency, but also opened several intriguing questions. First, no experimental observation of Bell-nonlocality exposure has been reported. Second, even though steering theory is relatively mature22,45,46,47,48, little is known about steering exposure. Steering features in the semi-DI description, where systems are described in terms of assemblages, given by quantum states describing the DD subsystems, weighted by the conditional probabilities describing the DI parties. Operational consistency relative to steering exposure was considered, in particular, in a definition of multipartite steering22, but based on models where each party is probabilistically either trusted or untrusted. On the other hand, a definition based on multipartite entanglement certification in semi-DI setups with fixed trusted-versus-untrusted divisions was proposed in ref. 49. There, bilocal hidden-variable models with an explicit quantum realization are considered, which automatically rules out potentially-conflicting fined-tuned models. Nevertheless, this has the side-effect of over-restricting the set of unsteerable assemblages, thus potentially overestimating steering. Third, exposure as a resource-theoretic transformation is yet unexplored territory. For instance, is it possible to obtain every bipartite assemblage via exposure from some multipartite one? What about Bell behaviors? Moreover, is there a single N-partite assemblage from which all bipartite ones are obtained via exposure?

These are the questions we answer. To begin with, we show that, remarkably, exposure of quantum nonlocality is a universal effect, in the sense that every bipartite Bell behavior (assemblage) can be the result of Bell-nonlocality (steering) exposure starting from some tripartite one. This highlights the power of exposure as a resource-theoretic transformation. However, we also delimit such power: we prove a no-go theorem for multi-black-box universal steering bits: there exists no single N-partite assemblage (with N − 1 untrusted and one trusted devices) from which all bipartite ones can be obtained through free operations of steering. Interestingly, in the universal steering exposure protocol, the starting behavior is not guaranteed to admit a physical realization, i.e., it may be supra-quantum50,51,52. Therefore, we also derive an alternative protocol that—albeit not universal—is manifestly within quantum theory. Moreover, we show that the output assemblage of such protocol is not only steerable but also Bell nonlocal (in the sense of producing a nonlocal behavior upon measurements by Charlie). This is notable as Bell nonlocality is a stronger form of quantum correlation than steering. We refer to this effect as super-exposure of Bell nonlocality. In turn, we provide a redefinition of (both multipartite and genuinely multipartite) steering to re-establish operational consistency. Finally, we experimentally demonstrate exposure as well as super-exposure. This is done using polarization and path degrees of freedom of two entangled photons generated by spontaneous parametric down-conversion, in a deterministic protocol.

Results

Steering and the semi-DI setting

Most of our discussion will be based on the semi-DI setting of Fig. 1a. We will not resort to quantum models of the black boxes; our definitions are based on the semi-DI setting alone, as befits its treatment as a resource for quantum tasks. Such systems are fully described by a Bell behavior \({{\boldsymbol{P}}}^{(AB)}:={\{{P}_{a,b| x,y}\}}_{a,b,x,y}\), with Pa,b∣x,y the conditional probability of outputs a, b given inputs x, y, for Alice and Bob, and an ensemble of conditional quantum states ϱa,b∣x,y for Charlie. These can be encapsulated in a hybrid object known as the assemblage \({\boldsymbol{\sigma }}:={\{{\sigma }_{a,b| x,y}\}}_{a,b,x,y}\), of sub-normalized conditional states σa,b∣x,y := Pa,b∣x,y ϱa,b∣x,y.

Unlike in Bell nonlocality or entanglement, semi-DI systems have a natural bipartition: the one separating the trusted devices from the untrusted ones, AB∣C. This is the bipartition with respect to which we define steering throughout, unless otherwise explicitly stated. We assume that σ satisfies the no-signaling (NS) principle, by virtue of which measurement-outcome correlations alone do not allow for communication. This implies that the statistics observed by Charlie should be independent of the input(s) of the remaining user(s). Mathematically, this condition reads

$$\mathop{\sum}\limits_{a,b}{\sigma }_{a,b| x,y}={\varrho }^{(C)},\quad \forall x,y,$$
(1)

where ϱ(C) is the reduced state on C. Furthermore, we also assume that Alice and Bob are NS, i.e., choosing their inputs does not provide them any communication,

$$\mathop{\sum}\limits_{a}{\sigma }_{a,b| x,y}\ {\rm{independent}}\ {\rm{of}}\ x,\quad \forall b,y,$$
(2)
$$\mathop{\sum}\limits_{b}{\sigma }_{a,b| x,y}\ {\rm{independent}}\ {\rm{of}}\ y,\quad \forall a,x.$$
(3)

The definition of steering in the AB∣C partition hinges on the impossibility of decomposing an assemblage σ as

$${\sigma }_{a,b| x,y}=\mathop{\sum}\limits_{\lambda }{P}_{\lambda }{P}_{a,b| x,y,\lambda }\ {\varrho }_{\lambda }.$$
(4)

Here, Pλ is the probability of the hidden variable Λ taking the value λ, each \({{\boldsymbol{P}}}_{\lambda }^{(AB)}:={\{{P}_{a,b| x,y,\lambda }\}}_{a,b,x,y}\) is a λ-dependent behavior, and ϱλ is the λ-th hidden state for C (locally correlated with AB only via Λ). However, different approaches have diverging positions on the set to which the distribution \({{\boldsymbol{P}}}_{\lambda }^{(AB)}\) may belong. Possibilities range5 from the full set of valid bipartite distributions to the most restricted set of factorizable ones (i.e., Pa,b∣x,y,λ = Pa∣x,λPb∣y,λ ∀ a, b, x, y). In ref. 49, steering is treated as equivalent to entanglement certification, hence each distribution \({{\boldsymbol{P}}}_{\lambda }^{(AB)}\) is required to be quantum-mechanically realizable. Our operational approach is defined in terms of assemblages only and aims to use them as resources, not for inferences on the quantum models that can produce them. It is thus best to ignore restrictions and consider, as a starting point, a general probability distribution. As such, σ is unsteerable if it admits a local hidden-state (LHS) model, defined by Eq. (4) with general \({{\boldsymbol{P}}}_{\lambda }^{(AB)}\); otherwise σ is steerable.

Importantly, a non-signaling σ does not imply non-signaling \({{\boldsymbol{P}}}_{\lambda }^{(AB)}\) for each λ (Imposition of the latter would be an additional requirement, one that is used in ref. 4 for yet another definition of steering in the literature.) In fact, LHS models can exploit hidden signaling between Alice and Bob as long as communication at the observable level (i.e., upon averaging Λ out) is impossible. This effect is known as fine-tuning44 and will turn out to be critical.

Steering exposure and Bell-nonlocality super-exposure

We begin by an exposure protocol for steering and Bell nonlocality that is universal in the sense of being capable of producing any bipartite assemblage (behavior) whatsoever from an appropriate tripartite assemblage (behavior) originally admitting an LHS (LHV) model. As in ref. 27, we exploit bilocal wirings as that of Fig. 1b, which makes Bob’s input y equal to Alice’s output a. This requires that Bob’s measurement is in the causal future of Alice’s. Indeed, after the wiring, systems A and B now behave as a single black box with input x and output b. In other words, exposure is a form of conversion from tripartite correlations into bipartite ones. Here, we restrict to the case of binary inputs and outputs (x, y, a, b ∈ {0, 1}) for simplicity, where we prove the following surprising result.

Theorem 1

(Universal exposure of quantum nonlocality). Any bipartite assemblage σ(target) or Bell behavior P(target) can be obtained via the wiring y = a on the tripartite assemblage σ(initial) or behavior P(initial), respectively, of elements

$${\sigma }_{a,b| x,y}^{(initial)}:=\frac{1}{2}{\sigma }_{b| x\oplus a\oplus y}^{(target)}$$
(5)

or

$${P}^{(initial)}(a,b,c| x,y,z)=\frac{1}{2}{P}^{(target)}(b,c| x\oplus a\oplus y,z),$$
(6)

where ⊕ stands for addition modulo 2. Moreover, σ(initial) and P(initial) admit respectively an LHS and an LHV models across the AB∣C bipartition, for all σ(target) and P(target).

That the initial correlations are mapped to the desired target is self-evident from Eqs. (5) and (6). What is certainly not evident is that the initial correlations are bilocal. This is proven in Supplementary Note A by construction of explicit LHS and LHV models. When the target assemblage (behavior) is steerable (Bell nonlocal), exposure of steering (Bell nonlocality) is achieved. Furthermore, apart from steerable, assemblages can also be Bell nonlocal in the sense of giving rise to nonlocal behaviors under local measurements47. Hence, when σ(target) is Bell nonlocal, a seemingly unsteerable system—i.e., one that admits an LHS decomposition—is mapped onto a Bell nonlocal one, which is outstanding in view of the fact that unsteerable assemblages form a strict subset of Bell-local ones.

The protocol highlights the capabilities of bilocal wirings as resource-theoretic transformations. Remarkably, such wirings compose a strict subset of well-known classes of free operations of quantum nonlocality (across AB∣C): local operations with classical communication (LOCCs)1 for entanglement, one-way (1W) LOCCs from the trusted to the untrusted parts40 for steering, and local operations with shared randomness27,32,33 for Bell nonlocality. However, there are also limitations to the capabilities of these wirings. In particular, in Supplementary Note E we prove a no-go theorem for universal steering bits in the NDI+1DD scenario [exemplified in Fig. 1c for N = 4]. That is, we show there that there is no N-partite assemblage, for all N, from which all bipartite ones can be obtained via arbitrary 1W-LOCCs.

Although the protocol above is universal, it is unclear whether it can actually be physically implemented in general. This is due to the fact that the tripartite initial correlations may be supra-quantum, i.e., well-defined non-signaling correlations that can however not be obtained from local measurements on any quantum state50,51,52,53. Physical protocols for Bell-nonlocality exposure were devised in refs. 27,28, but no such protocols have been reported for steering. Hence, we next derive an alternative example for both steering exposure and Bell-nonlocality super-exposure that is manifestly within quantum theory. This also exploits the bilocal wirings of Fig. 1b, but starting from a different initial assemblage. We describe the latter directly in terms of its quantum realization. Consider a tripartite Greenberger–Horne–Zeilinger (GHZ) state \((\left|000\right\rangle +\left|111\right\rangle )/\sqrt{2}\), with \(\left|0\right\rangle\) and \(\left|1\right\rangle\) the eigenvectors of the third Pauli matrix Z. Bob makes von Neumann measurements on his share of the state for both his inputs, for y = 0 in the Z + X basis and for y = 1 in the Z − X basis, with X the first Pauli matrix. Alice, however, makes either a trivial measurement, given by the positive operator-valued measure {\(\mathbb{1}\)/2, \(\mathbb{1}\)/2}, for x = 0, or a von Neumann X-basis measurement, for x = 1. For the resulting initial assemblage, σ(GHZ), the following holds (see Supplementary Note B for more details).

Theorem 2

(Physically-realizable exposure and super-exposure). The quantum assemblage σ(GHZ), of elements

$${\sigma }_{a,b| x,y}^{(GHZ)}=\frac{1}{8}\left\{{\mathbb{1}}+\frac{{(-1)}^{b}}{\sqrt{2}}\left[Z+x{(-1)}^{a+y}X\right]\right\}$$
(7)

admits an LHS model and, under the wiring y = a, is mapped to the assemblage of elements

$${\sigma }_{b| x}=\frac{1}{4}\left[{\mathbb{1}}+\frac{{(-1)}^{b}}{\sqrt{2}}\left(Z+xX\right)\right],$$
(8)

which is both steerable and Bell-nonlocal.

These results require a redefinition of steering in the multipartite scenario, since an assemblage can admit an LHS decomposition and still be steerable. We describe this redefinition, analogous to the one in ref. 27, before moving on to the experimental realization.

Consistently defining steering

The existence of subtle steering implies a stark inconsistency between the naive definition of steering from LHS decomposability, Eq. (4), and the notion of locality. Since the free operations that cause exposure are classical and strictly local (fully contained in the AB partition), it is reasonable that they are unable to create not only steering but also any form of correlations (even classical ones) across AB∣C. The alternative left is to redefine bipartite steering in multipartite scenarios such that, e.g., the assemblages in Eqs. (5) and (7) are already steerable. Formally, we need to exclude a subclass of LHS decompositions from the set of unsteerable assemblages.

To identify that subclass, let us apply the wiring y = a to a general σ fulfilling Eq. (4). This gives σ(wired), of elements

$${\sigma }_{b| x}^{({\rm{wired}})}:=\mathop{\sum}\limits_{a}{\sigma }_{a,b| x,a}=\mathop{\sum}\limits_{\lambda }{P}_{\lambda }\left(\right.\mathop{\sum}\limits_{a}{P}_{a,b| x,a,\lambda }\left)\right.{\varrho }_{\lambda }.$$
(9)

This is a valid LHS decomposition as long as the term within parentheses yields a valid (normalized) conditional probability distribution (of B given X and Λ). This is the case if every \({{\boldsymbol{P}}}_{\lambda }^{(AB)}\) in Eq. (4) is non-signaling. In that case, by summing over b and applying the NS condition, one gets

$$\mathop{\sum}\limits_{a,b}{P}_{a,b| x,a,\lambda }=\mathop{\sum}\limits_{a}{P}_{a| x,a,\lambda }\mathop{=}\limits^{{\rm{NS}}}\mathop{\sum}\limits_{a}{P}_{a| x,\lambda }=1,$$
(10)

which renders σ(wired) indeed unsteerable. However, this reasoning can in general not be applied if any \({{\boldsymbol{P}}}_{\lambda }^{(AB)}\) is signaling from Bob to Alice, i.e., if Alice’s marginal distribution for a depends on y (apart from x and λ). Therefore, we see that the inconsistency is rooted at hidden signaling. In fact, at the level of the underlying causal model, the phenomenon of exposure can be understood as a causal loop between such signaling and the applied wiring (see Fig. 2).

Fig. 2: Steering exposure as a causal loop.
figure 2

In the causal network underlying LHS models, given by Eq. (4), the hidden variable λ directly influences Charlie’s quantum state ϱ as well as the Alice and Bob’s outputs a and b, which are in turn also influenced by the inputs x and y, respectively. Even though the observed assemblage (after averaging λ out) is non-signaling, the model can still exploit hidden signaling (i.e., at the level of λ). For instance, for each λ, Alice’s output may depend (red arrow) on Bob’s input in a different fine-tuned way such that the dependence vanishes at the observable level. The wiring of Fig. 1b forces y = a, closing a causal loop that will in general conflict with the latter dependence for some λ. As a consequence, the final assemblage resulting from the wiring may not admit a valid LHS decomposition, exposing steering. Hence, the exposure can in a sense be thought of as an operational benchmark for hidden signaling in the LHS model describing the initial assemblage.

Full size image

To restore consistency, hidden signaling must be restricted. An obvious possibility would be to allow only for non-signaling \({{\boldsymbol{P}}}_{\lambda }^{(AB)}\)’s in Eq. (4). Interestingly, however, this turns out to be over-restrictive. Following the redefinition of multipartite Bell nonlocality27,28, we propose the following for bipartite steering in multipartite scenarios.

Definition 1

(Redefinition of steering). An assemblage σ is unsteerable if it admits time-ordered LHS (TO-LHS) decompositions both from A to B and from B to A simultaneously, i.e., if

$${\sigma }_{a,b| x,y}=\mathop{\sum}\limits_{\lambda }{P}_{\lambda }{P}_{a,b| x,y,\lambda }^{(A\to B)}{\varrho }_{\lambda }$$
(11)
$$=\mathop{\sum}\limits_{\lambda }{P}_{\lambda }^{\prime}{P}_{a,b| x,y,\lambda }^{(B\to A)}{\varrho }_{\lambda }^{\prime},$$
(12)

where each \({{\boldsymbol{P}}}_{\lambda }^{(A\to B)}\) is non-signaling from Bob to Alice and each \({{\boldsymbol{P}}}_{\lambda }^{(B\to A)}\) from Alice to Bob. Otherwise σ is steerable.

The validity of both time orderings simultaneously prevents conflicting causal loops. More precisely, if a wiring from Alice to Bob is applied on σ, one uses decomposition (11) to argue with the \({{\boldsymbol{P}}}_{\lambda }^{(A\to B)}\)’s [as in Eq. (10)] that the wired assemblage is unsteerable. Analogously, if a wiring from Bob to Alice is performed, one argues using the \({{\boldsymbol{P}}}_{\lambda }^{(B\to A)}\)’s from decomposition (12). Hence, no exposure is possible for TO-LHS assemblages, guaranteeing consistency with bilocal wirings (as well as generic 1W-LOCCs from trusted to untrusted parts) as free operations of steering. We note that, even though this redefinition prevents the exposure effect from creating steering, the effect still has, as illustrated by the exposure theorems, a relevant transformation power, especially when applied to steerable assemblages. As an example, there are assemblages that can only violate a Bell inequality across AB∣C after the exposure protocol.

On the other hand, when all λ-dependent behaviors in Eqs. (11) and (12) are fully non-signaling, then the assemblage is called non-signaling LHS (NS-LHS). There exist TO-LHS assemblages that are not NS-LHS, which proves that the latter is a strict subset of the former. In Supplementary Note C, we provide a quantum and a supra-quantum example of TO-LHS assemblages that are not NS-LHS.

This definition based on TO-LHS models is strictly different from previous definitions of steering in the literature. In ref. 4, \({{\boldsymbol{P}}}_{\lambda }^{({\boldsymbol{AB}})}\) from Eq. (4) is restricted to non-signaling distributions, which coincides with the NS-LHS definition. In ref. 49 \({{\boldsymbol{P}}}_{\lambda }^{({\boldsymbol{AB}})}\) is further restricted to quantum-realizable bipartite distributions, in what constitutes the quantum-LHS model, see Fig. 3. A fully factorizable \({{\boldsymbol{P}}}_{\lambda }^{({\boldsymbol{AB}})}\), as mentioned in ref. 5, represents an even further restriction, and the corresponding model only allows for classical correlations between Alice, Bob, and Charlie.

Fig. 3: Pictorial representation of inner structure of the set of all non-signaling assemblages in the tripartite scenario.
figure 3

Inclusion is strict for all depicted subsets: the set LHS of generic local-hidden-state (LHS) assemblages, the set TO-LHS of time-ordered LHS ones, the set NS-LHS of non-signaling LHS ones, and the set Q-LHS of quantum-LHS ones (see Supplementary Note C for details). The shaded region represents the set of assemblages with subtle steering. Bilocal wirings can expose such steering by mapping that region to the set of (bipartite) steerable assemblages.

Full size image

These examples have another consequence for the definition of steering. At times has the definition of steering been stated as entanglement that can be certified with the reduced information content of a semi-DI setting19,49. In fact, even with steering defined independently of entanglement certification, never to our knowledge had there been an instance of one being present without the other. We have nevertheless found cases of entanglement certification in the semi-DI scenario without steering, dissociating these two notions: the latter is sufficient, but not necessary, for the former. This is seen from the quantum-realizable examples of a TO-LHS assemblage that is not NS-LHS in Supplementary Note C. They can be decomposed as in Eqs. (11) and (12), but only with distributions \({P}_{a,b| x,y,\lambda }^{(A,B\to B,A)}\) that are signaling, hence, not quantum. As such, a quantum system without AB∣C entanglement is unable to produce such an assemblage, i.e., entanglement can be certified in AB∣C. On the other hand, since it is TO-LHS, the assemblage has no steering in the same bipartition (details in Supplementary Note C).

Furthermore, the redefinition above automatically implies also a redefinition of genuinely multipartite steering (GMS). We present this explicitly in Supplementary Note D. There, we follow the approach of ref. 49 in that a fixed trusted-versus-untrusted partition is kept. However, instead of defining GMS as incompatibility with quantum-LHS assemblages (i.e., with λ-dependent behaviors with explicit quantum realizations) as in ref. 49, we use the more general TO-LHS ones. This reduces the set of genuinely multipartite steerable assemblages safely, i.e., without introducing room for exposure. The dissociation of steering and entanglement certification also happens in this genuine multipartite case.

Experimental implementation

The exposure procedure was experimentally implemented using entangled photons produced via spontaneous parametric down-conversion. The experimental setup is shown in Fig. 4. A photon pair is generated in the Bell state \(\left|{{{\Phi }}}^{+}\right\rangle =\left(\left|00\right\rangle +\left|11\right\rangle \right)/\sqrt{2}\), where \(\left|0\right\rangle\) (\(\left|1\right\rangle\)) stands for horizontal (vertical) polarization of the photons54. The photons in the signal mode (s) pass through a calcite beam displacer (BD), which creates two momentum modes (paths) depending on the polarization. This results in a tripartite GHZ state, where the extra qubit is the path degree of freedom of the photons in s. Alice’s and Bob’s qubits are the polarization and path of the photons in mode s, respectively, while Charlie’s qubit is the polarization of the photons in mode i. Projective measurements onto all the degrees of freedom required for state tomography are performed as described below.

Fig. 4: Experimental setup.
figure 4

Two crossed-axis BBO crystals are pumped by a He-Cd laser centered at 325 nm, producing pairs of photons at 650 nm entangled in the polarization degree of freedom54. The signal (s) photon is sent through a BD which deviates only the horizontal-polarization component, producing a tripartite GHZ state on two photons using polarization and path degrees of freedom. Idler (i) photons are sent directly to Charlie’s polarization measurements. Signal photons are first measured in polarization by Alice, then Bob maps his path qubit onto a polarization qubit for his measurements. H stands for half-wave plate, Q for quarter-wave plate, and PBS for polarizing beam splitter.

Full size image

To implement the wiring from Fig. 1b, Alice’s polarization measurements are realized before Bob’s measurements onto the path degree of freedom. Alice’s results are read from the output of PBSA, which determines whether D2 (a = 0) or D3 (a = 1) clicks. For Alice’s trivial measurement (x = 0), crucial for the original assemblage to be LHS-decomposable, both her wave plates located before the imbalanced interferometer (represented by Δ) are kept at 0∘, and H@θ is adjusted to 22.5∘. The role of Δ is to remove the coherence between horizontal and vertical polarization components, ensuring that the photon exits PBSA randomly, independent of the input polarization state. For x = 1, Alice’s wave plates are set to project the polarization on the X eigenstates, the interferometer and H@θ (θ = 0∘) play no role. Bob performs his projective measurements by first mapping the path degrees of freedom onto polarization using BDs and then projecting the polarization state using his set of wave plates and PBSs, as was realized in ref. 55. To reconstruct the assemblage in Eq. (7), measurements for y = 0 and y = 1 are made in both detectors D2 and D3, varying the angle of the wave plates in Bob’s box. To collect the data corresponding to the wired assemblage (8) only the y = 0 measurement is made in D2 (a = 0) and only y = 1 is made in D3 (a = 1), enforcing that Bob’s input equals Alice’s output (y = a).

The assemblage σ(GHZ) was obtained experimentally by performing state tomography on Charlie’s system for each measurement setting and outcome of Alice and Bob. Sixteen density matrices (plotted in Supplementary Fig. S1) are obtained through maximum likelihood, and the assemblage presents a fidelity-like measure of 98.2 ± 0.2% compared to the theoretical one (see “Methods”). The experimental wired assemblage is shown in Fig. 5a, and returns a fidelity of 98.1 ± 0.6% with respect to the theoretical wired assemblage given in (8).

Fig. 5: Experimental results.
figure 5

Experimental assemblages after y = a wiring. a Real part of Charlie’s conditional density matrices, theoretical (top) and experimental (bottom). b Steering-witness histogram. The witness value is 1.015 ± 0.009, meaning that the experimental assemblage is more than one standard deviation above the steering threshold (dashed line). Compatibility of the tripartite experimental assemblage with the naive (LHS) definition of unsteerability [Eq. (4)]. c Histogram of the error of approximating the tripartite assemblage by an NS and an LHS assemblage, showing that the error of assuming the LHS decomposition is as small as that of the physically necessary NS assumption. d From the best NS approximation to the experimental data, histogram of the LHS-robustness, a measure of deviations from the set LHS. Even with all experimental error, there is only a residual amount of robustness, fully compatible with that of the theoretical LHS assemblage solely under finite-statistics error. All histograms come from Monte Carlo simulation assuming Poisson distributions.

Full size image

An exact LHS decomposition of the experimental assemblage is not feasible due to imperfections and finite statistics—in fact, assemblages reproducing raw experimental data exactly are not even physical, since they disobey the NS principle49. To show that the experimental tripartite assemblage is statistically compatible with an LHS decomposition, we proceed as follows: First, we assume the photocounts obtained for each measured projector are averages of Poisson distributions; with a Monte Carlo simulation, we sample many times each of these distributions and reconstruct the corresponding assemblages. Second, for each reconstructed assemblage, we find the physical (NS) assemblage that best approximates it through maximum-likelihood estimation, as well as the best LHS approximation for comparison. As an initial indication of LHS compatibility, the log-likelihood error of both approximations is extremely similar, see Fig. 5c. Third, for the NS approximations, we calculate the LHS-robustness56, a measure that is zero for all LHS assemblages. For comparison, we repeat the procedure starting with simulated finite-photocount statistics from the theoretical LHS assemblage from Eq. (7). In Fig. 5d we see that the experimental robustness has a sizable zero component and a distribution fully compatible with that of an LHS assemblage under finite measurement statistics.

To show that the experimental wired assemblage is steerable, we tested it on the optimal steering witness W with respect to assemblage (8) (see Supplementary Notes B). This returned a value 1.015 ± 0.009 ≰ 1 (theoretical: 1.0721 ≰ 1), where the inequality violation implies steering, see Fig. 5b. This allows us to conclude that the bipartite wired assemblage is indeed steerable. The experimental error was calculated using 500 assemblages also from a Monte Carlo simulation of measurement results with Poisson photocount statistics.

Using the same experimental setup, we can also experimentally demonstrate super-exposure of Bell nonlocality. As argued above, the initial experimental assemblage is compatible with an LHS model. Therefore, no matter what measurement Charlie makes, the corresponding Bell behavior will be compatible with an LHV model. Hence, we must only show that the experimental wired assemblage is Bell nonlocal. In ref. 47, a necessary and sufficient criterion for Bell nonlocality of assemblages was derived: Given Alice and Bob’s wired measurements (y = a) with input bit x and output bit b, to maximally violate a Bell inequality, Charlie performs von Neumann measurements in the 2Z + X and X bases, labeled by input bit z, obtaining binary output result c. They thus obtain 16 probabilities P(b, c∣x, z), which are used to calculate the Clauser–Horne–Shimony–Holt inequality57. We obtained an experimental violation of 2.21 ± 0.04 ≰ 2 (theoretical prediction: 2.29 ≰ 2), showing Bell nonlocality.

This experiment is sufficient to for a proof-of-principle demonstration of both exposures of steering and super-exposure of Bell nonlocality. We note that strict demonstration of these phenomena in their appropriate DI scenarios requires a realization with space-like separation between the parties (locality loophole), as well as high-efficiency source and detectors (fair-sampling assumption).

Discussion

We have demonstrated that the traditional definition of multipartite steering for more than one untrusted party based on decomposability in terms of generic bilocal hidden-state models presents inconsistencies with a widely accepted, basic notion of locality. We have also shown how, according to such definition, a broad set of steerable (exposure) and even Bell-nonlocal (super-exposure) assemblages would be created from scratch, e.g., by bilocal wirings acting on a seemingly unsteerable assemblage, i.e., an LHS one. A surprising discovery that we have made is the fact that exposure of quantum nonlocality is a universal effect, in the sense that all steering assemblages, as well as Bell behaviors, can be obtained as the result of an exposure protocol starting from bilocal correlations in a scenario with one more untrusted party. This highlights the power of exposure as a resource-theoretic transformation. However, we also delimit such power: we prove a no-go theorem for multi-black-box universal steering bits: there exists no single assemblage with many untrusted and one trusted party from which all assemblages with one untrusted and one trusted party can be obtained through generic free operations of steering. To restore operational consistency, we offer a redefinition of both bipartite steering in multipartite scenarios and genuinely multipartite steering that does not leave room for creating correlations from scratch. Finally, both steering exposure and Bell nonlocality super-exposure have been demonstrated experimentally using an optical implementation. This is to our knowledge the first experimental observation of exposure of quantum nonlocality reported, not only in semi device-independent scenarios but also in fully device-independent ones, as originally predicted in refs. 27,28.

Finally, we mention practical implications that our results might have. Steering in the scenario we work on, with a single trusted party, has been shown to be particularly relevant for the task of quantum secret sharing24,25. In it, the trusted party deals a secret to the untrusted parties, who must be able to access it only when cooperating, not independently. A form of steering that is only observable when such parties cooperate, as in the exposure protocol, fits this mold quite specifically. This indicates a potential application of our results, possibly in conjunction with the open question of other joint operations able to achieve exposure.

Methods

Experimental assemblages

Let us describe the quantum state and the assemblages produced in our experiment in more detail. Although we treat two of the qubits as black boxes, in order to ensure that the resulting assemblage is coming up from quantum measurements performed onto a GHZ, we first made a state tomography to determine the tripartite quantum state. This can be done without adding any optical element to the setup. By varying the angles on Alice’s quarter-wave plate and half-wave plate before the imbalanced interferometer, we set her apparatus to make any tomographic measurement in polarization if we set H@θ to 0∘. The tomographic projections for the path degree of freedom of photons in s and polarization of photons in i are done using the set of wave plates just before detectors D1 and D2, respectively. Using the collected coincidence counts we reconstructed the tripartite quantum state by maximum likelihood. The reconstructed density matrix is shown in Fig. 6. The experimental state presents fidelity with GHZ state equals to 0.981 ± 0.004.

Fig. 6: Real and imaginary parts of the experimental reconstructed GHZ state.
figure 6

Colors are for visualization purposes only.

Full size image

Each element of the tripartite assemblage is composed of Charlie’s conditional quantum state and the conditional probability Pa,b∣x,y for the black boxes. All sixteen experimental Charlie’s density matrices are shown in Supplementary Fig. S1 in comparison with the corresponding theoretical ones. The associated conditional probabilities are also shown.

For the wired assemblage, the expected conditional probability of each outcome is \(\frac{1}{2}\); the experimental values are 0.46 ± 0.01, 0.54 ± 0.01, 0.49 ± 0.01, 0.51 ± 0.01 (following the order in Fig. 5a). The imaginary components of the density matrix average to 0.05 ± 0.02 (theoretical: zero).

Assemblage fidelity

We can see by visual inspection that the experimental and corresponding theoretical assemblage elements shown in Fig. 5 and Supplementary Fig. S1 are similar. To quantify this similarity we use a mean assemblage fidelity between two assemblages σ1 = {P1(a∣x)ϱ1(a∣x)} and σ2 = {P2(a∣x)ϱ2(a∣x)} defined by

$$F({{\boldsymbol{\sigma }}}_{1},{{\boldsymbol{\sigma }}}_{2})=\frac{1}{{N}_{x}}\mathop{\sum}\limits_{{\bf{x}},{\bf{a}}}\sqrt{{P}_{1}({\bf{a}}| {\bf{x}}){P}_{2}({\bf{a}}| {\bf{x}})}{\mathcal{F}}\left({\varrho }_{1}({\bf{a}}| {\bf{x}}),{\varrho }_{2}({\bf{a}}| {\bf{x}})\right),$$
(13)

where x (a) is a list of inputs (outputs) of all black boxes, Nx is the number of different measurement choices, and \({\mathcal{F}}({\varrho }_{1},{\varrho }_{2})\) is the usual fidelity between two quantum states. The numerical values of assemblage fidelity in the main text are calculated with this definition. The above-defined fidelity can be seen as a mean of the fidelities of the quantum parts weighted by the square root of blackbox probabilities. It has the property of being 1 if all elements of the two assemblages are equal and vanish if all quantum states are orthogonal.