Introduction

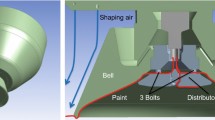
Knowing the thickness of a paint film on a high-speed rotary bell,1 especially near the periphery,2 has significance because film thickness in the region of departure contributes to the determination of average drop diameter in the subsequent spray.3 An example of an automotive body painting process, from supplied liquid through film deposition, is schematically shown in Fig. 1. As paint, which is a system of solvents and solutes, departs from the bell, it is shredded4 into an “infinity” of drops that can be approximated by a statistical distribution.5 Aerodynamic forces have a dependency on the initial tangential velocity of the departing drops. Thus, the eventual average drop diameter is influenced by a tentative balance between complex aerodynamic drop-shredding forces, drop-preserving forces of surface tension, and, if present, electrostatic forces.6 Larger drops are more vulnerable to aerodynamic shredding. However, as shredding reduces drop diameter, surface tension forces become relatively dominant, limiting further drop breakup.

Fig. 1
figure 1

Process flow—liquid paint enters the center of the bell, shear forces spread the liquid over the concave bell surface and accelerate it to the edge where it is atomized, and finally, air currents and electrostatics propel droplets toward deposition on the body panel

Full size image

The academic study of rotary atomization7 morphs into a tangible and financially quantitative industrial problem when considering the effects of variation in paint drop viscosity caused by solvent evaporation from the paint drop while they are inflight from the bell to final deposition on a body surface. A simplifying assumption is that the extrinsic solvent evaporation rate is proportional to drop surface area. Since a spherical drop has a surface area to volume ratio of three over the radius (3/r), at a constant intrinsic evaporation rate per unit area, the rate of change in solvent concentration within a drop is inversely proportional to drop radius. Compared to an average inflight drop, larger drops have a slower solvent concentration reduction rate, while smaller drops have a faster solvent concentration reduction rate. If a drop is significantly oversized, insufficient inflight solvent evaporation leaves it relatively solvent rich upon deposition at the car body. Therefore, the paint film has a higher likelihood of sagging due to low viscosity.

On the other hand, if a drop is significantly undersized, excess inflight evaporation leaves it solvent deficient upon deposition. The paint film can become too viscous to form a level surface, thereby contributing to an uneven finish colloquially known as “orange peel.” The desired rotary bell-induced spray has two important statistics: controllable drop size and narrow distribution, enabling a uniform and level paint film to satisfy customers.8

Background

Axisymmetric rotary bells profiles analyzed with the Navier–Stokes equations (NSE’s) in spherical9,10 or cylindrical coordinate systems are represented by schematics cross sections shown in Fig. 2.

Fig. 2
figure 2

Bell cross sections coincident with rotation axis in spherical or cylindrical coordinates

Full size image

Prior works by Hinze and Milborn,11 Orzechowski and Bayvel12 (h), Sun et al.,13 Ogasawra et al.14 (h), and Yang et al.15 are summarized in Table 1.

Table 1 Summary of prior works in common coordinate systems
Full size table

Table 1 summarizes simplified governing equations based on assumptions of steady state, a Newtonian fluid, thin film, in-film geometry defined by profile geometry, axisymmetric flow, axisymmetric derivatives, center-fed volumetric flow Q, no-slip and no-shear boundary conditions, high-speed, and point analysis. Point analysis implies all calculations are local instead of integrating from an upstream set of initial conditions constraining film thickness and velocity profiles. This last assumption leads to a singularity of an infinitely thick film at the center of rotation. However, since an actual rotary bell has a cap over the centrally located supply port that extends over a portion of the bell, point analysis becomes a reasonable assumption since the thickness is not calculated around the center of rotation.

Although the governing equations in Table 1 appear algebraically different, they are essentially equation (1) cast into different coordinate systems, along with different geometric references. The film thicknesses in Table 1 are the result of integrations that were simplified by implementing previously mentioned assumptions.

$$\frac{{d^{2} v_{{\tan }} }}{{dv_{{{\text{norm}}}}^{2} }} = \frac{{\rho R\omega ^{2} }}{\mu }\cos \psi$$
(1)

Equation (1) describes a pattern that emerges from analyses in familiar (spherical, cylindrical) coordinate systems. The film thickness at any point on a bell profile can be approximated in the context of a local normal-tangential coordinate system at a point on the bell profile by specifying the local angle \(\psi\) and other operating parameters. A schematic that describes this relationship is shown in Fig. 3.

Fig. 3
figure 3

Localized analysis

Full size image

Despite the apparent simplicity represented by equation (1) and Fig. 3, there is a hidden subtlety in analyzing a spherical bell profile with this approach. Since the angle \(\psi\) varies with radial position \(R\), and if the bell is of sufficient diameter, it is possible to find a location where the film thickness is minimum, beyond which, the film becomes thicker in the direction of flow. On the other hand, for profiles of constant polar angle, such as a cone or disk, the film thickness is strictly decreasing as the radial coordinate goes to infinity. In other words, for a bell surface profile that has an infinite radius of curvature, the film becomes forever thinning in the direction of flow. In contrast, in the case of a spherical surface, there is an inflection point, after which flow can proceed from thinner to thicker films. This article does not include an analysis of such flow conditions.

The bell cross section shown in Fig. 4 is casually different from those shown in Fig. 2. It does not have a surface profile coincident with a coordinate axis of a common coordinate system. An alternative coordinate system for analysis is defining a profile-following coordinate system. However, vector operators applicable to this surface-following coordinate system, such as those used in the vector form of the Navier–Stokes equations, will require derivation since they depend on the particular profile.

Fig. 4
figure 4

Example of blended profile

Full size image

As shown in Fig. 4, two questions will be answered with the introduction of a blended surface profile. First, does analyzing the film in the context of equation (1) provide a usable thickness profile in the case of a variable curvature bell surface? Second, does a Navier–Stokes formulation in surface-following coordinates, along with previously mentioned assumptions, simplify into the form of equation (1)? The answer to both of these questions is yes.

Example in literature

A bell profile was scaled from an illustration contained in Domnick et al.16 It consists of a substantially conical section with a surface angle, measured from a normal to the rotation axis, of about 28 degrees up to a radius of about 30 mm, and then blends into another substantially conical section with the surface angle of about 60 degrees and extends out to the peripheral radius of about 31.5 mm. The fluid had a viscosity of about 0.086 Pa-s viscosity and a density approximated as 1.0 gram per cc. Two different RPM curves are shown in Fig. 5, a 40,000-RPM curve and a 60,000-RPM curve. These curves agree with the data published by Domnick et al.16

Fig. 5
figure 5

Equation (1) applied to a bell with variable cone angles

Full size image

The curves shown in Fig. 5 had discontinuities at around the 30-millimeter radial position that were the result of lines connecting the points of local analysis between the two conical angles. Moreover, Domnick et al. included an ANSYS Fluent analysis that had similar results. Obtaining film thickness profiles based on localized calculations utilizing equation (1) does indeed have the ability to show useful results.

Surface-following coordinate system

In a mathematically elegant work published by Mogilevskii and Shkadov,17 although their analysis was tailored for an exceedingly more complex problem than a high-speed rotary bell, extensive simplification of the outward \(\left(\xi \right)\) momentum equation eventually yields equation (1). In their work, a plane curve with radial and vertical positions parameterized by arc length along the bell profile was revolved around the axis of rotation, thereby creating a surface-following orthogonal coordinate system. Since any particular bell profile defines a unique coordinate system, vector operators associated with this coordinate system required derivation. In the analysis of Mogilevskii and Shkadov, this paper attempts to fill in several intermediate steps that assist in recreating a derivation of their extraordinary work; however, derivations of results beyond select terms in the outwards \(\left(\xi \right)\) momentum equation were not included.

In Fig. 6, a plane on \(R,Z\) was parameterized by the coordinate \(\xi\), or arc length. A value of \(\eta\) is the distance normal to the curve at the point parameterized by \(\xi\). The angular position around the Z-axis is similar to the rotational coordinate in a “traditional” cylindrical coordinate system. Figure 7 and equation (2) are the keys to transformation between the planar systems of \(R,Z\) and \(\xi ,\eta\). Since \(\xi , \eta ,\) and unit vector for rotation around z (perpendicular to the page) are mutually orthogonal, this coordinate system is isomorphic to all orthogonal coordinate systems. It retains the property of invariance of differential length.

Fig. 6
figure 6

Plane curve in R, Z plane, revolved around the Z axis

Full size image
Fig. 7
figure 7

\(\left(r,z\right)=\left(R\left(\xi ,\eta \right),Z\left(\xi ,\eta \right)\right)=\left(R\left(\xi \right)-\eta {Z}_{\xi },Z\left(\xi \, \right)+\eta {R}_{\xi }\right)\)

Full size image

The invariance of length, or the L2 norm, in Hilbert Space can be expressed by equation (2). In this case, “x’s” represent the coordinates in a Cartesian \(\left(x,y,z\right)\) system, the “q’s” represent the coordinates in the surface-profile-following \(\left(\xi ,\eta ,\theta \right)\) system. The coefficients glm are the components of the metric tensor, or metric coefficients. They are defined by equation (3).

$${ds}^{2}={dx}_{i}\cdot {dx}_{i}=\frac{\partial {x}_{i}}{\partial {q}_{l}}\frac{\partial {x}_{i}}{\partial {q}_{m}}d{q}_{l}d{q}_{m}={g}_{lm}d{q}_{l}d{q}_{m}$$
(2)
$$\frac{\partial {x}_{i}}{\partial {q}_{l}}\frac{\partial {x}_{i}}{\partial {q}_{m}}={g}_{lm}$$
(3)

Orthogonality dictates there are only three diagonal coefficients in this metric tensor. Therefore, the length of a vector is defined by equation (4), where \(h_{{\left( i \right)}} ^{{\prime }} {\text{s}}\) are referred to as scale factors.18 This h is not the same as the previous h designating film thickness. Parentheses are used on the indices of each h to associate the scale factor with a particular coordinate and are not included in indicial operations. Finally, each \({h}_{\left(i\right)}\) is calculated according to equation (5).

$${ds}^{2}={h}_{\left(1\right)}^{2}{ds}_{1}^{2}+{h}_{\left(2\right)}^{2}{ds}_{2}^{2}+{h}_{\left(3\right)}^{2}{ds}_{3}^{2}$$
(4)
$${h}_{\left(i=\text{1,2},3\right)}=\sqrt{\frac{\partial {x}_{1}}{\partial {q}_{i}}\frac{\partial {x}_{1}}{\partial {q}_{i}}+\frac{\partial {x}_{2}}{\partial {q}_{i}}\frac{\partial {x}_{2}}{\partial {q}_{i}}+\frac{\partial {x}_{3}}{\partial {q}_{i}}\frac{\partial {x}_{3}}{\partial {q}_{i}}} i=\xi ,\eta ,\theta$$
(5)

Figure 7 substantiates a coordinate transformation of (\(\xi , \eta , \theta\)), where \(\theta\), in this context, is an angle around the axis of rotation, to (x, y, z). The Cartesian coordinate transformations are shown as equations (6), (7), and (8). In the (\(\xi , \eta , \theta\)) system, all points are \({\mathcal{R}}^{3}\) are longer reachable; therefore, analysis in this system is restricted to thin fluid films.17

$$x\left(\xi ,\eta ,\theta \right)=\left(R\left(\xi \right)-\eta {Z}_{\xi }\left(\xi \right)\right)\mathit{cos}\theta$$
(6)
$$y\left(\xi ,\eta ,\theta \right)=\left(R\left(\xi \right)-\eta {Z}_{\xi }\left(\xi \right)\right)\mathit{sin}\theta$$
(7)
$$z\left(\xi ,\eta ,\theta \right)=Z\left(\xi \right)+{R}_{\xi }\left(\xi \right)\eta$$
(8)

If equations (6), (7), and (8) are substituted into equation (5), the scale factors are obtained and shown as equations (9), (10), and (11). Deriving equations (9)–(11) relies on the identity \({C}^{2}+{S}^{2}=1\); however, equation (11) also relies on neglecting a \({\eta }^{2}\) term and the truncated binomial theorem, or \({\left(1+bx\right)}^{\alpha }=1+\alpha bx\).

$$\theta : {h}_{\left(3\right)}=1$$
(9)
$$\eta : {h}_{\left(2\right)}=R\left(\xi \right)-{Z}_{\xi }\left(\xi \right)\eta =r\left(\xi ,\eta \right)$$
(10)
$$\xi : {h}_{\left(1\right)}=1-\left({R}_{\xi }{\left(\xi \right)Z}_{\xi \xi }\left(\xi \right)-{Z}_{\xi }\left(\xi \right){R}_{\xi \xi }\left(\xi \right)\right)\eta =1-\mathcal{K}\eta (11)$$
(11)

Scale factors are the ratio of differential distances to differentials of the coordinate parameters.18 Once scale factors are known, vector operators can be derived using widely available gradient, material derivative, and Laplacian definitions. However, unit vectors in this surface-following system have derivatives; therefore, the derivation of associated vector operators becomes tedious.

Calculations of the unit vector derivatives were brilliantly explained by Happel and Brenner.19 Once derivatives of unit vectors are known, the gradient [equation (12)], the material derivative [equation (13)],20,21 and the Laplacian [equation (14)] 21 can be calculated and are shown as follows.

$$\nabla =\frac{1}{{h}_{i}}\frac{\partial }{\partial {q}_{i}}{\widehat{q}}_{i}$$
(12)
$${\left[u\cdot \nabla u\right]}_{i}=\frac{{u}_{j}}{{h}_{j}}\frac{{\partial u}_{i}}{{\partial q}^{j}}+\frac{{u}_{j}}{{h}_{j}{h}_{i}}\left({u}_{i}\frac{{\partial h}_{i}}{{\partial q}^{j}}-{u}_{j}\frac{{\partial h}_{j}}{{\partial q}^{i}}\right)$$
(13)
$$\Delta =\frac{1}{{h}_{1}{h}_{2}{h}_{3}}\left\{\frac{\partial }{\partial {q}_{1}}\left(\frac{{h}_{2}{h}_{3}}{{h}_{1}}\frac{\partial }{\partial {q}_{1}}\right)+\frac{\partial }{\partial {q}_{2}}\left(\frac{{h}_{1}{h}_{3}}{{h}_{2}}\frac{\partial }{\partial {q}_{2}}\right)+\frac{\partial }{\partial {q}_{3}}\left(\frac{{h}_{1}{h}_{2}}{{h}_{3}}\frac{\partial }{\partial {q}_{3}}\right)\right\}$$
(14)

Fitzpatrick, “after a great deal of tedious algebra,”21 which is an understatement, has an expanded form of [equation (14)], that is [equation (15)].

$$\begin{aligned} \left( {\nabla ^{2} A} \right)_{i} & = \nabla ^{2} A_{i} + \frac{2}{{h_{i} h_{j} }}\left( {\frac{1}{{h_{i} }}\frac{{\partial h_{i} }}{{\partial u_{j} }}\frac{\partial }{{\partial u_{i} }} - \frac{1}{{h_{j} }}\frac{{\partial h_{j} }}{{\partial u_{i} }}\frac{\partial }{{\partial u_{j} }}} \right)A_{j} \\ \quad & + \frac{h}{{h_{i} h_{j}^{2} }}\left[ {\frac{{A_{j} }}{{h_{i}^{2} }}\frac{{\partial h_{j} }}{{\partial u_{i} }}\frac{\partial }{{\partial u_{j} }}\left( {\frac{{h_{i}^{2} }}{h}} \right) - \frac{{A_{i} }}{{h_{j}^{2} }}\frac{{\partial h_{i} }}{{\partial u_{j} }}\frac{\partial }{{\partial u_{j} }}\left( {\frac{{h_{j}^{2} }}{h}} \right)} \right] \\ \quad & + \frac{{A_{j} }}{{h_{i} }}\frac{h}{{h_{j}^{3} }}\left[ {\frac{1}{{h_{j} }}\frac{{\partial h_{j} }}{{\partial u_{i} }}\frac{\partial }{{\partial u_{j} }}\left( {\frac{{h_{j}^{2} }}{h}} \right) + \frac{h}{{h_{j}^{2} }}\frac{\partial }{{\partial u_{i} }}\left( {\frac{{h_{j}^{2} }}{h}} \right)\frac{\partial }{{\partial u_{j} }}\left( {\frac{{h_{j}^{2} }}{h}} \right) - \frac{{\partial ^{2} }}{{\partial u_{i} \partial u_{j} }}\left( {\frac{{h_{j}^{2} }}{h}} \right)} \right] \\ \quad & - \frac{{A_{i} }}{{h_{i} h_{j}^{2} }}\left[ {\frac{2}{{h_{i} }}\left( {\frac{{\partial h_{j} }}{{\partial u_{i} }}} \right)^{2} - \frac{{\partial ^{2} h_{i} }}{{\partial u_{j}^{2} }}} \right]h = h_{1} h_{2} h_{3} \end{aligned}$$
(15)

If equations (12)–(15) are substituted into a vector form of the Navier–Stokes equations, along with kinematic and dynamic boundary conditions, an extensive nondimensionalization, and put into an inertial framework, this is the starting point of the work of Mogilevskii and Shkadov. However, if the \(\xi\) momentum equation is extensively simplified according to previous assumptions, equation (16) is obtained, and as seen in Fig. 7, \({R}_{\xi }\left(\xi \right)\) is equal to \(\text{cos}\theta\) in equation (1), thus, proving that an extensively simplified formulation of the Navier–Stokes equations in surface-following coordinates does indeed match the “pattern” seen in the more common cylindrical and spherical coordinate systems. Although a numerical answer can usually be obtained from equations (1) or (16), there is the possibility that additional physics were ignored. However, that is a complex and tedious analysis and not covered in this work. Equation (16) is a more general form than the equations in Table 1 since the bell surface is no longer constrained to a coordinate axis. Instead, it is defined by a revolved planar curve with radial and vertical position parameterized by arc length along the bell surface. Unfortunately, this equation does not indicate when it fails to predict actual fluid behaviors that result from the profile of \(R\left(\xi \right)\) and \(Z\left(\xi \right)\). However, it may prove useful as preliminary analysis or a numerical check of CFD results.

$$\frac{{d}^{2}{v}_{\xi }}{\partial {\eta }^{2}}=\frac{\rho R{\omega }^{2}}{\mu }{R}_{\xi }\left(\xi \right)$$
(16)

Conclusions

An analysis of the work of Mogilevskii and Shkadov17 was humbling; however, this article was not focused on what they did. On the other hand, it was focused on providing additional relevant subject matter to understand how they obtained results. Once deciphered, their article positively answered the question on the existence of a simple film model for a functionally defined and “within reason” surface profile of rotary a bell. Moreover, it provides a framework for considering analyses that are more complex. As expected, and proved, regardless of the coordinate system, the laws of physics should yield the same answer.