1 Introduction and rationale

What difficulties do students face to understand calculus concepts and to work on situations or tasks that involve variational reasoning? How should teaching and learning environments be framed to foster students development of resources and ways of thinking to approach calculus tasks? What is the role of digital technologies in students ways to represent, explore, understand, and apply calculus concepts to solve problems. Addressing these types of questions has led researchers in mathematics education, mathematicians, and teachers to develop a worldwide research agenda that has focused on curriculum issues, the role of students’ background and learning experiences in the transition from school to university mathematics, the design and implementation of learning activities, ways to foster and assess students’ learning, and the role and use of calculus textbooks in learning scenarios (Frank & Thompson, 2021). Research results, in these areas have shed light on ways to support teaching practices and ways to assess students’ understanding of calculus concepts.

Recently, researchers have been interested in analysing and documenting the extent to which the students understanding of foundational concepts studied in precalculus courses determines and shapes their ways to grasp calculus concepts and to approach calculus tasks. Thus, it is important to characterize the types of difficulties students exhibit to solve tasks that involve the use of foundational calculus concepts and to identify and discuss possible ways for students to overcome such difficulties to fully understand those concepts. To this end, we introduce a conceptual framework to address these foundational concepts in terms of recognizing the importance for learners to merge structurally and coordinate different meanings of the concept of derivative (Thurston, 1994). In this perspective, the students’ systematic use of a Dynamic Geometry SystemFootnote 1 (DGS) provides a route to discuss and understand calculus foundational ideas in terms of constructing and exploring concepts and problems dynamically. For this purpose, we analyse and discuss seminal calculus studies to shed light on what difficulties students encounter in their process of learning calculus foundational concepts and in solving related problems. Specifically, we identified tasks and problems in which calculus students exhibit limited understanding of concepts that are essential to work on variational tasks. Then, we illustrate and discuss how the systematic use of a DGS (GeoGebra) could provide a set of affordances for students to understand concepts such as the average rate of change that is crucial to make sense and work on tasks that involve variational reasoning. Thus, the research question that guided our inquiry was: How could students rely on DGS’ affordances to make sense, coordinate, and integrate different meanings associated with foundational ideas to grasp and apply the derivative concept? To elaborate and delve into this question, the content of this paper is organized around interrelated themes that include:

The presentation of features of a conceptual framework (Section 3) that explicitly acknowledges the importance for learners to think of the derivative concept in terms of interconnected facets or dimensions that they need to integrate and coordinate during their processes of understanding and applying the derivative concept in problem-solving activities.

The reviewing of themes regarding calculus curriculum reforms (Section 4) that address principles to support changes in high school curriculum frameworks and the importance of revisiting students’ understanding of foundational ideas that are relevant to grasp calculus concepts. In this section, a set of tasks that appears in some of the reviewed studies are discussed to illustrate ways in which the use of a DGS offers affordances to design an instructional route for students to understand and apply the concept of derivative. In the same section, we reflect on the extent to which the use of a DGS could provide students with an opportunity to extend their ways of reasoning to comprehend and apply the concept of derivative in problem-solving activities. Specifically, the construction of dynamic models of tasks or concepts demands that students think of problem elements in terms of geometric meanings that become essential to identify and explore mathematical relations within the model to work and solve the tasks.

In the looking back and reflections section, we disclose ways in which the use of a DGS offers a novel path to represent, explore, and approach tasks that involve foundational ideas and to work on calculus problems. Specifically, we discuss how technology affordances could be used to address essential calculus ideas and to illustrate how curriculum principles could be operationalized to engage students in variational reasoning.

Finally, in the concluding remarks section, we sketch a possible path to organize an instructional route for students to rely on digital affordances to understand calculus concepts and approach tasks that involve variational reasoning.

2 Background and literature review

Rasmussen et al. (2014) pointed out that millions of students enrol in calculus courses in secondary and tertiary education around the world. What core contents are included in calculus courses, both, in secondary and university education? How do students transit, in terms of reasoning, from high school mathematics to university calculus courses? Bressoud (2021, p. 521) stated that “… there is tremendous disparity across the country [US] in what courses are offered and how teachers are prepared to teach these courses. This is especially true for calculus in high school”. That is, educational systems might differ in terms of curriculum goals and countries’ research traditions and, there might be some differences in themes included in the calculus syllabus and in instructional approaches for a first calculus course; however, in general, there is a need to integrate accumulated research results to support and structure learning environments for students to robustly understand calculus concepts and to develop problem-solving proficiency. In this direction, Rasmussen et al. (2014) identified four main trends in calculus research: (i) the identification and characterization of students’ cognitive difficulties to learn calculus concepts; (ii) the study of what the students’ process to learn calculus concepts involves; (iii) the implementation of teaching innovations in calculus courses; and (iv) studies on the role of teachers or instructors’ knowledge, beliefs, and practices regarding students’ learning of calculus. The authors identified findings from several studies that have addressed the four research areas, and they recognize the importance of connecting those research results with ways to design and implement teaching/learning environments in which students have an opportunity to construct calculus concepts and to solve nonroutine problems. The idea is that mathematicians, mathematics educators, and instructors articulate what the authors call the Cycle of Knowledge that explicitly connects the production of knowledge (research results) with ways to frame and implement teaching or instructional practices. Rasmussen et al. (2014) also state that some research results have contributed to characterize how students learn basic or core calculus concepts and what difficulties they face during learning and solving calculus problems. They also suggest that there is a need to coordinate such results under an articulated conceptual or theoretical framework to support teaching practices. Furthermore, Silver (1990) recognized that there are different aspects of mathematics education research that can be applied to educational practices: (i) research findings or results are important to orient and structure learning environments; (ii) research methods and theoretical constructs, used in research studies, contribute to frame and support teaching practices; and (iii) the examples or tasks used in research studies could be applied to guide and foster learners’ development of mathematical thinking. Thus, we reviewed theoretical developments regarding ways of understanding calculus concepts and research results to identify relevant dimensions or facets that characterize what the students’ processes and ways to understand a mathematical concept entail. Specifically, it is recognized that the students’ understanding of the concept of derivative involves analysing and coordinating different meanings such as intuitive, operational, geometric, and formal definition associated with the concept in study (Thurston, 1994). Likewise, García et al. (2011) followed APOS theory to provide a genetic decomposition of the derivative concept that includes prerequisite knowledge (the function concept), graphical and analytical paths to construct a schema for the concept of derivative, graphical interpretation of the derivative, and the use and application of such concept. They reported that the participants in the study (mathematics major students taking first calculus course) were able to construct an underlying structure of the derivative scheme accordingly with its genetic decompositions. “…we assumed that these students provided evidence of being in the trans stage of the development of the derivative schema” (p. 1027). The students’ prerequisite component seems to play a crucial role in their construction of a coherent scheme of the derivative concept. In this paper, this component is extended to explicitly address themes such as average rate of change, linear approximation, and slope concepts.

It is recognized that the ways in which learners deal and delve into concept meanings and its application in solving calculus tasks contribute to the students’ development of a way of thinking to model and explore phenomena that involve parameters variation or changes. Further, the use of a DGS becomes a powerful tool for students to dynamically represent and analyse such variation. Although, the focus of this paper is on the construction of dynamic models of concepts and problems using a DGS, it is important to acknowledge that there are others online developments that students are encouraged to consult to enhance and contrast their concept understanding, and to rely on communication apps to continuously share and discuss their ideas and problem solutions with peers and their own teachers. The recent developments and availability of interactive Artificial Intelligence applications (ChatGPT) offer learners another way to bring and take into account diverse information and resources to explore mathematical concepts and problems. For instance, learners can introduce inputs or prompts to the ChatGPT regarding concept information or ways to solve calculus tasks and analyse the pertinence of the tool’s outputs to work on the problems or to extend their conceptual ideas and problem approaches and solutions (Santos-Trigo, 2024).

3 Conceptual framework: ways to understand the concept of derivative

Two related themes provide a rationale to frame this study: (i) The Thurston’ seminal work that shed light on the relevance of identifying and integrating different concept facets and meanings (intuitive, geometric, operational, formal, etc.) for learners to understand the concept of derivative and to solve problems; (ii) The students’ use of digital tools to represent and explore concept’s facets to transit from intuive or empirical ideas to operational and formal concept characterizations. It is recognized that the derivative is a cornerstone concept to study changes or variation in many mathematical and others disciplinary problems, and the use of a DGS provides affordances to dynamically model and study those changes.

3.1 On the concept of derivative

What does it mean to understand a mathematical concept? Specifically, what is it relevant in students’ understanding of the concept of derivative? To delve into these questions, we contend that the process of understanding a mathematical concept involves the integration and coordination of different facets or features embedded in the concept. What does it mean for learners to coordinate and integrate a set of dimensions or features of a concept? Thurston (1994) suggests that students gradually develop mathematical understanding of concepts, and this process might take different paths and it involves that students rely on their previous individual experiences and strategies to delve into the concept meaning and ways to operate and apply such concept. He identifies several dimensions of what understanding the concept of derivative of a function entails and all are relevant for students to grasp and apply such concept. In his own experience in learning and understanding this concept, he initially identified seven ways in which the derivative can be thought:

  1. (1)

    Infinitesimal: the ratio of the infinitesimal change in the value of a function to the infinitesimal change in a function [variable].

  2. (2)

    Symbolic: the derivative of \({x}^{n}\) is \({nx}^{n-1}\) the derivative of \(\text{sin}\left(x\right)\) is \(\text{cos}\left(x\right)\) the derivative of \(fog\) is \({f}^{\prime}og*{g}^{\prime}\), etc.

  3. (3)

    Logical: \({f}^{\prime}\left(x\right)=d\) if only if for every \(\epsilon\) there is a \(\delta\) such that when \(0<\left|\Delta x\right|<\delta\),

    $$\left|\frac{f(x+\Delta x)-f(x)}{\Delta x}-d\right|<\epsilon$$
  4. (4)

    Geometric: the derivative is the slope of a line tangent to the graph of the function, if the graph has a tangent.

  5. (5)

    Rate: the instantaneous speed of \(f(t)\), when t is time.

  6. (6)

    Approximation: The derivative of a function is the best linear approximation to the function near a point.

  7. (7)

    Microscopic: The derivative of a function is the limit of what you get by looking at it under a microscope of higher and higher power (p. 163).

Thurston recalls that he was introduced to each of these multiple derivative facets as something new and interesting in his school activities and in this route, the integration of those concept facets contributes to achieve a global understanding and ways to apply the concept in solving problems. In extending the derivative meanings and application, Carathéodory proposed a novel way to apply the concept of derivative. If f is differentiable at \(x=a\), then there is a function g continuous at \(x=a\) such that \(f\left(x\right)-f\left(a\right)=g\left(x\right)\left(x-a\right)\) (Kuhn, 1991). Accordingly, the function \(f\) has derivative at \(x=a\), if there is a function\(g\), continuous at \(x=a\), such that \(f\left(x\right)=f\left(a\right)+\left(x-a\right)g\left(x\right)\) for every \(x\) in an open interval that contains a. That is, \(f\left(x\right)-f\left(a\right)=g\left(x\right)\left(x-a\right)\) and this implies that a function has derivative at point \(x=a\) if the change \(f\left(x\right)-f\left(a\right)\) is continuously proportional to \(x-a\). Thus, the derivative of f at, a, is given by \({f}^{\prime}\left(a\right)=g\left(a\right)\).

To illustrate this derivative facet, let be \(f\left(x\right)={x}^{3}\) and any point\(x=a\). In this case, \(f\left(x\right)={a}^{3}+\left(x-a\right)\left({x}^{2}+ax+{a}^{2}\right)\). Using this representation of\(f\), we have that \(g\left(x\right)={x}^{2}+ax+{a}^{2}\) satisfies Carathéodory’s condition for the derivative, hence \({f}^{\prime}\left(a\right)=g\left(a\right)=3{a}^{2}\). Now using a DGS (GeoGebra), this algebraic procedure can geometrically be illustrated (Fig. 1).

Fig. 1
figure 1

The slope of the tangent to the graph of f at point \((a, f(a))\) is \(g(a)\)

Full size image

Thurston stated that “I also remember coming back to revisit these different concepts later with added meaning and understanding” (p. 164). That is, students’ understanding of concepts involves a continuous process to refine, test, contrast, and extend partial or initial concept comprehension.

3.2 Theoretical tenets to structure students problem-solving environments

Thurston’ reflection on the study of the derivative of a function provides information on what the process of understanding mathematical concepts entails and the importance of analyzing and reconciling intuitive, geometric, operational, and formal approaches to comprehend and deal with the concept. Furthermore, it becomes relevant to think of basic tenets to structure students’ problem-solving environments:

  1. (i)

    There are always multiple ways to characterize main features, properties, and interpretations of a concept and each one plays a relevant role for students to achieve and grasp its global understanding. Further, to analyse, work, and delve into each facet or concept dimension require that students activate different resources and strategies to represent, explore, carry out operations, and apply such concept. The integration of different concept dimensions is essential for students to understand it.

  2. (ii)

    The students’ understanding of a concept takes place gradually and demands that they continuously analyze and contrast what each interpretation involves including ways in which they relate and complement each other. Likewise, students need to revisit their initial ideas to constantly extend their concept understanding and ways to solve related problems.

  3. (iii)

    Each concept representation and interpretation contributes to students’ global concept understanding which becomes more robust or refined when students relate, connect, and transit, in terms of meaning, among the different concept interpretations. Thus, students’ construction and understanding of a concept is a continuous process in which they refine, test, extend ideas, and ways to apply such concept in problem-solving activities.

  4. (iv)

    Students examine and contrast concept dimensions and meaning through an inquiry process that involves posing and discussing questions and solving mathematical problems. That is, students are encouraged to conceptualize their learning in terms of dilemmas that need to be solved using mathematical resources and strategies (Polya, 1945; Santos-Trigo, 2024).

  5. (v)

    Students’ use of concrete, semiotic, or digital tools shapes their ways of reasoning and approaching mathematical tasks. Different tools might provide diverse ways for students to represent and work on mathematical problems, then, it becomes relevant to discuss in which ways students enhance or expand their concepts understanding and problem-solving approaches (Santos-Trigo, 2023, 2024).

3.3 The use of digital technologies to work and discuss mathematical tasks

The students’ systematic and coordinated use of digital technologies could provide grounds to apply and integrate research results into educational practices (Santos-Trigo, 2020, 2023). That is, digital technology affordances offer an opportunity for students to represent and explore calculus concepts in terms of coordinating visual, numeric (measuring attributes), and symbolic approaches to analyse variational phenomena (Hoffkamp, 2011). Indeed, students could rely on a DGS affordances to dynamically model and explore objects to visualize parameters behaviours within the model and detect patterns and relationships that are important to solve problems. Hiebert et al. (1997) recognize that a central activity for students to understand concepts is to present and communicate mathematical results to peers and teachers. Zengin (2018) proposes a teaching method that combines both individual and team work for students to understand concepts and to approach nonrutine tasks. Specifically, he idenfies five instructional stages (individual work, teamwork, scientific debate, self reflection, and institutionalization process) to foster students’ problem-solving approaches.

4 Principles to frame high school calculus curriculum and the role of foundational ideas to understand the concept of derivative

Based on research results, some educational systems have proposed calculus curriculum reforms. Frank and Thompson (2021) suggested that calculus reform in the US needs to focus on ways for students to examine and rethink the meaning associated with the concept of slope, average rate of change and function notation. To this end, principles to structure and support curriculum changes should include examples of mathematical tasks to illustrate ways in which such principles get implemented in learning scenarios.

4.1 Curriculum principles

Dreyfus et al. (2021) reviewed the influence and role of research results in high school curriculum proposals in Israel. Specifically, the use of task examples to illustrate and foster three principles to structure high school curriculum: The mathematical Reasoning principle, the Impact principle to connect mathematics knowledge (calculus) with everyday life and science events, and the Cultivation of ways of thinking from which concepts might emerge during the students’ learning experiences. That is, a distinguished feature in this calculus curriculum proposal was to include and discuss tasks that illustrate curriculum principles. In general terms, these principles provide information on types of tasks teachers should discuss in calculus courses and what features of mathematical practices should be emphasized in learning environments. How can the use of digital affordances support and contribute to the implementation of those principles? To address this question, we use GeoGebra to model some of the problems associated with the principles and illustrate paths to approach those tasks.

4.1.1 Reasoning

Involves preparing students to engage in critical thinking to understand definitions, the use of algorithms, to delve into theorems, to explain, justify, and to prove mathematical relations. That is, the goal is that students develop an inquiry approach to deal with mathematical tasks in which they examine definitions, formulate conjectures, explain theorems, and always look for arguments to validate and support mathematical relations. An example of a task to illustrate ways to foster students’ reasoning is:

In each statement below, choose the correct option and justify your claim.

  1. 1.

    A second degree polynomial has a point of inflection— always / sometimes / never.

  2. 2.

    A third degree polynomial has a point of inflection—always / sometimes / never.

  3. 3.

    A fourth degree polynomial has a point of inflection—always / sometimes / never (Dreyfus et al., 2021, p. 683).

To respond each statement, students need to discuss what inflection points mean in terms of the polynomial properties that can be explored by a graphic representation. That is, inflection points provide information regarding where the function changes concavity (from being “concave up” to being “concave down” or vice-versa). Another important characteristic of an inflection point is that it describes a position where the instantaneous rate of change of the function changes from being positive to negative or vice versa. Also, at these points the second derivative of the function, when exists, is zero and changes signs in an open interval. GeoGebra affordances are key tools to represent and explore visual and algebraically the properties of inflection points and can help grasp important properties of the function as a whole. Figure 2 shows an example of a third-degree polynomial \(f(x)\), point A is on the graph of the polynomial. And \({f}^{\prime}\left(x\right)\) and \({f}^{{\prime}{\prime}}\left(x\right)\) are the graph of first and second derivative of \(f(x)\), m is the slope of the tangent line to the graph of \(f(x)\) at point A. By moving point A along the graph of \(f(x)\), it is possible to visualize and determine the inflection point of the polynomial.

Fig. 2
figure 2

Connecting inflection points and second derivative

Full size image

4.1.2 Impact

Refers to the importance of connecting the study of mathematics with its application in everyday life, science, and engineering. The idea is that the study of the discipline is relevant for students to approach STEM subjects. Thus, students can rely on the notion of rate of change to analyze graphs that represent a variational phenomenon. Niss et al. (2007) recognize the importance for students to engage in modelling activities to connect the study of mathematics with the analysis and interpretation of real phenomena or problematic situations that appear outside the mathematics classroom.

…the term problem in a broad sense, encompassing not only practical problems, but also problems of a more intellectual nature that aim at describing, explaining, understanding or even designing parts of the world, including issues and questions pertaining to scientific disciplines (Niss et al., 2007, p. 8).

A task “clearing the bridge” that appeared in NCTM (2009) involves analyzing conditions for a tractor trailer to clear a bridge that was located at the base of a descending road (Fig. 3a). Indeed, it is common to find pictures in newspaper where trucks get stuck when passing an underpass. Why do trucks get stuck when they transit an underpass? The idea is to determine what information is needed to guarantee that a tractor trailer will clear the bridge.

Fig. 3
figure 3

a A trailer passing an underpass. b The locus of point S when point M is moved represents the variation of the truck’s height

Full size image

Figure 3b shows a dynamic model of the task that relates the position of the truck in terms of point M and its corresponding height (segment PK).

In a two dimensional model, the shape of the trailer could be thought as a rectangle, the wheels as circles, a segment as the height of the trailer, etc. Figure 3b represents a dynamic model of the problem in which segment PK represents the highest point of the trailer when passing under the bridge. Mobile point M controls the trailer movement.

When point M is moved along the lines, point S (with x-coordinate the same of M and y-coordinate height PK) describes a path that shows the variation of the length of segment PK (the height of the trailer). What is the locus of point S when point M is moved along the lines? Fig. 3b shows the locus of point S.

When the dimension of the rectangle are 3.50 cm side AD and 9 cm side AB, and the tilted angle 12.1 degrees, then a table of the coordinates of point S for different positions of point M is generated and Fig. 4 shows a fitted curve for those points. It is observed that the slope of the tangent line to the curve at T varies depending on the position of point T. Also, Fig. 4 shows that when the slope is zero, then maximum value for the height is reached and is 4.61. This means that the height of the bridge needs to be higher than 4.61 for the trunk to clear it.

Fig. 4
figure 4

Fitting the data by a polynomial of second degree

Full size image

In this task, learners have an opportunity to problematize a real situation, in this case, conditions for trucks to clear the bridge. In this process, they need to identify relevant data or information to model the situation. The construction of a dynamic model requires that students think of geometric objects and properties to ensemble such model. Furthermore, Fig. 4 shows the variation of truck’s height and learners can visualize its maximum value. In addition, by moving point M in the dynamic model, it is possible to generate a set of points for different positions of point S (Fig. 4) and to get a second-degree polynomial that fit those points. Then, point T is on the fit polynomial and the slope of a tangent to f at point T varies, when the value of the slope becomes zero, then the y-coordinate of point T is the highest value for the truck height. In approaching this task, several representations were used to first model geometrically the problem, then, collecting data through moving the trailer became important to generate points associated with the position of the trailer and the corresponding height. Based on these points, a fit polynomial was found and analyzed in terms of a variation of the slope of the tangent line to the graph at point T.

4.1.3 Cultivation

Involves providing condition to foster what Harel (2021) calls “an intellectual need” for students to create, understand, extend, and apply mathematical concepts. According to Dreyfus et al. (2021) “Cultivation refers to ways of creating intellectual ground fertile for a new concept to emerge naturally” (p. 685). To this end, students work on situations that are familiar to them through posing questions that lead them to generate and delve into new concepts. This construct is related to what Kilpatrick et al. (2001) call the productive disposition strand in which students develop an inclination to view or conceptualize mathematics as sensible, useful, worthwhile discipline that privileges reasoning and sense-making activities. To provoke students’ intellectual need to work on mathematical tasks, Harel (2021) proposed three interrelated principles for students to “…internalize, organize, and retain the mathematics they learn” (p. 710).

  • Duality principle: (a) Learners come with a set of ways of thinking, some desirable and some undesirable, that inevitably affect the ways of understanding we intend to teach them. (b) Learners develop desirable ways of thinking only through repeated application of proper ways of understanding.

  • Necessity principle: For students to learn what we intend to teach them, they must have a need for it, where ‘need’ refers to intellectual need.

  • Repeated-reasoning principle: Learners must practice reasoning in order to (a) internalize, (b) organize, and (c) retain ways of understanding and ways of thinking (p. 711).

The use of digital tools plays an important role in students’ development of an intellectual need since it offers a set of affordances to help thinking of and exploring different ways to approach mathematical tasks. In this perspective, finding a solution of a mathematical problem becomes a departure point for students to engage in mathematics discussions and practices. Santos-Trigo et al. (2016) provided an example in which high school students transformed an initial task in which they were asked to fold a corner of a rectangular sheet of paper to touch the opposite side AB as Fig. 5 shows. Here, they were asked to determine a position for point G (the folded corner D) in which side HI of triangle GHI gets its minimum value. To approach this task, the participants modeled the problem dynamically (Fig. 5). It is observed that when point G is moved along segment AB, the length of side HI, the area of triangle GHI and the area of triangle BHG change. With the use of GeoGebra, it is possible to graphically represent the behavior or variation of the length of HI (black curve), the area of triangle GHI (blue curve), and the area of triangle BHG (red curve) when point G is moved along the side AB. These curves can be parametrized to find maximum points. For example, K(x) represents the area of the family of triangles GBH that appears when point G is moved along AB. Point S has the distance AG as the x-coordinate and as y-coordinate the corresponding are of triangle BHG. The line that passes trough S is tangent to K(x) and when the slope of this line is zero, the area of triangle BHG gets its maximum value.

Fig. 5
figure 5

Folding vertex D of sheet ABDE to touch side AB

Full size image

In the construction and exploration of relations that emerged when point G is moved, a set of affordances such as dragging objects orderly, tracing objects loci, using sliders to move parameters, measuring objects’ attributes, etc. were essential to identify, analyze, and support mathematical relations that were relevant to solve and extend the tasks. That is, the activation of these tool affordances became a set of strategies for “…students to think of a kind of semantic proof based on visual arguments at the beginning and, afterwards, this contributes to open the way to more formal proofs by promoting links between learners’ empirical and deductive reasoning” (Santos-Trigo et al., 2016, p. 841). Furthermore, in terms of the cultivation principle, in this task, the use of GeoGebra demands that students think of a way to geometrically model the problem in terms of mathematical properties and then, the model exploration provoke an intellectual need to explore, analyze, and explain what elements with the model change or are invariants. In this perspective, they extend the initial task domain and pose new questions or related problems.

4.2 Highliting foundational ideas to understand calculus concepts through a dynamic approach

It has been recognized that students’ learning experiences in precalculus courses play an important role to understand calculus concepts and to approach calculus tasks. What are the main ideas and concepts that are essential for students to understand and apply calculus concepts? What type of learning experiences are important for students to meaningfully comprehend and deal with concepts such as average rate of change, slope, or linear approximation that are studied at the high school level? Frank and Thompson (2021) refer to the importance for high school students to understand key mathematical concepts to connect and transit from pre-calculus courses to the study of calculus at the university level. They stated that: “The meanings a student constructs throughout their prior schooling have the potential to provide a coherent platform that supports the student in developing conceptual understandings of key ideas in calculus” (p. 550).

Frank & Thompson pointed out that students’ understanding of basic concepts that appear in high school curriculum is crucial for them to develop calculus conceptual knowledge at the university level. They focused on three related areas: (i) the students’ development of variational reasoning, (ii) the students’ understanding and meaning of the concept of average rate of change; and (iii) the students’ representational use of function notation. In addition, they explored both secondary mathematics teachers’ understanding and meaning of the same three themes and ways in which they are addressed in precalculus textbooks. Frank and Thompson (2021) suggested that the students’ difficulties to grasp foundational concepts might become an obstacle for them to achieve a global understanding of calculus concepts.

Our examination of students’ meanings for key ideas in calculus revealed that students’ difficulties were often not specific to the calculus concept but instead rooted in meanings they likely developed in their prior schooling (p. 550).

Frank & Thompson relied on a questionnaire to document both teachers and students’ ideas regarding concepts that are studied in precalculus courses that are essential for students to understand calculus content at the university level. They concluded that teachers and students’ answers to questions that address conceptual meaning associated with variational reasoning, average rate of change, and the use of function notational systems reflect a segmented and uncoordinated knowledge that might affect and limit the students’ opportunities to understand and develop calculus concepts. Indeed, Frank and Thompson (2021) stated that “The data suggests U.S. teachers and students share many meanings for slope, average rate of change, and function notation and these meanings are unproductive for understanding calculus” (p. 561). They also indicate that calculus reforms in the U.S. need to focus on ways in which middle school and high school curricula and teachers could reconstruct meaning of foundational concepts that are important for students to understand calculus ideas to solve problems. Vargas et al. (2020) analysed problems or tasks included in high school textbooks in Spain that address the meanings of the derivative concept. They concluded that the textbooks privilege three meanings of the derivative concept: One that focuses on algebraic procedures, another that emphasizes the use of algoritms, and a third one that addresses concept geometric interpretations. They observed that, in general, textbooks favor more the use of algoritms or rules to solve the tasks than a conceptual comprehension involving the coordination of multiple meanings to approach the problems. Here, we propose to explicitly incorporate the use of a Dynamic Geometry System for students to represent, explore, and analyze foundational calculus concepts. Hoffkamp (2011) recognized that the use of a DGS (Cinderella) provide students with an opportunity to visualize and experience calculus variation and covariation ideas that contributes to an enrichement of concepts’ understanding. That is, the use of GeoGebra offers an opportunity for learners to delve into concepts in such a way that they could visualize, quantify variation, and observe concepts relations and their geometric meanings. Here, the construction and exploration of tasks’ dynamic models become important for students visualize and meaningful understand calculus concepts.

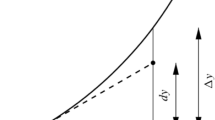
4.2.1 Variational reasoning and dependent variables

An item used in Frank and Thompson’ questionnaire to explore students’ variational reasoning appears in Fig. 6a (paper and pencil approach). A dynamic representation of this item is shown in Fig. 6b (using a DGS), there, dx is represented by slider d, and when d varies, it is observed that dy and \(\Delta y\) vary, but \(\frac{dy}{dx }=a\) remains constant. In this model, a slider is used to control the variation of x-coordinate, and line i is tangent to the graph of f at P.

Fig. 6
figure 6

a A question to explore variational reasoning (Frank & Thompson, 2021, p.552). b Moving d to observe the variation of dy and \(\Delta y\)

Full size image

Another item that involves describing the behavior of the changes in the dependent variable over an interval (Fig. 7a) could be examined by directly moving the corresponding parameters. In Fig. 7b, the slide d represents the increment of the value of x and the x-coordinate of point Q is x + d and as y-coordinate the corresponding function value. It is observed that the slope of the tangent line g to the graph of f describes how the changes of f behave for small increments of x and they are negative and increasing. Point A has x-coordinate equal to the x-coordinate of point Q and as y coordinate the slope m of g. The locus of A when d changes is a segment that shows that the slope values are increasing.

Fig. 7
figure 7

a An item that appears in (Frank & Thompson, 2021, p. 553). b Moving slider d to observe changes

Full size image

Clearly, the model presented in Fig. 7a differs from the one that appears in Fig. 7b. Instead of providing the graph, students might be required to construct it and then the GeoGebra affordances allow them to directly observe and explain the slope of g variation and its relationship with the function graph behavior.

The use of dynamic software for the demonstration and investigation of processes of change is recommended in the curriculum. And indeed, research studies have shown that students are more likely to understand the notion of derivative when learning incorporates technology (Dreyfus et al., 2021, p. 686).

Further, the use of GeoGebra could provide students with an opportunity to visually relate and coordinate changes in the graph representation of concepts (slope) and their corresponding numeric values. In this process, they are encouraged to construct meanings and referents of different aspects associated with the concept of derivative.

4.2.2 On nonroutine calculus tasks

Selden et al. (1989) carried out a study in which students who recently had taken and passed a first university calculus course were asked to solve five nonroutine problems. They found that the participants experienced serious difficulties to work and solve these problems. The problem statements did not explicitly include terms that appear in calculus courses (derivative, maximum or minimum values, slope, etc.), but to work and solve them required the use of calculus concepts. One of those problems was:

Find values of \(a\) and \(b\) so that the line \(2x+3y=a\) is tangent to the graph of \(f\left(x\right)=b{x}^{2}\) at the point where x = 3 (p. 48).

How could this problem be approached with the use of a DGS? How could the information or data in this problem be represented? To think of this problem geometrically implies that students recognize that there are families of lines and parabolas associated with the values of a and b. Thus, the use of sliders for values of parameters a and b leads to geometrically represent examples of those families. Figure 8a shows the graphs of lines and parabolas that are generated by varying parameters a & b. It can also be drawn a tangent line to the graph of f(x) at point x = 3, this line keeps the property of being tangent to the parabola at point \(x = 3\) when the parameter b takes different values. The graph of the linear function h(x) depends on values of parameter a, and for different values of this a, a family of lines is generated. Figure 8b shows for values of \(a = 3\) and \(b = -0.11\) both \(h(x)\) and the tangent line to the graph of \(f(x)\) coincide (the problem solution). This geometric and dynamic approach to represent and explore the problem provides basis to algebraically solve it.

Fig. 8
figure 8

a Using sliders to represent a family of lines and parabolas. b Finding values of a and b to determine the tangent line to f at x = 3

Full size image

4.2.3 The construction of dynamic configurations to analyze variational tasks through multiple approaches

When using a DGS, it is possible that learners construct their own dynamic configurations or model to analyze change of embedded attributes. For example, Fig. 9 shows a circle with center at the origin and radius R, point P on the positive x-axis and two lines tangent to the circle that pass through point P. The idea is that students move objects within this configuration and pose questions regarding the behavior of some objects’ attributes.

Fig. 9
figure 9

How does the area of the family of triangles, generated when P moves, behave?

Full size image

For instance, when moving point P along ray CQ, it is observed that points A and B move as well. A question might be, how does the area of triangle OAB change when point P is moved along ray CQ? (Fig. 9).

In Fig. 10, point D has the same X-coordinate as point P and as Y-coordinate the corresponding area of triangle OAB. What is the locus of point D when point P moves along ray CQ?

Fig. 10
figure 10

Showing the locus of point D when point P is moved along ray CQ

Full size image

This first approach to the problem shows that there is a position for point P in which the area of triangle OAB is maximum. In this case when the radius of the circle is 3 units, the maximum area of triangle OAB is reached when P is positioned at (4.24, 0). For any point I on the circular arc OCK, Fig. 11 shows that a family of rectangles IHOL can be drawn, point M has x-coordinate equal to the x-coordinate of point I and as y-coordinate the value of the area of rectangle IHOL. Thus, the locus of point M when point I moves along circular arc OCK is shown and the maximum area of the family of rectangles IHOL is reached when the rectangle becomes a square (Fig. 11).

Fig. 11
figure 11

When vertex I coincides with point A the rectangle becomes a square and its area corresponds to the maximum value of triangle OAB

Full size image

How can this visual or geometric approach be parametrized? If we assign coordinates to point \(A=(u,v)\) that is on the circle whose equation is \({x}^{2}+{y}^{2}={R}^{2}\), then.

$$v=\sqrt{{R}^{2}-{u}^{2}}.$$
(1)

Also, the equation of the line that passes through A and \(P=(t,0)\) can be expressed as

$$y=\left(-\frac{u}{v}\right)\left(x-t\right).$$

This line is perpendicular to the radius OA, which has slope \(v/u\). Now, since A lies on the tangent line, then.

$$v=-\frac{u}{v}\left(u-t\right).$$
(2)

By combining the previous relations, an expression for the area of triangle OAB is given by:

$$f\left(t\right)=uv=\left(\frac{{R}^{3}}{t}\right)\sqrt{1-\left(\frac{{R}^{2}}{{t}^{2}}\right)}.$$

From \(f^{\prime}\left(t\right)=0\), we obtain that the maximum value of the area of triangle OAB is reached when \(P=\left(\sqrt{2}R,0\right).\) For a circle radius \(R=3\), the area of OAB is

$$f\left(t\right)=\frac{27}{t}\sqrt{1-\frac{9}{{t}^{2}}}$$

If D is any point on the graph of \(f\), Fig. 12 shows the slope of the tangent line at D and when the slope corresponding value becomes zero, then function \(f(t)\) reaches its maximum value.

Fig. 12
figure 12

The slope value of the tangent line. Finding the maximum value of \(f(x)\)

Full size image

It is observed that a simple configuration that involves drawing a circle, a point on the positive x-axis and tangent lines to the circle through P, could lead students to formulate an area variation task. This task offers students the opportunity to reconcile visual, geometric and algebraic models as well as to illustrate that a maximum occurs when the derivative vanishes.

5 Looking back and reflections

Calculus courses have been and are an important subject in both high school and university mathematics curricula. To what extent do the contents and focus of high school calculus courses provide basis for students to prepare them to study calculus courses at university level? In general, university instructors often complain that calculus courses at high school level are mainly ruled-oriented and fail to provide conceptual grounds for students to enhance and advance their understanding of calculus concepts. Indeed, Frank and Thompson (2021) suggested that students’ knowledge and experiences about learning core ideas to understand calculus concepts such as variational reasoning, average rate of change, and the use of function notational system that they developed in their pre-university school courses are not consistent or robust enough to help them in their study of university calculus. To review and extend students’ knowledge about calculus foundational ideas, we propose that students rely on digital technology affordances to represent and explore dynamically calculus concepts and tasks.

To illustrate ways for students to activate technology affordances in approaching calculus problems, we selected some tasks used by Frank and Thompson (2021) and Dreyfus et al. (2021) to represent and explore variational reasoning and the concept of average rate of change in terms of connecting visual, graphic, and algebraic meanings. Thus, in Figs. 6b and 7b, the associated “sliders” control de variation of depending variables to observe not only what changes, but also how involved parameters change. Then, students have an opportunity to coordinate visual representation and numeric values of parameter behaviours. Törner et al. (2014) pointed out that “…the development of informal and intuitive knowledge through the use of dynamic tools, specially designed tasks and the progressive transition to formal knowledge is considered as an approach that can promote students’ conceptual understanding of calculus” (p. 554).

Figure 8a and b show that the use of a DGS to represent, explore, and solve a nonroutine task demands that learners think of the task in terms of geometric meaning of the involved concepts. In this case, the construction of a family of parabolas and lines and the representation of the concept of slope became relevant to geometrically approach the task in such a way that it could provide directions to model and solve the problem algebraically. Figure 2 illustrates how the use of examples are important to reason and support a mathematical statement.

The trailer task is an example in which a newspaper picture or information could be problematized by learners. In this case, analysing conditions for the trailer to clear a bridge. The geometric approach not only demands that problem-solvers reduce conditions to model the problem dynamically; but also, by the construction of a table of points of the locus of point S (Figs. 3b and 4), it provides information to consider a second-degree polynomial that fits the data. This representation leads to connect the slope of its tangent with the problem solution. This type of task shows the relevance for learners to connect real context situations with the use and impact of calculus concepts to solve problems.

Likewise, the “folding of a paper sheet task” shows that a routine task that appear in a calculus textbook can be transformed in a set of tasks to foster students’ problem-posing activities and mathematical reasoning. In addition, students can construct their own geometric or dynamic configuration by assembling mathematical objects and moving elements within the configuration. The construction of a dynamic configuration that involves simple figures provide students with an opportunity to observe how attributes (area, perimeters, etc.) vary or change within the configuration. Figures 11 and 12 show the area variation of a family of triangles and rectangles when a maximum area is reached. In addition, the information about the area variation provides elements to parametrize and model the phenomenon.

Throughout this paper, we emphasize that the study of mathematical concepts implies the students’ identification and analysis of different concepts dimensions or facets related to or embedded in the study of a particular concept. In this case, the concept of derivative is associated with several facets that include intuitive, visual, operational, formal, and geometric meanings. Thus, for students to develop a global and robust understanding of the derivative concept, they must transit, connect, and integrate several meanings associated with the concept. The use of digital affordances plays an essential role for learners to achieve such global comprehension of this concept. That is, in representing and exploring the concept dimensions, students have an opportunity to graph the function that represent the problem under study and to reconcile intuitive or visual analysis with the geometric interpretation of the derivative as the slope of the tangent line and to study the variation of the slope at different points of the corresponding function. Based on the review of recent calculus research studies it becomes crucial to revise, analyse, and extend the ways in which calculus’ foundation concepts are studied at pre-university education. Further, the students’ use of digital affordances offers a novel route for them to integrate and achieve global understanding of calculus concepts. In terms of the research question that guided the study: How could students rely on DGS’ affordances to make sense, coordinate, and integrate different meanings associated with foundational ideas to grasp and apply the derivative concept? We have shown that the consistent use of a DGS opens a new window for learners to dynamically model and explore foundational concepts and to approach tasks that involve variational reasoning. During the students’ construction of dynamic concept/problem model, they are required to think of the task in terms of geometric meaning of data or embedded concepts that lead them to identify and explore mathematical relations to solve the problems. The DGS’ affordances become relevant for students to transit from intuitive or empirical approach to formal solutions in terms of meanings that contribute to the students’ development of global understanding of the derivative concept.

6 Concluding remarks

It is recognized that the students’ development of mathematical understanding and problem-solving competencies go hand in hand with instructional goals, the types of activities that are implemented in learning environments and ways to assess students’ mathematical learning.

Learning spaces are complex environments in which teachers orchestrate diverse activities to foster and monitor students’ mathematical learning. In this process, students develop ideas, knowledge, strategies, and ways of thinking to deal with mathematical tasks (Schoenfeld, 2023). What does it mean that students learn calculus concepts and solve mathematical problems? Three related themes are important for students to develop global understanding of the concept of derivative and problem-solving competencies:

  1. 1.

    Variational reasoning. Students need to review and extend foundational ideas around variational reasoning to delve into the concept of average rate of change using a pertinent notational system.

  2. 2.

    The use of digital affordances. Students use of a DGS (GeoGebra) becomes important to geometrically represent and explore the different meanings associated with the concept of derivative. To this end, they need to think of concepts and calculus tasks in terms of properties that can be represented geometrically. For example, they can trace loci that describe area variation of a family of objects and to examine their properties in terms of the corresponding slope numeric and graphic changes. Thus, the students’ use of semiotic, concrete, and digital tools plays a crucial role in their construction of mathematical knowledge and problem-solving competencies.

  3. 3.

    Problematizing the learning task. Students need to conceptualize the study and understanding of calculus in terms of dilemmas that they need to discuss with peers and to present their solution to their classroom community (Santos-Trigo, 2007, 2024). In this context, they pose question and look for different ways to get answers and delve into concepts. This inquisitive approach is essential for students to achieve global concept understanding.

Finally, some research aspects and results in students’ construction of calculus concepts were important to structure the content of this paper. For instance, the theoretical construct regarding the concepts dimensions became relevante for students to achieve global understanding of the derivative concept (Thurston, 1994). Likewise, the examples or tasks implemented in different research studies to support the use of digital affordances for students to understand calculus foundations and the methods used to elicit students’ learning to foster mathematical practices contributed to answer the research question. Furthermore, research agenda in mathematics education needs to focus on the identification of different meanings and dimensions associated with the study of mathematical concepts and ways to use diverse technology affordances for students to constantly refine, coordinate, operate, and apply those concepts in problem-solving activities.