1 Introduction

Classroom observation instruments provide a theoretical framing for research into instructional practice (Bell & Gitomer, 2023), largely as summative evaluations of instructional practice and to provide evidence of teaching effectiveness (Charalambous & Praetorius, 2020; Kane & Staiger, 2012; Klieme et al., 2009; König et al., 2021). While there is agreement that mathematics instruction should focus on integrating conceptual understanding, procedural knowledge, and provide students opportunities to engage in mathematical practices (National Research Council, 2001), how to achieve these has led to multiple visions of high-quality mathematics instruction (Munter et al., 2015). Instruments measuring teaching quality may attend to generic aspects of effective teaching (Hamre et al., 2013; Klieme et al., 2009; Muijs et al., 2014), mathematics-focused dimensions (Hill et al., 2008), or take a hybrid approach (Lindorff et al., 2020; Schlesinger et al., 2018; Schoenfeld, 2018). The choice of tool foregrounds certain practices while backgrounding others. Thus, conclusions drawn from the use of any tool may rest on specific aspects of high-quality instruction or fail to highlight key practices that are unmeasured.

Literature on observation instruments often focuses on summative assessments of instructional quality and considers the ways in which the information provided within and across instruments presents valid and reliable information on teaching practice (Praetorius & Charalambous, 2018). We build on existing conversations around summative uses of observation instruments to consider formative improvement functions (Creemers et al., 2013; Kraft & Hill, 2020; Supovitz & Sirinides, 2018). Using observation instruments to improve teaching assumes the information provided delineates effective features of practice (Creemers et al., 2013) that can be taken up by teachers in actionable ways (White et al., 2022) and is aligned with contextually-valid visions of high-quality mathematics instruction (Bell & Gitomer, 2023).

In this exploratory study, we overlay two observation instruments, one focused on instructional practices that support students’ learning in mathematics and the other focused on practices that support students’ learning of algebra content specifically. We use these tools to analyze two consecutive algebra lessons taught by six different teachers. Considering observation scores alongside lesson videos, we closely examine what the scores signify in practice and consider what is foregrounded, backgrounded, and unmeasured. Our first aim is to illustrate the types of formative information provided by two instruments that attend to differing features of high-quality mathematics instruction and how overlaying those instruments changes that information. Second, as instrument developers, we seek to model a reflective process for those engaged in classroom observation research in which we examine how overlaying instruments illuminates strengths and limitations of the tools themselves.

2 Theoretical perspectives and literature review

2.1 Perspectives on high-quality mathematics teaching

The field has developed multiple frameworks to define and operationalize high-quality teaching practices in mathematics classrooms, linking classroom level factors to student outcomes (Creemers et al., 2013). Such studies have evolved from process-product approaches testing the relationship between teaching acts and student outcomes to those that consider groups of teaching practices in the context of content domains to connect teaching components to student learning (Seidel & Shavelson, 2007). Creemers and colleagues (2010, 2013) argue for dynamic models of educational effectiveness, as teaching and learning are adaptive and improving teaching requires attention to multiple levels. Classroom factors such as lesson structure, teachers’ actions, and use of time and resources are critical to supporting student outcomes.

Work identifying classroom practices that support student learning has yielded frameworks for assessing the quality of teaching across grades, content, and context. For example, the three-dimensional model of instructional quality (Klieme et al., 2009) posits three generic components of effective teaching practice that support student outcomes—classroom management, student support, and cognitive activation. Research has demonstrated their applicability in mathematics contexts (Praetorius et al., 2018) and multiple projects have drawn on this framework to evaluate teaching across settings (Baumert et al., 2010; König et al., 2021).

In addition to generic factors, researchers have also examined aspects of teaching that support students’ learning in content domains. In a meta-analysis of effectiveness studies, Seidel and Shavelson (2007) found domain-specific practices had the largest effect on student cognitive outcomes and frameworks have evolved to include subject-specific practices that support student learning (Schlesinger & Jentsch, 2016). For example, Schlesinger et al. (2018) theorized two additional mathematics-specific dimensions to the three-dimensional model described above, including mathematics subject-related practices and mathematics teaching-related qualities. Others have incorporated subject-specific characteristics of instruction such as the use of appropriate mathematical language, responses to students’ mathematical errors, mathematical sense-making activities, problem-solving, proof or modeling tasks, and mathematical depth (Klieme et al., 2009; LMTP, 2011; Matsumura et al. 2002; Schoenfeld, 2018).

Researchers studying teaching practices must consider how they are conceptualizing and measuring high-quality teaching (Schlesinger & Jenstch, 2016), whether the focus is on generic or domain-specific practices, and how those practices relate to student learning. High quality teaching is ideally both “successful” and “good,” (Fenstermacher & Richardson, 2005), encompassing practices that support intended outcomes and are disciplinarily worthwhile. However, there are multiple ways to define successful outcomes and certain teaching practices may be more successful at particular outcomes (Seidel & Shavelson, 2007) and perspectives may vary on what is considered disciplinarily important. In the U.S. for example, some visions of teaching quality center ambitious teaching practices that prioritize conceptual understanding, inquiry, and mathematical discourse (Hiebert et al., 2003; Lampert et al., 2010; Stein et al.1996). Other visions center practices that feature the teacher as expert and guide, prioritizing teacher-led modeling and explanation, guided practice, and corrective feedback (Doabler et al., 2015). Furthermore, visions of high-quality mathematics instruction are contextual; different countries exhibit different cultural patterns of teaching (Stigler et al., 2000; Bell et al., 2020) and differences in cultural values impact what is considered high quality (Cai et al., 2009; Givvin et al., 2009) and how teaching quality is measured.

2.2 Use of observation instruments to measure high quality mathematics instruction

Classroom observation instruments are tools that operationalize visions of high-quality teaching and assess instructional quality. Observation tools have evolved from quantifying easily observable teaching actions into more formalized systems capturing higher inference practices that support student learning outcomes (Bostic et al., 2021; Schlesinger & Jentsch, 2016). Some instruments measure generic teaching practices (Creemers & Kyriakides, 2007; Hamre et al., 2013; Muijs & Reynolds, 2010) and feature elements of effective teaching that cut across subject areas and can facilitate comparisons across domains and contexts (Lindorff, 2020). Other instruments focus on what we term domain-specific practices, aspects of high-quality teaching that support learning of a particular subject such as mathematics (Schlesinger & Jentsch, 2016). While these aspects may be a subset of more generic dimensions, researchers have shown the utility of domain-specific tools for understanding mathematics instructional quality (Boston, 2012; Hill et al., 2008; Schlesinger et al., 2018; Walkowiak et al., 2014). A third category of instruments are content-specific and focus on measuring teaching practices that support students to learn specific mathematics content such as algebra (Litke, 2020; Schoenfeld, 2018), such as focusing on teachers’ comparisons of algebraic solution methods (Star et al., 2015). A newer subset of instruments focuses on practices that improve access and opportunity in mathematics classrooms, for example, measuring equitable participation patterns (Reinholz & Shah, 2018) or teaching practices that support success for students traditionally marginalized in mathematics (Wilson, 2022).

Observation instruments have been used summatively to facilitate international teaching comparisons (Bell et al., 2020; Hiebert et al., 2003) or to connect teaching with student learning (Muijs et al., 2014). In the U. S., observation instruments feature as part of teacher evaluation systems (Kane & Staiger, 2012). The effectiveness of these tools for summative purposes hinges on whether they provide reliable and valid information about instructional quality. Research on observation instruments has evolved to encompass explorations of the validity and uses of these tools, such as their role in dynamic models of educational effectiveness (Creemers et al., 2010), the breadth and depth of factors necessary to determine a level of instructional quality, and whether instruments should measure generic or subject-specific teaching factors, or a synthesis of both (Charalambous & Praetorious, 2020). More recently, researchers have noted the potential for observation instruments to provide formative feedback on teaching to support instructional improvement efforts. For example, building from evidence that clusters of teaching practices range in difficulty, Creemers et al. (2013) demonstrate how observation instruments can be used in professional learning to support teachers to progress through stages of effective teaching. Kraft and Hill (2020) find that mathematics coaching grounded in teachers’ use of an observation tool yields positive impacts on instruction.

For observation instruments to support instructional improvement, they must provide actionable information teachers can use to deepen their instruction. Because what is measured holds value, tools serve to identify strengths, inform the focus of feedback, and impact the direction of instructional improvement (Bell & Gitomer, 2023; Boston & Candela, 2018). Generic, domain-specific, and content-specific observation tools may create different evaluations of quality and different pathways for instructional improvement (Hill & Grossman, 2013).

2.3 Theoretical perspective: formative uses of domain- and content-focused instruments

In Fig. 1, we conceptualize the overlapping, complementary nature of generic, domain-specific, and content-specific features of instructional quality and provide examples of where some features might fall.

Fig. 1
figure 1

Set of Factors of Instructional Quality in an Instructional Episode

Full size image

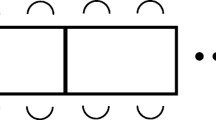
In Fig. 2, we illustrate how two hypothetical observation instruments might capture (solid dots) or not capture (open dots) specific components of instructional quality.

Fig. 2
figure 2

Factors of Instructional Quality Captured by Different Observation Instruments

Full size image

When used for formative purposes, observation instruments can identify strengths and provide actionable feedback. Educative observation instruments provide information about how teachers might improve or develop their practice (Stein & Matsumura, 2009; White et al., 2022). Formative uses foreground improvement and can inform professional learning (Creemers et al., 2013). How observation instruments align with instructional improvement goals is key (Stein & Matsumura, 2009) and, as shown in Fig. 2, each instrument could indicate different, though perhaps complimentary, areas of strength or improvement related to its specific focus.

In this study, we consider how overlaying instruments that foreground different aspects of high-quality mathematics instruction can provide a more complete picture, illuminating productive improvement pathways and helping address questions such as whether instructional moves and strategies were effective (or high-quality) for the targeted mathematical content (e.g., algebra) or processes (e.g., problem-solving versus guided discovery).

2.4 Frameworks overlayed in this study

Unlike studies that compare observation instruments or merge tools to develop synthesized frameworks (Charalambous & Praetorious, 2020; Lindorff et al., 2020; Litke et al., 2021; Panayiotou et al., 2021), we overlay two tools, one domain-specific and one content-specific.Footnote 1 We selected these tools as they support analyzing instruction at different grain sizes and foreground different aspects of high-quality mathematics instruction and likely provide different, but complementary, information. Furthermore, as instrument developers, we aim to model a reflective process to better understand the strengths and limitations of various protocols. We acknowledge these are not the only observation instruments we could have chosen for this analysis; however, we seek to illustrate collaborative work as called for by Bell and Gitomer (2023) and Lindorff et al. (2020) around using such tools to improve teaching.

2.4.1 Instructional quality assessment in Mathematics (IQA)

IQA is a domain-specific instrument and assesses instructional quality from a perspective of ambitious teaching, rooted in the constructs of Academic Rigor (Stein et al., 1996) and Accountable Talk (Michaels & O’Connor, 2015; Resnick & Hall, 1998). The Academic Rigor rubrics (Fig. 3) follow the progression of the cognitive demand of a task throughout a lesson. The Accountable Talk rubrics (Fig. 3) assess how classroom talk is accountable to the learning community and to the mathematics. Rubric descriptors frame each construct specific to mathematics teaching and learning (Boston, 2012).

IQA has been used to assess curriculum implementation (Boston, 2012), the impact of professional development on teachers’ instructional practices (Supovitz & Sirinides, 2018), the overall quality of mathematics instruction as an indicator of equitable learning opportunities (Boston & Wilhelm, 2017), and on teachers’ classroom practices (Candela & Boston, 2022). Developers and external researchers have examined the IQA’s concept-validity (Boston, 2012) and found positive correlations between IQA scores and students’ mathematical achievement (Matsumura et al., 2008). Research indicates two consecutive observations scored by two trained raters yields an internal consistency coefficient of 0.86 (Matsumura et al., 2008), with most studies reporting 75% or higher exact-point agreement between two trained raters (Boston & Wilhelm, 2017).

Fig. 3
figure 3

IQA Classroom Observation Rubrics

Full size image

2.4.2 Quality of instructional practice in algebra (QIPA)

QIPA is a content-specific instrument designed to identify instructional practice in contemporary algebra classrooms, which are typically teacher-centered and feature extensive instruction on procedures (Litke, 2020). The QIPA focuses on teaching practices that, while not unique to algebra, stem from research on students’ algebra learning.Footnote 2 QIPA measures elements in two broad categories of algebra teaching, described in Fig. 4. Teaching Procedures consists of three features that capture the ways in which instruction on procedures is connected to mathematical meaning, supports flexibility, and reflects a detailed, clear and organized presentation. These features of instruction have been shown to support students’ algebra learning specifically (Star et al., 2015). The second category reflects different types of connections teachers and students make between and among algebraic concepts and ideas, including connecting algebraic representations, connecting the algebra content of a lesson to other topics in algebra or to the broader domain of mathematics, and connecting abstract algebraic ideas to concrete or numeric underpinnings (Chazan & Yerushlamy, 2003; Fyfe et al., 2014; Sleep, 2012). Research using QIPA includes descriptive studies of algebra classrooms at both the secondary and post-secondary levels (Lamm et al., 2022; Litke, 2020; Litke et al., 2023). While a full validity study has not been conducted, analyses show moderate to relatively high rates of rater agreement, consistent with those of other instruments (Litke, 2020).

Fig. 4
figure 4

Features of Instruction in QIPA

Full size image

2.5 Research questions

We are interested in the information provided separately and together by two observation instruments focused on domain-specific and content-specific practices, particularly as it informs formative feedback provided to teachers. We ask: What information is provided by the domain-specific IQA and content-specific QIPA related to high-quality mathematics teaching in algebra? In what ways does overlaying the two instruments provide information about instruction and formative uses of the instruments themselves?

3 Methods

3.1 Data and sample

We conduct secondary analysis on data from a larger project aimed at understanding variations in enactments of two mathematics lessons using the same textbook taught by six different algebra teachers in the U.S. over two years (Dietiker et al., 2018). The project selected teachers and schools to reflect geographic variety in U.S. schools (rural, suburban, and urban) and diversity in school context (public comprehensive vs. private). The six teachers (pseudonyms Becker, Johnson, Lane, Randolph, Turner and Wilson) all had at least five years of teaching. All lessons came from College Preparatory Mathematics (CPM) Core Connections: Algebra (Dietiker et al., 2013), which the teachers had been using for a minimum of three years.

We focused on two consecutive lessons on quadratics that included a conceptual focus and the introduction of algebraic procedures. In an international comparison of teaching, Global Teaching InSights found instruction on quadratics relied heavily on algebraic approaches, rarely included connections between algebraic representations, and featured variability in cognitive demand and discourse (Bell et al., 2020), indicating this topic may be fruitful for considerations of formative feedback for teaching. This approach yielded 12 enactments (two per teacher). We had access to written curricular materials, videos and transcripts. As this was secondary data analysis, we did not participate in the sampling of teachers or lesson topics. However, we believe this sample to be appropriate for our analysis. CPM includes both conceptually focused elements and more bounded tasks using mathematical procedures (Choppin et al., 2022). This emphasis means the practices captured by both IQA and QIPA are likely to be evident, making this video sample useful for comparison purposes. Using consecutive lessons allows for a more robust opportunity to consider instructional practice than a single lesson, as we are able to capture the unfolding of related ideas. We reiterate our goal is not to evaluate instructional quality of sample lessons or teachers, but rather to engage in critical examination of the information provided by the instruments.

3.2 Description of sample lessons

The objective of Lesson A is for students to identify connections between graphic, symbolic, contextual, and tabular representations of quadratic functions, and connect the intercepts and vertex of a parabola to a contextualized situation. The central task is an exploration using a context in which four people launch a water balloon and compete for the longest and farthest toss (Fig. 5). Students create graphs and tables for each contestant, find the x-intercepts and vertex of each graph, and find the domain, range, and line of symmetry for one of the parabolas. Lesson A closes by asking what connections students can make between four algebraic representations.

Fig. 5
figure 5

Teacher Guidance and Lesson Tasks for Lesson A© CPM Educational Program 2024. All rights reserved. Used with permission

Full size image

The Lesson B objective is for students to find the x-intercepts of a quadratic algebraically and use the x- and y-intercepts to sketch the graph of a quadratic from its equation. This lesson is designed as guided discovery—the teacher supports students through a series of tasks introducing the Zero Product Property as a method for finding the x-intercepts of a quadratic function (Fig. 6). To close, students are asked to consider what connections they can make between representations of quadratic functions.Footnote 3  

Fig. 6
figure 6figure 6

Teacher Guidance and Lesson Tasks for Lesson B© CPM Educational Program 2024. All rights reserved. Used with permission

Full size image

3.3 Data analytic approach

We scored all enactments using both IQA and QIPA. We do not do so to evaluate the quality of teachers, but rather use scores to analyze the information provided by the instruments. While score reliability was not a central goal, prior work indicates a minimum of two lessons per teacher rated by two raters yields a stable indication of teachers’ practice (Matsumura et al., 2008). The second and third authors scored all lessons using IQA and the first author and a graduate student scored lessons using QIPA (Boston, 2012; Litke, 2020). IQA raters watched and scored lessons individually, marking evidence via time stamps, detailed notes, and transcript excerpts. Across rubrics, 0 represents the absence of the component, 1–2 represent lower-quality features of the component, and 3–4 represent higher-quality features. Raters shared individual scores and reconciled differences through discussion.

Lessons were scored with QIPA as part of a larger project (Litke et al., 2023). Raters scored each lesson independently, breaking lessons into 7.5-minute segments, and scoring the segment on each code using the rubric. Scores reflect the depth of enactment of each feature of instruction. Across instructional features, not present (1) indicates the absence of the feature, low (2) indicates brief or superficial enactment, mid (3) indicates more than brief but not well-developed enactment, and mid/high (4) and high (5) indicate more in-depth development or a segment characterized by a given feature. Segments were first scored for whether procedures were taught. If no procedures were taught in a segment, a score of not present was automatically assigned for the features related to teaching procedures. Interrater reliability across codes was similar, with an average of 70% exact agreement and 94% within-one agreement. Raters noted evidence and rationales for scores and met to reconcile scores through discussion using a consensus coding process. We generated lesson-level scores by averaging across segments for each feature. Because the number of segments vary and teachers may not attend to every practice in every segment, we also recorded maximal scores for each lesson.

To develop themes related to overlaying the instruments, we met to compare and discuss scores for each enactment. We drew on lesson scores, scoring notes, and the lessons themselves and first independently wrote memos (Corbin & Strauss, 2015) summarizing the information indicated by scores for each teacher and lesson. Next, each rater team created a memo for each teacher, summarizing the instructional strengths highlighted by their instrument, noting consistency or variations across lessons or teachers on individual rubrics, and interpreting scores in light of rubric descriptors and transcript excerpts. We then met to discuss these summaries, identifying patterns within and across instruments and enactments, taking note of where scores converged and where they varied (e.g., higher scores on IQA but lower scores on QIPA, or vice versa). Through this process, we generated additional memos that described emergent themes, both across lessons and teachers, returning to the video as needed to understand the information provided by rubric scores.

4 Findings

Our research questions focused on understanding the information provided by overlaying domain- and content-specific tools. We do not make generalizable claims about the quality of teachers or enactments, as doing so with such a small sample would be inappropriate. Rather, we use the instruments in an exploratory manner, describing the information they provide separately and overlaid with one another and consider their uses as formative tools.

4.1 Information about instructional quality provided by each instrument

In Table 1, we present IQA and QIPA scores for each lesson and teacher. IQA scores reflect lesson-level scores on each rubric while QIPA scores reflect a lesson-level average across all segments. For QIPA, we also present the maximal segment score for each lesson as averaging scores can obscure variation. We provide these scores as a descriptive summary.

Table 1 Teacher by Lesson Scores on IQA (top) and QIPA (bottom)
Full size table

IQA scores provide information about the extent to which teachers enact ambitious teaching practices and the depth and quality of mathematical discourse. We found both lessons featured high cognitive demand tasks, but all Lesson A enactments featured lower scores for task implementation than potential. Lesson B featured more variation in task implementation, with some maintaining and others lowering it. Scores also indicate teachers provided learning opportunities through questioning; but student contributions were characterized by short responses or procedural steps, rather than responses that connected strategies or offered mathematical explanations. Relatedly, while students explored important mathematical ideas during small group work, their contributions during whole-group discussions were limited. We found no instances of students linking mathematical contributions to other students’ ideas, indicating when discussion occurred it was primarily between teacher and student.

QIPA scores provide information about the extent to which instruction includes practices that provide opportunities for students to develop algebraic understanding. While no procedures were taught in Lesson A—in part due to the exploratory nature of the curricular materials—Lesson B featured explicit teaching of new procedures using a guided-discovery approach. Across all enactments, procedures were clearly presented and well-organized. In most enactments, teachers gave meaning to algebraic procedures to a modest degree, but enactments included less of a focus on supporting procedural flexibility. QIPA scores also show modest attention to connections between numeric and abstract algebraic ideas. We find variation in the degree to which teaching included connections between algebraic representations. The objectives and central tasks of both lessons reflected an emphasis on connecting representations of quadratic functions, yet while enactments included multiple representations, teachers and students seldom connected these representations explicitly.

4.2 Information provided by overlaying IQA and QIPA

We were interested in what could be learned about analyzing instructional quality from overlaying IQA and QIPA. Drawing on lesson scores, scoring memos, discussions, and lesson videos, we surface two main themes. First, we find in this sample, overlaying instruments allowed for consideration of practices that were foregrounded and backgrounded, particularly when the two instruments individually provided differing determinations of instructional quality for the same lesson. Second, overlaying the instruments showed ways that alignment between lesson and instrument influenced the information provided.

4.2.1 Layering instruments provides information for feedback and reflection

For a subset of enactments in this sample, the two instruments individually provided different conclusions about instructional quality. Moving beyond determination of whether these enactments reflect high-quality instruction, layering the instruments demonstrated strengths areas for growth that might not be considered with only a single lens. These differences relate to the ways in which the two instruments foreground aspects of high-quality instruction.

To illustrate this, we focus on Randolph’s lesson enactments. Through IQA, we find limited evidence of ambitious teaching practices across both lessons (Table 1). In particular, Lesson B features low-range IQA scores across most rubrics, indicating the enactment did not include high-quality instruction related to whole class discourse and building conceptual understanding of the Zero Product Property. IQA scoring notes and lesson memos show the teacher directed much of the work and while the task held potential for students to make meaning of mathematical ideas, Randolph often scaffolded students’ by providing explanations of concepts for them, rather than eliciting ideas from students or by walking students through problems rather than supporting their sense-making. Overall, the enactments featured limited opportunities for student discourse. Throughout both enactments, Randolph’s questions solicited explanations for how students arrived at their solutions, but students were not pressed for (and did not provide) explanations of their thinking or reasoning. Whole class discussion focused on sharing steps or reviewing students’ answers. These aspects of instruction are reflected in the lower scores on IQA accountable talk rubrics.

However, the same lesson segments when viewed through the lens of QIPA, include teaching practices that have potential to support students’ algebra learning, especially around algebraic procedures. Throughout the lesson, Randolph gave meaning to the Zero Product Property by explaining why solving for the x-intercepts was important (e.g., accurately sketching a parabola and finding its vertex), what the solution meant relative to the quadratic function (e.g., the x-value of the point where the y-value was 0), and giving mathematical meaning to the steps of the procedure (e.g., why factoring the quadratic is necessary in order to solve for the intercepts). While these explanations were brief, they permeated the lesson. In addition, Randolph employed a clear and organized note-taking structure, publicly recording the procedures in detailed and systematic ways and leveraging color to annotate solution methods.

Overlaying QIPA with IQA allowed for the identification of instructional strengths around different aspects of mathematics teaching, and for a richer depiction of the ways in which Randolph’s instruction might support (or better support) students’ conceptual and procedural understanding. To illustrate the ways in which overlaying the two instruments could provide richer guidance for a teacher, we present a short excerpt in which Randolph introduced the Zero Product Property.

Randolph drew from the curricular materials and asked a series of bounded questions using a series of numerical examples (“I am thinking of a number when I multiply that number by 5, I get 0. What is my number?,” “\( \frac{1}{4} \)times my number is 0. What’s my number?,” etc.). Through these, Randolph asked whether students noticed a pattern, then generalized that pattern:

Randolph: So a product is what you get when you multiply, right? It is your answer when you multiply. So if I have a zero product, what does that mean? That means that when I multiplied, my answer was?

Students: 0

Randolph: So what do you know about when you multiply and you get 0 as your answer, what do you know about the things that you multiplied?

Student: One of them has to be 0.

Randolph: One of them has to be 0. This was not news to you, was it? You guys already knew this when I brought up that slide? You were like yeah, yeah, yeah we get it. 5 times 0 is 0. -7 times a number is 0, it’s got to be 0. You guys all knew that, right? This is just giving it a name. The Zero Product Property. This is just telling me that when my answer to my multiplication, when my product is 0, one of the factors, one of the things being multiplied, has to also be 0. So let’s write that down. When the product is 0, hence the “zero product”, one of the things being multiplied must be 0. Why didn’t I say one of the numbers?

Student: Because it’s not always numbers.

Randolph: Because it’s not always a number. You could have a whole expression, couldn’t you? And then that expression has to equal 0? So this property is nothing you don’t already know to be true, it’s just now you have a name for it. You already knew that when you multiply two things and they equal 0, one of them has got to be 0. You just didn’t know that that was specifically called the Zero Product Property.

While this exchange exemplifies a teacher-centered approach using bounded questions (thus lower IQA scores), it also shows careful work to develop the property in ways that support students to make meaning of the ideas (thus higher QIPA scores). Throughout the enactment, Randolph periodically asked questions that provided opportunities for students to explain their mathematical work and thinking or make connections between ideas, but these were often followed by bounded questions that funneled students into brief or procedurally-focused responses. Here, Randolph asked students to make sense of the pattern (“what does that mean?”), but the question that followed funneled students into a meaning-making (“when I multiplied, my answer was?”). Layering the QIPA, we noted in this segment of the lesson, Randolph’s line of questioning provided the opportunity for students to build to a new abstract algebraic idea (the Zero Product Property) through numeric examples and developing a generalization.

From a perspective of ambitious teaching, this information indicates Randolph might be supported to shift to more student-centered instructional practices, such as providing students more opportunities for exploration, reasoning, or explanation. Using information from the QIPA formatively could support Randolph to understand strengths in the approach to introducing this property, while deepening the connections and meaning-making around the procedure, while IQA scores and descriptors might support Randolph to consider centering students in developing generalizations.

4.2.2 Information related to alignment between lesson and instrument

When overlaying QIPA and IQA, we find differences in the information they provide related to the alignment between the tool’s vision of high-quality instruction and the lesson itself. The consecutive lessons in this study had contrasting instructional emphases. When the lesson structure and vision of high-quality instruction emphasized by the observation instrument were not aligned, the information provided indicated lower quality instruction, despite the lesson including practices that support students’ mathematical learning. We provide three illustrative examples of how overlaying the two instruments in this study reflect these discrepancies.

One way lesson emphasis impacted the information the instruments provided was through the extent to which a lesson features whole class discussion. The IQA rubrics capture features of instruction during whole-class discussion around a mathematical task. Enactments without whole class discussion scored 0 on multiple IQA rubrics (see Table 1). Discussions that did not include students’ providing explanation or reasoning, scored lower on the accountable talk rubrics specifically. While teachers may have good reason for not conducting a whole-class discussion depending on their goals, aspects of high-quality mathematics instruction emphasized by IQA presume the inclusion of a discussion; its absence limits the formative information IQA is able to provide.

Second, overlaying instruments showed ways that alignment between instrument and curricular guidance influenced the information provided. The curricular materials for Lesson A featured tasks grounded in student exploration and inquiry, while Lesson B featured teacher-guided discovery and the introduction of an algebraic procedure. While ambitious teaching and high-quality teaching of procedures are not mutually exclusive, in this sample, this difference in emphasis led to differences in the amount and type of information provided by each instrument. IQA does not capture aspects of high-quality instruction when the focus is on procedural understanding; one reason for low scores across IQA rubrics was an instructional emphasis not aligned with what IQA is intended to capture. In contrast, QIPA was developed to measure high-quality teaching in more teacher-directed lessons such as those that introduce procedures; this instrument provided more information on these same enactments, allowing the rubric to be used to surface areas of strength and growth. Similarly, when lessons are more inquiry-focused (e.g., Lesson A) and do not feature the teaching of procedures, QIPA provides less information.

A third way alignment influenced the information provided was through the extent to which each instrument prioritizes teacher vs. student actions. Across multiple rubrics, IQA makes a distinction between who (teachers or students) is enacting certain behaviors. For example, high scores on Implementation rubrics require students, rather than the teacher, make connections, focus on making meaning, and provide explanations. The more scaffolding a teacher provides, implementation scores decline. Thus teacher-directed enactments often score lower on IQA elements, as there may be fewer opportunities for students to contribute in the ways privileged by IQA (as seen in Lesson B scores relative to Lesson A). In contrast, QIPA is designed to measure the depth of instructional features regardless of whether those features were teacher- or student-centered. The picture created by overlaying the two instruments could support teachers to identify strengths in their own explanations and connections while also surfacing ways in which teachers could do more to support students to generate these.

Overlaying instruments across consecutive lessons allowed for more and richer information as more components of high-quality mathematics instruction were measured. Rather than view the need for alignment at the lesson-level as a weakness in either tool, we suggest it underscores the importance of alignment between lens and lesson context and the benefit of looking at multiple, consecutive lessons with both frameworks. Because observation instruments center specific aspects of high-quality instruction, their focus foregrounds specific instructional strengths and areas for growth rooted in what they emphasize. While lower scores represent lower-quality instantiations of given practices, such scores may also indicate a misalignment between instruction and the tool. In this sample, overlaying instruments mitigated issues arising related to alignment between instrument and lesson format, curricular emphasis, or teachers’ role in instruction. Contrasting quality determinations across tools may not indicate contradictory information or measurement issues, but rather reflect complementary practices. Teachers who are enacting higher-quality ambitious teaching practices, may be supported by reflecting on finer-grained instructional practices that support students’ learning of algebra content. Teachers who demonstrate instructional strengths in more teacher-directed contexts can reflect on how they might surface students’ ideas through mathematical discourse.

5 Discussion and conclusion

In this study, we overlay two observation instruments—one domain-specific (IQA) and the other content-specific (QIPA). Building on work of those engaged in multi-instrument approaches to measuring teaching quality (Lindorff, 2020), we consider how overlaying tools can support their formative uses.

Our findings demonstrate how overlaying can provide specific and actionable feedback (White et al., 2022) beyond what one instrument alone could provide. For example, while sample lessons featured multiple algebraic representations, teachers and students did not always make explicit the connections between them, despite this being a stated goal of the lessons and focus of the curricular guidance. QIPA descriptors could support teachers to consider potential connections and use these to support deepening the conceptual focus of the lessons. IQA rubric descriptors could be used to support teachers in reflecting on who is linking representations, pressing students to explain their thinking about these connections, or linking their ideas with one another in whole group discussion.

Overlaying instruments also allowed for reflection on practices that support student learning beyond a single instrument’s vision of high-quality instruction. Each tool suggested different strengths or areas for improvement but overlaying them—particularly over two consecutive lessons—provided a more robust depiction of instructional practice to inform feedback. This was aided by the distinction between the domain and content foci of these two instruments. For example, many lesson enactments in this sample were characterized by teacher-centered instruction and included minimal mathematical discussion. When viewed only through the lens of IQA, feedback might take a deficit view of teacher-centered practices without consideration of how certain features of instruction highlighted through QIPA can support learning of specific content (e.g., teaching procedures in ways that connect to underlying mathematical concepts). Taking information provided by the two tools in tandem develops a more robust view of teachers’ strengths and has the potential to take an asset-based approach to feedback, supporting teachers to build on rather than reform current practice (Spangler, 2019).

In addition, overlaying instruments demonstrated how alignment between an instrument’s focus and a lesson’s instructional emphasis can influence formative feedback. In this sample, curricular guidance, opportunities for whole class discussion, and whose actions were of focus (teacher or student) influenced the amount and types of information provided. This finding indicates the importance of examining multiple lessons, even when instruments are used for formative purposes. Prior research (Matsumura et al., 2008), suggests the need for multiple observations in summative evaluations. For example, for IQA, two lessons provided a stable estimate of instructional quality when lessons aligned to the foci of the tool, but as many as eight lessons were needed when they were not (Wilhelm & Kim, 2015). For formative uses, stability of estimates are less of a concern, but there may be parallel reasons for relying on multiple observations. Analyzing two consecutive lessons allowed for more opportunity for alignment between lesson emphasis and tool as there were more opportunities for teachers to engage in practices that support student learning. Formative feedback might support teachers to reflect across lessons, considering how (and why) various practices were foregrounded or backgrounded. Future research could investigate the number of lessons needed to allow for robust reflection on practice and actionable information for improvement.

Our study is limited by our choice of instruments and small sample size. Different tools with different foci may identify additional ways that instruments complement or contradict one another; conducting similar work with other observation instruments is needed. Future research could overlay multiple such tools to consider whether and how the information provided supports instructional improvement. Overlaying instruments may also support teachers to consider practices at different stages of difficulty (Creemers et al., 2013). Furthermore, while we are concerned with formative feedback rather than summative evaluation, classroom observation research should ensure its alignment with student learning outcomes. We engaged in secondary data analysis and were unable to integrate student learning outcomes. Instead, we rely on previous research connecting the aspects of quality measured by IQA and QIPA to student achievement (Matsumura et al., 2008; Star et al., 2015). Additional work with larger samples could consider how the information provided through overlaying instruments relates to changes in student learning outcomes.

No one instrument will capture all aspects of high-quality mathematics instruction for every lesson. Different practices may support student learning for different types of lessons and mathematical content, and under different conditions. Regardless of the choice of tool, assumptions about what comprises high-quality instruction are embedded into all observation instruments. Classroom observation research should consider how the perspective of the lens used impacts conclusions about instructional quality and informs feedback for teachers. The field has begun to consider the merits of a synthesized framework for measuring instructional quality (Charalambous & Praetorius, 2020). Individual tools can have significant overlap but may also measure instruction at a grain size more suitable for supporting actionable feedback (Lindorff et al., 2020). But any one instrument can privilege a particular instructional orientation. Bell and Gitomer (2023) ask researchers to consider how multiple frameworks might support improvement across contexts.

We aimed to model a process by which scholars engaged in work with observation instruments might collaborate to consider the formative information provided by multiple tools. Lindorff and colleagues (2020) suggest scholars engage in such processes across contexts to further instructional quality research. We encourage those engaged in classroom observation research to overlay instruments and consider what doing so might contribute to research and practice. Overlaying tools from different country contexts could support dialogue around cultural dimensions of teaching and develop this global community. Layering generic tools such as the three-dimensional framework (Klieme et al., 2009) with domain- or content-focused tools could support teachers to reflect on the interaction between general pedagogical strategies and mathematics-specific aspects of teaching. Layering a domain-focused instrument with a tool focused on equitable participation (e.g., Reinholz & Shah, 2018) could support reflection on both students’ participation in mathematical discourse and meaning making, as well as how participation differs by demographic groups. Overlaying algebra-focused instruments with those focused on supporting the mathematical success of students from historically marginalized backgrounds (e.g., Wilson, 2022) could build knowledge around teaching practice in a key gatekeeper course. Teachers might be supported to learn and overlay instruments to reflect on their own practice (Candela & Boston, 2022; Supovitz & Sirinides, 2018), selecting tools aligned with their improvement goals.

If we wish classroom observation research to enhance the quality of mathematics teaching, we must offer a well-rounded vision of high-quality mathematics instruction, attuned to content and context. To do this, we must specify what is foregrounded, backgrounded, or absent in our measurement tools, acknowledging conclusions about instructional quality—including strengths, feedback, and areas of improvement—are framed and constrained by the tools used.