Promoting a set-oriented way of thinking in a U.S. High School discrete mathematics class: a case study

Abstract

In this case study, we investigate one teacher’s implementation of DNR-based combinatorics curriculum in their high school discrete mathematics class. By examining the teacher’s practices in whole-class discussions of two counting problems, we study how they advanced a variety of ways of thinking to support the development of a set-oriented way of thinking about counting. In particular, we find the teacher worked to build shared experience and understanding of mathematical ideas by grounding her teaching in students’ ways of understanding and leveraging students’ intellectual needs. In doing so, the teacher promoted a set-oriented way of thinking through attending to connections between sets of outcomes, counting processes, and formulas in student representations and justifications; elevated solutions employing process pattern generalization; and advanced the beliefs that counting problems can be solved in many ways and entail several types of mathematical activity.

1 Introduction

The value of discrete mathematics in K-12 curriculum is well-established (e.g. Hart & Martin, 2018; Kapur, 1970; NCTM 2000; Rosenstein et al., 1997), yet discrete mathematics is conspicuously absent from such curricula in the United States (Rosenstein, 2018), among other countries. Especially with its accessibility and practical applications in areas such as computer science, there has thus been both increased attention to the teaching and learning of discrete mathematics in the mathematics education community, and a renewed push to include discrete mathematics as an integral part of K-12 curriculum in the U.S.

As a branch of discrete mathematics, enumerative combinatorics is rife with opportunities to engage students in rich mathematical thinking. Even simple counting problems can draw students towards interpreting, representing, structuring, conjecturing, justifying, and generalizing in the process of counting, which can be leveraged to foster desirable mathematical ways of thinking. For example, researchers have documented how students meaningfully generalize, solve smaller, similar problems, think about equivalence, and attend to sets of outcomes as they solve counting problems (e.g. Lockwood, 2014; Lockwood et al., 2020; Lockwood & Reed, 2020; Maher et al., 2010).

Based on the potential of discrete mathematics to advance students’ thinking, Lockwood et al. (2020) call for a need for further research on the “kinds of classroom and teacher supports necessary to ensure that [rich] reasoning and rich thinking surface for students”. Studies situated in actual classrooms can provide valuable insights into precisely this—yet no such studies have been conducted in the U.S. or elsewhere. In this light, we present a case study of how one U.S. high school teacher implemented two counting problems in their discrete mathematics classroom, and address the following two interrelated questions:

• 1. What mathematical ways of thinking can be advanced with secondary students as they engage in counting problems?

• 2. What teaching practices can contribute to eliciting those ways of thinking?

2 Theoretical perspective

This study is grounded in the DNR theoretical framework (Harel, 2008a, 2008b) and Lockwood’s model of combinatorial thinking (Lockwood, 2013; Lockwood et al., 2015b). DNR contributes constructs necessary for framing our discussion of and answers to both research questions, and Lockwood’s model affords attention to characteristics of student thinking about counting problems.

2.1 DNR

DNR¹ is a system consisting of premises about learning, constructs, and instructional principles. In this study, we will make use of only a few relevant constructs and one central principle.

2.1.1 Mental acts, ways of understanding, and ways of thinking

In doing mathematics, humans engage in numerous mental acts such as counting, interpreting, representing, structuring, conjecturing, proving, generalizing, and problem-solving; these may occur in series or parallel. The cognitive products of a mental act carried out by a person are their ways of understanding (WoU) associated with that mental act, and the characteristics of these WoU are their ways of thinking (WoT).

We illustrate these constructs through examples relevant to our analysis: Attempts at counting often lead to a momentary shift of attention to listing, another mental act. A particular list is a WoU associated with listing, and a desirable WoT is for a list to be systematic. More generally, a list is a particular form of a representation, a WoU associated with the mental act of representing; representations may be verbal or written, where the latter includes drawings, lists, diagrams, expressions, and equations. As another example, attending to the underlying structure that causes a pattern to hold is a WoT referred to by Harel (2008a) as process pattern generalization (PPG).

2.1.2 The Necessity Principle

The Necessity Principle, a foundational principle in DNR, states: “For students to learn the mathematics we intend to teach them, they must have a need for it, where need refers to intellectual need, not social or economic need.” Harel (2008b) identifies five interrelated categories of intellectual needs, three of which are relevant to this study:

The need for computation encompasses one’s need to quantify, calculate and relate quantitative values, as well as develop efficient computation methods.

The need for communication refers to one’s needs to transform language into mathematical expressions (formulate) and externalize logical arguments and meanings of concepts (formalize).

The need for structure refers to one’s need to reorganize knowledge into a logical structure. Two important aspects of the need for structure are the need to make connections and the need to define objects to maintain invariance in a definition or maintain the form of an expression across varying contexts.

2.2 Combinatorial thinking

2.2.1 Lockwood’s model of combinatorial thinking

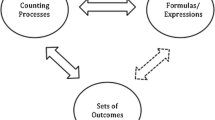
Lockwood’s model of combinatorial thinking highlights three components and the relationships between them. Formulas/expressions refer to mathematical expressions that yield numerical values. Mathematically equivalent expressions different in form are considered to be different. Counting processes refer to the enumeration procedures in which a counter engages as they solve a problem. Sets of outcomes refer to any set that can be associated with a counting process; this might be the desired set of outcomes being counted in a problem, an element, subset, or superset of the desired set, or any set that meaningfully bisects with such a set. Each component of the model is dialectically related with every other component (see Fig. 1).

Fig. 1

Lockwood’s (2013) model of combinatorial thinking

Through the lens of DNR, attending to sets of outcomes as an intrinsic component of solving counting problems is a desirable WoT associated with the mental act of counting. Grounded in the above model and DNR, Lockwood (2014) identified and illustrated the value of this WoT, and labeled it as a set-oriented perspective (henceforth “set-oriented way of thinking”/“SOWoT”).

2.2.2 Two characteristics of counting processes

In line with DNR, we consider individuals’ counting processes to be WoU, and characteristics of these counting processes to be WoT. In this study, we label two WoT characterizing observed counting processes: We say an individual’s counting process is a direct counting process if they count the elements of the desired set of outcomes once each, without repetition, and without considering any other outcomes outside this set. In contrast, we say an individual’s counting process is a counting process which corrects for intentional overcounting (henceforth “overcounting process”) if it considers some or all of the elements of the desired set of outcomes multiple times and/or outcomes not in this set, before accounting for the multiply-counted and/or extra outcomes to ensure that each element of the set is counted exactly once and that no other outcome is counted.

To contrast direct and overcounting processes, consider this problem (further discussed below): “In a group of 7 people, each person shook hands with everyone else exactly once. How many handshakes occurred?” Label the people with the numbers 1 through 7. A direct counting process might count the number of handshakes each person takes part in with a higher-numbered person in turn, yielding the expression $6+5+4+3+2+1+0$. An overcounting process might sum the number of hands shaken by each person, then consider that two hands are shaken in each handshake, yielding the expression $\frac{7\cdot 6}{2}$.

3 Curricular and instructional goals

This study is situated in a discrete mathematics classroom implementing DNR-based curriculum. The discrete mathematics course is a year-long course designed for grade 12 students (ages 17–18) in the U.S. who have already taken three years of high school mathematics. Outwardly, the course contains units on two-player impartial combinatorial games, graph theory, recursion, cryptography, and enumerative combinatorics (henceforth “counting”), but the goal underlying all of these units is to advance students’ WoT. Two of the authors of this study co-authored the counting unit and planned and provided professional development for the course. In particular, a primary aim across all units is to promote a transition from empirical reasoning to deductive reasoning (including PPG).

In line with DNR, the curriculum places a focus on problem-solving as the source of knowledge generation and sees productive struggle as crucial in knowledge construction. It sees students as co-constructors of knowledge, and places the onus on students to raise conjectures, justify them, and critique the reasoning of others; conversely, it sees teachers as orchestrators of this discourse, who can guide students through this work and leverage opportunities to elevate, value, and discuss student thinking. Practically, this means group tasks necessitating shifts in WoT are central to the curriculum and often take up the majority of instructional time, as these are rife for opportunities for students to solve problems and communicate ideas with others. Teachers are encouraged to elevate multiple problem-solving approaches, help students draw connections between different solutions, and welcome errors as being useful.

While the counting unit’s subject matter consists in reinventing the multiplication principle and the formulae for permutations and combinations, its underlying pedagogical aim is to advance students’ SOWoT, particularly with respect to structuring in a combinatorial context. As instructive examples of how the unit cultivates this WoT, consider the first two problems in the unit, henceforth called the Domino and Handshake problems, along with their accompanying instructions (see Fig. 2):

Fig. 2

The Domino and Handshake problems (from Vu et al., 2018)

Note that part (a) of the Domino problem is taken from Lockwood and Gibson (2016), and that the two problems can be considered analogous (Gick & Holyoak, 1983).

These two problems serve as an introduction to the larger unit in that they aim to give students genuine experiences with counting situations before labeling combinatorial ideas, and have them begin to develop desirable WoT about counting targeted over the course of the unit. These goals include, but are not limited to having students:

• 1. List examples of outcomes they are trying to count;

• 2. See value in being systematic in enumerating outcomes;

• 3. See value in a variety of structured representations (e.g. lists, tables, tree diagrams, expressions) in enumerating sets of outcomes;

• 4. Describe and compare the counting processes underlying representations to connect and reconcile differences between representations;

• 5. Become sensitive to the potential for undercounting or overcounting outcomes, and use and compare representations to identify, justify, and compensate for undercounting and overcounting

• 6. Use smaller cases to reason about more general cases.

4 Methods

In this study, we analyze empirical classroom data collected from one teacher’s (Ms. M) implementation of the Domino and Handshake problems in her high school discrete mathematics class. The real-world setting and our desire to understand and describe issues of cognition and instruction makes a case study an appropriate methodology for this study Yin (2011). We present our findings in vignettes, short narratives illustrating Ms. M’s targeted WoT and the teaching practices used to advance them.

4.1 Participants

The class consisted of 36 grade 12 students, and was offered in a large urban public school district in the southwestern United States where each high school in the district offered the course. In the year the data was collected, 92% of students in the school this class was taught at were BIPOC (Black, Indigenous, or people of color), 28% were considered socioeconomically disadvantaged, and 6% were English language learners (California Department of Education). Ms. M participated in professional development led in part by two of the authors detailing the implementation of DNR-based instruction in the context of this course, and had previously taught the course once, but had never taught the counting unit before. She was a resource teacher for the district, and took responsibility for training other teachers. However, she was not a DNR expert.

4.2 Context

The class spent 6 instructional hours on the Domino and Handshake problems. After introducing each problem, Ms. M routinely gave students time to work independently and in small groups while she circulated through the room listening to and probing into student thinking. During this time, she selected and sequenced students to present their WoU to the class (in the sense of Stein et al., 2008). During these presentations, Ms. M often asked clarifying or probing questions to the presenter or the class, created ad hoc problems, or encouraged student-to-student interaction between the class and the presenter. Of the time spent on the Domino and Handshake problems, approximately 47% was spent on small group work or discussions, while the remaining 53% was spent on student presentations and whole-class discussion. Ms. M had an atypical amount of freedom in teaching this course, as it was not subject to standardized testing, not a prerequisite for any other course and had a mostly self-selecting student population. At the same time, what could be done in her class was still limited by the constraints of teaching in a public school (e.g. class sizes, school schedules, and student fatigue).

4.3 Data collection and analysis

During the unit, video recordings of the class were collected. The lead author of the paper was present during a large majority of the instructional time in this unit. This data was originally collected for the purpose of curriculum evaluation, and its potential for research was only later realized.

Following Patton’s (2014) advice for conducting case studies and using grounded theory methods (in the sense of Corbin & Strauss, 1990), we took an iterative approach towards analyzing this data and refining our research questions, alternating between independently reviewing video recordings and meeting frequently to discuss and refine our observations, findings, and data analysis efforts. We independently reviewed the entirety of the video data across the unit (approximately 24 h across 24 instructional periods) and labeled the video with the names of presenters and participants and the form of classroom activity taking place (e.g. small-group work or student presentations and discussion of a WoU).

We agreed that whole-class discussions during the Domino and Handshake problems provided the most illuminating examples of the WoT Ms. M targeted while also shedding light on her teaching practices with a suitably low level of inference to support our conclusions. Based on applicability to the research questions, redundancy, and level of inference, 18 segments of interest emerged within the relevant video data. We summarized the events of each segment through the lens of DNR and Lockwood’s model by writing a short narrative indicating the WoU shown by participants, a description of any whole-class discussion that took place, Ms. M's teaching practices, and the WoT (e.g. PPG, SOWoT) evidenced by students and targeted by the instructor.

Next, we compared our claims and discussed our analyses of the WoU/WoT and teaching practices within the whole-class discussions of the two problems. In cases where we disagreed, we reviewed the video together. When the level of inference was too high, the claim was retracted. By the fifth round of analysis, we reached consensus in all cases. Then we more carefully transcribed and discussed the significance of the segments in which Ms. M’s teaching practices were clearly aimed at advancing an identifiable and desirable WoT, from which our results emerged in their final forms.

5 Results

In this section, we examine the whole-class discussion of the Domino and Handshake problems from our perspective as observers, and explore how the teacher, Ms. M, advanced three clusters of WoT: SOWoT, PPG, and beliefs about mathematics. In each of the following key episodes and their subsumed vignettes (marked V1–10), we claim that Ms. M promoted these WoT through:

• (Ep. 1) Attending to the encoding of outcomes (V1) and contrasting counting processes (V2) in student representations of the Domino problem, and subsequently leveraging students’ intellectual needs to necessitate reformulation (V3);

• (Ep. 2) Guiding students to draw connections between different sets of outcomes and their cardinalities through laying the groundwork for (V4), elevating (V5), and discussing (V6) a PPG-based solution to the Domino problem;

• (Ep. 3) Leveraging the need for structure in the Handshake problem through unstructured physical enactment (V7), surfacing multiple interpretations of the problem (V8), interpreting these representations via structured physical enactment (V9), and connecting the Handshake problem with the Domino problem (V10) to guide students to connect different interpretations, define desirable outcomes, and structure sets of outcomes in the Handshake problem.

At the end of each vignette, we provide a summary of how that vignette contributes to our answers to our research questions, through identifying the WoT advanced with students and the central teaching practices which contributed to eliciting those WoT. Each WoT described here is prefaced with either (SOWoT), (PPG), or (Beliefs) based on the cluster it lies in.

5.1 Episode 1: attention to representations

5.1.1 Vignette 1: attending to outcome encoding

After the Domino problem was introduced, a majority of students found a solution to part (a). Ms. M asked four students to present their work to the class. Figure 3 displays the first three students’ representations.

Fig. 3

(Top to bottom) Julia’s, Gloria’s, and Kai’s representations

We note that each of these representations symbolizes a domino differently; for example, Kai’s representation uses the symbol $x|y$ to mean a domino with $x$ dots on one half and $y$ dots on the other. We label the manner in which an outcome is symbolized in a representation the encoding scheme of that representation (in the sense of Lockwood et al., 2015a). During each respective presentation, Ms. M paused to attend to the representation’s encoding scheme, by asking questions of the presenter and/or the class, and pointing to and verbally describing examples of dominoes in each representation (see Fig. 4).

[Julia’s presentation] Ms. M: So would you agree that this represents a domino? … 5-5 and 5-6 … Those are two dominoes?

[Gloria’s presentation] Ms. M: What do these numbers at the top represent? …What does this represent [pointing to outcomes in the representation]?

[Kai’s presentation] Ms. M: So, when we see B/B right here, that means... a domino that has a blank half and a blank half...

Fig. 4

(Top, bottom-left, bottom-right) Ms. M attending to encoding schemes in Julia’s, Gloria’s, and Kai’s representations

Through elevating multiple students’ representations, which had different structures and encoding schemes, Ms. M consistently and repeatedly emphasized that outcomes can be represented differently, but one’s encoding scheme must be clear to other readers.

WoT: (Beliefs) Counting problems can be solved in more than one way (representationally).

Teaching Practices: Elevating multiple students' representations, which had different structures/encoding schemes.

5.1.2 Vignette 2: contrasting counting processes

During the presentations described in vignette 1, Ms. M surfaced students’ underlying counting processes by asking how they knew they had not under- or overcounted. We note that typically, Ms. M attended to overcounting, but not to undercounting. The first three presenters viewed this as being self-evident due to the systematic nature of their direct counting processes. Ms. M’s treatment of Gloria’s presentation was emblematic of how she handled the first three presenters.

[Gloria’s presentation] Ms. M: You’re answering the question of how you know you’re not overcounting when you said, “I already knew that I had 0-1, so I didn’t put the 1-0.” So, you’re making sure you’re not counting something twice by your system…

Before the fourth presentation, Ms. M promoted attending to the overcounting process underlying this representation, in contrast to previous representations’ direct counting processes (see Fig. 5):

Ms. M: So Noah’s approach was a little bit different than everybody else’s we’ve seen so far and I really want to highlight his approach because it’s going to shed [some light on] an important concept for us.

Fig. 5

Noah’s representation

Fig. 6

Class results for $101+100+\cdots+1$

After Noah’s presentation, Ms. M probed his thinking:

Ms. M: What do you see as different from your process than everybody else’s process?

Noah: … I just listed each domino by the number and then splitting it up.

Ms. M: What I see on yours that I don’t see on others is this crossing things out idea. Why did you have to cross things out?

Noah: Because they’re the same [as] other dominoes.

…

Ms. M: How did you determine which ones to cross out? What was your process for finding the repeats?

Noah: I don’t know. I just looked at it.

…

Ms. M: Noah’s approach was different because he listed all the possibilities… and crossed out the ones that were repeats.

Noah later realized he had missed all pairs of the form ‘n | Blank’; furthermore, we notice that the second column was written in descending order (unlike others) and some outcomes were crossed out and later re-added. This inconsistent structure placed Ms. M in an instructional dilemma. To meaningfully attend to the different sets needed to show how modifying Noah’s counting process could systematically count the desired set of outcomes, she would have had to reconfigure his representation. Ms. M reserved this issue until later (see vignette 4), and chose for the time being to highlight overcounting by removing elements of a superset to yield the desired set of outcomes as a broad counting process, saying “We really need to list all the possibilities and then cancel out all the repeats”.

WoT: (SOWoT) Overcounting processes can be effective ways to count; (Beliefs) Counting problems can be solved in more than one way (computationally)

Teaching Practices: Contrasting overcounting processes with direct counting processes

5.1.3 Vignette 3: leveraging students’ intellectual needs

After these selected presentations, Giovanni unexpectedly volunteered to present his solution, and offered an unsolicited generalization. He claimed that the cardinality of any set of dominoes containing 0 through $n$ dots on each half (henceforth “double-$n$ dominoes”) is $1+2+ \cdots +(n+1)$.

Giovanni: …if 20 is [the highest number of dots on a domino], I’m going to say $1+2+3+4$ until 21.

Ms. M: I know we have to process what Giovanni said a little bit… So, I wonder if we could use your individual method to try to count the number of dominoes [in part (b)] and then see if we can try to understand Giovanni’s method as well.

After students were given time to solve part (Beliefs) and connect their own counting method to Giovanni’s expression, Ms. M asked about a larger case:

Ms. M: If I said that on a domino you could have … up to 100 dots, how could we very quickly with a calculator figure out the total number of possible dominoes?

The class proceeded to add numbers in the sum $101+100+...+1$ in the order they appeared using a calculator, yielding eight different answers that Ms. M publicly recorded. In the ensuing whole-class discussion, she called students’ attention to the efficacy of their computational approaches (see Fig. 6):

Ms. M: Was this a very effective method for calculating the sum? … Wouldn’t it be nice if there was a shorter way? [Students reply affirmatively] … When we’re adding up large sums of numbers, [it’s] very difficult to not make a mistake [using this method].

A problematic situation arose for students as they implemented Giovanni’s computational approach. Through having students compute the sum on a calculator and publicly displaying the errors that entailed, Ms. M leveraged students’ needs for certainty and (avoiding) computation to necessitate computing the sum in a manner using fewer operations. In an informal conversation, Ms. M later communicated that she felt her class’s symbolic WoT stood in the way of them symbolically rearranging the sum into a different expression. In this light, as direct counting approaches had only led to expressions like Giovanni’s, she was able to necessitate a shift of attention to overcounting processes, and particularly Noah’s overcounting process as the only such process elevated at this point.

WoT: (Beliefs) Expressions can be reformulated in more than one way according to one’s purpose.

Teaching Practices: Leveraging students’ intellectual needs by handling a problematic situation.

5.2 Episode 2: connecting different sets of outcomes through PPG

5.2.1 Vignette 4: laying groundwork for a PPG-based solution

Immediately after the events of vignette 3, Ms. M elevated a representation she derived from Gloria and Noah’s earlier representations seen in vignettes 1 and 2.

Throughout this episode, for ease of communication we define several sets in reference to the generalized form of this representation: In an analogous table with row and column headings from 0 through $n$, let ${D}_{n}$ be the set of table entries along the main diagonal (that is, entries $i$-$j$ where $i=j$); ${U}_{n}$ be the set of upper-triangular table entries (where $i<j$); ${L}_{n}$ be the set of lower-triangular table entries (where $i>j$); and ${T}_{n}$ be the set of all table entries. Note that ${T}_{n}$ is the disjoint union of ${D}_{n}$, ${U}_{n}$, and ${L}_{n}$.

While attributing the approach to Noah, Ms. M pointed out that her table contained undesirable outcomes which should be removed, and had students circle all the “duplicates” (i.e. entries in ${U}_{6}\cup {L}_{6}$):

Ms. M: I wanted to come back to Noah’s idea… So I got all the possible combinations that I could have, but there are duplicates. So, I’m wondering if you could take a moment to circle all the duplicates.

Next, she invited students to share their observations. Bryan noticed that dominoes with two identical halves were positioned along the main diagonal. Cristina noticed that entries symmetric about this diagonal contained the same numbers. Ms. M then leveraged Bryan and Cristina’s WoU to ask students to physically enact a process to compensate for overcounting by crossing out every table entry in ${U}_{6}$ which represented removing those elements from the set of outcomes.

During and after this process, Ms. M explicitly named, pointed to, and highlighted each of the sets ${U}_{6}$,${D}_{6}$,${L}_{6}$, and ${U}_{6}\cup {L}_{6}$. She also counted $|{D}_{6}|$, $|{T}_{6}|$,$|{U}_{6}|$ and $|{D}_{6}\cup {L}_{6}|$.

In this vignette, Ms. M requested students to physically circle and cross out duplicate table entries to heighten their awareness of the presence and location of multiply-counted outcomes, and highlighted strategically useful sets of table entries and the symmetric structure of the table with the hope they could notice and generalize a pattern in the underlying structure of the sets of outcomes. Bryan and Cristina’s observations provide evidence that Ms. M’s observations were meaningful to a group of students. We see this as both an advancement of a SOWoT through an attention to sets of outcomes and their elements, and a precursor to the development of an overcounting process and a PPG-based solution to the problem.

WoT: (SOWoT) Attending to sets of outcomes and their elements.

Teaching Practices: Requesting physical manipulation of a representation; highlighting sets of outcomes, their cardinalities, and their structural relationships.

5.2.2 Vignette 5: elevating a PPG solution

After giving students time to work, Ms. M selected and invited Gabby to share and explain her solution to part (c).

Gabby began by examining the $n=3$ case with reference to Fig. 7. She identified the desirable set of outcomes here as ${L}_{3}\cup {D}_{3}$, and explained that its cardinality could be computed as $\frac{12}{2}+4$: The 12 represented $|{U}_{3}\cup {L}_{3}|$, the number of “repetitive dominoes” (i.e. “duplicates” from vignette 4), excluding “non-repetitive dominoes” (i.e. ${D}_{3}$). She divided by 2 to “cancel out repeats”, and added 4 to count the dominoes in ${D}_{3}$ (see Fig. 8).

Fig. 7

Ms. M’s table

Fig. 8

Ms. M’s treatment of the overcounted set of dominoes ($n=6$)

Ms. M promoted a SOWoT during Gabby’s presentation, through both selecting Gabby purposefully (a fact later confirmed in an informal conversation with Ms. M), and stepping in to point out that the numbers along the top and side of the table represented possibilities for the number of dots on each side of a domino. Later, Ms. M pointed out that examining small cases when searching for a pattern was a desirable problem-solving approach the class had previously been taught to use in the Games unit (see Fig. 9).

Fig. 9

Gabby’s table used in her initial explanation

After sharing her approach for the $n=3$ case, Gabby explained that in larger cases she needed to attend to the “sum of the whole picture”, or ${T}_{n}$. She realized she could generalize her approach through considering that $U_{n} \cup L_{n} = T_{n} D_{n}$, to get the formula $\frac{x - y}{2} + y$, where $x$ is “the total number of possibilities [in the table]”, or $\left| {T_{n} } \right|$, and $y$ is “the number of non-repetitive dominoes”, or $\left| {D_{n} } \right|.$ She explained the correspondence between the quantities $x$, $y$, $x - y$, $\frac{x - y}{2}$ and their associated subsets of $T_{n}$, and justified each operation in her formula:

Gabby: We can subtract $x-y$. $x$ is the number of possibilities within a set. Like the whole thing. Like for example, this is 16 [pointing to ${T}_{3}$], minus the total number of non-repetitive dominoes. We’re going to subtract the 4. And then divide it by 2 in order to get the dominoes that were once repeated, but not repeated anymore. And then we’re going to have to go back and add the 4 [referring to $|{D}_{3}|$] because remember, they were not repetitive. So we removed the ones that were repetitive [referring to ${D}_{3}$]… so we have to add them back.

In vignette 4, students attended to the structural relationship between${D}_{n}$, ${U}_{n}$, ${L}_{n}$, and ${T}_{n}$ when$n=6$. Gabby’s solution then evidenced PPG by attending to this structure for the $n=3$ case in relation to her overcounting process to justify the validity of her formula. In this way, Gabby’s explanation together with Ms. M’s support promoted a SOWoT. Through eliciting Gabby’s PPG-based explanation, Ms. M brought together and attended to the mental acts of counting, representing, structuring, formulating, and justifying.

WoT: (SOWoT) Formulas need to be grounded in sets of outcomes and counting processes; (PPG) Identifying and generalizing a structure; (Beliefs) Problem-solving entails multiple mental acts.

Teaching Practices: Asking for justification of a formula; Elevating solutions involving PPG.

5.2.3 Vignette 6: discussing Gabby’s explanation

After the events of vignette 5, Ms. M asked students to discuss Gabby’s explanation in groups before bringing the class back into a discussion to ask Gabby follow-up questions. Once the class’s questions had been addressed, Ms. M asked Gabby to highlight ${L}_{3}$ and ${D}_{3}$ with different colors on a blank copy of Fig. 7 for $n=3$ (see Fig. 10).

Fig. 10

A fresh table for $n=3$

Ms. M established the desired set of outcomes here as ${L}_{3}\cup {D}_{3}$, and that ${U}_{3}$ was not in this set as this was a set of “duplicates”. Ms. M then asked Gabby to repeat her computations by plugging values into her formula for the $n=3$ case, and explain in particular why $|{D}_{3}|$ was re-added at the end. To this, Gabby explained that $|{L}_{3}|$ could be computed as $\frac{12}{2}=6$, but that she still needed to add $|{D}_{3}|$ to get $|{L}_{3}\cup {D}_{3}|$, the total number of dominoes. In response, the class let out a collective “Oh!”. Ms. M then exclaimed, “That is the best sound in a math class ever!”.

Ms. M subsequently gave the class more time to internalize Gabby’s approach. She then asked Ken to re-explain Gabby’s WoU for $n=7$ (see Fig. 11):

Ms. M: Can you just go through and explain what each number is on the picture?

Ken: The 64 is everything inside this box [${T}_{7}$]. The 8 is this diagonal line cutting through right here [${D}_{7}$]. The two represents only one half [uses pen to hide $D_{7}$]… the 56 is everything on that board besides that diagonal line [$T_{7} \backslash D_{7}$]. The 28 is only one side. So either the top [$U_{7}$] or the bottom half [$L_{7}$], not including the diagonal line again and then adding the 8 back into the equation gives us that diagonal line on either the top or the bottom half.

Ms. M: Do we feel solid about this now?

Fig. 11

Ken’s presentation connecting Gabby’s formula to sets of outcomes for $n=7$

Ms. M played an active role throughout Ken’s presentation: She had conversations with him before, during, and after his presentation. Her teaching practices were guided by the goal of promoting the connections between relevant sets of outcomes and their cardinalities to help students better understand Gabby’s formula, which was ultimately successful: To her final question, the class indicated that they now felt comfortable with Gabby’s WoU.

WoT: (SOWoT) Connecting sets of outcomes and counting processes to justify a formula.

Teaching Practices: Asking a student to create and present a solution implementing another student’s approach in a different case.

5.3 Episode 3: connecting interpretations and structuring sets of outcomes

5.3.1 Vignette 7: leveraging the need for structure through unstructured physical enactment

Ms. M introduced the Handshake problem by reading part (a) aloud. She then immediately asked for seven volunteers to act out the situation:

Ms. M: You’re at a leadership conference. You’re getting to know one another. Make sure you shake hands with everybody else at the leadership conference. Go ahead.

The students shook hands without making a plan, and no apparent structure emerged. Afterwards, Ms. M asked:

Ms. M: Did everybody shake hands with everybody else? [Students reply affirmatively] How do you know?

Lori: We counted.

Ms. M: What did you count to?

Multiple students: Six. I counted to six.

Gabby: …I looked at their faces.

Ms. M did not comment further on either of these approaches, though her tone indicated skepticism about the latter approach.

Individuals’ counting processes are rooted in their conceptualizations of how they imagine or enact actions. Ms. M’s decision to have students externalize their conceptualizations of handshaking through physical enactment leveraged students’ need for systematicity (a form of the need for structure) in how they count by illustrating what can happen when one counts without a system in mind. Furthermore, Ms. M’s choice to attend to both the class’s and individual enactors’ viewpoints of how this enactment played out (i.e. from global and local combinatorial perspectives) set students up to interpret, and hence structure, the set of outcomes through multiple lenses. Vignettes 8 and 9 demonstrate that before she could successfully attend to students’ emergent counting processes, Ms. M had to surface, and eventually unify, her students’ multiple interpretations of a desirable outcome in this context.

WoT: (SOWoT) Counting processes should be systematic.

Teaching Practices: Requesting physical enactment of a scenario in a public space.

5.3.2 Vignette 8: Surfacing multiple interpretations

After giving students time to work on part (a), Ms. M asked two presenters to share WoU that each concluded there were 42 handshakes. From the perspective of both individuals, each was an example of direct counting. Felicia, a participant in the enactment from vignette 7, presented her solution from her perspective as an enactor. (We discuss the other representation—created by Dani—in vignette 9.) (see Fig. 12)

Fig. 12

Felicia’s representation for handshakes, with names removed for anonymity

Ms. M: Can you explain what you did, how you did it, and what you got?

Felicia: So, I figured if there was seven people, like doing handshakes, and then I labeled the people… and then I put that Benny shaked [sic] hands with six people because you wouldn’t have hands with yourself so it would be six for each person....

Ms. M confirmed with Felicia that she thought 42 handshakes took place, and followed by asking how she knew she was not undercounting or overcounting. To this, Felicia replied: “I only included the people that [each person] shook hands with, not themselves.” Immediately, a student raised a question about overcounting.

Benny: Can a handshake occur only one time?

Class Members: Yah. That’s my question. That’s all the questions.

Ms. M addressed Felicia’s encoding scheme, indicating an outcome that may have been counted twice (see Fig. 13).

Ms. M: Benny’s saying, Benny shook hands with John... and then John shook hands with Benny.

Fig. 13

Discussing overcounting in Felicia’s representation

Benny: But we would just ignore that, right? [Benny later clarified that he meant Felicia overcounted.]

Ms. M appealed to the physical enactment.

Ms. M: So when you guys were actually up here, John and Benny. Did you guys shake each other’s hands twice...

Class: No.

Ms. M: ...or did you guys shake each other's hands just once? Ah. You only shook each other's hand one time. So what are your thoughts over there... Dani?

Dani: I think like the way I see it is that like it counts per each person. Like, if I shake Gabby’s hand and Gabby shakes my hand it’s not going to cancel each other out because like we shook each other’s hand. In that case, like, it would be like that for everyone. So, because we shook each other’s hand it counts for one for me and one for her.

Despite Ms. M’s appeal to the physical enactment, Benny’s question and claim that Felicia’s WoU represented an overcount, and Ms. M’s attention to Felicia’s coding scheme, the WoU that there were 42 handshakes persisted in the class, launching a spirited public debate about how handshakes should be counted. The degree of enthusiasm and meaningful engagement during this five-minute segment is difficult to communicate here, so we offer some statistics: Of the 28 students visible on camera during this section, 16 raised their hands at some point during this debate, and 8 of these students spoke.

While most students in this debate argued for one side or the other, the final speaker claimed that depending on perspective, both interpretations could be considered correct:

Giovanni: They are both correct. It depends what do you want. Do you want the number of handshakes that happen or the number of people that shake hands?

Ms. M: Well said. It is a matter of interpretation… there are two ways to look at this problem… are we counting the number of handshakes or the total number of individual hands that have been shaken?

Ms. M attended to the central problem of defining outcomes by surfacing multiple interpretations of how a desirable outcome should be defined. Her choice to ask two students to present the WoU that there were 42 handshakes disequilibrated many students and sparked genuine public debate, leading them to attend more deeply to how elements of the desired set of outcomes are characterized.

WoT: (SOWoT) One’s solution to a counting problem depends on their interpretation and definition of a desirable outcome.

Teaching Practices: Elevating and handling opposing WoU; Attending to encoding schemes in a representation; Facilitating public debate.

5.3.3 Vignette 9: interpreting representations through structured physical enactment

After the events of vignette 8, Ms. M returned to Dani’s representation of part (a) of the Handshake problem, which originally concluded that 42 handshakes took place (see Fig. 14).

Fig. 14

Dani’s representation

Ms. M had 7 students come to the front of the room, labeled them with the numbers 1 through 7, and asked person 1 to act out what they saw in Dani’s tree. They shook everyone else’s hand in numerical order, after which Ms. M asked person 2 to continue the enactment. As person 2 shook hands with person 1, Ms. M paused the action to focus on the distinction between the number of hands being shaken and the number of handshakes occurring in the moment.

Ms. M: How many hands are being shaken right now?

Class: Two.

Ms. M: But how many handshakes are occurring?

Class: One.

Ms. M used this instance to institutionalize the WoU that a handshake is defined as an action occurring between two individual objects (hands), and the structural relationship entailed by this interpretation that the number of hands shaken is twice the number of handshakes. She reinforced this as person 2 continued to shake hands:

Ms. M: Go on through. Let’s count the number of hands that are shaken. We got two more, and then we got two more… [increments by two for every handshake]. So, how many hands were shaken? Individual little hands. We can count [person 2’s] hand more than once.

Class: 12.

Ms. M: And how many handshakes occurred?

Class: 6.

After further discussion about Dani’s representation, Ms. M elevated Benny’s direct counting approach represented by a different tree diagram (see Fig. 15).

Fig. 15

Benny’s representation

Again, Ms. M asked 7 students (labeled 1–7) to physically enact their interpretation of this representation. After person 1 had shaken hands with everyone else in numerical order, Ms. M asked:

Ms. M: Where should [person 1] go?

Class: [They should] sit down.

The externalization of Benny’s structured way to count handshakes through physical enactment created an experience that could be taken-as-shared by the class (Cobb et al., 1992). As the enactment continued similarly, Lori—who was previously counting the number of hands shaken—declared, “Oh! I get it”, and began to adjust her representation. Her comment sparked spontaneous conversations among students seated in small groups around the room as others also shifted their interpretations. Ms. M subsequently asked Lori to present her adjusted approach; in her presentation, she directly connected the physical enactments with her own representation (see Fig. 16).

Fig. 16

Lori’s representation of part (a) of the Handshake problem

Ms. M: Why did you need to divide 42 by 2 to get the 21 total handshakes?

Lori: Because there’s two people shaking hands and like how the people were in the front… you’re not going to shake everyone’s hand twice. It’s like eliminating that half.

Ms. M: So you’re eliminating the duplicates.

Lori: Yeah.

MM: Because we decided it’d be weird if I shake John’s hand, and then 30 seconds later, [John shakes my hand].

This demonstrates that, and how, Ms. M’s teaching action of asking students to interpret representations through physical enactment led Lori to recognize and account for double-counted handshakes. We characterize Lori’s approach as a case of adjusting for an unplanned overcount stemming from a shift in her interpretation of the desirable set of outcomes. This is in contrast to vignettes 6 and 10, where students anticipate and compensate for intentional overcounting.

By engaging students in physical enactments of their representations and pausing at key moments, Ms. M distinguished a handshake as separate from, but related to, the individual hands being shaken, established the structural relationship between the number of hands shaken and the number of handshakes, and institutionalized her definition of a desirable outcome. Her teaching practices promoted a SOWoT through attending to the connections between multiple interpretations of the problem and their induced sets of outcomes. This was a successful endeavor, as students were able to identify and compensate for overcounting to answer part (a) of the Handshake problem.

WoT: (SOWoT) Different solutions to a counting problem can sometimes be related through their definitions of a desired outcome; (Beliefs) Counting problems can be solved in more than one way

Teaching Practices: Institutionalizing particular WoU; attending to the meaning of outcomes in a requested physical enactment of a representation

5.3.4 Vignette 10: connecting the domino and handshake problems

After having students work through parts (b) and (c) of the Handshake problem, Ms. M asked Rebecca to present her solution to part (c) of the Handshake problem, which we characterize as employing an overcounting process and a PPG justification.

Rebecca: $x$ is the number of people and $y$ is the number of handshakes and from this table I color coded so you know which parts the equation comes from. [Motioning to the numbers across the top and left] This is the first person and this is the second person and it’s from 1 through 7… I think of this as a square. I square it to find the area. Highlighted in yellow [pointing to the upper-triangular region], those are duplicate handshakes. For example, [pointing at entry 1–2] person 1 shakes hands with person 2. Person 2 shakes hands with person 1 and I don’t want that. So that’s why [sic] the divide by 2 comes from. And in pink [motioning along the main diagonal], those are the doubles and I need to subtract that because person 2 can’t shake his own hand. And highlighted in primrose [pointing to the lower-triangular region], is the total number of handshakes. That’s what the $y$ is. For example, for 7, [if] I plug in 7 for $x$… [then] $y=21$.

Rebecca went on to call out commonalities and differences in the underlying structures of the sets of outcomes of the two problems, and in doing so observed how the Domino and Handshake problems are analogous:

Rebecca: Now this should look familiar to you because, compare this equation to the Domino problem. There are a couple of differences. For the Handshake [problem] $x$ is the number of people and for this one [pointing to Domino problem] $x$ is the number of dots plus a blank… I’m adding $x$ [pointing to $\frac{{x}^{2} + x}{2}$] because there can be doubles [motioning along the main diagonal], but in [the Handshake problem] a person can not shake his own hand.

Rebecca was grounded in sets of outcomes analogous to ${U}_{n}$, ${D}_{n}$, ${L}_{n}$, and ${T}_{n}$ (as defined in vignette 4), and drew parallels between her formula and Gabby’s formula (from vignette 5), noting their similar algebraic structure but explaining the differences in operations used. We also note that her representation of outcomes was analogous to that of Fig. 7 from vignette 4, and her overcounting process was analogous to that of Gabby’s solution (of the Domino problem).

Furthermore, Rebecca clearly anticipated and compensated for overcounting by leveraging geometric features of her representation (e.g. area of a square and symmetry in her tables) to include and subsequently account for instances of shaking one’s own hand and double-counted handshakes, and in doing so, she justified each operation used in her formula. Through including and compensating for the undesirable outcomes where people shake their own hands in the diagonal of the table and formula in Fig. 17a, b, she turned an unfamiliar structure into a familiar one to draw an analogy between the Domino and Handshake problems. We also note that she leveraged a small case to make conclusions about a general case, by attending to what remained invariant as the number of people increased (see Fig. 18).

Fig. 17

a Rebecca’s representation of part (c) of the Handshake problem. b A recreation of (a) for clarity

Fig. 18

Rebecca comparing the Domino and Handshake problems

In this way, Rebecca evidenced an internalization of Gabby’s solution, PPG, and a well-developed SOWoT. We see Rebecca’s spontaneous and fluid connections between formulas, counting processes, and sets of outcomes across different contexts as an example illustrating that, and how Ms. M found success in shaping students’ WoT associated with the mental acts of counting, interpreting, representing, generalizing, structuring, and justifying, and in particular a SOWoT.

WoT: (SOWoT) Overcounting processes can be effective ways to count; (PPG) Transforming an unfamiliar structure into a familiar one.

Teaching Practices: Soliciting a WoU that uncovered common structural elements between problems.

6 Discussion

We begin with a brief summary of our results, and structure the rest of our discussion thematically.

Summary The goal of the study was to examine WoT that can be advanced with students as they engage in counting problems, and teaching practices that can be used to elicit those WoT. We found that through her handling of the Domino and Handshake problems, Ms. M advanced three major clusters of WoT: SOWoT, PPG, and beliefs about mathematics. In our vignettes, we highlighted many of Ms. M’s teaching practices which contributed to eliciting these WoT, including asking for and leveraging both student presentations of multiple WoU and physical enactments, asking students to justify their reasoning, attending to students’ intellectual needs, and repeatedly elevating solutions involving PPG.

Relationships between clusters of WoT While we have grouped each WoT Ms. M advanced in our vignettes under one of three seemingly separate clusters, we emphasize these are interrelated through the idea that advancing a SOWoT can be mutually supportive of other WoT: In the process of strategically attending to the meaning of and relationships between different sets of outcomes, Ms. M advanced a variety of WoT connecting counting with other mental acts, including representing, justifying, organizing/structuring, and interpreting (and in doing so, also elevated the belief that problem-solving can entail multiple mental acts). In particular, PPG was vividly manifested during instances where students employed overcounting processes as a response to requests for justification of a formula, and in an attempt to share perceived structural similarities between problems.

Valuable teaching practices Ms. M frequently solicited presentations from students with PPG solutions useful in connecting sets of outcomes, counting processes, and formulas. During several such presentations, class members exhibited a desirable change in WoU, indicating how this was a successful teaching practice. This illustrates how PPG can serve as both a targeted WoT and a useful criteria for selecting presenters due to its explanatory power (Hersh, 1993). Ms. M also implemented the necessity principle in several instances and in several forms, through teaching practices such as facilitating public debate and requesting physical enactment. Her requests for physical enactment in the Handshake problem in particular advanced students’ SOWoT through attention to the structural relationship between two different interpretations of the definition of a desired outcome, showing the efficacy of this teaching practice. It can be difficult for teachers to attend to students’ intellectual needs: Problematic situations can arise spontaneously, and a teacher needs to decide in the moment which goals to pursue. Attempting to implement the necessity principle can be an act of bravery for many teachers and expresses a deep commitment to rehumanizing mathematics.

Rehumanizing mathematics We wish to elevate how Ms. M rehumanized mathematics (in the sense of Gutiérrez, 2018) for her students throughout these episodes. She sought to create robust learning opportunities using the cognitive tools students brought to her classroom, centering classroom discussion around student-created representations, and working to build shared understanding and appreciation of each others' WoU. In the Handshake problem, she used physical enactment to create a shared experience of mathematical ideas by helping students externalize their conceptualizations of handshaking processes. She also sought out and elevated alternative interpretations of the problem statement, and used them to spark public debate. Taken together, these teaching practices advanced students’ belief that mathematical knowledge is co-constructed by groups of people through problem-solving. These observations are consistent with Heinzman’s (2020) findings in interviews with a different discrete mathematics class Ms. M taught the following year, where students reported an improved sense of self-efficacy, agency, and belonging compared to their prior experiences learning mathematics.

The value of the Domino and Handshake problems While both the Domino and Handshake problems were in the discrete mathematics curriculum, Ms. M made active choices to bring these problems to her students, and in her handling of student solutions. In this light, we wish to discuss characteristics of these problems, and the value afforded by these characteristics in Ms. M’s classroom: The concrete nature of the first two parts of both problems provided opportunities to engage students in other mental acts in support of counting, including representing, interpreting, and structuring. The general nature of the last part of each problem also made them both amenable to pattern generalizing. In particular, the opportunity to attend to and count sets of outcomes using geometric structures encouraged mathematical thinking spanning domains (geometry, algebra, and counting). Finally, as a pair, the two problems were analogues, which encouraged discussion of the structural relationship between them. Not all counting problems are closely related to each other, nor do they all call for generalization. Nevertheless, we have demonstrated how, with careful instructional decisions, teachers can use enumeration tasks with these characteristics to advance desirable WoT in K-12 classrooms.

Conclusion This study gives us a better sense of the wealth and depth of WoT that can be advanced through the teaching of enumerative combinatorics, and teaching practices that can contribute to eliciting these WoT. In doing so, we act on the call for further research into and provide further evidence substantiating two of the five assertions about combinatorics cited by Lockwood et al. (2020): Specifically, our investigation into the WoT Ms. M advanced furthers the assertion that combinatorics fosters desirable mathematical practices, and our investigation of Ms. M’s teaching practices furthers the understanding of how combinatorics problems provide opportunities for rich mathematical thinking.

Our results suggest further investigation along several axes: They provide motivation to find instructional interventions leveraging other mental acts in support of counting, and determine whether such interventions are effective for advancing students’ WoT about counting. Additionally, they suggest the need to further explore how rich counting tasks like the Domino and Handshake problems can be more fully integrated throughout the K-12 curriculum, and how we can shape teacher professional training to guide them in leveraging the opportunities these problems afford to advance desirable WoT. Finally, they suggest the investigation of the mathematical WoT that can be advanced through the teaching of other discrete mathematics topics in the secondary classroom.