Finite Tree-Countermodels via Refutation Systems in Extensions of Positive Logic with Strong Negation

Abstract

A sufficient condition for an extension of positive logic with strong negation to be characterized by a class of finite trees is given.

1 Introduction

In this paper, extensions of positive logic with strong negation are studied. We give a sufficient condition (called the reduction property) for the completeness of such a logic with respect to the class of finite trees. The condition (implicitly) involves a certain refutation system employing Mints-style normal forms, and it generalizes some results in [5, 6]. Our completeness proof is constructive. As an example, the method is applied to the connexive logic C (introduced in [7]), an important non-classical logic.

2 Preliminaries

Let FOR be the set of all formulas generated from the set $\textsf{VAR}=\{p,q,p_1,p_2,\ldots \}$ of propositional variables by the connectives:

$\sim$ (strong negation), $\wedge$ (conjunction), $\vee$ (disjunction), $\rightarrow$ (implication).

Greek capital letters ($\Phi ,\Psi ,\ldots$) stand for finite sets of formulas. A literal is either a or $\sim \! a$, where $a\in \textsf{VAR}$. We define: $\varphi \leftrightarrow \psi =(\varphi \rightarrow \psi )\wedge (\psi \rightarrow \varphi )$ and $\varphi \Leftrightarrow \psi = (\varphi \leftrightarrow \psi )\wedge (\sim \!\psi \leftrightarrow \sim \!\varphi )$. Also $\Phi \longrightarrow \Psi =\bigwedge \Phi \rightarrow \bigvee \Psi$, where $\Psi \not =\emptyset$. (If $\Phi =\emptyset$ then $\bigwedge \Phi =p\rightarrow p$.) We write: “$\Phi ;\Psi$” for “$\Phi \cup \Psi$” and “$\Phi ;\psi$” for “$\Phi ;\{\psi \}$”.

Positive (Intuitionistic) Logic (Lp) is the set of all $\sim$-free formulas that are derivable from the axioms below by modus ponens ($\frac{\varphi \hspace{1em}\varphi \rightarrow \psi }{\psi }$).

• (Ax1) $\varphi \rightarrow (\psi \rightarrow \varphi )$

• (Ax2) $(\varphi \rightarrow (\psi \rightarrow \chi ))\rightarrow ((\varphi \rightarrow \psi )\rightarrow (\varphi \rightarrow \chi ))$

• (Ax3) $(\varphi \wedge \psi )\rightarrow \varphi$

• (Ax4) $(\varphi \wedge \psi )\rightarrow \psi$

• (Ax5) $(\varphi \rightarrow \psi )\rightarrow ((\varphi \rightarrow \chi )\rightarrow (\varphi \rightarrow (\psi \wedge \chi )))$

• (Ax6) $\varphi \rightarrow (\varphi \vee \psi )$

• (Ax7) $\psi \rightarrow (\varphi \vee \psi )$

• (Ax5) $(\varphi \rightarrow \chi )\rightarrow ((\psi \rightarrow \chi )\rightarrow ((\varphi \vee \psi )\rightarrow \chi ))$

By an extension of Lp we mean a set $\textbf{L}\subseteq \textsf{FOR}$ closed under subsitution and modus ponens and such that $\textbf{Lp}\subseteq \textbf{L}$. Extensions of Lp will also be called logics. We say that $\varphi$ is L-equivalent to $\psi$ iff $\varphi \leftrightarrow \psi \in \textbf{L}$.

A frame is a pair ${{{\mathcal {W}}}}=(W,R)$, where W is a non-empty set of points (worlds) and R is a reflexive, transitive relation on W. A model is a triple ${{{\mathcal {M}}}} = ({{{\mathcal {W}}}},V^+,V^-)$, where ${{\mathcal {W}}}$ is a frame and $V^+$ $(V^-)$ is a verification (falsification) valuation (that is, a function assigning to a propositional variable a the set of points at which a is true (false)) that satisfies the persistency condition: If $w\in V^+(a)$ ($w\in V^-(a)$) and wRx, then $x\in V^+(a)$ ($x\in V^-(a)$). The verification and falsification relations ($\models ^+$ and $\models ^-$) between ${{\mathcal {M}}}$ worlds and formulas are defined as follows.

${{{\mathcal {M}}}},w\models ^+a$ iff $w\in V^+(a)$   ${{{\mathcal {M}}}},w\models ^-a$ iff $w\in V^-(a)$ $(a\in \textsf{VAR})$

${{{\mathcal {M}}}},w\models ^+\varphi \wedge \psi$ iff ${{{\mathcal {M}}}},w\models ^+\varphi$ and ${{{\mathcal {M}}}},w\models ^+\psi$

${{{\mathcal {M}}}},w\models ^-\varphi \wedge \psi$ iff ${{{\mathcal {M}}}},w\models ^-\varphi$ or ${{{\mathcal {M}}}},w\models ^-\psi$

${{{\mathcal {M}}}},w\models ^+\varphi \vee \psi$ iff ${{{\mathcal {M}}}},w\models ^+\varphi$ or ${{{\mathcal {M}}}},w\models ^+\psi$

${{{\mathcal {M}}}},w\models ^-\varphi \vee \psi$ iff ${{{\mathcal {M}}}},w\models ^-\varphi$ and ${{{\mathcal {M}}}},w\models ^-\psi$

${{{\mathcal {M}}}},w\models ^+\varphi \rightarrow \psi$ iff for all x with wRx (${{{\mathcal {M}}}},x\models ^+\varphi$ implies ${{{\mathcal {M}}}},x\models ^+\psi$)

${{{\mathcal {M}}}},w\models ^-\varphi \rightarrow \psi$ iff for all x with wRx (${{{\mathcal {M}}}},x\models ^+\varphi$ implies ${{{\mathcal {M}}}},x\models ^-\psi$)

${{{\mathcal {M}}}},w\models ^+\,\sim \varphi$ iff ${{{\mathcal {M}}}},w\models ^-\varphi$

${{{\mathcal {M}}}},w\models ^-\,\sim \varphi$ iff ${{{\mathcal {M}}}},w\models ^+\varphi$

We say that a formula $\varphi$ is valid in a frame ${{\mathcal {W}}}$ (in symbols $\varphi \in \textsf{VAL}({{{\mathcal {W}}}}))$ iff for every model ${{{\mathcal {M}}}}=({{{\mathcal {W}}}},V^+,V^-)$ and $w\in W$, we have: ${{{\mathcal {M}}}},w\models ^+\varphi$.

The condition for “${{{\mathcal {M}}}},w\models ^-\varphi \rightarrow \psi$” is that for the logic C. However, it can be replaced with some other standard condition because it is not really used in our general result.

For convenience, we say that a set $\Phi$ of formulas is (not) true at w iff so is every $\varphi \in \Phi$.

The one-point frame $\circ =(\{x_0\},(x_0,x_0))$ will be especially important. We also write “$m=(\circ ,v^+,v^-)$” instead of “$(\circ ,V^+,V^-)$”, and “$m\models \varphi$” instead of “$m,x_0\models \varphi$”, where $\models \in \{\models ^+,\models ^-\}$.

We say that a logic L is complete with respect to a class W of frames (or L is characterized by W) iff $\textbf{L}=\bigcap \{\textsf{VAL}({{{\mathcal {W}}}}): {{{\mathcal {W}}}}\in \textbf{W}\}$.

We assume that every logic defined by an axiom system has a general characterization by a class $\textbf{W}_\textbf{L}$ of (possibly infinite) frames obtained by using canonical models (see e.g. [3]). The frames in $\textbf{W}_\textbf{L}$ are also referred to as L-frames.

By a generated frame we mean a frame ${{\mathcal {W}}}$ with a least point x (that is, xRy for all $y\in W$).

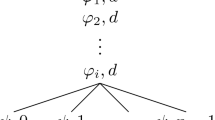
Let ${{{\mathcal {W}}}}_i$ be an $x_i$-generated frame $(1\le i\le k)$. Then $x_0({{{\mathcal {W}}}}_1,\ldots ,{{{\mathcal {W}}}}_k)$ is the $x_0$-generated frame shown below. (It is obtained from ${{{\mathcal {W}}}}_1,\ldots ,{{{\mathcal {W}}}}_k$ by adding a new root, and it resembles Jaśkowski’s construction from S. McCall, Polish Logic: 1920–1939.)

In this paper, we focus on the logics satisfying the following condition.

If generated frames ${{{\mathcal {W}}}}_1,\ldots ,{{{\mathcal {W}}}}_k$ are L-frames, then so is $x_0({{{\mathcal {W}}}}_1,\ldots ,{{{\mathcal {W}}}}_k)$.

In that case, we also say that $\textbf{W}_\textbf{L}$ is root-closed.

3 Normal Forms

Definition 3.1

A general form (cf. [1, 5]) is a formula

$$\begin{aligned} \alpha = \Delta ;\Gamma \longrightarrow \Theta \end{aligned}$$

where

$$\begin{aligned} \Delta = \{(a_i\rightarrow b_i)\rightarrow c_i: 1\le i\le k\} \quad (\text{ or } \Delta =\emptyset ) \end{aligned}$$

all $a_i,b_i,c_i$ are literals, $\Gamma$ is a finite set of formulas of the kind:

a or $a\rightarrow b$ or $a\rightarrow (b\rightarrow c)$ or $a\rightarrow b\vee c$, where a, b, c are literals, and $\Theta$ is a finite, nonempty set of literals.

The rank $r(\alpha )$ of $\alpha$ is k, which is the size of $\Delta$. (If $\Delta =\emptyset$ then $k=0$.)

Definition 3.2

A normal form is a general form such that:

If $a\rightarrow \gamma \in \Gamma$ then $a\in \Theta$.

Definition 3.3

Let $\alpha$ be a normal form. An L-model $(\circ , v^+,v^-)$ is called determined by $\alpha$ (symbolically, $m(\alpha )=(\circ , v^+,v^-))$ iff

$x_0\in v^+(\varphi )$ iff $\varphi \in \Gamma$, and $x_0\in v^-(\varphi )$ iff $\sim \!\varphi \in \Gamma$ ($\varphi \in \textsf{VAR}$).

Definition 3.4

An L special normal form is a normal form $\alpha$ (so $\alpha =\Delta ;\Gamma \longrightarrow \Theta$) with the property that $m(\alpha )\not \models ^+\alpha _0$, where $\alpha _0=\Gamma \longrightarrow \Theta$. (Recall that $m(\alpha )\models ^+\varphi$ stands for $m(\alpha ),x_0\models ^+\varphi$).

4 L Refutation System

The refutation system $\textbf{R}_\textbf{L}$ is defined as follows.

• Refutation axioms: All L special normal forms of rank 0.

• Refutation rules:

  Normalization rules: (Here $\Psi \not =\emptyset$).

  $$\begin{aligned}&{} \frac{\textstyle \varphi ;\Phi \longrightarrow \Psi }{\textstyle \varphi \vee \psi ;\Phi \longrightarrow \Psi }\hspace{2em} \frac{\textstyle \psi ;\Phi \longrightarrow \Psi }{\textstyle \varphi \vee \psi ;\Phi \longrightarrow \Psi }(R^{\vee }) \\{}&{} \frac{\textstyle \psi ;\Phi \longrightarrow \Psi }{\textstyle \varphi \rightarrow \psi ;\Phi \longrightarrow \Psi }\hspace{2em} \frac{\textstyle \varphi \rightarrow \psi ;\Phi \longrightarrow \Psi ;\varphi }{\textstyle \varphi \rightarrow \psi ;\Phi \longrightarrow \Psi }(R^{\rightarrow }) \end{aligned}$$

  Normal-form rules:

  $$\begin{aligned} \frac{\textstyle \alpha _1\ldots \alpha _k}{\textstyle \alpha }(R_\textbf{L})\hspace{2em} \frac{\textstyle \beta _i}{\textstyle \alpha }(R_i) \end{aligned}$$

  where $\alpha (=\Delta ;\Gamma \longrightarrow \Theta )$ is an L special normal form of rank $k>0$, and $\alpha _i=\Delta _i^-;b_i\rightarrow c_i;\Gamma ;a_i\longrightarrow b_i$, $\beta _i=\Delta _i^-;c_i;\Gamma ;(a_i\rightarrow b_i)\longrightarrow \Theta$, $\Delta _i^-=\Delta -\{(a_i\rightarrow b_i)\rightarrow c_i\}\hspace{1em} (1\le i\le k)$.

We say that a formula $\varphi$ is refutable (in symbols $\dashv \varphi$) iff $\varphi$ is derivable from refutation axioms by refutation rules. And we say that a logic L is $\textbf{R}_\textbf{L}$-complete iff for every normal form $\alpha$, we have: Either $\alpha \in \textbf{L}$ or $\dashv \alpha$.

Remark 4.1

Since $\textbf{Lp}\subseteq \textbf{L}$, we have:

• (i) The rule $R_i$ and all normalization rules have the property that $\varphi \rightarrow \psi \in \textbf{L}$, where $\psi$ is the premise and $\varphi$ is the conclusion.

• (ii) Every formula $\alpha _i$ is L-equivalent to $\Delta ;\Gamma \longrightarrow (a_i\rightarrow b_i)$.

• (iii) Every formula $\beta _i$ is L-equivalent to $\Delta ;\Gamma ;(a_i\rightarrow b_i)\longrightarrow \Theta$.

Definition 4.2

A formula $\varphi$ is L-reducible to a finite set $\Psi$ of formulas iff

• (i) $\Psi \longrightarrow \varphi \in \textbf{L}$.

• (ii) $\varphi$ is derivable from each $\psi \in \Psi$ by the normalization rules.

Corollary 4.3

If $\varphi$ is L-reducible to $\Psi$, then $\varphi \rightarrow \psi \in \textbf{L}$ for each $\psi \in \Psi$.

5 The Reduction Property

Definition 5.1

A logic L has the reduction property iff we have:

• 1. For any formula $\varphi$, there is a general form $\alpha _{\varphi }$ such that: $\varphi \rightarrow \alpha _{\varphi }\in \textbf{L}$, and if $\alpha _{\varphi }\in \textbf{L}$ then $\varphi \in \textbf{L}$.

• 2. Every general form $\alpha$ of rank k is L-reducible to some normal forms $\alpha _1,\ldots ,\alpha _n$ of rank k.

• 3. Let $\alpha$ be a normal form. If $m(\alpha )\models ^+\alpha _0$, then $\alpha _0\in \textbf{L}$.

Theorem 5.2

If a logic L has the reduction property, then L is $\textbf{R}_\textbf{L}$-complete.

Proof

Assume that L has the reduction property. We show, by induction on the rank of a normal form $\alpha$, that either $\alpha \in \textbf{L}$ or $\dashv \alpha$.

• (1) $k=0$. Then $\alpha =\alpha _0 =\Gamma \longrightarrow \Theta$.

Consider the model $m(\alpha )$. Either $m(\alpha )\models ^+ {\alpha }_0$ or $m(\alpha )\not \models ^+ {\alpha }_0$. If $m(\alpha )\models ^+\alpha _0$ then $\alpha _0\in \textbf{L}$ (by Definition 5.1(3)), so $\alpha \in \textbf{L}$. And if $m(\alpha )\not \models ^+\alpha _0$ then $\alpha$ is an L special normal form of rank 0, which is a refutation axiom, so $\dashv \alpha$. Hence, $\alpha \in \textbf{L}$ or $\dashv \alpha$.

• (2) $k>0$ and we assume that the theorem is true for normal forms of rank $<k$. Then $\alpha =\Delta ;\Gamma \longrightarrow \Theta$ and $\Delta \not =\emptyset$.

Consider the general forms $\alpha _i,\beta _i$ ($1\le i\le k$). They are of rank $<k$. By Definition 5.1(2), each of them is L-reducible to some normal forms of rank $<k$, which (by the induction hypothesis) are in L or refutable. So, all $\alpha _i,\beta _i$ are also in L or refutable (by Definition 4.2).

If some $\beta _i$ is refutable, then so is $\alpha$ (by $R_i$), so we assume that every $\beta _i\in \textbf{L}$. Then, the formula $\Delta ;\Gamma ;(a_i\rightarrow b_i)\longrightarrow \Theta$ is in L as well (by Remark 4.1(iii)). Now, if some $\alpha _i\in \textbf{L}$, then the formula $\Delta ;\Gamma \longrightarrow (a_i\rightarrow b_i)$ is in L, so it follows that $\alpha \in \textbf{L}$, and so we may assume that each $\alpha _i$ is refutable. Also, either $m(\alpha )\models ^+ {\alpha }_0$ or $m(\alpha )\not \models ^+ {\alpha }_0$. If $m(\alpha )\models ^+ {\alpha }_0$ then $\alpha _0\in \textbf{L}$ (by Definition 5.1(3)), so $\alpha \in \textbf{L}$. And if $m(\alpha )\not \models ^+ {\alpha }_0$ then $\alpha$ is an L special normal form, so $\dashv \alpha$ (by R).

Therefore, either $\alpha \in \textbf{L}$ or $\dashv \alpha$, as required. $\square$

6 $\textbf{R}_\textbf{L}$ Refutation Trees

The derivations in $\textbf{R}_\textbf{L}$ can be presented as refutation trees. By an $\textbf{R}_\textbf{L}$ refutation tree for a formula $\varphi$ we mean a finite immediate-successor tree ${\mathcal{R}\mathcal{T}}$ whose nodes are labelled with formulas and which satisfies the following conditions. (For any node x in ${\mathcal{R}\mathcal{T}}$, $\varphi (x)$ is the label of x).

• $\varphi$ is the label of the origin $x_0$.

• If x is an end node, then $\varphi (x)$ is an $\textbf{R}_\textbf{L}$ axiom.

• If $x_1,\ldots ,x_n$ are the immediate successors of a node x, then $\varphi (x)$ is obtained from $\varphi (x_1),\ldots ,\varphi (x_n)$ by an $\textbf{R}_\textbf{L}$ rule.

7 Finite Tree-Countermodels

Recall that a logic is an extension of Lp such that its general characterization $\textbf{W}_\textbf{L}$ is root-closed. By modifying some results in [4], we now transform refutation trees into countermodels.

Let ${\mathcal{R}\mathcal{T}}$ be an $\textbf{R}_\textbf{L}$ refutation tree for a normal form $\alpha$. We construct a finite tree-countermodel $({{{\mathcal {T}}}},V^+,V^-)$ as follows.

• First, we define the finite, reflexive, transitive tree ${\mathcal{R}\mathcal{T}}^{\uparrow }_{\circ }$ by taking the reflexive, transitive closure of the irreflexive, intransitive relation in ${\mathcal{R}\mathcal{T}}$.

• Second, we delete all nodes in ${{\mathcal{R}\mathcal{T}}}^{\uparrow }_{\circ }$ that are obtained by $R_i$ or a normalization rule, getting the subtree ${{\mathcal {T}}}$ of ${{\mathcal{R}\mathcal{T}}}^{\uparrow }_{\circ }$. Note that every node in ${{\mathcal {T}}}$ is either an end node or a node obtained by $R_\textbf{L}$, so the label of each node in ${{\mathcal {T}}}$ is an L special normal form.

• Third, we define valuations $V^+,V^-$ thus.

  $x\in V^+(\varphi )$ iff $\varphi \in \Gamma$, and $x\in V^-(\varphi )$ iff $\sim \!\varphi \in \Gamma$ ($\varphi \in \textsf{VAR}$).

  By inspecting the refutation rules, we can see that if y is a successor of x in ${{\mathcal {T}}}$, then a literal is in $\Phi '$ whenever it is in $\Phi$, where $\varphi (x)=\Phi \longrightarrow \Psi$ and $\varphi (y)=\Phi '\longrightarrow \Psi '$. So, the persitency condition is satisfied. Let ${{{\mathcal {M}}}}=({{{\mathcal {T}}}},V^+,V^-)$.

  Note that for any literal a, we have: ${{{\mathcal {M}}}},x_0\models ^+ a$ iff $m(\alpha )\models ^+ a$.

• Finally, for any node x in ${\mathcal{R}\mathcal{T}}$, we define its world $x^{\star }$ in ${{\mathcal {T}}}$ as follows. If x is an end node or obtained by $R_\textbf{L}$, then $x^{\star }=x$; and if x is obtained from $x_1$ by $R_i$ or a normalization rule, then $x^{\star }= x_1^{\star }$.

Lemma 7.1

If x is a node in ${\mathcal{R}\mathcal{T}}$, then $\varphi (x)$ is not true at $x^{\star }$.

Proof

(by induction on the number $n_x$ of nodes in the subtree of ${\mathcal{R}\mathcal{T}}$ generated by x).

• (1) $n_x=1$. Then $\varphi (x)$ is a refutation axiom, which is an L special normal form $\Gamma \longrightarrow \Theta$ (so $m(\alpha )\not \models ^+\alpha _0$). Since $x^{\star }=x$, we have: $\varphi (x^{\star })=\varphi (x)$. Hence, ${{{\mathcal {M}}}},x^{\star }\models ^+ a$ for every literal $a\in \Gamma$. Note that if $a\rightarrow \gamma \in \Gamma$ then $a\not \in \Gamma$ (otherwise, $a\in \Theta$ (because $\varphi (x)$ is a normal form) and $m(\alpha )\models ^+\alpha _0$, which is impossible). Thus, ${{{\mathcal {M}}}},x^{\star }\models ^+ a\rightarrow \gamma$ for all $a\rightarrow \gamma \in \Gamma$. Therefore ${{{\mathcal {M}}}},x^{\star }\not \models ^+\varphi (x)$.

• (2) $n_x>1$ and we assume that the theorem holds for the subtrees with fewer elements than $n_x$.

  • (2.1) $\varphi (x)$ is obtained from $\varphi (x_1)$ by $R_{i}$ or a normalization rule. Then $x^{\star }=x^{\star }_1$. Since $n_{x_1}<n_x$, by the induction hypothesis, $\varphi (x_1)$ is not true at $x^{\star }_1$. Hence $\varphi (x_1)$ is not true at $x^{\star }$. So, by Remark 4.1(i), $\varphi (x)$ is not true at $x^{\star }$ (because $\varphi (x)\rightarrow \varphi (x_1)$ is true everywhere).

  • (2.2) $\varphi (x)$ is obtained from $\varphi (x_1),\ldots ,\varphi (x_k)$ by $R_\textbf{L}$. Then $\varphi (x)=\Delta ;\Gamma \longrightarrow \Theta$ is an L special normal form of rank $k>0$, and $\varphi (x_i)=\Delta _i^-;b_i\rightarrow c_i;\Gamma ;a_i\longrightarrow b_i$ ($1\le i\le k$). Also

$x^{\star }=x$ (so $\varphi (x^{\star })=\varphi (x)$) and $n_{x_i}<n_x$ for all i. By the induction hypothesis, $\varphi (x_i)$ is not true at $x^{\star }_i$ ($1\le i\le k$), so $\Delta ;\Gamma \longrightarrow (a_i\rightarrow b_i)$ is not true at $x^{\star }_i$ ($1\le i\le k$) (by Remark 4.1(ii)). Hence, every $a_i\rightarrow b_i$ is not true at $x^{\star }_i$ and $\Delta ;\Gamma$ is true at each $x^{\star }_i$. So, every $a_i\rightarrow b_i$ is not true at $x^{\star }$ (because $x^{\star }$ precedes every $x^{\star }_i$). Also, $\Delta ;\Gamma$ is true at all $x^{\star }_i$, so $\Delta$ is true at $x^{\star }$ and every $a\rightarrow \gamma \in \Gamma$ is true at $x^{\star }$ (see (1) above). Of course, every literal in $\Gamma$ is true and $\Theta$ is not true at $x^{\star }$.

Therefore $\varphi (x)$ is not true at $x^{\star }$, as required. $\square$

Theorem 7.2

If a logic L has the reduction property, then L is characterized by the class of finite, reflexive, transitive trees.

Proof

Assume that L has the reduction property, and assume that $\varphi \not \in \textbf{L}$. Then, (by Definition 5.1(1)) its general form $\alpha _{\varphi }\not \in \textbf{L}$, and (by Definition 5.1(2)) $\alpha \not \in \textbf{L}$ for some normal form $\alpha$. So, by Theorem 5.2, $\alpha$ is refutable. Hence, by Lemma 7.1, $\alpha$ is not true at some point in some model based on a finite, reflexive, transitive tree. Thus, $\varphi$ is not true there either (because, by Corollary 4.3, $\varphi \rightarrow \alpha$ is true everywhere). Therefore, $\varphi$ is not valid in some finite, reflexive, transitive tree, which gives the result. $\square$

8 Example

The connexive logic C was introduced in [7] as the extension of Lp by the following axioms.

• (Ax 9) $\sim \!\sim \!\varphi \leftrightarrow \varphi$

• (Ax10) $\sim \!(\varphi \wedge \psi )\leftrightarrow (\sim \!\varphi \vee \sim \!\psi )$

• (Ax11) $\sim \!(\varphi \vee \psi )\leftrightarrow (\sim \!\varphi \wedge \sim \!\psi )$

• (Ax12) $\sim \!(\varphi \rightarrow \psi )\leftrightarrow (\varphi \rightarrow \sim \!\psi )$

Our refutation system $\textbf{R}_\textbf{C}$ is obtained from [5, 6] by the following straightforward modifications.

8.1 C Special Normal Forms

Proposition 8.1

$m(\alpha )\not \models ^+\alpha _0$ iff ${\Gamma }\cap \Theta =\emptyset$.

Proof

($\Rightarrow$) If ${\Gamma }\cap \Theta \not =\emptyset$, then $\alpha _0\in \textbf{C}$, so $\alpha _0$ is true everywhere, so there is no model on $\circ$ such that the formula $\alpha _0$ is not true.

($\Leftarrow$) Assume that ${\Gamma }\cap \Theta =\emptyset$. Then $m(\alpha )\not \models ^+\alpha _0$. $\square$

Corollary 8.2

A C special normal form is a normal form $\alpha$ such that ${\Gamma }\cap \Theta =\emptyset$.

8.2 The Reduction Property

Theorem 8.3

The logic C has the reduction property.

Proof

• 1. For any formula $\varphi$, the general form $\alpha _{\varphi }$ is constructed as follows.

  First, for every subformula $\psi$ of $\varphi$, we define a unique corresponding variable $a_{\psi }$ thus. If $\psi \in \textsf{VAR}$ then $a_{\psi }=\psi$, and if $\psi \not \in \textsf{VAR}$ then $a_{\psi }$ is a new variable.

  Second, we define the set $\Sigma _{\varphi }$ as follows.

  $$\begin{aligned} \Sigma _{\varphi }= & {} \{(a_{\psi _1}\otimes a_{\psi _2})\Leftrightarrow a_{\psi _1\otimes \psi _2}: \psi _1\otimes \psi _2\in \textsf{SUB}(\varphi ), \otimes \in \{\rightarrow ,\wedge ,\vee \}\}\\{} & {} \cup \{\sim \!\psi _1\Leftrightarrow a_{\sim \!\psi _1}: \sim \!\psi _1\in \textsf{SUB}(\varphi )\} \end{aligned}$$

  Third, we define: $\textsf{N}(\varphi ) = \Sigma _{\varphi }\longrightarrow a_{\varphi }$.

  Note that the Deduction Theorem and the Replacement Theorem below hold for C.

  $(\psi \Leftrightarrow \chi )\rightarrow (\varphi \Leftrightarrow \varphi (\psi /\chi ))$, where $\varphi (\psi /\chi )$ results from $\varphi$ by replacing some occurrences of $\psi$ with $\chi$.

  Thus (see [5]), it can be proved that

  $$\begin{aligned} \Sigma _{\varphi }\longrightarrow (\psi \Leftrightarrow a_{\psi })\in \textbf{C}\text { for any }\psi \in \textsf{SUB}(\varphi ). \end{aligned}$$

  Hence, in particular, $\Sigma _{\varphi }\longrightarrow (\varphi \Leftrightarrow a_{\varphi })\in \textbf{C}$, so $\Sigma _{\varphi }\longrightarrow (\varphi \rightarrow a_{\varphi })\in \textbf{C}$.

  Therefore, $\varphi \longrightarrow (\Sigma _{\varphi }\rightarrow a_{\varphi })\in \textbf{C}$, that is, $\varphi \longrightarrow \textsf{N}(\varphi )\in \textbf{C}$.

  Also, if $\textsf{N}(\varphi )\in \textbf{C}$ then $\varphi \in \textbf{C}$ (substitute $\psi$ for $a_{\psi }$).

  Finally, by using the axioms for $\sim$, we get the the general form $\alpha _{\varphi }$ C-equivalent to $\textsf{N}(\varphi )$, which gives the result.

• 2. Take any general form $\alpha$ of rank k. We have to show that $\alpha$ is C-reducible to some normal forms such that:

  ($*$) If $a\rightarrow \gamma \in \Gamma$ (so a is a literal), then $a\in \Theta$.

  Let $a\rightarrow \gamma \in \Gamma$, and let $\Gamma ^- =\Gamma -\{a\rightarrow \gamma \}$.

  Consider the C general forms

  $$\begin{aligned} \alpha ^1=\Delta ;\Gamma ^-;\gamma \longrightarrow \Theta \text { and }\alpha ^2=\Delta ;\Gamma \longrightarrow \Theta ;a \end{aligned}$$

  Of course, $\alpha ^1\wedge \alpha ^2\rightarrow \alpha \in \textbf{C}$. Also, $\alpha$ is dervable from both (so from some) $\alpha ^1,\alpha ^2$ by $R^{\rightarrow }$. Now, in $\alpha ^1$, we have $\gamma$ instead of $a\rightarrow \gamma$. If $\gamma$ is a literal, then the condition ($*$) is satisfied (because $a\rightarrow \gamma \not \in \Gamma ^-$). So assume that $\gamma$ is not a literal. Then $\gamma$ is either $b\vee c$ or $b\rightarrow c$, where b, c are literals.

  If $\gamma =b\vee c$ then we consider the general forms

  $$\begin{aligned} \alpha ^{1.1}=\Delta ;\Gamma ^-;b\longrightarrow \Theta \text { and } \alpha ^{1.2}=\Delta ;\Gamma ^-;c\longrightarrow \Theta \end{aligned}$$

  in which the $\rightarrow$-formula $a\rightarrow \gamma$ is eliminated. We have: $\alpha ^1\wedge \alpha ^2\rightarrow \alpha ^1\in \textbf{C}$, and $\alpha ^1$ is dervable from both (so from some) $\alpha ^{1.1},\alpha ^{1.2}$ by $R^{\vee }$. Hence, $\alpha$ is C-reducible to $\alpha ^{1.1},\alpha ^{1.2},\alpha ^2$, and $a\rightarrow \gamma$ satisfies the condition ($*$).

  And if $\gamma =b\rightarrow c$ then proceed as above, obtaining general forms in which $a\rightarrow \gamma$ satisfies the condition ($*$).

  Note that these transformations do not affect the rank k. Applying this procedure to the other $\rightarrow$-formulas in $\Gamma$, we, finally, get the result.

• 3. To prove that $m(\alpha )\models ^+\alpha _0$ implies $\alpha _0\in \textbf{C}$, suppose that $m(\alpha )\models ^+\alpha _0$ but $\alpha _0\not \in \textbf{C}$. Note that ${\Gamma }\cap \Theta =\emptyset$. (Otherwise $\alpha _0\in \textbf{C}$). Also, if $a\rightarrow \gamma \in \Gamma$ then $a\not \in \Gamma$ (because $\alpha$ is a normal form and $\alpha _0\not \in \textbf{C}$). Then $m(\alpha )\not \models ^+\alpha _0$, which is a contradiction.

$\square$

Corollary 8.4

• (i) C is $\textbf{R}_\textbf{C}$-complete.

• (ii) C is characterized by the class of finite, reflexive, transitive trees.

Remark 8.5

By straightforward modifications, similar results can be obtained for the connexive logic C3 (introduced in [2]).