Shape-based functional data analysis

Functional data analysis (FDA) is a fast-growing area of research and development in statistics. While most FDA literature imposes the classical $\mathbb {L}^2$ Hilbert structure on function spaces, there is an emergent need for a different, shape-based approach for analyzing functional data. This paper reviews and develops fundamental geometrical concepts that help connect traditionally diverse fields of shape and functional analyses. It showcases that focusing on shapes is often more appropriate when structural features (number of peaks and valleys and their heights) carry salient information in data. It recaps recent mathematical representations and associated procedures for comparing, summarizing, and testing the shapes of functions. Specifically, it discusses three tasks: shape fitting, shape fPCA, and shape regression models. The latter refers to the models that separate the shapes of functions from their phases and use them individually in regression analysis. The ensuing results provide better interpretations and tend to preserve geometric structures. The paper also discusses an extension where the functions are not real-valued but manifold-valued. The article presents several examples of this shape-centric functional data analysis using simulated and real data.

Comments on: Shape-based functional data analysis

Article 18 January 2024

Shape Analysis of Functional Data

On function-on-function regression: partial least squares approach

Article 07 January 2020

1 Introduction

Statistical analysis of functional data has become a prominent field of research and practice in recent years. The growing importance of this field stems from massive improvements in data collection, storage, and processing power, allowing one to view sampled data in near continuous time. Scientific, medical, and civilian domains provide many functional data types that require statistical tools for analysis and inferences. A prominent source of functional data in a modern digital society is visual, coming from cameras, imagers, and other sensors. Cameras have become a significant source for capturing information, especially in medicine, robotics, leisure, manufacturing, and bioinformatics. These devices produce a high volume of static images and video streams that can be viewed as functional variables with spatial and temporal indices. Analysis of such large data volumes requires modern statistical methods for representing and analyzing the information content pertinent to the overall goals.

Historically the analysis of functional data appeared in several places. For example, analyzing stochastic processes involves mathematical treatments of function spaces. One examines the sample paths of stochastic processes as random functional variables and defines functional operators and metrics for their statistical modeling. Several notable developments in stochastic processes, including the pioneering works of Grenander (1956, 1981), led the field in the early research. The more modern approach to functional data analysis (FDA) is due to the leadership of Ramsay, Silverman, and colleagues (Ramsay and Silverman 2005; Ramsay et al. 2009), who recognized the advantages of modeling functional variables explicitly and developed numerous computational procedures for statistically analyzing functional data. Through their fundamental contributions, FDA has become an important, active field in statistics, with significant involvement in various scientific and engineering fields. Several textbook-level treatments of FDA are now available (Ferraty et al. 2007; Hsing and Eubank 2015; Zhang 2013; Srivastava and Klassen 2016; Kokoszka and Reimherr 2017). Additionally, many review-type articles have also covered different aspects of FDA (Morris 2015; Wang et al. 2016).

Driven by the abundance of functional data and the emergence of exciting applications, the field of functional data analysis has proliferated in recent years. Naturally, there are multiple perspectives and research foci in this field. The traditional mainstream approaches seek convenient extensions of past multivariate techniques by adapting them to handling new challenges, including the infinite dimensionality of function spaces. Although convenient, this paper argues that these extensions often fail to provide interpretable and meaningful solutions. Specifically, we motivate and develop an alternative perspective natural for image and functional data. We argue that an essential aspect of functional data is their shape. Accordingly, one should seek statistical techniques that are cognizant of the shapes of functions. For scalar functions, shape relates to the number and heights of peaks and valleys but is less concerned with their placements. For instance, two bimodal functions are deemed to have similar shapes if the heights of their peaks and valleys are similar, but the locations of these extrema may differ. For planar and space curves, shape relates to the bends, corners, and regions of high curvatures. Functional data often represent the temporal evolution of a phenomenon of interest, and modes correspond to significant events in that process. For instance, in statistical analysis of COVID-19 data, the discussion has centered on the waves attributed to different mutations of the SARS-COV2 virus. Even though the waves occurred at different times in different geographical regions, they had similar impacts due to similar peak intensities. Here, the number and heights of waves are considered more important than the actual time occurrences of the waves. Similarly, in data depicting the consumption of utilities (electricity, gas, etc.) by individual households, the peaks correspond to high energy usage and are essential for planning by utility companies. As these and other examples presented later suggest, shapes are often the main focus in certain functional data.

The next issue is: How to mathematically define and quantify shapes of functions and develop statistical techniques to analyze these shapes? The shape is a geometric characteristic, and this pursuit requires essential tools from the differential geometry of functional spaces. Unfortunately, the widely used mathematical platform in FDA, namely the Hilbert structure provided by the $\mathbb {L}^2$ metric, does not provide meaningful results when analyzing shapes, and better alternatives are needed. While the vector space structure supported by the $\mathbb {L}^2$ metric may seem convenient and allows natural extensions of classical multivariate statistics to functional data, the results are counter-intuitive when we employ this metric for quantifying shapes. With this background, this paper has two broad goals: (1) motivate the need and importance of shape-based functional data analysis in broad application contexts, and (2) review and extend some essential tools for shape-based FDA.

We present some popular tools under both paradigms—the traditional FDA and the shape-based FDA—to compare and contrast the two approaches. Some popular tools in FDA include function estimation or curve fitting, functional PCA and dimensional reduction, functional ANOVA, and functional regression models. After reviewing the traditional approaches, we will develop similar concepts for shape data analysis of functions. Specifically, we will discuss the estimation of shapes from discrete observations, PCA and modeling of shape data, and regression models involving shape variables. We note that some of our developments are rather preliminary and serve as invitations to the readers to help advance this field.

Scope of this paper: Although functional data comes in many forms, with various combinations for domains and ranges, we will focus on functions of the type $f: I\rightarrow \mathbb {R}$ where I is a fixed interval. This restriction allows us to discuss statistical shape analysis of f for a broad audience without getting too technical. Of course, the cases where domain I is two- or three-dimensional, or the range space is $\mathbb {R}^d$ (for $d > 1$), are also of great interest. Most of the discussion presented here applies to these more general cases, albeit at a different computational cost and sometimes additional theoretical machinery. We will not go into these setups in this paper. One exception to this exclusion is functions of the type $f: I\rightarrow M$ where M is a nonlinear Riemannian manifold and I is still an interval. We will discuss an extension to these manifold-valued (or M-valued) functions as they have proven very pertinent in modern applications.

This paper highlights some developments at the crossroads of functional and shape data analysis. Being an overview, it focuses on the main ideas and avoids getting into algorithmic details or theoretical depths found in other, more technical literature. While most of the pedagogical material presented here is gleaned from the existing literature, there are some novel ideas presented in Sects. 3.5, 4.1, 4.3, and 5.1. It also lists some open problems in the field and invites interested researchers to take on these challenges. The rest of the paper is organized as follows. Section 2 summarizes the well-used $\mathbb {L}^2$ Hilbert structure for FDA and presents some standard statistical tools used in data analysis. Section 3 introduces the notion of the shape of scalar functions on one-dimensional domains and presents some examples. Some statistical tools for analyzing shapes of functional data are presented in Sect. 4. The paper then goes into manifold-valued or M-valued curves in Sect. 5 and outlines some preliminary ideas in that problem domain. It lists some open problems relating to shape-based FDA in Sect. 6, and finally, the paper ends with a summary.

2 Basic functional data analysis

To start the discussion, we review tools that form essential building blocks in current FDA techniques and practices. Underlying these tools is a popular and convenient Hilbert structure on functional spaces, and we start by summarizing this framework.

2.1 Current perspective

In the early FDA research, it seemed essential to develop techniques that are natural extensions of past multivariate methods. For statistical analysis, one needs to be able to compare, summarize, model, and test functional data. The definition of a metric (or distance) is central to achieving these goals. Accordingly, a standard mathematical platform for developing FDA is the Hilbert-space structure of square-integrable functions. The set of square-integrable functions is given by:

$$\begin{aligned} \mathbb {L}^2(I, \mathbb {R}) = \{ f: I\in \mathbb {R}: \Vert f\Vert < \infty \} \end{aligned}$$

where $\Vert f\Vert = \sqrt{\int _If(t)^2~dt}$. $\mathbb {L}^2(I, \mathbb {R})$ or simply $\mathbb {L}^2$ is a vector space endowed with a natural inner-product $\left\langle f,g \right\rangle = \int _If(t) g(t)~dt$. This Hilbert structure has been popular for several reasons:

Cross-sectional or pointwise analysis: Comparisons and summarizations of functional data under the $\mathbb {L}^2$ norm reduce to cross-sectional or pointwise computations. Here, pointwise implies that when studying a set of functions, say $f_1, f_2, \dots , f_n$, one uses the same argument t for all functions in a computation. Or, when studying covariance, one uses the same pair (s, t) for all observations. For example, the comparison of two functions $f_1, f_2$ under the $\mathbb {L}^2$ metric uses:
$$\begin{aligned} \Vert f_1 - f_2 \Vert = \left( \int _I(f_1(t) - f_2(t))^2~dt \right) ^{1/2}\,. \end{aligned}$$
In the integral, only the values of $f_1$ and $f_2$ at the same time t are compared; it never uses $f_1(t_1) - f_2(t_2)$ for $t_1 \ne t_2$.

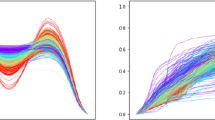
A matching of points across the two functions is also called registration, and the $\mathbb {L}^2$ norm uses vertical registration for comparing functions. The top row of Fig. 1 shows a pictorial illustration of this vertical registration. The left panel shows two functions, $f_1$ and $f_2$, and the middle panel shows that the functions are matched vertically, and only the vertical separations are considered. The right panel shows a pointwise linear interpolation between these functions $(1 - \tau ) f_1(t) + \tau f_2(t)$ indexed by $\tau \in [0,1]$. From a geometric perspective, this interpolation does not seem natural. The intermediate functions have shapes different from $f_1$ and $f_2$. In order to motivate a later discussion on shapes and shape-based interpolations, we illustrate a different registration in the bottom row. Here, the peak is matched with the peak and valley with valley across $f_1$ and $f_2$. This oblique registration provides a more natural interpolation of functions, as shown in the right panel, and it results from shape considerations presented later in this chapter.

When we seek the average of a set of functions under the $\mathbb {L}^2$ norm, we arrive at a familiar quantity, the cross-sectional mean:
$$\begin{aligned} \bar{f} = \mathop {\textrm{argmin}}_{f \in \mathbb {L}^2} \left( \sum _{i=1}^n \Vert f - f_i\Vert ^2 \right) \ ~~~~\Longrightarrow ~~~~ \bar{f}(t) = \frac{1}{n} \sum _{i=1}^n f_i(t), \ t \in I\,. \end{aligned}$$
Similarly, one can obtain cross-sectional variance using, $\sigma _f^2(t) = \left( \frac{1}{n-1} \sum _{i=1}^n (f_i(t) - \bar{f}(t))^2 \right) $, for any $t \in I$. Once again, we see that these summaries result from considering values of $f_i$’s synchronously, i.e., the averaging is pointwise. The top row of Fig. 2 shows COVID data for daily new infections, hospitalizations, and deaths in 25 European countries over the time period 09/2020–10/2022. The middle row shows the cross-sectional means as well as one-standard-deviation bands $(\bar{f}(t) - \sigma _f(t), \bar{f}(t) + \sigma _f(t))$ for these data. As these examples suggest, the mean function often shows a softening or disappearance of peaks and valleys due to poor alignment. In some cases, the opposite may happen, i.e., averaging of unaligned functions may create new peaks. While this cross-sectional averaging is useful in traditional statistical settings, especially when modeling data as a signal plus zero-mean noise, it can also result in the loss of structures in the original signal. The bottom row shows data for some individual countries; these plots have noticeably more peaks and valleys than the average $\bar{f}$. For instance, the daily infection rates of Spain, Italy, and Ukraine show multiple peaks (or pandemic waves) in 2022. However, these peaks are lost in the average profile of 25 countries. The need to preserve geometric structures when computing data summaries motivates the use of shape analysis.
Dimension reduction and multivariate approximation: Functional spaces are infinite-dimensional, presenting a big hurdle in statistical modeling and inferences of functional data. A natural course is to map the problem to a finite-dimensional vector space, either linearly or nonlinearly, and then apply standard tools from multivariate statistics. Since $\mathbb {L}^2$ is a familiar vector space, it provides many intuitive choices of orthonormal bases, allowing linear projections to finite-dimensional spaces. A set of functions ${{\mathcal {B}}}$ forms an orthonormal basis of $\mathbb {L}^2$ if: (i) for any $b_i, b_j \in {{\mathcal {B}}}$, we have $\left\langle b_i,b_j \right\rangle = \left\{ \begin{array}{cc} 1, &{} i = j \\ 0, &{} i \ne j \end{array} \right. $, and (ii) span$({{\mathcal {B}}})$ is dense in $\mathbb {L}^2$. For example, the set of Fourier functions: ${{\mathcal {B}}} = \{ 1, \frac{1}{\sqrt{2 \vert I\vert }}\sin (2 n \pi t), \frac{1}{\sqrt{2 \vert I\vert }}\cos (2 n\pi t), n = 1, 2, \dots \}$ provides a convenient orthonormal basis for elements of $\mathbb {L}^2$. For any $f \in \mathbb {L}^2$, we can write: $f(t) = \sum _{j=1}^{\infty } c_j b_j(t)$. In fact, the Parseval’s identity states that $\Vert f\Vert ^2 = \sum _{j=1}^{\infty } \left\langle f,b_j \right\rangle ^2$ for any $f \in \mathbb {L}^2$, relating the $\mathbb {L}^2$ vector space with the $\ell ^2$ vector space. This implies that the series $\sum _{j=1}^{J} \left\langle f,b_j \right\rangle ^2$ converges to finite value, and therefore, one can approximate $f \approx \sum _{j=1}^J c_j b_j$ for a large J, where $c_j = \left\langle f,b_j \right\rangle $. This approximation facilitates the replacement of f by a finite vector $c \in \mathbb {R}^J$, and the classical multivariate analysis becomes applicable. Many tools from multivariate statistics—principal component analysis, discriminant analysis, multiple hypothesis testing, etc.—have made their way into FDA through this relationship. As described in the next section, one can also use functional PCA, or fPCA, to learn an orthonormal basis from the data.

2.2 Essential FDA tools: curve-fitting, fPCA, regression

Given the cross-sectional or pointwise nature of the $\mathbb {L}^2$ metric, and the flat geometry (or vector space structure) of $\mathbb {L}^2(I,\mathbb {R})$, several ideas from multivariate statistics can be naturally extended to FDA.

2.2.1 Curve fitting

Theoretically, functions are represented on a continuous domain, but, in practice, one needs to discretize them for computing norms, inner products, averages, and covariances. This discretization requires evaluating functions at arbitrary points on the domain I. For example, given two discretized functions: $f_1$, sampled at points $\{t_{1,i} \in I, i=1,2,\dots ,n_1\}$ and $f_2$, sampled at points $\{t_{2,i} \in D, i=1,2,\dots ,n_2\}$, say we want to approximate their inner product $\left\langle f_1,f_2 \right\rangle $? One way is to fix the sampling of $f_1$ and to resample $f_2$ at the points $\{t_{1,i}, i=1,2,\dots ,n_1\}$. This resampling, in turn, requires curve fitting and is outlined next.

Given a set of time-indexed points $\{(t_{i}, y_i, i=1,2,\dots ,n) \in I\times \mathbb {R}\}$, where $t_i$s form an ordered set, one can fit a function according to a penalized squared-error criterion:

$$\begin{aligned} \hat{f}_1= & {} \mathop {\textrm{argmin}}_{f \in \mathbb {L}^2} \left( \sum _{i=1}^n (y_i - f(t_i))^2 + \kappa {{\mathcal {R}}}(f) \right) \end{aligned}$$

(1)

$$\begin{aligned} \hat{c}= & {} \mathop {\textrm{argmin}}_{c \in \mathbb {R}^J} \left( \sum _{i=1}^n (y_i - \sum _{j=1}^{J} c_j b_j(t_{i}))^2 + \kappa c^T M c \right) \,. \end{aligned}$$

(2)

The two equations are equivalent under the constraint $f(t) = \sum _{j=1}^{J} c_j b_j(t)$. The first equation states the problem in ${{\mathcal {F}}}$, while the second equation uses a finite basis to rephrase the problem in a vector space $\mathbb {R}^J$. Here, M is a pre-computed (roughness) matrix that comes from the inner products of derivatives of $b_j$s. For example, when using a second-order penalty, the entries of M are given by $M_{kl} = \left\langle \ddot{b}_k,\ddot{b}_l \right\rangle $. Figure 3 shows three examples of fitting curves for the sample size $n=10$. For each set of n data points, we plot three fitted curves corresponding to different values of the penalty coefficient $\kappa $. A smaller value of $\kappa $ allows more data fidelity, while a larger $\kappa $ favors a smoother fitted function. Once we have an estimated curve $\hat{f}$, we can resample it arbitrarily. For example, one can compute $\hat{f}$ at points needed to approximate an inner product with another function.

The curve fitting problem manifests itself in several ways in statistics, including regression (see Sect. 2.2.3). Similar to Eq. 2, one often uses an orthonormal basis for representing and estimating in regression models. Instead of choosing a pre-determined basis, one can also estimate basis functions from the training data, and fPCA (discussed next) is a standard solution.

2.2.2 fPCA and dimension reduction

Given a set of functions, one can use fPCA for dimension reduction and mapping some problems from a function space to a finite-dimensional vector space. As described in Marron and Dryden (2021), fPCA analysis has become a central tool in the preliminary inspection of functional data.

Let $\{f_i \sim \pi , i=1,2,\dots ,n\}$ where $\pi $ denotes a probability model on the function space ${{\mathcal {F}}}$. Let $\mu (t) = E_{\pi }[f_i(t)]$ denote the pointwise mean and let

$$\begin{aligned} C(s,t) = E[(f_i(t) - \mu (t))(f_i(s) - \mu (s))]\, \end{aligned}$$

denote the covariance function of $f_i$. Define ${{\mathcal {C}}}$ to be the linear operator on ${{\mathcal {F}}}$ associated with the function C(s, t) according to:

$$\begin{aligned} {{\mathcal {C}}}: {{\mathcal {F}}} \rightarrow {{\mathcal {F}}},\ \ \ {{\mathcal {C}}}(f)(t) = \int C(s,t) f(s)~ds\,. \end{aligned}$$

Since ${{\mathcal {C}}}$ is a bounded, linear, and self-adjoint operator, it admits a spectral decomposition ${{\mathcal {C}}} = \sum _{j=1}^{\infty } \sigma _i^2 \psi _j(s) \psi (t)$, where the eigenfunctions $\{\psi _j\}$ form an orthonormal basis of the function space ${{\mathcal {F}}} = \mathbb {L}^2$ (Hsing and Eubank 2015). Using the Riesz representation theory, we can represent any $f_i \sim \pi $ using the eigenfunctions $\phi _j$’s according to: $f_i(t) = \sum _{j=1}^{\infty } x_j \psi _j(t)$. Here, $\{x_j\}$ are scalar random variables that capture the variability of f. In practice, one can obtain this decomposition by discretizing the domain I and replacing the integral $\int _If_i(t) f_j(t)~dt$ by the summation $\delta \sum _{k} f_i(t_k) f_j(t_k)$ (assuming that $\{ t_k\}$ denotes the uniform partition of I with width $\delta $). This replaces the fPCA procedure with the finite-dimensional PCA using standard matrix algebra.

We demonstrate this idea with two examples. The top row of Fig. 4 shows two sets of functional data; the left set is for daily death rates for 25 European countries over a certain period, and the right set contains some simulated bimodal functions. These panels also show their cross-sectional means $\bar{f}$ in black. The second row shows the three principal directions of variation for the death-rate data: each panel contains three curves $\{\bar{f} - \sigma _j \psi _j, \bar{f}, \bar{f} + \sigma _j \psi _j\}$, for $j=1,2,3$, to capture how the function changes along $\psi _j$ direction. Intuitively, one would expect $\bar{f} \pm \sigma _j \psi _j$ to cover $\bar{f}$ from top and bottom, capturing the data’s vertical variability. However, this is not always the case. We see that in some places the curves $\bar{f} - \sigma _j \psi _j$, $\bar{f}$, and $\bar{f} + \sigma _j \psi _j$ actually intersect. This indicates the presence of horizontal variability, termed phase variability (made precise later in this paper) in the data. The definition and handling of phase variability is an essential tool in the shape analysis of functions. We use the simulated bimodal dataset from the top-right panel to further highlight this issue, with results shown in the bottom row. In this case, the variability is almost vertical for $j=2$ and $j=3$, but for $j=1$, the variability has a large horizontal component. Generally speaking, if some eigendirections move the peaks horizontally and others change their heights, their linear combinations can create or destroy peaks and valleys in the data. Thus, if one is concerned with preserving the modality (number of peaks), this $\mathbb {L}^2$-based fPCA is inappropriate. An alternate fPCA approach, based on shape analysis of function, has better properties and interpretability.

As these examples illustrate, one can use fPCA to gain some understanding of the functional data before further modeling and testing steps. The textbook (Marron and Dryden 2021) describes the strength of such PCA-based screening tools for functional and other nonlinear data.

2.2.3 Functional regression models

A central tool in statistical modeling is regression, and not surprisingly, a significant effort in FDA has been devoted to regression models involving functional variables. Most of these regression models rely on the $\mathbb {L}^2$ Hilbert structure (see Morris 2015 and references therein), either explicitly or implicitly. In broad terms, we have three scenarios for regression: (a) scalar responses and functional predictors or (Scalar-on-function regression); (b) functional responses and vector predictors or (Function-on-vector regression); and (c) functional responses and functional predictors or (Function-on-function regression). We will review the main ideas (parametric, semi-parametric, and nonparametric approaches) in each of these three categories:

Scalar-on-function regression: An initial model of this type, named functional linear regression model (FLRM) was introduced by Ramsay and Dalzell (1991) and expressed by Hastie and Mallows (1993) as:
$$\begin{aligned} {y}_i=\alpha _0+\left\langle f^x_i,\beta \right\rangle + {\epsilon }_i, \end{aligned}$$
(3)
where $\alpha _0 \in \mathbb {R}$ is the intercept, $\beta \in \mathbb {L}^2$ is the regression coefficient, $\{y_i \in \mathbb {R}\}$ are the responses, $\{f^x_i \in \mathbb {L}^2\}$ are the functional predictors, and ${\epsilon }_i \in \mathbb {R}$ are zero-mean, finite-variance random noise. If we express $\beta $ using an orthonormal basis $\beta (t) = \sum _{j=1}^J c_j b_j(t)$, then we can reduce the estimation of $\beta $ to a standard least squares problem. Subsequently, several authors (Cardot et al. 1999; Ahn et al. 2018; Reiss et al. 2017; Goldsmith and Scheipl 2014; Fuchs et al. 2015; Qi and Luo 2018; Luo and Qi 2017; Cai and Hall 2006), have studied and advanced this model. The variations include parametric models such as Shin (2009) which proposed functional partial-linear models extending Eq. 3 to include both functional and vector predictors. Similarly, Marx and Eilers (1999) proposed generalized functional-linear models via a known link function for exponential family responses; Gertheiss et al. (2013), Goldsmith et al. (2012) extended the literature to longitudinal functional-linear models via the introduction of the random effects into model (3); and (Yao and Müller 2010) introduced functional quadratic regression models that include full quadratic terms like $\int \int f^x_i(t){X}_i(s){\beta }_2(t,s)~dt~ds$ into model (3). Some semi-parametric approaches have been investigated as well. Specifically, functional single-index models or functional multiple-index models were proposed in Fan et al. (2015), Li et al. (2010), Marx et al. (2011), which incorporated nonlinearities in model (3) by involving smooth functions: ${y}_i=\alpha _0+\sum _{k=1}^K h_k(\left\langle f^x_i,\beta _k \right\rangle )+{\epsilon }_i$, where functions $h_k: \mathbb {R}\rightarrow \mathbb {R}, k=1,\ldots ,K,$ are unknown. Besides the parametric and semi-parametric approaches, the literature has fully nonparametric paradigm (Ferraty et al. 2007), where the model for the conditional mean $\mathbb {E}[y_i\mid f_i^x]$ is not only nonlinear but essentially unspecified. The common strategy here is to apply functional PCA on the predictors first and then apply smoothing methods to estimate the unspecified conditional mean function (Müller and Yao 2008; Wong et al. 2019; Zhu et al. 2014). One advantage of nonparametric approaches is that they are flexible and suitable for more general data spaces such as nonlinear Riemannian manifolds.
Function-on-vector regression: A basic linear function-on-vector regression model is given by
$$\begin{aligned} f^y_i(t)=\sum _{k=1}^K{x}_{ik} {\beta }_k(t) + {\epsilon }_i(t),\ t \in I\, \end{aligned}$$
(4)
where $f^y_i \in \mathbb {L}^2$ is the functional response, $\{{x}_{ik} \in \mathbb {R}, k=1,\ldots ,K\}$ are the predictors, and $\{{\beta }_k \in \mathbb {L}^2\}$ are functional coefficients representing the partial effect of predictor $x_{ik}$ on the response $f^y_i$ at position $t, i=1,\ldots ,n$. The set $\{{\epsilon }_i \in \mathbb {L}^2\}_{i=1}^n$ are the residual error deviations, frequently assumed to be a Gaussian process with covariance function ${{\varvec{\Sigma }}}(t, s)$, whose structure describes the within-function covariance. Sometimes the error deviations are split into a combination of individual random effect functions and white noise residual errors. This model assumes that the value of $f^y_i$ at time t depends only on the current value of $\sum _{k=1}^K{x}_{ik} {\beta }_k(t)$, and not the past or future values. Hence, it is often called a concurrent regression model (Wang et al. 2016).

A vast majority of existing parametric approaches to function-on-vector regression can be related back to model (4). The methods differ in how they smooth the mean function (or functional coefficient), with different choices of basis functions (e.g., principle components, splines, and wavelets) or regularization approaches, and also in how they model the correlation over t in the curve-to-curve deviations (see Morris 2015 and reference therein). We note that the function-wise independence assumption in model (4) is often violated in practice. In order to capture this correlation induced by the experimental design, there are two popular approaches: (i) specifying a function-wise covariance structure (Zhang et al. 2016) and (ii) adding random effect functions (Guo 2002; Scheipl et al. 2015). In contrast to the parametric approaches, which involve mean functions that are nonparametric in t but linear in x, some semi-parametric and nonparametric approaches, e.g., (Scheipl et al. 2015; Wood 2017), have been proposed where the idea of generalized additive model (Hastie and Tibshirani 1987) has been extended to model (4) via terms that are either parametric or nonparametric in x.

The goal of functional-on-vector regression models is often different from that of scalar-on-function regression models. Here the focus is on estimation of ${\beta }_k(t)$, followed by either testing whether ${\beta }_k(t)={0}$ or assessing for which t we have ${\beta }_k(t)\ne {0}$. Thus, some hypothesis testing problems and estimation of confidence bands problems have been thoroughly investigated in Fan and Zhang (2008) and Zhu et al. (2014), and Zhu et al. (2012). A special case arises when the predictor is a scalar variable, such as time. In this case, one can view the problem of regression as a simple curve fitting. Rich literature exists on fitting curves to time series data on both Euclidean (see Sect. 2.2.1) and non-Euclidean domains (see Sect. 5.1).
Function-on-function regression: The third situation is when both the predictors and responses are functions. Compared to the first two categories, little work has been done on function-on-function regression problems. A function-on-function regression model with unconstrained surface coefficient ${\beta }(s, t)$ was first proposed in Ramsay and Dalzell (1991):
$$\begin{aligned} f^y_i(t)= {\beta }_0(t)+\int f^x_i(s) {\beta }(t,s)ds+ {\epsilon }_i(t) = \beta _0(t) + (A_{\beta }f^x_i)(t) + {\epsilon }_i(t), \end{aligned}$$
(5)
which can be treated as an extension of (3) when the scalar response y is replaced by $f^y \in \mathbb {L}^2$ and the coefficient function ${\beta } \in \mathbb {L}^2(I\times I, \mathbb {R})$ varies with t and s, leading to a bivariate coefficient surface. Corresponding to $\beta $, there is a linear operator $A_{\beta }: \mathbb {L}^2\rightarrow \mathbb {L}^2$ that operates on $f^x_i$. Also, model (5) can be treated as an extension of (4) by changing the inner product from a finite space to a function space ($\mathbb {L}^2$).

The estimation in this situation is challenging because the model (5) faces issues present in both scalar-on-function regression and functional-on-vector regression settings, including (i) regularizations of the predictor function, coefficient surface in both dimensions and structural modeling of within-function correlation in the residual errors (Ivanescu et al. 2015; Wu and Müller 2011); and (ii) specification of function-wise correlation when the response curves are correlated (e.g., covariance structure or random effect functions) (Meyer et al. 2015; Scheipl et al. 2015).

So far, we have summarized essential items from the current FDA, with functional data treated as elements of the Hilbert space $\mathbb {L}^2$. Next, we introduce a novel perspective where the shapes of functions, rather than full functions, become the main focus.

3 Shapes: motivation, definition, and analysis

This section starts with some applications motivating the need to focus on the shapes of functions. Then, it introduces a formal definition of shape and presents some essential tools for shape analysis.

3.1 Motivation for shape analysis

Generally, the shape refers to the number and heights of extremal points in a function. For instance, it could simply refer to the number of modes in functions or can include the heights of these modes also. (We will present a precise mathematical definition in the next section but keep the discussion abstract for now.) In some situations, one is more interested in the number and (relative) heights of modes of a function than their locations. For example, this has been the case in COVID research, where the shapes of COVID curves (daily infection rates, hospitalization counts, death rates, etc.) are the main focus. Significant peaks in these data curves represent waves of infections and are medically attributed to a new mutation of the SAR-Cov2 virus. The emphasis is on detecting and characterizing these waves and their impacts on different populations. The top left panel of Fig. 5 shows the plots of hospitalization rates (per million) over time for several European countries. The period covered here is from April 1, 2020, to July 1, 2021. Different countries had major waves at different asynchronous times, but still, there was an underlying pattern to the waves for the region as a whole. This pattern is evident if we align the peaks and valleys of these curves in some way, as shown in the middle panel. Most countries had three big waves centered around 05/20, 12/20, and 05/21. Some countries also had an additional small wave during 03/21. The rightmost panel shows the time-warping functions used to align the original functions.

To gauge public interest in COVID vaccine developments and research, we studied data from Google trend counts for the word “vaccine." The bottom left panel of Fig. 5 shows the plots of normalized search frequencies over time for several countries worldwide. The search period is from October 11, 2020, to October 2, 2021. Once again, notice that although the peak searches are at different time points in different countries, the underlying trends of the change in vaccine popularity are similar. This pattern becomes clear once we align the peaks and valleys, as shown in the middle panel.

These examples indicate that peaks and valleys broadly capture the shapes of scalar functions, and properly aligning them across observations helps elucidates their shapes. The question arises: How can we mathematically represent the shapes? How can we quantify the similarities and dissimilarities between the shapes of functions naturally and effectively? As mentioned, a classical and obvious choice would be the $\mathbb {L}^2$ norm. However, the $\mathbb {L}^2$ norm has several limitations in this regard, leading to counterintuitive results. Figure 6 demonstrates the problem in using $\mathbb {L}^2$ norm to analyze shapes of functions. In both panels, functions $f_1$ (red line) and $f_2$ (blue line) have a similar shape, i.e., the same number and the same heights of peaks. The magenta line $f_3$ in the left panel illustrates a flatter unimodal function, while $f_3$ in the right panel represents a constant function. Note that $d_{13}$, the $\mathbb {L}^2$ distance between functions $f_1$ and $f_3$, is smaller than $d_{12}$ in both examples. The functions with the same shapes have larger $\mathbb {L}^2$ distances than the totally different functions. Thus, using the $\mathbb {L}^2$ norm verbatim to quantify the shape differences leads to counterintuitive results.

3.2 Definition: shape of a function

The main question is: How can we quantify the notion of shape of a scalar function mathematically precisely? Most commonly, the shape is associated with the count of the peaks of a function. For instance, one may consider unimodal functions (Fig. 7(left)) to be similar in shape and bimodal functions (Fig. 7(right)) to be different from the unimodal functions but similar to each other. Further, it also seems pertinent to include the heights of these peaks in the shape discussion. Any two bimodal functions with similar heights of their corresponding peaks (and valleys) will have similar shapes compared to two bimodal functions with very different heights of their peaks (and valleys). The locations of the peaks or valleys in I seem less useful in defining shapes. In other words, the horizontal movements of peaks, often called the phase variability (Marron et al. 2014, 2015), do not affect the shape of a function. The vertical translation is another transformation that preserves the shape: $f(t) \mapsto f(t) + c$, $c \in \mathbb {R}$. Together these properties lead to the notion of invariance of shape. While these qualitative discussions are meaningful, one needs precise mathematical representations to develop statistical models and inferences. We need frameworks that respect our intuitive notions of shape and facilitate statistical analyses.

We introduce a group of time-warping functions to help develop a precise notion of shape. Let $\Gamma $ denote the set of all orientation-preserving diffeomorphisms of I to itself. A diffeomorphism is a smooth, invertible function, and its inverse is smooth. Naturally, such a diffeomorphism preserves the boundaries of I. Notably, this set $\Gamma $ is a group with composition being the group operation. For any $\gamma _1, \gamma _2 \in \Gamma $, the function $\gamma _1(\gamma _2(t)) = (\gamma _1 \circ \gamma _2)(t)$ is also in $\Gamma $. The identity element of $\Gamma $ is the identity function $\gamma _{id}(t)= t$, and for every $\gamma \in \Gamma $, we have a $\gamma ^{-1} \in \Gamma $ such that $\gamma \circ \gamma ^{-1} = \gamma _{id}$. Why is $\Gamma $ being a group important? As we will see later, the group structure of $\Gamma $ is critical in establishing certain invariant properties of shapes.

In the discussion on traditional FDA, we used ${{\mathcal {F}}} = \mathbb {L}^2$, the set of square-integrable functions, as the function space. In the shape-based FDA, we will use a restricted set. Let ${{\mathcal {F}}}$ be the set of all absolutely-continuous functions on the interval I. For any $f \in {{\mathcal {F}}}$ and $\gamma \in \Gamma $, the composition $f \circ \gamma $ is said to be time-warping of f by $\gamma $. This operation only moves the values in the graph of f horizontally; no points move vertically. An example of this warping is illustrated in Fig. 8. In the FDA literature, this is also called changing the phase of f. Any two functions $f_1$ and $f_2$ are said to have the same shape if they differ only in their phases, i.e., there is $\gamma \in \Gamma $ such that $f_1 = f_2 \circ \gamma $. Since $\Gamma $ is a group, and every $\gamma $ has an inverse, this also implies that $f_1 \circ \gamma ^{-1} = f_2$. Furthermore, one can check that this denotes an equivalence relationship; we will denote it by $f_1 \sim f_2$. One can check that if $f_1 \sim f_2$ and $f_2 \sim f_3$, we have $f_1 \sim f_3$. The equivalence class of a function f is denoted by the set $[f] = \{f \circ \gamma : \gamma \in \Gamma \}$. In mathematics, one calls the set [f] the orbit of f under $\Gamma $. Any two equivalence classes are either disjoint or equal. With this setup, we are now ready to provide a formal definition of the shape of a function.

Definition 1

(Shape of a function) For any function f, its equivalence class [f] under the equivalence relation $\sim $ is called the shape of f. The set of all shapes ${{\mathcal {S}}} = \{ [f]: f \in {{\mathcal {F}}}\}$ is called the shape space of functions. It is also denoted by the quotient space ${{\mathcal {F}}}/\Gamma $.

The shape is a property that does not lend to Euclidean calculus, and that causes a major difficulty in representing and quantifying shapes. One cannot simply add, subtract, or scale shapes. In order to compare and quantify shapes, one needs a proper metric on the set ${{\mathcal {S}}}$, and several choices are discussed in the literature. In an approach called elastic shape analysis (Srivastava and Klassen 2016), this distance is as follows. Define the square-root velocity function (SRVF) of a function $f \in {{\mathcal {F}}}$ to be $q \in \mathbb {L}^2$, where $q(t)= \text{ sign }(\dot{f}(t)) \sqrt{\vert \dot{f}(t) \vert }$. The use of SRVFs in shape analysis is motivated by several properties. Please refer to the book (Srivastava and Klassen 2016) for a detailed development. It is important to note that SRVF is a bijection from ${{\mathcal {F}}}$ to $\mathbb {L}^2$ (up to a constant), and one can reconstruct f from its SRVF q. That is, given (q, f(0)), the original function is given by $f(t) = f(0) + \int _0^t |q(s)| q(s) ds$. However, since the vertical translation of a function is usually shape-preserving, the SRVF q is sufficient to describe the shape of f.

If the SRVF of f is q, then the SRVF of $(f \circ \gamma )$ is given by $(q \circ \gamma ) \sqrt{\dot{\gamma }}$. We will denote the last quantity by $q \star \gamma $ for brevity. It is interesting to note that for all $q \in \mathbb {L}^2$ and $\gamma \in \Gamma $, we have:

$$\begin{aligned} \Vert q \star \gamma \Vert ^2 = \int _I((q \circ \gamma ) \sqrt{\dot{\gamma }})^2~dt = \int _Iq(s)^2~ds = \Vert q\Vert ^2\,. \end{aligned}$$

(6)

In other words, the transformation $q \mapsto q \star \gamma $ is norm preserving. Notably, the same does not hold for $\mathbb {L}^2$ norm and time warping, i.e., in general $\Vert f \circ \gamma \Vert \ne \Vert f\Vert $ except for some special cases. Hence, the shortcomings of traditional methods in registration and shape analysis. We caution that even though the mapping $q \mapsto q \star \gamma $ is unitary, not all the unitary mappings can be expressed in this fashion. Even if a mapping $q \mapsto \tilde{q}$ is unitary and results from such a transformation, it is not straightforward to find the corresponding $\gamma $ analytically, but the numerical solutions exist.

Analogous to the definition of shape as an equivalence class $[f] \subset {{\mathcal {F}}}$, we can define the shape of an SRVF q by $[q] = \{ q \star \gamma : \gamma \in \Gamma \}$. The shape difference between any two curves is given by comparing their equivalence classes:

$$\begin{aligned} d_s([q_1], [q_2]) = \inf _{\gamma \in \Gamma } \Vert q_1 - (q_2 \star \gamma )\Vert = \inf _{\gamma \in \Gamma } \Vert q_2 - (q_1 \star \gamma )\Vert \,. \end{aligned}$$

(7)

If $\gamma ^*$ is the optimizer for the middle term in Eq. 7, then the functions $f_1$ and $f_2 \circ \gamma ^*$ are said to be optimally aligned. That is, for any $t \in I$, the vertical registration of $f_1(t)$ with $f_2(\gamma ^*(t))$ best aligns the peaks and valleys in the two functions. The quantity $d_s$ is called the shape metric and is used to impose a metric structure on ${{\mathcal {S}}}$. If any two functions are optimally aligned, then they do not have any phase variability between them.

The isometry condition (Eq. 6) mentioned above is of fundamental importance in shape-based FDA. There are several interesting consequences of that condition that are critical in shape analysis. We list some of them below without proofs but refer the reader to Srivastava and Klassen (2016) for the full list.

If $\gamma ^*$ is in the set $\arg \inf _{\gamma \in \Gamma } \Vert q_1 - (q_2 \star \gamma )\Vert $, then ${\gamma ^*}^{-1}$ is an element of the set $\arg \inf _{\gamma \in \Gamma } \Vert q_2 - (q_1 \star \gamma )\Vert $. That is, the optimization problem stated in Eq. 7 is inverse consistent.
For any $q_1, q_2 \in \mathbb {L}^2$ and $c \in \mathbb {R}_+$, the solution $\arg \inf _{\gamma \in \Gamma }\Vert q_1 - c (q_2 \star \gamma )\Vert $ does not depent on c. Consequently, we have that the identity function $\gamma _{id}$ is in the set $\arg \inf _{\gamma \in \Gamma }\Vert q_1 - c (q_1 \star \gamma )\Vert $. That is, a multiplication by a positive constant does not change the phase of a function.
The quantity $d_s$ is a proper metric on the shape space ${{\mathcal {S}}} = {{\mathcal {F}}}/\Gamma $. That is, it satisfies symmetry, positive-definiteness, and the triangle inequality.

In general, there is no readily available expression for optimization over $\Gamma $ in Eq. 7. However, a well-known numerical procedure called dynamic programming (Bertsekas 1995) has been used for several problems, including optimal path finding on discrete graphs. If we discretize I using T partition points, then the computational complexity of this algorithm is $O(T^2k )$ where k dictates bounds on the slope of $\dot{\gamma }$ during optimization. Note that the mapping $t \mapsto \gamma (t)$ provides the optimal slanted matching (between $f_1$ and $f_2$) referred to in Sect. 2.1.

Why not use the quantity $ \Vert f_1 - (f_2 \circ \gamma )\Vert $ (instead of $ \Vert q_1 - (q_2 \star \gamma )\Vert $) for minimization in Eq. 7. After all, the $\mathbb {L}^2$ norm is a popular tool in FDA for comparing functions! The problem is that using $ \Vert f_1 - (f_2 \circ \gamma )\Vert $ leads to a degeneracy: one can severely distort $f_2$ by time warping and arbitrarily reduce that cost function. This phenomenon is called the pinching effect. Figure 9 shows an example of pinching in the top row. To avoid pinching, many past papers have used a penalized optimization approach:

$$\begin{aligned} \inf _{\gamma \in \Gamma } \Vert f_1 - (f_2 \circ \gamma )\Vert ^2 + \lambda {{\mathcal {R}}}(\gamma ), \end{aligned}$$

(8)

to perform functional alignment and phase removal. Here, ${{\mathcal {R}}}$ denotes a penalty term on $\gamma $ and is introduced to avoid severe distortion of $f_2$. Despite its popularity (Eq. 8 is at the heart of past efforts in functional alignment including PACE (Tang and Müller 2008; Yao et al. 2005)), this formulation is fundamentally flawed. Figure 9 illustrates some of the issues resulting from this approach. The figure starts with two functions $f_1, f_2$ (top left) and studies their pairwise alignment using the penalized-$\mathbb {L}^2$ given in Eq. 8. The first column shows the optimal alignment of $f_2$ to $f_1$, and the second column aligns $f_1$ to $f_2$. The third column shows the optimal $\gamma $s for the two cases: $\gamma _1$ and $\gamma _2$. In order to study the symmetry of this solution, we compute their composition $\gamma _1 \circ \gamma _2$ in the fourth column. The first three rows correspond to solutions for different $\lambda $s. When $\lambda = 0$ or no penalty, the solution has inverse symmetry, i.e., $\gamma _1 \circ \gamma _2 = \gamma _{id}$, but this solution exhibits the pinching effect or degeneracy of the solution. As $\lambda $ increases, the pinching and alignment decrease, and the solution becomes inverse asymmetric. The bottom row shows the solution from the elastic approach (Eq. 7); it is perfectly inverse asymmetric, the alignment level is impressive, and no choice of parameter is involved.

When we get functional data for analysis, we cannot be certain just by visual inspection if it contains phase variability on not. We want to automate that decision, i.e., we want a method that separates the phase only if needed but leaves the data unchanged if the data is already aligned. Equation 7 provides this situation, while Eq. 8 does not. Consider the results in Fig. 10. Here, we take two functions that are perfectly aligned already, $f_1(t) = \sin (2 \pi t)$ and $f_2(t) = 2f_1(t)$. Ideally, an alignment algorithm should leave them unchanged, but applying Eq. 8 results in significant distortions depending on the penalty. Also, note this method’s lack of inverse consistency when the penalty is present. In contrast, Eq. 7 leaves the functions unchanged as desired.

So far, we have discussed alignment and shape comparisons of two functions. What if we are given a set of n functions $f_1, f_2, \dots , f_n$, and we want to analyze or visualize their shapes? Let $q_1, q_2, \dots , q_n$ represent their SRVFs. Then, solve for their mean $\mu $ according to an iterative computation:

$$\begin{aligned} \mu = \frac{1}{n} \sum _{i=1}^n (q_i \star \gamma _i),\ \text{ where }\ \ \gamma _i = \mathop {\textrm{argmin}}_{\gamma \in \Gamma } \Vert \mu - (q_i \star \gamma )\Vert ^2 \,. \end{aligned}$$

(9)

These are two mutually dependent equations, and one iterates between them until convergence to solve for the mean shape $\mu $. The resulting optimal warpings $\{\gamma _i^*\}$ capture the data’s horizontal or phase variability, so we call them their phases. After optimal alignment to the mean, the only information left in the aligned functions $\tilde{f}_i = f_i \circ \gamma _i$ are the heights of the peaks and valleys, and we define them as the shapes. Figure 11 illustrates the utility of elastic alignment of data with three examples. The first two rows are simulated data, and the third row presents the data for new COVID deaths in 25 European countries from September 2020 to July 2021. Column (A) presents the original functions. We compute the mean function with and without elastic alignment and show the time point-wise variance on the mean function, colored by the scaled variance level. As shown in column (B), the variance and shape differences are significant over most of the domain I before functional alignment. However, after the elastic alignment using SRVF, the shape differences are primarily seen in the peaks of the functions (column (C)), which reflects the accurate information in the shape pattern of the data. More importantly, the misalignment errors that often overwhelm sample shape variance have been removed.

3.3 Alignment and clustering comparison

Next, we present a comparative study on registering functions and clustering shapes. We compare the functional data registration and clustering results using the elastic approach and a pairwise functional data synchronization method used in the PACE package (Tang and Müller 2008; Yao et al. 2005).

Figure 12 presents the results of an experiment on aligning functions using SRVFs and PACE. The data are made up of simple shapes that have been time-warped using random warping functions. We start with three types of basic shapes as shown left in panel (A): unimodal $g_1$ (red), bimodal $g_2$ (blue), and trimodal $g_3$ (yellow). Then, we generate random time warping functions $\gamma _i$’s with the model $\gamma _i = t + z_it(t-1)$, where $z_i \sim U[-1,1]$. Next, we apply these random time warping functions $\gamma _i, i=1,\dots ,90$ ((A) right) to the simple shapes, respectively, to simulate functions $ \{f_i\} = \{g_1 \circ \gamma _i: i = 1,\dots ,30 \} \cup \{g_2 \circ \gamma _i: i = 31,\dots ,60 \} \cup \{g_3 \circ \gamma _i: i = 61,\dots ,90\} $. Note that the 90 randomly warped functions ((A) left) fall into three clusters (30 unimodal, 30 bimodal, and 30 trimodal), with only phase variability separating functions inside a cluster.

The results in panel (B) show that the SRVF framework succeeds in removing phases and discovering the tri-cluster structure. The results from alignment tools in the PACE package are not as good, as there is still a substantial amount of phase variability in the data. The distance heatmaps in panel (C) further quantify the alignment results. They show matrices of pairwise $\mathbb {L}^2$ distances between functions (after the joint alignment by each method) as images. Functions aligned with SRVF show much tighter three clusters, with larger intercluster and smaller intracluster distances.

To quantify clustering performance, we compare the resulting clusters with the original three shapes (unimodal, bimodal, and trimodal) used in data simulation. If a function with one shape gets clustered with functions of different shapes, we label it an error. In this experiment, the SRVF registration gets an accuracy of 90/90, the PACE registration has an accuracy of 69/90, and the original (randomly warped) functions without registration have an accuracy rate of 64/90.

3.4 Shape discovery

What is the effect of using the shape metric (Eq. 7) for alignment and averaging functions? Figure 13 shows the enhancement of geometrical features due to temporal alignments of functions. The top row is a repeat from Fig. 2 showing the cross-sectional mean and variance for daily infections, hospitalizations, and death counts for 25 European countries. The bottom row has similar statistics, but the phase variability has been removed this time, and only the shape variability is left. The two results—top and bottom—provide different pictures of the summary statistics in the FDA. One can interpret the bottom row as discovering and focusing on the shape variability in the data. Notably, one can better recognize the waves in pandemic data after alignment than before.

3.5 Extension: modal shape analysis

We have developed a notion of shape via an equivalence relation; a shape is an equivalence class of functions that are within time warping of each other. There is a different mathematical representation of this class that can be extended to a more abstract notion of shape. This notion, relating to the number of modes in a function but independent of their heights, can be helpful in some contexts. We develop this representation next. To understand this representation, consider the following result.

Lemma 1

Let $f_0 \in {{\mathcal {F}}}$ be any function such that the set $E = \{ x \in I\mid \dot{f}_0 = 0\}$ has measure zero. For such an $f_0$, there is a unique piecewise-linear function $f_{0,p} \in [f_0]$.

See Theorem 1 in Lahiri et al. (2015) for a proof. This lemma can be understood as follows. On any interval between adjacent peak and valley, the function $f_0$ is monotonic and can be time-warped into a straight line. Since these domains are disjoint, and their union is I, we can concatenate these piecewise warpings to form a full warping function $\gamma $ on I such that $f_{0,p} = f_0 \circ \gamma _0$ is piecewise linear. Note that the boundary points of I are either peaks or valleys. (One can extend this concept to include constant functions on intervals, but we avoid that situation here to keep the discussion simple.)

Any piecewise-linear function is representable by a sequence of heights denoting the ordered peaks and valleys. Assuming that the number of peaks is finite, the length of this vector is variable but finite. Note that in shape analysis, the locations of these geometric features are irrelevant and hence are dropped from the notation. Only the heights are kept. For instance, a vector of heights $\textbf{x}= (x_0+,x_1-,x_2+,x_3-,x_4+, x_5-,x_6+,x_7-)$ represents a piecewise-linear function with peaks at $x_0, x_2, x_4, x_6$, and valleys at $x_1, x_3, x_7$. The ‘+’ mark denotes a peak, and ‘-’ denotes a valley. Naturally, there are some constraints that the elements of $\textbf{x}$ should satisfy. For instance, any valley $x_i-$ should be lower than its neighboring peaks $x_{i-1}+$ and $x_{i+1}+$. Such a vector describes a piecewise linear function and its entire shape class. One can construct a piecewise linear function $f_{0,p}$ from its vector ${{\mathcal {X}}}$ by placing these peaks and valleys at points $t_i = i/n, i=0,1,\dots ,n+1$ and connecting them by straight lines. This construction leads to an equivalence class: $[f_{0,p}] = \{f_{0,p} \circ \gamma \mid \gamma \in \Gamma \}$. The reader can verify that $[f_{0,p}]$ is equal to $[f_0]$.

What is the advantage of this vector-based shape representation? One cannot directly compare the shapes of functions by comparing their corresponding vectors. In other words, even though a vector represents the shape, the set of shapes is still not a vector space. One runs into the same registration problem discussed earlier. Different functions may have vectors of various sizes, and comparing them requires registering elements of these vectors. Lahiri et al. (2015) has studied this registration of piecewise linear functions using such vector representation. We are going to use this vector to extend our notion of shape.

Mode count as shape: A more general notion of shape, relative to the one stated Definition 1, counts the number of its modes or peaks and ignores their heights. For instance, labeling a function as bimodal implies that it has two peaks (and valleys around these peaks) but does not specify the heights of these peaks (and valleys). In terms of a vector description, one can capture it using a string of polarities $\textbf{m} = (-, +, -, +, -)$. Compared to the vector $\textbf{x}$ above, this $\textbf{m}$ does not contain information about the heights $x_i$s attached to these polarities. There is a many-to-one relationship from $\textbf{x}$ to $\textbf{m}$: for a bimodal function

$$\begin{aligned} (-, +, -, +, -)\equiv & {} \{ (x_1-, x_2+, x_3-,x_4+, x_5-)~\mid ~ \nonumber \\{} & {} \quad x_i \in \mathbb {R}, x_2> x_1, x_2> x_3, x_4> x_3, x_4 > x_5\}\,. \end{aligned}$$

(10)

In Fig. 7, all the functions in the left panel have the same modal shape and can be represented by $(-,+,-)$. Similarly, all the functions in the right panel have the same shape and are represented by $(-,+,-,+,-)$. Some past literature has used the number of modes as shapes of functions, especially for constraining probability density functions in their estimation (Cheng et al. 1999; Hall and Huang 2002; Bickel and Fan 1996; Wegman 1970; Rao 1969; Birge 1997). However, in practice, those past efforts have mostly been restricted to unimodal functions, and the current discussion goes much further.

In summary, the shape of a function can be characterized in terms of its extreme values in several ways. Under one definition, shape description includes geometric features such as the heights and counts of the peaks and valleys (ignoring their placements). In another definition, we ignore the heights also and only count the extremal points.

4 Essential shape data analysis tools

Now that we have established a definition or two of shape, how can we use these notions in statistical data analysis? We start with the problem of fitting a given shape to discrete data.

4.1 Shape-constrained curve fitting

As discussed in Sect. 2.2.1, in the FDA, one needs techniques to fit continuous functions to the given observed (noisy, discrete) data for multiple reasons. One of the motivations is to be able to resample these fitted functions at arbitrary points to allow for comparisons with other functions. Section 2.2.1 described a basic nonparametric approach that uses a penalized, least-squares objective function to fit elements of $\mathbb {L}^2$ to given data. The only constraint in this approach is the penalty imposed on the roughness of the fitted function to encourage smoother solutions. Otherwise, this approach is entirely unconstrained and nonparametric.

In shape data analysis, one is often concerned with fitting shapes, rather than functions, to the given data. Given a set of time-indexed points $\{(t_{i}, y_i) \in I\times \mathbb {R}\}$, we are interested in fitting a function f but with the constraint that $f \in [f_0]$ for some given $f_0 \in {{\mathcal {F}}}$. In other words, the unknown function f is assumed to be in the shape class of a known function $f_0$. Since $[f_0] = \{ f_0 \circ \gamma \mid \gamma \in \Gamma \}$, the problem changes to finding an appropriate $\gamma $ according to:

$$\begin{aligned} \hat{\gamma }= & {} \mathop {\textrm{argmin}}_{\gamma \in \Gamma } \left( \sum _{i=1}^n (y_i - f_0(\gamma (t_i)))^2 + \kappa \int _0^1 \dot{f}_0(\gamma (t))^2 \dot{\gamma }(t)^2~dt \right) , \ \text{ or } \nonumber \\ \hat{\gamma }= & {} \mathop {\textrm{argmin}}_{\gamma \in \Gamma } \left( \sum _{i=1}^n (y_i - f_0(\gamma (t_i)))^2 + \kappa \int _0^1 \dot{\gamma }(t)^2~dt \right) \,. \end{aligned}$$

(11)

The difference between the two is that the roughness penalty is imposed on $\gamma $, instead of $f_0 \circ \gamma $, in the second equation.

Comparing this optimization with that in Eq. 1, we notice that when we optimize over full $\mathbb {L}^2$, we can exploit the vector space structure and reach a simple least-square solution. However, now the search is restricted to the set $[f_0]$, or equivalently over $\Gamma $, and the role of $\gamma $ in this setup is nonlinear. One cannot reach a straightforward solution since $[f_0]$ is not a vector space. Taking a numerical approach, we use the dynamic programming algorithm (Bertsekas 1995; Srivastava and Klassen 2016) to solve the second formulation. We refer the reader to these references for the implementation details but only present some examples. Figure 14 shows an example where we generate random data from a sine function $\sin (2\pi t)$ to form the observations $\{y_i\}$s. The green points denote these observations, the pink curve is $f_0$, and the other curves are $f_0 \circ \hat{\gamma }$ for different values of the penalty weight $\kappa $. (Here, we use the penalty on $\gamma $ directly, i.e., use the second option in Eq. 11.) The $f_0$ used here is different in shape from the sine function used to generate the original data, so we don’t expect a perfect fit here. The right panel shows the corresponding $\hat{\gamma }$s for different $\kappa $ values. We can see that as $\kappa $ increases, the time warping functions get increasingly closer to $\gamma _{id}$.

Remark 1

Several other published techniques can also potentially provide an element of the correct shape class in function estimation. However, they do not ascribe any notion of optimality to that solution. For example, by modifying the bandwidth, one can easily fit a k-modal function to the data using a kernel estimator. It is not enough to provide an element of the correct shape class; the answer should be optimal somehow. In our approach, Eq. 11 defines an optimality criterion, and the dynamic programming algorithm helps find the optimal solution.

The previous section also developed a more abstract notion of shape that is purely based on the modal count and ignores the heights of the peaks and valleys. One can imagine an estimation problem where only the mode count is provided a priori instead of the equivalence class $[f_0]$ of the function. In other words, given observed data $\{(t_{i}, y_i) \in I\times \mathbb {R}\}$, how can we estimate a function that is constrained to have a fixed number, say k, of peaks? Interestingly, there is rich literature on estimating probability densities under shape constraints. However, that literature is basically restricted to elementary shapes, e.g., unimodal density estimation (Cheng et al. 1999; Hall and Huang 2002; Bickel and Fan 1996; Wegman 1970; Rao 1969; Birge 1997). Dasgupta et al. (2018), Dasgupta (2019) has developed a general mathematical framework for fitting mode-constrained functions to the given data with an arbitrary number of modes. The formulation involves solving a penalized-ML problem on both the placements and heights of the peaks. Figure 15 shows an example of this estimation. The blue dots represent the data points $\{(t_{i}, y_i)\}$ and three function estimates under k-modal constraint with $k=1$, $k=2$, and $k=3$. A recent paper (Kim et al. 2023) studies the complementary problem of estimating the number of peaks in the functional data using a novel geometric representation termed peak-persistence diagram. This estimation of the number of peaks, combined with the shape-constrained function estimation procedure, provides an end-to-end solution to the inference problem.

4.2 Shape-based fPCA

An essential FDA tool mentioned in Sect. 2.2.2 is dimension reduction using PCA. We often need to approximate functions with finite-dimensional vectors to be able to apply multivariate statistical analysis. For instance, we perform fPCA to develop generative models of functional data. Here, we introduce a novel perspective on capturing variability in functional data while focusing on preserving shapes. We call the approach shape fPCA to contrast it with the previously discussed fPCA analysis.

We have discussed earlier the process of extracting shapes from functional data by registering or time-warping the given functions $\{f_i\}$. Instead of analyzing the original functions, we decompose the data into two more interpretable parts: phases and shapes. Consequently, we perform the fPCA of these components separately. Let the SRVFs of the aligned functions $\{\tilde{f}_i\}$ be $\{\tilde{q}_i\}$. We can obtain the covariance function of these SRVFs and reach the directions of principle variability in the given shapes by conducting the SVD of the covariance function, $C_s = U_s\Sigma _s V_s^T$. Note that we are computing the PCA in the SRVF space of the aligned functions (the phase is already separated). This is why we call it the shape fPCA. To perform fPCA of the phase terms, we compute their own SRVFs according to $q_{\gamma _i}^* = \sqrt{\dot{\gamma }_i^*}$. Then, we can obtain the directions of principal variability in phase space by using the covariance function of these $\{q_{\gamma _i}^*\}$. Note that the SRVFs of phase functions should have unit $\mathbb {L}^2$ norm. In practice, we impose that condition by normalizing any SRVF that does not satisfy unit normality.

Shown in panels (A) and (B) of Fig. 16 are two examples of simulated datasets with low phase variability and high phase variability, respectively. The remaining panels show illustrations of the shape and phase PCA of these two datasets. The second column shows the first dominant direction of the shape fPCA, and the third column shows the first dominant direction of phase PCA by plotting the functions from $\mu -\sigma $ to $\mu +\sigma $ in each case. The two datasets differ only in the level of their phase variability but are similar in shapes. The example shown in panel (B) has more significant phase variability, as illustrated by a more extensive deformation in the first principal direction of phase PCA. Also, since we separately analyze the shape and phase variability, the first shape PC is perfectly vertical and shows the explicit variability in the height of peaks and valleys. This separation of phase and shape components helps us understand the nature of data when dealing with underlying scientific questions.

Once we get the shape-PCA principal directions, we can calculate the principal coefficients as $c_{s,ik} = \left\langle q_i,U_{s,k} \right\rangle $ and $c_{p,ik} = \left\langle q_{\gamma _i}^*,U_{p,k} \right\rangle $. $\{c_{s,ik}\}$ and $\{c_{p,ik}\}$ are the finite-dimensional Euclidean representations of the aligned (shapes) and phase functions. Then, one can impose probability models on the principal coefficients and generate randomly sampled shapes $\tilde{h}$ and phases $\tilde{\gamma }$ using their respective PCA bases $U_s$ and $U_p$. The compositions $\tilde{f} = \tilde{h} \circ \tilde{\gamma }$ provide random elements of the function space ${\mathcal {F}}$ according to the underlying probability model. Panel (C) in Fig. 16 presents two examples of randomly generating functions according to independent Gaussian distributions on the principal coefficients. We first generate random principal coefficients of the first three dominant shape fPCA directions following the Gaussian distributions and then reconstruct the random shape and warping functions $\tilde{h}$ and $\tilde{\gamma }$, as shown in the second and third column. The fourth column shows their compositions, i.e., the randomly sampled functions following the Gaussian distribution. For comparison, we follow the same model for the fPCA of given functional data directly (without shape and phase separation) and generate random functions shown in the first column. The functions modeled with shape fPCA are more consistent with the original functions, especially when large phase variability exists in the original data (second row in panel (C)).

4.3 Shape regression methods

Section 2.2.3 discussed some basic regression models involving random functions as inputs, either as predictors, responses, or both. Now, we shall consider situations where the interest lies in the shapes of these functions as regression variables. In other words, the phase components are treated either as nuisance variables wholly or of relatively less importance. Therefore, it becomes essential to separate the phase and shape components and treat them appropriately. The question is: What is the definition of phase for shape regression? Not surprisingly, this definition may differ from the one used for function registration or shape fPCA.

We aim to modify, adapt, and apply the models presented in Sect. 2.2.3 to the problem of shape regression. As stated, these models do not account for the phase variability in functions and require some modifications. We use equivalence classes of functions rather than individual functions as variables to represent shapes. Thus, a regression model should not depend on which specific elements of the equivalence classes are selected. Since the only variability inside an equivalence is due to phase, a shape regression model should be invariant to the phase variability. There are several ways to accomplish this:

Direct maps to and from shape spaces: The natural idea is to utilize mappings intrinsic to the shape space ${{\mathcal {S}}}$ and use them as conditional means in shape regression models. For example, one can use a map $h: {{\mathcal {S}}} \rightarrow \mathbb {R}$ for scalar-on-shape regression or a map $h: {{\mathcal {S}}} \rightarrow {{\mathcal {S}}}$ for shape-on-shape regression. The question is: How to define these maps that are intrinsic to a shape space? Many of the past functional regression models are essentially linear (although some involve using a link function to introduce nonlinearity). Since ${{\mathcal {S}}}$ is nonlinear, one cannot directly apply those ideas here. Recall that in Sect. 3.5, we established a vector notation $\textbf{x}_f = (x_0^+, x_1^-, \dots )$ to capture the shape of a function f. The elements of this vector are the heights of the extrema of f. (Also note that the set of valid $\textbf{x}$ is not a vector space due to different dimensionalities and relative height constraints.) The design of valid and interpretable mappings from the shape representative x to a response space $\mathbb {R}$, when the dimensions of $\textbf{x}$ are variable, remains challenging.
Pre-registration: Another, albeit less intrinsic, approach is to work with individual functions but remove the phase variability via an additional optimization step. Depending on the context, one can do this removal for all functions—responses, predictors, or both. For instance, in a scalar-on-shape problem, one can apply optimization over $\gamma _i$s stated in Eq. 9 to obtain the shape-phase pairs $\{( \tilde{f}_i, \gamma _i) \}$ from the predictor functions $\{f_i\}$. Then, discard the phases and use the shapes $\{ \tilde{f}_i\}$ as if they are elements of ${{\mathcal {F}}}$. This approach is called pre-registration because it removes the phases before regression analysis starts, while practical, it has several problems: (1) The relationship between predictors and responses is not utilized in this phase removal. It only uses the information within the functions that form the predictors. Thus, in the context of regression, this approach is sub-optimal. (2) A complete pre-removal of phase only makes sense when phases are a non-informative nuisance in regression models. If the phases carry some information relevant to the predictor-response relationship, one should not throw them out completely.
Registration inside regression model: Another way to focus on the shape is to formulate an optimization problem similar to Eq. 9 but in conjunction with a regression model. That is, redefine and isolate the phase as a part of the regression analysis, not in a pre-processing step. This approach has the advantage of letting the context guide the definition of phase rather than using the previous definitions. For example, suppose we apply this approach to the scalar-on-shape problem. In that case, the definition (and subsequent removal) of the phase from the predictor functions will also depend on the response variable. By definition, this phase-shape separation should perform better than the pre-registration approach.
Separate and include both shape and phase in regression: Lastly, we mention an option that separates phase and shape using Eq. 9, and instead of discarding the phases, includes them (along with shapes) as separate regression variables. For example, consider the scalar-on-shape regression problem. Let $\{(f_i, y) \in {{\mathcal {F}}} \times \mathbb {R}\}$ denote the prediction-response pair data and let $\{ f_i \equiv ( \tilde{f}_i, \gamma _i) \}$ denote the shape-phase separation of functional predictors using Eq. 9. Then, we can include both $\{ \tilde{f}_i\}$ and $\{ \gamma _i\}$ as predictors in this approach for predicting the response $\{y_i\}$.

In this paper, we will pursue the third option, namely that of registration inside a regression model. This leads to a new definition of the phase, different from the one used for functional alignment and shape fPCA. We start the discussion by studying the consequences of ignoring phase variability in the classical functional regression models when they (phases) are indeed nuisance variables.

4.3.1 Consequences of ignoring phase variability

What happens when we use the full functions $\{f_i\}$, instead of their shapes, in situations where only the shapes carry the relevant information? In other words, how does the presence of random and uninformative phases affect the performance of a classical regression model? We use some examples to investigate this question. Consider Eq. 9 that defines the decomposition of a function $f_i$ into its shape $[f_i]$ (represented by $\tilde{f}_i$) and the nuisance transformation $\gamma _i$. Since current methods work with $f_i$, instead of $[f_i]$, they contain arbitrary transformations $\gamma _i$.

Scalar-on-function regression model: We start with the case of phase variability in functional predictors. Consider the simple, functional linear regression model mentioned in Eq. 3. Given the data $\{(y_i, f^x_i)\}$, we have techniques for estimating the regression coefficient $\beta $. Suppose, instead of observing precise $f^x_i$s, one observes $\tilde{f}^x_i = f^x_i \circ \gamma _i$, where $\gamma _i \in \Gamma $ is an arbitrary time-warping of $f^x_i$s which is independent of $y_i$. In other words, the shapes are given to us as arbitrary elements of their orbits. This scenario is similar to having errors in the time indices for functional data and has been discussed in Carroll et al. (2006).

We use a simulation experiment to demonstrate this issue, with results shown in Fig. 17. The main idea is to quantify the deterioration of prediction performance as the amount of random warping in the predictor functions increases. The left panel shows the predictors $\{f^x_i\}$ used in these experiments. For a fixed $\beta _0$, we simulate responses $y_i$s using Eq. 3, and use the data $\{f^x_i, y_i\}$ to estimate the model parameters, including $\hat{\beta }$. Using this estimated $\hat{\beta }$, we predict the response variable for predictors that are now contaminated by time-warping $\{\tilde{f}^x_i\}$. We quantify prediction performance using $R^2$ and study its value as the warping noise increases. The warping functions used in this experiment are $\gamma _i(t) = t + \alpha _i t (1-t)$, where $\alpha _i \sim U(-a, a)$; larger the value of a, larger is the warping noise. The middle two plots show examples of warping functions for $a = 0.02$ and $a=1$. The last panel shows a plot of $R^2$ versus a (averaged over 200 runs)—a superlinear performance decay due to the introduction of random phases and the resulting misalignments.

Function-on-scalar regression model: As a different example, we now demonstrate consequences of random phases in the response variable. Consider the following function-on-vector regression model:

$$\begin{aligned} f^y_i(t)=x_{i,1}{\beta }_1({t})+x_{i,2}\beta _2({t})+\epsilon _i({t}),~i=1,\ldots ,n,\ \ t\in [0, 1]\, \end{aligned}$$

(12)

where $f^y_i \in {{\mathcal {F}}}$ is a functional response, $(x_{i,1},x_{i,2}) \in \mathbb {R}^2$ are Euclidean predictors, $\epsilon _i \in {{\mathcal {F}}}$ represents the measurement error, and $(\beta _1, \beta _2) \in {{\mathcal {F}}} \times {{\mathcal {F}}}$ are prespecified functional coefficients. Given samples $\{(f^y_i, x_{i,1}, x_{i,2})\}$, the smoothing techniques can be adopted for estimating $\beta _1$ and $\beta _2$. The main issue with this framework is that it fails to account for potential misalignment in the functional responses. Suppose that instead of observing $\{f^y_i\}$, one observes $\tilde{f}^y_i(t) = f^y_i(\gamma _i(t))$, with the random warping functions $\gamma _i(t) = t + \alpha _i t (1-t)$. Here $\alpha _i \sim U(-a,a)$, and a are set as 0, 0.05, 0.1, 0.3, 0.5, 0.7, 1, respectively.

The results from this simulation experiment are shown in Fig. 18. In this simulation, the sample size $n=50$, the predictors $\{(x_{i,1}, x_{i,2})\}_{i=1}^n$ were independently generated from multivariate normal distribution with covariance matrix $\Sigma = \begin{pmatrix} 1 &{} 0.6 \\ 0.6 &{} 1 \end{pmatrix}$, and the measurement error $\{\epsilon _i\}_{i=1}^n$ were independently generated from a Gaussian process $GP({0},0.5^{\Vert {s}-{s}'\Vert })$. The main idea is to quantify the estimation accuracy of functional coefficients as the bound a increases. The true values of functional coefficients $\beta _1({t})$ and $\beta _2({t})$ with predefined patterns are shown in the left two panels of Fig. 18. The functional responses $\{f^y_i({s})\}_{i=1}^n$ were simulated through Eq. 12, then contaminated via warping functions. Then, the functional coefficients were estimated using this data via the local linear kernel smoothing method (Fan and Zhang 1999). To quantify estimation errors, we use two metrics: mean integrated absolute error (MIAE) and mean integrated squared error (MISE). As shown in the last two panels of Fig. 18, both MIAEs and MISEs for these two coefficient functions increase as the amount of misalignment (i.e., the bound a) increases.

Now, we discuss some techniques for using shape variables in regression models that can nullify the presence of arbitrary phases in the data.

4.3.2 Scalar-on-shape regression

Scalar-on-shape is a natural problem that frequently arises in statistical shape analysis. Applications include regression of clinical measures of diseases using shapes of physiological or anatomical measurements. For example, Physionet (https://physionet.org/) is a website devoted to datasets that study relationships between physiological measurements (functional data) of human subjects and clinical outcomes relating to health. Similarly, other shape data has been used to predict Euclidean outcomes by solving the scalar-on-shape regression problems. Specifically, let $\{[f^x_i],y_i\}_{i=1}^n$ be the observed data, where $[f^x_i]$ is an element of a shape space $\mathcal {S}$, and $y_i \in \mathbb {R}$ is a Euclidean variable. Then, the scalar-on-shape regression model (Lin et al. 2019; Niu et al. 2019; Lin and Yao 2021) can be written as

$$\begin{aligned} y_i=g([f^x_i])+\epsilon _i,~ i=1,\ldots ,n, \end{aligned}$$

(13)

where $g:\mathcal {S}\rightarrow \mathbb {R}$ is the regression function on $\mathbb {R}$, and $\{\epsilon _i\}_{i=1}^n$ are independent errors. Several kernel-based approaches have been used to estimate the unknown function $g(\cdot )$, including extrinsic approaches that model Gaussian processes on the embedding space of $\mathcal {S}$ (Lin et al. 2017) or on the tangent space of $\mathcal {S}$ (Lin and Yao 2021). Intrinsic approaches use Brownian motion sample paths generated on the shape space $\mathcal {S}$ (Niu et al. 2019). The shape spaces in these cases may differ from those in the current paper.

Earlier, we discussed several approaches for incorporating shapes in a regression model. In the pre-registration approach, phase separation or alignment is performed independently of the response variable. In other words, the values $\{y_i\}$ do not play any role in the alignment. In contrast, the registration-inside-regression approach, where the phase separation is a part of the estimation of model parameters, seems more natural. An example of this approach is the so-called elastic functional regression model (Ahn et al. 2020, 2018; Lin and Yao 2018; Tucker et al. 2019; Wang et al. 2016):

$$\begin{aligned} y_i=g\left( \sup _{\gamma _i\in \Gamma }\langle \beta ,f_i^x*\gamma _i\rangle \right) +\epsilon _i,~ i=1,\ldots ,n, \end{aligned}$$

(14)

where $g(\cdot )$ is a single index function and $f_i^x*\gamma _i=(f_i^x\circ \gamma _i)\sqrt{\dot{\gamma _i}}$. For alignment, one can represent the predictor $f_i^x$ in the pre-shape space using the square-root velocity function (SRVF) transformation (Srivastava and Klassen 2016). Compared to the pre-alignment-based approaches, the elastic functional regression model is more powerful as the phase separation is performed inside the regression model. In addition, the model (Eq. 14) has nice theoretical properties, including nonlinear relationship captured by the function $g(\cdot )$, invariance to the phase, and identifiability of the coefficient $\beta $ (Ahn et al. 2020).

4.3.3 Shape-on-scalar regression

In order to model the relationships between shape responses and covariates of interest in Euclidean space, various approaches can be grouped into two broad categories: extrinsic regression and intrinsic regression. To understand these two categories better, let $\{[f^y_i],x_i\}_{i=1}^n$ be the observed data, where $[f^y_i]$ is an element of a shape space $\mathcal {S}$, and $x_i \in \mathbb {R}^p$ is a Euclidean variable. In the extrinsic regression framework, the shape responses $\{[f_i^y]\}_{i=1}^n$ are usually embedded onto a subspace in the higher dimensional Euclidean space $\mathbb {R}^m$. Then, the classical regression models in that space are applied, and the estimated models and predictions are projected back onto the original shape space. Specifically, given the covariate x, the estimated extrinsic model, i.e., $\hat{g}(x)$, is derived as

$$\begin{aligned} \hat{g}(x)={h}^{-1}\left( \mathop {\textrm{argmin}}_{q\in \mathbb {R}^m}\Vert q-\tilde{g}(x; \{{h}([f^y_i]),x_i\}_{i=1}^n)\Vert \right) , \end{aligned}$$

(15)

where ${h}: \mathcal {S}\rightarrow \mathbb {R}^m$ is an embedding of $\mathcal {S}$ onto some subspace in $\mathbb {R}^m$ and ${h}^{-1}$ is the corresponding inverse embedding map. Here, $\tilde{g}(x; \{{h}([f^y_i]),x_i\}_{i=1}^n)$ is an estimator of the relationship between the embeddings ${h}([f^y_i])\in \mathbb {R}^m$ and covariates of interest $x_i$ and an example is the kernel-based estimator (Lin et al. 2017, 2019). However, for these extrinsic approaches, the local shape geometry is not well-preserved through the embedding map $h(\cdot )$ and the existence of the inverse embedding map $h^{-1}(\cdot )$ to the shape space is not always guaranteed (Tsagkrasoulis and Montana 2018).

In contrast, the intrinsic approaches are natural generalizations of regression models from Euclidean spaces to non-Euclidean shape geometries, typically using exponential maps and tangent space representations. Specifically, we denote the tangent space at $[f_i^y]\in \mathcal {S}$ by ${T}_{[f_i^y]}(\mathcal {S})$ and the inner product of ${u},{v}\in {T}_{[f_i^y]}(\mathcal {S})$ by $\langle {u},{v}\rangle $. For any ${v}\in {T}_{[f_i^y]}(\mathcal {S})$, there is a unique geodesic curve $\xi : [0,1]\rightarrow \mathcal {R}$, with initial conditions $\xi (0)=[f_i^y]$ and $\xi '(0)={v}$. The exponential map at $[f_i^y]$, $\textrm{exp}_{[f_i^y]}(\cdot ): {T}_{[f_i^y]}\mathcal {(S)}\rightarrow \mathcal {S}$ is locally diffeomorphic and defined as $\textrm{exp}_{[f_i^y]}({v})=\xi (1)$. Meanwhile, the inverse exponential map is defined as $\textrm{exp}^{-1}_{[f_i^{y}]}(\cdot ): \mathcal {S}\rightarrow {T}_{[f_i^y]}(\mathcal {S})$. Then, one can apply a commonly used geodesic regression model:

$$\begin{aligned} {[}f^y_i] = \textrm{exp}_{\kappa (x_i)}({\epsilon }_i),~~~\kappa (x_i)\in \mathcal {S}, \epsilon _i\in {T}_{\kappa (x_i)}(\mathcal {S}), \end{aligned}$$

(16)

where $\textrm{exp}_{\kappa (x_i)}(\cdot ): {T}_{\kappa (x_i)}(\mathcal {S})\rightarrow \mathcal {S}$ is the exponential map at $\kappa (x_i)$, and ${T}_{\kappa (x_i)}(\mathcal {S})$ is the corresponding tangent space. Model (16) involves two key terms: the conditional mean shape $\kappa (x_i)$ and the error $\epsilon _i\in \mathcal {T}_{\kappa (x_i)}\mathcal {S}$. The conditional mean shape $\kappa (x_i)$ can be treated as a link function including the typical parametric setting, i.e., $\textrm{exp}_{\mu }(\textbf{B} x_i)$, where $\mu \in \mathcal {S}$ and columns in $\textbf{B}$ are coefficient vectors lying in the tangent space ${T}_{\mu }(\mathcal {S})$ (Fletcher 2013; Kim et al. 2014; Cornea et al. 2017; Zhang 2020), and some other nonparametric settings, such as the link function model, i.e., $g(x_i)$, where $g(\cdot )$ is an unknown map from $\mathbb {R}^p$ to the shape space $\mathcal {S}$ (Shi et al. 2009; Stöcker and Greven 2021; Xiong et al. 2022). On the other hand, the error term ${\epsilon }_i$ can be specified using parametric, such as the Riemannian Normal (RN) distribution (Fletcher 2013), semiparametric, such as the first-order moment condition (Shi et al. 2009; Cornea et al. 2017), or completely nonparametric models (Kim et al. 2014).

In the intrinsic approaches, the shape response $[f^y_i]$ should be an orbit of a pre-shape space under the rotation group (Srivastava and Klassen 2016). In practice, it is common to take a representative element of the pre-shape space, aligned or rotated appropriately through some preprocessing steps. However, there are several limitations of geodesic regression models caused by using the pre-aligned elements, including (i) misalignment issue in pre-aligned responses (Ahn et al. 2018; Zhang et al. 2018; Shin and Oh 2020; ii) non-optimal alignment due to imaging heterogeneity (Huang 2019); and (iii) lack of spatial correlation structure in modeling (Fletcher 2013; Kim et al. 2014). To address these limitations, a geodesic factor regression model (Huang et al. 2021) is proposed as follows:

$$\begin{aligned} \psi (f^y_i \circ \gamma _i) \mid x_i,z_i \sim \text {RN}\left( \textrm{exp}_{\psi (\mu )}(\textbf{B}{x}_{i}+\varvec{\Lambda }z_i),\sigma \right) ,~z_i\sim {\text {N}}(0,\textbf{I}_q), \end{aligned}$$

(17)

where $\psi (\cdot )$ is a one-to-one map such that the preshape space is equivalent to a unit hypersphere, and $\gamma _i$ denotes the time warping that forms the individual nuisance transformation. Compared to the pre-aligned elements, the time warpings $\{\gamma _i\}$ in model (17) are applied on preshapes and learned inside the regression model itself. In addition, compared to other intrinsic approaches, the spatial correlation structure in model (17) is established as a low-dimensional representation, including latent factors through a factor analysis framework on the tangent space and error term modeled using the isotropic RN distribution (Pennec 2006).

Some other important topics related to shape-on-scalar regressions have also been investigated in existing literature, including hypothesis testing (Shi et al. 2009, 2012; Cornea et al. 2017; Huang et al. 2021) and longitudinal shape analysis (Fishbaugh et al. 2012; Durrleman et al. 2013; Gerig et al. 2016; Kim et al. 2017; Bône et al. 2018; Chakraborty et al. 2018; Nava-Yazdani et al. 2019; Zhang et al. 2023). For the hypothesis testing problems, one is interested in investigating the comparison of shape responses across different groups or detecting the change in shapes across time. Taking the geodesic regression model (16) with $\kappa (x_i)=\textrm{exp}_{\mu }(\textbf{B} x_i)$ as an example, the scientific question can usually be formulated as the following hypothesis:

$$\begin{aligned} \mathbf{H_0:}~\beta _j= 0~~\text{ vs. }~~\mathbf{H_1:}~\beta _j\ne 0, \end{aligned}$$

(18)

where $\beta _j$ is the coefficient corresponding to the j-th covariate of interest, $j=1,\ldots ,p$. Different test statistics, such as the Score test statistic (Shi et al. 2009, 2012) and Wald test statistic (Cornea et al. 2017; Huang et al. 2021), are constructed, and their asymptotic properties under $\mathbf{H_0}$ are derived as well. In practice, the parametric bootstrap procedure is also proposed to derive the empirical distribution and the p-value (Huang et al. 2021). For the longitudinal shape analysis, the linear mixed effects model (LMEM) can be extended in many ways to the shape space. Specifically, let $\{f^y_{i,j},x_{i,j}, j=1,\ldots ,m_i\}_{i=1}^n$ be the longitudinal observed data, where $f^y_{i,j}$ is the shape from the i-th subject at the j-th time point, and $x_{i,j}$ is the corresponding covariates. Then, a natural extension of LMEM (Kim et al. 2017) can be written as

$$\begin{aligned} f^y_{i,j}=\textrm{exp}_{\mu _{i,j}}({\epsilon }_{i,j}),~\mu _{i,j}=\textrm{exp}_{\kappa (x_{i,j})}(\textbf{U}_iz_{i,j}),~\kappa (x_{i,j})=\textrm{exp}_{\mu }(\textbf{B}x_{i,j}), \end{aligned}$$

(19)

where $\textbf{B}$ represents the fixed effect in the tangent space ${T}_{\mu }(\mathcal {S})$ while $\textbf{U}_i$ represents the random effects in another tangent space ${T}_{\kappa (x_{i,j})}(\mathcal {S})$. Some other methods are also adopted to capture the temporal correlations among the longitudinal shapes, such as the deformation model (Fishbaugh et al. 2012; Durrleman et al. 2013; Gerig et al. 2016; Bône et al. 2018), recurrent neural network (Chakraborty et al. 2018), and functional data analysis (Zhang et al. 2023).

4.3.4 Shape-on-shape regression

Finally, we consider the regression setup where both the predictor and the response variables are shapes of functions. This problem arises, for example, when one is interested in modeling changes in anatomical shapes after a medical intervention. The shape of a function before the treatment can be used to model its shape after the treatment. One can use such a regression model to test the efficacy of the intervention. This shape-on-shape regression is the most challenging of the shape regression setups because of the complexity of both the predictor and the response. Consequently, there is limited literature on this topic currently.

Let $[f^x_i], [f^y_i]$ denote the shape of the predictor and response, respectively. To develop shape-on-shape regression, we seek a model of the type:

$$\begin{aligned}{}[f^y_i] = {{\mathcal {A}}}_{\beta }([f^x_i]) \oplus [\epsilon _i]\, \end{aligned}$$

(20)

where ${{\mathcal {A}}}_{\beta }$ is an operator from the shape space ${{\mathcal {S}}}$ to itself and $\oplus $ represents an operation where the effect of additive noise $\epsilon _i$ on only the shape is considered, its effect on the phase is ignored. Associated with ${{\mathcal {A}}}_{\beta }$ is a surface $\beta (s,t)$ that represents the coefficient of regression, similar to the function-on-function model presented in Eq. 5. The key requirement here is that the model should not depend on the phases of either $f^x_i$ or $f^y_i$. One way to define the operator ${{\mathcal {A}}}_{\beta }$ is through a special inner product $\left\langle \langle \beta (s, \cdot ),f\rangle \right\rangle \triangleq \left\langle q_{\beta }(s,\cdot ),q_f \right\rangle $, where $q_{\beta }(s,\cdot ),\ q_f$ are the SRVFs of $\beta (s,\cdot )$ and f, respectively. Note that the quantity $\left\langle \langle \beta (s,\cdot ),f\rangle \right\rangle $ is a function of s but represents a shape rather than an element of ${{\mathcal {F}}}$. To motivate this definition, we mention the isometric property of SRVFs that states: $\left\langle q_{\beta }(s,\cdot ),q_f \right\rangle = \left\langle q_{\beta }(s,\cdot )\star \gamma ,q_f \star \gamma \right\rangle \, \text{ for } \text{ any }\ \ \gamma \in \Gamma $. One consequence of this property is that:

$$\begin{aligned} \sup _{\gamma \in \Gamma } \left\langle q_{\beta }(s,\cdot ),q_f \star \gamma \right\rangle = \sup _{\gamma \in \Gamma } \left\langle (q_{\beta }(s,\cdot ) \star \gamma _1),(q_f\star \gamma _2) \star \gamma \right\rangle \,. \end{aligned}$$

That is, the supremum of the inner product is unaffected by the phases of $q_f$ and $q_{\beta }(s,\cdot )$. Thus, using SRVFs and this invariance to time-warping helps define the desired operator ${{\mathcal {A}}}$: ${{\mathcal {A}}}_{\beta }([f])(s) = \sup _{\gamma \in \Gamma } \left\langle q_{\beta }(s,\cdot ),q_f \star \gamma \right\rangle $. Putting these ideas together, we reach a regression model:

$$\begin{aligned} q_i^y(s) = \left( \left( \sup _{\gamma _i \in \Gamma } \left\langle q_{\beta }(s,\cdot ),q_{f_i^x} \star \gamma _i \right\rangle + \epsilon _i(s) \right) \star \gamma ^y_i(s) \right) \,. \end{aligned}$$

The inclusion of the last $\gamma ^y_i$ implies that $f^y_i$ is observed with an arbitrary phase. The additive noise $\epsilon _i \in {{\mathcal {F}}}$ affects not just the shape but also the phase of the mean function. However, the effect on phase is nullified by the inclusion of an arbitrary phase $\gamma ^y_i$ in the model. The estimation of $\beta $ corresponds to the optimization:

$$\begin{aligned} \hat{\beta } = \mathop {\textrm{argmin}}_{\beta } \sum _{i=1}^n \left( \inf _{\gamma ^y_i \in \Gamma }\Vert (q^y_i\star \gamma ^y_i) - \sup _{\gamma _i \in \Gamma } \left\langle q_{\beta },q_{f^x_i} \star \gamma _i \right\rangle \Vert ^2 \right) \end{aligned}$$

(21)

Of course, there are several potential variations of this model and one can choose according to the situation. Experimental evaluations of this model and its application to real data are left for future efforts.

5 Manifold-valued functions

A significant portion of FDA literature is focused on scalar or Euclidean vector-valued functions on domain I. However, in mathematics, the concept of functional variables and function spaces is much broader. It also includes functions where the range spaces are non-Euclidean. In this section, we consider the shapes of functions of the type $f:I\rightarrow M$, where M is a Riemannian manifold. In the previous sections, we have relied on SRVFs to analyze shapes of function, but now M is a nonlinear manifold, and the nature of SRVFs changes. Since SRVFs are essentially scaled derivatives of functions, and derivatives on manifolds correspond to tangent vectors, we cannot directly compare tangent vectors of different functions. We will need additional tools like parallel transport that allows one to transport tangent vectors from one point to another and then compare SRVFs.

To keep the discussion non-technical, we will assume that the functions are smooth, i.e., and one can compute as many derivatives of f as needed. The Riemannian structure of M allows us to compute intrinsic distances and other geometric quantities on M as needed. As a simpler visual example, we can use $M = \mathbb {S}^2$ to help facilitate the discussion. Such functions are also called manifold-valued curves or trajectories (Zhang et al. 2018a, b). For instance, when M is the shape space of objects the M-valued functions have been called shape curves (Kenobi et al. 2010; Kume et al. 2007; Jupp and Kent 1987; Su et al. 2011).

Given a Riemannian structure on M, one can define a distance $d_M: M \times M \rightarrow \mathbb {R}_+$ such that the length of the shortest path (or geodesic) between any two points $p, q \in M$ equals $d_M(p,q)$. This geodesic length can be used to establish a sample mean on M as follows. For a set of points $\{ p_i \in M, i=1,2,\dots ,n\}$ sampled from a distribution, their sample mean is defined to be:

$$\begin{aligned} \bar{p}_n = \mathop {\textrm{argmin}}_{p \in M} \sum _{i=1}^n d_M(p, p_i)^2. \end{aligned}$$

(22)

This quantity has alternatively been called the Karcher, intrinsic, or Fréchet mean. There is a well-known algorithm for estimating this mean from the given data, and we will not repeat it here (Le 2001; Le and Kendall 1993; Srivastava and Klassen 2016). We point out that there also exist tools for computing sample median (Fletcher and Venkatasubramanian 2009; Pennec et al. 2019) and sample modes on manifolds and help derive robust statistical inferences (Deng et al. 2022). Such summarizing tools can be readily used for computing pointwise summaries of M-valued functions.

One can also establish a notion of the sample covariance but not directly on the manifold M. Since M is not a vector space, this computation is performed on the manifold’s tangent space, a vector space. Let $T_{\bar{p}_n}(M)$ denote the space of vectors tangents to the manifold M at the sample mean $\bar{p}_n$. For each observation $p_i$, we can map it to the tangent space according to $p_i \mapsto v_i$, $v_i = \exp _{\bar{p}_n}^{-1}(p_i)$. It is the analog of the different $p_i - \bar{p}_n$ in a Euclidean space and can then be used to compute the sample covariance matrix according to $\hat{C} = \frac{1}{n-1} \sum _{i=1}^n v_i v_i^T \in \mathbb {R}^{m \times m}$. Note that the vectors $v_i$s are elements of the same tangent space, so they can be treated as Euclidean and analyzed conventionally. For instance, one uses singular value decomposition of $\hat{C}$ to perform PCA, and this approach is called a tangent PCA or TPCA. TPCA results in tangential directions on M at the point $\bar{p}_n$, which can then be mapped on M to visualize principal (geodesic) paths on M. This TPCA on M, in turn, helps facilitate pointwise fPCA of M-valued functions.

5.1 Essential tools for M-valued functions

In order to perform data statistical analysis of M-valued functions, we need some basic tools. Similar to the previous sections, one can develop a core set of tools for analyzing M-valued functions.

1.
Curve fitting: The problem of fitting scalar functions on I can be extended to estimating M-valued functions using the optimization:
$$\begin{aligned} \hat{f} = \mathop {\textrm{argmin}}_{f \in \mathbb {L}^2(I,M)} \left( \sum _{i=1}^n d_M(y_i, f(t_i))^2 + \kappa {{\mathcal {R}}}(f) \right) \, \end{aligned}$$
(23)
where ${{\mathcal {R}}}(f)$ is a measure of roughness of f. Some common choices of ${{\mathcal {R}}}(f)$ are:
$$\begin{aligned} \int _I\left\langle \dot{f}(t),\dot{f}(t) \right\rangle _{f(t)}~dt\ \ \ \text{ or }\ \ \ \int _I\left\langle \frac{D \dot{f}(t)}{dt},\frac{D\dot{f}(t)}{dt} \right\rangle _{f(t)}~dt\,. \end{aligned}$$
Here, $\dot{f}(t)$, $\frac{D \dot{f}(t)}{dt}$ denote the velocity and acceleration along f(t), respectively. $\frac{D}{dt}$ represents a covariant derivative, ensuring the derivative is tangent to the manifold. For any function $f: I\rightarrow M$, the ordinary derivative $\dot{f}(t)$ lies in the tangent space $T_{f(t)}(M)$ automatically, so the first derivative need is already covariant. However, the second ordinary derivative, $\ddot{f}(t)$, may not necessarily be in the tangent space and requires an additional projection to make it tangential and $\frac{D \dot{f}(t)}{dt}$ is that projection.

Comparing Eq. 23 with Eq. 1, we see that the terms are simply the manifold analog of Euclidean terms. The Euclidean square error is replaced by the manifold distance $d_M$ squared error. The solutions to this problem are also called smoothing splines, and there is now extensive literature on estimating smoothing splines from noisy, discrete data. Numerous papers including (Noakes et al. 1989; Camarinha et al. 1995; Crouch et al. 1999; Hofer and Pottmann 2004; Machado et al. 2006; Machado and Leite 2006; Samir et al. 2012) have studied variations of these problems and their computational solutions. The problems of fitting smooth curves and interpolating between landmark-based shape representations, called shape curves have been studied by Dryden, Kent, and collaborators (Jupp and Kent 1987; Kenobi et al. 2010; Kume et al. 2007). A common thread among these solutions is the need to evaluate the Riemannian curvature tensor on M. While this tensor is available for some of the commonly used manifolds in statistics (unit spheres, positive-definite matrices, and some shape manifolds), it is generally not the case. This limits the past developments on spline-type techniques for fitting curves to M-valued data. Also, these methods are helpful only when the time samples are reasonably dense. In the case of temporally sparse data, there is insufficient information to provide meaningful dense interpolations. Zhang et al. (2023) utilized a flattening approach for interpolating in the shape space of 3D subcortical objects using sparse data points.

Figure 19 shows an example of fitting smoothing splines to points in a shape space of 3D curves. The specific shape space used in this example is not developed here explicitly, as we use it only as an example. The top left shows four shapes observed at time points $t=1,6,11, 16$, and the bottom left shows a spline interpolation between them using elastic shape analysis. This elastic interpolation uses an optimal registration of points between successive curves, shown in the top right. The bottom-right panel shows a piecewise-linear interpolation between the given 3D curves for comparison. One can see that the spline curve in shape space better preserves the geometric features (bends and twists) in the newly interpolated shapes.
2.
Cross-sectional statistics: As an essential tool for summarizing M-valued functional data, one would like to compute cross-sectional or pointwise averages. Given a set of functions $\{f_i:I\rightarrow M\}$, we assume they are temporally registered. For any $t \in I$, the points $\{f_i(t)\}$ correspond to each other in some interpretable way. Then, for any $t \in I$, we can compute summaries of the points $\{f_i(t) \in M\}$ using the sample mean defined in Eq. 22. This results in a cross-sectional mean function $\bar{f}: I\rightarrow M$ that represents the functions mean of all $f_i$s. Using the inverse exponential map mentioned above, we can compute the tangent vectors $v_i(t) = \exp _{\mu (t)}^{-1}(f_i(t))$ and form a sample covariance matrix $\hat{C}(t)$. This sample matrix can be used to perform TPCA at each tangent space separately. One shortcoming of this idea is that we are not using covariances of $f_i(t)$s across times to help determine the principal directions of complete functions. In that sense, this process is not a functional PCA but a collection of individual M-valued TPCAs. (In contrast, the analysis in Sect. 2.2.2 used the full fPCA of functions.) The complete functional data analysis requires defining a cross-covariance between $f_i(t)$ and $f_i(s)$, which requires additional machinery.

Figure 20 shows examples of cross-sectional statistics for functions on $M = \mathbb {S}^2$. The left column shows original data sets: the top shows Swainson hawks’ migration paths, and the bottom shows trajectories of recent hurricanes originating in the Atlantic Ocean. The middle columns show their cross-sectional mean as the central curve. It also shows cross-sectional covariances at some chosen points using ellipses to depict 2D covariance matrices. It is noticeable that in the top examples, the ellipses are oriented along the mean function direction. This indicates that these functions are not well registered, i.e., they have large phase variability. We discuss the tools for registering M-valued functions next.

5.2 Flattening using parallel transport

Another way to analyze M-valued functional data is to transform them into Euclidean functions and then apply the Euclidean techniques discussed earlier. Naturally, there are multiple ways to “flatten" M-valued functions. A naïve approach is to choose a global reference point $p_0$ on M and map each point $f_i(t)$ to the tangent space $T_{p_0}(M)$ using the inverse exponential maps $f_t(t) \mapsto \exp _{p_0}^{-1}(f_i(t))$ (Su et al. 2014). However, this mapping can introduce a large distortion in the pairwise distances between points, especially when the points are scattered away from $p_0$ on M. An alternative is to use the parallel transport of tangent vectors, which reduces the distortions but uses the time derivatives of functions (Zhang et al. 2018a, b). This approach has also been called unrolling or unwrapping in the shape analysis literature (Kume et al. 2007).

To make the discussion concrete, we will assume $I= [0,1]$. For a function $f_i: [0,1] \rightarrow M$ let $\dot{f}_t(t)$ denote the velocity vector along $f_i$ at times t. By definition, this velocity $\dot{f}_i(t)$ is an element of the tangent space $T_{f_i(t)}(M)$. Using $f_i(0)$ as the reference point, we parallel transport (please refer to the definition of the parallel transport in Srivastava and Klassen 2016) this vector along the curve to reach a tangent vector at the starting point $f_i(0)$; we denote it by $(\dot{f}_i(t))_{f_i(t) \rightarrow f_i(0)}$. Repeating it for all $t \in [0,1]$ results in a function $v_i(t): I\rightarrow T_{f_i(0)}(M)$ with values in a vector space $T_{f_i(0)}(M)$.

One wants to use the flat nature of initial tangent spaces $T_{f_i(0)}(M)$ to analyze data. However, there is still one hurdle left in that the vector spaces $T_{f_i(0)}(M)$ are different for different observation indices i. Thus, one cannot directly compare functions lying in different spaces. To reconcile this, we can compute their mean $\bar{f}(0)$ of the set $\{f_i(0), i=1,2,\dots ,n\}$ on M and treat it as a global reference point. In other words, we transport all the curves $v_i$ from $f_i(0)$ to this global reference point to bring all the functions to the same coordinate system; Call these functions $g_i: I\rightarrow T_{\bar{f}(0)}(M)$. Since $g_i$s are functions in the same vector space, one can directly apply the tools discussed in Sect. 2. For example, we can perform phase-shape separation and temporal register these curves. The rightmost column of Fig. 20 shows the cross-sectional mean and covariances after the data have been registered in this way. Notice that the ellipses are now mainly oriented perpendicular to the curves rather than along them.

5.3 Shapes of M-valued curves

The next question is: What is the notion of shapes for M-valued functions or trajectories? Similar to Sect. 3.2, one can define the time-warping group on I and define the shape as an equivalence class. The time warping of a function $f: I \rightarrow M$ does not alter the graph (and thus the shape) of f and is called a re-parameterization of f. The re-parameterization group, $\Gamma $, is shape-preserving and thus needs to be removed when we focus on shapes of M-valued functions. (Re-parameterization here also performs temporal registration of functions across observations.) Similar to Definition 1 for Euclidean functions, we can define a notion of shape here.

Definition 2

(Shape of a function) For any function $f: I\rightarrow M$, its equivalence class $[f] = \{ f \circ \gamma : \gamma \in \Gamma \}$ is called the shape of f. The set of all shapes ${{\mathcal {S}}}_M = \{ [f]: f \in {{\mathcal {F}}}\}$ is called the shape space of functions.

In order to compare shapes of such functions, the notion of square-root velocity functions (SRVF) has been extended to the transported SRVFs (Su et al. 2014; Zhang et al. 2018b, a). Define the transported square-root velocity function (TSRVF) of f to be

$$\begin{aligned} q(t)= \left( \frac{\dot{f}(t)}{\sqrt{\Vert \dot{f}(t)\Vert }}\right) _{f(t) \rightarrow f(0)} \,. \end{aligned}$$

The subscript $f(t) \rightarrow f(0)$ denotes the parallel translation of the scaled tangent vector $\frac{\dot{f}(t)}{\sqrt{\Vert \dot{f}(t)\Vert }}$ from f(t) to f(0) along f. Consequently, the function q is a function on I with values in the tangent space $T_{f(0)}(M)$. Note that one can reconstruct f from its SRVF q and the seed point f(0). That is, given (q, f(0)), the original function $f(t) = exp_{f(0)}(\oint _0^t \Vert q(t)\Vert (q(t))_{f(0) \rightarrow f(t_{-})} dt)$. Here, $\oint $ denotes the covariant integration of the vector q(t) from f(0) to a point $f(t_{-})$ just before t.

The TSRVF of a function $f:I \rightarrow M$ is a function $q:I: T_{f(0)}(M)$. Thus, TSRVFs of different functions take values in different tangent spaces. In order to register and compare any two of them, we need to parallel transport them to the same space. For example, consider two M-valued functions $f_1, f_2: I \rightarrow M$ and their TSRVFs $q_i: I \rightarrow T_{f_i(0)}(M)$. If we parallel transport $q_1(t)$ from $f_1(0)$ to $f_2(0)$ along a geodesic, for all $t \in I$, resulting in $q_1^{\parallel }(t)$, then we can compare them in the same way as the scalar functions are handled in Eq. 7.

$$\begin{aligned} d_s([q_1], [q_2]) = \inf _{\gamma \in \Gamma }\left\| q_1^{\parallel } - (q_2 \star \gamma )\right\| \,. \end{aligned}$$

(24)

Figure 21 shows an example of this registration for two $\mathbb {S}^2$-valued functions. The left panel shows the original functions $f_1, f_2$ with colors depicting their parameterizations. The middle panels show the registration using Eq. 24, and the function $f_1$ is now re-parameterized using the optimal $\gamma $. The optimal warping is shown in the right panel.

Similar to Eq. 9, this framework for pairwise shape comparisons can be extended to phase-shape separation for a set of M-valued functions. Further statistical analyses, including shape summaries and regression models, can also be pursued in a similar manner although with some additional computational challenges.

6 Some open problems

In this section, we list some open problems for future research in the field of shape-based FDA. This is not a comprehensive list and contains only the most relevant problems.

Adaptive definition of phase of functions: As highlighted in this paper, the definition of phase (and this shape) of a function is not universal. Early in Sect. 3.2, we defined phase of a function as the time-warping (of I) that facilitates optimal alignment of peaks, valleys, and slopes between functions. Later on, in Sect. 4.3, we defined the phase differently for the regression models. Here, the phase is time warping of variables that optimizes the prediction power from the predictor to the response. In other situations requiring some other statistical aims, the phase can have yet another definition. One needs to develop adaptive definitions of phases of functions according to the situation, and reconcile their behaviors across definitions.
Direct maps to and from shape spaces for regression models: Section 4.3 outlines several ways to develop statistical regression models involving shape variables. We focused on approaches that involve explicit phase-shape separation, but methods that use direct maps to and from shape spaces (quotient spaces) are yet to be developed. These maps must be invariant to the time-warping of functions to focus solely on their shapes. Some general nonparametric approaches involving kernels and shape metrics can be applied here (Ferraty and Vieu 2006), but techniques that further exploit shape space geometry are currently missing.
Theoretical foundations for FDA of M -valued functions: The textbook (Hsing and Eubank 2015) provides a comprehensive theoretical foundation for FDA under the standard Hilbert geometry for scalar- or Euclidean-valued functions. The literature lacks a similar, foundational treatment of M-valued functions. Therefore, several tools are lacking when it comes to FDA of M-valued functions. For example, the computation of covariance for M-valued functions in Sect. 5.1 treated each point along the function independently. In other words, that process did not define a joint covariance operator for all pairs of times (s, t), as is usually the case in fPCA. We were able to define a full (s, t)-indexed covariance but only after using a flattening approach, not in an intrinsic way on the manifolds. This field requires a lot of work to reach the maturity level of Euclidean FDA.
Beyond scalar functions: Note that while our primary focus in this paper is on functions of the type $f:I\rightarrow \mathbb {R}$, where I is a one-dimensional space, several of the ideas presented here also apply to curves of the type $f: I \rightarrow \mathbb {R}^d$ for $d > 1$. For $d > 1$, the notion of shapes and shape statistics remain the same. However, one important difference between $d=1$ and $d > 1$ is that time warping does not change the graph of the function for $d > 1$. Figure 22 shows an example with $d = 2$. The leftmost panel shows a curve $f: I\rightarrow \mathbb {R}^2$ in blue under the uniform parameterization (equally spaced points). For the $\gamma $ function shown in the second panel, the time warping of the coordinate functions $f_x \mapsto f_x \circ \gamma $, $f_y \mapsto f_y \circ \gamma $ are shown in the last two panels. The curve $(f_x \circ \gamma , f_y \circ \gamma )$ goes through the same points as $(f_x, t_y)$ but at a different rate, as can be seen by a different spacing of points. The blue and red curves do completely coincide, but one has been shifted for display purposes. The statistical shape analysis of such Euclidean curves $f: I \rightarrow \mathbb {R}^d$ is a well-developed field but has been left out of the discussion here.
Beyond interval domains: Another way to generalize scalar functions is to study $f:[0,1]^k\rightarrow \mathbb {R}^d$, where $k > 1$. For example, the case of $k=2$ corresponds to shape analysis of images and surfaces, interesting and well-studied problems (Jermyn et al. 2017; Laga et al. 2017). A number of papers have covered shape analysis of surfaces and registration of images, but statistical treatments for such high-dimensional objects remain a wide-open field. For instance, the problem of using their shapes in regression models is yet to be developed.

7 Conclusion

The presence of functional data in many scientific disciplines has led to rapid growth in research and the application of functional data analysis. This paper outlines a novel approach to functional data analysis where the focus is on the shape of functions rather than full functions. The shape of a function is characterized by the number and heights of its peaks and valleys, or even just the number on extrema in some cases. This shape-based FDA often provides more interpretable results as it better preserves the geometric structures in functional data when compared to the traditional approach. The paper uses examples and illustrations to present broad ideas for function estimation, shape fPCA, and shape regression models as candidates for their current FDA counterparts.

References

Ahn K, Tucker JD, Wu W, Srivastava A (2020) Regression models using shapes of functions as predictors. Comput Stat Data Anal 151:107017
Article MathSciNet Google Scholar
Ahn K, Derek Tucker J, Wu W, Srivastava A (2018) Elastic handling of predictor phase in functional regression models. In: Proceedings of the IEEE conference on computer vision and pattern recognition workshops, pp. 324–331
Bertsekas DP (1995) Dynamic programming and optimal control. Athena Scientific, Belmont
Google Scholar
Bickel PJ, Fan J (1996) Some problems on the estimation of unimodal densities. Stat Sin 6(1):23–45
MathSciNet Google Scholar
Birge L (1997) Estimation of unimodal densities without smoothness assumptions. Ann Stat 25(3):970–981
Article MathSciNet Google Scholar
Bône A, Colliot O, Durrleman S (2018) Learning distributions of shape trajectories from longitudinal datasets: a hierarchical model on a manifold of diffeomorphisms. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 9271–9280
Cai TT, Hall P (2006) Prediction in functional linear regression. Ann Stat 34(5):2159–2179
Article MathSciNet Google Scholar
Camarinha M, Leite FS, Crouch P (1995) Splines of class $c^k$ on non-Euclidean spaces. IMA J Math Contr Inform 12:399–410
Article Google Scholar
Cardot H, Ferraty F, Sarda P (1999) Functional linear model. Stat Probab Lett 45(1):11–22
Article MathSciNet Google Scholar
Carroll RJ, Ruppert D, Stefanski LA, Crainiceanu CM (2006) Measurement error in nonlinear models: a modern perspective. Chapman & Hall/CRC, Boca Raton
Book Google Scholar
Chakraborty R, Yang C-H, Zhen X, Banerjee M, Archer D, Vaillancourt D, Singh V, Vemuri B (2018) A statistical recurrent model on the manifold of symmetric positive definite matrices. Advances in neural information processing systems 31
Cheng M-Y, Gasser T, Hall P (1999) Nonparametric density estimation under unimodality and monotonicity constraints. J Comput Graph Stat 8(1):1–21
MathSciNet Google Scholar
Cornea E, Zhu H, Kim P, Ibrahim JG, Initiative ADN (2017) Regression models on Riemannian symmetric spaces. J Royal Stat Soci: Series B (Stat Methodol) 79(2):463–482
Article MathSciNet Google Scholar
Crouch P, Kun G, Leite FS (1999) The de casteljau algorithm on the lie group and spheres. J Dyn Contr Sys 5:397–429
Article MathSciNet Google Scholar
Dasgupta S (2019) Shape based function estimation. PhD thesis, Florida State University, Dept of Statistics
Dasgupta S, Pati D, Jermyn IH, Srivastava A (2018) Shape-constrained and unconstrained density estimation using geometric exploration. In: 2018 IEEE Statistical signal processing workshop (SSP), pp. 358–362
Deng X, Sarkar R, Labruyere E, Olivo-Marin J-C, Srivastava A (2022) Characterizing cell populations using statistical shape modes. In: 2022 IEEE 19th International symposium on biomedical imaging (ISBI), pp. 1–5
Durrleman S, Pennec X, Trouvé A, Braga J, Gerig G, Ayache N (2013) Toward a comprehensive framework for the spatiotemporal statistical analysis of longitudinal shape data. Int J Comput Vision 103(1):22–59
Article MathSciNet Google Scholar
Fan J, Zhang W (1999) Statistical estimation in varying coefficient models. Ann Stat 27(5):1491–1518
Article MathSciNet Google Scholar
Fan J, Zhang W (2008) Statistical methods with varying coefficient models. Stat Interface 1(1):179
Article MathSciNet Google Scholar
Fan Y, James GM, Radchenko P (2015) Functional additive regression. Ann Stat 43(5):2296–2325
Article MathSciNet Google Scholar
Ferraty F, Vieu P (2006) Nonparametric functional data analysis: theory and practice. springer series in statistics. Springer, New York
Google Scholar
Ferraty F, Mas A, Vieu P (2007) Nonparametric regression on functional data: inference and practical aspects. Austr N Z J Stat 49(3):267–286
Article MathSciNet Google Scholar
Fishbaugh J, Durrleman S, Piven J, Gerig G (2012) A framework for longitudinal data analysis via shape regression, SPIE. Med Imaging: Image Process 8314:1015–1021
Google Scholar
Fletcher PT, JS. Venkatasubramanian S (2009) The geometric median on Riemannian manifolds with application to robust atlas estimation. Neuroimage 45
Fletcher PT (2013) Geodesic regression and the theory of least squares on Riemannian manifolds. Int J Comput Vision 105(2):171–185
Article MathSciNet Google Scholar
Fuchs K, Scheipl F, Greven S (2015) Penalized scalar-on-functions regression with interaction term. Comput Stat Data Anal 81:38–51
Article Google Scholar
Gerig G, Fishbaugh J, Sadeghi N (2016) Longitudinal modeling of appearance and shape and its potential for clinical use. Elsevier
Gertheiss J, Goldsmith J, Crainiceanu C, Greven S (2013) Longitudinal scalar-on-functions regression with application to tractography data. Biostatistics 14(3):447–461
Article Google Scholar
Goldsmith J, Scheipl F (2014) Estimator selection and combination in scalar-on-function regression. Comput Stat Data Anal 70:362–372
Article MathSciNet Google Scholar
Goldsmith J, Crainiceanu CM, Caffo B, Reich D (2012) Longitudinal penalized functional regression for cognitive outcomes on neuronal tract measurements. J Royal Stat Soci: Series C (Appl Stat) 61(3):453–469
MathSciNet Google Scholar
Grenander U (1956) On the theory of mortality measurement: part ii. Scand Actuar J. https://doi.org/10.1080/03461238.1956.10414944
Article Google Scholar
Grenander U (1981) Abstract inference. Wiley, New York
Google Scholar
Guo W (2002) Functional mixed effects models. Biometrics 58(1):121–128
Article MathSciNet Google Scholar
Hall P, Huang L-S (2002) Unimodal density estimation using kernel methods. Stat Sin 12(4):965–990
MathSciNet Google Scholar
Hastie T, Mallows C (1993) [A statistical view of some chemometrics regression tools]: discussion. Technometrics 35(2):140–143
Google Scholar
Hastie T, Tibshirani R (1987) Generalized additive models: some applications. J Am Stat Assoc 82(398):371–386
Article Google Scholar
Hofer M, Pottmann H (2004) Energy-minimizing splines in manifolds. In: SIGGRAPH
Hsing T, Eubank R (2015) Theoretical foundations of functional data analysis, with an introduction to linear operators. Wiley, Chichester
Book Google Scholar
Huang C (2019) Advanced statistical learning methods for heterogeneous medical imaging data. PhD thesis, The University of North Carolina at Chapel Hill
Huang C, Srivastava A, Liu R (2021) Geo-farm: geodesic factor regression model for misaligned pre-shape responses in statistical shape analysis. In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp. 11496–11505
Ivanescu AE, Staicu A, Scheipl F, Greven S (2015) Penalized function-on-function regression. Comput Stat 30(2):539–568
Article MathSciNet Google Scholar
Jermyn IH, Kurtek S, Laga H, Srivastava A (2017) Elastic shape analysis of three-dimensional objects. Synthesis lectures on computer vision #12. Morgan and Claypool Publishers, San Rafael
Jupp PE, Kent JT (1987) Fitting smooth paths to spherical data. J Roy Stat Soc: Ser C (Appl Stat) 36(1):34–46
MathSciNet Google Scholar
Kenobi K, Dryden IL, Le H (2010) Shape curves and geodesic modeling. Adv Appl Probab 97:567–584
Google Scholar
Kim HJ, Adluru N, Collins MD, Chung MK, Bendlin BB, Johnson SC, Davidson RJ, Singh V (2014) Multivariate general linear models (mglm) on Riemannian manifolds with applications to statistical analysis of diffusion weighted images. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2705–2712
Kim HJ, Adluru N, Suri H, Vemuri BC, Johnson SC, Singh V (2017) Riemannian nonlinear mixed effects models: analyzing longitudinal deformations in neuroimaging. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2540–2549
Kim WM, Dasgupta S, Srivastava A (2023) Peak-persistence diagrams for estimating shapes and functions from noisy data arXiv:2305.04826 [stat.ME]
Kokoszka P, Reimherr M (2017) Introduction to functional data analysis. Texts in statistical science. Chapman & Hall/CRC, Boca Raton
Google Scholar
Kume A, Dryden IL, Le H (2007) Shape-space smoothing splines for planar landmark data. Biometrika 94:513–528
Article MathSciNet Google Scholar
Laga H, Xie Q, Jermyn IH, Srivastava A (2017) Numerical inversion of SRNF maps for elastic shape analysis of genus-zero surfaces. IEEE Trans Pattern Anal Mach Intell 39(12):2451–2464
Article Google Scholar
Lahiri S, Robinson D, Klassen E (2015) Precise matching of pl curves in $\mathbb{R} ^{n}$ in the square root velocity framework. arXiv: Differential Geometry
Le H (2001) Locating frechet means with application to shape spaces. Adv Appl Probab 33(2):324–338
Article MathSciNet Google Scholar
Le HL, Kendall DG (1993) The Riemannian structure of Euclidean shape spaces: a novel environment for statistics. Ann Stat 21(3):1225–1271
Article MathSciNet Google Scholar
Li Y, Wang N, Carroll RJ (2010) Generalized functional linear models with semiparametric single-index interactions. J Am Stat Assoc 105(490):621–633
Article MathSciNet Google Scholar
Lin Z, Yao F (2021) Functional regression on the manifold with contamination. Biometrika 108(1):167–181
Article MathSciNet Google Scholar
Lin L, St. Thomas B, Zhu H, Dunson DB (2017) Extrinsic local regression on manifold-valued data. J Am Stat Assoc 112(519):1261–1273
Article MathSciNet Google Scholar
Lin L, Mu N, Cheung P, Dunson D et al (2019) Extrinsic gaussian processes for regression and classification on manifolds. Bayesian Anal 14(3):887–906
Article MathSciNet Google Scholar
Lin Z, Yao F (2018) Intrinsic riemannian functional data analysis. arXiv preprint arXiv:1812.01831
Luo R, Qi X (2017) Function-on-function linear regression by signal compression. J Am Stat Assoc 112(518):690–705
Article MathSciNet Google Scholar
Machado L, Leite FS (2006) Fitting smooth paths on Riemannian manifolds. Int J Appl Math Stat 4:25–53
MathSciNet Google Scholar
Machado L, Leite FS, Hüpper K (2006) Riemannian means as solutions of variational problems. LMS J Comput Math 9:86–103
Article MathSciNet Google Scholar
Marron JS, Dryden IL (2021) Object oriented data analysis. CRC Press, Boca Raton
Book Google Scholar
Marron JS, Ramsay JO, Sangalli LM, Srivastava A (2014) Statistics of time warpings and phase variations. Electr J Stat 8(2):1697–1702
MathSciNet Google Scholar
Marron JS, Ramsay JO, Sangalli LM, Srivastava A (2015) Functional data analysis of amplitude and phase variation. Stat Sci 30(4):464–484
Article MathSciNet Google Scholar
Marx BD, Eilers P (1999) Generalized linear regression on sampled signals and curves: a p-spline approach. Technometrics 41(1):1–13
Article Google Scholar
Marx BD, Eilers P, Li B (2011) Multidimensional single-index signal regression. Chemom Intell Lab Syst 109(2):120–130
Article Google Scholar
Meyer MJ, Coull BA, Versace F, Cinciripini P, Morris JS (2015) Bayesian function-on-function regression for multilevel functional data. Biometrics 71(3):563–574
Article MathSciNet Google Scholar
Morris JS (2015) Functional regression. Ann Rev Stat Appl 2:321–359
Article Google Scholar
Morris JS (2015) Functional regression. Annu Rev Stat Appl 2:321–359
Article Google Scholar
Müller H-G, Yao F (2008) Functional additive models. J Am Stat Assoc 103(484):1534–1544
Article MathSciNet Google Scholar
Nava-Yazdani E, Hege H-C, Tycowicz Cv (2019) A geodesic mixed effects model in kendall’s shape space. In: Multimodal brain image analysis and mathematical foundations of computational anatomy, pp. 209–218. Springer, New York
Niu M, Cheung P, Lin L, Dai Z, Lawrence N, Dunson D (2019) Intrinsic gaussian processes on complex constrained domains. J Royal Stat Society: Series B (Stat Methodol) 81(3):603–627
Article MathSciNet Google Scholar
Noakes L, Heinzinger G, Paden B (1989) Cubic splines on curved spaces. IMA J Math Control Inf 6(4):465–473
Article MathSciNet Google Scholar
Pennec X (2006) Intrinsic statistics on Riemannian manifolds: basic tools for geometric measurements. J Math Imag Vis 25(1):127
Article MathSciNet Google Scholar
Pennec X, Sommer S, Fletcher T (2019) Riemannian geometric statistics in medical image analysis. Academic Press, London
Google Scholar
Qi X, Luo R (2018) Function-on-function regression with thousands of predictive curves. J Multi Anal 163:51–66
Article MathSciNet Google Scholar
Ramsay JO, Dalzell CJ (1991) Some tools for functional data analysis. J Royal Stat Soci: Series B (Methodol) 53(3):539–561
MathSciNet Google Scholar
Ramsay JO, Silverman BW (2005) Functional data analysis, 2nd edn. Springer, New York
Book Google Scholar
Ramsay JO, Hooker G, Graves S (2009) Functional data analysis with R and MATLAB. Use R! Springer, New York
Book Google Scholar
Rao BLSP (1969) Estimation of a unimodal density. Sankhyā: Ind J Stat, Series A (1961–2002), 31(1):23–36
Reiss PT, Goldsmith J, Shang HL, Ogden RT (2017) Methods for scalar-on-function regression. Int Stat Rev 85(2):228–249
Article MathSciNet Google Scholar
Samir C, Absil P-A, Srivastava A, Klassen E (2012) A gradient-descent method for curve fitting on Riemannian manifolds. Found Comput Math 12(1):49–73
Article MathSciNet Google Scholar
Scheipl F, Staicu A, Greven S (2015) Functional additive mixed models. J Comput Graph Stat 24(2):477–501
Article MathSciNet Google Scholar
Shi X, Zhu H, Ibrahim JG, Liang F, Lieberman J, Styner M (2012) Intrinsic regression models for medial representation of subcortical structures. J Am Stat Assoc 107(497):12–23
Article MathSciNet Google Scholar
Shin H-Y, Oh H-S (2020) Robust geodesic regression. arXiv preprint arXiv:2007.04518
Shin H (2009) Partial functional linear regression. J Stat Plann Infer 139(10):3405–3418
Article MathSciNet Google Scholar
Shi X, Styner M, Lieberman J, Ibrahim JG, Lin W, Zhu H (2009) Intrinsic regression models for manifold-valued data. In: International conference on medical image computing and computer-assisted intervention, pp. 192–199. Springer
Srivastava A, Klassen E (2016) Functional and shape data analysis. Springer, New York
Book Google Scholar
Stöcker A, Greven S (2021) Functional additive regression on shape and form manifolds of planar curves. arXiv preprint arXiv:2109.02624
Su J, Dryden IL, Klassen E, Le H, Srivastava A (2011) Fitting optimal curves to time-indexed, noisy observations of stochastic processes on nonlinear manifolds. J Image Vis Comp Rev 30:428–442
Article Google Scholar
Su J, Kurtek S, Klassen E, Srivastava A (2014) Statistical analysis of trajectories on Riemannian manifolds: bird migration, hurricane tracking, and video surveillance. Ann Appl Stat 8(1):530–552
Article MathSciNet Google Scholar
Tang R, Müller H-G (2008) Pairwise curve synchronization for functional data. Biometrika 95(4):875–889
Article MathSciNet Google Scholar
Tsagkrasoulis D, Montana G (2018) Random forest regression for manifold-valued responses. Pattern Recogn Lett 101:6–13
Article Google Scholar
Tucker JD, Lewis JR, Srivastava A (2019) Elastic functional principal component regression. Stat Anal Data Min: ASA Data Sci J 12(2):101–115
Article MathSciNet Google Scholar
Wang J-L, Chiou J-M, Müller H-G (2016) Functional data analysis. Annu Rev Stat Appl 3(1):257–295
Article Google Scholar
Wang JL, Chiou JM, Müller HG (2016) Functional data analysis. Annu Rev Stat Appl 3:257–295
Article Google Scholar
Wegman EJ (1970) Maximum likelihood estimation of a unimodal density II. Ann Math Stat 41(6):2169–2174
Article MathSciNet Google Scholar
Wong RKW, Li Y, Zhu Z (2019) Partially linear functional additive models for multivariate functional data. J Am Stat Assoc 114(525):406–418
Article MathSciNet Google Scholar
Wood SN (2017) Generalized additive models: an introduction with R. Chapman and Hall/CRC, Boca Raton
Book Google Scholar
Wu S, Müller HG (2011) Response-adaptive regression for longitudinal data. Biometrics 67(3):852–860
Article MathSciNet Google Scholar
Xiong D, Ying S, Zhu H (2022) Intrinsic partial linear models for manifold-valued data. Inform Process Manag 59(4):102954
Article Google Scholar
Yao F, Müller HG (2010) Functional quadratic regression. Biometrika 97(1):49–64
Article MathSciNet Google Scholar
Yao F, Müller H-G, Wang J-L (2005) Functional data analysis for sparse longitudinal data. J Am Stat Assoc 100(470):577–590
Article MathSciNet Google Scholar
Zhang Y (2020) Bayesian geodesic regression onriemannian manifolds. arXiv preprint arXiv:2009.05108
Zhang J-T (2013) Analysis of variance for functional data. CRC Press, Boca Raon
Book Google Scholar
Zhang L, Baladandayuthapani V, Zhu H, Baggerly KA, Majewski T, Czerniak BA, Morris JS (2016) Functional car models for large spatially correlated functional datasets. J Am Stat Assoc 111(514):772–786
Article MathSciNet Google Scholar
Zhang X, Shi X, Sun Y, Cheng L (2018) Multivariate regression with gross errors on manifold-valued data. IEEE Trans Pattern Anal Mach Intell 41(2):444–458
Article Google Scholar
Zhang Z, Klassen E, Srivastava A (2018) Phase-amplitude separation and modeling of spherical trajectories. J Comput Graph Stat 27(1):85–97
Article MathSciNet Google Scholar
Zhang Z, Su J, Klassen E, Le H, Srivastava A (2018) Rate-invariant analysis of covariance trajectories. J Math Imag Vis 60(8):1306–1323
Article MathSciNet Google Scholar
Zhang Z, Wu Y, Xiong D, Ibrahim JG, Srivastava A, Zhu H (2023) Lesa: longitudinal elastic shape analysis of brain subcortical structures. J Am Stat Assoc 118(541):3–17
Article MathSciNet Google Scholar
Zhu H, Li R, Kong L (2012) Multivariate varying coefficient model for functional responses. Ann Stat 40(5):2634
Article MathSciNet Google Scholar
Zhu H, Yao F, Zhang H (2014) Structured functional additive regression in reproducing kernel Hilbert spaces. J Royal Stat Soci: Series B (Stat Methodol) 76(3):581–603
Article MathSciNet Google Scholar
Zhu H, Fan J, Kong L (2014) Spatially varying coefficient model for neuroimaging data with jump discontinuities. J Am Stat Assoc 109(507):1084–1098
Article MathSciNet Google Scholar

Download references

Acknowledgements

The authors are grateful to the Editors Profs. Ana M. Aguilera and José M. Angulo for their kind invitation to write this article. They are also thankful to the three anonymous reviewers for their helpful comments and feedback. The authors thank the creators of several public datasets used in this paper for making the data public. Finally, they acknowledge the Grant Nos. NSF DMS 1953087 and NIH R01 GM135927 for partial support of this research.

Author information

Authors and Affiliations

Department of Statistics, Florida State University, Tallahassee, FL, 32306, USA
Yuexuan Wu, Chao Huang & Anuj Srivastava
Department of Epidemiology, University of Washington, Seattle, WA, 98195, USA
Yuexuan Wu

Authors

Yuexuan Wu
View author publications
You can also search for this author in PubMed Google Scholar
Chao Huang
View author publications
You can also search for this author in PubMed Google Scholar
Anuj Srivastava
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Anuj Srivastava.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this article

Cite this article

Wu, Y., Huang, C. & Srivastava, A. Shape-based functional data analysis. TEST 33, 1–47 (2024). https://doi.org/10.1007/s11749-023-00876-9

Download citation

Received: 09 December 2022
Accepted: 11 July 2023
Published: 22 August 2023
Issue Date: March 2024
DOI: https://doi.org/10.1007/s11749-023-00876-9

Keywords

Mathematics Subject Classification

62R10

Use our pre-submission checklist

Avoid common mistakes on your manuscript.