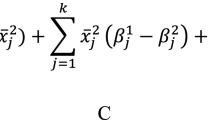1 Introduction

Latent Markov (LM) models (Bartolucci et al. 2013, 2014) permit parsimonious and flexible modeling of univariate and multivariate longitudinal data. A particularly attractive feature is that random effects are time-varying, and their discrete distribution, based on k support points, can usually approximate well almost any true underlying distribution of random effects. Local and global decoding allow to assign subjects, at each measurement occasion, to their most likely hidden state (or sequence of hidden states). Consequently, the latent classification can then be seen as a model-based time-varying clustering (Bulla et al. 2012; Dias et al. 2015; Punzo and Maruotti 2016) based on k groups. A generalization to a different number of groups at each time occasion has recently been proposed (Anderson et al. 2019a, b). A limitation is that the association rule between the multivariate outcome and the latent indicators is based on posterior probabilities and therefore not available in closed form. Assignment of a new measurement to a latent cluster is cumbersome, especially if the outcome configuration has not been observed in the data. Furthermore, a score that increases (or decreases) with the likelihood of belonging to a cluster of interest could be in general very useful to practitioners.

A good example is given by our motivating application on assessment of material deprivation, a direct measure of poverty (Sen 1981), in Europe. The official household-level questionnaire is based on nine binary items. Our main issue is how to classify as poor/not poor a new family, based on its nine-dimensional binary profile, and ranking families with respect to their propensity to material deprivation. It is underlined in Atkinson (2003) and Dotto et al. (2019) that a simple counting approach has an unsatisfactory classification performance for this task. It also, clearly, leads to several ties when using it to rank families. The simple counting approach is equivalent to computing linear combinations, with equal weight assigned to of the items. It has been seen also more in general to have limitations from the quality of measure point of view. See for instance Najera Catalan (2017), Cafiero et al. (2018), and De Andrade and Tavares (2005) specifically for panel data. Counting in fact implicitly assumes that all items have the same discrimination power (i.e., they are equally related to the latent trait), unidimensionality (Linacre 2009), and the specific objectivity or measurement invariance of the scale. On the other hand, use of a map of each of the \(2^9=512\) possible configurations to the \(k=2\) latent states (poor/not poor), as provided by a multidimensional latent Markov model for instance, is cumbersome and makes it impossible to rank families. A heuristic two-step strategy for dimension reduction was used in Dotto et al. (2019) for panel data recorded in Greece, Italy and U.K. At the first step, a basic latent Markov model with the nine-dimensional binary outcome, no covariates, and \(k=2\) latent states is estimated. At the second step, a score, corresponding to a weighted sum of the active indicators, is targeted. To do so, weights are estimated by maximization of the Spearman correlation between the unidimensional score and posterior probabilities of being materially deprivated in a given year. Albeit provingly better than simple item counting, this heuristic method is clearly informal and not necessarily optimal. It is also restricted to a one-dimensional projection.

Our main task in this work is that of building optimal scores (obtained as weighted sums of a multivariate outcome, repeatedly observed over time) able at discriminating among subjects belonging to classes of a discrete latent trait (e.g., poor/non-poor; low/medium/high propensity to buy, etc.). Unidimensional scores can be used for ranking, bidimensional scores for graphical representations, and so on. We also report on how to choose the score dimensionality, and to assess how well scores reproduce the variability in the original data. Weights can be used to directly and simply compute a score for a newly measured subject. We are especially interested in the case in which no covariates are used and \(k=2\), since it is by far the most common situation in which a score is desired: the use of \(k=2\) classes leads to binary discrimination, and absence of covariates indicates that all relevant information is used in the scoring system. All other cases might be of interest too in applications and are briefly discussed below. Weighted sums can also be seen as lower-dimensional projections of longitudinal measurements, which relates our method to the more general literature on dimension reduction for longitudinal data (e.g., Hall et al. 2006; Jiang and Wang 2010); more specifically in relation to latent Markov models. For instance, in Vogelsmeier et al. (2019) a multivariate continuous outcome is assumed to follow a factor model, with loadings that are state-dependent and follow a latent Markov model. The literature on dynamic dimensionality reduction methods is actually very rich, see for instance Jung et al. (2011), Xia et al. (2016), Song et al. (2017), Bai and Wang (2015), Maruotti et al. (2017), Ando and Bai (2017) and Chen et al. (2020).

Clearly, our method is also an extension of dimension reduction approaches for cross-sectional categorical data (e.g., Collins et al. 2002; de Leeuw 2006; Lee et al. 2010; Landgraf and Lee 2015), like logistic PCA and logistic SVD. See also Cagnone and Viroli (2012) and Yamamoto and Hayashi (2015). Logistic PCA extends Pearson’s initial formulation of principal component analysis by seeking a rank-r projection of the data which is as close to the original data as possible, therefore being model-agnostic. Logistic SVD is a similar approach based on exponential families, where the objective is expressed as a function of PC scores. Many methods mentioned above are also restricted to either binary multivariate data or continuous multivariate data, while our approach will be designed for any multivariate outcome, including a mix of binary, categorical and continuous variables.

Our approach can be summarized as follows: we assume each weighted sum of a multivariate outcome follows a latent Markov model, where weights are orthonormal. We then optimize a measure of latent class separation over the weight space, in the spirit of more classical methods for dimension reduction. Our basic assumption is that latent scores are Gaussian in general. This is straightforward when working with continuous multivariate outcomes. We give a technical justification below for more general cases, but note that this assumption is common in various fields. For instance, in several psychometric applications multivariate binary data give rise to Gaussian latent variables. It shall be noted that our model-based approach provides a natural way of treating (informative or ignorable) missing values, which can be dealt with as usually done with latent Markov models (Bartolucci et al. 2013; Bartolucci and Farcomeni 2015, 2019; Maruotti 2015; Marino and Alfó 2015; Marino et al. 2018). See also Geraci and Farcomeni (2018) for the dimension reduction context in general. A notable by-product is that missing scores can be imputed by generating predictions.

The rest of the paper is as follows: in the next section we formalize and justify our model for multivariate binary outcomes and time-fixed weights. We then obtain optimal weights in Sect. 2.1 and discuss multidimensional projections with orthogonal weights in Sect. 2.2. In Sect. 3 we provide some extensions: general outcomes, covariates, time-dependent weights. Simulations are reported in Sect. 4, while in Sect. 5 we describe our motivating application on poverty in Europe. Some concluding remarks are given in Sect. 6.

The methodology proposed in this paper has been implemented in R functions which can be downloaded from https://github.com/afarcome/LMdim.

2 Basic model for binary outcomes

Let \({Y}_{it}\), \(t=1,\ldots ,T_i\), \(i=1,\ldots ,n\), denote an H-dimensional vector of binary outcomes measured on the ih subject at time t; with \(T=\max _i T_i\). Our problem in this paper is how to define optimal one-dimensional summaries \(S_{it}(w)=\sum _{h=1}^H Y_{ith} w_h\) through weight vectors w, where for each w \(S_{it}(w)\) follows a first-order latent Markov model (to be more formally specified below). In what follows we will suppress dependence on w for ease of notation whenever possible. Our main idea is based on directly modeling \(S_{it}(w)\) and selecting the optimal w as the one that best separates the latent groups. Constraints are needed for identifiability and to avoid issues with unboundedness of the objective function; in this work, we use the classical unit-norm bound \(\sum _{j=1}^H w_j^2 = 1\).

Let \(U_{it}\) denote an unobserved discrete random variable with support \(1,\ldots ,k\), where k is known. We make the assumption that \(S_{it}(w)\) is conditionally Gaussian and follows a unidimensional latent Markov model, as follows:

$$\begin{aligned} S_{it}(w) | w, U_{it}=j \sim N(\xi _j,\sigma ^2), \end{aligned}$$
(1)

where \(\xi _j\) is a group-specific latent intercept and \(\sigma ^2\) is the variance. A justification of the Gaussian assumption is given at the beginning of Sect. 3. Note that (1) is identified as long as we constrain \(\xi _{j}<\xi _{j+1}\) for \(j=1,\ldots ,k-1\); see also Bartolucci et al. (2013) for a more general discussion. The model is completed by assumptions of local independence, that is, that conditionally on \(U_{it}\) the outcome is independent of the past measures and on the distribution of the latent variable \(U_{it}\). Commonly a first-order homogeneous Markov chain is specified, with \(\Pr (U_{i1}=c)=\pi _c\) and \(\Pr (U_{it}=d|U_{i,t-1}=c)=\pi _{cd}\). The transition probabilities are collected in a transition matrix \(\Pi \).

More formally, we assume that the multivariate longitudinal outcome is a deconvolution, with unknown weights, of a univariate score which in turn follows a latent Markov model.

2.1 Optimal dimension reduction

Each set of weights \(w_1,\ldots ,w_H\) corresponds to a unidimensional projection \(S_{it}(w)\) of the vector \(Y_{it}\), associated with parameters \(\xi (w)\), \(\sigma ^2(w)\), \(\pi (w)\) and \(\Pi (w)\). In parallel with principal component analysis, we define optimality for a vector of weights as the maximization of a measure of (group) variability. In our setting, there are different criteria that can be put forward to measure group variability in latent Markov models. These clearly must involve the latent intercepts \(\xi _1(w),\ldots ,\xi _k(w)\).

Let \(p_{tj}(w) = \Pr (U_{it}=j)\), where \(p_{1j}=\pi _j(w)\) and \(p_{tj} = \sum _h p_{t-1,h}(w)\pi _{hj}(w)\) for \(t>1\) denote the prior probability that the ith subject is in latent state j at time t. Let also \({{\tilde{\xi }}}_t(w) = \sum _j p_{tj}\xi _j(w)/\sum _j p_{tj}\). At population level, we propose to measure latent group separation through the weighted deviance

$$\begin{aligned} D(w) =\sum _j \sum _t p_{tj}(w) (\xi _j(w) - {{\tilde{\xi }}}_t(w))^2. \end{aligned}$$
(2)

In words, we define the (absolute) maximal separation as the situation in which latent intercepts \(\xi _j(w)\) are maximally far apart and subjects are maximally spread over groups at each time point. The principle behind this idea is similar to the assessment of dependence in latent Markov models proposed in Farcomeni (2015). Deviance (2) is an absolute measure of group separation, where intra-class variability is weighted by time-specific class proportions. Of course, there are several other objective functions that can be put forward. A relative measure of separation is presented in Magidson (1981), while several other can be found in Vermunt and Magidson (2016) and are implemented in the software Latent GOLD. Another possibility would be to minimize a measure of cluster overlap, e.g., the one proposed in Steinley and Henson (2005). In this work, we prefer using (2) since it is a direct and absolute measure of separation, and it is directly connected with the ability of the final score to separate the occasion-specific measurements into clusters that are balanced (since more heterogeneous \(p_t\) clearly decrease D(w) when the \(\xi \) vector is held fixed) and distant (since when the entries of \(\xi \) are closer to each other, D(w) decreases if \(p_{t}\) is held fixed). We mention here that modification of the objective function is straightforward, and simulations lead to similar conclusions also if for instance the Magidson (1981) index is used.

One should in principle maximize D(w) in (2) with respect to w to obtain the optimal set of weights by construction. In practice, population parameters corresponding to each set of weights are unknown, hence the consistent surrogate objective function

$$\begin{aligned} {{\hat{D}}}(w) =\sum _j \sum _t {{\hat{p}}}_{tj}(w) ({\hat{\xi }}_j(w) - {\bar{\xi }}_t(w))^2. \end{aligned}$$
(3)

must be used, where \({\hat{\xi }}_j(w)\), \({\hat{\sigma }}^2(w)\), \({{\hat{\pi }}}(w)\) and \({{\hat{\Pi }}}(w)\) denote the MLE associated with weights \(w_1,\ldots ,w_H\); \({{\hat{p}}}_{1j}={\hat{\pi }}_j(w)\), \({{\hat{p}}}_{tj} = \sum _h {{\hat{p}}}_{t-1,h}(w){\hat{\pi }}_{hj}(w)\) for \(t>1\), and \({\bar{\xi }}_t(w)= \sum _j {{\hat{p}}}_{tj}{\hat{\xi }}_j(w)/\sum _j {{\hat{p}}}_{tj}\). Optimization of (3) is not straightforward since the MLE associated to model (1) must be obtained for each candidate set of weights w.

We proceed using an iterative procedure, combining an inner and an outer optimizer. The outer optimizer maximizes (3) using a numerical method (like the Nelder-Mead procedure or a genetic algorithm (Scrucca 2013)). In order to proceed without constraints the objective function is optimized in \({\tilde{w}} \in {{\mathcal {R}}}^H\), with \(w={\tilde{w}}/\sqrt{\sum _j {\tilde{w}}_j^2}\). Numerical outer maximizers in general proceed iteratively, computing the objective function at several points. For each, that is, conditionally on the current value for w, the inner optimizer uses a classical EM-type algorithm for obtaining the MLE of a latent Markov model with a continuous outcome (Bartolucci et al. 2013). The outcome in the working latent Markov model is \(S_{it}(w)\), where w is the currently evaluated vector of weights. By-products of the optimization procedure are, clearly, the MLE at the optimal projection and the optimal score \(S_{it}({\hat{w}})\).

2.2 Optimal multidimensional projections

Suppose now that multidimensional dimension reduction is desired. Call \(w^{(z)}\) the zth vector of weights, with \(z=1,2,\ldots ,r\), \(r\le H\). Similarly, denote \(S_{it}(w^{(z)})= \sum _{j=1}^H w_j^{(z)} Y_{itj}\).

In order to estimate \(w_j^{(z)}\), we optimize (3). When \(z>1\), this is done subject to further constraints on the weights. In this work, we pursue an orthogonality constraint. Formally, in order to obtain \({\hat{w}}^{(z)}\), we optimize (3) subject to

$$\begin{aligned} \sum _{j=1}^H w_j^{(z)}w_j^{(h)} = 0 \end{aligned}$$
(4)

for all \(h<z\), and additionally, as before, that \(\sum _j w_j^{(z)}w_j^{(z)}=1\).

The constrained optimization problem can be solved either simultaneously, that is, by maximizing

$$\begin{aligned} \sum _{j=1}^r {{\hat{D}}}(w^{(j)}) \end{aligned}$$
(5)

subject to orthonormality constraints of \(w^{(1)},\ldots ,w^{(r)}\); or sequentially, that is, obtaining the zth optimal set of weights only after the first \(z-1\) have been found. In the first case, the objective function argument is the vectorization of the H by r unconstrained matrix \({\tilde{w}}\), where w is the Q matrix in the QR-decomposition of \({\tilde{w}}\). Use of the QR decomposition is particularly convenient since an efficient algorithm can be used to map an unconstrained vector to an orthonormal matrix. For each \({\tilde{w}}\), the objective function is computed after r EM-type inner optimization procedures for obtaining the r MLEs corresponding to \(w^{(1)}, \ldots , w^{(r)}\). The inner procedures can be easily parallelized for computational convenience.

In the second case, in order to compute \({\hat{w}}^{(z)}\), the first \(z-1\) solutions are held fixed. The objective function argument is a unidimensional vector \({\tilde{w}}^{(z)}\), where \(w^{(z)}\) is the zth column of the Q matrix in the QR-decomposition of the matrix whose first \(z-1\) columns are \(w^{(1)},\ldots ,{\hat{w}}^{(z-1)}\) and the zth is \({\tilde{w}}^{(z)}\). This is a very convenient way of mapping an unconstrained vector to a unit-norm vector that is orthogonal with all previously computed vectors of weights. A single inner optimization procedure now suffices to obtain the MLE associated with the current value of \(w^{(z)}\).

Our numerical experiments have indicated that the sequential procedure is less dependent on initial solutions (that is, less likely to be trapped into local optima) and slightly quicker than the simultaneous procedure.

The quality of each projection is measured, by definition, by the weighted deviance (3). This is not a standardized measure. Clearly, due to (4), \({{\hat{D}}}({{\hat{w}}}^{(z)}) \le {{\hat{D}}}({{\hat{w}}}^{(h)})\) and

$$\begin{aligned} \sum _{j=1}^z {{\hat{D}}}({{\hat{w}}}^{(j)}) \ge \sum _{j=1}^h {{\hat{D}}}({{\hat{w}}}^{(j)}) \end{aligned}$$

for all \(z\ge h\). Consequently, calling \(D_{\max } = \sum _{j=1}^H {{\hat{D}}}({{\hat{w}}}^{(j)})\) we have that a standardized measure of the quality of the jth score is given by \({{\hat{D}}}({{\hat{w}}}^{(j)})/D_{\max }.\) The latter is the proportion of separation that is retained by the jth score. This measure is standardized, with a minimum of zero for scores in which latent groups are perfectly overlapped, and a maximum of one when only one score gives non-zero separation.

2.3 Goodness of fit

It should be made clear that separation and goodness of fit are two different matters, and our approach targets separation of the latent variable. This is only indirectly pursuing goodness of fit, which therefore should be checked alongside separation. Even in cases in which the cumulative degree of separation \(\sum _{j=1}^z {{\hat{D}}}({{\hat{w}}}^{(j)})/D_{\max }\) is large enough, we recommend selecting a larger number of scores in case goodness of fit is not acceptable.

Ideally, we would need a measure of how well an optimal score S can approximate the data Y, which is very cumbersome with binary (or even mixed) outcomes. We thus propose a measure that is based on the following interpretation of LM models: in LM models the outcome, be it the multivariate profile Y or the score S, can be assumed to be measuring, with error, a discrete latent variable. All information about the latent variable is summarized by the posterior probabilities \( \Pr (U_{it}=j\ |\ Y), \) and \(\Pr (U_{it}=j\ |\ S)\), respectively. We point the reader to Bartolucci et al. (2014) both for further discussion and computation of these quantities at the MLE. The latter is a direct by-product of our estimation procedure. We therefore propose that if posterior probabilities agree, then data Y are well explained by the score S. It shall be pointed out that, since we are measuring association between vectors of probabilities, we should use a log-ratio transform Aitchison (2011). When \(k=2\), for simplicity, we directly compute the squared Spearman correlation between the estimated \(\Pr (U_{it}=1\ |\ Y)\) and \(\Pr (U_{it}=j\ |\ S)\).

3 General model for mixed outcomes and extensions

Let now \({Y}_{it}\), \(t=1,\ldots ,T_i\), \(i=1,\ldots ,n\), denote an H-dimensional vector of continuous, binary and/or ordinal outcomes.

We begin by discussing justification of the assumption that \(S_{it}\) is Gaussian in general. When \(Y_{it} \in {{\mathcal {R}}}^H\), the most common parametric assumption is that of a multivariate Gaussian distribution, possibly after transformation. Since any linear combination of Gaussian distributions is Gaussian, \(S_{it}\) is exactly Gaussian under this assumption. In case different distributional assumptions are used for \(Y_{it}\), the assumption that \(S_{it}\) is Gaussian is only a working approximation, which is usually guaranteed as H grows by some form of central limit theorem.

Let us now consider discrete outcomes. Suppose \(Y_{ith} \in \{0,1,\ldots ,c_h-1\}\), that is, there are \(c_h\) categories for the hth variable. These can be ordered or unordered. If all outcomes are unordered, one can simply define \(c_h-1\) binary dummy variables \(Z_{itl}=I(Y_{ith}=l)\), \(l=1,\ldots ,c_h-1\). It is straightforward to see that Bernoulli assumptions on \(Z_{itl}\), which correspond to general multinomial assumptions on \(Y_{ith}\), lead to \(\sum _l w_l Z_{itl}\) begin distributed according to a Poisson-Binomial law. The Poisson-Binomial indeed is the distribution of a weighted sum of independent and non-identically-distributed random indicators. A detailed description, with a strategy for efficient evaluation of its probability mass function, can be found in Hong (2013). An ordered outcome \(Y_{ith}\) can be treated similarly after letting \(Z_{itl}=I(Y_{ith}\ge l)\), \(l=1,\ldots ,c_{h-1}\). Our point here is that the Poisson-Binomial is well approximated by a Gaussian distribution as soon as H is large (by Lyapunov central limit theorem), with \(H\ge 6\) very often being sufficient. See also Deheuvels et al. (1989).

The reasoning above can be directly extended to mixed-type outcomes. Without loss of generality assume that \(Y_{ith}\), for \(h=1,\ldots ,H_1\), is continuous for some \(1<H_1<H\); and for \(h=H_1+1,\ldots ,H\) it is binary. Call \(S_{it}=\sum _h w_h Y_{ith}\), \(S_{it}^{(1)}=\sum _{h=1}^{H_1} w_h Y_{ith}\) and \(S_{it}^{(2)}=\sum _{h=H_1+1}^H w_h Y_{ith}\). Clearly the distribution of \(S_{it}\) is the same as the distribution of \(S_{it}^{(1)}+S_{it}^{(2)}\), where \(S_{it}^{(1)}\) and \(S_{it}^{(2)}\) are independent conditionally on \(U_{it}\) as assumed above. Consequently, \(S_{it}\) (conditionally on \(U_{it}\)) is the sum of two independent Gaussian (or at least approximately Gaussian) random variables.

We can then use an assumption as (1), even conditionally on a vector of covariates \(x_{it}\), associated with coefficients \(\beta \):

$$\begin{aligned} S_{it}(w) | w, U_{it}=j,x_{it} \sim N(\xi _j+x_{it}'\beta ,\sigma ^2), \end{aligned}$$
(6)

Use of covariates in (6) has direct consequences on the interpretation of the results. When no covariates are used, \({\hat{\xi }}_j\) is simply the latent group mean of the projected score. When covariates are included, groups are defined after adjustment, that is, comparing measurements as if they had the same covariate configuration. Accordingly, since weights are (still) chosen to maximize (3), and \(\beta \) parameters do not appear in the formula, the final score maximizes the distance among latent groups after adjusting for covariates. That is, \(S_{it}({\hat{w}})\) maximizes (on average) the distance among subjects belonging to different latent states when they share the same covariate configuration.

Given our underlying assumptions, algorithms proposed in Sects. 2.1 and 2.2 can still be used to obtain optimal orthonormal weights under (6) and (3).

3.1 Time-dependent weights

The models considered so far involve time-fixed weights \(w_1,\ldots ,w_H\). This is appropriate when, as in our application, dimension reduction is used to obtain a score which can be compared across different time points, in order to monitor time trends. On the other hand, in other cases one might want to target the goodness of fit, capture dynamics in the weights rather than in the scores, or even assess the assumption that weights are time-fixed. An extension of our approach in this direction is straightforward, where the new variables are defined as

$$\begin{aligned} S_{it}(w_t^{(z)}) = \sum _{j=1}^H w_{jt}^{(z)} Y_{itj}, \end{aligned}$$

and these are still assumed to follow (6) in general. The constrained optimization problem, on the other hand, should be specified in slightly different way. While the objective function is still (5), in order to obtain interpretable and identifiable solutions, we put forward the following set of constraints:

$$\begin{aligned} {\left\{ \begin{array}{ll} \sum _{j=1}^H (w_{jt}^{(z)})^2 = 1 \ \forall \ t,\forall \ z\\ \sum _{j=1}^H w_{jt}^{(z)}w_{jl}^{(h)} = 0\, \forall \ t,\forall \ z\, \forall \ l,\forall \ h<z \end{array}\right. } \end{aligned}$$

Namely, weights are normalized to unit norm at each time occasion; and weights of the zth score are orthogonal to the weights of the hth score, with \(h<z\), for all time points.

Unsurprisingly, we can still use the same optimization procedure to solve the problem, but at the price of a longer computational time since the dimension of the outer optimization problem is multiplied by T. It shall be finally made clear that interpretation of scores changes at each time point, making it quite difficult to compare new variables over time.

4 Simulations

In this section, we illustrate our procedure with a simulation study.

Data were generated by considering \(H =\{ 5,10 \}\) Binomial outcomes, \(T = \{4, 6\}\) occasions, \(n = \{500, 1000, 2000\}\) observations and \(k=2\). The outcomes follow a multivariate binary latent Markov model where latent states are drawn at random with uniform initial probabilities. Transition matrices are set so that transitions from the first to the second and second to first latent states have probability 10%. Subject time-specific success probabilities follow a logit model with latent intercepts generated from a standard Gaussian distribution. Note therefore that the data generating process is not (1), and our model is consequently misspecified.

For each combination of the experimental factors (H, T, n), we generate \(B=500\) data sets and compare the following approaches: our model with only the first (D1), the first three (D3) and first five projections (D5); the logistic PCA with only the first (LogPCA1), the first three (LogPCA3), and the first five projections (LogPCA5); the logistic SVD with only the first (LogSVD1), the first three (LogSVD3), and the first five projections (LogSVD5); the naive approach based on equal weights (Naive); the heuristic method (Heur) proposed by Dotto et al. (2019). Note that the last two methods are restricted, by definition, to a single projection. We recall here also that Dotto et al. (2019) approach is based on weight calibration after the estimation of the parameters of a multivariate latent Markov model.

Our proposal has been initialized using the output of logistic SVD as implemented in the R package logisticPCA (Landgraf and Lee 2015). Logistic PCA and logistic SVD use an eigen decomposition as starting values (as default in the R package just mentioned). For the naive and heuristic approaches, we use deterministic starting points, as implemented in the function est_lm_basic included in the R package LMest (Bartolucci et al. 2015).

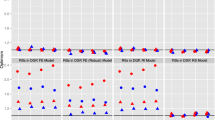
Figures 1 and 2 display the boxplots of the weighted deviance, at convergence, over the different scenarios and model specifications.

Fig. 1
figure 1

Distribution of the weighted deviance when \(H=5\) for different values of sample size n, time occasions T and number of projections Proj. For \(\hbox {Proj}=1,3,5\), we consider our proposed model (D), compared with logistic SVD (LogSVD), logistic PCA (LogPCA) and when \(\hbox {Proj}=1\) also with the counting approach (Naive) and the heuristic method of Dotto et al. (2019) (Heur). Results are based on \(B=500\) replicates

Full size image
Fig. 2
figure 2

Distribution of the weighted deviance when \(H=10\) for different values of sample size n, time occasions T and number of projections Proj. For \(\hbox {Proj}=1,3,5\), we consider our proposed model (D), compared with logistic SVD (LogSVD), logistic PCA (LogPCA) and when \(\hbox {Proj}=1\) also with the counting approach (Naive) and the heuristic method of Dotto et al. (2019) (Heur). Results are based on \(B=500\) replicates

Full size image

It can be seen that in almost all scenarios our proposal leads to a larger weighted deviance, and hence to more separated clusters, than competitors. This difference cumulates over the number of projections, and it becomes more and more apparent with increasing number of projections.

The naive approach of giving equal weights to all items, as could be expected, always yields the worst performance. Surprisingly enough, the heuristic approach of Dotto et al. (2019), despite being more variable, sometimes outperforms more formal methods like logistic PCA and logistic SVD.

As regard computational time, Table 1 shows times in minutes needed to obtain the results in different settings, using our non-optimized R code on a standard laptop. We believe that these are very reasonable running times.

Finally, to assess the effect of parameter initialization, we focus on the scenarios where \(H=5\), \(n=500\) and \(T=4,6\). In Table 2, we report statistics about differences in weighted deviance at convergence when comparing different parameter initializations: random, logistic PCA and logistic SVD. We find no evidence of strong dependence of the results on the specific initialization strategy, albeit the moderate standard deviation suggests that it might be wise to compare different starting solutions in general.

5 An optimal scoring system for material deprivation in three European countries

Data come from the longitudinal component of the EU-statistics on income and living conditions, the EU-Silc survey. We have data on households interviewed each year in U.K., Italy and Greece over the period 2010–2013. We use the balanced panel, therefore ending up with a total of \(n=1199\) Greek, \(n=2836\) Italian and \(n=1298\) U.K. households; each interviewed \(T=4\) times. Microdata as shared by EUROSTAT include less than 0.5% missing values. For simplicity, we work with the listwise complete cases.

The severe material deprivation indicator, defined by Eurostat (2012), corresponds to a lack of least four of the following \(H=9\) items:

  1. 1.

    the ability to keep the house adequately warm;

  2. 2.

    to have one-week annual holiday away from home;

  3. 3.

    capacity to afford a meal with meat, chicken, fish or equivalent protein every second day;

  4. 4.

    capacity to face unexpected expenses;

  5. 5.

    whether the household has a telephone;

  6. 6.

    whether the household has a color TV;

  7. 7.

    whether the household has a washing machine;

  8. 8.

    whether the household has a car;

  9. 9.

    whether the household is free of arrears on mortgage, rent, utility bills or loans.

The 9-item list is fixed for all EU countries.

Table 1 Median computation time (IQR in parenthesis), in minutes, when \(k=2\) and \(H=5\) for our model based on the first (D1), first three (D3) and all projections (D5)
Full size table
Table 2 Mean, median and standard deviation (SD) of differences in optimal weighted deviance of the first projection when \(H=5\), \(n=500\), \(T=4,6\)
Full size table

To explore the impact of the assumptions behind the counting approach adopted by Eurostat, first of all we compare the weighted deviance of unidimensional projections of different approaches, for four panel data sets: the households of each of three countries, and the entire data based on \(n=5333\) households pooled together. Results are reported in the upper panel of Table 3.

Table 3 Weighted deviance of projections for data on material deprivation in Europe, as obtained with different methods
Full size table

It is clear from Table 3 that our proposed approach (D1) outperforms all competitors. The heuristic method proposed in Dotto et al. (2019) does not compare well for this data set, as it outperforms only the naive approach based on equal weighting (as formally shown in Dotto et al. (2019)). Good results are provided by logistic PCA and logistic SVD in terms of group separation, but D1 improves the objective function by a minimum of 2.3% (for U.K.) to a maximum of 17% (for Greece). An advantage of D1 it that is also more interpretable, since a latent Markov model (whose parameters and interpretation are reported below) is estimated for the projected score.

We also evaluated our approach with time-dependent weights. This generalization does not seem to be useful for the data at hand, though. For instance, for D1, we obtain weighted deviances of 1.524, 1.388, 1.162 and 1.432 for Greece, Italy, U.K. and the pooled data, respectively. Since a fourfold increase in the number of weights leads to an increase in weighted deviance of only about 2% for Greece, and less than 1% in the other cases, we have decided not to pursue this route further. We therefore report only results involving time-fixed weights.

Further evidence of the good ranking and classification performance of our approach can be provided by externally validating the resulting scores. We do so through an assessment of their association with the equivalised disposable income, and with an indicator of the employment status (which was zero if no member of the household was working full time). In each of the four data sets, the scores obtained with our method were more strongly associated with these two variables than all other methods. Associations were measured through the Spearman correlation for equivalised disposable income, and the point bi-serial correlation for employment status.

Finally, as an assessment of goodness of fit, we report squared Spearman correlation between posterior probabilities for the material deprivation class obtained using D1 vs using the entire data. For Greece, this correlation is 0.947, for Italy 0.940, for U.K. 0.892, for the entire data set 0.939. We can thus conclude that, after projection, variability in the data at hand is well explained.

Optimal weights for method D1 are reported in the left panel of Table 4, as \({\hat{w}}^{(1)}\). In all cases, these scores can be seen as an overall measure of material deprivation, as weights have concordant signs (with the exception of item 5 in Greece and U.K., whose weight is anyway close enough to zero to be deemed negligible). It can be seen that the first four items and the last in general receive a strong weight. The fifth to eighth item are on the other hand probably not as important for discrimination. These items all regard possession of a good (namely: a telephone, a TV, a washing machine and a car). The first three goods are top priority in these countries regardless of poverty status: in the pooled data set only two households do not have at least one telephone (for a prevalence of 0.04%), three do not have a TV (0.06%), and sixteen (0.3%) do not have a washing machine. On the other hand, it is not surprising that owning a car is (jointly) not discriminating poor and not poor households as in several areas a car is not needed (e.g., the metropolitan area of London) and in other (e.g., more rural) areas it is almost essential. Our weighting system indicates that these four items might be eliminated from the questionnaire, at least when restricting the survey to these countries.

Some weights are also slightly different over countries. Ability to keep the house warm (item 1) seems important in Greece and Italy but less in U.K., where probably heathing is a priority. On the other hand, ability to have a holiday away from home (item 2) is crucial in U.K. but less important in Italy and Greece, where holiday spots (e.g., the seashore in the Summer) might be close to home. Less marked, and probably less relevant to classification, differences are seen for the other items. This suggests that, as also noted by Dotto et al. (2019), there might be some differential item functioning within and between countries. This needs to be tackled in order to produce meaningful and comparable classifications.

Table 4 Optimal weights for the first (\({\hat{w}}^{(1)}\)) and second (\({\hat{w}}^{(2)}\)) projection obtained with our approach in Greece (GR), Italy (IT), U.K. and for the pooled data (Pool)
Full size table

Since the scores are used directly, estimates for \(\xi \) and \(\sigma \) might not be of primary interest. On the other hand, initial and transition probabilities provide useful information. In Table 5, we report estimates for each country and the pooled data set. It can be seen that risk of deprivation in a given (e.g., the initial) year is quite large, especially in Greece, but persistent deprivation (as defined by persistence in the latent status of deprivation for the entire observation period) is not. See Dotto et al. (2019) for a more detailed discussion on this point. More importantly, all (homogeneous) transition matrices have slightly large values on the off-diagonal elements, with 16–24% probability each year to move from the deprived (D) to the non-deprived (ND) status, and 5–15% probability to move from the non-deprived to the deprived status. Overall, given that \({\hat{\pi }}_\mathrm{{D,ND}}>{\hat{\pi }}_\mathrm{{ND,D}}\) in all cases, we can claim that propensity to material deprivation has declined in each country over the observation period, from 2010 to 2013.

Table 5 Initial (upper panel) and transition (lower panel) probabilities for the optimal scores estimated for Greece (GR), Italy (IT), U.K. and for the pooled data (Pool)
Full size table

We conclude this section producing bi-dimensional projections, whose overall percentage of explained deviance is reported in the lower panel of Table 3. Once again, our proposal outperforms the competitors. Weights for the second projection are reported in the right panel of Table 4. Results indicate the while the first projection is, as noted above, a measure of overall material deprivation; the second projection has a different slightly interpretation over the four data sets. For Greece, the second projection is clearly just an indicator of arrears; for Italy, the second projection is contrasting item 1 with item 2, revealing preferences for poor households: the second score will have large values for households unable to keep the house warm but going away from home on holiday at least 1 week per year; and small values for households whose house is warm but unable to take holidays away from home. A similar interpretation can be given to the second score for the pooled data. Finally, for U.K. the second score is contrasting item 4 with item 2, which has a similar interpretation to the Italian second score after item 1 (which is top priority in U.K.) is replaced with item 4.

6 Conclusions

It is intuitive and clearly demonstrated in this work and in Dotto et al. (2019) that oftentimes obtaining linear combinations through equal weighting might be inefficient.

We have proposed a method to perform dimension reduction and clustering of continuous, discrete, nominal and binary multivariate outcomes repeatedly observed over time. Our proposal can also very naturally work with multivariate outcomes of mixed nature (e.g., continuous and binary). The method is based on optimization of a measure of separation of the latent clusters. A by-product of our approach is a vector of parameter estimates for a latent Markov model, which the linear projection is assumed to follow. The projected scores can be simply used as new variables, as usual. Clustering is also a natural by-product, given that subjects can be assigned to a latent state using estimated posterior probabilities for the underlying latent Markov model. A simple alternative is to directly threshold the scores. This might be convenient in order to efficiently assign new observations to clusters. We have not discussed for brevity how to do so and point the reader to references like Zheng and Heagerty (2004) and Barbati and Farcomeni (2018). Clearly, score thresholding is useful only when at least some labels are observed.

In our implementation, we have used a specific measure of group separation, given in (3). Expression (3) gives an absolute measure of variability, while a relative measure is obtained by expressing the model as a function of class-specific variances and taking those into account. Use of other group variation functions is straightforward given our numerical outer optimization strategy. In our example and a subset of simulations, we have seen that use of other measures, anyway, does not modify the comparative merits of our proposal with respect to other methods like logistic PCA and logistic SVD.

In summary, we have presented a method for dimension reduction in longitudinal data of mixed type that leads to new variables as linear combinations of the multivariate outcome. Unlike similar approaches, the method can deal quite simply with repeated measures, use of weights allows us to compute projected measurements on new subjects directly, and the underlying latent Markov model is interpretable and naturally leads to cluster labels (e.g., poor/not poor). Optimization of an objective function leads to optimal separation by construction.

Further improvements in our approach can be made by tackling the following assumptions. First of all, our approach is parametric in nature, being based on the assumption that linear combinations are Gaussian and follow a latent Markov model. Secondly, being based on nested optimizations (an inner optimization for estimating the parameters of each latent Markov model, and an outer optimization for the weights), it is computationally intense. In our implementation, we have used Fortran routines of the R package LMest (Bartolucci et al. 2015), and computational times are more than reasonable for the real and simulated examples shown; but we do not expect this approach to scale well to much larger data sets. Finally, the assumption that weights are orthogonal is useful for interpretation and for having the possibility of plotting scores. On the other hand, interpretation might be difficult in certain applications. One possibility is to put forward a pseudo-rotation, by relaxing orthogonality constraints. This can be done for instance by penalizing the objective function for the degree of non-orthogonality of the weights (e.g., Farcomeni 2017).