Model predictive control for compliant feed drives with offset-free tracking behavior

Abstract

Industrial machine tool feed drives are predominantly controlled by cascade control due to their low tuning complexity and inherent robustness. However, the cascaded structure requires the inner cascades to have higher dynamics than the outer cascades, which limits the achievable dynamic accuracy. Direct control approaches, which substitute the position and velocity cascade, offer the potential to utilize the unused potential. A promising approach is model predictive control (MPC), which optimizes the manipulated variable with a plant model along a prediction horizon. However, model uncertainties between the nominal model and the real plant lead to tracking errors. Therefore, this paper presents, a linear MPC (LMPC) and an adaptive MPC (AMPC) with an additional integral action to robustly compensate for model mismatches. Both controllers use a compliant model, are real-time capable with a sample rate of ${{2}\,\textrm{kHz}}$ and consider state and input space constraints. The AMPC accounts for position-varying stiffness and friction. The controllers are experimentally compared with classical P-PI cascaded control on a ball screw drive. They show a tracking error reduction of ${{37}{\,\%}}$ (LMPC) and ${{44}{\,\%}}$ (AMPC) during a high speed motion profile and an increase in bandwidth of ${{180}{\,\%}}$ (LMPC) and ${{184}{\,\%}}$ (AMPC), resulting in significantly improved dynamic accuracy.

1 Introduction

The positioning with controlled feed drives is a key task in production engineering [1]. The dynamic positioning accuracy of feed drives determines the quality and efficiency of machine tools in production processes during motion [2]. Feed drives are responsible for the feed movement of the workpiece or tool, and thus generating a relative movement between them [3]. A ball screw drive is often used as a feed drive in machine tools. It transmits the rotary motion of the electric motor via the spindle to the nut, thus converting the rotary motion into a linear axis motion. Ball screw drives are characterized by low friction and high efficiency, but their spindle stiffness depends on the load position [4, 5], resulting in position-variant machine dynamics. This degrades the achievable control performance if it is not considered in the control design.

Nowadays, cascaded P and PI controllers are well established in industry for position, velocity and current control, due to the fact that they are straightforward to parameterize and disturbances are compensated in the inner cascades. The integral action of the PI velocity controller of a drive system is required to achieve offset-free tracking behavior [6]. Although cascaded controllers are generally effective and straightforward to implement, the cascaded structure limits the dynamics, as the inner cascade must be faster than the outer [7]. The utilised controller has a significant influence on the tracking error dynamics and the disturbance behavior.

A possible increase in the dynamics of feed drives is considered by a model-based method of direct drive control. Model predictive control $\hbox {(MPC)}$, which is increasingly used for high dynamic processes, is applied. To investigate this potential for improvement, a model predictive controller is being implemented on a ball screw drive. $\hbox {MPC}$ uses a dynamic behavior process model, not only in the design phase, but also in the operation of the controller on the real plant [8]. Based on this model, a prediction is made for several time steps. An integrating behavior must be considered in the design of model predictive control to compensate for mismatches between the model and the real plant.

Therefore, the novelty of this paper is to provide a $\hbox {MPC}$ formulation that combines a compliant mechanical model, including the position-varying stiffness of the ball screw, with an integral disturbance compensation for offset-free tracking despite errors due to using a low-order prediction model. Two $\hbox {MPC}$ approaches with different linearization strategies are presented and experimentally compared with the state-of-the-art cascaded control with velocity and acceleration feedforward on a test bench with respect to their potential dynamic improvement.

The paper is organized as follows. Section 2 discusses relevant publications for feed drive control. Based on Sect. 2, the control design is presented in Sect. 3. Thereby, the plant model and the fundamentals of the $\hbox {MPC}$ formulation are discussed. The proposed $\hbox {MPC}$ formulations with the selected state space are validated with test bench data in Sect. 4. Therefore, the test bench is explained in more detail, the model identification is conducted and the controller performance is compared. A conclusion is given at the end, which completes the presented paper.

2 State of the art $\hbox {MPC}$ for drive systems

$\hbox {MPC}$ has been used in recent decades to control systems with slow dynamics, as they offer more time for solving the optimization problem [9]. However, the increase in computation power and solver speed allows to aim for systems with faster dynamics, such as robot joint control [10], feed drives [9] or piezoactuated systems with sampling rates up to 10 kHz [11].

Various $\hbox {MPC}$ structures have been established for drive systems. Berners et al. use a $\hbox {MPC}$ instead of a position controller in the cascaded form in [12]. Others use a direct approach, where a $\hbox {MPC}$ is used to control the axis position using the servo torque as the manipulated variable [7, 9, 13]. The replacement of the current controller gained some traction as well, e.g. by controlling a permanent magnetic synchronous machine (PMSM) [14]. An overview of current control with $\hbox {MPC}$ is given in [15].

There are already several automated solutions for parameter determination, e.g. a genetic algorithm for designing the $\hbox {MPC}$ parameters [12]. Dong et al. present a Markov algorithm in [16] and Stenger et al. use a Bayesian algorithm in [17] for the parameterization.

For the application in industrial machine tools, the $\hbox {MPC}$ can also be adjusted to more than one axis, such as a biaxial-system [18, 19] or a tool center point control for a five-axis-system [20]. [19, 20] control the system only indirectly via the motor encoder and therefore do not consider a compliant feed drive. In [18], a compliant feed drive is considered, but only simulation results are presented and the disturbance behavior is not analysed. This paper focuses on high dynamic profiles with small tracking errors and analyses the position-dependent stiffness on a single axis.

Fig. 1

Source of ballscrew and motor image: Neubauer et al. [21], CC BY license

P-PI structure with feedforward control

The advantage of $\hbox {MPCs}$ is the explicit consideration of constraints, but these are not considered in every implementation. In [13, 22, 23] constraints for the $\hbox {MPC}$ are considered and implemented. In other approaches, the constraints are not taken into account in order to reduce the computational time [19] or because the feedforward control or path planning already takes them into account [12].

It is also possible to use the $\hbox {MPC}$ for path planning to determine an optimal trajectory. In [24] a control approach with two $\hbox {MPCs}$ is presented to control a machine tool. One generates the reference trajectory in the time domain based on a trajectory in the position domain and transfers it to the other $\hbox {MPC}$, which directly controls the machine tool [24].

Industrial feed drives require offset-free tracking, which is achieved by the integral action in cascaded control, e.g. in the velocity controller. As direct $\hbox {MPC}$ has no such integral action, and due to the mismatch between the nominal model and the real plant, steady-state errors remain [25]. One approach to achieve offset-free tracking is to modify the plant model to take the input rate as a new input, which introduces an integral action [7]. Another approach is to extend the plant model by a disturbance model [25].

As shown before, there are numerous approaches in the state of the art for using a $\hbox {MPC}$ to increase the dynamic path accuracy of machine tool feed drives. However, none of these publications take into account the nonlinearity of friction and the position dependence of spindle stiffness in the prediction model. Furthermore, only [7] proposes a solution to avoid the control error inherent in direct control due to model errors. Therefore, this paper presents a model predictive control for offset-free tracking behavoir of machine tool feed drives taking into account the position dependence of the spindle stiffness.

3 Control design

The concept considered in this paper is based on replacing the position and velocity controller with an $\hbox {MPC}$. The cascaded control structure established in the industry is shown in Fig. 1. From the inside out, the controller consists of a current control loop, a velocity control loop and a position control loop. The P position controller reacts to the position error of the desired position value $x_d$ and the actual load position $x_l$. The controller output, which is the desired motor velocity $v_d$, is calculated using the measured velocity from the table and transferred to the PI velocity controller as a control error. The current controller is located in the inner cascade. The cascaded control structure in Fig. 1 also has an additional feedforward control for velocity $v_{FF}$ and acceleration $a_{FF}$. For this purpose, the desired velocity and desired acceleration are derived from the desired setpoint position by assuming a rigid model, i.e. no compliance between motor and load. The setpoints are then added to the corresponding control error. The acceleration is multiplied by $\lambda = m/\left( i_S k_M \right)$ to calculate the corresponding value for the current with the mass m, the transmission ratio $i_S$ and the torque constant $k_M$.

Within this paper we replace the position and velocity control loop with an $\hbox {MPC}$ (see Fig. 2). The $\hbox {MPC}$ directly provides the desired motor current based on the measured encoder value from the ball screw drive to control the motion.

Fig. 2

Source of ballscrew and motor image: Neubauer et al. [21], CC BY license

Model predictive control structure

3.1 Plant model

The plant model is used for model prediction in the controller. Therefore, it is critical to the overall system performance. The chosen model must represent a compromise between modeling accuracy and computation time. However, a more detailed model may lead to numerical and identification issues and even deteriorate the overall prediction quality. In this paper, we choose to use a two-mass oscillator structure, since the sensor values (motor current, motor position and table position) can be used directly and, with numerical differentiation for the velocities, no observer needs to be implemented.

The two-mass model is sketched in Fig. 3. We follow the convention that motor-side variables are denoted with index $(\cdot )_m$ and load-side variables with index $(\cdot )_l$. For ease of interpretation, the model is posed in purely translational coordinates, i.e., the motor side is converted from rotational to axial motion via the transmission ratio $i_S$ $\hbox {m/rad}$. $m_l$ describes the load mass and $m_m = J_m/i_S^2$ the mass of the motor and spindle of the ball screw drive, which is proportional to the inertia moment $J_m$. The degrees of freedom are the translational motor motion $x_m = \theta _m i_S$ with the measured motor encoder angle $\theta _m$ and the load position $x_l$. Further, the position-varying spring stiffness is described by $k(x_l)$ and the damping constant by d. In addition, a frictional force $F_F$ is applied to both masses.

Fig. 3

Schematic model of the ball screw drive system used for model-based control

This model is able to reproduce the dominant compliant mode, while neglecting higher modes. A typical ball screw drive characteristic is found in the frequency variation of the dominant mode due to the time-varying spindle length. This is considered by a position-dependent spindle stiffness k, where the ansatz function

$$\begin{aligned} k(x_l) = \frac{k_0}{k_1 + x_l} + k_2 \end{aligned}$$

(1)

depending on the position $x_l$ is used for a ball screw drive with one fixed and one free bearing. This is loosely motivated by the physical stiffness modeling based on Hooke’s law [3]:

$$\begin{aligned} k_\textrm{rot} = \frac{G I_T}{l_0 + l_\textrm{eff}} \text { and } k_\textrm{ax} = \frac{E A}{l_0 + l_\textrm{eff}} \end{aligned}$$

(2)

for the rotatory and the axial case with shear modulus G, torsional moment $I_T$, Young’s modulus E, spindle cross-section area A and unused spindle length $l_0$. The damping d is in general challenging to model [26] and, hence, assumed to be constant.

The resulting state space for the two-mass model in Fig. 3 with combined static friction $F_{F}$ is

$$\begin{aligned} \varvec{\dot{x}} =&\varvec{A}(x_l) \varvec{x} + \varvec{b} u + \varvec{F}_F(\varvec{x}) \nonumber \\ =&\begin{bmatrix}0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ -\frac{k(x_l)}{m_m}&{} \frac{k(x_l)}{m_m} &{} -\frac{d}{m_m}&{} \frac{d}{m_m} \\ \frac{k(x_l)}{m_l} &{} -\frac{k(x_l)}{m_l} &{} \frac{d}{m_l} &{} -\frac{d}{m_l}\end{bmatrix} \varvec{x} + \begin{bmatrix}0\\ 0\\ \frac{i_S}{m_m}\\ 0\end{bmatrix} u \nonumber \\&- \begin{bmatrix}0\\ 0\\ \frac{1}{m_m} \\ 0 \end{bmatrix} F_F \\ y&= \varvec{c}^{\textrm{T}} \varvec{x} = \begin{bmatrix} 0&1&0&0 \end{bmatrix} \varvec{x} \nonumber \end{aligned}$$

(3)

with state vector $\varvec{x} = \begin{bmatrix}x_m&x_l&\dot{x}_m&\dot{x}_l\end{bmatrix}^{\textrm{T}}$, input u being the motor torque and transmission ratio $i_S$ of the ball screw. The static friction force $F_F = F_{F,m} + F_{F,l}$ is combined on the motor side. Note, that the states are transformed to linear positions, but the input u is the motor torque, which results in expressions of the same magnitude and, hence, is beneficial for the optimization problem convergence. The torque u can then be converted via the torque constant $k_M$ into the desired motor current $i_d = u / k_M$. To determine the state space from (3), the unknown parameters have to be identified. These are identified in the frequency domain by optimizing to the frequency response using input and output measurements from the test bench. The transfer function for parameter identification is determined from the desired torque to the table position. The two-mass oscillator is optimized to the transfer function $G(s) = X_l(s)/U(s)$. The friction $F_F$ is modeled with static characteristics of the Stribeck-Model [27] as two superimposed functions ($F_{F,m}$, $F_{F,l}$). Note, that the Coulomb friction of the load side is mapped to the motor side and identified in combination with the motor friction as identifying separate friction models would require additional, non-standard sensors (e.g., force sensing in the ball screw nut) or significant velocity differences between motor and table, which are challenging to achieve without damaging the feed drive. To identify the friction characteristics, trajectories with constant velocities were used to measure the respective mean friction force. The least-squares error is then minimized by particle swarm optimization using the friction $F_F = F_{F,m} + F_{F,l}$ with

$$\begin{aligned} F_{F,i}(\varvec{x}) &= \textrm{sign}(v) \Bigg (F_{c,i} + (F_{s,i} - F_{c,i}) \textrm{e}^{\left( -|\frac{v}{v_{s,i}}|^{\delta _i} \right) } \Bigg ) \nonumber \\& \quad + F_{v,i} v , \quad \text { for } i=\{m,l\}. \end{aligned}$$

(4)

Due to a missing integrator and the fact, that there is a mismatch between the two-mass model and the test bench, the $\hbox {MPC}$ will show a steady-state error. To achieve an offset-free $\hbox {MPC}$,  Pannocchia showed in [25] different design methods to eliminate this error. One method is to add an additional integrating state, which is usually described as a disturbance [25]. The system dynamics from (3) is extended accordingly to:

$$\begin{aligned} \varvec{\dot{x}}&= \varvec{A}(x_l) \varvec{x} + \varvec{b} u + \varvec{b}_d d + \varvec{F}_F(\varvec{x}) \nonumber \\ y&= \varvec{c}^{\textrm{T}} \varvec{x} + c_d d \nonumber \end{aligned}$$

(5)

where d is the known disturbance.

In this study, two different $\hbox {MPC}$ formulations are used to control the feed drive motion. The first one is a linear $\hbox {MPC}$, indicated by LMPC, which means that it cannot take into account the friction and the position-dependent stiffness. The second $\hbox {MPC}$ is able to consider the friction and the varying stiffness at each time step and is called adaptive $\hbox {MPC}$, in the following AMPC. The discontinuous Stribeck function from (4) is approximated by a hyperbolic tangent for finite derivatives for the AMPC formulation. Therefore, the signum function is replaced by $\textrm{tanh}(\beta v)$ with $\beta = 1 \cdot 10^3$, which determines the slope at the origin. For the linearization of (3), a distinction is made between the linear and the adaptive $\hbox {MPC}$. The linear $\hbox {MPC}$ is linearized at the spindle position with maximum stiffness and without considering the nonlinear friction terms using $\varvec{x}_s = \varvec{0}$. For the adaptive $\hbox {MPC}$, a linearization is executed at each sampling step $t_k$ around the current (measured) state $x(t_k)$. The linearizations are listed in (5) and (6).

$$\begin{aligned} \varvec{A}_\textrm{LMPC}&= \frac{\partial \left( \varvec{A}\left( x_l\right) + \varvec{F}_F(\varvec{x})\right) }{\partial \varvec{x}}\bigg \vert _{\varvec{x} = \varvec{x}_s},\\ \varvec{A}_\textrm{AMPC}&= \frac{\partial \left( \varvec{A}\left( x_l\right) + \varvec{F}_F(\varvec{x})\right) }{\partial \varvec{x}}\bigg \vert _{\varvec{x} = \varvec{x}(t_k)} \end{aligned}$$

(6)

Finally, for real-time application the continuous model is discretized by the forward Euler method. Since the LMPC cannot consider the friction and the position-dependent stiffness, the friction is neglected and a constant stiffness k is realised by the discretisation. The AMPC, on the other hand, takes into account the friction and the varying stiffness at each time step. The discretization is described as follows

$$\begin{aligned} \varvec{x}_{k+1}&= \varvec{x}_k + T_s \left( \varvec{A}_{{\mathcal {C}}} \varvec{x}_k +\varvec{b} u_k +\varvec{b}_d d_k\right) , \\ {}&\text { for } {\mathcal {C}} \in \{\text {LMPC}, \nonumber {\text {AMPC}}\} \end{aligned}$$

(7)

with $f_s = 2~\textrm{kHz}$ and $T_s = 1/f_s$, where we use the index $(\cdot )_k$ as shorthand notation for time step $t_k$ of the discrete signal. The Euler discretization does not destabilize the system here due to the fast sample rate of the position controller.

3.2 $\hbox {MPC}$ formulation

The $\hbox {MPC}$ is designed to control the feed drive model (7). The model predictive controller solves a quadratic optimization problem in each sampling step $t_k$ to determine the optimal motor torque for the ball screw drive. The optimization is based on minimizing the cost function

$$\begin{aligned} J_k &= \sum _{i=1}^{N} \left\Vert e_{k+i\vert k} \right\Vert _{Q_{\textrm{c}}}^2 \nonumber \\ + \quad &\sum _{i=0}^{N-1} \left\Vert u_{k+i \vert k} - u_{k+i-1 \vert k} \right\Vert _{R_{\mathrm{c,\Delta u}}}^2, \end{aligned}$$

(8)

with the predicted tracking error $e:= y_d - y$ between the desired and predicted load position and the manipulated variable change for a prediction horizon of N steps. The prediction horizon length in (8) should be long enough to predict at least half the period of the model eigenfrequency, i.e.

$$\begin{aligned} N \ge \frac{\pi }{T_s}\sqrt{\frac{m}{k}}~. \end{aligned}$$

(9)

The cost function also includes a constant gain $Q_c$ and $R_{c,\Delta u}$ to weight the cost function. The weighting terms depend on the number of plant output variables $n_y$ and the number of manipulated variables $n_u$ with $Q_{\textrm{c}} \in {\mathbb {R}}^{n_y\times n_y}$ and $R_{\mathrm{c,\Delta u}} \in {\mathbb {R}}^{n_u\times n_u}$. $Q_c$ penalises the tracking error and $R_{c,\Delta u}$ penalises the output variation to reduce high frequency oscillations in the manipulated variable. To improve the tracking behavior, we use the fact that for computerized numerical control (CNC)-guided axis motion the dynamic trajectory of each axis is known in beforehand. Hence, for each step k, the cost function is provided with the desired axis positions $\{y_d(k+i), i=1,\ldots ,N\}$. With the system dynamics (7) and box-constraints for valid states and inputs the overall optimization problem becomes

$$\begin{aligned} u_k^* =&\arg \min _{u} J_k \\ \text {s.t.} \qquad&\varvec{x}_{k+1} = \varvec{x}_k + T_s \left( \varvec{A}_{{\mathcal {C}}} \varvec{x}_k +\varvec{b} u_k +\varvec{b}_d d_k\right) \nonumber \\&\varvec{x}_k \in [\varvec{{\underline{x}}}, \varvec{{\overline{x}}}] \nonumber \\&\varvec{u}_k \in [\varvec{{\underline{u}}}, \varvec{{\overline{u}}}] \nonumber \end{aligned}$$

(10)

and its solution at each time step $t_k$ results in the optimal motor torque $u_k^*$. For the numerical solution the optimization problem is stacked into a general quadratic program (QP) problem, which is solved using the active-set algorithm from the $\hbox {MPC}$ toolbox in Matlab.

4 Validation

The proposed $\hbox {MPC}$ formulations are implemented on a ball screw drive test bench. The cascaded P-PI controller is running at a sample time of $4~\textrm{kHz}$ and the $\hbox {MPCs}$ at $2~\textrm{kHz}$. The validation is conducted on a test bench, which is described in more detail in the following section.

4.1 Experimental setup

To analyze the controllers on a physical system, a test bench with common industrial implementations is used. The test bench for experimental validation is shown in Fig. 4. A linear motion is generated by a servo motor actuating the machine table via a ball screw drive (Steinmeyer 3526/40.40.6.3) with diameter of 40 mm and transmission ratio of $0.04/(2\pi )$ $\hbox {m/rad}$. The mounted table has a mass of $\sim$ 400 kg and a motion range of 0.75 m. The ball screw is driven by a Siemens PMSM (1FT7085-7WF71-1ML1) with a rated torque of 38 Nm, which is equipped with a motor encoder with a resolution of 20481/rev ($\approx$ 3.1$\,\upmu\mathrm{m}$ axial). The load position $x_l$ is measured using a linear measurement system (Heidenhain LS187C) with a grating period of 0.5$\,\upmu \mathrm{m}$ and an accuracy grade of 3$\,\upmu\mathrm{m}$ . A specific characteristic of the experimental setup is a linear direct drive (LSP200U-RU2-BN), which is mounted parallel to the guide rails under the machine table. The direct drive can apply a maximum force of $\hbox {13.2}\,\mathrm{kN}$ and is used to simulate disturbance forces. The current control loop for motor and linear direct drive are running on an industrial control unit (CU320-2 DP) via a terminal module (TM31). The velocity and position controller and the motion generation are running on a dSPACE rapid prototyping system (DS1006 processor board) at a sampling frequency of ${{4}\,{\mathrm{kHz}}}$. The control functionality is developed in Matlab Simulink and compiled with code generation for the target architecture of the rapid prototyping system. The desired torque u is provided as an analog voltage $\in \pm {{10}\,{V}}$ to avoid additional dead times of a digital fieldbus. Thus, the industrial control unit runs in torque control mode with only the current control loop running locally.

Fig. 4

The ball screw drive test bench used for validation

4.2 Model identification

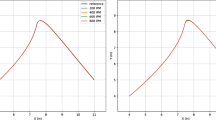
To identify the state space model parameters, first the unknown friction parameters from equation (4) have to be determined. For this purpose, different constant velocities are used and the corresponding force is calculated (see $\text {F}_{\text {F,meas}}$ in Fig. 5). Thus, the friction can be identified. These measured values are used to perform a nonlinear least-squares curve fitting. The friction function from equation (4) is used and approximated to the measured values. The result can be seen in Fig. 5.

Fig. 5

Approximation of the friction

The parameters ($k_0$, $k_1$ and $k_2$) for the position-dependent stiffness from (1) also have to be identified. For this purpose, the frequency response is performed at different positions and the stiffness is determined with a parameter identification in the frequency domain in positive and negative travel direction, respectively. The frequency response is evaluated with a sine sweep on the velocity at different positions and depending on the direction. For each frequency response, the stiffness is identified (see $\text {k}_{\text {meas}}$ in Fig. 6). The position-dependent stiffness is evaluated at different table positions over the entire travel distance. Thereby, a nonlinear least-squares curve fitting was performed for the varying spring stiffness parameters from (1). The damping d is assumed to be constant. The parameter identification result is shown in Table 1. With the identified parameters, the position-dependent stiffness can now be taken into account and the curve is shown in Fig. 6 with the measured values.

Fig. 6

Approximation of the position-dependent stiffness

The masses for the motor $m_m$ and the table $m_l$ were not considered in the parameter identification, as they can be determined from datasheet values and the CAD model, and were set to fixed values, which are listed in Table 1. All identified parameters for the two-mass model from (3) are listed in Table 1.

Table 1 Identified parameters for the state space model

4.3 Controller performance

The controllers are compared on the test bench and the behavior is evaluated in terms of trajectory tracking and disturbance rejection. Four different excitation signals are used to investigate the behavior in the time and frequency domain. The excitation signals used and their parameterization are shown in Table 2.

4.3.1 Validation trajectories

The trajectory tracking behavior in the time domain is validated on a time-optimal trajectory with a trapezoidal acceleration profile, which is a common speed profile in machining [28, Sect. 5.4.3]. This trajectory is called s-profile and the parameters used are shown in Table 2 with dynamic configuration.

Table 2 Feed parameters of the reference inputs

In the frequency domain, the trajectory tracking is validated with a transfer function using a pseudo-random-binary-sequence (PRBS) excitation. To determine the disturbance rejection behavior, disturbance forces are applied to the table using a force-controlled linear direct drive, which is mounted underneath the table (cf. Fig. 4). The time domain behavior is shown with a disturbance step, while for the frequency domain a disturbance chirp signal is used as excitation for the compliance transfer function. Both motions are performed with small table velocities ($\dot{x}_s = \hbox {0.01}\, \mathrm{m/s}$) to avoid the nonlinear friction domain.

4.3.2 Evaluation criteria

In the following, three different error types are defined, which are used for the comparison of the controllers. Thus, a statement can be made based on the quality of the error deviation. The tracking error $e_x = x_d - x_l$ refers to the deviation between the desired position signal $x_d$ and the actual load position $x_l$. As error measures in time domain we use the mean absolute error $J_{x}(e) = 1/M \sum _{i=1}^M \vert e_x \vert$, the standard deviation $\text {std}(e) = \sqrt{1/(M-1) \sum _{i=1}^M \left( e_x - J_{x}(e) \right) ^2}$ and the maximum $\text {max}(e)$ of the tracking error.

4.3.3 Controller parameterization

To validate the controllers experimentally, their parameters need to be tuned. For a fair comparison, the cascaded controller with velocity and acceleration feedforward control and the $\hbox {MPCs}$ are tuned according to the maximum peak criteria from [29], where the maximum peak of the sensitivity is defined as

$$\begin{aligned} M_{S} = \max _{\omega } \vert S(j\omega ) \vert \end{aligned}$$

(11)

and is typically required to be $\le 2$ ($\hbox {6} \, \mathrm{dB}$) [29]. The sensitivity function is defined as $S(j\omega ) = E_x(j\omega )/X_d(j\omega )$. The value of $M_{S}$ is also a measure of robustness, which is explained in detail in [29]. Before tuning the controller, it is necessary to determine the measured disturbance of the $\hbox {MPC}$. The disturbance is defined as the integrated error between the desired and the actual position, as $d = K_n \int e_x \,dt$. The integrator gain is set to the integral gain value of the PI controller. The disturbance only affects the plant output and is included in the cost functional, resulting in $\varvec{b}_d = \varvec{0}$ and $c_d = -1$. The $\hbox {MPC}$ can be adjusted and for this purpose three parameters have to be tuned: the prediction horizon length N, the weighting $Q_c$ and weighting $R_{c,\Delta _u}$. The weightings $Q_c$ and $R_{c,\Delta _u}$ have been parameterized for maximum bandwidth under the constraint of a worst-case sensitivity peak of $M_S\le \hbox {6}\,\mathrm{dB}$. For controller performance evaluation, the bandwidth $f_{\text {B}}$ is used and is defined as the lowest frequency at which the sensitivity $\vert S \vert$ crosses the $\hbox {-3}\,\mathrm{dB}$ for the first time from below [29]. To find the lower estimation of the prediction horizon length N the equation from (9) with $T_s=\hbox {0.5} \,\mathrm{ms}$ results in

$$\begin{aligned} N \ge \frac{\pi }{T_s} \sqrt{\frac{m_l}{k(x_{l,\max })}} = \frac{\pi }{T_s} \sqrt{\frac{412.6}{5.22\cdot 10^7}} = 17.66 \end{aligned}$$

(12)

The influence of the prediction horizon is shown in the experimentally determined sensitivity transfer function in Fig. 7 using the linear $\hbox {MPC}$. The figure shows that the prediction horizon has a great influence on the controller performance. The longer the horizon in Fig. 7, the smaller the peak and, since it is a new optimization problem, also a higher bandwidth $f_{\text {B}}$.

Fig. 7

Influence of the prediction horizon on the sensitivity function with LMPC

However, an increase in the horizon is also accompanied with a decrease in tracking behavior. According to equation (9), a lower estimation can be established. In the further course of the study a prediction horizon of $N = 18$ is used because it satisfies the maximum peak criteria. The velocity controller of the cascaded control was designed with loop-shaping and the position controller subsequently with the maximum peak criteria.

Fig. 8

Sensitivity analysis of the controllers in the frequency domain

4.3.4 Experimental validation

Figure 8 shows the comparison of the cascaded controller with velocity and acceleration feedforward control and the model predictive controllers in the frequency domain with the sensitivity function. For this purpose, a PRBS was used as reference input. In Fig. 8 it can be seen that the $\hbox {MPCs}$ have a significantly higher bandwidth and almost the same peak (to which they were tuned). To stay in the frequency domain, we analyze the disturbance behavior in the following. A disturbance chirp has been applied to the machine table as a disturbance force. Figure 9 shows that disturbances with low frequencies are better compensated by the $\hbox {MPCs}$.

Fig. 9

Disturbance rejection behavior in frequency domain

However, frequencies in the range of $f \in \left[ 40, \, 80 \right] \textrm{Hz}$ are better compensated by the cascaded controller with feedforward control. The controllers were also compared in the time domain. Disturbance behavior and reference tracking are examined in more detail. Figure 10 shows the disturbance rejection behavior in time domain. The $\hbox {MPCs}$ show a smaller error in case of a disturbance and reacts faster to the disturbance than the cascaded controller.

Fig. 10

Disturbance rejection behavior in time domain

For reference tracking in time domain, a s-profile for $x_s \in \left[ 0,\, 0.7\right] \textrm{m}$ is used to evaluate the tracking performance on the test bench.

Fig. 11

Position and tracking error for P-PI and $\hbox {MPCs}$ for the reference trajectory

In Fig. 11, the upper figure shows the desired reference trajectory $x_d$ and the table position $x_l$, and the control error $e_{x,i}$ is shown below. The control error of the $\hbox {MPCs}$ are significantly reduced, especially in the acceleration phase for $t \in \left[ 0, \, 0.2 \right] \textrm{s}$. Due to the offset-free $\hbox {MPC}$, the error is reduced during constant travel and no steady-state error remains. Table 3 shows the error measures in time domain for the tracking behavior from Fig. 11 as well as the frequency domain performance from Fig. 8.

Table 3 Performance of the controllers

4.4 Discussion

The $\hbox {MPCs}$ show a significant increase in bandwidth and thus the potential of the presented $\hbox {MPC}$ formulations for the control of machine tool feed drives.

A current limitation of the discussed approaches is the iterative parameter tuning during commissioning on the real plant. Therefore, future research is needed towards automated model-based controller tuning for safe parameterization on the plant. Another limitation is the accuracy of the low-order prediction model. A more complex prediction model could be selected for improvement. However, higher order models have a more complex parameter identification and the optimization problem at each control step requires more computational effort. Furthermore, the low-order model formulation directly supports the extension to other drive systems, such as robot joints or rack and pinion drives.

The transferability of the application to feed drive axes in machine tools depends on their specific design, especially the coupled mechanical behavior, as well as the process. By taking the dominant natural vibration into account in the model, this is also dampened by the controller. Cascade control cannot actively dampen resonances, so a significant increase in bandwidth can also be expected on machine tools. If a single resonance does not dominate, then a different model must be used for the $\hbox {MPC}$, but the remainder of the proposed methodology can still be used. More challenging is the integration of the optimization problem into the control system, which requires direct access to the control system interfaces. On the frequency converter this is currently impossible, but the trend of modern CNC controls to open interfaces, as with the open data layer of Rexroth CtrlX, allows an integration of the controllers here.

5 Conclusion

A model predictive controller for compliant feed drives was presented. Motivated by the increase in dynamics and to investigate the direct $\hbox {MPC}$ potential, two $\hbox {MPC}$ structures with integral action have been proposed, a linear one (LMPC), which is linearized once during the controller design phase, and an adaptive controller (AMCP), which is linearized locally at each time step, hence considering nonlinearities and the position-dependent stiffness of the ball screw spindle. The proposed approaches have been implemented and evaluated on a ball screw drive test bench. Compared to state-of-the-art cascaded P-PI controller, the $\hbox {MPCs}$ demonstrates the potential of a model-based controller with an increase in bandwidth of up to ${{184}{\,\%}}$. Moreover, the $\hbox {MPCs}$ reduce the peaks during acceleration by ${{59.41}{\,\%}}$ (LMPC) and ${{61.35}{\,\%}}$ (AMPC) and thus improve the tracking behavior. Furthermore, disturbance rejection has been improved by reducing the maximum error for a step disturbance force by ${{46.74}{\,\%}}$ (LMPC) and ${{45.88}{\,\%}}$ (AMPC). Future work will consider the integration of the offset-free controllers directly in the numerical control, the transferability to other drive systems as well as the data-driven identification of more accurate models.