1 Introduction

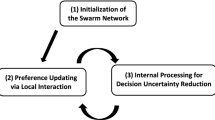
Fast yet reliable methods for consensus decision-making under localized communication play a critical role in artificial swarms, enabling them to decide on and perform tasks autonomously under uncertainties. This paper presents an efficient and scalable consensus algorithm for a swarm of artificial agents with limited sensing, communication, and processing capabilities. Consensus decision-making within this paper refers to achieving an agreed-upon decision among a finite number of available options, also known as a best-of-N problem (Valentini et al., 2017). Each agent’s preference toward these options is modeled as a probabilistic mass function (PMF). The option with the highest preference, the exhibited decision, determines the agent’s current state. This preference distribution in each agent dynamically changes as it communicates with its neighbors, i.e., other agents within the direct communication range. State transition occurs when the exhibited decision changes. Therefore, individual agents are viewed as probabilistic finite state machines (PFSMs).

PFSM-based methods have been previously explored in swarm decision-making. Several considered a probabilistic model consisting of a few control states or phases. For example, two-state PFSMs have been adopted for various applications, including stay or walk (Cambier et al., 2021; Lee et al., 2021), move forward or rotate (Shan & Mostaghim, 2021), and disseminate or explore (Valentini et al., 2016). The states may also include multiple directions of movements (Cai & Lynch, 2022) or interactions with the environment (Bodi et al., 2012). In these works, a probabilistic controller defined by customized transition functions determines the state transition. Another form of PFSM, similar to our setting, is based on a finite number of distinctive states, each representing an independent option (Bartashevich & Mostaghim, 2021). In Bartashevich and Mostaghim (2021), a swarm of robots utilized the evidence theory to collect color information of the environment and stored each color as a state in the PFSMs where local communication using fusion rules updated the states. This method achieved a high consensus rate (\(99-100\%\)) with up to five options in the PFSM through repeated exploration and dissemination phases. These previous works based on PFSMs were demonstrated for \(N \le 7\), limiting their applications to a relatively small number of available options.

In the presented work, distinctive options are expressed as uniquely assigned index numbers (IDs). For example, each agent may have N embedded algorithms corresponding to different swarm behaviors. Upon consensus, all or the majority of the agents in the swarm show the same exhibited decision. Simultaneously executing the algorithm associated with this decision, the swarm shows a collective behavior, such as shape formation, aggregation, or foraging. The amount and types of information exchanged among the neighbors are limited to the exhibited decision ID and the level of certainty calculated based on the entropy of the preference distribution. The entropy-based measure used in the method captures increasing uncertainty as the number of options increases while also reflecting the distribution characteristics (e.g., highly concentrated vs. uniformly distributed). Preference learning in each agent is performed by updating its preference distribution, considering the exhibited decisions and associated certainty levels received from the neighbors. Technical contributions of the presented method are summarized below:

  • Scalability. The algorithm is scalable with respect to the number of options (N) and the swarm size (n). The amount of information exchanged at the local level among the neighbors remains constant, making the algorithm suitable for a large value of N in best-of-N decision-making problems. The scalability was tested for \(N \in [2, 1000]\) and \(n \in [100, 1000]\).

  • Reliability. The algorithm showed a high convergence rate, over 90% in most of the experiments involving fixed random networks (i.e., randomly created networks that assume all nodes and connections remain fixed during consensus) and 100% in dynamic random networks (i.e., randomly created networks whose connections among the nodes dynamically change during consensus), under different conditions.

  • Applicability. Applicability of the algorithm for best-of-N consensus problems was tested in simulations involving 100 mobile agents in a confined environment and \(2-9\) beacons fixed in the environment serving as the available options perceived and evaluated by the agents. Three experimental scenarios involved (1) all beacons with the same range and quality, (2) the beacons with the same quality but different ranges, and (3) the beacons with the same range but different qualities. Within the scope of this work, we assume the quality and range are independent and do not interact with each other.

2 Related works

Consensus decision-making problems in artificial swarms can be roughly divided into two categories, depending on whether the swarm has infinite or finite options. The options are infinite if the decision domain is on a continuum, such as finding an optimal pathway in a 2D or 3D space (Amorim et al., 2021; Jadbabaie et al., 2003; Kwon et al., 2014; Turgut et al., 2008; Ferrante et al., 2012, 2014). A consensus problem with finite options requires the swarm to collectively select one among possible options that best satisfies specified conditions. Following the definition and classification method proposed in Valentini et al. (2017), this is referred to as “a discrete consensus problem” under the taxonomy of collective decision-making processes. Such consensus problems are commonly called the best-of-N problems. The best-of-N problems can be further classified into symmetric, if all options are equal in qualities and costs (Prasetyo et al., 2018; De Masi et al., 2020; Garnier et al., 2007), or asymmetric, if options are unequal in their qualities (e.g., different signal strengths (Kernbach et al., 2009; Schmickl et al., 2009; Arvin et al., 2012; Lee et al., 2018a), sites in various sizes (Garnier et al., 2009; Campo et al., 2011; Schmickl et al., 2006), frequencies (Parker & Zhang, 2009), task completion levels (Parker & Zhang, 2010)), costs (e.g., path length/time (Schmickl & Crailsheim, 2008; Montes de Oca et al., 2011; Campo et al., 2010)), or both (Reina et al., 2017). As demonstrated in these works, what entails the option qualities and costs depends on experimental scenarios and individual swarm agents’ capabilities. Commonly considered best-of-N scenarios include finding the largest or smallest site for the swarm agents to aggregate (Garnier et al., 2009; Campo et al., 2011; Schmickl et al., 2006), finding the shortest pathway among finite options (Schmickl & Crailsheim, 2008; Garnier et al., 2007; Montes de Oca et al., 2011; Campo et al., 2010), or finding the best quality source or signal (Kernbach et al., 2009; Schmickl et al., 2009; Arvin et al., 2012; Parker & Zhang, 2009; Lee et al., 2018a, b). Many existing works focused on the problem with binary options, such that \(N=2\) (Shan & Mostaghim, 2021; Garnier et al., 2009; Campo et al., 2011; Schmickl et al., 2006; Schmickl & Crailsheim, 2008; Garnier et al., 2007; Montes de Oca et al., 2011; Campo et al., 2010; Schmickl et al., 2009; Arvin et al., 2012; Parker & Zhang, 2009), while some others considered \(3 \le N \le 100\) (Lee et al., 2021; Cai & Lynch, 2022; Bartashevich & Mostaghim, 2021; Kernbach et al., 2009; Lee et al., 2018a, b).

The consensus process requires interaction among the swarm agents either indirectly or directly. The indirect interaction may occur through peer observations or modifying the environment without directly exchanging information among the agents. Indirect interaction eliminates the need for agent-to-agent communication mechanisms but requires a method for observing other agents or making and detecting the environmental traces. In the indirect-interaction methods, the consensus process is often tied with a specific consensus scenario, e.g. aggregating at the largest or smallest site (Garnier et al., 2009; Campo et al., 2011), finding the strongest signal source (Kernbach et al., 2009; Schmickl et al., 2009; Arvin et al., 2012), or selecting the shortest path (Sugawara et al., 2004; Garnier et al., 2007; Fujisawa et al., 2008; Mayet et al., 2010). Therefore, one swarm system developed for a specific application is usually not applicable to different scenarios.

Direct interaction indicates that the agents within the communication range exchange certain information. Depending on what data is sent and received and what internal processing is performed, the consensus strategies based on direct communication often apply to multiple, possibly more complex scenarios. In a voter model (Liggett, 1999; Rogers & Gross, 2013), each robotic agent replaced its opinion with the opinion of a randomly selected neighbor. In Valentini et al. (2014), the algorithm was adjusted to allow the agents to examine the qualities of the options. The opinion pooling method in DeGroot (1974) considered the consensus of a group of fully connected agents. Each carries a subjective opinion and updates it by pooling opinions from the rest of the group. Combining opinion pooling with a negative updating strategy, consensus towards the best opinion from the population size 10 to 100 with an adjustable pooling size was demonstrated (Lee et al., 2018a, b). The opinion pooling method requires each agent to collect all other agents’ probability distributions at each iteration. However, our method only requires the ID of the most preferred option and the level of certainty exchanged among the agents within the local communication range (‘neighbors’) in a loosely connected network. In Liu and Lee (2020), a scalable consensus algorithm applicable for loosely connected networks was presented, but it required the network topology to remain fixed during the consensus process and thus is not applicable for dynamic networks.

Some other widely adopted methods, also based on direct communication among the neighbors, include the majority rule (Wessnitzer & Melhuish, 2003), k-unanimity rule (Brutschy et al., 2012; Scheidler et al., 2015), and the frequency method (Parker & Zhang, 2009). The majority rule requires each agent to check the opinions of its neighbors and update the opinion to the majority’s (Wessnitzer & Melhuish, 2003). This method was combined with differential latency (Montes de Oca et al., 2011; Valentini et al., 2013), allowing the agents to rest for the duration determined by the environmental bias, e.g., a shorter differential latency for a shorter path (Goss et al., 1989). In the k-unanimity rule (Brutschy et al., 2012; Scheidler et al., 2015), each agent stores up to k opinions from the latest k neighbors. When k stored opinions are identical, the agent changes its opinion to be the same. The frequency-based method aims to select the best among finite options whose qualities can be quantitatively evaluated (Parker & Zhang, 2009). Each robot in the swarm can directly evaluate the quality of the opinion it favors and periodically sends “recruit” messages at a frequency proportional to the quality of the opinion. These three methods have been proven scalable over n and N. Considering their relevance, these three methods were employed for comparative evaluations in our selected best-of-N consensus problems.

The rest of the paper is organized as follows. Section 3 presents the entropy-based local negotiation and preference updating algorithms for swarm consensus, and Sect. 4 evaluates the presented method for its scalability and reliability under different conditions. Section 5 provides the comparative evaluations and discusses the results.

3 Entropy-based consensus algorithm

This section presents the distributed consensus decision-making algorithm for best-of-N problems in artificial swarm systems. It is based on each agent’s preference distribution over N options, updated via local negotiation among the neighbors within the communication range.

3.1 Problem formulation

We consider an artificial swarm of autonomous agents (also referred to as robots hereinafter) with relatively low-level computational and processing capacities and limited wireless communication capabilities without centralized control. Each robot with a limited memory capacity may have N embedded swarm algorithms, where only one can be executed at a time. These algorithms may represent physical behaviors, each corresponding to a specific swarm behavior when the agents in the swarm simultaneously execute the same algorithm. For example, each robot is programmed to find two nearby neighbors and position itself in the middle of the two, keeping a certain distance. If a group of agents executes the same algorithm, they will form a connected loop.

The swarm consisting of n agents is denoted as \(\mathcal {S} = \{A_1, A_2, \cdots , A_n\}.\) Each agent, \(A_i\) for \(i \in \{1, 2, \cdots , n\}\) has N available options, \(\mathcal {Q} = \{q_1, q_2, \cdots , q_N\}.\) The qualities or costs of these options may be symmetric or asymmetric. Decision-making within the context of this paper is defined as the swarm agents selecting a specific \(q_j \in \mathcal {Q}\) through local negotiations. Neighbors of \(A_k\) include the agents within the communication range of \(A_k\), such that \(\mathcal {N}_k = \{N^k_1, N^k_2, \cdots , N^k_r \}\) where \(0\le r \le n-1\). We note that \(\Vert \mathcal {N}_k\Vert = 0\) if \(A_k\) is isolated and \(\Vert \mathcal {N}_k\Vert = n-1\) when it is connected to all other agents in the swarm. The individual agent has a preference for N possible options. The preference is modeled as a PMF:

$$\begin{aligned} \vec {p}_k = [p^k_1, p^k_2, \cdots , p^k_N]^T \in \mathcal {R}^N \end{aligned}$$
(1)

where \(\sum _{i=1}^{N} p^k_i = 1\) for \(A_k\). The index of the most preferred option is the exhibited decision of \(A_k\), denoted as \(D_k = index(\max \{p^k_1, p^k_2, \cdots , p^k_N\})\). For example, if \(\vec {p}_k = [0.2, 0.5, 0.3]^T\), \(\max \{p^k_1, p^k_2, p^k_3\} = 0.5\) and \(D_k = 2\). Perfect consensus (100% convergence) requires all agents in the swarm to exhibit the same decision. Otherwise, a user-defined consensus criterion may be used. For example, if 90% convergence is required, a consensus is achieved when 90% of all agents in the swarm exhibit the same decision.

3.2 Local negotiation and internal updating

The presented consensus algorithm is based on each agent’s exhibited decision \(D_k\) and the level of certainty defined as

$$\begin{aligned} \Omega _k = \frac{1}{H_k+1} \end{aligned}$$
(2)

where \(H_k\) is the discrete entropy on \(A_k\)’s preference distribution, such that

$$\begin{aligned} H_k = -\sum _{i=1}^{N} p^k_i \log _2 p^k_i. \end{aligned}$$
(3)

The maximum certainty, \(\Omega _k = 1\), is achieved when \(p^k_j = 1\) and \(p^k_i = 0\) for all \(i=1, \cdots , N\) where \(i \ne j\), resulting in \(H_k =0.\) As \(H_k\) increases, \(\Omega _k\) decreases. For N available options, the range of \(\Omega\) is given by

$$\begin{aligned} \frac{1}{1+\log _2 N} \le \Omega \le 1. \end{aligned}$$

For example, consider three agents in the swarm \(\mathcal {S}= \{A_1, A_2, A_3\}\) with \(N = 4\), such that \(\mathcal {Q}=\{q_1, q_2, q_3, q_4\}\). Individual preferences are given by \(\vec {p}_1 = [0.9, 0.1, 0, 0]^T\), \(\vec {p}_2 = [0.7, 0.1, 0.1, 0.1]^T\), and \(\vec {p}_3 = [0.25, 0.25, 0.25, 0.25]^T.\) It is obvious that \(A_1\) and \(A_2\) exhibit the highest preference towards \(q_1\), while \(A_3\) shows a uniform distribution. Calculated decisiveness values for the three agents are \(\Omega _1 = 0.6807\), \(\Omega _2 = 0.4243\), and \(\Omega _3 = 0.3333\). While a statistical measure of variation (e.g., standard deviation (SD)) may play a similar role in measuring the level of certainty, it does not properly capture increasing uncertainty as N increases. For example, the SD of a uniform distribution over N options is zero regardless of N. On the other hand, \(\Omega\) for a uniform distribution decreases as N increases, such that \(\Omega =0.3333\) when \(N=4\) while \(\Omega = 0.2124\) when \(N=10\).

Local negotiation involves each agent exchanging limited information with its neighbors. In the proposed method, this involves the index of the highest preference among N options and the level of certainty, such that

$$\begin{aligned} \mathcal {I}_k= \{(D_{N_1^k}, \Omega _{N_1^k}), (D_{N_2^k}, \Omega _{N_2^k}) \cdots , (D_{N_r^k}, \Omega _{N_r^k})\}. \end{aligned}$$
(4)

\(\mathcal {I}_{k}\) is the information received by \(A_k\) from its r neighbors. Preference updating for \(A_k\) can be expressed as \(f: (\vec {p}_k, \Omega _k) \oplus \mathcal {I}_{k} \rightarrow (\vec {p}_k^{new}, \Omega _k^{new}).\) The specific formula used for this is

$$\begin{aligned} \vec {p}_k^{new} = \left[ \frac{\vec {p}_k + \sum _{i=1}^{r} \lambda ^k_i\vec {\Omega }_{N^k_i}}{\sum _{j=1}^{N}\left( \vec {p}_k(j) + \sum _{i=1}^{r}\lambda ^k_i\vec {\Omega }_{N^k_i}(j) \right) } \right] . \end{aligned}$$
(5)

We note that \(\vec {\Omega }_{N^k_i}\) is an N-by-1 vector with \(\Omega ^k_i\) on the \(j^{th}\) element, where j is the index of the exhibited decision of \(N^k_i\), and zeros for the rest. The weight denoted as \(\lambda ^k_i\) determines the relative attribute of the neighbors’ exhibited decisions in \(A_k\)’s preference updating process. If defined as a fixed constant applied to all agents, every agent’s opinion equally contributes to the consensus process. The \(\lambda\) value can also represent the quality associated with the specific exhibited decision or fidelity of \(N_i^k\). Theoretically, it may have any non-negative real value, where \(\lambda =0\) indicates ignorance of that neighbor’s opinion. Considering that \(\vec {p}_k\) is a PMF and \(0<\Omega \le 1\), the range of \(0 < \lambda \le 0.5\) allows each agent to consider its own and neighbor’s opinions in a balanced manner. The effect of \(\lambda\) in convergence performance when a fixed constant value is used across all agents is further discussed in Sect. 4.2. Section 5 utilizes \(\lambda\) to differentiate available options’ qualities.

4 Algorithm evaluation

This section evaluates the algorithm using randomly created networks where the nodes represent the swarm agents. We consider N abstracted options (i.e., represented by the ID numbers) without associated qualities or costs, where all agents are initialized with random preferences toward them. Therefore, successful convergence aims to achieve an agreed-upon decision among all options. This evaluation is meaningful when the swarm has to collectively perform a task among many options whose priorities or qualities are unknown or do not matter.

4.1 Experimental design and settings

Performance is measured by the convergence rate, the number of iterations required for convergence, and consensus outcome in terms of the following four aspects: 1) effect of \(\lambda\); 2) scalability over an increasing swarm size (n) and an increasing number of options (N); 3) effect of the network connectivity (c), i.e., the average number of neighbors each node can directly communicate with; and 4) effect of the seeds, i.e., a small subset of nodes in the swarm with the same exhibited decision with the maximum certainty, in governing the convergence performance and consensus result. A strict convergence criterion is applied here, requiring all nodes to exhibit the same decision. In most successful convergence cases, the number of iterations was below 100. Therefore, the upper limit of 250 iterations was set for the experiments in this section to determine successful convergence. MATLAB is used to construct an abstracted simulation environment for testing its scalability and convergence performance. All experiments were conducted on an Alienware Aurora R9 desktop computer with the Windows 10 system. This computer has an Intel i7-8700k CPU, 32.0GB RAM, and an NVIDIA GTX 1080Ti display adapter.

4.2 Effect of \(\lambda\)

The value \(\lambda\) in (5) represents how much the specific neighbor’s decision affects the internal updating process in each agent. While different \(\lambda\) may be assigned for individual neighbors or available options, this section examines the convergence behavior when a fixed value is used for all agents. We consider a random network consisting of 100 nodes (\(n=100\)) with the average connectivity \(c=5\), where each node has a randomly distributed initial preference over 10 options (\(N=10\)). The values for n and N were arbitrarily selected while \(n=100\) is viewed large enough to form a swarm (Motsch & Tadmor, 2014; Wedin & Hegarty, 2015; Zhang et al., 2017; Matni & Horowitz, 2014; Green et al., 2007), and N is comparable to (if not larger than) the number of options typically considered in related works (Parker & Zhang, 2009; Wessnitzer & Melhuish, 2003; Brutschy et al., 2012; Scheidler et al., 2015). The value of c was selected to be relatively small for a loosely connected network while being sufficient for convergence based on the analyses discussed in Sect. 4.4.

The evaluation of \(\lambda\) involved three cases: (1) 100-node fixed networks (i.e., the network configuration and connectivity remain unchanged during the consensus process), (2) 100-node dynamic networks (i.e., connections among the nodes randomly change at each iteration while maintaining the overall connectivity), and (3) 100-node fixed networks with five connected seeds (i.e., the special nodes exhibit the same decision with \(\Omega =1\)). In the first two cases, all agents were initialized with random preference distributions for ten options. A successful consensus was determined by the swarm converging to any of these options. The third case involved five directly connected nodes randomly selected as the seeds. All seeds showed the same exhibited decision with \(\Omega = 1\), and a successful consensus was determined when all nodes converged to the decision advocated by the seeds.

We performed 500 trials for each \(\lambda\), ranging from 0.05 to 0.5 with 0.05 increment. Figure 1 shows the results from the three experiments. The lines show the convergence rates; the bar graphs with error bars show the average number of iterations required for convergence and the SD. First, in the fixed networks, the convergence rate (solid-magenta lines) increased until \(\lambda = 0.2\) and remained at around 90%. The average number of iterations for convergence (blue bars) also showed a similar trend. We observed that convergence failures were mostly caused by two conflicting decisions dividing the swarm into two equal-sized groups. Second, in the dynamic networks, the result showed 100% convergence (dash-green lines) regardless of the \(\lambda\) values. The problems of two conflicting decision groups were not observed in the dynamic networks because the connection changes broke such conflicts. The average number of iterations (orange bars) also decreased as \(\lambda\) increased until around \(\lambda = 0.3\). The last set of experiments involving the seeds showed a high convergence rate (\(>95\%\), dash-blue lines) in all \(\lambda\) values except when \(\lambda = 0.05.\) The convergence rate was at the highest (\(97.6\%\)) when \(\lambda = 0.3\). The number of iterations for convergence (gray bars) was significantly lower than the other two experiments while showing the same decreasing trend as \(\lambda\) increases. Based on these results, we considered \(\lambda =0.3\) for the experiments in the following subsections.

Fig. 1
figure 1

Convergence rate and average number of iterations versus \(\lambda\) for a fixed and dynamic networks, and b fixed networks containing 5 connected seeds

Full size image

4.3 Scalability

Scalability is one of the most fundamental criteria required for distributed swarm algorithms. To evaluate the scalability, we employ fixed random networks with i) \(N=10\) for varying network sizes of \(n=100\) to 1, 000 with an increment of 100 and ii) \(n = 100\) for varying numbers of options ranging from \(N=2\) to 1, 000, where \(c=5\). As observed in Sect. 4.2, the convergence rate was 100% in all experiments employing dynamic networks. Therefore, we adopted fixed networks to observe the consensus performance changes over different n and N. We conducted 500 trials and recorded the convergence rate (%) and the average number of iterations with the SD for each n and N. Figure 2 shows that the convergence rate remained consistent at above 90% and the number of iterations and the SD increased as n increased from 25.8 (SD=13.1) when \(n=100\) to 67.1 (SD=35.4) when \(n=1,000\). Figure 3 shows that the convergence rate also remained consistent at around 90% as N increased from 2 to 1,000 with an irregular step size. The average number of iterations increased at a low rate from 17.5 (SD=9.2) when \(N=2\) to 37.4 (SD=16.3) when \(N=1,000\).

Fig. 2
figure 2

Convergence performance versus swarm size (n) with \(N=10\)

Full size image
Fig. 3
figure 3

Convergence performance versus the number of options (N) with \(n=100\)

Full size image

4.4 Effect of network connectivity

To evaluate the effect of network connectivity c, we consider fixed random networks with \(n=100\) with varying connectivity (\(c=3, \cdots , 20\)). Three examples on the top of Fig. 4 visualize the networks when \(c = 3, 7, 20\). The connectivity c indicates the average number of directly connected nodes from each node. The graph in Fig. 4 shows the convergence rate (blue) and the average number of iterations until the consensus (orange) over increasing c value. The data is based on the results from 500 trials for each c. The convergence rate rapidly increased from 24.0% to 90.2% as c changed from 3 to 5 and remained high afterward. The average number of iterations required for consensus decreased as c increased. However, the increased network density also indicates that each node (or agent) receives more data from the neighbors at each iteration, requiring increased computing and processing loads and thus taking longer. Therefore, a high network density may not be desirable if individual agents have limited capabilities. Moreover, if the agents are mobile, c would dynamically change for each agent, and thus requiring or assuming a high value of c may not be realistic. We used \(c=5\) for other evaluation settings considering these aspects.

Fig. 4
figure 4

Convergence performance with respect to the connectivity of the swarm network

Full size image

4.5 Effect of the number of seed nodes

Evaluation of how the number of seeds affects the convergence performance considered two cases of random networks, one with \(n=100\) and the other with \(n=200\). The percentage of the seed nodes changed from 1 to 8%. Figure 5a shows the overall convergence rate for each case. The blue and orange bars indicate the successful consensus towards the seeds’ decision when \(n=100\) and \(n=200\), respectively. The successful consensus toward the seeds’ decision increased as the percentage of the seeds increased in both cases, while the larger network (\(n=200\)) outperformed the smaller one (\(n=100\)). With 5% or more seeds, we observed almost guaranteed successful consensus. Figure 5b shows the average number of iterations decreased as the seed percentage increased in both cases of \(n=100\) and \(n=200\).

Fig. 5
figure 5

Convergence performance with respect to seed percentage under two different swarm sizes: \(n=100\) and \(n=200\)

Full size image

5 Comparative performance evaluation

This section compares the algorithm with existing, well-known methods, i.e., the majority rule, frequency-based method, and k-unanimity method. We adopt classical best-of-N target selection scenarios, commonly used for implementing consensus decision-making algorithms (Seeley & Buhrman, 2001; Parker & Zhang, 2009; Valentini et al., 2017).

5.1 Experimental scenarios and simulation environment

The experiments consider N options represented by beacons in a confined circular arena. These beacons are fixed in the environment, while the swarm agents are mobile. Under this setting, three specific best-of-N problems were considered:

  1. 1.

    All beacons have the same quality and communication range (symmetric problems).

  2. 2.

    The beacons have the same quality but different communication ranges (asymmetric problems involving options with the same quality and different costs).

  3. 3.

    The beacons have the same communication range but different qualities (asymmetric problems involving options with the same cost and different qualities).

We assume each beacon has a designated communication range and quality, and the agents within this range can receive the quality information broadcasted by the beacon. The communication range of the beacon can be viewed as the associated cost (Valentini et al., 2017). The beacon qualities may be defined differently depending on individual algorithms. All four methods, including the presented and three existing algorithms, were employed for Experiments 1 & 2. Experiment 3 involved only the entropy and frequency methods because the majority and k-unanimity rules do not have embedded mechanisms to consider different qualities of the options. It is possible to modify these algorithms to allow the beacon qualities to be accounted for. However, we formulated the experiments without significant arbitrary modifications in the algorithms because the convergence performance can be differently affected by how we modify them. For Experiment 3, beacon qualities were taken into account by \(\lambda\) values in the entropy method and frequency values in the frequency method proportional to the beacon qualities. In the previous section, we used a strict convergence criterion of all agents exhibiting the same decision. This criterion is not practical when beacons continuously affect mobile agents. Therefore, we now consider successful consensus when 90% of the swarm agents reach the same decision.

Fig. 6
figure 6

Unity experimental environment (a) and UGV model (b) with two sphere colliders defined for collision avoidance and consensus communication range

Full size image

A simulation environment was created using the Unity game engine to facilitate the above experimental scenarios. Unity offers an easy user interface, a robust physics engine (i.e., Nvidia PhysX engine integration), and a rich integrated development environment (Mattingly et al., 2012). It has also been used for robotic swarm simulations involving Unmanned Ground Vehicles (UGVs) (Lim et al., 2021; Le et al., 2014) and Unmanned Aerial Vehicles (UAVs) (Anand et al., 2019). Figure 6a shows 100 UGVs (i.e., mobile swarm agents) in a circular arena with the radius \(r=15\) meters(m) enclosed by 18 wall segments with six beacons fixed in the environment along the walls. These beacons can be viewed as available abstracted options or environmental biases (i.e., \(\mathcal {Q}=\{q_1, q_2, \cdots , q_6\}\)). Figure 6b shows a simple UGV model adopted for this simulation. This model has the following components: a collider determining the collision avoidance range (Collider 1); another defining the communication range (Collider 2); a 3D robot model; and a decision indicator for visualizing the agent’s exhibited decision using a distinctive color. Each mobile agent has the following capabilities:

  • Locomotion: It moves freely on a 2D surface within the enclosed arena at a fixed speed of 1.5 m-per-second (m/s).

  • Collision avoidance: It has an embedded collision avoidance algorithm that makes each agent either wait or detour when encountered by another agent within the boundary defined by Collider 1.

  • Localized communication: It can communicate with its neighbors within 2 m. Based on the communication range (Collider 2) and the defined movement speed, the swarm maintains a loosely connected network with the average connectivity measured at around \(c=2.07\). The default communication frequency is 10 Hz.

  • Consensus decision making: Each agent can participate in the consensus process based on the selected algorithm.

Fig. 7
figure 7

A successful trial using entropy-based consensus method. Snapshots at a 0 s, b 6 s, c 12 s, and d 18 s were recorded

Full size image

To implement our consensus algorithm for the experimental scenarios, each beacon is viewed as a stationary agent with a fixed preference, i.e., affecting mobile agents’ preferences without changing itself. The preference vector of the \(j^{th}\) beacon is modeled as

$$\begin{aligned} \vec {p}_j = [0, \cdots , 0, 1, 0, \cdots , 0]^T \in \mathcal {R}^N \end{aligned}$$
(6)

with 1 in the \(j^{th}\) element and zeros for the rest, where N is the total number of beacons (\(j\le N\)). We used \(\lambda = 0.3\) for all mobile agents, while individual beacons have different \(\lambda\) values representing their relative qualities, such that

$$\begin{aligned} \lambda _j = Q_j\cdot \lambda \end{aligned}$$
(7)

where \(Q_j\) represents the quality of the \(j^{th}\) beacon and ranges from 0 to 1. Figure 7 shows a simulation result with 100 mobile agents and six beacons with assigned qualities. All mobile agents converged to the ‘red’ beacon’s decision with the highest quality within about 18 s. We note that each mobile agent updates its preference at the local level while moving in the environment and communicating with its mobile neighbors. The number of iterations for consensus in individual agents varies, and therefore, we used the total time in seconds for measuring convergence speed.

5.2 Existing methods employed for comparison

To allow comparisons with existing algorithms, the following assumptions were made: (1) agents can only communicate with each other via local communication within a fixed distance (i.e., 2 m in this work, where the radius of the circular arena is set to be \(r=15\) m); (2) the communication frequency is fixed at 10 Hz, except for Experiment 3 where the frequency-based method uses the frequency to represent the decision quality (ranging from 1 to 10 Hz); (3) each mobile agent’s locomotion speed is consistent at 1.5 m/s; (4) each beacon is viewed as a stationary agent with a fixed exhibited decision.

The three existing consensus methods considered for comparative evaluation are briefly reviewed below:

  • Majority rule (Wessnitzer & Melhuish, 2003): This method aims to achieve consensus by having individual agents update their decisions with the majority’s decision observed from their neighbors. For example, if an agent can communicate with five neighbors, and three of them exhibit the same decision, then this agent changes its decision to the one shared by these three. Iterations continue until all agents in the swarm reach a consensus.

  • Frequency-based method (Parker & Zhang, 2009): In this method, each agent in the swarm periodically sends a “recruit" message with its decision at the frequency proportional to the associated quality. Therefore, agents with a higher quality decision send the recruit messages more frequently than those with a lower quality decision and thus tend to govern the convergence towards the highest quality decision.

  • K -unanimity rule (Brutschy et al., 2012; Scheidler et al., 2015): Consensus using this method can be achieved by individual agents updating their decisions after meeting k agents in a row that all exhibit the same decision. For example, if \(k=3\), each agent stores up to 3 decisions exhibited by the latest 3 neighbors and updates its decision to the decision commonly exhibited by the three latest neighbors.

5.3 Results from comparative evaluations

The consensus performance is evaluated by the successful convergence rate and the average time required for convergence. As stated earlier, we consider that consensus is achieved when 90% of the mobile agents in the swarm converge to a common decision among N options represented by N beacons. Experiments employed 100 mobile agents (\(n=100\)) and a varying number of beacons (\(N=2,3,6,9\)). For each experimental setting, 100 trials were conducted with a time limit of 1,000 s. If the swarm does not reach a consensus within this time limit, the trial is regarded as non-convergence.

5.3.1 Equal-quality, equal-range beacons: Experiment 1

We first tested consensus performances of the four methods in the symmetric option scenario when all beacons have equal communication range (10 m in diameter) and frequency (10 Hz) for each case of \(N = 2,3,6,9\). Figure 8 shows the results using pie charts and bar graphs. Blue indicates successful convergence to any beacon’s decision, and red shows non-convergence. Bar graphs with error bars show the average time for convergence with the SD. Except for the frequency method, the other three showed 100% successful consensus in all symmetric option cases without significant differences in time for convergence. In most cases, the frequency method failed to reach consensus when \(N\ge 6\), such that only 6% convergence when \(N=6\) and 1% when \(N=9\). Even in convergence cases, it took significantly longer than other methods.

Fig. 8
figure 8

Results from Experiment 1 - symmetric options: consensus performance of 4 consensus methods: (1) entropy-based method, (2) majority rule, (3) frequency-based method, and (4) k-unanimity rule

Full size image

5.3.2 Equal-quality, unequal-range beacons: Experiment 2

This experiment involves beacons that communicate at the same frequency but with different communication ranges. This setting is similar to the problem involving multiple sites with varying sizes where consensus aims for converging to the largest site. Two sets of beacon ranges were considered for each N: one set involving one of the beacons with a significantly longer range than the rest and the other set with gradually different beacon ranges. Figure 9 shows the results using the same color scheme. Successful consensus towards the beacon with the largest communication range is shown in blue; non-convergence is shown in red in the pie charts. We also report the consensus towards a beacon decision other than the best in orange. Our entropy-based method outperformed the other methods in this asymmetric option scenario showing the highest successful consensus rate towards the best option in all eight cases. When convergence towards any beacon is considered, i.e., the blue and orange areas combined in the pie charts, the entropy, frequency, and majority methods showed 100% convergence, whereas the entropy method showed slightly faster convergence than the other two. Similar to the results from Experiment 1, the performance of the frequency method began to significantly deteriorate when \(N=9\) with the gradually differing range options.

We further analyzed the statistical significance of the results shown in Fig. 9. Two-sample testing between population proportions was applied to the pairs of the presented entropy-based method and each of the three employed methods to determine if the difference in the convergence rate towards the best option is significant (Ott & Longnecker, 2015). In all cases except for two, the entropy-based method showed better convergence performance with significant differences. The results from the entropy and frequency methods when \(N=3\) with the beacon diameters of \(\{12, 10, 8\}\) and \(N=6\) with the beacon diameters of \(\{14, 12, 10, 8, 6, 4\}\) showed no statistical differences, resulting in \(z=0.9936\) and \(z=0.3415\), respectively. In all cases, the frequency method took significantly longer for convergence than the rest.

Fig. 9
figure 9

Results from Experiment 2 - asymmetric options: consensus performance of 4 consensus methods: (1) entropy-based method, (2) majority rule, (3) frequency-based method, and (4) k-unanimity rule

Full size image

5.3.3 Unequal-quality, equal-range beacons: Experiment 3

This experiment employs the frequency-based method (Parker & Zhang, 2009) and the presented entropy-based method only because the other two are not readily suitable for this scenario. In the entropy method, the frequency of communication among the mobile agents remains consistent at 10 Hz, with the \(\lambda\) value defined in (7) determining the quality of each beacon. In the frequency method, the frequency of communication is proportional to the quality of the exhibited decision (ranging from 1 to 10 Hz). For each N, we considered two sets of beacon frequencies, similar to Experiment 2: the first set involved one beacon with a significantly higher frequency than the rest, and the second had gradually changing frequencies. Figure 10 shows the results using the same color scheme. Both methods showed high consensus rates and fast convergence speeds in all cases, especially when one of the beacons has a significantly higher frequency. When \(N=3\) with beacon frequencies of (6, 5, 4), the entropy method showed a 98% convergence rate towards the first beacon, whereas the frequency method showed 100%. When \(N=6\) with gradually different beacon frequencies, the success rates were 96% using the entropy method and 100% using the frequency method. When \(N=9\) with gradually different beacon frequencies, the success rates were 97% using the entropy method and 99% using the frequency method. Two-sample testing between population proportions was also applied to the case when \(N=9\) with the beacon frequencies of \(\{9, 8, 7, 6, 5, 4, 3, 2, 1\}\). The result showed no significant difference between the two results (\(z=1.5410\)). In all other cases, the frequency method showed a 100% convergence rate; thus, no further statistical analysis was applied.

Fig. 10
figure 10

Results from Experiment 3 - asymmetric options: consensus performance of 2 consensus methods: (1) entropy-based method, and (2) frequency-based method

Full size image

6 Discussion and conclusion

This paper presented a new consensus algorithm for a swarm of artificial agents with limited sensing, communication, and processing capabilities. The algorithm was evaluated for its scalability in terms of the swarm size (n) and the number of options (N), reliability with a high convergence rate under different experimental conditions, and applicability for best-of-N consensus scenarios. We assumed that all agents have the same N options in the presented work. However, a minor algorithm modification allows individual agents to have different or dynamically changing options. For example, individual agents may have limited knowledge about the available options and start learning new options as they communicate with their neighbors. If an agent receives the exhibited decision ID with the certainty value from its neighbor that does not belong to the existing options, the agent may extend the decision domain and redistribute the preferences based on the existing and received information. The agent must also receive any information or data about this new option in this case. This dynamic option scheme will be a useful extension of the algorithm in the interest of real-world applications of swarm robotics.

The presented preference updating algorithm in (5) has one parameter, \(\lambda\), which may represent different properties or roles. In Sect. 4, we considered the same \(\lambda\) value for all agents and observed the convergence behavior in three cases, i.e., fixed networks, dynamic networks, and fixed networks with seed nodes, for comprehensive evaluations. These experimental settings may apply to real-world scenarios. For example, the fixed network case may represent a connected IoT system with many sensor nodes for monitoring large facilities, such as power plants. Based on the sensor data, a consensus may be performed to identify the highest risk area. Experiments with dynamic networks were intended to represent mobile swarm networks, where the local connections among the mobile agents would dynamically change. The experiments with the seeds may apply to the cases when a small subset of a swarm perceives critical information (or an upper-level command), and this subset must govern the consensus process.

As stated earlier, \(\lambda\) can be used for each agent to assign different trust values for its neighbors or to represent the qualities of the exhibited decisions as demonstrated in Sect. 5. The specific role(s) of \(\lambda\) may be determined for each application and the capabilities of individual agents. For example, robotic agents in a swarm can observe and detect the ‘well-being’ conditions of the neighboring robots within the sensing range. Each agent updates its preference while giving a higher weight to the healthy neighbors and a lower weight to those unwell. If the consensus aims for the swarm to determine the shortest path, \(\lambda\) may be inversely proportional to the distance traveled for available paths. Further evaluations encompassing commonly adopted swarm consensus scenarios may be followed to fully understand the roles and effects of \(\lambda\) and possibly develop a method to optimize this value given n, N, and problem-specific conditions.

In fixed networks, the presented algorithm achieved over 90% successful consensus in most cases. Most convergence failures employing the presented entropy-based method were associated with the swarm converging into two comparable-sized groups with two conflicting decisions. To break the symmetry, our algorithm may be combined with the frequency-based method (Parker & Zhang, 2009; Liggett, 1999). Any method involving asynchronous message sending or any algorithm that randomly selects partners for communication may be considered to resolve this issue. Such problems were not observed in the experiments employing dynamic networks.

Comparisons with three well-known methods (i.e., majority rule, frequency-based method, and k-unanimity rule) demonstrated the algorithm’s applicability in three best-of-N experimental scenarios. Within the experimental scenarios and settings presented in this paper, the entropy-based method could be directly applied to these experimental settings and performed reliably in all cases. When equal-quality, equal-range beacons were adopted (Experiment 1), three methods except for the k-unanimity performed similarly well. With equal-quality, non-equal range beacons (Experiment 2), the presented entropy-based algorithm outperformed the other three regarding the convergence rate and the number of iterations. In the scenario with unequal-quality, equal-range options (Experiment 3) comparing only the entropy and frequency methods, the frequency method showed a slightly higher convergence rate, but the difference was insignificant. Despite the demonstrated potential, the results in Sect. 5 must be viewed with caution. We employed these algorithms as described in Seeley and Buhrman (2001); Parker and Zhang (2009); Valentini et al. (2017). Many variations and improved algorithms exist, and this paper does not discuss their relative performances. Likewise, the presented algorithm can be improvised for specific consensus problems.

7 Disclaimer

The views, opinions and/or findings expressed are those of the author and should not be interpreted as representing the official views or policies of the Department of Defense or the U.S. Government.