The Cu–Sn System: A Comprehensive Review of the Crystal Structures of its Stable and Metastable Phases

Abstract

The present works assesses the knowledge concerning the crystal structures of phases in the Cu–Sn system having their high relevance due to their occurrence in bronze alloys and soldered systems. The crystal structures of the terminal solid solution phases α-Cu and β-Sn and of the stable main intermediate phases β, γ, ε-Cu₃Sn, δ-Cu₄₁Sn₁₁, ζ-Cu₁₀Sn₃, η-Cu₆Sn₅ and η′-Cu₆Sn₅ and some metastable phases appear to be well established in the literature, but details can be intriguing. This paper attempts to review apparently or truly contradictory structure models derived from experimental diffraction data for the different phases, revealing limiting knowledge in some cases. These results are also analyzed regarding the results of first-principles calculations making use of various model structures. The review is also used to highlight exemplarily problems, which can be experienced upon widespread, “routine” means of phase identification, in particular x-ray diffraction (on polycrystalline specimens) and electron backscatter diffraction.

1 Introduction

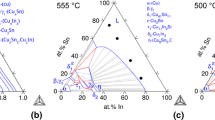
Knowledge on the phases of the binary Cu–Sn system, their heterogeneous equilibria and phase transformations can serve as basis for the understanding of the constitution of a variety of technologically highly relevant alloy systems like bronze alloys and the reaction zones of solders. Reports on the constitution of the binary Cu–Sn system are, therefore, among the classics of phase-diagram research.^[1,2,3,4] The currently most widely used phase diagram might be that reported by Raynor in 1944^[5] and later reproduced prominently by Hansen and Anderko,^[6] or by Saunders and Miodownik.^[7] This diagram is also contained in a prominent collection of binary alloy phase diagrams,^[8] as reproduced in Fig. 1(a). However, note that some changes in detail have been proposed in some later works, as it concerns the β/γ equilibrium and the equilibria involving the Cu₆Sn₅ intermetallic¹ (η and η′ phase in Fig. 1).^[9,10,11,12] Instead of trying to incorporate these insights into Fig. 1(a), alternate versions suggested by later works are shown in Fig. 1(b-d).

Fig. 1

Phase diagram Cu–Sn at 1 atm. (a) Version as originally constructed by Raynor ^[5] and adapted in modified form from ^[8]. Further, updates as suggested by (b) Leineweber et al. ^[12], (c) Liu et al. ^[13], and (d) Fürtauer et al. ^[9] are shown. All subfigures were redrawn from the original in a simplifying manner. Blue: continuous/second order transition lines

Soon after the advent of x-ray diffraction, atomic structure models for the Cu–Sn phases were proposed. This apparently started with the Cu-rich terminal solution and on the ε phase (ε-Cu₃Sn) investigated by Bain.^[14,15] Reports continued over time, including classic studies, which were fundamental in working out what is now known as the Hume-Rothery electron-per-atom rules for the occurrence of different crystal structure in brass-like systems,^[16,17] towards the latest experimental information on the incommensurate structure of the metastable η′′ phase.^[11,18] Some recent reviews have included insights related to the Cu₆Sn₅ intermetallic.^[19,20] Experimental information on crystal structures is, nowadays, supplemented more and more by first-principles calculations on periodic model structures, starting perhaps by an influential work dealing with the Cu₆Sn₅ intermetallic.^[21] A very recent work dealt with crystal structures considered as relevant for ε-Cu₃Sn.^[22]

The present work aims at reviewing the knowledge about crystal structures occurring in the Cu–Sn system. Basic information on crystal structures usually accompanies reviews on the phase constitution as in.^[6,7] However, it turns out, as it is also the case for other binary systems, that the wide range of experimental and theoretical information including their interpretation in the original works appears contradictory and can cause confusion. This is often caused by inappropriate appreciation of early works and by uncritical appreciation of database entries like from the ICSD^[23] or from Pearson’s Handbook.^[24] In view of this, the present work does not only try to explore the definite, “true” crystal structure for each phase but also discusses the partially true or apparently contradictory structure models for each phase or group of phases, also considering some subtleties in the crystallographic descriptions. Thereby, this review might serve as a guide for scientists applying all kinds of phase identification during microstructure analysis. This work also points out areas of limited knowledge and understanding. Such areas might be addressed in future experimental and theoretical studies.

2 Remarks on Crystal Structure Information

In the thermodynamic sense, a crystalline phase is a structurally homogenous state of matter under some complete or constrained equilibrium with properties that change continuously upon change of externally controlled state variables (e.g., composition, temperature, and pressure). Discontinuities in some, e.g., thermodynamic properties imply occurrence of a phase transition. A discontinuous evolution of a crystal structure also implies such a transition and thus existence of different phases (apart from the case of an isomorphous transition). Most of the transitions are of 1^st order according the Ehrenfest’s classification and show discontinuity, e.g., in entropy and volume over the transition. Some transitions between structurally related phases, however, do not have to show such discontinuities. Discontinuities then only occur for higher-order derivatives of the volume or entropy. Such transitions are frequently designated as 2^nd or higher order according to Ehrenfest, but often the term continuous (e.g., in volume and entropy) is used as a general term, which also can cover λ-type transitions. In the present work the designation continuous transition will be employed.

We will discuss crystal structure mainly in terms of the atomic structure implied by space group symmetry, the unit cell, and the fractional coordinates of the atoms.² These data have typically been derived by means of diffraction experiments that focus on the information contained in Bragg peaks.

Assessing reports on crystal structures in the literature is complicated by the following facts:

• (a) The same crystal structure can be described in many ways, many of them are perfectly reasonable. This concerns a few choices, e.g., choice of the origin of the unit cell, choice of translation vectors spanning the unit cell (common for triclinic and monoclinic symmetry) or choice of one out of 6 permutations of orthogonal basis vectors for orthorhombic crystals. Analysis of different descriptions for possibly equivalent structures can be supported using software to standardize the crystallographic description.^[25,26] Different descriptions of a given crystal structure are usually referred to as setting. Settings involving different choices of basis vectors to span the unit cell can (but do not need to be) associated with different Hermann–Mauguin symbols, which correspond, however, to the same space group number in the International Tables for Crystallography A.^[27]3

• (b) At first glance, two described crystal structures may be regarded as essentially different if there is a significantly different size of the primitive unit cell or if they are described with space groups with different space group numbers according to.^[27] If such different crystal structure models exist for some kind of sufficiently similar crystalline material, such information first implies essentially different phases. However, this does not have to be the case. Different quality of diffraction data can reveal features (e.g., additional weak reflections), which were not visible in other, e.g., earlier studies. The perpetual search for an improved interpretation of diffraction data but also the simple oversight of symmetry elements implied by a structure solution may also lead to structure models with a level of atomic ordering which is not supported by the diffraction data (overdetermined structure model). As it is often the case in science, the interpretation of an experiment is, to some degree, influenced by the individual scientist’s (artist’s) interpretation of the data. Comparison of diffraction patterns simulated based on the respective reported structure models might reveal the possibility that such apparently different structure models might be simply different interpretations of quite similar diffraction data. In such cases it must be analyzed whether the experimental evidence presented in the different works is really supporting the substantially different structure models to an extent that these different models may imply really different, distinct phases. A special case is that of an incommensurately modulated structure with continuously varying vector describing the spatial structure modulation. In such a case higher-dimensional crystallography can be used to describe structures, which might otherwise imply different types of unit cells, within a unified scheme, thereby providing a single structure model for a specific phase.

It turns out that most of the complications described above actually must be considered upon analyzing the crystal structures of the phases in the Cu–Sn system.

Some remarks should also be made on crystal structures or phases studied by first-principles calculations. Such calculations are typically done on well-ordered structure models, where the quantities derived from relaxed structure models (lattice parameters, atomic coordinates, energies, electronic structure) and the associated local energy landscape about some distortions (elastic constants and phonon energies) can be used to make predictions for real or virtual phases. However, not every structure model considered in first-principles calculations should be conceived as separate phase as some authors tend to claim in their works. Otherwise one could construct infinitely many phases. Furthermore, in particular the study of a single disordered phase by first-principles calculations typically requires consideration of various carefully selected model structures (e.g., specific types of superstructures^[28]). The information from first-principles calculations can be valuable in complementing experimental data on crystal structures and their stability.

3 Assessment of the Crystallographic Literature on the Cu–Sn System

3.1 Organization of the Data

The data for the stable solid solutions and intermediate phases with some metastable derivatives is discussed with increasing Sn contents in Sects. 3.2-3.8. Crystal structures of further metastable phases or transitional states are reported in Sect. 3.9, while further hypothetical structures will be considered in Sect. 3.10.

In each section, the review starts discussing experimental findings concerning lattice parameter data and atomic structure and its symmetry. Generally the Strukturbericht notation^[29] is used to denote crystal structure types, sometimes also indicating the prototype structure or other symbols (for a listing, see Appendix A). Further, if no Strukturbericht symbol is available, the Pearson symbol^[30] or some ad-hoc structure names may be employed to differentiate between different structure models.

Reference will be made to powder x-ray diffraction (PXRD⁴), single crystal x-ray diffraction (SCXRD) and selected-area electron diffraction (SAED) and other transmission electron microscopy (TEM) techniques. For brevity, it was decided generally not to systematically review temperature-dependent lattice parameters/coefficients of thermal expansion. Values given in kX units (and values, although given as Å, which obviously are in kX) are multiplied by 1.00202 to arrive at values in Å.^[31] If values were calculated from wave lengths strongly deviating from present day ones, the values were directly corrected considering these values. Such modified values are marked with the note “corrected!”.

Later, in the corresponding section, results from first-principles calculations are reviewed by summarizing their main results in tables, if more than one work is relevant for the corresponding section. As pointed out above, this typically happens on periodic model structures which try to reflect some essence of the structural and thermodynamic properties of real phases. The vast majority of this data has been obtained by applying density functional theory (DFT), using different variants of the generalized gradient approximation (GGA),^[32,33] which may be regarded as standard to capture thermodynamic properties of inorganic materials.^[34] Energy and relaxed structure geometry from such calculations refer to the static atomic structure at 0 K (neglecting zero-point vibrations). It is noted that the absolute unit-cell volume depends on the detailed setting of the calculations, even when applying different variants of the GGA. No attempt is made to compare data from different first-principles works on the same model structure as it concerns slight variations of the unit cell volume. Mainly, data giving special insight into the structure geometry, composition-dependent structure changes and the energy hierarchy of competing structure models will be reviewed. Also, elastic properties are cited, usually listing the bulk modulus B implied by the calculations. If single-crystal elastic constants are available, typically in terms of the components of the Voigt-type 6 × 6 matrix and its components ${C}_{ij}$ with $i, j$ = 1…6), the calculated Hill average of the bulk modulus B will be reported. To quantify elastic anisotropy implied by the reported single-crystal elastic constants, the “universal elastic anisotropy index” ${A}^\text{U}$ according to Ref. [35] will be used, where elastic isotropy implies a value of ${A}^\text{U}=0$. Details on elastic anisotropy are, however, only discussed if ${A}^\text{U}>0.6$ holds (which will be rarely the case). Below this value, the elastic anisotropy will be regarded as small (and not sufficiently interesting). Note that ${A}^\text{U}=0.6$ corresponds for cubic materials to a Zener anisotropy index $A=2{C}_{44}/\left({C}_{11}-{C}_{12}\right)$ of $A=2$ (or some values below 1). The quite isotropic A1-type metals aluminum and iridium attain values of $A=1.3$ and 1.5, whereas more anisotropic Ni and Cu attain values of 2.2 and 3.3 (values from Ref. 36). Only in certain cases calculations have been performed in the literature on Cu–Sn phases which consider phonon energies allowing to draw conclusions on T > 0 K properties.

In the tables summarizing the first-principles calculations, the column “Types of results” may contain the following abbreviations: LP: (relaxed) lattice parameters, FC: relaxed fractional coordinates (or other details on the relaxed atomic structure), B: bulk modulus, SCEC: single-crystal elastic constants (in such a case bulk modulus data are not mentioned separately), E: Energies with respect to some reasonable reference, ES: analysis of the electronic structure, e.g., the electronic density of states; T > 0 K: considerations on the thermodynamics at $T>0 \,\mathrm{K}$.

3.2 α-Cu–Sn Terminal Solution Phase

Bain^[15] first reported the increase of the lattice parameter of the A1 structure (cubic Cu type, Pearson symbol cF4, space group $Fm\overline{3 }m$) with increasing Sn content. In this work the substitutional character of the solid solution was anticipated, like the α-Cu–Zn solution studied in the same work. Later Weiss^[37] presented more detailed lattice-parameter values for the α-Cu–Sn phase, which increased with increasing Sn content. These data were compared with measured mass-density values of the same alloys which were lower than the calculated densities for a simple substitutional solid-solution model. These findings were interpreted in terms of substitution of more than one single Cu atom by one Sn atom. This was, however not confirmed by a subsequent study by Mehl et al.^[38] While the composition-dependent lattice parameters agreed well with the data by the earlier authors, the mass-densities determined were larger and highly consistent with the simple substitutional model.

There were additional works on composition-dependent lattice parameters revealing their increase with increasing Sn content of the α phase; parts of the works also considered mass-density data directly confirming the simple substitutional model: Owen and Iball,^[39] Isawa and Obinata,^[40] Haase and Pawlek,^[41] Gulyaev and Trusova,^[42] Andresen,^[43] Nuding and Ellner.^[44] The data from the latest work^[44] are exemplarily shown in Fig. 2, revealing a linear dependence of the lattice parameter a_A1 on atomic fraction x_Sn of the alloy, as long as it is single-phase. The data of this work appear to agree well with most of the other works, except for Ref. 43 which reported deviations from linearity. However, in view of the other data this non-linearity seems to be caused by experimental or reproduction errors.

Fig. 2

Lattice parameter of the terminal α-Cu–Sn solid solution phase with cubic A1 structure as a function of alloy composition according to Nuding and Ellner ^[44] as measured by PXRD of quenched samples at ambient temperature. The open data point for 10.5 at% Sn has been stated to be from a two-phase alloy. The vertical line indicates the boundary of the single-phase region at the annealing temperature of 600 °C

Owen and Iball,^[39] as well as Haase and Pawlek^[41] analyzed the evolution of the lattice parameter a_A1 of the α-Cu–Sn solid solution during phase transformations to reveal composition changes occurring during heat treatments at low temperature, revealing the decreasing solubility limit with decreasing temperature. Unmixing is enhanced by coldwork prior to heat treatment. Thereby, different phases may precipitate upon low-temperature annealing of α. Besides equilibrium ε,^[45] also non-equilibrium ζ and δ may develop.^{[45,46,47,48]}

The increase of the lattice parameters in a substitutional solid solution is straightforwardly attributed to the larger size of the Sn substituting smaller Cu atoms. The associated local static atomic displacements caused by the mismatching sizes of Sn and Cu atoms leads to a decrease of the reflection intensities (static Debye−Waller factor), as studied by Guseva et al.^[49] and Webb.^[50] Cohen et al. probed these displacements by means of extended x-ray absorption fine structure (EXAFS) analysis,^[51] and revealed that an Sn atoms is surrounded by 12 atoms at an average distance of 2.63 Å, while for Cu 2.55 Å has been observed as interatomic distance.

3.3 β and γ Phase

The β and γ phases are thermodynamically stable at high temperatures; see Fig. 1. During quenching and ageing at lower temperatures, they decompose dramatically (martensite formation) or in a subtle fashion, e.g., by precipitation, where interpretation of diffraction data recorded at ambient temperature might be difficult; see also below. Already Hume-Rothery^[16] anticipated an A2 crystal structure (cubic W type, Pearson symbol cI2, space group $Im\overline{3 }m$) for the β high-temperature phase; Fig. 3(a).

Fig. 3

A2-related crystal structures considered for the β/γ-Cu–Sn high-temperature phases: Cubic unit cells in clinographic view for the (a) A2 structure (β phase, $Im\overline{3}m$), (b) possibly existing B2 superstructure reported as separate phase in Ref. 13 ($Pm\overline{3}m$), (c) D0₃ superstructure (γ phase, $Fm\overline{3}m$). (a, b) have been drawn using pie charts representing the partial occupancies by Cu and Sn atoms for a hypothetical composition of 25 at.% Sn, being the composition also allowing the idealized order D0₃ shown in (c). (d) Atoms located on a $\left( {1\overline{1}0} \right)_{{{\text{D}}0_{3} }}$ plane intersecting the origin as in gray in (c)

Westgren and Phragmén^[52] were apparently the first to report lattice parameters of quenched β phase of 15 at.% Sn yielding a lattice parameter of a_A2 = 2.979 Å (corrected!), where this alloy also seemed to be affected by decomposition processes having occurred during quenching. It was noted in the same work that alloys with compositions corresponding to the γ field (referred to as β′ in Ref. 52) could not be successfully quenched. Therefore, a direct study of the crystal structures of the β and γ phases became a typical task for high-temperature diffraction methods.

The apparently first high-temperature diffraction study was high-temperature PXRD on α and β phase by Andrews and Hume-Rothery,^[53] confirming the A2 structure of the β phase. In a short note, Hendus and Knödler^[54] reported a D0₃ superstructure (cubic Fe₃Al type, cF16, space group $Fm\overline{3 }m$) for the γ phase, being a typical superstructure of the A2 structure; see Fig. 3(c). The corresponding high-temperature PXRD studies were described in much more detail by Knödler,^[55] reporting composition-dependent values ${a}_{\mathrm{A}2}$ referring to the A2 subcell (= ${a}_{\mathrm{D}{0}_{3}}/2$) at two different temperatures. These data were replotted in Fig. 4, including also later data by Fürtauer et al.^[9] determined for a somewhat different temperature. Notably, the data imply a nonlinear increase of ${a}_{\mathrm{A}2}$ with the atomic fraction of Sn, with a decreasing slope above about 20 at.% of Sn. In another work reporting an apparently diffusionless formation of δ on cooling (see Sect. 3.4), Knödler^[56] discusses the possible presence of vacancies in high-Sn content γ phase. Such vacancies can well be reason for the reduced slope of the lattice parameters versus atomic fraction of Sn evident in Fig. 4. In view of the rapid formation of δ from γ, Knödler^[56] appeared to imply that these vacancies in the γ phase are already ordered like in δ; see also Sect. 3.4. The present author, however, regards this as unlikely. While it is quite plausible that a high and composition-dependent vacancy content is present in equilibrium-γ phase (stabilized by configurational entropy), it is unlikely that these vacancies are ordered. Such vacancies are typically sufficiently mobile to become ordered only during quenching; see considerations of δ′ upon quenching in Sect. 3.4.

Fig. 4

Composition-dependent lattice parameters of the β and γ phases obtained from high-temperature PXRD analysis due to Knödler ^[55] (605 °C, 710 °C; corrected!) and Fürtauer et al. ^[9] (700 °C) as a function of alloy composition. There is no visible discontinuity upon the transition from β to γ, e.g., as indicated for 710 °C by the two right-most vertical dotted lines

There have been structural studies conducted at elevated temperatures, which to some extent challenge the view on the equilibrium phase constitution under equilibrium conditions as depicted in Fig. 1(a). Nishiyama et al.^[57] performed high-temperature SAED on a Cu-14.8at.% Sn alloy. At 650 °C, i.e., well “within” the β field, they observed a diffraction pattern indicative for presence of a D0₃ superstructure. The corresponding superstructure reflections, however, disappeared upon stepwise heating to 750 °C. Assuming correctness of the Sn content of that work, this observation might imply shifts of the phase boundaries as compared to those depicted in Fig. 1(a). Liu et al.^[13] performed high-temperature SAED, which suggested presence of a phase with distinct B2-type ordering (due to composition, of course, with imperfect ordering; cubic CsCl type, cP2, space group $Pm\overline{3 }m$; see Fig. 3b). Moreover, due to a lack of clear evidence for any type of two-phase region like that between β and γ given in Fig. 1(a), the authors proposed the transitions to occur continuously, as indicated by corresponding transition lines in Fig. 1(c). Fürtauer et al.^[9] conducted high-temperature PXRD and were unable to detect signs of the B2 structure, but also proposed the transition between β and γ to occur continuously; see Fig. 1(d). Continuous character of the these phase transitions was also adopted in the course of thermodynamic modeling.^[13,58]

It should be noted that in Ref. 57 also the presence of pronounced phonon-induced diffuse scattering was observed occurring in planes perpendicular to ${\langle 111\rangle }_{\mathrm{A}2} \parallel {\langle 111\rangle }_{\mathrm{D}{0}_{3}}$, as indicative of mutual shifts of the corresponding close-packed atomic chains and being indicative for the tendency to develop ω-like phases; see Sect. 3.9.2.

First-principles calculations on model structures relevant for the β and γ phases have been performed only for the ideal D0₃ structure with Cu₃Sn composition^[59,60]; see Table 1. Ramos de Debiaggi et al.^[59] reported a particularly positive energy of formation from the elements in comparison with ε-Cu₃Sn (see Sect. 3.6). As also mentioned by Daeumer et al.^[22], the energy of formation values reported by Qu et al.^[60] might be affected by errors. That latter work reports single-crystal elastic constants, which imply elastic instability of D0₃-Cu₃Sn due to $\frac{1}{2}\left({C}_{11}-{C}_{12}\right)<0$. That elastic instability, however, pertains to the considered static structure at 0 K, and reflects the generally low value of $\frac{1}{2}\left({C}_{11}-{C}_{12}\right)$ for β-brass like phases, which typically decreases with decreasing temperature. The temperature, at which the value of $\frac{1}{2}\left({C}_{11}-{C}_{12}\right)$ of a cubic β-brass like phase gets negative is essentially the lower limit of stability of that phase.^[61]

Table 1 Summary of first-principles electronic structure calculations of model structures relevant for the β and γ phases of the Cu–Sn system

Upon leaving the stable β and γ fields towards low temperatures, there is driving force for structure changes which can occur in various forms.^{[55,56,62,63,64,65,66,67,68,69]} Already quenching may introduce considerable structural changes. Figure 5, for example, summarizes the results of the systematic PXRD work by Knödler^[55,56] on alloys quenched from 700 °C to –183 °C and reheated to ambient temperature for PXRD. The different types of products identified by this method are indicated. The corresponding results will be discussed in more detail in the corresponding later Sects. 3.4 (δ′), 3.5 (ζ′), 3.6 (ε′), and 3.9.3 (martensite), whereby it needs to be emphasized here that the primes accompanying the phase labels indicate in most cases (but not always) a crystal structure deviating from that of the stable version of the phase. However, further phases than those reported by Knödler may also develop in quenched β/γ, as shown in Sects. 3.9.1 (A3 type α′) and 3.9.2 (ω). For convenience, Fig. 5 also contains the martensite start and finish temperatures^[68] as well as an extrapolation of an estimated ${T}_{0}$ line between the β and the γ phases. Below this line there is a driving force for ordering from A2 towards the D0₃ superstructure of γ. Indeed, detailed investigation of alloys quenched from the β-phase region appear to reveal this order according to SAED, ^[68,70] as it especially reflected by the order present in the developing martensites, see Sect. 3.9.3.

Fig. 5

Phase diagram Cu–Sn redrawn after Knödler^[55] (compare Fig. 1(a)) depicting in red the composition ranges within which certain types of products are obtained upon quenching β or γ phase to –183 °C and reheating to ambient temperature, at which PXRD analysis has been performed. These products have been labeled Mart. (different types of martensites indicated in green at the bottom according to^[71]; see Sect. 3.9.3), δ′, ζ′ and ε′. An estimated T₀ line for β/γ makes it plausible that A2 → D0₃ (β₁) ordering may occur during quenching prior to reaching the martensite start/end temperatures M_S/M_F^[68,70]

3.4 Cu₄₁Sn₁₁ Intermetallic (δ etc.)

The similar but different cubic crystal structures of the γ-brass like phases in the Cu–Zn, Cu–Al and Cu–Sn systems were recognized as early as 1926 by Westgren and Phragmén.^[17] It was found that the corresponding δ-Cu–Sn phase has a face-centered cubic Bravais lattice with lattice parameter of 17.95 Å (corrected!). In combination with mass-density values and the composition of the phase, several 416 atoms per unit cell was derived.

Two years later, it was pointed out by the same authors^[52] that formulas like Cu₅Zn₈^[72] and Cu₉Al₄ (cited as personal communications in Ref. 52; published as^[73]) derived from crystallographic work, would imply 21:13 electrons per atoms. Accordingly, the formula Cu₃₁Sn₈ was derived for the δ phase. The 20.5 at.% Sn implied by this formula, indeed, corresponds to the composition of this phase at the eutectoid temperature of 350 °C (see Fig. 1a), and is within the homogeneity range of δ according to data by Owen et al. ^[39,74], e.g., 20.4–20.7 at.% at 550 °C. However, the Cu₃₁Sn₈ formula cannot easily be reconciled with the mentioned 416 atoms per face-centered cubic unit cell if one requires perfect atomic ordering. SCXRD evidence was reported by Bernal^[75] in the same year, without arriving at a definite structure model. In any case, the space group $F\overline{4 }3m$, which is also accepted today, was proposed. Bernal also derived the formula Cu₄₁Sn₁₁ which is compatible with the 416 atoms per unit cell implying a Pearson symbol cF416, although the Sn content of 21.2 at.% implied by the formula is located outside the homogeneity range of the δ phase according to^[39,74] and Fig. 1. Lattice parameters as a function of alloy composition were published by Owen et al.^[39,74]. The corresponding δ-phase rich (mainly two-phase) alloys were equilibrated at different temperatures and quenched to ambient temperature, at which the PXRD experiments were conducted. Figure 6 shows the course of the cubic lattice parameter a_δ versus alloy composition for alloys quenched from 550 °C.^[74] In the same figure, the limits of the independently assessed homogeneity range from the same Ref. 74 are indicated, which corresponds to a width of about 0.4 at.%. These limits show that only one point should correspond to a single-phase alloy. Therefore, the alloy-composition dependent lattice parameter in the present case mainly reflects the overall change of the lattice parameter over the narrow homogeneity range (estimated evolution indicated in Fig. 6) and does not show the actual evolution with composition of the phase as it was the case in Fig. 4. Consistent with the narrower homogeneity range at lower temperatures, the range of observed lattice parameters observed decreases.^[74]

Fig. 6

Alloy-composition dependent lattice parameter a_δ (corrected!) of the δ-Cu₄₁Sn₁₁ phase of a series of alloys equilibrated at 550 °C and quenched^[74]. In the same work the homogeneity range was determined as indicated by the vertical lines. Therefore, only the alloy at 20.5 at.% Sn should be single phase, and the lattice parameter at lower or higher Sn contents pertains to saturated δ in equilibrium with the indicated phases. The dashed blue lines depict some estimated course of the lattice parameter, serving as a guide to the eye

The description of the atomic structures of γ-brass like phases is usually based on a four-shell cluster introduced by Bradley and Thewlis^[72] for the γ-Cu–Zn phase with its already mentioned ideal formula Cu₅Zn₈. The crystal structure of the latter has a body-centered cubic Bravais lattice, which can be derived from a 3 × 3 × 3 supercell of the A2 structure. This supercell would contain 2 × 3³ = 54 atoms. However, two atoms are removed from the origin and the center of the unit cell, yielding the body centered cubic Bravais lattice mentioned above, with 52 atoms per 3 × 3 × 3 supercell, i.e., 1/27 of the atomic sites become vacant. The empty space generated by such vacancies is filled by a symmetry-breaking ($m\overline{3 }m$ → $\overline{4 }3m$ point group symmetry for the vacancy site) collapse of the cube of atoms around the vacancy towards an inner and an outer tetrahedron (IT, OT); see Fig. 7(a). This two-shell IT-OT cluster is typically considered along with two further shells composed of an octahedron (OH) and of a cuboctahedron (CO) of atoms, resulting in a 26-atom, four-shell IT-OT-OH-CO cluster.

Fig. 7

Representation of the crystal structure of δ-Cu₄₁Sn₁₁. Partial site occupation is indicated by pie charts. (a) Single IT-OT-OH-CO cluster with different atomic colors for each cell (also indicated as margins in (c) and (f)). (b-f) Sections through the face diagonal of a cubic unit cell showing the atoms with fractional coordinates x, x, z, which is sufficient to establish the occupation (“coloring”) of the sites derived for the different structure models (or mixed occupation by Cu and Sn). (b, c) Stepwise derivation of a structure model as discussed by Knödler ^[56] by (b) removal of atoms at the coordinates Z: 0,0,0, Q: ¼, ¼, ¼, H: ½, ½, ½, and T: ¾, ¾, ¾ starting from a D0₃ structure “Cu₃Sn” and (c) at the end with the same composition and atomic shifts establishing a γ-brass-like structure with $F\overline{4}3m$ symmetry. The about 20.5 at.% Sn was proposed to be achieved by a partial substitution of the Sn sites by Cu (not shown). (d-f) Results of the single-crystal x-ray diffraction analyses by (d) Arnberg et al. ^[76], (e) Booth et al. ^[77] and (f) Misra et al. ^[78], where in all cases the same principal occupation schemes of the cluster shells by Sn are achieved but with different choices of the unit cell origin and, in case of (f) orientation of the atomic coordinates with respect to the chosen unit cell. The respectively occurring positions in the clusters are indicated with reference to the positions Z, Q, H and T, as discussed in the text

The magnitude of the lattice parameter of the δ-Cu₄₁Sn₁₁ phase from Ref. 17 implies that the structure has a 2 × 2 × 2 supercell as compared to the structure of Cu₅Zn₈, i.e., it is an 6 × 6 × 6 supercell with respect to A2:

$${\mathbf{a}}_{{\updelta}} = 6{\mathbf{a}}_{{{\text{A}}2}} .$$

(3.4.1)

The crystal structure can be described in terms of four crystallographically independent IT-OT-OH-CO clusters. Each shell of a cluster corresponds to a different atomic site, resulting a total of 16 crystallographically independent sites in space group $F\overline{4}3m$. Some positions of each site are located on a diagonal plane, e.g., parallel to $\left( {1\overline{1}0} \right)$, of the cubic unit cell, intersecting the unit cell’s origin; see also.^[79] Hence, the results of structural analysis in terms of the “coloring” of these sites (i.e., their preferential occupation by Cu and Sn) and in terms of the atom’s displacements away from the ideal positions (derived from the A2 structure) can well be visualized based on such sections. Figure 7(c-f) summarizes the corresponding structure information from the literature. For the following discussion, the different clusters on the positions 0 0 0, ¼ ¼ ¼, ½ ½ ½, and ¾ ¾ ¾ within the unit cell are denoted as Z, Q, H and T (see e.g.,^[78]).

The earliest detailed atomic structure model for the δ phase was presented by Knödler.^[56] He derived his model from the D0₃ structure (see Fig. 3c) of the γ high-temperature phase, removing from a 3 × 3 × 3 supercell the atoms at the positions 0 0 0, ¼ ¼ ¼, ½ ½ ½, and ¾ ¾ ¾ and the ones equivalent by the $F\overline{4 }3m$ symmetry; see Fig. 7(b). Afterwards the atoms were shifted by magnitudes adopted from similar structures published in the literature,^[72] as illustrated in Fig. 7(c) in comparison to Fig. 7(b). In this way, each of the IT-OT-OH-CO clusters Z, Q, H and T contains three shells occupied by Cu and one shell by Sn atoms. Focusing on the positions of the Sn atoms in the clusters, these clusters can be denoted as Z-CO_Sn, Q-IT_Sn, H-OH_Sn, and T-OT_Sn; see Fig. 7(c). Considering the multiplicities of the sites, the thus resulting structure model implies 312 Cu and 104 Sn atoms per unit cell, which corresponds to the initial composition Cu₃Sn of an ideal D0₃ structure. In order to comply with the actual phase composition (assumed as Cu₃₁Sn₈/20.5 at.% Sn in^[56]), a random substitution of the Sn sites by Cu was proposed.

The first systematic structure refinement on the basis of quantitative SCXRD data was carried out by Arnberg et al.^[76], with single crystals from a Cu-20.6 at.% Sn alloy equilibrated at 550 °C giving a PXRD-based lattice parameter of 17.965 Å. Mass-density measurements gave the expected 416 atoms per face-centered unit cell. These authors noted that within Knödler’s^[56] model the cluster with Sn atoms on the IT shell implied unrealistically short Sn–Sn distances. Indeed, in the course of their structure refinements it turned out that these IT sites contain only Cu atoms, resulting in an IT-OT-OH-CO cluster that is free from Sn atoms; see Q-0_Sn in Fig. 7(d) versus Q-IT_Sn in Fig. 7(c). Neglecting the mixed occupancy refined for some sites, the sites add up to 328 Cu and 88 Sn atoms, corresponding to the formula Cu₄₁Sn₁₁/21.5 at.% Sn. Hence, the Sn content is too high in view of the alloy composition and known homogeneity range of the δ phase. The refined mixed site occupations do not resolve the still too high Sn content of 21.3 at.% Sn, whereby, however, the standard deviations of the refined occupancies are so large that the difference to the alloy composition becomes insignificant. The main structure principle identified by Arnberg et al.^[76] was a reasonably uniform distribution of the large Sn atoms within a matrix of smaller Cu atoms, avoiding short Sn-Sn distances, which was also identified as the reason that (predominant) occupation of an IT by Sn as proposed by Knödler^[56] was regarded as unlikely.

Subsequent SCXRD work by Booth et al.^[77] based on a single crystal isolated from an alloy of 20.5 at.% Sn does not generally change the picture with respect to the main sites of the Sn atoms; see Fig. 7(e). The description of the crystal structure differs from Arnberg et al.^[76] by a shift of the origin. Thereby, only one fractional occupation was refined, assuming Cu atoms and vacancies on one IT site; see Fig. 7(e). This refined model implies 412 atoms per unit cell. This appeared to be supported by mass-density measurements of the corresponding alloy, which gives 413 atoms per unit cell. In any case, the refined structure model has resulted in a too Sn-rich composition.

More recently, Misra et al.^[78] confirmed the basic Sn distribution from the previous work,^[76,77] using a Sn-poor alloy composition for the crystal described in the main publication (20.2 at.% Sn). Here, too, a different setting was chosen, i.e., choice of origin and general rotation of the atomic sites within the unit cell. More sites with (Cu, Sn) mixed occupation were considered, resulting in a composition closer to the equilibrium homogeneity range after refinement (20.7 at.% Sn). In corroboration to Ref. 76, Misra et al.^[78] found a significant partial occupation of the Sn site in the CO_Sn cluster by Cu, which probably plays a key role in obtaining a composition of lower Sn content than the 21.5 at.% implied by the basic Sn distribution connected with the formula Cu₄₁Sn₁₁. In any case, Knödler’s^[56] model derived from the D0₃ structure was already very close to what has been determined in the subsequent analyses.

Knödler^[56] also observed indicators for domains within large grains of the δ phase by means of optical microscopy on polished and etched cross sections under different illumination conditions. According to Laue backscattering diffraction, the crystal orientation appeared homogeneous, and the planar boundaries were thus determined to be oriented parallel {110}_δ. While no origin of this domain formation has been suggested, the only type of orientation domains compatible with the $\overline{4 }3m$ crystal class are 90° orientation domains, which correspond to inversion domains. Of these only two types should exist, while micrographs, however, may indicate more types of domains. Such inversion domains occur in various γ-brass like phases with boundaries on the cubic {110} planes.^[80] Assuming inversion symmetry of the diffraction pattern, crystal specimens containing inversion domains give the appearance of true single crystals using the employed diffraction techniques. Experimental confirmation of the character of these domains in the δ phase is still pending.

The only electronic structure calculations involving a δ-Cu₄₁Sn₁₁-related structure model were included in the study by Misra et al.^[78] It is likely that the large number of atoms per primitive unit cell has precluded further studies. In this work, working with the ideal distribution of Sn (too Sn-rich as compared to reality; see above), a pseudogap was found that electronically stabilizes the structure, as expected for a corresponding Hume-Rothery phase; see also Sect. 4.1.

There are several reports of Cu₄₁Sn₁₁ intermetallic forming under non-equilibrium conditions which might exhibit structures different from the equilibrium δ phase. First, Knödler^[55,56] performed a PXRD analysis at ambient temperature on a γ phase of 15.8–21.3 at.% Sn, which was quenched from 700 to −183 °C and reheated for measurement. The diffraction patterns in this compositional range appear to show reflections characteristic for the δ phase (see Fig. 5), which have some composition-dependent intensity, but details were not reported.^[56,81] While mass densities and lattice parameters showed a peculiar composition dependence, the derived number of atoms per δ-phase unit cell showed a clear decrease with composition as shown in Fig. 8. Based on the underlying A2 structure (2 × 6³ = 432 atoms per δ unit cell), absence of vacancies would yield about 14.5 at.% Sn according to that plot, whereas at 20–20.5 at.% Sn a value of 416 atoms per unit cell is encountered, in agreement with the ideal unit cell content of the equilibrium δ phase. Also the 412–413 atoms per unit cell found by Booth et al.^[77] (see above) is contained on the Sn-rich side in the range observed by Knödler.

Fig. 8

Composition dependence of the number of atoms per face-centered cubic δ unit cell of “δ′” type Cu–Sn obtained by quenching from 700 °C to –183 °C ^[56] (redrawn and modified). The values were obtained from experimentally determined mass densities, the lattice parameters, and the composition of the alloy, which was assumed to be single-phase

It has also to be noted that Knödler has designated the γ → δ′ transformation as diffusionless (even “martensitic”), implying that already existing ordered vacancies would only have to collapse in the sense of the transition of Fig. 7(b) towards Fig. 7(c). Such a simple view is, however, precluded by the unlikely (long-range) order of the vacancies in γ; see Sect. 3.3. In the whole discussion it has to be kept in mind that the states observed in^[55,56] need not to be homogeneous, i.e., it cannot be excluded that local-scale precipitation (retaining coherence of the structure) does occur in spite of all quenching efforts; see also works mentioned in the following.

A second group of reports deal with SAED on Cu₄₁Sn₁₁ intermetallic, which has formed in as-water quenched γ phase (14.8 at.% Sn,,^[69] 16.5 at.% Sn^[82,83]). The corresponding patterns show systematic shifts of non-A2/D0₃ reflections from their ideal positions expected for the δ phase. These shifts have not been interpreted in detail and suggest some incommensurate way by which the structure features of the δ phase have developed. Quenching of the γ phase paused at 180 °C has led to less pronounced shifts,^[83] see also comments on ω phase in Sect. 3.9.2. Stable or metastable δ having developed in later stages of precipitation from α or upon decomposition of β apparently does not show structural peculiarities.^[48,84]

The third report on metastable δ-related material was by Saunders and Miodownik,^[85] who prepared Cu–Sn thin films by sputter deposition. The PXRD patterns of films of 11.5 and 19.5 at.% Sn deposited at a substrate temperature of 450 °C were interpreted in terms of presence of a “simple” γ-brass like crystal structure (referred to as γ′) with thus having half of the lattice parameter of ${a}_{\gamma \mathrm{^{\prime}}}=\frac{{a}_{\delta }}{2}$ than the equilibrium δ phase. Apparently, no reflections were encountered which require doubling of the unit cell as for the normal δ-phase. This could imply a different Cu versus Sn order in the structure. Alternatively, the order corresponds to the δ phase, but faulting of the structure broadens characteristic reflections precluding their detection and thus suggesting a smaller unit cell. Like in the first case, details on the detected diffraction evidence are missing. Likewise, it was not checked whether the alloys were homogeneous on a local scale.

3.5 Cu₁₀Sn₃ Intermetallic (ζ etc.)

Hamasumi and Nishigori^[86] were the first to report a phase which they labeled ε, which is now known as ζ phase. This phase is only stable at elevated temperatures with a narrow homogeneity range around the composition Cu₁₀Sn₃; see Fig. 1(a). Soon after, Carlsson and Hägg^[87] performed PXRD analysis of Cu₁₀Sn₃-containing alloy with 21.8 at.% Sn equilibrated at and quenched from 595 °C to ambient temperature. They derived a primitive hexagonal Bravais lattice with $a_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }}$ = 7.331 Å and $c_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }}$ = 7.864 Å (corrected!) and labeled the corresponding phase γ′. Using the measured mass density and alloy/phase composition, the authors concluded the presence of 26 atoms in the unit cell (Pearson symbol hP26). The reflection intensities suggested (misleadingly; see below) that the thus observed crystal structure was a direct derivative of a A2 structure, i.e., a structure which results from atomic ordering and introduction of vacancies accompanied by slight atomic displacements. The observed unit cell can be derived from the A2 unit cell according to

$$\begin{gathered} {\mathbf{a}}_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} = 2{\mathbf{a}}_{{{\text{A}}2}} - {\mathbf{b}}_{{{\text{A}}2}} - {\mathbf{c}}_{{{\text{A}}2}} \hfill \\ {\mathbf{b}}_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} = - {\mathbf{a}}_{{{\text{A}}2}} + 2{\mathbf{b}}_{{{\text{A}}2}} - {\mathbf{c}}_{{{\text{A}}2}} \hfill \\ {\mathbf{c}}_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} = \frac{3}{2}\left( {{\mathbf{a}}_{{{\text{A}}2}} + {\mathbf{b}}_{{{\text{A}}2}} + {\mathbf{c}}_{{{\text{A}}2}} } \right) \hfill \\ \end{gathered}$$

(3.5.1)

Thereby, the meaning of the subscript ${\text{LT-Cu}}_{10} {\text{Sn}}_{3}$ will be explained later and currently refers only to this type of unit cell. Without unit cell distortion, Eq 3.5.1 implies ideal lattice parameter values $a_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} = b_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} = \sqrt 6 a_{{{\text{A}}2}}$, $c_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} = 3\sqrt 3 /2a_{{{\text{A}}2}}$ leading to an axial ratio of $c_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} /a_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} = 3\sqrt 2 /4 = 1.061$. However, the above-mentioned lattice parameter values yield a ratio of 1.073, i.e., a deviation of 1.1% from the ideal value. The unit cell transformation according to Eq 3.5.1 starting from the A2 basis structure yields 27 atoms per hexagonal unit cell. In view of the 26 atoms per unit cell implied by the mass-density measurements, it was concluded that 1/27 of the atomic sites are empty, i.e., the same fraction as in the δ phase; see Sect. 3.4. Assuming a vacant atomic site at the origin of the unit cell and $P\overline{3}1m$ space group symmetry (a subgroup of the $Im\overline{3}m$ symmetry of the A2 structure), different possible distributions of Cu and Sn have been discussed.^[87]

Lenz and Schubert^[88] re-investigated the crystal structure using SCXRD employing quantitatively evaluated photographic films, based on crystal specimens isolated from alloys quenched to ambient temperature. The geometry of the diffraction pattern was compatible with the unit cell according to Eq 3.5.1. Analysis of the reflection intensity data yielded a structure model which has the same 26 atoms per unit cell (hP26) as derived above from the mass-density data. The new model, however, essentially differs from the model by Carlsson and Hägg.^[87] While the intensity data in Ref. [88] suggested 6/mmm Laue symmetry, a convincing structure model could only be derived within space group $P6_{3} /m$ (Laue group 6/m), assuming twinning by merohedry. Optical microscopy on metallographic cross-sections of the quenched alloy revealed presence of domains which can be related to the twinned character of the specimen, i.e., supporting the deduced low symmetry.

The authors referred to the thus characterized Cu₁₀Sn₃ intermetallic as metastable Cu₁₀Sn₃(m) (see below), while it is referred here to as ${\text{LT-Cu}}_{10} {\text{Sn}}_{3}$. The crystal structure (see Fig. 9) can be characterized by atomic chains running along the $\left[ {001} \right]_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} \parallel\user2{ }\left[ {111} \right]_{{{\text{A}}2}}$ direction, i.e., along the close-packed direction of the A2 structure: two chains with two Cu atoms per unit cell (accommodating the single vacancy per unit cell⁵), two chains with three Cu atoms, and six chains with (ordered) 2 Cu and 1 Sn atoms. With respect to the ${\text{LT-Cu}}_{10} {\text{Sn}}_{3}$ supercell, the atoms of these chains are located approximately at fractional coordinates x = m/3 and y = n/3 with m and n being integers; see Fig. 9(a). This actually corresponds to what one also expects from an A2-derived structure according to Eq 3.5.1, as in the model by Carlsson and Hägg.^[87] The levels of the atoms with respect to the a-b plane (Fig. 9b) are, however, essentially different from a structure resulting from symmetry reduction starting from the A2 structure. This follows directly from the hexagonal space group symmetry $P6_{3} /m$ which is not a subgroup of the cubic space group $Im\overline{3}m$ of the A2 structure. Instead, new symmetry elements are generated by the shifts of the atomic chains mainly along $\left[ {001} \right]_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }}$.⁶

Fig. 9

Crystal structure models derived for ζ-Cu₁₀Sn₃ ^[89,90], compare also Fig. 10. (a) Structure model according to Lenz and Schubert (LT, space group $P6_{3} /m$ ^[88]), with view along $\left[ {00\overline{1}} \right]_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }}$ depicting the contents of a unit cell in a range of fractional coordinates somewhat extended beyond 0 ≤ x, y ≤ 1. The green rectangle shows the range of atoms, which are viewed along ${\mathbf{a}}_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} + {\mathbf{b}}_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }}$ in (b, c); the atoms notably are located at different levels with respect to the a-b plane. The purple rhomb further indicates the extent of the hexagonal unit cell suggested for the thermodynamically stable HT phase ^[91], where the pure Cu chains become equivalent by translation (purple rectangles in (a) and (b)). (b) Structure model of Lenz and Schubert ^[88] with the mirror planes indicated on z = ¼, ¾ as blue lines and (c) LT′ structure model space group $P6_{3}$ of Brandon et al. ^[90], with the Sn atoms placed at z = ¼, but with the dotted lines representing the broken mirror planes. The arrows show the most pronounced atomic displacements of some Cu atoms breaking the mirror planes suggesting the $P6_{3}$ rather than the $P6_{3} /m$ symmetry; see text

While in the course of an early high-temperature PXRD work, Hamasumi and Morikawa^[92] did not detect perceptive structure differences between quenched material and such at equilibrium temperature, Knödler^[55,81] suggested such differences to exist, without reporting further details. High-temperature PXRD at 600 °C by Lenz and Schubert^[91] revealed the absence of many weak reflections expected due to the ${\text{LT-Cu}}_{10} {\text{Sn}}_{3}$ structure model,^[88] allowing the use of a unit cell of three-fold smaller volume; compare Fig. 9(a), purple rhomb. As compared to Eq 3.5.1 the basis vectors can be written as

$$\begin{aligned} {\mathbf{a}}_{{{\text{HT-Cu}}_{10} {\text{Sn}}_{3} }} =& - {\mathbf{b}}_{{{\text{A}}2}} + {\mathbf{c}}_{{{\text{A}}2}} \hfill \\ {\mathbf{b}}_{{{\text{HT-Cu}}_{10} {\text{Sn}}_{3} }} =& {\mathbf{a}}_{{{\text{A}}2}} - {\mathbf{c}}_{{{\text{A}}2}} \hfill \\ {\mathbf{c}}_{{{\text{HT-Cu}}_{10} {\text{Sn}}_{3} }} =& \frac{3}{2}\left( {{\mathbf{a}}_{{{\text{A}}2}} + {\mathbf{b}}_{{{\text{A}}2}} + {\mathbf{c}}_{{{\text{A}}2}} } \right) \hfill \\ \end{aligned}$$

(3.5.2)

The correspondingly derived phase/structure model is referred here to as ${\text{HT-Cu}}_{10} {\text{Sn}}_{3}$, whereas the authors of Ref. 91 used the notation “Cu₇₋Sn₂ (600)” with the 600 evidently referring to the 600 °C at which the state has been characterized. Semi-quantitative evaluation of the intensities of the reflections suggested an overfilled Na₃As structure with $P6_{3} /mmc$ symmetry, where the non-integer number of atoms per unit cell (defect variant of D0₁₈, Pearson symbol hP8.67) implies a formula Cu_3.33Sn. It was proposed that the unit cell contains two chains with (ordered) 2 Cu + 1 Sn atoms and one Cu chain with (disordered; in average) 2.67 atoms per chain (and translation period along ${\mathbf{c}}_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} =$ ${\mathbf{c}}_{{{\text{HT-Cu}}_{10} {\text{Sn}}_{3} }}$). The latter chains, which are equivalent by symmetry in the ${\text{HT-Cu}}_{10} {\text{Sn}}_{3}$ structure model, have been emphasized in Fig. 9(a, b) by purple rectangles. Note that this description of the structure, which seems in line with the text from,^[91] differs from the corresponding entry in the ICSD database,^[23] collection code 629,281, which is, however, stated to be derived from.^[91]

Without reference to Refs. 88 and 91, Brandon et al. ^[90] reported a further SCXRD study on quenched Cu₁₀Sn₃. The measurement was done with more advanced counter-based intensity data as compared to the techniques used in Refs. 88 and 91. The unit cell reported in this study was compatible with Eq 3.5.1, but the intensity data were reported to show $6/m$ Laue symmetry, in contrast the intensity data in Ref. 88 (see above). While it was reported that a structure model in $P6_{3} /m$ symmetry could be refined (likely closely corresponding to the ${\text{LT-Cu}}_{10} {\text{Sn}}_{3}$ model in^[88]), it was pointed out that a symmetry reduction (retaining the unit cell according to Eq 3.5.1) to polar $P6_{3}$ symmetry did sufficiently improve the R-factors of the refinement to justify the increase in the number of refined structure parameters. Hence, a structure model referred to here as ${\text{LT}}^{\prime}{\text{-Cu}}_{10} {\text{Sn}}_{3}$, was published.^[90] The symmetry reduction is mainly caused by shifts of one kind of Cu atoms; see arrows in Fig. 9(c). The fractional coordinates of these Cu atoms deviate from a P6₃/m model by Δz = 0.02 corresponding to a displacement of 0.1–0.2 Å.

Wang and Konno^[47] were apparently the only ones who critically considered the structure model from^[90] (${\text{LT}}^{\prime}{\text{-Cu}}_{10} {\text{Sn}}_{3}$) compared to that from^[88] (${\text{LT}}^{\prime}{\text{-Cu}}_{10} {\text{Sn}}_{3}$). They performed SAED on corresponding intermetallic having formed metastably by discontinuous precipitation instead of ε upon ageing Cu-8.6at.% Sn alloy. Observation of 101_LT/LT′ and 201_LT/LT′ reflections was taken as evidence in favor of the ${\text{LT}}^{\prime}{\text{-Cu}}_{10} {\text{Sn}}_{3}$ structure model. Test calculations by the present author confirm that indeed the atomic model for ${\text{LT}}^{\prime}{\text{-Cu}}_{10} {\text{Sn}}_{3}$ from^[90] predicts significantly larger structure factors for these reflections (which are, in any case, small) than it is the case for the LT model.^[88] However, checks by the present author reveal that these differences are not a direct consequence of the different space group symmetries of the two models, but a consequence of the detailed atomic coordinates derived for the different structures. It is possible, e.g., to impose inversion symmetry on the LT′ model from^[90] yielding $P6_{3} /m$ symmetry including merging atomic sites on average positions. The resulting ${\text{LT-Cu}}_{10} {\text{Sn}}_{3}$ structure model with fractional coordinates somewhat differing from those in Ref. 88 has still relatively large structure factors for the mentioned reflections. In any case, dynamic diffraction effects were apparently not considered in Ref. 47 in concluding that the 101_LT/LT′ and 201_LT/LT′ reflections were too strong for the $P6_{3} /m$ model.

The different structure models derived for Cu₁₀Sn₃ intermetallic (apart from the outdated one^[87]) have symmetries related by group-subgroup relationships depicted in Fig. 10. As also pointed out in Refs. 88 and 91 the crystal structures are closely related with to those of Cu₃P and Cu₃As, but also to similar structures in the Cu–Sb and Cu–Ge systems. Many, also apparently contradictory structure models exist for hexagonal/trigonal phases in these systems,^{[89,93,94,95,96,97]} and a considerable part with similar unit cells as given by Eq 3.5.1 and 3.5.2. The phase transitions and complex structure chemistry implied in these works indicate that Cu₁₀Sn₃ may also exhibit more complicated structures including disorder than previously thought.

Fig. 10

Group-subgroup scheme (Bärninghausen tree) following Ref. 98 for the different structure models for ζ-Cu₁₀Sn₃ with Pearson symbol and space group symbols, with intermediate space groups without separate model in grey. LT-Cu₁₀Sn₃ ^[88] and LT′-Cu₁₀Sn₃ ^[90] correspond to the usually considered models, based on single-crystal x-ray diffraction analysis, while it had been concluded from in-situ powder x-ray diffraction that at the actual equilibrium stability temperature of 600 °C the HT-Cu₁₀Sn₃ structure would be stable ^[91] with a smaller unit cell and likely dynamically disordered atomic structure. Note that the trigonal structure model from Ref. 87 can be regarded as outdated and could also not be easily included in the present tree

There seem to be two original works dealing with Cu₁₀Sn₃ in the ${\text{LT-Cu}}_{10} {\text{Sn}}_{3}$ and ${\text{LT}}^{\prime}{\text{-Cu}}_{10} {\text{Sn}}_{3}$ form by electronic structure calculations^[59,99]; see Table 2. Ramos de Debiaggi et al.^[59] considered the LT′ structure (P6₃) and determined a positive energy of formation from Cu and β-Sn as well as relaxed structure parameters. Analysis of the resulting fractional coordinates show even closer agreement with higher $P6_{3} /m$ symmetry than the experimental structure from Ref. 90, which raises some doubt as to whether the use of the lower symmetry is really justified. Liu et al.^[99] adopted the LT structure ($P6_{3} /m$) and calculated structure parameters and elastic constants, the latter not implying a considerable anisotropy. From considering a number of Cu-containing intermetallics, it was concluded that the relaxed lattice parameters of the considered Cu₁₀Sn₃ deviated from the experimental values to a larger extent than it was the case for the other intermetallics (while they well agreed with the previous work^[59]).

Table 2 Summary of first-principles electronic structure calculations of model structures relevant to the Cu₁₀Sn₃ intermetallic

However, none of these first-principles works attempted to resolve the likely flat and complicated energy landscape with respect to atomic displacements in Cu₁₀Sn₃ to confirm whether the $P6_{3}$ ${\text{LT}}^{\prime}{\text{-Cu}}_{10} {\text{Sn}}_{3}$ structure has really a lower energy than the $P6_{3} /m$ ${\text{LT-Cu}}_{10} {\text{Sn}}_{3}$ version. From the present author’s point of view, the relevance of a polar $P6_{3}$ LT′ is even questionable if it had a somewhat lower DFT energy and if it suggested an improved structure refinement as in Ref. 90: While the local atomic displacements, e.g., of the Cu atoms could be real (and motivated by lower energy), they need not to be spatially correlated as implied by the LT′ structure model. Hence, the $P6_{3}$ LT′ structure could possibly be some kind of overdetermined crystal structure model, here possibly artificially pressing diffraction effects of non-periodic features affecting the diffraction data into a periodic structure model.

As shown in Fig. 5, the studies of Knödler^[55,81] on γ phase alloys quenched from 700 °C to –183 °C revealed also a compositional window around the actual stability range, where the alloys show PXRD patterns (taken at ambient temperature) indicative for the LT/LT′-Cu₁₀Sn₃ structure (referred to as ζ′).

There are a number of publications which have reported observation of Cu₁₀Sn₃-like solid, e.g., in form of precipitates, often developing upon decomposing α or β/γ under non-equilibrium conditions,^[47,82] with one of these works already mentioned above. There have also been reports on a smaller hexagonal unit cell with ${\mathbf{c}}_{{{\text{LT-Cu}}_{10} {\text{Sn}}_{3} }} /3$ (implying Pearson symbol hP9, ignoring possible vacancies) in quenched and aged β phase, based on x-ray diffraction on multi-variant single crystal specimens^[100] or on SAED.^[101] Similarity of the resulting crystal structures with ζ-Ag–Zn phase was proposed, while no reference has been made to structure models for phases of the Cu₁₀Sn₃ intermetallic existing at the time of the respective works. Hence, it was not examined whether the available diffraction data provided evidence, e.g., for the larger LT unit cell according to Eq 3.5.1.

3.6 Cu₃Sn Intermetallic (ε etc.)

Bain^[14] first reported the basic A3 crystal structure (hexagonal Mg type, hP2, space group $P6_{3} /mmc$) for the ε phase using PXRD data. Soon after, Jones and Evans^[102] reported lattice parameter values: $a_{{{\text{A}}3}}$ = 2.752 Å, $c_{{{\text{A}}3}}$ = 4.322 Å (corrected!), implying an axial ratio of $c_{{{\text{A}}3}} /a_{{{\text{A}}3}}$ = 1.572 which is much smaller than the ideal value of $2\sqrt {2/3}$≈ 1.633.^[102] Westgren and Phragmen^[52] reported, for that unit cell, lattice parameters to range from $a_{{{\text{A}}3}}$ = 2.753 Å, $c_{{{\text{A}}3}}$ = 4.329 Å (Cu rich) to $a_{{{\text{A}}3}}$ = 2.761 Å, $c_{{{\text{A}}3}}$ = 4.329 Å (Sn rich; both sets of values corrected!), which was stated to imply a few tenths % homogeneity range. This range is compatible with experimental data for the homogeneity range obtained from metallographic analyses of equilibrated alloys,^{[39,74,103,104]} implying some extension of the homogeneity range towards < 25 at.% Sn. Figure 11 shows the alloy-composition dependent evolution of the lattice parameters $a_{{{\text{A}}3}}$ and $c_{{{\text{A}}3}}$ for a series of mainly biphasic alloys equilibrated at 420 °C,^[74] reflecting the lattice parameters’ changes over the homogeneity range indicated by the vertical lines, as assessed in the same work. These changes confirm the decrease of $c_{{{\text{A}}3}} /a_{{{\text{A}}3}}$ with increasing Sn content, as already evident from the data given in Ref. 52. Data presented in figures in Refs. 104 and 105 confirm the same trend.

Fig. 11

Alloy-composition dependent evolution of the lattice parameters of ε-Cu₃Sn (pertaining to the A3-type unit cell; see Fig. 12) as determined by PXRD at ambient temperature of Cu–Sn alloys equilibrated at 420 °C and predominantly containing this phase ^[74]. In the same work the homogeneity range was determined as indicated by the vertical lines. The data reflect the decreasing axial ratio $c_{{{\text{A}}3}} /a_{{{\text{A}}3}}$ with increasing Sn content. The dashed blue lines depict some course of the lattice parameters as a guide to the eye

However, it has already been shown by Bernal^[75] based on SCXRD that typical Cu₃Sn intermetallic shows long-range occupational ordering of Cu versus Sn on the sites of the underlying A3 structure. In this publication and publications from later decades diffraction evidence was obtained which was used to arrive at different translation lattices and structure models. The distributions of Cu versus Sn implied by the most important models have been depicted in Fig. 12 in form of a hexagonal close-packed layer. Each of these layers allows construction of a unique three-dimensional A3-based structure by hexagonally stacking (“ABAB”) the corresponding layer under the constraint to avoid Sn-Sn nearest-neighbor contacts, which is achieved by placing Sn atoms of a given layer on top of the centers of Cu triangles of an adjacent layer. Availability of such triangles is ensured by the rectangle and triangle motifs of the Sn atoms in all types of layers under consideration (R and T layers as discussed by Beck^[106,107]).

Fig. 12

Illustration of the hexagonal close-packed layers contained in the most relevant superstructure models for ε-Cu₃Sn based on an A3 structure. Note that the shown layers are stacked such that they avoid next-neighbor contacts of the Sn atoms: (a) D0₁₉ structure as experimentally observed only recently ^[108]. This structure has earlier served as starting point to generate the other structures by periodically introducing APBs (possible positions indicated in light green), (b) D0_a structure likely existing as ε′ resulting from rapid transformation of γ-high temperature phase, and (c, d) the most important long-range APB (green dashed lines) variants as $oS64$ or $oS80$ superstructures. They are likely being special cases of an incommensurately modulated structure ^[109]. Note that the basis vectors are indicated regardless of the employed origin of the unit cell

The description and discussion of the ordered models will start with structures pertaining to likely equilibrium ε-Cu₃Sn. The first superstructure unit cell described by Bernal^[75]7 was later confirmed by Carlsson and Hägg,^[87] Brooks and Gillam^[110] and Müller and Lidin.^[109] The base centered orthorhombic “eightfold” supercell (Fig. 12d) contains 64 atoms and will be correspondingly denoted by the Pearson symbol oS64, which will be also used for the structure itself due to a lacking Strukturbericht symbol. The basis vectors are:

$$\begin{gathered} {\mathbf{a}}_{oS64} = 2\left( {{\mathbf{a}}_{{{\text{A}}3}} + {\mathbf{b}}_{{{\text{A}}3}} } \right) \hfill \\ {\mathbf{b}}_{oS64} = 8\left( {{\mathbf{a}}_{{{\text{A}}3}} - {\mathbf{b}}_{{{\text{A}}3}} } \right) \hfill \\ {\mathbf{c}}_{oS64}\quad = {\mathbf{c}}_{{{\text{A}}3}} \hfill \\ \end{gathered}$$

(3.6.1)

with ideally (no metrical distortion; see below) $a_{oS64} = 2a_{{{\text{A}}3}}$, $b_{oS64}$ = 8 × $\sqrt 3$ a_A3 and $c_{oS64} = c_{{{\text{A}}3}}$. Schubert et al.^[111], Watanabe et al.^[112] and Müller and Lidin^[109] have alternatively described some “tenfold” superstructure” (Fig. 12c), implying a Pearson symbol $oS80$ with unit cell basis vectors

$$\begin{gathered} {\mathbf{a}}_{oS80} = 2\left( {{\mathbf{a}}_{{{\text{A}}3}} + {\mathbf{b}}_{{{\text{A}}3}} } \right) \hfill \\ {\mathbf{b}}_{oS80} = 10\left( {{\mathbf{a}}_{{{\text{A}}3}} - {\mathbf{b}}_{{{\text{A}}3}} } \right) \hfill \\ {\mathbf{c}}_{oS80}\quad = {\mathbf{c}}_{{{\text{A}}3}} \hfill \\ \end{gathered}$$

(3.6.2)

with ideally (no metrical distortion; see below) $a_{oS80}$ $= 2a_{{{\text{A}}3}}$, $b_{oS80} = 10\sqrt 3$ a_A3 and $c_{oS80} = c_{{{\text{A}}3}}$.

For the $oS64$ superstructure, already Bernal apparently has suggested an orthorhombic space group symmetry, corresponding in Hermann–Mauguin notation and applying the standard axes setting, to Cmcm (compatible with the choice of axes implied Eq 3.6.1–2). This space group turns out to be correct for both the $oS64$ and $oS80$ superstructures^[109,112]; see what follows.

Schubert et al.^[111] were the first to report a detailed structure model for the $oS80$ supercell, however, without reference to some explicitly formulated space-group symmetry. The structure is depicted in Fig. 12(c). In Ref. [111] this structure has been discussed in terms of a D0₁₉ superstructure for Cu₃Sn (compare Fig. 12a), which contains a periodic arrangement of antiphase boundaries (APBs, referred to as “Verwerfungen”) at 0.4 = 40% (APD density; “Verwerfungsdichte” in^[105,111]) parallel to (010)_oS80. Hereby, the D0₁₉ superstructure can be described by a supercell with

$$\begin{gathered} {\mathbf{a}}_{{{\text{D}}0_{19} }} = 2{\mathbf{a}}_{{{\text{A}}3}} \hfill \\ {\mathbf{b}}_{{{\text{D}}0_{19} }} = 2{\mathbf{b}}_{{{\text{A}}3}} \hfill \\ {\mathbf{c}}_{{{\text{D}}0_{19} }} = {\mathbf{c}}_{{{\text{A}}3}} , \hfill \\ \end{gathered}$$

(3.6.3)

and the suitable locations for APBs are parallel to one set of the planes $\left\{ {1\overline{1}00} \right\}_{{{\text{D}}0_{19} }}$. One possible set of locations is indicated by light-green dashed lines in Fig. 12(a). The APB densities as given in Refs. 105 and 111 refer to the average fraction of APBs on these lines, where, however, it has to be kept in mind that placement of APBs on adjacent light-green lines not enclosing Sn atoms will cancel their respective effect. Therefore, at maximum ½ of the light-green lines may become APBs, i.e., the maximum APB density is ½. This results in the orthorhombic D0_a/Cu₃Ti type ordering. To describe this structure, three choices of axes are considered here (only one shown in Fig. 12b), which are distinguished by Hermann–Mauguin symbols:

$$\begin{gathered} {\mathbf{a}}_{Pmnm} = 2\left( {{\mathbf{a}}_{{{\text{A}}3}} + {\mathbf{b}}_{{{\text{A}}3}} } \right) = {\mathbf{b}}_{Pmmn} = {\mathbf{b}}_{Pnmm} \hfill \\ {\mathbf{b}}_{Pmnm} = {\mathbf{a}}_{{{\text{A}}3}} - {\mathbf{b}}_{{{\text{A}}3}} = {\mathbf{c}}_{Pmmn} = - {\mathbf{a}}_{Pnmm} \hfill \\ {\mathbf{c}}_{Pmnm}\quad = {\mathbf{c}}_{{{\text{A}}3}} = {\mathbf{a}}_{Pmmn} = {\mathbf{c}}_{Pnmm} \hfill \\ \end{gathered}$$

(3.6.4)

The standard choice of axes for space group number 59 of the D0_a structure has the n glide plane perpendicular to the [001] direction,^[27] leading to the space group symbol Pmmn. A setting corresponding to Pmnm has been used by Schubert et al.^[111] and has the axes parallel to those given in Eq 3.6.1-2. Finally, the setting Pnmm was used by Knödler,^[55,67] which is also the commonly used choice of axes for the 2H/γ′₁ martensite; see Sect. 3.9.3.⁸ In the absence of distortions away from pseudohexagonal metrics (see below) one obtains lattice parameter values a_Pmnm = 2 $a_{{{\text{A}}3}}$, b_Pmnm = $\sqrt 3 a_{{{\text{A}}3}}$ and c_Pmnm = c_A3.

As already noted in Ref. [111], the D0_a ordering is actually closer to the $oS64$ and $oS80$ ordering than to the D0₁₉ ordering. With respect to the D0_a ordering, the APB density of the $oS80$ structure would amount only to 0.1 = 10%.

The SCXRD analysis reported in Ref. [111] relied on rotation camera-based film methods with semiquantitatively measured reflection intensities. Based on these data, some systematic displacements of the atoms were educed to occur along the [010]_oS80 direction, i.e., away from the atoms’ ideal positions originating from the underlying A3 structure. In a later SCXRD work, Watanabe et al.^[112] were able to rely on much better counter-based intensity data. The crystal structure analysis resulted in a description of the complete crystal structure in Cmcm symmetry, using up-to-date crystallographic language to present the atomic structure, including a complete set of fractional coordinates referring to the standard space group origin.^[27] The atomic displacements of the Cu atoms were found to be much larger than those of the Sn atoms and to disagree with the displacements proposed in Ref. 111. The displacements reflect the space requirements of the large Sn atoms and are pronounced near the APBs. The Sn sites were refined to contain 2% Cu atoms, resulting in a composition corresponding to 24.5 at%, which is within the composition ranges determined in Refs. 103 and 104. Müller and Lidin^[109] also reported SCXRD based on ε-Cu₃Sn crystal specimens from alloys equilibrated at 200–550 °C. Either the $oS64$ or the $oS80$ superstructure (both Cmcm symmetry) were used to evaluate the SCXRD data, depending on the better agreement of the positions of the reflections in the SCXRD data with the positions predicted by these structure models. Thereby, occurrence of these superstructures did not depend in a characteristic fashion on the equilibration temperature. Independent from the type of superstructure, the atomic displacements with respect to the ideal A3 positions were again reported in terms of fractional coordinates, but they were not analyzed in detail. They seem to largely agree with those found in Ref. 112. It should be noted that refinement of the occupancies of the Cu sites implied slightly Cu-rich compositions, as in Ref. 112.

Burkhardt^[104] and Burkhardt and Schubert^[105] already realized that the actual positions of the superstructure reflections typically did neither exactly correspond to those expected due to the $oS64$ or to the $oS80$ superstructure (corresponding to APB densities of 0.375 or 0.4 with respect to D0₁₉ or 0.125 or 0.1 with respect to D0_a; see also above). Instead, an apparent continuum of values could be discerned from the positions of the reflections. From these positions, it was possible to determine values for APB densities.^[104,105] Numerical data of APB densities for different alloy compositions⁹ reported by Burkhardt^[104] have been plotted in Fig. 13. Some systematic dependence of the APB density on the equilibration temperature and the alloy (and likely also the phase) composition seems to be present.

Fig. 13

Antiphase boundary (APB) density with respect to the D0₁₉ superstructure as measured by diffraction techniques at ambient temperature after quenching from an annealing temperature T. Filled data points: Results from PXRD using numerical data from ^[104], and data from plots in Refs. 104 and 105 for different alloys. The compositions are given in at.% Sn. The lines have been added to guide the eye. Open circles: Results from SCXRD from stoichiometric alloys ^[109]. The APD densities corresponding to the $oS64$ and $oS80$ superstructures have been marked by arrows

Müller and Lidin^[109] also evaluated their above-mentioned SCXRD data in terms of allowing non-discrete values of APD densities. For that they designed a 3 + 1 dimensionally modulated structure model having the $oS64$ and $oS80$ superstructures as special cases. The employed superspace group was of the type Xmcm(0q₂0)00, with X representing the 4-dimsional translations 0000 and ½00½. Thereby, the average structure has Cmcm symmetry with basis vectors corresponding to those of the Pmnm unit cell defined in Eq 3.6.4, i.e., ${\mathbf{a}}_{{{\text{av}}}} = {\mathbf{a}}_{Pmnm}$ etc. and a modulation vector of the type ${\mathbf{q}} = q_{2} {\mathbf{b}}_{{{\text{av}}}}^{\user2{*}}$ with ${\mathbf{b}}_{{{\text{av}}}}^{\user2{*}}$ being the corresponding reciprocal lattice vector. Accordingly, the value of q₂ determines the positions of the satellite reflections in reciprocal space, whereby with $q_{2} = 0.1$, resp. 0.125, the reflection positions correspond to those of the $oS64$ and $oS80$ superstructure, respectively. It can be shown that the value of q₂ corresponds to the APB density with respect to the D0_a structure, while $1/2 - q_{2}$ corresponds to the APB density with respect to the D0₁₉ structure employed previously.^[104,105] Using this model, the authors re-analyzed the SCXRD data, which was initially evaluated in terms of either the $oS64$ or the $oS80$ superstructures, considering now the satellite reflection positions upon data reduction and thus arriving at continuous values for q₂ for each set of crystal data. For crystals obtained from alloys treated at different temperatures, the values of $1/2 - q_{2}$ have been included in Fig. 13. In contrast to the data from Ref. 104 there is no evident systematic equilibration-temperature dependence of the data, as already expected from the data analysis using the $oS64$ and $oS80$ approximant superstructures (see above).

The non-systematic behavior of the data from^[109] contrasting the systematic behavior of the data from^[104] evident in Fig. 13, may have two reasons. (i) In Ref. 109 a Cu-25 at.% Sn alloy was melted and slowly cooled in the furnace. This helped developing coarse crystals upon solidification, favorable for retrieving crystals for SCXRD analysis but unfavorable for short diffusion paths impeding reduction of segregation during the following heat treatments. Hence, compositional control is difficult in correspondingly solidified alloys. In contrast to this, in^[104,105] arc melting has been employed, leading to finer microstructures upon solidification and shorter diffusion paths. Moreover, more detailed composition control was attempted and likely achieved, which was possible by apparently deliberately employing two-phase samples. Under equilibrium conditions, in such alloys the ε phase attains the high- or low-Sn content boundary of its phase field allowing to obtain crystallographic parameters for these boundary compositions, which may not be exactly known but may be well defined. (ii) Establishment of equilibrium values of the APB density requires thermal activation and may become slow at low temperatures.

The ideal relations between lattice parameters pertaining to the different orthorhombic superstructure cells have been given above as they hold in the absence of distortions away from a pseudohexagonal metric. There are only few reports on such distortions. Burkhardt and Schubert have considered the ratio $2b_{Pmnm} /a_{Pmnm}$ pertaining to a subcell defined according to Eq 3.6.4, corresponding to the average structure of the modulated structure model introduced by.^[109] This ratio assumes a value of $\sqrt 3$ in the case of a pseudohexagonal lattice metric. In^[104,105] it was pointed out that the cases of $2b_{Pmnm} /a_{Pmnm} > \sqrt 3$ and $2b_{Pmnm} /a_{Pmnm} < \sqrt 3$ constitute inequivalent, distinguishable states. Based on lattice parameters derived from SCXRD film data from Ref. 111 a value of $2b_{Pmnm} /a_{Pmnm} = 1.728$ was calculated. This deviation from $\sqrt 3$ by −0.2% is smaller than that for most of the other analyzed related crystal structures^[104,105] and might be close to insignificant in view of the only 0.01 Å precision with which the lattice parameters were given in Ref. 111. It had been stated simultaneously that splitting of fundamental reflections (i.e., those already expected for the A3 basis structure) in PXRD patterns was not detected^[104]; such a splitting would be direct evidence for a deviation of $2b_{Pmnm} /a_{Pmnm}$ from $\sqrt 3$. Lattice parameters determined by Knödler^[55] show even a closer agreement of $2b_{Pmnm} /a_{Pmnm}$ with $\sqrt 3$ when measured at ambient temperature. Knödler also reported that the $2b_{Pmnm} /a_{Pmnm}$ ratio decreases to values significantly below $\sqrt 3$ at elevated temperature as shown by PXRD.^[55] Note, however, that even in the case of non-visibility of such a splitting, a metrical distortion can be determined by careful analysis of the PXRD data including the reflections due to long-range ordering. This was demonstrated in the case of η′-Cu₆Sn₅^[113] (see also Sect. 3.7).

The reduction of crystal-class symmetry from $6/mmm$ for a virtual (hypothetical) A3 structure to mmm for the actual orthorhombic structure(s) of ε-Cu₃Sn ($6/mmm$ → $mmm$) is characterized by a ratio of the orders of the point groups of 24/8 = 3,^{[114,115,116,117]} suggesting the possible formation of 3 orientational twin domain states due to ordering. High-resolution electron microscopy has been used to image the periodic occurrence of the APBs^[22,116] and the occurrence of twin domains.^[116] Moreover, more complex APB structures have been observed.^[116] However, notably, the previously discussed works reporting SCXRD analysis of the crystal structure of ε-Cu₃Sn (typically working with crystal specimens with sizes up to above 100 μm) did not—as it is common practice—report issues with twinning, i.e., mutual presence of several twin orientations in the investigated crystal specimens.^{[109,111,112]} This suggests that a sufficiently large domain size appears to have developed during the respective alloys’ heat treatments.

Upon quenching of γ-Cu₃Sn from 700 °C, Knödler observed development of a type of orthorhombic Cu₃Sn referred to ε′-Cu₃Sn.^[55,67] The PXRD data of ε′ was interpreted in terms of the D0_a/Cu₃Ti-type structure; see Fig. 12(b) and Eq 3.6.4 for its unit cell. Schubert et al.^[111] originally formulated such a crystal structure as an extreme type of the periodic APB-containing ε, without claiming its occurrence in reality. Such an ε′ structure was also encountered by Seemann and Knödler after quenching a Cu₃Sn alloy from liquid.^[118] It had been argued^[55,67] that due to the close agreement of the Cu versus Sn ordering in the $\left\{ {220} \right\}_{{{\text{D}}0_{3} }}$ planes of the D0₃ structure of γ-Cu₃Sn (see Fig. 3d) and the $\left\{ {002} \right\}_{{{\text{D}}0_{{\text{a}}} }}$ planes of the D0_a structure of ε′ (see Fig. 12b) that the ordering of the latter is due to a diffusionless/martensitic γ → ε′ transition^[55,67] referring to the Burgers lattice correspondence between A2 and A3.^[119] It was further argued that the ε′ is likely only a metastable transitional structure on the path from γ to APB-containing (with respect to ε′) ε-Cu₃Sn. Upon inducing the ε′ → ε transformation, the ε appears to grow at the cost of ε′ instead of continuously changing the APB density.^[55] Strikingly, while at above 600 °C ε-Cu₃Sn (of unspecified composition) was reported to show the $oS64$ superstructure, after quenching the intermetallic appeared to contain significant amounts of ε′ more alongside with ε with apparent $oS80$ superstructure.^[55] This may hint at a surprising difficulty to retain the APB state from elevated temperature by quenching to ambient temperature and might shed some new light on the apparently continuous change of the APB density with composition reported previously^[104,105] and the difficulty of other works to discern systematic temperature dependent trends. In this context in can be mentioned that irregular spacing of APBs have been observed by van Sande et al.^[116] upon liquid quenching from 1000 °C.

While Ref. [67] reported an ideal pseudohexagonal metric of ε′, Ref. [55] later reported (at 293 K) lattice parameters implying $2b_{Pmnm} /a_{Pmnm} < \sqrt 3$ contrasting the nearly ideal pseudohexagonal lattice parameters as found for equilibrium ε measured at 20 °C. Subsequent work by Brooks and Gillam^[110] performed mainly by PXRD reported experimental results on a small orthorhombic cell, D0_a type Cu₃Sn obtained by quenching from the 700 °C (i.e., from γ phase), closely agreeing with the results reported by Knödler^[55,67] for his ε′-Cu₃Sn.

Cold work applied to powders having the long-period ordered ε and or small-unit cell ε′ superstructures, leads to suppression of most of the superstructure reflections. While the labeling by Brooks and Gillam^[110] suggests that plastic deformations suppresses all superstructure reflections (Table 1b of this work), according to the present author’s judgement two of the remaining reflections are actually superstructure reflections and indicate some remaining long-range order. The remaining reflections imply introduction of irregular APBs, since it is these remaining superstructure reflections, which are least affected by changes in the APB density or by introduction of these with respect to the D0_a superstructure.¹⁰ It is to be kept in mind, however, that Knödler has noted in contrast to Ref. 110 that cold work of ε′-Cu₃Sn would transform it to ε-Cu₃Sn. Brooks and Gillam^[110] also presented more detailed considerations which might be supporting evidence for the martensitic character of the γ → ε′ transition.

Relatively recently, Sang et al.^[108] reported first evidence for formation of the actual D0₁₉ type superstructure to occur (see Fig. 12a). This superstructure had been considered above, as constituting, together with D0_a, an extreme case with respect to the periodic APB models for the orthorhombic superstructure of the ε phase. According to the scheme from Refs. 104 and 105 the D0₁₉ structure has an APB density of 0; compare also Fig. 13. The alloy studied in Ref. 108 was apparently analyzed in an arc-melted and as-solidified state, which hinders easy interpretation of the results. Using TEM including SAED, the Cu₃Sn dendrites were identified to be of D0_a superstructure (ε′), whereas Cu₃Sn in the interdendritic space was identified to be of the D0₁₉ structure. The TEM analysis notably revealed presence of irregularly arranged APBs on $\left\{ {1\overline{1}00} \right\}_{{{\text{D}}0_{19} }}$ planes. These correspond to the orientation of the APBs in the orthorhombic variants; see above. Note that already in a very early work, Linde^[120] had reported PXRD data with superstructure reflections interpreted in terms of an apparently hexagonal supercell with ${\mathbf{a}}_{{{\text{Linde}}}} = 2{\mathbf{a}}_{{{\text{A}}3}}$ and ${\mathbf{c}}_{{{\text{Linde}}}} = 2{\mathbf{c}}_{{{\text{A}}3}}$. However, no structure model had been proposed. Some of the superstructure reflections reported in that work appear compatible with the D0₁₉ structure model, while others (those with uneven l_Linde) are incompatible. Already Carlsson and Hägg^[87] reported that their observations on ε-Cu₃Sn were incompatible with those from Ref. 120 neither did subsequent work confirm Linde’s observations.

In an attempt to simulate the time-dependent evolution of domain structures in ε-Cu₃Sn, Oguma et al.^[121,122], have developed a time-dependent Ginzburg − Landau model for microstructure evolution, taking the D0₁₉ structure as the equilibrium structure, where, consequently, only APB boundaries but no twin boundaries occur due to hexagonal point group symmetry 6/mmm of the adopted D0₁₉ structure. The used model parameters resulted in APBs which indeed appear to be compatible with those observed in Ref. 108.

First-principles calculations have been carried out for a variety of model structures already discussed for the Cu₃Sn intermetallic. An overview is presented in Table 3. In general, computational, and experimental data, in particular atomic coordinates, agree well. For example, Chen et al.^{[123,124,125,126]} confirmed, for the first time, that the fractional atomic coordinates obtained from first-principles calculations reflect well the above-mentioned atomic displacements experimentally determined by Watanabe et al.^[112].

Table 3 Summary of first-principles electronic structure calculations of model structures relevant for the Cu₃Sn intermetallic

Works reporting single-crystal elastic constants for the various considered structures yield A^U values below 0.5, which implies, in view of the $A^{\text{U}} = 0.6$ criterion outlined in Sect. 3.1, a small degree of elastic anisotropy, irrespective of the considered superstructure type. Ramos de Debiaggi et al.^[59] found similar bulk moduli for both considered structure types (D0_a, $oS80$), while in the case of Qu et al.^[60], these values differ to some extent. Discussion of these differences in view of the varying calculation settings is beyond the scope of the present review.

A couple of works have computed the energy of formation values derived from the static structures for the different model structures^[22,59,60]. Figure 14 shows the energies per atom for the $oS80$ and D0₁₉ superstructures relative to D0_a. The latter was chosen as a reference for the pragmatic reason that this structure has been considered in all the works relevant for this comparison. Obviously, the energy hierarchy of the structures varies from work to work. While in the case of Ramos de Debiaggi et al.^[59] and Daeumer et al.^[22] the energies per atom differ only by a few meV, the differences by Qu et al.^[60] are significantly larger.¹¹ The newest work by Daeumer et al.^[22] obtained the lowest energy for D0₁₉ and found a somewhat monotonously decreasing energy from D0_a to D0₁₉ with changing APB density (the authors even use a different measure of the APB density than those discussed above) as revealed by considering even further model structures including the $oS64$ superstructure. It should also be noted that, if the D0₃ structure (γ phase; see Sect. 3.3) was considered,^[59,60] its energy is some 10 meV/atom higher than that of the considered ε/ε′-Cu₃Sn structures, which is compatible with its instability at low temperatures.

Fig. 14

Energies of different superstructures for ε/ε′-Cu₃Sn relative to that of the D0_a superstructure obtained by first-principles calculations according to Ramos de Debiaggi et al. ^[59], Qu et al. ^[60] and Daeumer et al. ^[22]. Note that the latter work also considered more structure and frozen phonon calculations to estimate T > 0 K effects

Daeumer et al.^[22] were also the first who have considered $T > 0 \, {\text{K}}$ thermodynamics and defect chemistry based on first-principles calculations to compare the energies of different Cu₃Sn superstructures. However, the calculations did not predict a T-dependent change of the energetic hierarchy, which could possibly explain the occurrence of different types of structures for ε-Cu₃Sn. It was also made likely that excess Cu may substitute Sn close to the APBs.

A definitive experimental study of the evolution of the equilibrium values of the APB densities in ε-Cu₃Sn requires careful composition control (as achieved in early work^[104,105]) but also should attempt to demonstrate reversibility of temperature-induced changes and should get some information about the kinetics of such changes. As described, the available first-principles calculations seem to imply very small differences in energies of the different structures and, therefore, small driving forces for structure changes, which suggests sluggish kinetics. Powder diffraction can play an important role for that purpose, as changes in the APB densities cause appreciable shifts in the superstructure/satellite¹² reflection positions.^{[104,105,109]} A complete interpretation of such phenomena should, in any case, also consider the probability that upon a diffusionless γ → ε′ transformation, an unusual high vacancy content from the γ phase (see Sect. 3.3) is initially retained in the developing ε/ε′, where a likely much lower (temperature dependent) equilibrium vacancy content prevails. Prior to the vacancies have annihilated, there will be consequently enhanced diffusion kinetics that may influence the evolving APB arrangement.

3.7 Cu₆Sn₅ Intermetallic (η, η′, etc.)

The literature on the crystal structures related to the η and η′ equilibrium phases (see Fig. 1(a) and (e)) and the Cu-rich metastable η′′ phase of the Cu–Sn system turns out to be highly confusing. Therefore, the current view on the structure is briefly summarized, before reporting the evolution of scientific knowledge also including some detours.

The high-temperature η phase has a disordered B8₂/B8₁ (or Ni₂In/NiAs) crystal structure with hexagonal $P6_{3} /mmc$ symmetry; see Fig. 15(a). The Sn atoms form a hexagonal close packed/A3-like arrangement, with the Cu(1) atoms on the octahedral sites surrounded by 6 Sn atoms and the Cu(2) atoms on the trigonal–bipyramidal interstices (partial occupancy δ) surrounded by 5 Sn atoms. This gives the general formula Cu_1+δSn; see also Table 4, which can be used to indicate the composition in a way closely related with the crystal structure. A recent experimental assessment on the extent of the homogeneity range implies that the Cu(2) sites can assume occupancies δ ranging from 0.24–0.17.^[12] The composition given by the formula Cu₆Sn₅ corresponds to Cu_1.20Sn, i.e., δ = 0.2, which is within this range. The ideal B8₂ (Ni₂In type) structure is characterized by a fully occupied 2d site with δ = 1, whereas the ideal B8₁ (NiAs type) structure corresponds to δ = 0. This is the background of referring to structures with 0 < δ < 1 as B8₂/B8₁ structures, as done also here. The short notion B8 will be used to accompany basis vectors, or indices representing lattice directions and lattice planes, whereas in a series of papers the present author has used the index h for that purpose. As it will be described in more detail below when reviewing the literature, the η′ and η′′ are low-temperature phases with long-range ordered arrangement of the Cu(2) atoms.^[11,18,134]

Fig. 15

Crystal structure of the disordered B8₂/B8₁ η-Cu–Sn phase (Cu₆Sn₅, Cu_1+δSn; subscript: B8) (a) Clinographic drawing of a hexagonal unit cell, which was augmented by further atoms to illustrate the trigonal–bipyramidal coordination of Cu(2) atoms (partial occupation indicated by pie-chart presentation). Additionally, the basis vectors for the unit cell of the average structure are given (subscript av), which is basis for a modulated structure description of various ordered phases. (b-e) depict the transformed (Eq 3.7.1) A2 structure, as well as the B8₂/B8₁ structure due to atomic displacements along $\left[ {001} \right]_{{{\text{B}}8}} \parallel \user2{ }\left[ {111} \right]_{{{\text{A}}2}}$. (d)-(e) depict the atoms being located on the planes indicated by dotted lines in (b-c), further illustrating the structural changes from the transformed A2 structure to the B8₂/B8₁ structure. The numbers are the z-fractional coordinates indicating the level above the a-b plane

Table 4 Atomic sites relevant for the crystal structure of the disordered B8₂/B8₁ η-Cu–Sn phase (Cu₆Sn₅, Cu_1+δSn) or in general T_1+δB (T: transition metal, B: main-group element; Ni₂In/NiAs type) with respect to the standard choice of origin of space group $P6_{3} /mmc$ and placing the Sn atoms on the 2c (and not the 2d) sites

However, the above description based on an A3 arrangement of the Sn atoms neglects that the η/η′/η′′-Cu–Sn phases and many related transition-metal (T) − main-group element (B) phases T_1+δB of B8₂/B8₁ structure have a unit cell (or subcell) with a very small axial ratio $c_{{{\text{B}}8}} /a_{{{\text{B}}8}}$. In the case of an ideal A3-type arrangement (as used above to describe the arrangement of the Sn atoms), this ratio would be $c_{{{\text{B}}8}} /a_{{{\text{B}}8}} = 2\sqrt {2/3} \approx 1.633$. However, as pointed out, e.g., in Refs. 135,136,137, in the phases discussed the ratio is much closer to $c_{{{\text{B}}8}} /a_{{{\text{B}}8}} = \sqrt {3/2}\approx 1.225$. If the latter ratio holds, certain reflections inequivalent by hexagonal symmetry assume the same d spacing and thus position in PXRD patterns. In fact, although the reflection positions in such PXRD patterns can be reconciled with those expected from a (primitive) cubic unit cell, the symmetry group of the disordered B8₂/B8₁ crystal structure ($P6_{3} /mmc$) has no cubic supergroups. It is, nevertheless, possible to arrive at the hexagonal/trigonal unit cell based on a cubic A2 structure by

$$\begin{aligned} {\mathbf{a}}_{{{\text{B}}8}} =\;& {\mathbf{a}}_{{{\text{A}}2}} - {\mathbf{b}}_{{{\text{A}}2}} \hfill \\ {\mathbf{b}}_{{{\text{B}}8}} =\; &{\mathbf{b}}_{{{\text{A}}2}} - {\mathbf{c}}_{{{\text{A}}2}} \hfill \\ {\mathbf{c}}_{{{\text{B}}8}} =\;& {\mathbf{a}}_{{{\text{A}}2}} + {\mathbf{b}}_{{{\text{A}}2}} + {\mathbf{c}}_{{{\text{A}}2}} \hfill \\ \end{aligned}$$

(3.7.1)

The directly transformed A2 structure contains close-packed atomic chains along the $\left[ {0001} \right]_{{{\text{B}}8}} \parallel \left[ {111} \right]_{{{\text{A}}2}}$ directions on three levels with respect to the a-b plane: Fig. 15(b, d). A B8₂ structure is then attained by mutually shifting these chains so that two out of the three chains per ${\mathbf{a}}_{{{\text{B}}8}}$–${\mathbf{b}}_{{{\text{B}}8}}$ mesh attain the same level and the third chain attains a level differing from the other ones by one half of the atomic distance within the chain. Retaining the translation lattice according to Eq 3.7.1, the atomic positions of the B8₂ structure are obtained by preferential site occupation and by shifts of the chains relative to each other; Fig. 15(c, e). Note that similar considerations can be applied to the structure of the Cu₁₀Sn₃ phase (see Sect. 3.5), and that the scheme used corresponds to that upon formation of the ω phase from A2; see Sect. 3.9.2.

Laves and Wallbaum^[136] were the first to establish the B8₂ resp. B8₂/B8₁ structure model for transition-metal (T) rich phases with B8₁-base structure, many of them turning out to occur (even only) as superstructures in later research. Laves and Wallbaum^[136] dealt with binary phases in the Ni–In, Cu–In and Cu–Ge and some other systems (but not Cu–Sn). The positions of the transition-metal T(2) atoms, which occur in excess to the ideal TB composition (T(1)B) of the B8₁ structure, were concluded from evaluated intensities from PXRD data to be what has been described as trigonal–bipyramidal sites above. These excess sites were, however, referred to as tetrahedral sites in Ref. 136, whereas the actual centers of gravity of the B atoms tetrahedra in an A3 structure (irrespective of the axial ratio) are located as pairs slightly away from the trigonal–bipyramidal positions; compare Table 4. Nevertheless, the term tetrahedral sites for what is referred to here as trigonal–bipyramidal sites has also been used in some other works in the context of the η-related Cu–Sn phases.^[138]

In any case, the crystal structures related to the Cu₆Sn₅ intermetallic have neither been considered by Laves and Wallbaum,^[136] nor in a later review.^[137] It seems that it was only since the works by Lidin and coworkers in the 1990s,^{[134,135,139,140]} that the special characteristics of the B8₂/B8₁ structure with partial occupation of the trigonal–bipyramidal sites has also been applied systematically to the crystal structures of the Cu₆Sn₅ intermetallic (while it may have been self-evident for some scientists). Note that the Cu(2)/T(2) atoms were also referred to as being located within a so-called 11-vertex Edshammar polyhedron formed by 5 Sn atoms (the same as considered for the trigonal bipyramid) and a trigonal prism formed by Cu(1) atoms; see e.g., Refs. 134, 135, and 139.

Accordingly, two points must be kept in mind when reviewing, in the following the crystal structure data:

(i) In the pre-1990s, the position of the Cu(2) atoms in Cu₆Sn₅ was never really determined and it remained largely matter of speculation and the structure was often incompletely referred to as B8₁/NiAs-type.

(ii) Already pre-crystal-structure analysis phase diagram research (e.g.,^[3]) had distinguished between two main stable forms/phases of the Cu₆Sn₅ intermetallic, i.e., what is referred to as η and η′. Nevertheless, some works on crystal structures do not point out whether the structure analysis is supposed to refer to η and η′.

Westgren and Phragmen^[52] reported on SCXRD and PXRD data a B8₁ structure with $a_{{{\text{B}}8}} =$ 4.199 Å, $c_{{{\text{B}}8}} =$ 5.097 Å (corrected!; $c_{{{\text{B}}8}} /a_{{{\text{B}}8}} = 1.214$). However, composition and mass density of the investigated material implied a Sn content smaller than 50 at.% Sn and excess Cu atoms with respect to a B8₁-CuSn at some unspecified sites. This complied with the finding that the lattice parameters increase with increasing Cu content of the phase.

Bernal^[75] reported results of SCXRD analysis on specimens isolated from an alloy of undescribed history. The observed reflections were interpreted in terms of a superstructure cell $a_{{{\text{Bernal}}}} = 5a_{{{\text{B}}8}} = 20.90$ Å,$c_{{{\text{Bernal}}}} = 5c_{{{\text{B}}8}} =$ 25.16 Å (corrected!). This publication probably uses the formula Cu₆Sn₅ in crystallographic context for the first time and proposes 50 formula units Cu₆Sn₅ per superstructure unit cell, implying 2.4 Cu atoms and 2 Sn atoms per B8 unit cell. The positions of the Cu atoms in excess to a CuSn composition were not discussed. These results were confirmed by Carlssen and Hägg.^[75]

Goria^[141] reported results of SCXRD and PXRD analyses. The author concluded that the data could be reconciled with a hexagonal unit cell smaller than that reported by Bernal^[75]: $a_{{{\text{Goria}}}} = a_{{{\text{B}}8}} = 4.19$ Å, $c_{{{\text{Goria}}}} = 5c_{{{\text{B}}8}} =$ 25.25 Å (corrected!).

Gangulee et al.^[138] reported crystallographic parameters of η high-temperature phase (quenched from 210 °C; $a_{{{\text{B}}8}} =$ 4.192 Å, $c_{{{\text{B}}8}} =$ 5.037 Å), and η′ phase (quenched after 49 d at 170 °C; $a_{{{\text{Bernal}}}}$ = 5 × 4.174 Å, $c_{{{\text{Bernal}}}}$ = 5 × 5.016 Å). The latter showed unspecified superstructure reflections which were stated to be compatible with the supercell due to Bernal.^[75] Unfortunately, it is not clear whether the lattice parameters were determined using PXRD or SCXRD data. In any case, the authors noted them to contract by about 0.4% from the η to the η′ phase, implying a volume contraction of 1.2% (see discussion below). The investigated alloys appeared to contain simultaneously ε-Cu₃Sn and Sn, i.e., they were inhomogeneous and not in equilibrium. The authors seem to propose occupation of the trigonal–bipyramidal sites by the Cu atoms in excess to a formula CuSn (i.e., Cu(2)) as a possible route to reconcile the Cu-rich composition with the B8-type structure. The order–disorder transformation η ⇄ η′ was discussed in terms of some “electronic origin”, either by inducing some kind of antiphase boundaries parallel to $\left( {001} \right)_{{{\text{B}}8}}$ or by order formation on the trigonal–bipyramidal sites, reducing configurational entropy (as it turns out to be the case; see what follows).

Further work^[142,143] reported formation of the superstructure reflections visible in PXRD data in agreement with the supercell reported by Bernal.^[75] In the course of a study of the Au–Cu–Sn system Karlsen et al.^[144] also reported the lattice parameters of quenched high-temperature η phase with $a_{{{\text{B}}8}} = 4.215$–$4.219$ Å and $c_{{{\text{B}}8}} = 5.103$–$5.108$ Å. This range was explicitly attributed to a varying composition of the η phase. Thereby, in the passing, the authors referred to a variable degree of filling of the trigonal–bipyramidal sites by Cu as means to vary the composition. Peplinski et al.^[145] reported high-quality PXRD data ($a_{{{\text{B}}8}} = 4.2062$ Å and $c_{{{\text{B}}8}} = 5.0974$ Å) of high-temperature η phase quenched from 240 °C, without concluding new details on the atomic structure of the disordered phase.

The study by Larsson et al.^[134] represented a breakthrough. The authors investigated, using SCXRD, PXRD and TEM/SAED, an intermetallic extracted from Cu-80 at.% Sn alloy heated to 500 °C and slowly cooled to solidify, leached with hydrochloric acid (dissolving the β-Sn) and further annealed at 180 °C. This allowed determination of the monoclinic crystal structure of the η′-Cu₆Sn₅ low-temperature phase (C2/c, mS44). This structure typically occurs as small orientation domains. Superposition of the diffraction patterns of the domains mimics hexagonal Laue symmetry, explaining that Bernal^[75] had arrived at a large hexagonal supercell; see above. It was the TEM/SAED analysis with high spatial resolution which allowed determination of the C-centered monoclinic supercell from single-domain regions according to:

$$\begin{gathered} {\mathbf{a}}_{{\upeta\prime}} = {\mathbf{a}}_{{{\text{B}}8}} + {\mathbf{b}}_{{{\text{B}}8}} - 2{\mathbf{c}}_{{{\text{B}}8}} \hfill \\ {\mathbf{b}}_{{\upeta\prime}} = - {\mathbf{a}}_{{{\text{B}}8}} + {\mathbf{b}}_{{{\text{B}}8}} \hfill \\ {\mathbf{c}}_{{\upeta\prime}} = 2{\mathbf{a}}_{{{\text{B}}8}} + 2{\mathbf{b}}_{{{\text{B}}8}} + {\mathbf{c}}_{{{\text{B}}8}} \hfill \\ \end{gathered}$$

(3.7.2)

SCXRD from a (domain-)twinned specimen was used to solve the crystal structure. The C-centered unit cell according to Eq 3.7.2 was expected and confirmed to contain two formula units Cu₆Sn₅. An ordered distribution of Cu(2) atoms on 1/5 of all trigonal–bipyramidal sites was found and illustrated in terms of the projection of the Cu(2) atoms along ${\mathbf{b}}_{{\upeta\prime}} = - {\mathbf{a}}_{{{\text{B}}8}} + {\mathbf{b}}_{{{\text{B}}8}}$. This is redone in Fig. 16, where the rectangular grid corresponds to the positions of the trigonal–bipyramidal sites in that projection. As ${\mathbf{b}}_{{\upeta\prime}} = - {\mathbf{a}}_{{{\text{B}}8}} + {\mathbf{b}}_{{{\text{B}}8}}$ is a translation vector of the superstructure and as, for a given grid position, there is only one trigonal–bipyramidal site within one periodic unit ${\mathbf{b}}_{{\upeta\prime}}$, such a schematic unequivocally represents the distribution of the Cu(2) atoms in the superstructure.

Fig. 16

Rectangular grid representing the positions of the trigonal bipyramidal sites in B8₂/B8₁ structures as resulting from projection along the vector $- {\mathbf{a}}_{{{\text{B}}8}} + {\mathbf{b}}_{{{\text{B}}8}}$. This grid is used to illustrate the distribution of the Cu(2) atoms in various ordered real or approximant structure models for Cu₆Sn₅ intermetallic which have in common $- {\mathbf{a}}_{{{\text{B}}8}} + {\mathbf{b}}_{{{\text{B}}8}}$ as translation vector: η′^[134] (see Eq 3.7.2), η⁸ and η⁶ (structure model implies Cu₅Sn₄ = Cu_1.25Sn composition) ^[139] and η⁴⁺¹ (structure model: Cu₄₆Sn₃₇ = Cu_1.243Sn) ^[146], where the unprimed basis vectors pertain to the unit cells given in the original works and the primed ones to a unified scheme introduced in Ref. 18. The green ellipse highlights an ac-type pair of Cu(2) atoms as illustrated in Fig. 17. a_av and c_av label the basis vectors of the average structure used within the framework of the modulated structure description of the η′′ phase but also for η′, η⁸ and η⁴⁺¹ (see Eq 3.7.4; see also Fig. 15a)

One year later the same authors published SAED data^[139] of Cu₆Sn₅-intermetallic containing alloy quenched from 350–405 °C. Again, domain structures were encountered, while the reflections indicating long-range ordering in SAED differed from those expected due to the structure model of the η′ phase.^[134] From the patterns and geometric considerations, two further (super)structure models, referred to η⁸ and η⁶ were derived, both having the Cu-rich composition Cu₅Sn₄ = Cu_1.25Sn. Both the structure models have translation lattices with $- {\mathbf{a}}_{{{\text{B}}8}} + {\mathbf{b}}_{{{\text{B}}8}}$ as a lattice vector. Hence, also for these structures the Cu(2) distribution can be illustrated within the rectangular grid in Fig. 16. Notably, no evidence for such η⁸ and η⁶ structures were found using PXRD. Soon after, Lidin and Larsson reviewed the insights on long-range ordering in different B8₂/B8₁-related intermetallic phases.^[140]

Ghosh and Asta^[21] presented qualitatively analyzed PXRD data as a function of heat treatment temperature by comparing individual observed versus predicted reflections. The PXRD patterns showed superstructure reflections due to η′ ordering for alloys annealed at ≤ 150 °C, whereas no superstructure reflections occurred for alloys annealed above 222 °C and quenched. In addition to first-principles calculations (see below), the authors presented mass-density values attributed to η and η′, which were stated to be calculated from literature data compiled in Ref. 140. These calculations gave 8448 kg/m³ and 8270 kg/m³. Assuming the same composition Cu₆Sn₅ for both cases, these values imply an increase in volume upon ordering by 2.1%. Therefore, volume change due to ordering has the opposite direction than what has been reported by Gangulee et al.^[138]. It was implied that such volume changes acting in the intermetallic within solder joints should lead to severe stresses and thus to cracking, as in particular pointed out by Nogita et al.^[147,148]. The idea of an order-induced volume change has caused considerable research activity on the kinetics of the ordering transitions in the Cu₆Sn₅ intermetallic. Many works also considered the influence of further chemical elements on the ordering; see^[19,20] and citations therein.

Taking into account the impact of the density/volume change calculated by Ghosh and Asta^[21] on subsequent research, the present author has tried to reproduce the density values of 8448 kg/m³ and 8270 kg/m³ based on the numerical data published in Ref. 140. The new calculation results in 8449 kg/m³ for the structure data reported for the η⁸ phase and 8278 kg/m³ for the structure data reported for η′. Data pertaining to the η phase were not reported in Ref. 140. Therefore, it is taken as likely that the value attributed to η in Ref. 21 actually should pertain to η⁸. It is argued here, that using density data calculated from η⁸ and η′ is inadequate to estimate a density change upon the η → η′ transition due to three reasons: (i) All arguments are based on an ordering transition at constant composition, i.e., without occurrence of diffusive phase transition with further participating phases. However, already the η⁸ structure model implies a composition Cu_1.25Sn versus the composition Cu_1.20Sn of η′. (ii) Although the data were determined on an alloy quenched from high temperature, a structure showing a superstructure like η⁸ might not be adequate to represent the disordered η phase. (iii) The lattice-parameter data on η⁸ originating from Ref. 139 were due to some standard SAED analysis known to be imprecise, and potentially rather inaccurate as compared to XRD, in particular PXRD. All this can, in the worst case, render sign and magnitude of the density difference meaningless. See also what follows.

In the course of some more extended activities by Nogita and coauthors dealing with the phase-transformation behavior of Cu₆Sn₅, Wu et al.^[146] reported a new “phase” labeled η⁴⁺¹. Its structure was derived from SAED patterns, which were found to differ from such expected for η⁸, and the structure model was checked by Rietveld refinement against PXRD patterns, although some misfit of the positions of superstructure reflections could be encountered. This superstructure has a very large unit cell and an ideal composition Cu₄₆Sn₃₇ (Cu_1.243Sn). The structure model was described with triclinic P1 symmetry, but in a subsequent work it was suggested that the atomic structure was compatible with monoclinic symmetry.^[18]

Wieser et al.^[113] focused on the metric distortion caused by the η′ ordering, i.e., the distortion of the unit cell away from an ideal pseudohexagonal one. For that purpose, PXRD data from η′ generated in a Cu/Sn diffusion couple were evaluated. That metrical distortion was determined to be particularly small but still significant. The comparison with different sets of lattice parameter values from the literature revealed, on the one hand, good agreement with the PXRD data by Larsson et al.^[134]. On the other hand, the comparison revealed that first-principles calculations usually failed to reveal the experimentally observed distortion, probably due to the very small energy changes associated with the distortions.^[113] In view of this, the distortion implied by the first-principles calculations will not be discussed below.

In a series of further works, Wieser et. al^[10] and Leineweber et al.^[11,12] have shown that, in a temperature range around 165–172 °C, η′ and (more Sn-rich) η coexist in diffusion couples, leading to separate sets of Bragg reflections detectable by PXRD of quenched diffusion couples. Moreover, two-phase alloys equilibrated in the two-phase regions ε + η and η + melt at temperatures between 380 °C and 240 °C and quenched to ambient temperature revealed a systematic variation of the hexagonal lattice parameters of the η phase. In order to estimate the composition of the different phases under consideration, it was proposed that the volume per hexagonal B8 unit cell varied linearly with the occupancy δ of the Cu(2). While the absolute lattice parameter values were related to experimental data, the composition (δ) dependent change was taken from first-principles calculations. The formula is

$$V_{{{\text{B}}8}} = V_{{{\text{B}}8}}^{*} \left[ {1 + A\left( {\delta - 0.2} \right)} \right]$$

(3.7.3)

where $V_{{{\text{B}}8}}^{*}$ is the value for δ = 0.2, and $A = 0.259$.^[10] In case of the ordered phase, $V_{{{\text{B}}8}}^{*} = 78.141\,$Å ^[11,113] has been recommended, where $V_{{{\text{B}}8}}$ has to be chosen as the corresponding fraction of the unit cell used to describe the ordered structure, e.g., 1/10 of the volume of the conventional C-centered monoclinic superstructure cell of η′. Since it was found that the partitionless transition to ordered intermetallic (η′′; see what follows) results in a very minor volume decrease of 0.13% (which refutes much larger changes previously proposed^[21,138]), the above values for $V_{{{\text{B}}8}}^{*}$ and A were recommended only for long-range ordered Cu₆Sn₅. Instead, an increased (by 0.13%) value of $V_{{{\text{B}}8}}^{*} = 78.243$ Å was recommended for disordered η phase.^[11]

Upon annealing high-Cu content η phase, e.g., with δ = 0.23–0.24 at 165 °C,^[11] alloys were produced which showed PXRD patterns with order-related reflections different from those expected for previously reported η′, η⁸, η⁶ and η⁴⁺¹. Nevertheless, the positions of the observed reflections were relatively similar (but still different) to the positions of the superstructure reflections predicted for the η⁴⁺¹ structure model. Eventually, the experimental PXRD patterns were reconciled with an incommensurate structure model of what was referred to the η′′ phase, which was described in C2/m(q₁0-q₃)00 superspace group symmetry.^[11,18] This description uses a pseudo-orthorhombic monoclinic average structure with C-centered unit cell with

$$\begin{gathered} {\mathbf{a}}_{{{\text{av}}}} = {\mathbf{a}}_{{{\text{B}}8}} + {\mathbf{b}}_{{{\text{B}}8}} \hfill \\ {\mathbf{b}}_{{{\text{av}}}} = - {\mathbf{a}}_{{{\text{B}}8}} + {\mathbf{b}}_{{{\text{B}}8}} \hfill \\ {\mathbf{c}}_{{{\text{av}}}} = {\mathbf{c}}_{{{\text{B}}8}} \hfill \\ \end{gathered}$$

(3.7.4)

The splitting of certain fundamental reflections in PXRD patterns reveal some significant intrinsic distortion away from a hexagonal metrics, particularly by a β_av lattice angle deviating from 90°, as allowed by the monoclinic symmetry. The values of q₁ and q₃ in the superspace group symbol are real numbers which describe the positions of the satellite reflections with respect to the reciprocal lattice of Eq 3.7.4, where q₃ ≈ 2q₁. As indicated in Fig. 1(b) the η′′ phase is thought to be only metastable, i.e., its ordering is only achieved upon partitionless ordering of Cu-rich η phase. The η′′ phase is metastable relative to more Cu-poor η (or η′) and ε-Cu₃Sn.^[11,12]

As elaborated in Refs. 11 and 18, the η′, η⁸, and η⁴⁺¹ structures can also be described as modulated structures using the same type of average structure, Crenel occupation modulation and C2/m(q₁0-q₃)00 symmetry as employed for the η′′ phase. The descriptions of these structures imply q₃ = 2q₁ = 2(1 − δ) to hold exactly. That exact relation is well compatible with the experimental evidence for the η′ phase (δ = 0.2),^[113,134] which, thereby, appears to be a lock-in phase of the incommensurate η′′ phase showing deviations from q₃ = 2q₁ = 2(1 − δ); see above. In contrast to this, the η⁸ (δ = 0.25)^[139] and η⁴⁺¹ (δ = 0.243)^[146] structures actually are not phases (although that term had been used in Ref. 146), but they are rational approximant structures to the incommensurately modulated structure of η′′ phase. It is believed that the diffraction experiments in the corresponding works were performed on η′′ phase, which, however, was interpreted in terms of the η⁸ and η⁴⁺¹ structures. Thus, these structures were probably derived in the respective works in the natural desire to find an easy, commensurate structure explaining the diffraction data. Deviations from q₃ = 2q₁ were difficult to detect in view of the relative imprecision of standard SAED techniques (as compared to PXRD) to determine lattice parameters and accurate superstructure/satellite peak positions. Indeed, slightly misfitted satellite reflection positions were already evident in the Rietveld fits made using the η⁴⁺¹ structure model on the basis of PXRD data, as shown in Ref. 146; see above. In any case, the alloys in Refs. 139 and 146 were heat treated at high temperatures so that η phase was Cu-rich before cooling. This means that the quenching performed in Ref. 139 was probably not sufficiently rapid to prevent ordering or, alternatively, ordering was induced by the electron beam. Such effects had already been discussed in Ref. 139 and might also be responsible for development of ordering leading to the SAED patterns interpreted in terms of the η⁶ structure. The latter structure cannot be regarded as an approximant to the η′′ structure, and experimental evidence has not been reported after the structure’s first encounter in Ref. 139.

It has been analyzed in detail in Ref. 18 that in the η′ structure the trigonal bipyramids formed by the ordered Cu(2) atoms together with their surrounding 5 Sn atoms (Cu(2)Sn₅) are isolated in the sense that these surrounding Sn atoms are not shared by other such units. At higher Cu contents (δ > 0.2) this is not possible. According to the structure refinement of the η′′ phase and in agreement with the structure models for η⁸ and η⁴⁺¹ (and also for η⁶, which is less related with the other structures), only ac-type edge-sharing Cu(2)Sn₅ double units (Cu(2)₂Sn₈) are developed upon increasing the Cu content starting from δ = 0.2, while a and c pairs (vertex sharing, respectively) are not formed. This implies that ac pairs are energetically more favorable than a pairs and c pairs. The geometry of a, c and ac pairs is illustrated in Fig. 17.

Fig. 17

Illustration of the geometry of the different types a, ac and c of close pairs Cu(2)–Cu(2) possible in a B8₂/B8₁-Cu_1+δSn structure. (a) Represented in an abstracted way adopting the same grid as in Fig. 16. (b-d) Clinographic view including the Sn atoms. In the experimentally known structures (see Fig. 16), however, only edge-shared ac pairs appear to occur

Ambient-temperature lattice parameters reported for Cu₆Sn₅ intermetallic from the reviewed literature has been compiled in Fig. 18. Pseudo-hexagonal lattice parameters were taken for the ordered phases. Lattice parameters a_B8 and c_B8 as determined by the author’s group^{[10,11,12,18]} reveal a linear behavior if c_B8 is plotted versus a_B8, as visible by the thicker black curve connecting the values for δ = 0.166 and δ = 0.237. The varying lattice parameters are evidently a consequence of the δ-dependent unit cell volume. The compositional range implies a volume change of 1.8%, while the effect of ordering had been estimated to be 0.1%; see above. The data imply a nearly constant axial ratio c_B8/a_B8, which is apparently quite independent of the degree of order, which is in contrast with the strong changes in similar Ni–Sn phases, showing, however, different ordering.^[149,150] Further published data seem to fit the data from the present author’s group. However, some other data deviate significantly. These include the data by Gangulee et al.^[138], shedding doubt on the general reliability of the lattice parameters of this work, which were used to propose substantial shrinkage of the lattice dimensions upon ordering.

Fig. 18

Hexagonal and pseudohexagonal lattice parameters $a_{{{\text{B}}8}}$ and $c_{{{\text{B}}8}}$ determined from Cu₆Sn₅ intermetallic (quenched η phase or ordered structures), plotted in a $c_{{{\text{B}}8}}$ vs. $a_{{{\text{B}}8}}$ fashion. The composition is represented by iso-lines of constant occupancy δ of the trigonal–bipyramidal sites (calculated via $a_{{{\text{B}}8}} , c_{{{\text{B}}8}}$ and Eq 3.7.3 using the coefficients for the η phase). Additional isolines indicate the axial ratios, where the ideal value is $\sqrt {3/2}$ ≈ 1.225; see text. Black squares mark data from the author’s group, in particular, limiting compositional values for η ^[12] (Cu_1.116Sn and Cu_1.237Sn) and values for ordered η′ ^[113] and η′′ ^[18]. Further points are data published by authors given in the legend ^{[52,75,134,138,141,144,145,151]}

A recent ambient-temperature neutron diffraction study by Aurelio et al.^[151] using Rietveld refinement on η-Cu–Sn phase quenched from 300 °C confirmed the B8₂/B8₁-type occupation of the trigonal–bipyramidal sites by Cu(2) for the first time explicitly for the disordered η phase. The occupancy of the Cu(2) site was refined to 0.22, which is in very good agreement with the value of 0.214 calculated by Eq 3.6.3 via the lattice parameters (contained in Fig. 18) and is in reasonable agreement with the Sn-rich boundary of the homogeneity range at 300 °C implied by the phase diagram in Fig. 1(b).

It is to be noted that the version of the popular ICSD database^[23] (data release 2022.2) does not yet contain an appropriate entry for the high-temperature η-Cu–Sn phase. Hence, scientists who base some of their research on superficially retrieved structure models taken from databases are in danger to use the outdated atomic structure models derived from.^[52,138]

As mentioned above, a crucial step for the determination of the crystal structure of η′ was an adequate interpretation of the diffraction pattern from a “single-crystal specimen”, which typically consists of six types of orientation domains.^[134] Later, in the case of the η′′ phase, Leineweber et al.^[12] traced back the number of 6 types of orientation domains to the ratio of the orders of the point groups of the high-temperature η phase (point group 6/mmm, order: 24) and of the low-temperature η′′ phase (point group 2/m, order 4); see Sect. 4.4. Martin et al.^[152,153] identified the domain structure of η′′ phase by EBSD analysis using advanced pattern matching methods.

First-principles calculations have been performed considering a series of model structures for the different phases of the Cu₆Sn₅ intermetallic; see Table 5. Note that a significant part of these studies involved substitution of Cu or/and Sn by further elements; nevertheless, such studies are included, as long as they provide relevant information on a binary reference structure. An early study by Ghosh and Asta^[21] considered the η′, η⁸ and η⁶ structures as well as B8₁-CuSn and B8₂-Cu₂Sn as endmembers of the B8₂/B8₁-Cu_1+δSn solid solution. A B8₂-derived CuSn₂ has also been considered. The energies of formation are plotted in Fig. 19 vs atomic fraction of Sn to reveal the stabilities of these structures relative to the elements. Unsurprisingly, B8₂-Cu₂Sn and B8₂-CuSn₂ are energetically uncompetitive, i.e., outside the range of Fig. 19, as also noted by the authors. Somewhat surprisingly, B8₁-CuSn is so stable that the energies of η′, η⁸ and η⁶ structures are located above the tie line connecting the energies (of formation) of Cu and of B8₁-CuSn, indicating their metastability with respect to Cu + B8₁-CuSn. This does not consider possible equilibria with lower-Sn content Cu–Sn phases, which, however, cannot change the picture. The authors^[21] attributed the observation of more Cu-rich phases than “CuSn” (even at temperatures below the melting point of β-Sn) to T > 0 K effects. Later data of Ramos de Debiaggi et al.^[59] basically confirmed these findings. Comparison of the fractional coordinates determined in Refs. 21 and 59 from the first-principles calculations do not show noteworthy deviations from the experimental values (η′)^[134] or from those estimated from geometric considerations (η⁸, η⁶).^[139]

Table 5 Summary of first-principles electronic structure calculations of model structures relevant for the Cu₆Sn₅ intermetallic

Fig. 19

Energies of formation (with respect to A1-Cu + β-Sn) of Cu₆Sn₅ related model structures (η′, η⁸, η⁶ and hypothetical B8₁-CuSn) vs. atomic fraction of Sn according to first-principles calculations by Ghosh and Asta ^[21]. The energy values for η′, η⁸, η⁶ are located above the tie line connecting Cu and B8₁-CuSn, indicating the metastable character of their static structures at T = 0 K

Due to the importance of the hexagonal η phase, there have also been attempts to model aspects of this hexagonal phase via first-principles calculations. Apart from the B8₁-CuSn and B8₂-Cu₂Sn^[21,59] this has also been attempted for the Cu₆Sn₅/Cu_1.2Sn composition. First-principles calculations typically require consideration of well-ordered model structures of correct composition which are believed to be somehow “representative” for the disordered structure. In order to represent η phase, Jiang^[164] considered some not fully specified supercell of the B8₁ structure with missing Sn atoms accounting for the Cu₆Sn₅ composition, in deviation from the above-described structural knowledge that was also available at that time. Schwingenschlögl et al.^[157] were the first to use models based on a simple hexagonal supercell of the type a_rrs = ra_B8, b_rrs = rb_B8, a_rrs = sc_B8 with r = 1 and s = 5. Accordingly, the model will be referred to, in short, as 115 model. However, this type of supercell does not imply a unique distribution of the Cu(2) over trigonal–bipyramidal sites. In fact, there are 5 distinguishable distributions shown in Fig. 20, labeled 115(a) to 115(e). Although only indirectly evident from the description,^[157] the model 115(e) appears to have been used for the calculations, which is also supported by the use of exactly this model structure in works by authors from the same research group,^[160,172] and by apparently independent groups.^{[161,163,165,170]} In another work, Zhou et al.^[162] referred to Ref. 157 for their 115-type structure. Drawings in Ref. 162, however, appear to depict a 115(a) structure (see Fig. 20a), implying that the first principles calculations of this work are based on this structure. Only Yi et al.^[175] have explicitly considered all possibilities from 115(a) to 115(e), and found that the 115(d) model structure has the lowest energy.

Fig. 20

Cu(2) distribution in the hexagonal model structures labeled 115(a)-(e) employed for η-Cu₆Sn₅ in a series of works, illustrated using a rectangular grid similar to Fig. 16. The colored lines illustrate the types a, ac and c of close pairs Cu(2)–Cu(2) illustrated in more detail in Fig. 17. Note that (a)-(e) do not agree with the sequence (1)-(5) in Ref. 175. The least favorable energy obtained by first-principles calculations was obtained for the 115(b) structure ^[175], which suggests a particularly unfavorable character of the c-type Cu(2)–Cu(2) pairs contained only in this structure

Several works using first-principles calculations have considered both results from the η′ phase and some model structures for the η phase with Cu₆Sn₅ composition. The corresponding energy differences E(η) – E(η′) are listed in Table 5, and may be compared with experimental enthalpy differences with a maximum of 4.5 meV/atom^{[157,161,162,165]} (also lower values have been assessed in the literature; see^[21] for details). Evidently, the obtained absolute energy differences in Table 5 are far too high. This is most evident for Jiang et al.^[164], which is, however, attributable to the highly unrealistic character of the of the Sn-vacancy containing η model structure. The 115 structure variants 115(a)-115(e) give values much closer, but still are by a magnitude larger than the mentioned 4.5 meV/atom from experiments.^{[157,161,162,165]} A single value reported by Shao et al.^[161] is, in contrast to the other works, even unrealistically negative, without the authors having commented on this point.

As illustrated in Fig. 20 by means of the colored lines, adopting the same code as in Fig. 17, each Cu(2) atom of every 115 structure is involved in a-type Cu(2)–Cu(2) pairs. There are, in fact, six of such a-type pairs for a given Cu(2) of this kind within the plane perpendicular to the c_B8 direction. This type of T(2)–T(2) pairs does not occur in any reported ordered B8₂/B8₁ structure having low δ values; see e.g.,.^[140] Such a-type pairs are automatically created for every supercell with m = 1, i.e., a_B8 and b_B8 are retained as translation vectors upon superstructure construction. In the opinion of the present author this extreme type of order is unlikely to exist as short-range order in the η phase. Hence, at least the energetic and elastic properties of the 115 structure models unlikely represent the true properties of η, while predictions concerning electronic bonding properties might be better.

While the structures 115(a)-115(e) are similar with respect to occurrence of the a-type Cu(2)–Cu(2) pairs, they differ with respect to occurrence of the ac- (115(a)) and c-types (115(b)) of pairs. Notably, the energies calculated for 115(a)-115(e)^[175] yield the highest energy for 115(b) and thus imply an unfavorable character of c-type Cu(2)–Cu(2) pairs. Note, however, that ac pairs occur for η′′ and their approximants η⁴⁺¹ and η⁸ (see above) and both c- and a-type pairs do occur for higher δ values for ordered B8₂/B8₁-Ni_1+δSn phases (including “Ni₃Sn₂”).^[149,177] More detailed analysis of the energies of differently ordered Cu_1+δSn model structures might contribute to a better understanding of the configurational energetics of the Cu₆Sn₅ related intermetallics.

3.8 β-Sn Solid Solution

β-Sn has an A5 structure with I4₁/amd space group symmetry^[178,179] and Pearson symbol tI4. β-Sn solid solution has up to about 0.1 at.% equilibrium solubility for Cu; see Fig. 1(a) but also.^[180] Westgren and Phragmén reported no change of lattice parameters of β-Sn upon equilibrium saturation by Cu.^[52] Kane et al.^[181] reported that Sn-4at.%Cu liquid quenched at –190 °C yields supersaturated β-Sn solid solution, however, without reporting crystallographic details allowing for conclusions about the fashion by which type of point defects Cu is inserted into the A5 structure of β-Sn.

In view of this lack of knowledge, it is worthy to mention the high and highly anisotropic impurity diffusivity of Cu in solid β-Sn, which was attributed to an interstitial character of this diffusivity.^[182] This implies that at least a part of the Cu atoms occupies interstitial positions in β-Sn. Direct experimental evidence for such interstitial impurity atoms in β-Sn, appears, however, to be lacking. Note that more evidence exists for impurity diffusion in lead (A1 structure but higher homologue of Sn in the periodic table of the elements) and some other metals, see e.g.,.^[183,184]

Much more recently, Liu et al.^[185] presented results of first-principles calculations on interstitial and substitutional Cu, Ag, Au, Zn and Cd atoms in β-Sn. In the same work molecular dynamics simulations on diffusion were carried out. In particular the interstitial incorporation of Cu atoms within channels of the β-Sn structure running along the tetragonal [001] direction is predicted, as well as an interstitial character of the diffusion.

3.9 Metastable Phases Not Yet Discussed

3.9.1 hcp-Based α′ Phase

The α′ phase with A3 structure was first described by Deruyttere^[62] to develop upon some kind of bainitic decomposition of β/γ phase in a Cu-16.5at.% Sn alloy at 300 °C together with the evidently more Sn-rich δ phase. Therefore, the α′ phase must have a lower Sn content than corresponding to the alloy composition. PXRD data of α′ revealed lattice parameters of a_A3 = 2.606 Å, c_A3 = 4.272 Å. These values are much smaller than those implied by diffraction data of the A3-based Cu₃Sn intermetallic (ε/ε′) occurring very close to 25 at.% Sn; see Sect. 3.6. The axial ratio of α′ is with ${c}_{\mathrm{A}3}/{a}_{\mathrm{A}3}=1.639$ much closer and slightly larger than the ideal 1.633 value, than it is the case for Cu₃Sn. Deruyttere had estimated the composition of the A3-type phase to have 8 at.% Sn by some kind of not fully specified comparison of the interatomic distances with those in α-Cu–Sn solid solution. Note that 8 at.% Sn is still well within the homogeneity range of the α phase at somewhat elevated temperatures above 300 °C; see Fig. 1(a). Later, De Bondt and Deruyttere^[186] investigated the same types of alloys by TEM, in particular, by SAED. It was found that the α′ was heavily faulted and does not correspond to ideal A3 structure, as evidenced by systematic shifts of certain Bragg reflections. The faulting of α′ was attributed to the deformation processes required by the particle’s growth being constrained by the harder δ particles forming prior or during the bainitic transformation.

Saunders and Miodownik^[85,187,188] generated α′ phase with A3 structure by sputter deposition of Cu-12 at.% Sn thin layers onto substrates having temperatures below 200 °C, together with A1 α-solid solution, as characterized by grazing incidence PXRD. The reported^[85] lattice parameters of $a_{{{\text{A}}3}} = 2.625$ Å and $c_{{{\text{A}}3}} = 4.26$ Å and thus $c_{{{\text{A}}3}} /a_{{{\text{A}}3}} = 1.623$ approximately agree with.^[62,186] Further α′ phase was obtained by electrodeposition by Cavallotti et al.^[189], contained in Cu–Sn layers with 12–18 at.% Sn. With increasing Sn content, the axial ratio decreased from 1.633 to 1.622 (no further detailed data were given).

Juskenas et al.^[190] reported A3 lattice parameters alongside with those from A1 solid solution determined from electrodeposited layers having total compositions of 4.6–16.3 at.% Sn. The PXRD patterns as shown in Ref. 190 appear to evolve continuously with increasing Sn content, being A1-like at low Sn content, although A3 lattice parameters were determined alongside those of A1. Already from about 11.3 at.% a feature interpreted as 100_A3 reflection of the A3 phase was visible in the patterns. However, as pointed out by Wilkens,^[191] the presence of such a feature needs not be indicative of an actual Bragg peak, but may already originate from continuous streaking of intensity in reciprocal space due to layer faulting in the A1 structure (stacking faulting, twinning). Thereby, the reflection-like feature becomes visible as a consequence of the reciprocal space integration typical for PXRD techniques.^[192] With alloy compositions above 12/14 at.% Sn, however, peaks corresponding to 101_A3 reflections become clearly visible while the characteristic A1 reflections disappear. Note that a series of prominent reflections are attributable to both the A1 and A3 structures, including the very prominent reflection 111_A1/002_A3. Such peak overlap severely impedes the reliable determination of independent sets of lattice parameters for separate A1 and A3 phases from the same specimen as seemingly attempted in^[190] even if both structures would be present simultaneously, which is, however, highly doubtful.

The lattice parameters of α′ phase Cu–Sn are analyzed together with data from ε/ε′-Cu₃Sn in Sect. 4.1.

3.9.2 ω Phase

An ω phase has first been discovered in Ti-base alloys. It forms from the A2 structure, usually in small amounts, as an alternative to formation of the A3-type low-temperature phase.^[193] Its formation is driven by a dynamic instability associated with mutual displacements of atomic chains along $\langle111\rangle_{{{\text{A}}2}}$. Within the stability range of the A2-related phase, the ω phase is preceded by presence of low-energy phonons. These can lead to characteristic diffuse scattering^[193] which occurs together with effects due to the low elastic modulus ½(C₁₁–C₁₂). The latter is associated with the Bain/Burgers transformation path towards martensite; see Sect. 3.9.3. It was this type of mutual displacements of atomic chains along $\langle111\rangle_{{{\text{A}}2}}$ which has already been discussed in the context of the ζ-Cu₁₀Sn₃ and Cu₆Sn₅ (see Sects. 3.5 and 3.7). In a high-temperature SAED study on β phase in Cu-14.8 at.% Sn alloy, Nishiyama et al.^[57] encountered pronounced diffuse scattering attributed to atomic vibration associated with displacements of $\langle111\rangle_{{{\text{A}}2/{\text{D}}0_{3} }}$.

SAED evidence for actual ω phase within Cu-16.5 at.%Sn alloy held in the γ region and water quenched was presented by Vandermeulen and Deruyttere.^[83] The corresponding diffraction features were observed along with other decomposition products (α′ and δ′). The basis vectors of the ω phase are given by

$$\begin{aligned} {\mathbf{a}}_{{\upomega}} =& {\mathbf{a}}_{{{\text{A}}2}} - {\mathbf{b}}_{{{\text{A}}2}} = {\mathbf{a}}_{{{\text{B}}8}} \hfill \\ {\mathbf{b}}_{{\upomega}} =& {\mathbf{b}}_{{{\text{A}}2}} - {\mathbf{c}}_{{{\text{A}}2}} = {\mathbf{b}}_{{{\text{B}}8}} \hfill \\ {\mathbf{c}}_{{\upomega}} =& \frac{1}{2}\left( {{\mathbf{a}}_{{{\text{A}}2}} + {\mathbf{b}}_{{{\text{A}}2}} + {\mathbf{c}}_{{{\text{A}}2}} } \right) = \frac{1}{2}{\mathbf{c}}_{{{\text{B}}8}} . \hfill \\ \end{aligned}$$

(3.9.2.1)

The ω structure can occur in 4 different orientation variants with respect to the (possibly ordered) A2 matrix. The structure has P6/mmm symmetry and the Strukturbericht symbol can be given as C32 in accordance with the AlB₂-type structure (Pearson symbol hP3). It was noted in^[83] that the ω phase particles will diffract coherently with the A2 matrix, and the mutual arrangement of these particles will cause shifts of certain reflections in a way generally known for ω phase.^[193] It was concluded from specimens quenched with different cooling rates that the ω phase precedes the formation of the δ (δ′) phase. Certain reflections of the ω and the δ phase coincide in position in reciprocal space, which requires special attention when interpreting SAED patterns. In addition, due to the coherent diffraction with the β/γ matrix and due to misfit strains, even the reflections specific to ω, do not reflect the true (strain-free) lattice parameters of the ω. Approximate values can be obtained from the lattice parameters of the A2/D0₃ matrix considering the lattice correspondence in Eq 3.9.2.1, i.e., $a_{{\omega}} = \sqrt 2 a_{{{\text{A}}2}}$ and $c_{{\omega}} = \sqrt 3 /2a_{{{\text{A}}2}}$.

The consequences of the ordering present in the parent D0₃ type γ matrix upon transformation to ω have been considered by Zakharova and Duchenko^[194]13: A quadrupling of the basis vector c_ω is expected due to order inherited from the parent structure, leading to a structure model as shown in Fig. 21(c). The authors in^[194] derived $a_{4\upomega} = a_{\upomega} = 4.21$ Å and $c_{4\upomega} = 4c_{{\upomega}} = 11.11$ Å based on SCXRD and SAED on Cu-15.5 at.% Sn. However, as also pointed out in this work, the reflections attributed to a quadrupling of the ${\mathbf{c}}_{{}}$ axis, coincide with the positions of the reflections due to the δ phase. The derivation of an “s phase” and an “L phase” (definitely related with ω) to occur in quenched and aged Cu-15at%Sn^[101] has to be handled with care for similar reasons.

Fig. 21

Structure of ω phase for a model composition at 25 at.% Sn with selected sets of fractional coordinates indicated. Pie chart presentations of atoms reflect the fractional occupation by the different types of atoms with (a,b) disordered structure and (c) ordered structure according to ^[194]: (a) Projected along-c_ω with dotted line presenting the section plane used in (b) and (c)

3.9.3 Martensites at < 16 at.% Sn

This section deals with the products obtained by quenching of the high-temperature phase β/γ to what is labeled in Fig. 5 as Mart.. The likely martensitic transformation towards ε′ as well as the unlikely martensitic transformations towards δ′ and ζ′, all at > 16. at.% Sn contents, have already been described above. The complex and perhaps confusing literature on these martensites occurring for < 16 at.% Sn must be read against the following background:

• Crystallographic studies of martensites (formed from β brass-type phases or other austenites¹⁴) have typically been performed by very specialized groups dealing with very special challenges: Long-range stacking order including its faulting as well as the effect of substitutional ordering, all superposed by a high level of irregularity in the atomic structure. A specific language has been apparently developed ad hoc to describe these structures, with notions which got fixed often prior to characterization of the atomic structure. Space groups and fractional coordinates of crystallographically independent atoms are less-frequently used. It should be noted, in particular, that in martensite literature, regardless of the binary brass-type system, the disordered A2 austenite is referred to as β, the D0₃ type ordered austenite as β₁ (corresponding to the γ phase) and B2 ordered austenite as β₂. The indices are frequently—but not always—retained when labeling the martensite to indicate its ordering inherited from the austenite, which may have formed during quenching.

• Many insights were obtained by in-depth studies on certain alloy systems and then transferred to other systems by analogy but with less experimental evidence. For example, much of what appears to apply to the Cu–Sn system was first (and often in more detail) elaborated for the Cu–Al system.

Only after the bulk of the crystal structure studies on Cu-based martensites had been conducted in the 1960-1980s, Otsuka et al. published a systematic analysis of typical polytypic structures with substitutional order taking into account conventional space group symmetry,^[196] suggesting a revision of the description of a series of polytypes. Cortie and Mavrocordatos^[197] referred to the confusion that has arisen in literature by incorrect translations and differing naming conventions.

Although PXRD has been used extensively in the early days of the investigations, the powers of TEM-based techniques, including SAED have been increasingly exploited^[198,199] to reveal the characteristics of complicated crystal structures embedded in complex microstructures. However, as mentioned elsewhere in the present work, under routine conditions SAED is relatively insensitive to small distortions of the unit cell and often does not provide reliable lattice parameters.

Already Isaichev and Salli^[65] have found that the martensite start and finish temperatures are composition dependent and that low and high Sn contents appear to develop different types of martensites, as indicated in Fig. 5 based on later data. Systematic, mainly SAED-based conclusions on the composition dependent structural behavior (see Table 6) were provided in a conference paper by Warlimont and Härter,^[71] tracing basically back to results from a diploma thesis.^[200] The structural behavior was reviewed later,^{[68,199,201,202]} taking also into account newer insight. It appears that all experimentally observed martensite structures are ordered close-packed structures differing by their stacking sequence. The ordering is evidently inherited from an D0₃ structure of the austenite, which was either present at the annealing temperature or which has developed after having crossed the T₀ line during quenching, but above the martensite start temperature M_S; see Fig. 5. Disordered martensites have not been reported in the Cu–Sn system, while they have been reported to occur for very low Al contents in the Cu–Al system.^[203] Because of the Bain or Burgers lattice correspondences (towards D0₂₂ or D0_a, Fig. 22(a)), the close-packed layers are of the type as shown in Fig. 22(b), and show the same ordering pattern as for the D0_a structure of ε′-Cu₃Sn; see Fig. 12(b). However, due to the lower Sn content of the presently considered martensites the Sn site will have to be partially occupied by Cu, and there might be further antisite disorder. The stacking sequence can also be modified on a local “crystal structure level” by introduction of stacking faults due to slip on close-packed planes, which is one of the acting mechanisms of lattice invariant shear (LIS; the other mechanism is twinning). LIS occurs to ensure transformation in accordance with an invariant plane strain within the phenomenological theory of martensite crystallography (PTMC).^[204]

Table 6 Compositional ranges for occurrence of different types of martensites

Fig. 22

Crystal structures of the Cu–Sn martensites at < 16 at.% Sn (a) Path of the phase transition within the phenomenological theory of martensite crystallography starting from the D0₃ structure (β₁; neglecting the partial occupation of the Sn sites by Cu): The Bain or Burgers transformations/stretches, leading to D0₂₂ or D0_a, is followed by a lattice invariant shear (LIS), leading in the course of slip to the long-range polytypes, whereas D0_a leaves the crystal structure unchanged on a local atomic level; (b) top: one close-packed layer with ordering inherited from D0₃ austenite, and bottom: Projected relative positions of the Sn atoms in the layers A/A′, B/B′ and C/C′

The type of martensite with the lowest Sn-content has been labeled frequently as β′, e.g., in,^[65,71] but in view of the ordered character of the corresponding martensites it could actually be called β₁′. Warlimont and Härter^[71] seems to be unspecific on the order for the low-Sn compositional range, but diffraction patterns shown in Refs. 200 and 205 e.g., for 13.7 at.% Sn,^[200] reveal the ordered character. The reported polytype has 11 layers until the layer sequence can be regarded as “closed” along the stacking direction. Given the usual ABC stacking notation (see also^[199] for some details) the sequence reads

$$\left| {{\text{ABC}}/{\text{BCA}}/{\text{CAB}}/{\text{AB}}/} \right|.$$

(3.9.3.1)

Thereby the “|” symbols enclose the periodic unit of the closed stacking sequence (i.e., the next unit again starts with A), and the “/” symbols denote the positions of (intrinsic) stacking faults, each of which can be conceived to be produced by slip via a Shockley partial dislocation. This stacking sequence can alternatively be described by the Zhdanov symbol

$$\left| {2\underline {1} 2\underline {1} 2\underline {1} 1\underline {1} } \right|$$

(3.9.3.2)

with the numbers denoting the stacking direction of a given layer with respect to a previous one (positive or negative). In agreement with a systematic compilation,^[206] this polytype has $P\overline{3}m1$ symmetry in the absence of ordering and can be described by a conventional unit cell according to

$$\begin{aligned} {\mathbf{a}}_{{\text{P}}} =& {\mathbf{a}}_{{{\text{A}}3}} \hfill \\ {\mathbf{b}}_{{\text{P}}} =& {\mathbf{b}}_{{{\text{A}}3}} \hfill \\ {\mathbf{c}}_{{\text{P}}} =& \frac{n}{2}{\mathbf{c}}_{{{\text{A}}3}} \hfill \\ \end{aligned}$$

(3.9.3.3)

where P = 11H with a 11H being Ramsdell-like symbol adopting the philosophy of,^[207] and where n = 11.

Regarding the arrangement of the Sn/Al-enriched sites in the close-packed layers, Warlimont and Wilkens have proposed two different ordering schemes for β₁′-Cu–Al^[205,208] as well as,^[209] which, however, both contain next-neighbor contacts Al–Al and can thus be regarded as unlikely. Close neighbors are prevented when alternately unprimed and primed layers according to Fig. 22(b) are stacked upon each other.^[207,210] This implies a stacking sequence of^[207]15

$$\left| {{\text{AB}}^{\prime}{\text{C}}/{\text{B}}^{\prime}{\text{CA}}^{\prime}/{\text{CA}}^{\prime}{\text{B}}/{\text{A}}^{\prime}{\text{B}}/{\text{A}}^{\prime}{\text{BC}}^{\prime}/{\text{BC}}^{\prime}{\text{A}}/{\text{C}}^{\prime}{\text{AB}}^{\prime}/{\text{AB}}^{\prime}/} \right|.$$

(3.9.3.4)

In view of the alternate sequence of the primed and unprimed layers, and the uneven number of layers in the closed period unit of the disordered stacking sequence, there are now 22 layers per periodic unit length. The unit cell for this structure can be described with

$$\begin{gathered} {\mathbf{a}}_{{{\text{P}}^{\prime }}} = - {\mathbf{a}}_{{{\text{A}}3}} + {\mathbf{b}}_{{{\text{A}}3}} \hfill \\ {\mathbf{b}}_{{{\text{P}}^{\prime }}} = \left( {{\mathbf{a}}_{{{\text{A}}3}} + {\mathbf{b}}_{{{\text{A}}3}} } \right) \hfill \\ {\mathbf{c}}_{{{\text{P}}^{\prime }}} = \frac{{n^{\prime }}}{2}{\mathbf{c}}_{{{\text{A}}3}}. \hfill \\ \end{gathered}$$

(3.9.3.5)

In the present case one may refer to this model as 11H′ with n′ = 22. The choice of axes has been similarly used in the majority of martensite literature, where such an pseudoorthorhombic unit cell has been adopted (^[207] may be noted as an exception). As it concerns the basal layer, the axes in Eq 3.9.3.5 corresponds to the Pnmm setting in Eq 3.6.4). The present author has shown, also using the software FINDSYM,^[211] that the symmetry of the 11H′ is monoclinic, agreeing with C2/m space group symmetry after transformation into a conventional unit cell.

In contrast to Ref. 71, Nishiyama et al.^[212] concluded, based on TEM/SAED, that an unusual 4H type polytype for “banded” martensite occurs in an Cu-14.8 at.% Sn alloy quenched from 700 °C to 0 °C. However, the diffraction patterns shown did not contain the stacking direction containing the decisive reflections indicative for the stacking sequence. Indeed, a reinvestigation by some authors^[213] identified a polytypic structure which was earlier also found by Nishyama and Kajiwara for β₁′-Cu–Al^[210] and briefly reported for Cu–Sn.^[214] This likely invalidated the results from.^[212] The model implies a stacking sequence being closed after 9 layers and is most frequently referred to as 9R (3R in^[199,207]). Stacking sequence and Zhadanov symbols correspond to:

$$\begin{aligned}&\left| {{\text{ABC}}/{\text{BCA}}/{\text{CAB}}/} \right| \\ &\left| {2\underline {1} 2\underline {1} 2\underline{1} } \right|, \end{aligned}$$

(3.9.3.6)

implying in view of Eq 3.9.3.3 a value of n = 9. This structure is also the known crystal structure of stable Sm while that of the 11H polytype is unknown as a stable structure. Ordering according to Fig. 22(b) implies due to the alternate occurrence of primes a doubling of the unit cell dimension in stacking direction:

$$\left| {{\text{AB}}^{\prime}{\text{C}}/{\text{B}}^{\prime}{\text{CA}}^{\prime}/{\text{CA}}^{\prime}{\text{B}}/{\text{A}}^{\prime}{\text{BC}}^{\prime}/{\text{BC}}^{\prime}{\text{A}}/{\text{C}}^{\prime}{\text{AB}}^{\prime}/} \right|.$$

(3.9.3.7)

We will refer to this model as 9R′ (frequently 18R can be found in the literature), and n′ = 18 for use in Eq 3.9.3.5. A smaller centered monoclinic (with angle considerably differing from 90°) can be constructed from this structure model, which has space group symmetry compatible with C2/m.

In the context of β₁′-Cu–Al, there has been some debate about the relevance of experimental evidence supporting the more complicated 11H/11H′ structure model as compared to the simpler (and for β₁′-Cu–Al, older) 9R/9R′ structure model.^{[207,209,215,216,217,218]} The general arguments also apply to β′/β₁′-Cu–Sn. To understand the discussion, two points should be mentioned:

• Although the unit cells of the 11H/11H′ and 9R/9R′ structure models may not appear compatible at first glance, the diffraction patterns (e.g., SAED or PXRD) are quite similar.

• As can be seen from SAED and diffraction line broadening in PXRD, the structure is not strictly periodic, i.e., both ideal structure models are not perfectly realized due to irregularities in the stacking sequence. This leads to characteristic line broadening/streaking along the stacking direction and to some systematic shifting of reflections away from the ideal positions implied by the structure models.

In fact, both structure models imply some kind of regular distribution of stacking faults with respect to an underlying A1/D0₂₂ structure; see Fig. 22(a). In the 11H/11H′ model, there is a stacking fault density¹⁶ of 4/11 = 0.364 of the close-packed planes, whereas the 9R/9R′ model implies a density of 1/3 = 0.333. It was argued in Ref. 205 that according to considerations using the PTMC, the stacking fault density should be larger than 1/3, e.g., a value of 0.355 was predicted for β′/β₁′-Cu–Al.^[203] However, the question remains, whether the excess stacking faults are that regularly distributed within the real stacking sequence to justify the introduction of a more complicated structure model (11H/11H′) distinct from simpler models (9R/9R′).

It should be noted that there are different views on the stacking-faulted structures.^[199,201] On the one hand, one can claim that the actual crystal structure of the β′/β₁′ martensite is the D0₂₂ structure provided that the actual transformation proceeds via the Bain path (see Fig. 22(a); or A1 structure if the structure is disordered). The containing stacking faults are then a consequence of the LIS and regarded as defects within the D0₂₂ structure. On the other hand, the PTMC considerations can also be performed assuming a direct transformation into, let’s say, the 9R/9R′ model, using a different lattice correspondence including shuffling of the atoms. In that case the stacking faults are taken as part of the structure model, and much less additional LIS is required to achieve an invariant plane strain. In fact, it has been speculated that the 9R/9R′ model is a distinct structure (phase?) “in its own right”, possibly exhibiting particular stability due to electronic reasons.^[207] As it concerns stoichiometric Cu₃Al, however, electronic structure calculations do not imply that this is the case^[219]: The 9R/9R′ polytype shows intermediate stability as compared to the energetically most favorable D0_a structure (only hexagonal stacking) and the least favorable D0₂₂ structure (only cubic stacking). Estimates for T > 0 K do not change the energetic hierarchy, which is, however, expected to change for lower Al content. However, this does not necessarily imply a preference of some complicated polytypes as compared to the simple A1 or A3. Indeed, Kajiwara^[220,221] plastically deformed Cu–Al martensite with 9R′ polytypic structure yielding A1-type material as shown by PXRD, rendering the cubic stacking sequence more stable than the 9R′ polytype. However, the same author also found more complicated polytypes with long stacking sequences to develop by SAED.^[222]

On to the Sn-rich side of the considered composition range (see Table 6), the martensites referred to as γ₁′ exhibit the D0_a structure, which is also found for ε′-Cu₃Sn; see Sect. 3.6. This structure can be regarded as a 2H polytype (A3, stacking sequence $\left| {{\text{AB}}} \right|$) with ordering leading to that D0_a superstructure (2H′, stacking sequence $\left| {{\text{AB}}} \right|$). It is compatible with Eq 3.9.3.3 and 3.9.3.5 with P = 2H as well as n = n′ = 2, and has Pnmm symmetry for this choice of axes; compare Eq 3.6.4. This structure was first proposed by Isaichev^[66] based on SCXRD on multi-domain material formed from γ (β₁) after quenching from 700 °C, drawing an analogy to similar work on Cu-rich Cu₃Al phase.^[223] This structure identification was confirmed in later works by PXRD^[224] and TEM/SAED techniques.^[71,214]

The β₁′′ martensite found at intermediate compositions (see Table 6), appears to be a composite consisting of the crystal structures contained in β₁′ and γ₁′.^[71] Thereby, it appears (also considering findings from Cu–Al and ternary martensites) that the β₁′ fraction is more of the 9R′ than of the 11H′ type,^{[199,216,225]} suggesting that in β₁′′ martensite the stacking fault density expected to be present in excess to a density of 1/3 (9R′ polytype) is not realized in the form of a largely homogeneous 11H′ polytype (9R′ + 2H′), but in terms of larger 2H′ regions.

It should also be noted that the occurrence of the different types of martensites is not only a matter of composition, but also on the state of stress, which can also be inhomogeneous in the course of a martensitic transformation.^[226]

There seems to be a lack of composition-dependent, accurate PXRD-based lattice parameters of Cu–Sn martensites. Lattice parameter values were apparently only reported for γ₁′: For 15.5 at.% Sn, Isaichev^[66] derived a_2H′ = 4.56 Å, b_2H′ = 5.37 Å, c_2H′ = 4.32 Å (corrected!) from SCXRD from a multidomain specimen. For 15.0 at.% Sn, Soejima^[224] obtained a_2H′ = 4.558 Å, b_2H′ = 5.402 Å, c_2H′ = 4.358 Å from evaluating a PXRD pattern, whereas corresponding patterns from lower Sn contents were not evaluated quantitatively. For 15.1 at.% Sn, Härter^[200] showed PXRD-based reflection positions which yield a_2H′ = 4.525 Å, b_2H′ = 5.379 Å, c_2H′ = 4.321 Å. The orthorhombic distortion implied by these sets of lattice parameters in the language of^[104,105] (see Sect. 3.6) is given by $2b_{Pmnm} /a_{Pmnm} = 2a_{{2{\text{H}}}} /b_{{2{\text{H}}}}$ values which are 2–3% smaller than $\sqrt 3$. As argued in Refs. 199 and 201, the same direction of distortion is expected from the differences in the atomic sizes of Cu and Sn. A figure shown in^[71] shows that this distortion seems to increase with increasing Sn content over the existence range of the Cu–Sn martensites as listed in Table 6. However, the lattice parameter data underlying this evolution have seemingly not been published separately. In this context, it has to be mentioned that in a review, Pandey et al.^[202] have calculated lattice parameters using the various lattice correspondences of the type cited above using the lattice parameters from Soejima,^[224] which pertain to the Sn-rich γ₁′ with 2H′ structure, thus ignoring the likely considerable composition dependence of the lattice parameters. While such lattice parameters may be well suited to simulate SAED patterns, the corresponding values are likely poor starting values for, e.g., evaluation of PXRD patterns.

Remarkably, for the strongly non-stoichiometric compositions around 15 at.% Sn, the mentioned orthorhombic distortion is significantly larger than the distortions (in the same direction) encountered for ε/ε′-Cu₃Sn existing around 25 at.%; compare Sect. 3.6. A reason for this is not evident, although it might be related to the quite different axial ratios c_A3/a_A3, which are analyzed in more detail in Sect. 4.1.

In the overall context one may note the publication by Dey and Quader.^[227] The authors performed PXRD analysis on Cu-15.1 at.% Sn alloys quenched from 620 °C (referred to as β′) and reported a tetragonal unit cell. No suitable structure model has been presented, and it appears that the strong reflections may be related to the above-mentioned structure models.

3.9.4 A_f-Cu–Sn

Kane et al.^[181] studied Cu–Sn alloys, which were splat-quenched on a Cu substrate at −190 °C. In case of 65–90 at.% Sn, according to PXRD investigations at the quenching temperature, the alloys contained a hexagonal primitive A_f structure (referred to as γ). This crystal structure has one atom at the origin of the hexagonal unit cell (Pearson symbol, hP1; space group P6/mmm), and a structure which had first been reported for HgSn_6-10^[228] .¹⁷ In case of the Cu-65 at.% Sn alloy, the authors^[181] reported lattice parameters $a_{{{\text{A}}_{{\text{f}}} }} = 3.188$ Å, $c_{{{\text{A}}_{{\text{f}}} }} = 2.976$ Å and coexistence with “CuSn”, being probably Cu₆Sn₅ intermetallic of unspecified degree of order and lattice parameters. For 80 and 90 at.% Sn, the A_f phase (of unspecified lattice parameters) coexisted with supersaturated Sn (with unspecified lattice parameters), which was claimed to contain at least up to 4 at. % Cu under the quenching conditions; see also Sect. 3.7. This implies in the absence of coring, a composition range of the A_f phase within 65 and 80 at.% Sn. Upon heating to ambient temperature, the A_f phase is reported to decompose gradually to “CuSn” + β-Sn. Although the authors have labeled the A_f phase as metastable, they did not exclude that this phase might be an equilibrium phase, e.g., at the formation temperature. In fact, the authors restricted the notion metastable to temperatures at which atomic mobility is sufficient to allow for diffusive phase transformations.

3.9.5 Other Structures Considered in the Literature

Two publications have reported first-principles calculations on model structures different from those discussed in the previous sections. The considered structures and the types of results elaborated have been compiled in Table 7.

Table 7 Summary of electronic structure calculations on further Cu–Sn crystal structures discussed in Sect. 3.10

Ramos de Debiaggi et. al.^[59] performed first-principles calculations on model structures from the Cu–Sn and Cu–In systems. Experimentally determined structure models from both systems have served as model structures for both systems. Hence, a series of structures known for Cu–In were considered as Cu–Sn model structures. Lachmann et al.^[229] considered three different related CuSn₂ structures in the context of thermodynamic modeling of (Nb,Cu)Sn₂ ternary solid solutions that only exist on the Nb-rich side.

In both cases the energy of formation for the considered model structures are positive, and obviously more positive than that of model structure corresponding to structures of stable Cu–Sn phases.

4 Discussion

4.1 General Systematics of the Crystal Structures

In 1926 Hume-Rothery^[16] reported detailed constitution and crystal structure investigations of the Cu–Zn, Cu–Al and Cu–Sn systems, as well as, to some extent, of similar systems of the higher homologues Ag, Au, and Cd. In acknowledgement of still incomplete experimental evidence on the crystal structures, he proposed that the intermediate A2-type phases (or phases with A2-based superstructures) do not form at a characteristic atomic fraction but at a characteristic electron-to-atom ratio,¹⁸e/a, of 3/2. In the same year, Westgren and Phragmen,^[17] generalized this idea by demonstrating the structural analogies between a series of phases in the Cu–Zn, Cu–Al and Cu–Sn systems occurring at specific values of e/a. This included the analogy between the α solid solution, the β/γ phase, the δ phase and ε phases of the Cu–Sn system with structurally similar (but not necessarily exactly isostructural) phases in the prototypical Cu–Zn system: α brass, β and β′ brass, and γ brass. This was the basis for what is now known as the “valence electron concentration” rules for formation of certain types of Hume-Rothery phases^[230,231]. Table 8 summarizes the most important Cu–Sn phases and their e/a values.^[16] In this table the β′₁ martensite has been included together with the α solid solution phase, adopting the view of β′₁ as stacking-faulted D0₂₂ structure, which is an A1-based superstructure; see Sect. 3.9.3. In fact, the upper compositional limit of 14 at.% Sn of β′₁ (see Table 6) corresponds to an e/a value found as upper limit of stability of the α-brass phases,^[230] justifying this assignment. In Table 8, the crystal structures occurring for the Cu₁₀Sn₃ and Cu₆Sn₅ intermetallics are assigned to a group of electron-rich phases being vacancy-containing A2 variants in the broad sense of Lenz and Schubert^[91] and Schubert.^[232,233] In these works, the authors proposed that the specific ordered incorporation of vacancies in an A2 structure, which leads to the γ-brass structure (→ δ-Cu₄₁Sn₁₁ in the Cu–Sn system), corresponds to a mechanism which is also responsible for formation of other structures which can be conceived to result from introduction of vacancies into an A2-type structure. Such structures appear to develop at even higher e/a ratios than it is the case for γ-brass structures. Having such a principle in mind, the high e/a values of up to 1.84 calculated for Sn-rich γ-high temperature phase having the D0₃ superstructure of A2 (see Table 8), going beyond the e/a range of the typical β phase, supports the idea of a high vacancy content in this phase, as pointed out in Sect. 3.3.

Table 8 Interpretation of Cu–Sn phases as brass-like or Hume-Rothery phases

Both the α′ (see Sect. 3.9.1), the ordered γ′₁ 2H′ martensite (see Sect. 3.9.3) and the ε/ε′-Cu₃Sn phases are derived from an A3 structure. In general, as argued by Saunders and Miodownik,^[188] the preference of such A3 structures as compared to the A1 structure of the terminal solid solution is a consequence of a composition- or e/a-dependent stacking fault energy, which eventually becomes negative at sufficiently large Sn contents. Furthermore, it was reported in Ref. 188 that the metastable α′ phase (the same holds for γ′₁ martensite) with its c_A3/a_A3 ≈ 1.633 has stable analogues at similar e/a in systems Cu–Si, Cu–Ge and Cu–Sb.

Lattice parameter values $a_{{{\text{A}}3}}$ and $c_{{{\text{A}}3}}$ belonging to the A3-related phases are plotted in Fig. 23. The lines of constant $c_{{{\text{A}}3}} /a_{{{\text{A}}3}}$ ratio reveal that the scatter of experimental data pertaining to the α′ of varying composition from Ref. 190 (containing also small values of $a_{{{\text{A}}3}}$ and $c_{{{\text{A}}3}}$ originating to more A1-like faulted material) lies around the ideal axial ratio of $2\sqrt {2/3 }$≈ 1.633 up to the maximum e/a = 1.49. The data from other sources for α′ and for γ′₁ agree within the scatter. However, the lattice parameters pertaining to whatever form of Cu₃Sn (e/a = 1.75) imply a much lower $c_{{{\text{A}}3}} /a_{{{\text{A}}3}}$ ratio. In the general field of brass-like phases, the A3-related phases are typically called ζ and ε; see 3^rd and 4^th column of Table 8. However, as noted by Massalski and King,^[230] the electronic structures of ζ and ε type brasses are not fundamentally different and the $c_{{{\text{A}}3}} /a_{{{\text{A}}3}}$ axial ratios are expected to decrease continuously with increasing e/a. Distinct ζ- and ε-type equilibrium phases only seem to occur in systems in which the ε-type phase is ordered and, thereby, achieves thermodynamic stabilization leading to a miscibility gap to the disordered ζ-type phase. This situation seems to prevail in the systems Cu–Ge,^[234] Cu–Sb^[235] and Ag–Sn.^[236] While the ε-type ε/ε′-Cu₃Sn is clearly ordered under equilibrium conditions, this is less clear for the α′ phase formed under non-equilibrium conditions, while the order in the γ′₁ martensite phase should be regarded as inherited from the austenite and is not necessarily in equilibrium at the temperature at which the martensite is stable against decomposition.

Fig. 23

Pseudohexagonal and hexagonal lattice parameters of different Cu–Sn phases with A3-like crystal structure (including superstructures) plotted in a $c_{{{\text{A}}3}}$ vs. $a_{{{\text{A}}3}}$ fashion and with the numbers indicating the assessed atomic fraction of Sn in %. Isolines are given for the atomic volume (which increases with Sn content) and for the axial ratios. The ideal axial ratio amounts $2\sqrt {2/3}$ ≈ 1.633; see text. Data are due to true or apparent α′ ^[62,85,190] (see Sect. 3.9.1), due to high-Sn content ε-Cu₃Sn ^[74] (see Sect. 3.6) and γ′₁ martensite ^[200,224] (averaged basal plane lattice parameters; see Sect. 3.9.3)

The only phases that are not of the Hume-Rothery type in the discussed sense are the A_f/hP1 phase and the β-Sn solid solution.

4.2 Assessed Likely Stable and Metastable Crystal Structures

When it comes to a final assessment of the crystal structures of what should be regarded as the stable and metastable phases of the Cu–Sn system, the task is to identify what the corresponding stable solid (crystalline) phases are. This is relatively simple in the case of the phases stable at 1 atm and somewhat elevated temperature, because these should correspond to the stable phase fields of the binary system. Figure 1(a) seems still appropriate for identification of these single-phase fields (apart from the low-temperature α-Sn not discussed here, because there are no data on the influence of Cu on this phase). For these single-phase fields the discussions in Sect. 3 lead to the structure types listed in Table 9.

Table 9 Crystal structure models regarded as relevant from the current literature

What is different as compared to the crystal structures indicated in the review by Saunders and Miodownik?^[7] Although quantitative data are lacking, there is evidence that the ζ-Cu₁₀Sn₃ phase adopts a partially disordered D0₁₈/Na₃As structure (labeled HT in the present work) in its high-temperature stability range,^[91] whereas the low-symmetry P6₃ structure^[90] had been indicated in.^[7] The latter LT′ structure (alternatively LT^[88]) is likely only that of a metastable phase forming partitionless ordering upon sufficiently rapid cooling.

As it concerns the ε phase, in Ref. 7 the $oS80$ structure determined in detail by Watanabe et al.^[112] had been indicated as the crystal structure. As shown here, indicating this structure as a crystal structure for the ε phase is not wrong, but not the whole story. The $oS64$ structure and intermediates have also been observed, whereas the relevance of the occasionally observed D0₁₉ extreme is still unclear. Hence, it was decided to choose the general modulated structure model described in 3 + 1 dimensional superspace symmetry Xmcm(0q₂0)00 with variable parameter q₂ from Ref. 109 as the crystal structure of the ε phase. As indicated, the real energy landscape as a function of q₂, temperature and composition is still to be explored, whereby this exploration is likely obstructed by the apparently complicated kinetics of changes of q₂.

The η high-temperature phase was identified as B8₁ structure type in Ref. 7, which is, again, not entirely wrong. However, this structure type designation fails to indicate the quite relevant way, how the Cu atoms realizing a lower Sn content than 50 at.% (δ > 0) are incorporated. Hence, we refer here to the intermediate Ni₂In/NiAs structure as B8₂/B8₁, a term similarly used by authors, who, after the publication of Ref. 7, dealt in some depth with such structures and their ordered versions.^[140] These authors also were involved in the determination of the long-range ordered structure of η′-Cu₆Sn₅,^[134] after publication of the review article.^[7]

It is more difficult to assess the structures of metastable phases. In general, a metastable phase can be regarded to be a locally ergodic region in configurational space as described in detail in Ref. 237. Thereby, the configurational space consists of all structural degrees of freedom of the arrangement of the atoms. Metastable states have a sufficient lifetime to establish some (only) constrained equilibrium with respect to such degrees of freedom, e.g., at fixed composition. However, the states resulting from some phase transformations, frequently contain lots of nonperiodic one- and higher-dimensional structural features (microstucture), which are difficult to be separated from what might be regarded as the ergodic periodic crystal structure. Under the constrained equilibrium these defects do not heal out before other degrees of freedom allow formation of more stable structures. The controversy described in Sect. 3.9.3, whether the 11H′ martensite or 9R′ martensite models (plus stacking faults) is the appropriate structure model for certain β′₁-Cu–Al martensites (a discussion which might apply also to β′₁-Cu–Sn) can be regarded as an example for the difficulty in identifying an appropriate (periodic) structure model based on a heavily faulted crystal structure. In any case, the diffraction effects associated with the microstructure can strongly broaden and transfer intensity from Bragg peaks to diffuse scattering, altogether complicating interpretation of the diffraction patterns. In PXRD, effects can become invisible due to the broadening of the Bragg peaks. This might also be the case for versions of δ brass mentioned in Sect. 3.4. The present author is unable to offer a general way to tackle these fundamental problems to unequivocally identify and distinguish different metastable phases of the Cu–Sn and to identify appropriate structure models. Instead, for pragmatic reasons, the model structures regarded as definitely relevant in view of the literature have been included in the corresponding part of Table 9. As a results, the decision to include some proposed structure models was more conservative than in Ref. 7.

4.3 Volume versus Composition

Analysis of the composition-dependence of the volume per atom (or per mole atoms) of solid and liquid materials based on mass-density data or crystallographic data can be used to reveal composition-dependent bonding effects in the corresponding system.^{[238,239,240]} Such an analysis is usually done by identifying deviations from linearity of the volume with the molar fraction(s) over the whole compositional range, often referred to as Zen’s law (volume version of Vegard’s law; the term Biltz’s law is also sometimes used).^[241,242] If that bonding behavior is approximately structure independent, the agreement of a particular set of crystallographic data with further (e.g., new) data for the given or for a related system, can be used as a plausibility check of that set of crystallographic data.

The evolution of the volume per atom (in short: atomic volume) calculated from selected ambient-temperature crystallographic data for selected solid Cu–Sn phases is plotted in Fig. 24. Figure 24(a) includes also the predicted values given by Zen’s law of the average atomic volume $v\left( {x_{{{\text{Sn}}}} } \right)$:

$$v\left( {x_{{{\text{Sn}}}} } \right) = \left( {1 - x_{{{\text{Sn}}}} } \right){}_{{}}^{0} v_{{{\text{Cu}}}} + x_{{{\text{Sn}}}} {}_{{}}^{0} v_{{{\text{Sn}}}} .$$

(4.3.1)

Fig. 24

Composition-dependent atomic volume evolution derived from crystallographic data obtained at ambient temperature. (a) Overview with lines representing Zen’s law linear evolution over the entire compositional range (Eq 4.3.1), and fits to the low-Sn (Eq 4.3.2) and high-Sn content data (Eq 4.3.3); (b) same data depicting the excess volumes with respect to Zen’s law. Points pertaining to data from α-Cu–Sn solid solution ^[44] and β-Sn ^[179], as well as data for β ^[52], δ ^[74], ζ ^[88] and ε ^[74] and η′ ^[113]. The black dashed line further indicates the atomic volume of the A_f/hP1 metastable phase ^[181] for the estimated compositional range. (c-e) Zoomed ranges depict the data for selected intermetallics with vertical dashed lines reflecting the assessed homogeneity ranges: (c) δ with data from 480 °C ^[74] and (d) ε with data from 420 °C ^[74], with the solid data points corresponding to those included in (a,b). (e) Data point from Ref. 113 and evolution assessed for the η phase ^[11] plotted as line over the maximum compositional stable extension homogeneity range assessed in Ref. 12

Here, ${}_{{}}^{0} v_{{{\text{Cu}}}} = 11.81$ ų is the atomic volume for pure Cu^[44] and ${}_{{}}^{0} v_{{{\text{Sn}}}} = 27.04$ ų for pure β-Sn,^[179] in the latter case adopting the allotrope stable at 20–25 °C. Consideration of the low-temperature α-Sn allotrope (diamond/A4 structure) with ${}_{{}}^{0} v^{\prime}_{{{\text{Sn}}}} = 34.16$ Å^{3 [243]} would lead to considerably different values.

The difference between the experimental average volume values and the results of Eq 4.3.1 visible already from Fig. 24(a) is the excess volume (volume of formation), which is shown in Fig. 24(b). While the excess volume is negative for most of the data (see below), only in the case of the metastable A_f/hP1 phase there seems to be positive excess volume at its estimated composition; see Sect. 3.9.4. This indicates a less metallic character of the chemical bonding in this kind of outsider among the discussed Cu–Sn phases, or alternatively, an incomplete structure model for this material. For example, the positive excess volume would easily get negative, if there were “interstitial” atoms in the hP1 structure, i.e., more than 1 atom per unit cell. The other metastable phases have not been included in Fig. 24 for sake of simplicity, but the available crystallographic data do not imply noteworthy differences in the atomic volume as compared to the stable phases.

It was already determined by Massalski and King^[230] that the partial atomic volumes of the two components of a series of Hume-Rothery type α and β phases have basically identical partial atomic volumes. These partial atomic volumes are obtained by the usual tangent construction as axes intercepts at (in case of Cu–Sn) x_Sn = 0% ($v_{{{\text{Cu}}}}^{*}$) and x_Sn = 1 = 100% ($v_{{{\text{Sn}}}}^{*}$). Indeed, when inspecting the data in Fig. 24(a,b) it turns out that the atomic volumes of the stable intermediate phases up to ε-Cu₃Sn can be well approximated by

$$v\left( {x_{{{\text{Sn}}}} } \right) = \left( {1 - x_{{{\text{Sn}}}} } \right){}_{{}}^{0} v_{{{\text{Cu}}}} + x_{{{\text{Sn}}}} v_{{{\text{Sn}}}}^{*}$$

(4.3.2)

with $v_{{{\text{Sn}}}}^{*} = 21.6$ų$= 0.80{}_{{}}^{0} v_{{{\text{Sn}}}}$ (obtained by linear regression). The remaining data for the Sn-rich part, can be approximated analogously by:

$$v\left( {x_{{{\text{Sn}}}} } \right) = \left( {1 - x_{{{\text{Sn}}}} } \right)v_{{{\text{Cu}}}}^{*} + x_{{{\text{Sn}}}} {}_{{}}^{0} v_{{{\text{Sn}}}}$$

(4.3.3)

with $v_{{{\text{Cu}}}}^{*} = 10.2$ ų $= 0.84{}_{{}}^{0} v_{{{\text{Cu}}}}$. Since no composition-dependent crystallographic data are available for the β-Sn terminal solid solution (see Sect. 3.8), the coefficients in Eq 4.3.3 were determined only based on the two data points for η′-Cu₆Sn₅ and β-Sn. Both Eq 4.3.2 and 4.3.3 have been included in Fig. 24.

The negative excess volume of the crystalline Cu–Sn phases was previously recognized in the literature.^[44,244] With regard to the α-Cu–Sn solid solution, this was already noted by Bain.^[15] Based on their composition-dependent lattice parameter values of α-Cu–Sn (see Sect. 3.2), Nuding and Ellner^[44] derived a linear evolution similar to Eq 4.3.2. There, it turned out that the value of $v_{{{\text{Sn}}}}^{*} \left( {x_{{{\text{Sn}}}} } \right) < {}_{{}}^{0} v_{{{\text{Sn}}}}$ for α-Cu–Sn was still significantly larger than the value for the solid solution of Ni and Co, which was connected with available 3d states for bonding with Sn in the case of Ni and Co. Similar trends were determined for the higher homologues of Ni and Co. Notably, the “volume size factors” calculated from the values in Eq 4.3.2 and Ref. 44 agree well with values already compiled by King^[238] upon reviewing literature data.

The global trends implied by Eq 4.3.2–3 appear also to be relevant when it comes to analysis of the composition-dependence of the atomic volume within narrow homogeneity ranges, as shown in Fig. 24(c-e). Figure 24(c, d) depict exemplary data pertaining to the δ and ε phases, corresponding to lattice parameter data already in depicted in Fig. 6 and 11. In both cases, few points pertain to single-phase materials as implied by the margins of the narrow homogeneity ranges indicated by vertical dashed lines. The composition dependences of the volume within these ranges evidently run largely parallel to lines given by Eq 4.3.2. The experimental volumes are, however, only by about 0.7% larger than predicted by Eq 4.3.2 in the case of δ (Fig. 24(c)), whereas in the case of ε such a difference appears even absent in view of the experimentally scatter of the data; see Fig. 24(d).

Figure 24(e) shows the vicinity of the data point for the ordered η′-Cu₆Sn₅ as well as the values according to Eq 4.3.3, which intersects this data point exactly since the coefficients of this equation were determined (only) from the data points of η′-Cu₆Sn₅ and β-Sn; see above. Figure 24(e) also includes the results from Eq 3.7.3, using the coefficients for the disordered η phase. For that purpose, the dark-green line depicts the atomic volume $v = V_{{{\text{B}}8}} /\left( {4 + 2\delta} \right)$ versus the atomic fraction $x_{{{\text{Sn}}}} = 2/\left( {4 + 2\delta} \right)$ for the maximum extension of the compositional range for the stable η phase. Notably, these values derived by considerations based on results of first-principles calculations and experimental data^[10,11] (see Sect. 3.7) also give a composition-dependent trend compatible with the global course according to Eq 4.3.3 derived from the atomic volumes of η′-Cu₆Sn₅ and β-Sn. Note, that the considerations leading to Eq 3.7.3 assumed linearity of the unit cell volume with the compositional parameter $\delta$, which is mathematically incompatible with a linear evolution of the atomic volume with $x_{{{\text{Sn}}}}$. In view of the narrow compositional range relevant for the Cu₆Sn₅ intermetallic in Fig. 24, the deviation of the composition-dependent volume according to Eq 3.7.3 from linearity in $x_{{{\text{Sn}}}}$ is negligible. In any case, the similar composition dependences of the atomic volumes due to Eq 3.7.3 and 4.3.3, confirm that the considerations leading to these equations are valid.

4.4 Consequences of Orientation Domain Formation

The review in Sect. 3 has included the microstructural level as it concerns the formation of characteristic orientation variants of a given crystal structure, especially but not only when this occurred because of a phase transformation. The formation of more or less well-characterized types of domains due to formation of low-symmetry structures has been reported for the δ phase,^[56] Cu₁₀Sn₃ (ζ),^[88] ε/ε′ phase,^[116] η′ and η′′ phases.^[134,152] For each of these cases, a high-symmetry structure can be identified to occur as high-temperature phase (see Table 10), except for the case of ε/ε′-Cu₃Sn. The low-symmetry phase is then an ordered version of the high-symmetry structure. Retaining some kind of framework of the high-symmetry structure, only distinct orientations of the low-symmetry structure are expected to occur. In case where the symmetry elements of the low-symmetry phase are perfectly aligned along those of the parent high-symmetry phase (see e.g.,^[245]), the number of orientation variants is given by the ratio of the orders of the point groups of the high and of the low-symmetry phases,^[114,115] as listed in Table 10. Also in the case of the ε/ε′-Cu₃Sn phase, domains seem to appear.^[116] In any case, occurrence of such orientation domains is eased by the low energies of characteristic orientational (grain) boundaries.

Table 10 Point group symmetries of high-symmetry structures/phases and low-symmetry counterparts in the Cu–Sn system, rationalizing the variants of orientation domains in the low-symmetry phase in terms of the ratio of the orders of the respective point groups

Equal volume fractions of the small orientation domains in multidomain “single crystals”, can lead to diffraction patterns that show the symmetry of the high-symmetry structure but with more reflections. This has been encountered in some previous SCXRD studies.^[88,134] Ignoring the influence of such domains on the diffraction pattern might then lead to inappropriate interpretation of diffraction data in terms of a typically too large high-symmetry unit cell as it happened to Bernal,^[75] and as pointed out upon identification of the true structure of the η′ phase.^[134]

The ordering characterizing the various low-symmetry phases involves only a part of the atomic structure, while a large part of the structure closely corresponds to that of the high-symmetry structure. Therefore, the diffraction pattern will largely correspond to that of the high-symmetry phase. Only, e.g., the presence of certain and usually relatively weak superstructure reflections or superstructure Kikuchi bands allows identification the actual orientation domains. This effect is often referred to as pseudosymmetry.

That pseudosymmetry often turns out to be a problem in EBSD analysis. The present author was involved in a study,^[152,153] where it was shown that uncareful use of standard (Hough space) evaluation methods may even suggest that the domain orientations of η′′ can be distinguished. That apparent success was, however, not confirmed when trying to verify the domain structure by comparison with the back-scatter contrast. That comparison, however, succeeded when applying more advanced pattern matching to identify domain orientation. In that case, also the absolute domain orientations were verified by direct analysis symmetry breaking features in the EBSD patterns.

It is predicted here that the pseudosymmetry problem also exists for the other Cu–Sn phases listed in Table 10. For example, there are numerous EBSD based studies on ε-Cu₃Sn that are not listed here. In many cases Hough-space indexing methods using one of the orthorhombic structure models have been applied. If the analysis is used to only discriminate the ε-Cu₃Sn phase against other phases (often a Cu₆Sn₅ related phase), this is not a problem. However, when the crystallographic orientation is of concern, problematic results can be obtained. For example, the measurements will imply information on crystal orientation, which may not be reliable, leading to incorrect texture information on some microstructure being studied. Ideally, unsuccessful identification of a domain orientation should lead to “pixeled” inverse pole figure maps due to random assignment of the different domain orientations. Depending on details of the structure model and algorithm used for indexing, however, a bias towards specific domain orientations can occur without that decisive features distinguishing the different orientations are really used. This then can lead to an apparently unique orientation determination and thus largely non-pixeled EBSD inverse pole figure maps. However, the orientation information obtained in such cases may be incorrect.

In a study on ε-Cu₃Sn, Daeumer et al.^[22] determined the full orientation of corresponding crystallites with respect to its orthorhombic symmetry. Thermal conductivity measured for many of such crystallites was used to derive the complete thermal conductivity tensor of ε-Cu₃Sn in crystal coordinates. A quite conventional Hough-space analysis of the Kikuchi patterns was apparently used for determination of the crystals’ orientations, with some grains excluded from the analysis due to non-unequivocal assignment of the orientation. Unpublished attempts in the present author’s group to unequivocally index (high-quality) EBSD patterns of ε-Cu₃Sn using Hough-space methods and any of the orthorhombic structure models failed: it was impossible to distinguish the orientations which differed by multiples of 120° around the pseudohexagonal axis. In any case, the Eigenvalues of the thermal conductivity tensor determined in Ref. 22 pertaining to the directions perpendicular to the pseudohexagonal $\left[ {0001} \right]_{{{\text{A}}3}} = \left[ {001} \right]_{oS80}$ direction were found to be quite similar. Consequently, the impact of incorrect orientation determination would likely be small as it concerns the thermal conductivity tensor.

Distinction of domains of a pseudosymmetric crystal structure based on EBSD patterns is only relevant if the regions of uniform domain orientation are sufficiently large such that no overlapping patterns containing the diffraction features of differently oriented domains are obtained. If the domain sizes get smaller, it becomes more and more difficult to adequately resolve the domain structure, even though the data and evaluation settings would, in principle, be able to tackle the pseudosymmetry problem. In the limit of very small domains, EBSD analysis from the diffraction perspective basically corresponds to the situation of the perfectly twinned crystals occasionally encountered in SCXRD analysis; see above.

Different crystal orientations developing from a single crystal are typically also found for martensites and the ω phase. In such cases, there is not necessarily a group-subgroup relationship between original and transformed phases, and the symmetry elements do not necessarily coincide in both phases due to a larger rotation. In such cases the number of orientation variants (typically 24 for martensites) and 4 for the ω phase can be derived via the concept of the intersection group^[245] considering the actual orientation relationship.

5 Concluding Remarks

In this article the crystal structure information of different phases in the Cu–Sn system was reviewed. This task had to consider the idea that every thermodynamically distinct crystalline phase should be characterized by a certain crystal structure with given symmetry (translation lattice and space group symmetry), and that different crystal structures imply different phases. This required a review of the different structure models derived in different experimental studies and analysis of true or apparent contradictions in the results and possible inappropriate assumptions made in previous works, e.g., that high-temperature atomic structures can be retained by quenching. Undercomplex or incomplete early partial structure models and possibly overdetermined structure models could be identified for various phases, reflecting the often hierarchical crystal structures, giving also rise to pseudosymmetry issues, becoming especially evident in the course electron backscatter diffraction analysis.

It turned out that the stable phases can be derived from the A1, A2 or A3 structures (“fcc”, “bcc” and “hcp”), which can—in an extended view—be regarded as Hume-Rothery (brass-like) phases with the type of crystal structures controlled to a major extent by the electron-to-atom ratio. Thereby, electron-rich A2-related structures appear to contain characteristic vacancies. The high-Sn content A_f/hP1-type is the only intermediate phase with a crystal structure not related to these principles.

Appendix A

See Table 11

Table 11 Strukturbericht notation used in the present paper