Photoluminescence Study of As Doped p-type HgCdTe Absorber for Infrared Detectors Operating in the Range up to 8 µm

Abstract

A HgCdTe photodiode grown by chemical vapor deposition (MOCVD) on a GaAs substrate operating in the long-wave infrared (LWIR) range was characterized using photoluminescence (PL) measurements. At high temperatures, the PL spectrum originates from a free-carrier emission and might be fitted by a theoretical expression being the product of the density of states and the Fermi–Dirac distribution. At low temperatures, the PL spectrum consists of multiple emission peaks that do not originate solely from the energy gap. Such spectra are not unambiguous to interpret due to the prominence of different optical transitions. Spectral response (SR) measurements were used to determine the energy gap (E_g) and extract the band-to-band transition from the PL spectra. PL peaks visible within the band gap were fitted by a Gaussian distribution. To identify the sources of individual emission peaks, excitation power dependence analysis was conducted. Band-to-band, free-to-bound, acceptor-bound exciton, and defect-bound exciton transitions were identified. At low temperatures, transitions are mainly impurity-related, with shallow impurity levels estimated to be 6 meV and 16 meV for the donor and acceptor, respectively, while deep-level impurities were associated with V_Hg. The latter transition with an energy of about 78 meV does not vary with temperature. Its relative positions with respect to the energy gap is 0.8 E_g at 18 K and 0.67 E_g at 80 K.

Introduction

Detectors operating in the long-wave infrared (LWIR) range (8–12 µm) are used in many industrial and scientific applications. Despite the competing technologies’ development, mercury–cadmium telluride (Hg_1−xCd_xTe) is still the main material for infrared (IR) detectors in that spectral range.^1,2 A variable energy gap without a significant change in the lattice constant allows for the design of the complex heterostructures. Well-controlled molar composition and doping profiles are enabled by advanced epitaxial techniques, such as molecular beam epitaxy (MBE)³ and metal–organic chemical vapor deposition (MOCVD).⁴ The p-type doping of HgCdTe with arsenic (As), which has a low diffusivity in HgCdTe, allows for high-quality detection devices.^5,6 Although As shows amphoteric behavior, it occupies both metal and nonmetal sites, exhibiting donor and acceptor characters. In the MBE technique, an ex situ thermal annealing process is required to activate the As as a shallow acceptor with a lower activation energy than that of the intrinsic mercury vacancies (V_Hg).⁷ The inherent advantages of the epitaxial growth are better utilized when the doping is achieved in situ, at most with post-growth low-temperature annealing. Toward this goal, an in situ acceptor doping in the MOCVD technique is not a problem with AsH₃ or TDMAAs used as acceptor precursors; however, AsH₃ causes the incorporation of As–H pairs in addition to As, which act as recombination centers. The AsH₃ substitution by TDMAAs resulted in higher carrier lifetimes.⁸ It should also be noted that epitaxial growth with external p-type doping can produce additional Hg vacancies. All this makes p-type doping of HgCdTe layers extremely interesting in terms of impurity level studies.

Photoluminescence (PL) is a method for analyzing band transitions and shallow impurity states, which often exhibit low volume density and are therefore difficult to detect by absorption measurements. The PL spectra line width and the peak energy provide information about the concentration of dopants and their type, material homogeneity, or composition fluctuations. There have been relatively few PL studies of As-doped HgCdTe, and most of them were related to mid-wave infrared (MWIR) epilayers grown by MBE.^9,10,11 All the reported data show that at low temperatures, the PL spectrum consists of multiple emission peaks that do not originate solely from the energy gap but are mainly impurity-related.

In this paper, the PL results for a p-type Hg_1−xCd_xTe absorber (x = 0.22) used for high-temperature photodiodes operating in the LWIR range are presented. The PL measurements are recorded as a function of temperature, from 18 K to 300 K. Additional spectral response (SR) measurements are used to determine the energy gap (E_g) and to extract the band-to-band transition from the PL spectrum. Next, to determine the origin of all visible transitions, an analysis of the PL intensity versus excitation power has been carried out.

Sample and Experimental Details

The analyzed HgCdTe epilayer was grown in an Aixtron AIX-200 MOCVD system on a 2-inch ©. 5 cm) (100) GaAs substrate and CdTe buffer layer. Growth was carried out at a temperature of about 350 °C and the mercury zone at 170 °C using the IMP technique.^12,13 The As doping was achieved using a TDMAAs precursor. A cadmium flush during the nucleation process allowed (100) orientation growth. A detailed description of the MOCVD growth of HgCdTe (100) epilayers can be found in Ref. 14. The crystallographic orientation is important for the level of As dopant activation during MOCVD growth. The high level of acceptor doping in our laboratory is an order of magnitude higher for the (100) orientation than for the (111) one.⁸ In turn, a residual donor concentration is an issue during p-type doping at a low level. The best results reported in our laboratory disclosed the residual donor concentration at the level of mid-10¹⁴ cm⁻³ for the HgCdTe (100) epilayers.¹⁵

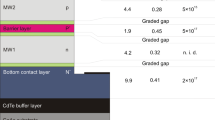
The entire detection structure consists of several layers: N⁺/p/T/P⁺/n⁺, as shown in Fig. 1a. From the substrate, the first layer is the wider-band gap N⁺ contact layer, next is the p-type active layer, then the wider-band gap P⁺ barrier, and finally an n⁺ cap-contact layer. The transient layer T parameters are conditioned by interdiffusion processes during the MOCVD growth.

Fig. 1

The LIWR N⁺/p/T/P⁺/n⁺ HgCdTe heterostructure (a) and photoluminescence measurement setup with a HgCdTe sample (b).

For the PL measurements, the HgCdTe N⁺/p/T/P⁺/n⁺ structure was chemically etched in a Br:HBr solution diluted with deionized water (50:50:1, Br:HBr:H₂O) to reveal a p-type absorber layer (Fig. 1b). The PL characteristics were measured using a FT-IR Bruker Vertex 70v spectrometer with the liquid nitrogen-cooled MCT DS316 detector. The PL was measured in step-scan mode¹⁶ with a lock-in amplifier. A 637-nm line laser chopped mechanically with a frequency of 100 Hz was used as an excitation source. The spot size of the laser on the sample had a diameter of 1.5 mm. The PL measurements were made in the temperature range from 18 K to 300 K and the laser excitation power from 35 mW to 200 mW. The sample was in a helium cryostat with a temperature stabilization system. All the measurements were carried out in a vacuum.

For the SR measurements, a detector in a mesa-type structure was chemically etched to the bottom N⁺ contact layer. The electric area of the detector was 7.85 × 10^–5 cm^2.. The structure was back-side-illuminated through the GaAs substrate. The SR characteristics for the HgCdTe photodiode at selected temperatures and at the bias voltage of − 0.5 V are presented in Fig. 2a. The medium-doped p-type absorber with a thickness of 3 μm and a molar composition x = 0.22 provided the detector cut-off wavelength (λ_cut-off) of 8 μm at 195 K, 7.7 μm at 210 K, 7.45 μm at 230 K, and 6.75 μm at 300 K. The SR peak value at 5.6 μm was ~ 3.20 A/W for all the temperatures which translates into a quantum efficiency of 72%. The SR measurements are also helpful in determining the energy gap of the absorber. The λ_cut-off , which corresponds to the E_g , was determined for the point where the detector response drops to 50% of the peak value.¹⁷

Fig. 2

Characteristics of LWIR N⁺/p/T/P⁺/n⁺ HgCdTe photodiode measured at selected temperatures from 195 K to 300 K: spectral characteristics with − 0.5 V bias voltage (a), I–V characteristics (b), and dark current and R₀A (c).

The HgCdTe (100) photodiode showed a high crystallographic quality, which is associated with limited tunnel currents (Fig. 2b).¹⁸ The dark current density (J_DARK) for a bias voltage of − 0.2 V varied from 23 A/cm² to 0.5 A/cm² with decreasing temperature (Fig. 2c). This result is comparable to the literature data for this type of device.¹⁹ R₀A and J_DARK have been compared to the theoretical “Rule 07” ²⁰. The slope of the J_DARK characteristic deviates from “Rule 07”, the cause of which may be a different photodiode design. Auger suppression is visible in the non-equilibrium N⁺/p/T/P⁺/n⁺ HgCdTe photodiode, but higher dark currents are due to shorter Shockley–Reed–Hall lifetimes. However, the experimental R₀A values are of the same order as “Rule 07”.

Optical Transitions in p-type HgCdTe

The temperature-dependent PL transitions showed a variable nature starting from free carrier transitions at high temperatures to the occurrence of impurities (or dopant)-related transition contributions at moderate temperatures, and finally to the full contribution of the impurities-related transitions at low temperatures. A schematic of the carrier transitions in a p-type HgCdTe with the As shallow acceptor level of $E_{{\text{a}}}$ is shown in Fig. 3. The temperature-dependent transitions can be explained according to the $E_{{\text{F}}} \sim T$ expression, where $E_{{\text{F}}}$ is the Fermi level and $T$ is the temperature.

Fig. 3

Schematics for temperature-dependent carrier transitions in the p-type HgCdTe with a shallow acceptor level of ${E}_{a}$: high T (a), moderate T (b), low T (c); solid and dotted lines denote the allowed and not allowed transitions, respectively. Adapted from Ref. 7.

The temperature dependence of the location of the Fermi level in HgCdTe determines the possibility of transitions from shallow levels, regardless of the growth method and the sources of the impurities. At high temperatures, the acceptor level $E_{{\text{a}}}$ is fully ionized (A^‒), which means that is always occupied by electrons (Fig. 3a), and the Fermi level is above the acceptor level. Electrons can participate in the absorption process to the conduction band (CB) but cannot transit from the CB band to the $E_{{\text{a}}}$ level. As a result, only electron transitions from the CB to the valence band (VB) are visible in the PL signal. At moderate temperatures (Fig. 3b), the thermal ionization of the dopant level decreases with the Fermi level close to the acceptor level, but only some of the dopants are ionized (A^‒/A⁰, where A⁰ denotes the non-ionized acceptor level). In this case, holes in $E_{{\text{a}}}$ can capture electrons and contribute to both absorption and emission. Electron transitions from the CB to the $E_{{\text{a}}}$ level provide a contribution to the PL emission spectra. At low temperatures (Fig. 3c), holes in the $E_{{\text{a}}}$ level are frozen, and the Fermi level is below the acceptor level, which in this case is non-ionized (A⁰). Only electrons from the VB can be excited to the CB, and only the intrinsic absorption is visible. In turn, excited electrons can recombine with holes in the $E_{{\text{a}}}$ level together with holes in the VB. What is more, the contribution of the CB–$E_{{\text{a}}}$ transition increases, which is evident in the increase in the intensity of this transition in the PL spectrum.

The CB–VB transition energy is equal to the energy gap, $E_{{\text{g}}}$. Then, the PL intensity can be described as the product of the joint density of states and the probability that the particle occupies a state with the energy $E$^21,22:

$$ I_{{{\text{PL}}}}^{{{\text{CB}}{-}{\text{VB}}}} \left( E \right) = A_{1} \left( {E - E_{{\text{g}}} } \right)^{1/2} \exp \left( { - (E - E_{{\text{g}}} )/k_{{\text{B}}} T} \right), $$

(1)

where $A_{1}$ is the scaling factor for CB–VB recombination and $k_{{\text{B}}}$ is the Boltzmann constant.

The below-band-edge emission model which additionally incorporates an Urbach tail is^23:

$$ \begin{aligned} I_{{{\text{PL}}}}^{{{\text{CB}}{-}{\text{VB}}}} \left( {E \le E_{{{\text{cr}}}} } \right) & = A_{1} K\exp \left( {\frac{\sigma }{{k_{{\text{B}}} T}}\left( {E - E_{{{\text{cr}}}} } \right)} \right) \\ & \quad \times \exp \left( { - (E - E_{{\text{g}}} )/k_{{\text{B}}} T} \right), \\ \end{aligned} $$

(2)

where $E_{{{\text{cr}}}}$ is the energy of transition (or crossover) between Eqs. 1 and 2, $K$ is a parameter chosen to ensure that the transition is a smooth one, and $\sigma$ describes the slope of the Urbach tail. The continuity and smoothness of the function given by Eqs. 1 and 2 are assured when $E_{{{\text{cr}}}} = E_{{\text{g}}} + k_{{\text{B}}} T/2\sigma$ and $K = \left( {k_{{\text{B}}} T/2\sigma } \right)^{{1/2}}$.

Because the transition energy of the $E_{{\text{a}}}$ level is lower than the VB–CB transition energy, the absorption edge energy is red-shifted. The PL intensity due to the recombination of a free electron from the CB with a hole located at the acceptor level $E_{{\text{a}}}$ can be expressed as:

$$ I_{{{\text{PL}}}}^{{{\text{CB}}{-}E_{{\text{A}}} }} \left( E \right) = A_{2} \left( {E - \left( {E_{{\text{g}}} - E_{{\text{A}}} } \right)} \right)^{1/2} \exp \left( { - E - (E_{{\text{g}}} - E_{{\text{A}}} )/k_{B} T} \right), $$

(3)

where $A_{a}$ is the scaling factor for CB–$E_{{\text{a}}}$ recombination.

Figure 4 shows the temperature-dependent PL spectra for the p-type Hg_1−xCd_xTe absorber (x = 0.22). The asymmetric shape of the PL signal at 300 K can be attributed to a free electron emission from the CB to the VB, related to the sharp broadening of the high-energy side of the PL peak accounted for by the Boltzmann carrier distribution function, and by a small proportion of localized states related to the sharp slope of the Urbach tail at the low-energy side of the PL peak. Therefore, the PL spectrum can be well-fitted by Eq. 2, while the $E_{{\text{g}}}$ can be determined from Eq. 1. Additionally, the determination of the $E_{{\text{g}}}$ from PL measurements can be confirmed by comparison with the SR measurements. Plotting the PL and SR results in one graph gives a precise result (Fig. 5). The blue solid line corresponds to the PL measurement and the green dashed line corresponds to the SR measurement. The red dotted line is a theoretical $I_{{{\text{PL}}}}$ function calculated by Eq. 1. It can be seen that the $E_{{\text{g}}}$ determined from the PL spectrum is close to the value determined at the 50% of the SR peak value. With decreasing temperature, additional lower-energy optical transitions appear (see Fig. 4). At 240 K and 140 K, one additional transition is visible (peak 2), while at 40 K, there are two more (peaks 3 and 4). In the case of narrow-band HgCdTe, it is difficult to observe the free exciton energy level. The free exciton ground state energy for Hg_1−xCd_xTe (x = 0.22) is 0.37 meV. Thus, all the transitions are mainly impurity-related. All four emission processes overlap and produce a broad peak. Peak 1 disappears in the PL spectrum, and therefore determination of the $E_{{\text{g}}}$ from the SR measurements becomes useful to extract the CB–VB transition. At low temperatures, the PL peak from a single emission process is symmetrical and can be fitted by a Gaussian shape with a good approximation. However, it should be noted that, for this type of line shape, the $E_{{\text{g}}}$ , as well as other determined energies, e.g. $E_{{\text{a}}}$, are expected to be $k_{{\text{B}}} T/2$ below the PL peak maxima.^16,21

Fig. 4

Temperature-dependent PL spectra measured for the p-type Hg_1−xCd_xTe absorber (x = 0.22) in the temperature range from 40 K to 300 K.

Fig. 5

PL and SR normalized spectra for the p-type Hg_1−xCd_xTe absorber (x = 0.22) at 300 K; the blue solid line corresponds to the PL measurement, the green dashed line corresponds to the SR measurement, and the red dotted line is a theoretical ${I}_{\text{PL}}$ function calculated by Eq. 1 (Color figure online).

Figure 6 shows the temperature dependance of the $E_{{\text{g}}}$ determined from the PL and SR measurements. The emission-edge energy for the analyzed sample is consistent with the theoretical Hansen relationship for x = 0.22.²⁴ The energies for the remaining transitions were calculated taking the PL peak position minus $k_{{\text{B}}} T/2$. Peak 2 is already visible at 240 K, and its energy is shifted by 6 meV towards lower energies with reference to the band gap for the entire temperature range. This suggests that it is attributed to a donor level–VB transition (Te_Hgwhen the antisite of Te occupies the Hg site or As_Hg- when As occupies the Hg site). Literature data present these transition energy values as ~ 20 meV for Te_Hg and ~ 9 meV for As_Hg.^7,25 Peaks 3 and 4 become visible at temperatures below 100 K. The transition energy of peak 3 is ~ 16 meV below the $E_{{\text{g}}}$. This transitions may be related to the CB–acceptor level created by the As occupying the Te site (As_Te). Literature data present this transition energy value as ~ 17 meV for As_Te.^7,25 Peak 4 is fixed at the same energy of about 78 meV in the entire analyzed temperature range. Such a dependence of the transition energy on temperature has already been reported and has been defined as a deep defect transition.²⁶ With reference to the $E_{{\text{g}}}$, its position is 0.8 $E_{{\text{g}}}$ at 18 K and 0.67 $E_{{\text{g}}}$ at 80 K. Peaks 2 and 3 are red-shifted by a constant value with reference to the $E_{{\text{g}}}$. These transitions may be related to the deep level created by the V_Hg.

Fig. 6

Temperature dependence of the PL peaks energy for the p-type Hg_1−xCd_xTe absorber (x = 0.22); the ${E}_{\text{g}}$ was determined from the PL and SR measurements and is compared to the Hansen relationship.²⁴

To determine the origin of all vthe isible transitions, an analysis of the PL intensity versus excitation power was carried out. The PL signal for 18 K as a function of excitation power is shown in Fig. 7. The measurement results show four peaks varying in PL intensity. Peak 1 is barely visible, peak 2 has the highest PL intensity, but as the excitation power decreases from 200 mW to 35 mW, while the intensity of peak 3 becomes comparable to the intensity of peak 2.

Fig. 7

PL signals versus excitation power energy for the p-type Hg_1−xCd_xTe absorber (x = 0.22) at 18 K.

The change in energy as a function of excitation power is shown in Fig. 8a. A shift toward lower energies with decreasing excitation power can be seen for peaks 1, 2, and 3 by 12 meV, 10 meV, and 8 meV, respectively. On the other hand, for peak 4, there is no visible energy shift for different excitation powers. To finally identify the origin of these emission peaks, a power law dependence study was conducted:

$$ I_{{{\text{PL}}}} \propto P^{\alpha } , $$

(4)

where ${I}_{\text{PL}}$ is the intensity of the PL peak for a given excitation power, $P$, and the exponent $\alpha$ indicates the type of transition.²⁶ Figure 8b shows PL intensity versus an excitation power approximated by Eq. 4. The extracted exponent factor for peak 1 is $\alpha$ = 1. Thus, it can be concluded that peak 1 corresponds to a band-to-band transition. For peak 2, $\alpha$ > 1 and equals 1.2, while, for peaks 3 and 4, $\alpha$ < 1 and equals 0.5 and 0.7, respectively. It can be concluded that peak 2 corresponds to a free-to-bound transition, while peak 3 and 4 are attributed to acceptor-bound exciton and defect-bound exciton transitions, respectively.²⁷

Fig. 8

PL peak energy (a) and PL intensity (b) versus excitation power for the p-type Hg_1−xCd_xTe absorber (x = 0.22) at 18 K.

Conclusions

The PL spectra for HgCdTe LWIR N⁺/p/T/P⁺/n⁺ heterostructure is difficult to interpret. In this paper, PL is presented for a temperature range of 18–300 K. Additional spectral response measurements were used to determine the energy gap and to extract the band-to-band transition from the PL spectrum. Next, to determine the origin of all visible transitions, an analysis of the PL intensity versus excitation power was carried out. The emission-edge energy for the analyzed sample is consistent with the theoretical Hansen relationship for x = 0.22. Next, to determine the origin of all the visible transitions, an analysis of the PL intensity versus excitation power was carried out. Band-to-band, a free-to-bound, acceptor bound exciton, and defect bound exciton transitions were identified. Shallow impurity levels are estimated to be 6 meV, and 16 meV for As_Hg as a donor and V_Hg as acceptors, and a deep level associated with V_Hg, respectively. The latter transition with the energy of about 78 meV does not vary with temperature. Its relative positions with respect to the energy gap are 0.8 $E_{{\text{g}}}$ at 18 K and 0.67 $E_{{\text{g}}}$ at 80 K.