Introduction

The performance of organic-based microelectronic devices is affected by the characteristics of the organic molecules utilised in their fabrication, as well as their optical and electrical properties.1 Thus, organic materials have risen in popularity because of their numerous applications in photonic devices such as organic light-emitting diodes (OLEDs), organic photovoltaics (OPVs), and organic solid-state lasers.2,3,4,5 Coumarin and its derivatives have received a considerable interest in industry in the form of dye lasers and high-efficiency dye-sensitized solar cells due to their interesting and promising optical features, such as fluorescence in visible light, significant Stokes shifts, high quantum yields, and solubility.6 Recently, a few studies have focused on the relationship between the molecular structure and optical properties of coumarin to gain better knowledge of the electronic operational principles, which may result in more efficient coumarin derivatives for optical device applications.7,8 Coumarin 6 (C6), a chromophore of the highly conjugated coplanar molecule, has been identified and employed as a fluorescent dye for staining organelles or medical materials9,10 and as a high-gain medium in tunable and amplifier lasers.11,12 C6 has generated substantial attention in optoelectronic applications after its successful introduction as an effective dopant in organic light-emitting diodes (OLEDs).13,14 Such as OLEDs with low turn-on voltages were fabricated in polyvinylcarbazol (PVK) doped with C6 deposited using ink-jet printing15 and spin coating.16 Also, Ismail et al. used C6 dye was used as a donor material in bulk heterojunctions (BHJ),17 and they studied the effect of tbe dye on light harvesting and photocurrent of the P3HT:PCBM solar cell.18 The performance of N719 sensitized nanocrystalline TiO2 DSSC19 was examined by adding C6 to the electrolyte, which improves not only the short-circuit current but also the fill factor and device efficiency.

Recently, our group performed DFT and TDDFT calculations20 to investigate the effect of attaching two different acceptor groups (–COOH and –CN) to C6 dye on the electronic structure and optical properties of the novel dyes and the use of these dyes as sensitizers for DSSCs. A thorough investigation of the fabrication and characterization of Coumarin 6 polycrystalline or amorphous thin films for use in organic multilayer optoelectronic devices is required. To achieve this goal, C6 thin films were obtained using the technique of thermal evaporation in this study, and their structure was investigated in terms of X-ray diffraction and FTIR spectroscopy, whereas the optical properties such as refractive index n and optical band gap energy were derived from the measurements of the transmittance and reflectance. Using a single oscillator model, the dispersion of the refractive index was explored and analyzed. In addition, we computed the nonlinear optical parameters χ(3) and n(2). We also examined the effect of annealing on the structural and optical properties of as-deposited C6 thin films.

Experimental Technique

C6 (Scheme 1) was obtained from Sigma-Aldrich, and C6 thin films were deposited onto clean quartz surfaces for optical and structural studies using Edward's coating unit (E 306A). A quartz crystal monitor, FTM5, was used to regulate the evaporation rate (0.3 nm/s) and the thickness of the evaporated films (260 nm). A group of these films was annealed in air at 373 and 398 K for 2 h before progressively cooling to room temperature. X-ray diffraction patterns for C6 as-deposited and annealed thin films were obtained using an XRD system equipped with a Rigaku RINT 2100 diffractometer. Chemical structural characterizations of the powder, as-deposited, and annealed thin films were performed at room temperature using FTIR spectroscopy (Jasco Model 6100) with a resolution of 1 cm-1 in the spectral range 400–4000 cm−1. Surface characterization of the prepared C6 thin films was examined by AFM (NT-MDT, Russia). The transmittance T(λ) and reflectance R (λ) measurements were carried out at normal incidence at room temperature in a wide wavelength range between 200 and 2500 nm using a double-beam JASCO-670 UV computer-controlled spectrophotometer for all the investigated films.

Scheme 1
scheme 1

Molecular structure of C6 Dye.

Full size image

The optical constants of the studied thin films such as the absorption coefficient, α, absorption index, k, and the refractive index, n, at different wavelengths, λ, were computed using the following equations21,22,23:

$$ \alpha = \frac{1}{d}\ln \left[ {\frac{{(1 - R)^{2} }}{2T} + \sqrt {\frac{{(1 - R)^{4} }}{{4T^{2} }} + R^{2} } } \right] $$
(1)
$$ k = \frac{\alpha \lambda }{{4\pi }} $$
(2)
$$ n = \frac{1 + R}{{1 - R}} + \sqrt {\frac{4R}{{(1 - R)^{2} }} - k^{2} } $$
(3)

where d is the film thickness with experimental errors ±2.5%.

Results and Discussion

Structural Properties

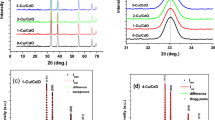
C6 in powder form exhibits an XRD pattern, which is seen in Fig. 1a. It is clear from the pattern that the C6 powder is polycrystalline, as shown by the presence of several diffraction peaks of various intensities. C6 has a triclinic structure (CCDC reference:1294096) with space group \(P\overline{1 }\) and lattice parameters a = 8.962 Å, b = 11.136 Å, c = 8.922 Å, α = 95.14°, β = 104.50°, and γ = 86.74°.1,24,25 The XRD patterns of the investigated thin films are presented in Fig. 1b, indicating that the as-deposited and annealed C6 thin films are partially crystallized. The intensity of the prominent peak at 2 =13.7° increases when the annealing temperature is raised. This result might be explained by rearrangements in the film atomic structure, which boosts their crystallinity.26 The average crystallite size D was estimated using Scherrer's equation27,28

$$ D = \frac{{K_{S} \lambda }}{\beta \cos \theta } $$
(4)
Fig. 1
figure 1

XRD pattern of (a) powder and (b) the investigated thin films.

Full size image

where θ is Bragg’s angle, β is the FWMH in radians, λ = 0.15406 nm for an X-ray wavelength of CuKα, and KS= 0.94 is a constant known as the shape factor. Crystallite sizes estimated using Scherrer’s equation are listed in Table I. Crystallite size values are in the nanoscale, confirming the nanostructural properties of the as-deposited and annealed films. In addition, the nano-size nature of the as-deposited and annealed thin films is represented in the broadening or FWHM of the (011) plane diffraction peak in the thin film pattern, which is bigger than that of the source powder of C6. The broadening of the (011) plane's diffraction peak may be attributed to tiny crystallites, which result in significant surface scattering and hence cause a significant broadening of the diffraction peak. During film deposition and post-annealing, it is possible for some strain and dislocation to occur in the film. The dislocation density, δ, has been estimated using Williamson and Smallman's formula29 as the length of dislocation lines per unit volume of the crystal using crystallite size values (D).

$$ \delta = \frac{1}{{D^{2} }} $$
(5)
Table I Structural parameters for C6 powder, as-deposited and annealed thin films
Full size table

The microstrain, εs derived from the following equation27:

$$ \varepsilon_{s} = \frac{\beta \cos \theta }{4} $$
(6)

The number of crystallites per unit surface area, Nc, can be calculated using the following formula27,28,30:

$$ N_{c} = \frac{d}{{D^{3} }} $$
(7)

The values of δ, εs, and Nc at different annealing temperatures are given in Table I. As seen in the table, the microstrain, dislocation density, and a number of crystallites all decrease with increasing annealing temperature, while the crystallite size increases. The decrease in the concentration of lattice flaws (point defects) near the grain boundary areas causes this phenomenon. At higher annealing temperatures, the development of high-quality C6 thin films is demonstrated by lower microstrain and dislocation density. The increased diffusion of species and the formation of films with bigger crystallites were aided by the thermal energy complete by annealing.

The infrared spectrum is a widely used and successful method for determining the molecular structure of a wide variety of materials, both organic and inorganic. The infrared spectra of the C6 powder and thin films in various forms are shown in Fig. 2 in the spectra range 600–2000 cm−1. Table II includes the peak’s locations and assignments, which match the C6 powder spectra's stated places. Because C6 molecules do not disintegrate during the thermal evaporation process and C6 films have excellent chemical stability and stoichiometric films, this indicates that C6 is a good choice for thermal deposition. AFM is used to analyze and evaluate the surface morphology, roughness, and grain size of the thin film before and after annealing. Figure 3 illustrates the changes in the microstructure before and after different annealing treatments. It is plain to observe that the form of the grains varies throughout the annealing process and that the grain boundaries fade as the grains merge. The as-deposited thin film has a root-mean-square (RMS) roughness of 2.618±0.03 nm while the RMS value for the annealed thin film is 7.385±0.03 nm. The increase in the roughness of the C6 thin film surface is a result of particle agglomeration and coalescence. As predicted, the surface morphology of the films varies with increasing the annealing temperature. This is consistent with the XRD and demonstrates that increasing the annealing temperature modifies the thin film structure.

Fig. 2
figure 2

FTIR spectra of powder and the investigated thin films.

Full size image
Table II Peak positions and assignments for C6 powder, as-deposited and annealed thin films
Full size table
Fig. 3
figure 3

AFM images for (a) as-deposited and (b) annealed thin films.

Full size image

Optical Properties

The T(λ) and R(λ) spectra of as-deposited and annealed thin films in the wavelength range 200–2500 nm are shown in Fig. 4. All films become almost transparent in the non-absorbing zone (i.e., R + T = 1) at longer wavelengths (λ > 750 nm) owing to the negligible energy loss due to scattering. Absorption occurs because of the inequality (A+R + T=1) at lower wavelengths (λ < 750 nm), which is referred to as the absorbing area. In addition, the annealing temperature pushes the transmittance edge to higher wavelengths, making it easier to see through the material. Because light scattering occurs on rough surfaces, it is often considered that the transmittance of a film decreases with grain size in the visible light range.31,32 As a result, the annealing is expected to have an impact on the gap. Increasing the annealing temperature of C6 thin films decreases the optical reflectance of the as-deposited film, as shown in Fig. 4.

Fig. 4
figure 4

The optical transmission T(λ) and reflection R(λ) for as-deposited and annealed thin films.

Full size image

Figure 5 illustrates the absorption coefficient of the as-deposited and annealed C6 thin films, which has a value in the range of 105 cm−1. Three bands are seen in these spectra. The Q band is associated with a transition from the ground state to the first excited state (S0→S1), while the Soret (B) band corresponds to a strongly allowed transition from the ground state to the second excited state (S0→S2). The Q and Soret (B) bands are often assigned to π →π* singlet transitions.33 A band designated N appears in the ultraviolet region at 225 nm due to the intrinsic transition of C6 (n→π*).28 Using Tauc's relation, which describes the interband absorption coefficient as a function of energy in the region of the absorption edge, it is usual to investigate both the types of optical transitions and the magnitude of the energy gap at the basic absorption edge in numerous organic thin films34:

$$ \alpha h\nu = A\left( {h\nu - E_{g} } \right)^{r} $$
(8)

where \(h\nu \) is the photon energy, A is a constant called the band tailing, \({E}_{g}\) is the energy of the optical band gap, and r determines the type of the optical transition, when r = 2, the best fit of the experimental data to Eq. 8 is achieved. This means that the electronic transition is an indirect allowed transition, as seen in Fig. 6 by plotting \({(\alpha h\nu )}^{1/2}\) versus \(h\nu \) for the as-deposited and annealed films. Values of optical energy gap for each electronic transition are obtained by extrapolating the straight lines parts of the curves to \({(\alpha h\nu )}^{1/2}=\) 0 and are tabulated in Table III. The optical energy gaps \({E}_{g}^{Q}\) , \({E}_{g}^{B}\) and \({E}_{g}^{N}\) correspond to the optical absorption in the Q band, Soret (B) and N energy bands, respectively. The calculated energy gap for Q band \({E}_{g}^{Q}\) between HOMO and LUMO orbitals of as-deposited C6 film is in good agreement with the reported values.35 The reduction in the energy gap values (e.g.,a redshift) with higher annealing temperatures is attributed to an increase in crystallite size as well as a decrease in lattice defect concentration at the grain boundary.36,37 Additionally, a shift in the relative locations of the valence (HOMO; π orbitals) and conduction band (LUMO; π *orbitals) might minimize the energy gap, which occurs from the thermal energy generated during annealing.37,38 The behaviour of the energy gap values in C6 films as a function of annealing temperature appears to be comparable to that observed in previously reported organic films.36,37,38,39,40

Fig. 5
figure 5

Absorption coefficient, α for as-deposited and annealed thin films as a function of hν.

Full size image
Fig. 6
figure 6

(ahν)1/2 versus hν for C6 thin films (a) as-deposited, (b) annealed at 373 K and (c) annealed at 398 K.

Full size image
Table III Variation of the optical band gap of C6 thin films for different annealing temperatures.
Full size table

Dispersion Analysis of the Refractive Index n

The complex refractive index N = n–jk of electromagnetic waves travelling through thin films is frequency-dependent, while the refractive index n which is the real part of the complex refractive index is velocity-dependent and carries information about electronic polarisation.37,41 The imaginary component (extinction coefficient, k) is proportional to the decay or damping of the applied electric field's oscillation amplitude. The spectra of the k(λ) curves for the investigated thin films are presented in Fig. 7. As shown in Fig 7, the k for as-deposited and annealed C6 thin films approach a minimum value at about 900 nm. After that, k increases again with an increasing wavelength, which is a characteristic feature of the presence of free carriers in C6 film.42,43,44 When the annealing temperature was raised, the peak locations changed slightly toward a longer wavelength (redshift) and their intensity increased. This behavior may be explained by the fact that the crystallite size grows as the annealing temperature increases. Figure 8 represents the change in n as a function of λ for as-deposited and annealed C6 films. It is found that annealing changes the locations of the peaks a lot, which is related to changes in the structures of the thin films. The fluctuation of the refractive index n with wavelength (dispersion of n) is also a critical optical property of thin film materials used to transmit electromagnetic waves.43 The dispersion curve was analysed using the two-zone method (see Fig. 8). Numerous peaks in the refractive index are seen in the first region at λ<750 nm. When absorption occurs inside this zone, n reverts to its original orientation when absorption decreases to the non-absorbing region (second region) λ> 750 nm.37 Additionally, n drops gradually as λ increases in this area. This is known as normal dispersion.37 The normal dispersion behavior is caused by the effect of the resonance between the incident electromagnetic radiation and the electron's polarization, which couples electrons in C6 films to the oscillating electric field. The n in the second region can be analyzed using the single-oscillator model suggested by Wemple-DiDomenico (WDD) using the following equation45:

$$ n^{2} = 1 + \frac{{E_{d} E_{o} }}{{E_{o}^{2} - \left( {h\nu } \right)^{2} }} $$
(9)

where \({E}_{o}\) and \({E}_{d}\) are the single-oscillator energy and oscillator dispersion energy, respectively. \({E}_{d}\) indicates the average strength of interband optical transitions and is connected to variations in the structural order of the material; nevertheless, the \({E}_{o}\) is considered the material's average energy gap value. The \({E}_{d}\) and \({E}_{o}\) values can be easily obtained from the slope \({({E}_{o}{E}_{d})}^{-1}\) and the intercept \(({E}_{o}/{E}_{d})\) by plotting of \({({n}^{2}-1)}^{-1}\) versus \({(h\upsilon )}^{2}\) for as-deposited and annealed films as illustrated in Fig. 9. The obtained values of \({E}_{d}\) and \({E}_{o}\) are given in Table IV. As the annealing temperature increases, the values of \({E}_{d}\) are decreased while the values of \({E}_{o}\) are increased. Extrapolating the linear part of the dispersion relationship towards \(h\nu =0\) gives the infinite wavelength dielectric constant \({\varepsilon }_{\infty }\). Also, the static refractive index \({n}_{o}\), can be used to calculate using the formula (\({\mathrm{n}}_{\mathrm{o}}=\sqrt{{\varepsilon }_{\infty }}\)). The values of \({\varepsilon }_{\infty }\) and \({n}_{o}\) C6 thin films are tabulated in Table IV.

Fig. 7
figure 7

Extinction coefficient, k for as-deposited and annealed thin films as a function of wavelength.

Full size image
Fig. 8
figure 8

Reflective index, n for as-deposited and annealed thin films as a function of wavelength.

Full size image
Fig. 9
figure 9

(n2−1)−1 versus (hν)2 for as-deposited and annealed thin films.

Full size image
Table IV Optical parameters of C6 thin films for different annealing temperatures
Full size table

The dielectric constant at high frequency \({\varepsilon }_{L}\) can be calculated by analyzing the refractive index \(n\) data as follows. In the transparent region, the relation between the refractive index, n, the high frequency dielectric constant, \({\varepsilon }_{L}\), and the wavelength \(\lambda \), is given by the relation46,47:

$$ n^{2} = \varepsilon_{L} - \left( {\frac{{e^{2} }}{{4 \pi^{2} c^{2} \varepsilon_{o} }}} \right)\left( {\frac{N}{{m^{*} }}} \right)\lambda^{2} $$
(10)

where e is the electronic charge, \({\varepsilon }_{o}\) is the vacuum permittivity \(N/{m}^{*}\) is the ratio of charge carrier concentration to the effective mass of the charge carriers. The variation of \({n}^{2}\) vs. \({\lambda }^{2}\) for C6 films is shown in Fig. 10. At longer values of wavelengths the dependence of \({n}^{2}\) on \({\lambda }^{2}\) is linear, which can be extrapolated to zero wavelength (λ2 =0) to calculate the high-frequency dielectric constant \({\varepsilon }_{L}\) and the slope of this linear part can be used to evaluate the value of \(N/{m}^{*}\). The plasma frequency ωp can calculated as following based on the Drude model40,48:

$$ \omega_{p}^{2} = \frac{{e^{2} N/m^{*} }}{{\varepsilon_{o} }} $$
(11)
Fig. 10
figure 10

n2 versus λ2 for as-deposited and annealed thin films.

Full size image

The values of these parameters are listed in Table IV. It is obvious that the value of ε∞< εL, may be attributed to the contribution of free charge carriers to the polarisation process occurring within the material when light illuminates it.37 Moreover, the decreasing values of ε∞ and εL with the annealing temperature increases may be ascribed to the reduction of lattice vibration and bound carriers in the transparent zone.

Dielectric Characterization

The dielectric constant ε* is a critical element in the manufacture and design of highly efficient optical-electronic systems. The complex dielectric function is written as \({\varepsilon }^{*}(\omega )={\varepsilon }_{1}(\omega )+{\varepsilon }_{2}(\omega )\) with the real ε1 and imaginary ε2 parts of components. The optical constant components can be derived from n and k using the following formulas22,28:

$$ \varepsilon_{1} \left( \omega \right) = n^{2} - K^{2} \,{\text{and}}\, \varepsilon_{2} \left( \omega \right) = 2{\text{nK}} $$
(12)

The ε1 and ε2 components of the dielectric constant are shown as a function of the photon energy hv of the investigated C6 thin film in Fig. 11. Through the interaction of incoming photons and electrons, the presence of peaks in the dielectric spectrum identifies the type of material and offers information on the electronic structure of the material. As seen in Fig. 11, increasing the annealing temperature of C6 thin films resulted in a decrease in the ε1 and ε2. The decrease in the dielectric constants of C6 thin films as annealing temperatures increase might be a result of a decrease in net polarisation produced by a decrease in the net alignment of dipoles within materials generated by the electric field during thermal annealing.49,50,51,52 The dissipation factor (loss tangent, tan δ) is a property of dielectric materials that measure their intrinsic energy dissipation due to the molecule's inability to realign them in response to an applied alternating electric field and may be estimated using the following equation21,22:

$$ \tan \delta = \frac{{\varepsilon_{2} }}{{\varepsilon_{1} }} $$
(13)
Fig. 11
figure 11

The variation of (a) the ε1 and (b) the ε2 part with hν for as-deposited and annealed thin films.

Full size image

The plot of tan δ vs. \(h\nu \) for the investigated C6 thin films is shown in Fig. 12. The peaks in the spectra represent the mean energy dissipation of C6 thin films owing to interband transitions. As the temperature increases, tan δ switches to a higher frequency, suggesting a thermally triggered process.52,53 The volume energy loss function (VELF) and surface energy loss function (SEF) are two well-known variables that measure the rate at which high-energy electrons lose energy while traveling through the medium (SELF). The following relationship22 connects VELF and SELF to the real and imaginary terms of a dielectric function:

$$ {\text{VELF = }} - {\text{Im}}\left( {\frac{1}{{\varepsilon^{*} }}} \right) = \frac{{\varepsilon_{2} }}{{\varepsilon_{1}^{2} + \varepsilon_{1}^{2} }} $$
(14)
$$ {\text{SELF}} = - {\text{Im}}\left( {\frac{1}{{\varepsilon^{*} + 1}}} \right) = \frac{{\varepsilon_{2} }}{{(\varepsilon_{1} + 1)^{2} + \varepsilon_{1}^{2} }} $$
(15)
Fig. 12
figure 12

The variation of tanδ with hν for as deposited and annealed thin films.

Full size image

The results are illustrated in Fig. 13 which shows that both VELF and SELF follow the same behavior with the incident photon energy. Additionally, energy loss due to free charge carriers travelling through the bulk material (VELF) is greater than energy loss due to free charge carriers traversing through the surface at certain peaks that define the C6 thin film (SELF). The real σ1 and imaginary σ2 parts of the optical conductivity can be determined using the ε1 and ε2 parts of the dielectric constant as stated by following expressions28,54:

$$ \sigma_{1} = {\upomega }\varepsilon_{0} \varepsilon_{2} \,{\text{ and}}\, \sigma_{2} = {\upomega }\varepsilon_{0} \varepsilon_{1} $$
(16)
Fig. 13
figure 13

The variation of (a) VELF and (b) SELF with hν for as-deposited and annealed thin films.

Full size image

The σ1 and σ2 parts of the optical conductivity of the investigated C6 thin film as a function of hν are illustrated in Fig. 14. The reduction in optical conductivity of C6 thin films σ1 and σ2 as annealing temperatures rise might be due to changes in crystallinity and charge carrier concentration. The variation in optical conductivity follows the same pattern as the change in dielectric constant.

Fig. 14
figure 14

The variation of (a) σ1 and (b) σ2 for as-deposited and annealed thin films as a function of hν.

Full size image

Nonlinearity in C6 Thin Films

Nonlinear optical materials exhibit fascinating properties such as second harmonic generation, sum and difference frequency generation, optical parameter amplification, and wave mixing and can be used in a wide variety of applications including optical computing, image manipulation and processing, data storage, and parametric oscillators.55 The Wemple-DiDomenico (WDD) parameters (Eo and Ed) are related to the nonlinear optical susceptibility, χ(3) through the following relationship45,54,56:

$$ \chi^{\left( 3 \right)} = A\left[ {\chi^{\left( 1 \right)} } \right]^{4} = A\left[ {\frac{{E_{o} E_{d} }}{{4\pi \left( {E_{o}^{2} - \left( {h\nu } \right)^{2} } \right)}}} \right]^{4} $$
(17)

where \(A = 1.7 \times {10}^{-10}\)(for \({\chi }^{(3)}\) measured in esu) and has the same value for all materials that is assumed to be frequency independent, for \(h\nu \to 0\) one can obtain:

$$ \chi^{\left( 3 \right)} = 1.7\left[ {\frac{{n_{o}^{2} - 1}}{4\pi }} \right]^{4} = 1.7\left[ {\frac{{E_{d} }}{{4\pi E_{o} }}} \right]^{4} \times 10^{ - 10} $$
(18)

The nonlinear refractive index \({n}_{2}\) can be calculated by the following relation45:

$$ n_{\left( 2 \right)} = \frac{{12 \pi \chi^{\left( 3 \right)} }}{{n_{o} }} $$
(19)

The estimated values of nonlinear refractive index \({n}_{(2)}\) and \({\chi }^{(3)}\) (esu) when \(h\nu \to 0\) for the investigated films are listed in Table IV. The decreases in values of \({n}_{(2)}\) and \({\chi }^{(3)}\) as the annealing temperature increased was attributed to the decrease in Eg as the annealing temperature increased. This demonstrates that the nonlinear optical characteristics of C6 are very temperature sensitive.

Conclusions

In this study, the structural, morphological, and optical characteristics of C6 thin films were significantly impacted by the thermal annealing. An increase in crystallite size with annealing temperature was seen in the XRD patterns. The crystallite size values are in the nanometer range, indicating that the as-deposited and annealed films have nanostructure characteristics. The fact that the molecular structure of C6 films does not change as the annealing temperature goes up is proof that they are chemically stable. The indirect energy band gaps of corresponded to the Q, B, and N bands. The redshift in the indirect band gap for C6 films is observed due to the improved crystallinity of the thin film with higher annealing temperatures. Dispersion parameters \(({ E}_{o}\),\({E}_{d}\), no and \({\varepsilon }_{\infty }\)), dielectric parameters (\(\mathrm{N}/{\mathrm{m}}^{*}\),\({\varepsilon }_{L}\), ωp), optical conductivity constants, and the loss energy functions (VELF and SELF) are correlated to the annealing temperatures. The calculated χ(3) and \({n}_{(2)}\) are on the order of ~10−13 and ~10−12esu, respectively at \(h\nu \to 0\). Lastly, these findings should be considered for linear and nonlinear optical properties recommend that the C6 film is good candidate for NLO applications in photonic and optoelectronic devices.