Introduction

Copper is a key element for de-carbonization, renewable energy technologies, and achieving a circular economy.[1] When paired with a Peirce–Smith converter, the Flash Smelting Furnace (FSF) has the lowest environmental impact and CO\(_2\) emissions of all modern copper smelting technologies.[2] However, significant disadvantage of the FSF is that up to 5 pct of the concentrate feed is carried over as flue dust into the down-stream waste heat boiler (WHB).[3] The flue dust generates various operational challenges, such as dust buildup, formation of accretions throughout the WHB, and surface fouling on the cooling surfaces in the convection section.[4,5,6] Flue dust catalytically promotes the undesired oxidation from SO2 to SO3, especially at temperatures around 750 °C.[7] SO3 can combine with water, forming corrosive H2SO4, if the gas temperature decreases below the acid dew point. Hence, the WHB is usually designed for a minimum temperature of 350 °C, as this can lead to equipment damage and downtime.[8] Hence, gaining more insight into the formation of accretions can help optimize the process and increase the boiler availability.[9]

The following operational goals can be derived regarding flue dust management in the WHB:

  1. 1.

    Minimization of flue dust carry-over through the gas uptake.

  2. 2.

    Oxidation and sulfatization of the unreacted sulfidic concentrate to decrease the dust stickiness.[10]

  3. 3.

    Maximization of dust collection within the radiation section.

  4. 4.

    Minimization of dust buildup.

  5. 5.

    Minimization of dust entering the convection section, hence, minimization of surface fouling and catalytic SO3 formation.

Experimental studies in the WHB are challenging. For this reason, Computational Fluid Dynamics (CFD) models are often used to optimize the WHB design.[11,12,13,14] In 1997 and 1999, the flue dust capture efficiency in the WHB radiation section was calculated with an Eulerian–Eulerian model and an Eulerian–Lagrangian approach, respectively.[12,13] It was found that the Eulerian–Lagrangian approach, which allows flue dust particles to be tracked, leads to very different results. The Eulerian–Eulerian approach predicted that the capture efficiency of particles with a diameter below 50 μm would be 30 pct. With the second approach, these particles did not sediment either in the radiation or in the convection section.

The results of another CFD study showed that sharp corners promote dust buildup, making a smoother, aerodynamic design favorable.[14] However, this geometric change also led to a bypass of the main flow, shifting the buildup of dust to the convection section. The insertion of two baffle plates led to a more uniform flow and helped the sulfatization air and main gas flow mix.

Another study confirmed that baffle plates can improve the flow pattern.[15] However, not all baffle plate modifications showed this positive effect. While a baffle plate halfway into the radiation section improved the gas cooling when paired with elevation of the radiation ceiling, including more radiation plates lengthwise did not further enhance the flow pattern. A study by Reference 16 provides similar findings. In their model, a short baffle plate was beneficial for reducing the dead volume within the radiation section, while a long baffle plate was less advantageous.

Initially mainly consisting of copper and iron sulfides and oxides, the flue dust can oxidize and form sulfates under the WHB process conditions. This chemical reaction releases heat, potentially softening the flue dust and promoting accretion formation.[17] The dust sulphatization was included in a CFD model based on kinetics developed by Reference 19 as a dual-layer shrinking-core particle model.[18] This mechanism was tested on a CFD case with a single particle, revealing that particles with a diameter of 100 μm react completely to sulfates, while particles with a diameter of 1000 μm form a thick sulfate layer inhibiting further reaction.

This mechanism was then included in a CFD model for an industrial-scale WHB, composing of the gas uptake and radiation section.[20] As a sticking criterion, it was assumed that the particles’ stickiness does not depend on the impact on the wall, but on the mass balance of gravity, friction, and thermophoretic force. The evolution of accretion layers was calculated in a transient fashion, using time-dependent particle tracking. Based on the previously described sulfatization mechanism, the grade of conversion was calculated for the accretion layers. Routines were developed and used to calculate the layer thickness and their thermal resistance. It was shown that this approach is applicable for an industrial-scale WHB model for a physical time of up to 60 minutes. In that time, the evolving dust buildup hindered the heat flux through the cooling surface significantly.

Industrial experience shows that flue dust is sticky only above a dust-softening temperature \(T_{\rm soft}\). This principle can be used to predict the accretion pattern in the industrial-scale WHB model. A study preceding this work investigated the effect of the dust-softening temperature on the dust accretion formation in a steady state using a standard baffle plate modification.[21] It was found that accretions in the convection section are minimized by increasing the dust-softening temperature, proving the capability to reduce accretions by altering the dust mineralogy. However, later it was found that setting the dust-softening temperature to 700 °C produces the best agreement with the accretion pattern in the real WHB.

However, a steady-state calculation can neither predict the dynamic growth of the accretion layer, nor take into consideration the resulting increase in the boiler temperature. The aim of this study is to extend previous CFD models by including the accretion layer growth over a time of 24 hours, while tracking the change in the WHB temperature profile. The increase in thermal resistance caused by the dust layer is calculated using the approach described in Reference 20. A quasi-steady-state approach is proposed to enable the calculation of long physical times. The influence of different baffle plate modifications on accretion formation and dust sedimentation is estimated using three different baffle plate designs.

Methods—Computational Fluid Dynamics

The fluid dynamics are calculated based on the incompressible, steady-state Navier–Stokes equations in the CFD tool ANSYS Fluent 19.2. For turbulence, the \(k{-}\omega \) SST model was used. The \(k{-}\omega \) SST combines the \(k{-}\epsilon \) and the \(k{-}\omega \) models depending on the wall distance, making it suitable for near-wall and free stream conditions.[22] Its implementation can be found in Reference 22. Radiation was considered via the Discrete-Ordinates model, since the P1 model can lead to overestimation of the heat flux.[23,24] The implementation can be found in Reference 25. The physical properties of the gaseous phase were estimated via the temperature-dependent polynomials from the ANSYS Fluent database.[25]

The flue dust was calculated with the Lagrangian–Eulerian approach, which allows particle tracking. This approach divides the total flue dust mass flow into representative parcels, which will follow typical flue dust trajectories. The trajectories are calculated with a force balance; in this case, only the drag forces and gravity were considered. The number of particles in a parcel NP depends on the dust mass flow \({\dot{m}}_{\rm s}\), the mass of a dust particle \(m_{\rm p},\) and the time step \(\varDelta t\).[25]

$$\begin{aligned} NP=\dot{m}_\text{s}\cdot \frac{\varDelta t}{m_{\rm p}} \end{aligned}.$$
(1)

The statistic effects of turbulent dispersion on the particle trajectories are considered by calculating ten representative particles for each parcel. The heat transfer between the gaseous and particulate phases was taken into account using two-way coupling. This coupling also determines how the particulate phase influences the gaseous phase by including additional forces in the energy and momentum balances.[25]

CFD Simulations

Setup of Three WHB Geometries and Calculational Meshes

Fig. 1
figure 1

Setup of WHB and connection to FSF. The calculational domain is marked in blue, the red arrows show the flow direction of the off-gas, and the blue arrow shows the oxygen inlet. The three baffle plate designs are marked in black, orange, and red (Color figure online)

Full size image

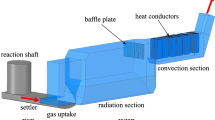
Figure 1 shows the WHB and its connection to the FSF via the gas uptake. The calculational domain is marked in light blue. The domain is 60 m long, 20 m high, and 10 m wide. The off-gas stream enters the domain via the gas uptake, which is set angular to the WHB. This leads to an asymmetric flow field at the entrance of the radiation section. Additional oxygen is injected via an inlet at the gas uptake roof. The baffle plate and three rows of boiler tubes are located within the radiation section. The baffle plate designs were developed with the following design considerations:

Baffle plate Design 1 is located in the last third of the radiation section and has a comb structure to minimize the pressure drop.

Design 2 is located in the first half of the radiation section; it has a comb structure but protrudes deeper into the radiation section. This modification is intended to increase the particle sedimentation while shielding the following boiler tubes from dust buildup.

Design 3 is a solid plate in the first half of the radiation section, set at an angle and with a rounded edge. This design was chosen to lead to a similar flow pattern as Design 2 without compromising on the cooling performance of the subsequent heat conductors. The smooth shape also minimizes particle dispersion, thereby reducing the extend of the accretion layer in the WHB.

The convection section has six rows of cooling screens and boiler tubes, which are approximated by rectangular plates. Flue dust particles can leave the domain via the bottom of the gas uptake, the radiation or convection section, or follow the main flow through the outlet towards the electrostatic precipitator (ESP).

Fig. 2
figure 2

Slice at center line through calculational mesh using the example of WHB with baffle plate Design 1. Refined areas are marked in red (Color figure online)

Full size image

In Figure 2, the calculational mesh is depicted using the example of the WHB with baffle plate Design 1. It consists of 50 million tetrahedral cells including a prismatic wall-adjacent layer, in which the \(y^+\) value was monitored to remain below 500. The large mesh is required due to the very different length scales in the domain, the tetrahedral cells allow a flexible meshing of the complex geometric shapes. A mesh convergence study showed that refinements at the radiation section entrance, below the oxygen inlet, around the baffle plate, the heat conductors and in the convection zone facilitate the correct estimation of the heat transfer and flow behavior.

Boundary conditions

Table I summarizes the inlet conditions for the FSF off-gas and the oxygen injection at the radiation section roof; the outlet is set as a pressure outlet.

Table I Inlet Conditions of FSF Off-Gas and Oxygen Injection, Calculated from Standard Process Conditions of the Real WHB
Full size table

The flue dust enters the domain with the same velocity and temperature as the off-gas through the off-gas inlet. The thermal and physical properties of the dust and the accretion layers and the dust particle size distribution are given in Section III–A–2.

The heat transfer coefficients of all cooling walls were adapted in an iterative procedure to fit a temperature profile from an industrial-scale WHB at standard operation, since the local heat transfer coefficients within the WHB are unknown.

Calculation of the local deposition rate

Table II summarizes the properties of the flue dust and the developing accretion layer. The physical properties were derived from Reference 26. The particle size distribution is typical for copper concentrate and is depicted in Figure 4.

Table II Inlet Conditions and Physical Properties of the Flue Dust and the Developing Accretion Layer
Full size table

Two User-Defined Functions (UDFs) are needed to calculate the formation of dust layers[18]:

  1. 1.

    The first UDF calculates the mass flow of sticky particles onto each wall cell. Particles are considered sticky, if they hit a wall with a temperature above the softening temperature \(T_{\rm soft}\) of 700 °C. The mass flow is saved in the respective cell memory and accumulates with increasing physical time.

  2. 2.

    The second UDF calculates the thickness of the resulting dust layer (see Section III–A–3), using a time ratio to enable long physical times. Afterwards, the new heat transfer coefficient is calculated based on the assumption that the dust buildup functions as an insulating layer.

Figure 3 shows the modeling of dust buildup in a schematic fashion in comparison to reality. In the real WHB, dust particles below the dust-softening temperature will be reflected from the wall, despite not necessarily fully elastically as in the model. Sticky particles above the critical temperature will stick to the wall, changing the WHB wall surfaces. Unlike the real dust buildup, the model does not include the geometric changes that come with dust layer formation, or the possible stickiness of the wall itself. Additionally, the dust layer is calculated per cell, with no smoothing between cells with different layer heights. A maximum layer thickness of 40 cm was implemented to prevent unphysically high local thermal resistances. In reality, the flue dust layer will be removed regularly by a hammer system, which is not included in the model. Hence, the observed temperature changes will be higher than in reality, making the temperature calculation a worst-case approximation.

Fig. 3
figure 3

Modeling of dust layer formation: comparison of reality and model (see Ref. 21)

Full size image

Estimation of the dust layer thickness

CFD simulations are often not suitable for calculating long physical times due to the computational effort. In this case, the short time scale for the fluid flow needs to be combined with the comparatively slow accretion buildup. Therefore, the fluid flow was calculated in steady state, while the mass of the injected Lagrangian particle streams equaled the flue dust mass flow in the real WHB for a physical time of 20 minutes, using a different time scale to reduce the computational effort. Hence, the dust layer thickness \(X_{\rm layer}\) is defined with the mass of deposited particles \(m_{\rm deposit, model}\), the cell area \(A_{\rm cell}\), the dust density \(\rho _{\rm dust}\) and the physical time step of 20 minutes:

$$\begin{aligned} X_{\rm layer}=\frac{{\dot{m}}_{\rm model}}{{\dot{m}}_{\rm reality}} \cdot \frac{m_{\rm deposit, model}}{A_{\rm cell} \cdot \rho _{\rm dust}} \cdot \varDelta t \end{aligned},$$
(2)

The de-coupling of the two time scales is reflected in the following algorithm, where the flow properties are calculated in a steady state, while the local deposition rate of the Lagrangian particles is calculated based on the converged solution[27,28,29]:

  1. 1.

    Calculation of steady flow until solution is converged.

  2. 2.

    Injection of Lagrangian particles with steady-state particle tracking.

  3. 3.

    Calculation of dust buildup thickness per cell as shown in Eq. [2].

  4. 4.

    Calculation of new wall heat transfer coefficient as described in the following.

  5. 5.

    Start of the new loop.

The new wall temperature \(h_{\rm wall, new}\) with the insulating dust layer is calculated with a modified function by Reference 20, neglecting the influence of the steel wall:

$$\begin{aligned} h_{\rm wall, new}= \left( \frac{X_{\rm layer}}{k_{\rm layer}} + {\frac{1}{h_{\rm conv,ext}}} \right) ^{-1} \end{aligned}.$$
(3)

Hence, the new wall heat transfer coefficient \(h_{\rm wall, new}\) depends on the external heat transfer coefficient \(h_{\rm conv,ext}\) and is reduced by the thermal resistance originating from the dust layer, consisting of the layer thickness \(X_{\rm layer}\) and the layer conductivity \(k_{\rm layer}.\)

Numerical Setup

The commercial CFD tool ANSYS Fluent 19.2 was used for the CFD simulations with the numerical setup as shown in Table III. When convergence was reached, the mass balance was closed below 0.02 pct and the energy balance was closed below 0.5 pct for all baffle plate designs.

Table III Numerical Setup
Full size table

Results and Discussion

Dust Capture Efficiency

Figure 4(a) shows the particle size distribution at the inlet and compares it to the resulting distribution at the outlet for all baffle plate modifications. In the WHB, the \(x_{50}\) decreases from 30 μm to approx. 14 μm for baffle plate Designs 1 and 3. For Design 2, the median value \(x_{50}\) is at approximately 12 μm. A size-dependent segregation is observable for all baffle plate designs, with coarse particles more prone to sedimentation and accretion formation in the WHB, meaning the \(x_{50}\) is lowered by half. However, only baffle plate Design 2 is able to decrease the \(x_{50}\) by another 2 μm more. In contrast, Design 3 does not change the particle size distribution compared to Design 1. Hence, the rounded baffle plate design does change the flow pattern enough to promote the sedimentation or accretion formation of coarse particles.

This finding is confirmed by the particle settling per section as depicted in Figure 4(b). In Design 1, over 85 pct of all sedimented particles either fell back into the flash smelting furnace settler or left the WHB through the outlet to the ESP; 4.7 pct settled in the radiation section, the remaining 8.0 pct in the convection section. This general distribution is only influenced to a minor extent by the baffle plate design. Moving the baffle plate closer to the gas uptake leads to a larger number of particles falling back into the furnace. This effect might be caused by stronger recirculation at the beginning of the radiation section and accounts for a 2.5 pct improvement for Design 2 and a 5.0 pct improvement for Design 3. Since the particle size distribution used at the WHB inlet originates from copper concentrate and, thus, might be coarser than the real flue dust, this effect might be less pronounced in reality. The sedimentation in the radiation section remains almost unchanged, leading to the conclusion that the direction of the flow downwards does not necessarily lead to enhanced sedimentation. However, an influence on sedimentation was visible in the convection zone. For Design 2, the settling improved by 16 pct, and for Design 3, it decreased by 17 pct. It can be concluded that leading the flow downwards early in the radiation section and increased dispersion are beneficial for the settling in the convection section, as the flow enters the convection section at a lower level (see Figure 5 for reference).

Figure 4(c) shows the distribution of accretions on the walls of the WHB after 12 h. Compared to Design 1, the previously explained recirculative flow pattern at the beginning of the radiation section leads to increased accretion formation in the gas uptake. Although this can be uncomplicated close to the FSF settler, where high temperatures might re-melt the accretions, at the connection of the gas uptake and the radition section this might cause operational challenges.

The largest share of accretions can be found on the radiation section walls, a situation that can be reduced by altering the baffle plate design. For Design 2, the share of accretion is reduced from 50.7 to 46.0 pct; for Design 3, it falls further to 44.4 pct. This reduced accretion formation seems to be influenced by two factors: (i) the accretion formation on the baffle plate and (ii) the reduction of particle dispersion. For Design 2, 4.4 pct of the reduction is directly caused by increased accretion formation on the baffle plate, preventing the particles from forming accretions elsewhere. This shows that part of the improvement seen in Figure 4(a) is due to flue dust being captured on the baffle plate in the form of accretions. For Design 3, only 0.3 pct can be explained in this fashion. Instead, the rounded design leads to less dispersion, minimizing the total area of accretion formation.

While the accretions on heat conductors in the convection section are not significantly influenced by the changed design, the heat conductors in the radiation section profit from the shielding by baffle plate Design 2, exhibiting 12.75 pct fewer accretions compared to Design 1. Design 3 does not exert this protecting function, leading to accretion formation comparable with that in Design 1. The accretions on the convection section walls are not influenced significantly and range from 7.0 to 5.37 pct of the total accretion formation. This entire analysis is limited by the total thickness limit of 40 cm, so thicknesses exceeding this value are not taken into consideration.

Fig. 4
figure 4

Dust capture with baffle plate modification: (a) particle size distribution at outlet, (b) dust collection, and (c) accretion formation in the WHB

Full size image

Accretion Formation Analysis over 24 Hours

Figure 5 shows the accretion formation in the entire WHB after 2, 12, and 24 hours. The accuracy of this prediction was ensured by comparison of the predicted accretion patterns to those from the real WHB. For Design 1 in Figures 5(a) through (c), the first accretions form in the gas uptake and in the entrance of the radiation section, especially at the top-left part of the radiation section roof. After 12 h, accretions can be seen in the center-lower part of the radiation section walls. The accretions are widespread and indicate that the flue dust is very widely dispersed. At the entrance of the convection section, the accretion pattern shows that the gas flow is focused on the upper part of the convection section. For Design 2 in Figures 5(d) to (f), the accretions are less focused on the top-left corner of the radiation section, indicating that the flow is more widely dispersed in the beginning of the radiation section compared to Design 1. The baffle plate pushes the gas flow downwards, leading to more accretion formation on the side walls of the radiation section. After the baffle plate, the flow starts to recirculate as clearly seen in Figure 5(d). After 12 h, the entire radiation section is covered in accretions, with a focus on the upper part of the walls in the first half of the radiation section. Compared to Design 1, the flow enters the convection section in a less focused manner, leaving a more even coating of accretions at the beginning of the convection section. For Design 3 in Figures 5(g) through (i), the flow is directed from the left to the right side at the solid baffle plate, creating a second accretion risk zone at the right-hand edge of the baffle plate. This phenomenon becomes clearer after 12 and 24 hours, showing large accretion zones following the streamlines. After the baffle plate, a dead zone is indicated by a lack of accretion. The flow is then directly aimed at the first two heat conductor rows, which is very disadvantageous compared to the other two designs. In contrast, the accretion formation at the beginning of the convection section is comparable to Design 2. The accretion zone lengthens with time in all designs, which is caused by increasing temperatures, the further dispersion of dust, and the thickness limit used.

Fig. 5
figure 5

Accretion formation in the entire WHB over 2, 6, and 24 h

Full size image

Figure 6 shows the accretion formation on the baffle plate and on the first two rows of heat conductors in the convection section after 24 hours for all baffle plate designs.

Fig. 6
figure 6

Accretion formation on the baffle plate ((a) through (c)) and on the first two rows of heat conductors in the radiation section ((d) through (f)) after 24 h

Full size image

All accretion patterns on the baffle plates given in Figures 6(a) through (c) confirm the bias of the flow towards the left side. While the baffle plates in Design 1 and Design 3 have a comparable area, indicating a similar accretion pattern, the larger area of baffle plate Design 2 is more heavily covered in flue dust, as already shown in Figure 4(c). Baffle plate Design 1 is located after the heat conductors, which are depicted in Figures 6(d) through (f). Hence, it cannot shield the heat conductors from accretions, which are again biased towards the left-hand side of the domain. Baffle plate Design 2 is located in front of the heat conductors and is longer than them, thus, completely shielding them. The comb-like structure does not prevent all sticky particles from hitting the heat conductors, so the accretion layer is evenly thinner than in Design 1 without the bias of the accretions changing. Due to the dust layer formation model depicted in Figure 3, local geometric changes due to the dust layer thickness cannot be observed in this study. This includes potential blockages in the comb-like structure of the baffle plate, which could increase the pressure drop further. Design 3 effectively shields the upper half of the heat conductors but directs the flow to the lower half, leading to increased accretion formation over the entire width of the WHB. In total, the accretion formation on the heat conductors in the radiation section is not minimized by using Design 3, as already shown in Figure 4(c).

Figure 7(b) shows the temperature increase caused by accretion formation over the course of 24 hours. Since the temperature increase is limited by the maximum accretion thickness and does not take into account the regular accretion removal in the WHB, the temperature is much higher than in the real WHB. All temperatures were measured in a cube with a side length of 10 cm placed at the end of the convection section, where a temperature probe is located in the real WHB (see Figure 7(a)). Design 1 shows the lowest initial temperature, which increases almost linearly by 52 °C over a period of 24 hours. Since the flow changes slightly with the temperature profile, small deviations from the linear increase are visible between 4 and 10 hours. When the same heat transfer coefficient is assumed for the baffle plate, Design 2 leads to an initial temperature that is 23 °C higher than for Design 1. The final temperature increase is 39 °C and the final temperature stabilizes after 20 hours. This is due to particles being captured on the baffle plate; as soon as the maximum layer thickness is reached, the temperature cannot increase much further. In contrast, Design 3 starts at a comparable temperature to Design 2 but increases by 31 °C in the first hour. After 24 hours, it reaches the highest final temperature of 484 °C. In this case, the streamlined baffle plate leads the flow from the left to the right side of the radiation section, creating another accretion risk zone and, thus, worsening the heat transfer rapidly.

Fig. 7
figure 7

Temperature sampling location and temperature increase for all baffle plate designs over 24 h

Full size image

Conclusions

This study evaluated the effect of the baffle plate design on the sedimentation and accretion formation of flue dust, examining the decreasing cooling performance of the WHB over the course of 24 hours. Moving the baffle plate forward in the radiation section increases the settling in the convection section slightly while leaving the settling in the radiation section almost unchanged. Instead, the baffle plates showed increased accretion formation, thus, “capturing” the particles before they could settle. Design 2 moved the accretion risk zone to the front of the radiation section, while shielding the following heat conductors. While this led to a higher initial temperature, this design was found to produce the lowest temperature increase in the model. In contrast, Design 3 produced a smaller accretion risk area as there was less dispersion, but it had the highest impact on the cooling performance.

Based on this study, the following design recommendations can be derived:

  1. 1.

    Moving the baffle plate forward can push the flow downwards, leading to slightly more sedimentation and minimizing the dead zone in the lower part of the radiation section. However, the baffle plate is covered in flue dust accretions quickly, decreasing its cooling performance.

  2. 2.

    Streamlined design leads to smaller accretion risk zones, but emphasizes the existing ones. In operation, these risk zones should be easy to clean, otherwise the cooling performance might be impacted.

  3. 3.

    Dispersive designs increase the size of the accretion risk zone but lead to a more even coating with flue dust, making the expected temperature increase slower.