Introduction

Copper is one of the key metals for the circular economy. It combines unique physical properties with the ability to be used as a solvent for other industrial metals.[1] In 2019, the Flash Smelting Furnace (FSF) accounted for 67 pct of worldwide copper smelting.[2] Developed in 1949, the FSF is based on the auto-thermal smelting of copper concentrates, producing copper-rich matte, slag, and off-gas that is high in sulfur dioxide.[3,4] The FSF is an advantageous technology for smelting copper concentrates, both from an economic and an environmental point of view.[5] Its main advantages are as follows: (i) it saves energy by using the chemical energy bound in the concentrate and (ii) it produces off-gas with a high concentration of \(\hbox{SO}_{2}\) that can be captured as sulfuric acid.[3,5]

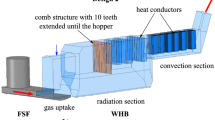
The FSF is followed by a horizontal process unit, the Waste Heat Boiler (WHB).[6] It connects the FSF to the acid plant and has the following functions: i) cooling the off-gas to approx. \(400\,^{\circ }\hbox{C}\) while keeping the \(\hbox{SO}_{2}\) content high and recovering heat from the copper production process, ii) dust precipitation, and iii) providing conditions which allow only the desired chemical reactions to occur (e.g., dust sulfation by oxygen injection).[7] The process conditions in the WHB are harsh, with high inlet temperatures and large amounts of (semi-)molten, often sticky dusts, making experimental studies challenging.[7,8]

Despite its downstream position,[9] stated that the WHB should not be considered as a “tail-end” process unit. Instead, the WHB is often a bottleneck for the whole production process.[8] As a study on Jinlong’s copper FSF in 2002 showed, failures in the WHB were responsible for 36 pct of all furnace downtime.[10]

Furthermore, the recovery of heat as pressurized vapor minimizes the operational costs and has an important impact on the overall energy balance of the process.[11,12] As shown by Reference 5, 29.3 pct of the process heat leaves the furnace with the off-gas, proving the enormous potential for energy recovery.[5]

The WHB is sensitive to problems with flue dust handling.[10,13,14] Above its softening temperature and depending on its mineralogical composition, flue dust can become sticky, forming accretions in the radiation section[13,12,15,16,17] or lead to surface fouling and blockages in the convection section.[8,12,13]

Dust accretions are usually removed regularly by a hammer system integrated within the WHB.[7,11] However, many industrial reports describe other approaches to minimize problems with flue dust. These can be distinguished into three mechanisms: (i) adding additional oxygen or air for after-burning and dust sulfation,[13,16,18,19] (ii) adding additional substances to change the flue dust properties (e.g., soda ash[20]), and (iii) changing the temperature and velocity profile within the WHB.[16,21,22] The last approach is based on the limited temperature range for flue dust to be sticky, meaning that rapid cooling and dust removal in the radiation section can prevent surface fouling in the convection section.[21,22]

The physical and thermal properties of flue dust have been investigated in various studies focusing on the particle size distribution,[23,24] the chemical and mineralogical composition,[18,24,25] and the thermal, insulating properties of flue dust.[23] Reference 26 focused on flue dust after the electrostatic precipitator downstream of the WHB. It was found that flue dust forms either mechanically, by convective transport, or chemically, by the condensation of species while the gas cools. Comparable studies exist for the accretions from the gas uptake and radiation section.[19,27]

Not only industrial experience but also Computational Fluid Dynamics (CFD) simulations can provide new insights into the complex flow behavior in the WHB.[4,7] Previous CFD studies focused on dust flow and settling in the radiation section.[28,29] In 1997, the dust-laden gas flow was modeled with an Eulerian–Eulerian approach, which does not allow single particle tracking.[28] Additionally, some calculations were performed in which the influence of dust was modeled by correlations. In the first approach, physical interaction between the phases was considered using an Algebraic-Slip model. Heat transfer in the gaseous phase was considered, while the particles were modeled isothermally in a two-dimensional calculational domain. It was found that the settling of dust particles in the radiation section is size-dependent. Only particles with a diameter above \(20\,\mu\hbox{m}\) settled in the first dust hopper. No particle accumulation occured in the second dust hopper. In total, the WHB reached a capture efficiency of 40 pct for large particles of \(100\,\mu\hbox{m}\) and 30 pct for small particles below \(50\,\mu \hbox{m}.\)

In 1999, this model was extended to include off-gas recirculation in a three-dimensional model.[29] The additional off-gas inlet was found to change the main flow significantly. 30 pct dead volume was found in the radiation section, a figure which was lowered to 15 pct by modifying the boiler geometry. The dust flow was calculated using an Eulerian–Eulerian and an Eulerian–Lagrangian approach. While the first approach led to results comparable to the previous study, the Eulerian–Lagrangian approach showed that uniformly-sized, \(50\,\mu \hbox{m}\) dust particles follow the main gas flow. The influence of dust stickiness was not considered; instead, the dust particles were elastically reflected from the boiler walls.

A more recent study by Reference 30 focused on the three-dimensional gas flow and heat transfer in a WHB including radiation via the P1 model and air leakages from the dust hoppers. The description of the P1 radiation model can be found in Reference 31. The influence of dust was calculated via empirical correlations. The total heat transfer was found to comprise 83 to 93 pct of radiative heat transfer. While including a baffle plate halfway into the radiation section and elevating the radiation ceiling improved the gas flow and heat transfer, including more baffle plates did not further enhance the heat transfer.

A study by Reference 32 investigated the influence of design modification on the gas flow and heat transfer throughout the WHB. The positive influence that an additional oxygen inlet and the first baffle plate exerted on the overall flow was confirmed in that study. Furthermore, the modification of the conjunction between the gas uptake and WHB was found to allow a more uniform gas flow.

The aim of the present study is to provide more insight into the physical dust behavior in the three-dimensional WHB. Phenomena such as size-dependent particle settling and the formation of flue dust accretions will be investigated with an Eulerian–Lagrangian approach. The evaluation of flue dust accretions depending on the dust softening temperature has not been investigated yet. Therefore, a new sticking function for flue dust is developed. Finally, physical risk factors for flue dust accretions and suitable operational recommendations will be derived from the CFD model.

Methods

Computational Fluid Dynamics

To simulate the fluid flow and heat transfer, the incompressible, stationary Navier–Stokes equations are calculated. For that purpose, the k–\(\omega \) SST (shear stress transport) turbulence model was chosen, as it is suitable for a wider range of flows than the industrially more often used k–\(\epsilon \) model.[33] Its implementation can be found in Reference 31. A pre-study showed that the P1 model overestimated the radiative heat flux while decreasing the numerical stability, as already described in Reference 34. All the physical properties of the gas were derived from temperature-dependent polynomials in the FLUENT Database.[31] Radiation was modeled with the Discrete-Ordinates (DO) radiation model.

The influence of dust loading was modeled with a Lagrangian–Eulerian approach, which is valid for a particle volume fraction up to about 10 to 12 pct. This assumption is valid for the current setup. The discrete second phase is calculated as representative parcel trajectories, which include heat and mass transfer between the continuous and the discrete phases. Each trajectory is considered to be a parcel of particles, which all sum up to the complete mass flow rate. The particles are assumed to be spherical (see backscattered electron (BSE) images in Reference 25). The forces acting on the particle are assumed to consist only of drag forces and gravitational force. For spherical particles, the drag coefficient \(C_\text{D}\) is calculated with constants a1 to a3.[35]

$$\begin{aligned} C_\text{D}=a_1 + \frac{a_2}{\text{Re}} + \frac{a_3}{\text{Re}^2} \end{aligned}$$
(1)

Forces originating from rotation (e.g., the Magnus lift force) or shear (e.g., the Saffman force, virtual mass force) are negligible or not valid for the present particle shape and density and viscosity ratios of the particles and fluid. The influence of the discrete phase on the continuous phase is included via additional forces in the momentum and heat balance. This approach is known as two-way coupling. The influence of turbulent dispersion was calculated using the Random Walk Model with three representative particles for each trajectory.

Preparation and Analysis of Dust Samples

Dust samples from the electrostatic precipitator were analyzed regarding their particle size distribution and morphology. Due to the electrostatic separation procedure, the primary particles form large aggregates. For the backscattered electron (BSE) microscope analysis, an aggregate was randomly chosen, cut, and embedded in epoxy resin.

The granulometric analysis was carried out by laser diffraction, using dry dispersion. Before this procedure, the aggregates were carefully deagglomerated manually.

CFD Simulations

Computational Domain and Mesh

Figure 1 shows the WHB geometry in connection to the flash smelting furnace. The WHB is joined to the FSF via the gas uptake. In order to obtain the correct flow pattern at the WHB inlet, the gas uptake is included in the calculation domain, which is marked in blue. The WHB consists of a radiation section and a convection section. A transverse baffle plate is located in the last third of the radiation section. The convection section is filled with six rows of heat conductors. This is a geometric simplification compared to the usual tube banks and is used to decrease the size of the calculational mesh required. The entire domain is approx. \(60\,\hbox{m}\) in length, \(20\,\hbox{m}\) in height, and \(10\,\hbox{m}\) in width.

Fig. 1
figure 1

Setup of WHB and connection to FSF. The calculational domain is marked in blue, the red arrows show the flow direction (Color figure online)

Full size image

For this computational domain, a mesh convergence study with three meshes was conducted. The first step taken was to investigate the effect achieved by refining areas around the baffle plate and in the convection zone. The refinement lowers the outlet temperature by \(7\,^{\circ }\hbox{C}\) and stabilizes the convergence. Adding an additional refinement in the near-wall zone by including a prism layer lowered the outlet temperature by an additional \(19\,^{\circ }\hbox{C}\) to \(451\,^{\circ }\hbox{C}.\) The maximum outlet temperature deviation in the calculated meshes is therefore 3.7 pct.

The resulting mesh is shown in Figure 2. It consists of 38  million tetrahedral cells and the wall-adjacent cell layer was designed as a prism layer. The mesh is locally refined around the baffle plate and in the convection section. This allows the correct capture of flow characteristics in the gaps between the baffle plate segments and between the heat conductors. The maximum \(y^+\) value was monitored to ensure that it remained below 500, although the enhanced wall treatment in the k–\(\omega \) SST model is insensitive to the wall resolution.

Fig. 2
figure 2

Calculation mesh with zoom into refined areas. The inlet is marked in green, the outlet in red, and the cooled area in blue (Color figure online)

Full size image

Boundary conditions

As shown in Figure 2, the gas flow enters the domain through the gas uptake, which joins the FSF and the WHB. Its inlet conditions are summarized in Table I. As a boundary condition, the inlet volume flow was set to \(63\,\hbox{kNm}^{3}/\hbox{h}\) at a temperature of \(1350\,^{\circ }\hbox{C},\) which are typical process parameters for an industrial-scale WHB.[30] The flue dust enters the domain at the same velocity and temperature; the density \(\rho \) and heat capacity \(c_\text{p}\) were derived from Reference 23. The particle size groups for the analysis of accretion risk areas were chosen in the typical particle size range of flue dust as given in Reference 25. Each particle size group has the same number of flue dust particles, since the flue dust accretions are evaluated only qualitatively and not for a specific particle size distribution. However, the particle size groups can be easily adapted to a measured particle size distribution with this setup.

Table I Inlet Conditions of FSF Off-Gas and Flue Dust Particles, Calculated From Standard Process Conditions of an Industrial-Scale WHB
Full size table

The walls, the baffle plate, and the heat conductors in the radiation and convection zones are cooled. The heat transfer coefficients are set to obtain a realistic temperature profile (see Figure 2). This adaptation procedure has already been described by References 28, 29, and 30. The heat transfer coefficients in the authentic WHB are unknown as the different surfaces are not evenly coated with flue dust. The geometric simplification of the heat conductors makes the further calibration of the heat transfer necessary. Since the calculation of accretion risk zones depends on the temperature profile, the heat transfer must be adapted when evaluating another WHB geometry. In this case, the average outlet temperature is \(450\,^{\circ }\hbox{C}.\)

The discrete flue dust particles can leave the domain via the bottom of radiation and convection zone and move to the dust hoppers or via the outlet and move to the ESP. Using particle sampling in these areas, the size-dependent settling behavior in the WHB can be visualized.

Sticking function

Sticking functions can be used to define the conditions under which particles will be captured on walls and might depend on factors such as the particle/wall temperature or its Weber number, as described in Reference 36. In this case, the particle temperature was the criterion for stickiness because industrial experience shows that dust particles are sticky at temperatures above \(700\,^{\circ }\hbox{C}.\) This concept has already been described for other kinds of fly ashes, where deposits are formed easily once the melting temperature of fly ash is reached.[37] This sticking function was applied to all walls. Thereby, the particles are elastically reflected, if they are below the softening temperature. If they are above the softening temperature, the sticking function applies. This dust softening temperature was set to \(700\,^{\circ }\hbox{C}\) based on industrial experience. Thus, whenever a particle hits the wall and sticks, its trajectory is ended and it is saved as a count in the memory of the adjacent cell. This principle is visualized in Figure 3.

This simplified approach does not account for the stickiness of the wall itself, the influence of the chemical or mineralogical composition of the particle, or the angle of the particle impact. Therefore, it does not reflect the actual sticking behavior of dust, which is unknown for the WHB. Instead, it is a visual approach to the locations of critical zones in the three-dimensional domain.

Fig. 3
figure 3

Schematic explanation for the sticking function

Full size image

Numerical Setup

The commercial CFD tool ANSYS Fluent 19.2 was used for the CFD simulations. The numerical setup is summarized in Table II. When selecting the convergence criteria, the mass balance was closed to \(10^{-5}\) pct, and the energy balance was closed to \(10^{-4}\) pct.

Table II Numerical Setup
Full size table

Results and Discussion

Size-Dependent Flue Dust Settling and Representative Particle Trajectories

The particle trajectories can be divided into three categories, for which example trajectories and the separation curve are given in Figure 4. The particle sizes are sorted according to their average particle track length in the WHB, from the shortest track to the longest:

  1. 1.

    Coarse flue dust \(>100\,\mu\hbox{m}\): Most particles fall back into the FSF settler. A smaller fraction reaches the radiation section to settle. This size group forms accretions only in the lower part of the gas uptake, opposite to the inlet. This kind of accretion is caused by the inlet flow setup opposite the wall and might not relate to an actual phenomenon, since the high temperatures above the molten bath might cause the accretions above to melt and fall back into the bath (Figure 4(a)).

  2. 2.

    Medium-fine flue dust 10 – \(100\,\mu\hbox{m}\): Most particles reach the radiation section or the convection section. Medium-fine particles form accretions comparable to the ones of coarse flue dust and minor accretions in the radiation zone (Figure 4(b)).

  3. 3.

    Fine flue dust \(<10\,\mu\hbox{m}\): Fine particles mainly follow the gas flow without sedimentation. This particle size group should be mainly related to the ESP dust. These particles form accretions throughout the WHB (Figure 4(c)).

Fig. 4
figure 4

Typical trajectories of flue dust particles depending on flue dust diameter ((a) through (c)) and resulting separation curve (d)

Full size image

The particle trajectory analysis shows that there is size-dependent sedimentation in the WHB, which is in accordance with the findings from previous CFD models.[28,29] Sampling studies by References 25 and 26 show that this phenomenon is also seen in industrial-scale WHBs and leads to the separation of flue dust compositions. In general, coarse flue dust is mainly formed mechanically by carry-over and breakage of concentrate from the FSF, while very fine flue dust can also be formed chemically by condensation. From the findings above, it can be concluded that chemically formed flue dust can be especially critical for flue dust accretions in the WHB, especially in the convection zone.

Figure 4(d) depicts the particle separation curves derived from the CFD model and visualizes the particle behavior explained above. It shows that particles with a diameter between \(10\,\mu\hbox{m}\) and \(100\,\mu\hbox{m}\) make up the main share of WHB dust. Most larger particles fall back into the furnace and thus are not visible in the WHB flue dust. This situation does not apply to any larger particle agglomerates that may form within the radiation section. The agglomeration of particles is not included in this model. Small particles below \(10\,\mu\hbox{m}\) leave the WHB to form ESP dust, although Figure 4(d) indicates that there might be some carry-over from particles below \(70\,\mu\hbox{m}.\) The validation of this ESP dust prediction with the help of a sampling study can be found in Section IV–C.

Evaluation of Risk Zones for Flue Dust Accretions

Figure 5 shows the accretion pattern as predicted by the CFD model. Figure 5(a) shows the accretions throughout the computational domain. Region A is hit by the highest number of sticky particles, since it is located directly opposite the flow inlet. It must be mentioned that the very high temperatures in Region A might cause the accretions to melt and fall back into the FSF settler. Because of this, the accretions right above the metal bath are of lesser interest.

From that point on, the accretions follow the main flow. When entering the radiation section, the flow is biased towards the left side, which is closer to the FSF reaction shaft. This phenomenon was described for this type of WHB in Reference 7. Until the baffle plate (B), the flow and the accretion risk zone even out, as depicted in Figure 5(b).

In Figure 5(c), the accretions at the heat conductors (C) and the streamlines are given. It can be seen that the first two rows of the heat conductors are especially prone to accretion formation, since the temperature is above the dust softening temperature. Furthermore, the center of heat conductors is especially affected, as the main flow is directed at it. Figure 5(d) summarizes the accretion formation per WHB section. With decreasing temperatures along the length of the WHB, the accretion formation decreases. Hence, \(84\,\text{pct}\) of all sticky particles form accretions in the gas uptake and the radiation zone. The baffle plate accounts for \(2\,\text{pct}\) of all accretions. While the convection zone walls are less affected (\(4\,\text{pct}\)), the heat conductors seem to function as a filter for the remaining sticky particles, with \(10\,\text{pct}\) of all accretions found there.

When the character of dust is altered, e.g., by chemical reactions, this might influence the dust softening temperature. In Figure 6, the results of a parameter study for \(T_\text{soft}\) are summarized. Increasing the dust softening temperature by \(50\,^{\circ}\hbox{C}\) to \(750\,^{\circ}\hbox{C}\) is seen to keep the convection section cleaner in terms of accretions; the amount of the latter is reduced by 68 pct with regard to the heat conductors, as shown in Figure 6(c). Increasing \(T_\text{soft}\) further to \(800\,^{\circ}\hbox{C}\) leads to 99 pct fewer accretions at the heat conductors (see Figure 6(d)). When lowering \(T_\text{soft}\) by \(50\,^{\circ}\hbox{C},\) the accretion risk zone grows until it includes the entire third row of heat conductors as shown in Figure 6(b), which increases the number of sticky particles by \(102\,\text{pct}\) compared to the original setup. Lowering \(T_\text{soft}\) further to \(600\,^{\circ }\hbox{C}\) does not increase the accretion risk zone, but increases the dust accretions by another \(64\,\text{pct}\) (see Figure 6(a)).

This parameter study regarding \(T_\text{soft}\) shows the potential of changing the dust mineralogy towards higher melting and softening temperatures, for example, by oxidizing the sulfides in the flue dust. A higher \(T_\text{soft}\) will keep accretion formation within the radiation section, preventing blockages and surface fouling in the convection section. On the other hand, this shows the need to determine \(T_\text{soft}\) more exactly to refine the model further.

Fig. 5
figure 5

Accretion risk zone analysis

Full size image
Fig. 6
figure 6

Parameter study for particle softening temperature \(T_\text{soft}\)

Full size image

Using the previously described approach for prediction of accretion risk zones, the following principles should be taken into account when attempting to minimize the formation of flue dust accretions:

  1. 1.

    Direct particle–wall collisions can lead to accretions, if the particles or the walls are above the softening temperature, and thus should be avoided. However, it should be considered that bends in the flow might be beneficial for the sedimentation of coarse particles, for example, as caused by baffle plates.

  2. 2.

    The angular gas uptake design leads to asymmetric accretion formation within the first half of the radiation section. Also, flow separation at the WHB entrance causes particle dispersion and thus contributes to larger accretion zones. Hence, the gas uptake design is an important influence factor on the accretion formation within the radiation section.

  3. 3.

    Gas cooling should be as rapid as possible to stop dust entering the convection zone while still sticky. With the present WHB setup, this could be achieved by enlarging the heat transfer surfaces and reducing the amount of stagnant fluid.

  4. 4.

    Low-melting components of the dust have the potential to cause serious accretion formation. Hence, a high-melting dust mineralogy is advantageous.

Validation with Dust Samples from Electrostatic Precipitator

Figure 7 shows an inverted BSE image of the agglomerated ESP dust sample, depicting the complexity of the flue dust composition with regard to particle morphology and composition. Expected phases such as concentrate and slag inclusions and condensed zinc were found. A large number of sub-micron particles are visible, validating the separation curve given in Figure 4(d). The largest particle found is a concentrate inclusion with a diameter of approx. \(85\,\mu \hbox{m}\) including a sulfate layer. No particles above \(100\,\mu \hbox{m}\) were seen, supporting the CFD finding that particles of this size either fall back into the furnace settler or settle in the radiation section.

Fig. 7
figure 7

Inverted BSE image of agglomerated ESP dust sample

Full size image

Figure 8 shows the cumulative distribution \(Q_3\) as determined by laser diffraction, depending on the dispersion pressure used for dry dispersion. The cumulative distributions are independent of the dispersion pressure, which can be interpreted that the particles are strongly agglomerated. This might be caused by capillary condensation binding the very fine particles firmly when electrostatically separated from the gas flow. Overall, the particle sizes are larger than previously reported in the literature or as expected from the BSE images. Compared to the findings by Reference 25, who determined a \(x_{50}\) of approx. \(5\,\mu\hbox{m}\) with a water-dispersed sample, the \(x_{50}\) with dry dispersion is approx. \(20\,\mu\hbox{m}.\) The dry dispersion might be a preferable approach for determining the size distribution, because it includes the water-soluble sulfate layers around the primary particles. However, the manual deagglomeration described in Section II–B was apparently not sufficient, causing an overestimation of the particle size. This also includes the appearance of particles above \(100\,\mu\hbox{m},\) which are predicted neither by BSE images nor by CFD results. For future granulometric analysis, it might be beneficial to choose a different means of deagglomeration, e.g., pretreatment with a high shear mixer. Therefore, the particle size distribution from BSE images might be advantageous for ESP dust.

Fig. 8
figure 8

Averaged cumulative particle size distribution as analyzed with laser diffraction of five measurements per dispersion pressure setting. At \(x_{50},\) the standard deviation is below \(1\,\mu\hbox{m}\) for all runs

Full size image

Conclusion

In this study, the settling of flue dust and accretion formation in a copper FSF WHB was investigated using a 3D CFD model. The settling of flue dust was validated pointwise with BSE images of the ESP flue dust. In accordance with the literature, the sedimentation of particles in WHB was found to be dependent on the particle size. Risk areas for flue dust accretions were predicted for the entire WHB domain. While the accretions in the radiation zone were not influenced by changes in the dust softening temperature, the convection zone was kept accretion-free by increasing the dust softening temperature to \(750\,^{\circ }\hbox{C}\).

Based on these results, the following risk factors for flue dust accretions are distinguishable:

  1. 1.

    A non-optimized flow field, which leads to many particle/wall collisions or fails to separate coarse flue dust from the main flow.

  2. 2.

    Slow cooling of the gas flow, causing the potential zone for flue dust accretions to grow

  3. 3.

    Sticky flue dust, which contains many low-melting mineralogical components.

To operate the WHB with maximum operability, the following recommendations can be made based on the CFD model: (i) cooling in the radiation zone should be rapid, to prevent flue dust from entering the convection zone in a sticky state and (ii) there should be special focus on the critical, low-melting flue dust components.