Introduction

The tundish, working as a buffer and distributor of molten steel between ladle and mold, plays a key role in affecting the performance of casting machine. Tundish design varies widely, owing to differences in the end products, number of strands, and operating parameters. Focusing on the superior steel quality, a modern casting tundish is designed to ensure the homogeneity of liquid steel and enhance the inclusion removal.[1,2,3,4]

To study liquid steel mixing behavior in tundish, residence time distribution (RTD) is widely used for analyzing liquid mixing. Using RTD in flow mixing analysis in chemical reactor, was initially proposed by MacMullin and Weber in 1935[5]; thereafter Danckwert carried out a study of mixing performance in non-ideal reactors using RTD theory.[6] Since then, RTD has been widely used as an important indicator to analyze industrial reactors.[7]

Residence-time distribution analysis in tundish can be derived through a pulse injection of tracer at the inlet and monitoring its concentration at the outlet. RTD data analysis can provide mean residence time, volume fractions of flow regimes (plug flow, mixed flow and dead zone) in the tundish.[8,9,10,11] Many RTD studies were focusing on the optimization of flow control devices in the tundish, such as weir and dam,[12,13,14] turbulence inhibitor[15,16,17] and gas curtain.[18,19,20] These studies led to a considerable improvement in understanding various flow phenomena associated with tundish operations. However, RTD theory is also limited in following two aspects: (i) The probability function of residence time cannot disclose the local mixing states (e.g. the locations of short-circuiting flow and dead zone) inside the tundish, which are critical for the performance analysis; (ii) A long computing time is often required to capture the long-time tail of RTD curve, especially for the tundish with a large turnover time.

Mean age, introduced by Danckwerts, is defined as the average time of all material passing through a given location in a continuous system.[21] To measure a complete distribution of mean age requires multiple sampling across an entire system, which is impractical and expensive. However, it is viable to calculate the mean age distribution using CFD model. In comparison with the transient RTD model, the low computing costs and accurate predictions of mean age using CFD were demonstrated in the research of ventilation and building,[22,23] water science[24] and chemical reactors.[25,26]

The author recently employed a simulation-based digital design method to optimize the performance of tundish.[27,28] The long computing time is an issue that occurred when using the transient RTD model, particularly for the large number of case studies. The mean age model based on the steady-state solution is therefore of interest, although it is relative obscurity in the metallurgical applications. This innovative approach will enable researchers to perform parameter studies to a wider extent. Moreover, the spatial distribution of mean age can provide considerable insight of melt mixing in tundish.

The purpose of present work is threefold: (i) To apply mean age theory for melt mixing analysis in tundish; (ii) To compare the results using mean age and RTD theory; (iii) To introduce a new criterion, melt change efficiency (MCE), which can be used for the design optimization of the tundish.

Model Description

CFD Model

CFD software STAR-CCM + V.15 (Siemens PLM software, Plano, TX) was used in this study.[29] The assumptions made for the mathematical model are described below:

  • The model is based on a 3D standard set of the Navier–Stokes equations.

  • Nonisothermal and steady-state flow is calculated.

  • Density of fluid is constant.

  • The realizable k-ε model is used to describe the turbulence.

  • The free surface is flat and is kept at a fixed level. The slag layer is not included.

Transport equation

In the CFD model, the conservation of a general flow variable ϕ, for example, the density, momentum, within a finite control volume can be expressed as a balance between the various processes. The calculation of single-phase incompressible flow is accomplished by solving the mass and momentum conservation equations. The equations solved in CFD code are written in a general form as:

$$ \rho \frac{{\partial \overline{\phi }}}{\partial t} + \rho \overline{{u_{j} }} \frac{{\partial \overline{\phi }}}{{\partial x_{j} }} - \frac{\partial }{{\partial x_{j} }}\left[ {\Gamma_{{\phi ,{\text{eff}}}} \frac{{\partial \overline{\phi }}}{{\partial x_{j} }}} \right] = S_{\phi } $$
(1)

where ϕ represents the solved variable, Гϕ,eff is the effective diffusion coefficient, Sϕ is the source term, xj are the Cartesian coordinates, uj are the corresponding average velocity components, t is the time and ρ is the density.

Equations [2] through [5] are used to describe the continuous phase.[30]

$$ {\text{Continuity}}:\,\frac{{\partial \left( {\rho u_{j} } \right)}}{{\partial x_{j} }} = 0 $$
(2)
$$ {\text{Momentum}}:\,\rho u_{j} \frac{{\partial u_{i} }}{{\partial x_{j} }} = - \frac{\partial P}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \mu_{t} } \right)\left\{ {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right\}} \right] + \rho g_{i} $$
(3)

Realizable k–ε model:[31]

$$ \frac{\partial }{\partial t}\left( {\rho k} \right) + \frac{\partial }{{\partial x_{j} }}\left( {\rho ku_{j} } \right) = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{k} }}} \right)\frac{\partial k}{{\partial x_{j} }}} \right] + G_{k} + G_{b} - \rho \varepsilon - Y_{M} + S_{k} $$
(4)
$$ \frac{\partial }{\partial t}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial x_{j} }}\left( {\rho \varepsilon u_{j} } \right) = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\mu + \frac{{\mu_{t} }}{{\sigma_{\varepsilon } }}} \right)\frac{\partial \varepsilon }{{\partial x_{j} }}} \right] + \rho C_{1} S\varepsilon - \rho C_{2} \frac{{\varepsilon^{2} }}{{k + \sqrt {v\varepsilon } }} + C_{1\varepsilon } \frac{\varepsilon }{k}C_{3} G_{b} + S_{\varepsilon } $$
(5)

where k is the turbulent kinetic energy; ε is the turbulent energy dissipation rate; µ is the molecular viscosity; µt is the turbulent viscosity; Gk represents the generation of turbulent kinetic energy due to the mean velocity; YM symbolizes the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate; υ is the kinematic viscosity; σk and σε are the turbulent Prandtl numbers for k and ε, respectively.

The success of numeric prediction methods depends to a great extent on the performance of the turbulence model used. The realizable k–ε model was applied in the current study, which is a two-layer approach using fine mesh that resolve the viscous sublayer.

Residence-time distribution

To calculate the RTD curve, a transport equation of tracer concentration is used (Eq. [6]). For an incompressible steady-state flow with constant density, the scalar transport equation is solved at each time step once the fluid field is calculated.

$$ \frac{\partial C}{{\partial t}} + \frac{{\partial u_{j} C}}{{\partial x_{j} }} - \frac{\partial }{{\partial x_{j} }}\left[ {D_{{{\text{eff}}}} \frac{\partial C}{{\partial x_{j} }}} \right] = 0 $$
(6)

where Deff is the turbulent effective diffusivity, defined as

$$ D_{{{\text{eff}}}} = D_{m} + \frac{{\nu_{t} }}{Sc} $$
(7)

where Dm is the molecular diffusivity, νt is the turbulent viscosity and Sc is Schmidt number with a constant value of 0.7.

To solve Eq. [6], boundary conditions are given as following:

$$ {\text{Inlet}}:\,C\, = \,{1}\, \, \left( {t\, \le \,{\text{injection}}\,{\text{time}}} \right),\quad C\, = \,0 \, \left( {t\, > \,{\text{injecting}}\,{\text{time}}} \right) $$
(8)
$$ {\text{Outlet}}:\,\,\frac{\partial C}{{\partial x_{n} }}\, = \,0\quad \left( {x_{n} \,{\text{is}}\,{\text{the}}\,{\text{normal}}\,{\text{direction}}} \right) $$
(9)
$$ {\text{Wall}}\,{\text{and}}\,{\text{surface}}:\,{ }\frac{\partial C}{{\partial x_{n} }}\, = \,0\quad \left( {x_{n} \,{\text{is }}\,{\text{the}}\,{\text{normal}}\,{\text{direction}}} \right) $$
(10)

Mean age

The transport equation for mean age in a steady flow was derived from a pulse tracer input by Spalding,[32] Sandberg,[33] Liu[34] and Russ.[35] (see APPENDIX)

$$ \frac{{\partial u_{j} a}}{{\partial x_{j} }} - \frac{\partial }{{\partial x_{j} }}\left[ {D_{{{\text{eff}}}} \frac{\partial a}{{\partial x_{j} }}} \right] = 1 $$
(11)

To solve Eq. [11], boundary conditions are given as:

$$ {\text{Inlet}}\quad a\, = \,0\quad \left( {{\text{fresh}}\,{\text{liquid}}\,{\text{of}}\,{\text{zero - age}}} \right) $$
(12)
$$ {\text{Outlet}}\,\frac{\partial a}{{\partial x_{n} }}\, = \,0\quad \left( {x_{n} \,{\text{is}}\,{\text{the}}\,{\text{normal}}\,{\text{direction}}} \right) $$
(13)
$$ {\text{Wall}}\,{\text{and}}\,{\text{surface}} \,\frac{\partial a}{{\partial x_{n} }}\, = \,0\quad \left( {x_{n} \,{\text{is}}\,{\text{the}}\,{\text{normal}}\,{\text{direction}}} \right) $$
(14)

Geometry, mesh and boundary conditions

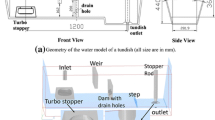
A single-strand tundish (51 tons) for casting slab product was studied in the present work. The geometric dimensions are illustrated in Figure 1.

Fig. 1
figure 1

Dimensions of a single-strand tundish with flow control devices of dam, weir and turbulence inhibitor (a) side view (b) front view (unit: mm)

Full size image

The volume mesh was generated in Star-CCM + V.15 with the option of trimmer and prism layer. Three prism layers were generated next to all the walls. A base mesh size of 0.006 m was used for the simulation of the tundish. The average y + value near the wall boundary is 3. A half tundish was simulated through its symmetry plane. The CFD model possesses a total of 3.5 million trimmer cells in the computing domain.

No-slip conditions were applied on walls for the liquid phase. A constant mass flow was used at the inlet. The outflow boundary condition was applied at the outlet. A wall function was used to provide the near-wall boundary conditions for solving the transport equations. Zero mass flux was applied at walls and top surface for solving the passive scalar equation. At t = 0–2 seconds the mass fraction of tracer at the inlet was set to be equal to 1. When t > 2 seconds, it was given as zero. The concentration of the tracer at the outlet was monitored from t = 0 to 2600 seconds and the RTD curves were obtained from the numerical calculation. A summary of input parameters and boundary conditions used for CFD simulations are given in Table I.

Table I Input Parameters and Boundary Conditions Used for Water Model and CFD Model
Full size table

Solution procedure

The discretized equations were solved using the semi-implicit method for the pressure-linked equations (SIMPLE) algorithm. The second-order upwind scheme was applied to calculate the convective flux in the momentum equations. The solution was considered to be converged when the residuals of all solved variables were less than 1 × 10−4. The under-relaxation parameters for solving pressure, velocity and turbulence equations were 0.3, 0.7 and 0.8, respectively. To calculate the RTD curves in the prototype, the flow fields were first calculated in steady-state. Then, the transient calculations were performed to solve the tracer passive scalar equation. The steady-state calculations were performed to solve the passive scalar equation of mean age.

Model validation and verification

Model verification and validation (V&V) are essential parts of the model development process if CFD models will be used with sufficient confidence in industrial applications.[36] Quantitative V&V of CFD calculations are usually performed by comparing the model predictions against trustworthy data. A reliable assessment of the CFD model requires the calculations to be undertaken with complete control over the numerical errors and uncertainties to avoid erroneous conclusions.[37]

A CFD benchmark exercises were recently performed by the author to determine appropriate modelling strategies.[38] In that work, the crucial aspects of CFD simulations in the tundish were addressed with the reference data of fluid flow from the three-dimensional Laser Doppler Anemometry (LDA) measurements.[39] Six mesh sizes (0.0045, 0.005, 0.0055 mm, 0.006, 0.0065, 0.007 m) were compared. Six RANS turbulence models were compared, including Standard k–ε, Realizable k–ε, V2F k–ε, Elliptic blending k–ε and shear stress transport k–ω. Three convection discretization schemes were compared, including the first-order upwind scheme, the second-order upwind scheme and the third-order MUSCL. Based on the results of the CFD benchmark exercise, a recommended modelling setup for tundish flow simulation is the mesh size 0.006 m, realizable k–ε turbulence model and second-order upwind discretization scheme. A flow field comparison between the LDA measurement and the CFD prediction is shown in Figure 2(a). Figure 2(b) shows the validation of CFD predicted RTD curves in a water model with two configurations, (i) bare tundish and (ii) tundish equipped with gas curtain.[40] Figure 2(c) displays the validation of CFD predicted transient heat transfer in a non-isothermal water model of tundish.[41] The established best practice guidelines (BPG) in tundish simulation were applied in the present study.

Fig. 2
figure 2

Validation and verification of CFD model for tundish simulations (a) fluid flow (Reprinted from Ref. [38], under the terms of the Creative Commons CC BY license https://creativecommons.org/licenses/by/4.0/), (b) RTD (Reprinted from Ref. [40], under the terms of the Creative Commons CC BY license https://creativecommons.org/licenses/by/4.0/ ) and (c) heat transfer (Reprinted from Ref. [41], under the terms of the Creative Commons CC BY license https://creativecommons.org/licenses/by/4.0/)

Full size image

Water Model

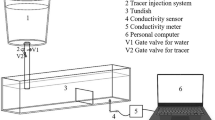
The water model is following the principle of geometry and dynamic similarity. Dynamic similarity should satisfy the similarity criteria of Froude. Then, liquid velocity, volumetric flow rate and time ratio between the model and the prototype can be described as a function of geometric scale factor (λ). The geometric scale factor λ is 1:2. Table I lists the parameters of the water model, obtained by the dynamic similarity.[19,40]

The water model was made of plexiglass, with a wall thickness of 10 mm. Once the water reached to the level of 600 mm and was stabilized, 200 mL salt saturated solution was used as the tracer injecting through the tundish inlet in 2 seconds. One conductivity probe was used to record conductivity at the outlet of the tundish. The pulse stimulus–response technique was applied to obtain RTD curves. Afterwards, the time and the concentration were transformed to a dimensionless value to compare the obtained flow characteristics. The average values of three repetitions were used for data analysis.

Flow Characterization

Residence-Time Distribution

RTD is a statistical representation of the time spent by an arbitrary volume of the fluid in vessel. The direct way of finding RTD curve uses a nonreactive tracer. RTD curve can be plotted based on the outlet concentration measured in experiment or calculated by CFD model. In a plug flow reactor, the response to a pulse input is that all fluid elements leave the vessel with the same residence time (Figure 3(a)). In a completely mixed flow reactor, the fluid elements leave the vessel over a range of residence time (Figure 3(b)). When a device operates between these two conditions, there is a degree of plug flow resulting in an initial monitored concentration peak, and a degree of mixed flow resulting in the concentration tails (Figure 3(c)).[42]

Fig. 3
figure 3

Residence-time distribution function under three conditions of (a) plug flow, (b) mixed flow and (c) arbitrary flow

Full size image

Tundish is assumed to contain three flow regimes: plug flow, mixed flow and dead zone. A combination of the plug flow and mixed flow volumes can be termed as an active volume. The volumetric flow rate (Q) through the tundish can be divided in Qa (through the active region) and Qd (through the dead region).

The dead volume fraction (Vd/Vt) and the active volume fraction (Va/Vt) are calculated through Eqs. [15] through [18]. Based on the RTD analysis, the dead volume fraction can be used as a criterion for tundish design. Theoretical residence time (τ) is given by:

$$ \tau = {{V_{t} } \mathord{\left/ {\vphantom {{V_{t} } Q}} \right. \kern-\nulldelimiterspace} Q} $$
(15)

where Vt is the volume of tundish, and Q is the volumetric flow rate.

Mean residence time is presented in Eq. [16].[43]

$$ \overline{\tau } = \frac{{\mathop \smallint \nolimits_{0}^{2\tau } tC\left( t \right){\text{d}}t}}{{\mathop \smallint \nolimits_{0}^{\infty } C\left( t \right){\text{d}}t}} $$
(16)

Dead volume fraction,

$$ \frac{{V_{d} }}{{V_{t} }} = 1 - \frac{{Q_{a} }}{Q}\theta_{{{\text{mean}}}} = 1 - \frac{{Q_{a} }}{Q} \cdot \frac{{\overline{\tau }}}{\tau } $$
(17)

where, θmean is the dimensionless mean residence time, the term Qa/Q is the area under the C-curve from τ = 0 to 2, and represents the fractional volumetric flow rate through the active region.

Active volume fraction,

$$ \frac{{V_{a} }}{{V_{t} }} = 1 - \frac{{V_{d} }}{{V_{t} }}. $$
(18)

Mean Age

Melt change efficiency (MCE) is introduced as a new criterion to evaluate how quick melt in tundish is replaced by fresh melt from ladle during casting, when the mean age theory is applied. It is described as the ratio between the turnover time (τn) and the actual melt change time (τm), as shown in Eq. [19]. τn is defined as the shortest possible time it takes to replace all the melt in the tundish, which is equal to the theoretical residence time (τ), as defined in Eq. [15]. τm is twice of the volume-averaged mean age of the melt (av), taking the ideal plug flow as a reference.

$$ \varepsilon_{m} = \frac{{\tau_{n} }}{{\tau_{m} }} = \frac{{\tau_{n} }}{{2 \cdot a_{v} }} $$
(19)

For an ideal plug flow (Figure 4(a)), the time that takes to change all the melt in the vessel is equal to the turnover time. Therefore, MCE is 100 pct and the volume-averaged mean age is half of the turnover time. In terms of a perfect mixed flow (Figure 4(b)), the concentration is the same in the vessel all the time. The volume-averaged mean age equals to the turnover time and the melt change efficiency is 50 pct. In a short-circuiting system, a large fraction of the melt flow resides a short time without passing the whole vessel volume. The melt change efficiency maybe less than 50 pct (Figure 4(c)).

Fig. 4
figure 4

Melt change efficiency under three conditions: (a) plug flow, (b) mixed flow and (c) short-circuiting flow

Full size image

Results

Multiple case studies, divided into three groups, were carried out in order to proof the viability of the mean age method in tundish. The mean age CFD model were applied to study the influence of flow control device of weir + dam (Case 1) and the outlet position (Case 2) on the performance of tundish water model. The simulated mean age results were compared with physical experiment results and results from RTD model. In Case 3, it compared the CFD results of mean age model and RTD model when applying different dam height in the prototype tundish. The studied cases of the tundish simulation are listed in Table II.

Table II List of Studied Cases of the Tundish Simulation
Full size table

Case 1: Bare and Weir + Dam Installed Tundish Configuration (Water Model)

Flow characteristics and RTD analysis

Case 1 has two sub-cases, (i) Case 1a—bare tundish and (ii) Case 1b—tundish equipped with weir and dam. In Case 1b, the modelled tundish has geometric details of the weir and dam as: A, 1000 mm; B, 600 mm; C, 100 mm; D, 360 mm (Figure 1). Figure 5 shows the contour plots of the predicted velocity (upper part), the image of line integral convolution (LIC) of velocity (middle part) and velocity vector (down part) on the symmetry plane of the water model. LIC has the advantage that all structural features of the vector field can be displayed.[44]

Fig. 5
figure 5

Contour plot, line integral convolution of velocity and velocity vector on the symmetry plane of the water model (a) Case 1a-bare and (b) Case 1b-weir + dam

Full size image

The inlet jet with high velocity flows down to the bottom of the tundish and spreads rapidly near the bottom. To clearly visualize the data, the clipping range of velocity is set at 0–0.2 m/s. In the inlet chamber (Figure 5(b)), the flow is driven along the side wall, then moves back to the entering jet. It forms counter flows near the inlet region. A part of the incoming stream is confined near the inlet owing to the presence of the weir. Meanwhile, another flow part with high momentum moves underneath the weir and downstream towards the outlet direction. The presence of a dam reorients the flow after the weir, driving the flow vertically towards the top surface. A large recirculation loop is formed in the outlet chamber. The low velocity regions occur in the upper right corner of the tundish, the lee of weir and dam, as well as the recirculation center.

Figure 6 presents the transient tracer dispersion in the water model at 10, 15 and 20 seconds. In the bare tundish, the inlet stream hits the bottom and spreads rapidly near the entry zone. The flow partially moves along the bottom and then reached the outlet. The existence of the weir and dam changes the flow path. As exhibited in Figure 6(b) (at 15 and 20 seconds), the dam drives the incoming stream moving upwards to the top surface, and then flowing towards the outlet. The flow path is prolonged. The weir reveals the function of confining the turbulence flow within the inlet chamber, leading to a better mixing in this region.

Fig. 6
figure 6

Tracer dispersion at 10, 15 and 20 seconds in water model (a) Case 1a-bare and (b) Case 1b-weir + dam

Full size image

Figure 7 shows the comparison of the measured RTD curves in the water model between Case 1a and Case 1b. The RTD curve of Case 1a shows a less breakthrough time and a higher peak value. The RTD curve of Case 1b reveals a smoother shape, which indicates that the flow characteristics were improved using the weir and dam. The results of data analysis are listed in Table III. The mean residence time of Case 1a and Case 1b is 484.3 and 562.1 seconds, respectively. The dead volume fraction of Case 1a and Case 1b is 25 and 14 pct, respectively.

Fig. 7
figure 7

Comparison of measured RTD curves in water model (Case 1a-bare; Case 1b- weir + dam)

Full size image
Table III Data Analysis of RTD Curve and Mean Age Distribution
Full size table

Mean age and melt change efficiency

Figure 8 presents the contour plots of mean age on the symmetry plane of the water model. To obtain a clear plot, the clipping range of mean age is set at 0–800 seconds. The mean age theory integrated with CFD provides comprehensive spatial variation in mean age. The plots clearly illustrate the mean age distribution from low (blue) to high (red), which also describes the location of dead zones (red regions). The lowest mean age region is near the inlet due to the young material feed. Case 1b shows a lower mean age in inlet chamber than Case 1a, indicating a stronger mixing effect due to the existence of the weir. In the outlet chamber of Case 1b, the dead zone is located in the center of the recirculation loop and in the lee of the dam. The predicted mean age distribution in Figure 8 matches well visually to the flow patterns in Figures 5 and 6.

Fig. 8
figure 8

Contour plots of mean age on the symmetry plane of the water model (a) Case 1a-bare and (b) Case 1b-weir + dam

Full size image

Figure 9 displays the contour plots of mean age at the outlet of the water model (zoomed-in view). They show very tight mean age distributions around the mean value. The mean age at the outlet varies from 613.6 to 617.3 seconds for Case 1a, and from 590 to 612.9 seconds for Case 1b. The flow through the small outlet pipe is relatively fast as an effective plug flow, which leads to the narrow distribution of the mean age at the outlet. In Figure 7, the x-axis varies from time zero to the dimensionless time of 3 (physical time, 0–1900 seconds). The measured tracer concentration has a broader distribution (0–1900 seconds) at the outlet compared to the calculated mean age at the outlet (613.6–617.3 seconds, 590–612.9 seconds in Figure 9). The reason is that the calculated mean age is a steady-state solution of Eq. [11] and the measured RTD records a transient data sequence. The mean age a(x) at the outlet can only provide the spatial distribution at the position x rather than the temporal distribution for materials passing through x, as expressed in Eq. [A3]. The tundish equipped with the weir and dam shows a relatively wider mean age distribution (22.9 seconds) compared to the bare case (3.7 seconds), owing to the large gradient of mean age in the outlet chamber.

Fig. 9
figure 9

Contour plots of mean age at outlet of the water model (a) Case 1a-bare and (b) Case 1b-weir + dam

Full size image

According to the definition, the mass-flow averaged mean age at exit should be equal to the theoretical residence time (turnover time) in a flow system with single inlet/outlet.[45] As listed in Table III, the mass-flow averaged mean age at the outlet is 615.4 and 598.8 for Case 1a and Case 1b, respectively. They are 0.2 pct difference away from the turnover times, indicating an excellent mass balance in the CFD calculations.

The volume-averaged mean age (av) of Case 1a and Case 1b is 579.2 and 462.5 seconds, respectively. The fluid becomes relatively young with the installation of weir and dam, indicating a better mixing of Case 1b. The turnover time (τ) of Case 1a and Case 1b is 616.7 and 599.4 seconds, respectively. Installation of weir and dam decrease the fluid volume in the tundish, thus leading to the decrease of turnover time (Case 1b). The melt change efficiency (MCE) can be calculated using Eq. [19]. MCE is 53.2 and 64.8 pct for Case 1a and Case 1b, respectively. The result reveals that the flow control devices (weir and dam) can improve the mixing and material exchange in the tundish. RTD data analysis shows the same tendency based on the dead volume fraction (Vd/Vt).

Case 2: Outlet Position (Water Model)

Case 2 has two hypothetical sub-cases with different outlet position, (i) Case 2a, horizontal distance between inlet and outlet 0.4 m; (ii) Case 2b, horizontal distance between inlet and outlet 1.6 m. The normal horizontal distance between inlet and outlet is 3m.

Flow characteristics and RTD analysis

Figure 10 shows the contour of the predicted velocity on the symmetry plane of the water model for Case 2a and Case 2b. The inlet jet hits the bottom of the tundish and spreads rapidly near the bottom. A counter flow pattern forms on the left side of the inlet jet for the both cases. Significant short-circuiting occurs due to the short horizontal distance between inlet and outlet. On the right side of the tundish, a broad low velocity region appears in both cases. For Case 2a, the velocities at the right side of the top surface are close to zero.

Fig. 10
figure 10

Contour plot of velocity on symmetry plane of water model (a) Case 2a-outlet position 1 and (b) Case 2b-outlet position 2

Full size image

Figure 11 presents the RTD curves through the numerical simulations. For Case 2a, the calculated peak concentration occurs at a very short time, 2 seconds. The peak value of dimensionless concentration is 49, which is much greater than a normal value 0.9 in Figure 7. A sharp rising in the tracer concentration indicates a short-circuiting flow which is undesirable for the tundish operation. A large dead volume exists in the tundish. As listed in Table IV, the mean residence time of Case 2a and Case 2b is 304 and 420 seconds, respectively. The dead volume fraction of Case 2a and Case 2b is 76 and 54 pct, respectively. According to the RTD results of Case 2a, Case 2b and Case 1a, it can be concluded that the increase of horizontal distance between inlet and outlet can decrease the dead volume fraction in tundish.

Fig. 11
figure 11

Comparison of measured RTD curves in water model between two cases model (Case 2a, outlet position 1; Case 2b, outlet position 2)

Full size image
Table IV Data Analysis of RTD Curve and Mean Age Distribution (Outlet Position)
Full size table

Mean age and melt change efficiency

Figure 12 displays the contour plots of mean age on the symmetry plane of the water model for Case 2a and Case 2b. The clipping range of mean age is set at 0–800 seconds. Young material is in the left side of tundish, close to the inlet. The short-circuiting path with smaller mean age is easily distinguishable from the inlet to the outlet. In the right side of tundish (Case 2a), the high mean age means that the young material is mixed very slowly in this region. The main mechanism for the young material to enter this region is by diffusion. However, low velocity in this region leads to low turbulent diffusion and slow mixing. In Case 2b, the mean age decreases in the right side of tundish compared to Case 2a.

Fig. 12
figure 12

Contour plot of predicted mean age on symmetry plane of water model (a) Case 2a-outlet position 1 and (b) Case 2b-outlet position 2

Full size image

Figure 13 shows the contour plots of mean age at the outlet of the water model for Case 2a and Case 2b (zoomed-in view). Case 2a shows a wider distribution compared to Case 2b. The left side has a relative low mean age, indicating most of the young material flows through this region. This is reasonable since the inlet is at the left side. Based on the mean age plots of Case 2a (Figure 13), Case 2b (Figure 13) and Case 1a (Figure 9(a)), it can be concluded that an increase of horizontal distance between inlet and outlet results in a more uniformed distribution of mean age at the outlet plane. As listed in Table IV, the mass-flow averaged mean age at the outlet plane is 608.4 and 614.1 seconds for Case 2a and Case 2b, which is 1.3 and 0.4 pct difference away from the turnover times.

Fig. 13
figure 13

Contour plots of mean age at the outlet of the water model (a) Case 2a-outlet position 1 and (b) Case 2b-outlet position 2

Full size image

As shown in Table IV, the volume-averaged mean age (av) of Case 2a and Case 2b is 890.7 and 635.5 seconds, respectively. The increased horizontal distance between inlet and outlet results in a decrease of mean age in the tundish. The turnover time (τ) of Case 2a and Case 2b is equal, 616.7 seconds. The predicted melt change efficiency (MCE) is 34.6 and 48.5 pct of Case 2a and Case 2b, respectively. The result reveals a short-circuiting flow for both Case 2a and Case 2b because their MCE values are less than 50 pct, as shown in Figure 3(c). The result of MCE is consistent with the dead volume fraction analyzed by the RTD. That is to say, a higher dead volume fraction means a lower melt change efficiency by the comparison of the two cases.

Case 3: The Height of the Dam (Prototype)

Case 3 has three sub-cases, including (i) Case 3a, low dam height-160 mm; (ii) Case 3b, medium dam height—360 mm and (iii) Case 3c, high dam height—560 mm. The geometric details of weir and dam are: A, 1000 mm; B, 600 mm; C, 100 mm (in Figure 1). The prototype tundish was equipped with weir, dam and turbulence inhibitor.

Flow characteristics and RTD analysis

Figure 14 shows the contour of the predicted velocity and streamline on the symmetry plane of the water model for Case 3. When the tundish was equipped with a turbulence inhibitor, the entering flow reoriented towards the top surface and formed recirculation loops in the inlet chamber. The appearance of turbulence inhibitor drove flow towards the surface with less turbulence. The flow patterns in the inlet chamber are almost the same for the three cases. In the outlet chamber, the existence of the weir and dam drives the incoming stream moving upwards to the top surface, and then flowing towards the outlet. A clockwise recirculation loop is observed in the three cases, with slightly different shape due to the different dam height. The low velocity regions can be observed in the lee of weir and dam, upper right corner and center of the recirculation loops in the outlet chamber.

Fig. 14
figure 14

Calculated streamline and contour plot of velocity on symmetry plane of prototype tundish (a) Case 3a-low dam; (b) Case 3b-medium dam and (c) Case 3c-high dam

Full size image

Figure 15 displays the calculated RTD curves in the prototype tundish of the studied cases. The three curves have the similar shape. Only slight difference can be observed in the figure. The RTD data analysis is listed in Table V. The calculated mean residence time of Case 3a, Case 3b and Case 3c is 732.0, 730.0 and 723.0 seconds, respectively. The dead volume fraction of Case 3a, Case 3b and Case 3c is 24.7, 23.1 and 22.6 pct, respectively. The results reveal that an increase of dam height leads to a decrease of dead volume, thus improving the mixing performance of the tundish.

Fig. 15
figure 15

Comparison of calculated RTD curves in prototype tundish between cases (Case 3a, low dam; Case 3b, medium dam; Case 3c, high dam)

Full size image
Table V Data Analysis of RTD Curve and Mean Age Distribution
Full size table

Mean age and melt change efficiency

Figure 16 shows the contour plots of mean age on the symmetry plane of the prototype tundish for Case 3. The clipping range of mean age is set at 0–1132 seconds. In the inlet chamber, a large low mean age region is observed due to the function of the turbulence inhibitor. The distributions of mean age of the three cases are similar. In the outlet chamber, a high mean age region is observed in the center of the clockwise recirculation loop where the velocity is low (Figure 14). The shape of the dead zone varies with the dam height. The upright corner is not so dead after all even though the velocities are low in this region. This is mainly due to the high rates of turbulent diffusion in this region, which increases the mixing of the materials and higher the mean age in this region.

Fig. 16
figure 16

Contour plot of predicted mean age on the symmetry plane of prototype tundish (a) Case 3a-low dam; (b) Case 3b-medium dam and (c) Case 3c-high dam

Full size image

Figure 17 shows the contour plots of mean age at the outlet plane of prototype tundish for the three cases (zoomed-in view). Case 3a (low dam) shows a different shape of mean age distribution compared to Case 3b and Case 3c. The left side of outlet has a relatively high mean age for all three cases since the dead zone is located at the left of the outlet pipe. A narrow distribution of mean age is observed at the outlet plane for the three cases, less than 40 seconds. As listed in Table V, the mass-flow averaged mean age at the outlet plane is 841.3, 830.6 and 820.0 seconds for the three cases, respectively. They are 0.2 pct difference away from their theoretical residence times, indicating an accurate solution of the CFD calculations.

Fig. 17
figure 17

Contour plots of mean age at outlet plane of prototype tundish (a) Case 3a-low dam; (b) Case 3b-medium dam and (c) Case 3c-high dam

Full size image

The volume-averaged mean age (av) of Case 3a, Case 3b and Case 3c is 613.0, 596.0 and 584 seconds, respectively. The fluid becomes relatively young when increasing the dam height, indicating a better mixing. The turnover time (τ) for the three cases is 843.0, 832.0 and 822.0 seconds, respectively. The predicted melt change efficiency (MCE) is 68.8, 69.8 and 70.4 pct for Case 3a, Case 3b and Case 3c, respectively. This result indicates that a high dam can improve the material exchange in the prototype tundish. The variance of MCE between the three cases is small, less than 1.6 pct. The variance of RTD analysis (Vd/Vt) between the three cases is also small, less than 2.1 pct. It is interesting to notice that both MCE and RTD can identify the small variance between the studied cases and draw the same conclusion, a better mixing caused by a higher dam. This means that the mean age theory can be effectively used for the design optimization.

Discussions

Computing Time

One advantage of the mean age method is the computing time and numerical accuracy. The steady-state mean age model appears to be more accurate than the RTD model since the transient solution inherently introduces numerical error due to the dependency on the time step. The computing time required for the mean age solution is two orders of magnitude smaller than that required for a full transient solution, as shown in Figure 18. Full transient means that the model simultaneously solves the tracer concentration equation together with all other transport equations at each time step. The total physical time and the time step is set to be 2600 and 0.5 seconds, respectively. Transient tracer means that the model solves the steady-state flow field in the first step. After that, only a tracer transport equation is solved at each time step using the steady-state solution of the flow field. Mean age means that all transport equations are solved at the steady-state condition. A full transient solution of a selected case requires computing time of 150 hours using an engineering workstation with 12-core and 64GB of RAM. Such long computing time is not practical for industrial demands when the sensitivity analysis of large parameter sets is needed for the design optimization. A transient tracer case needs computing time of 50 hours to get a solution. To use the mean age model, it only requires computing time of 1 hour. Therefore, the mean age model can be most practically applied in the industry because a few hundred cases are commonly required for a detailed product design. However, it is also worth noting that the mean age model has the limitation since it provides stead-state solution using the averaged information in temporal domain. For a flow system with the focus on the transient phenomena, the conventional RTD model has the advantage over the mean age model.

Fig. 18
figure 18

Computing time using different modelling methods

Full size image

Where is the Dead Zone?

Another advantage of the mean age method is that it can display the location of dead zone inside the tundish by post-processing the CFD solution. The RTD curves from the exit contains no information regarding the spatial distribution of dead zone. Dead zone means inefficient use of the tundish volume and should be avoided, or at least minimized. Figure 19 illustrates the dead zone location which is commonly recognized by the metallurgists.[1,43,46] The dead zones may occur in the sharp corner, and also in the lee of dam or weir, as marked in Figure 19.

Fig. 19
figure 19

Representation of melt flow in a tundish having dead zones

Full size image

However, a large volume of dead zone is detected by the 3D contour plot of the mean age in the prototype tundish (Figure 20). The range of mean age is set from 1100 to 1406 seconds (maximum). It is not surprising from physical reasoning. A region with closed streamlines can be observed in the outlet chamber due to the big clockwise recirculation loop (Figure 14b). Any fluid captured in the vortex may recirculate for a long time, resulting in the increase of mean age. Here, an interesting question arises: how to define the dead zone, using “slow moving” or “slow mixing”? The dead zones marked in Figure 19 were generally considered as slow moving due to the low velocity; however, some of them are not so “dead” from the perspective of mean age, for example, in the lee of weir and at the upright corner (Figure 16). This is mainly due to the strong turbulent diffusion between the main flow paths and these low velocity regions. The passive tracers can be diffused into and out of these low velocity regions across the streamlines at the high rates. In addition, their volumes are very small. Therefore, slow mixing is a more appropriate definition of the dead zone. Based on this definition, the chemical reaction, inclusion behavior and intermixing of casting product during the ladle changeover operation can be studied using dead volume fraction as a criterion.

Fig. 20
figure 20

Three-dimensional contour plot of calculated mean age in prototype tundish

Full size image

Conclusions

Mean age theory based on the spatial distribution of mean age was presented to characterize the mixing performance of tundish. A new criterion, melt change efficiency, is defined to evaluate how quick the melt in tundish can be replaced by the fresh melt from ladle during casting. Multiple case studies were carried out to test the feasibility of the new theory and criterion. The main conclusions of this study can be drawn as below:

  1. 1.

    The developed mean age model in tundish can be solved using CFD under steady-state condition. The computing time using mean age method is two orders of magnitude faster than the full transient analyses.

  2. 2.

    Two sub-cases, bare tundish and tundish with weir and dam, are studied in Case 1 (water model). The solutions of mean age were well validated with the tracer dispersion and measured RTD curves from the water model experiment. The predicted MCE increases with the installation of weir and dam, indicating a better mixing compared to the bare case.

  3. 3.

    Two sub-cases with different outlet positions were studied in Case 2 (water model). Increasing the horizontal distance between inlet and outlet can increase MCE in the tundish. The short-circuiting paths are clearly observed in Case 2a and 2b where MCE is both less than 50 pct.

  4. 4.

    Three sub-cases with varied dam height are included in Case 3 (prototype tundish). The results of mean age distributions reveal that the high dam can decrease the volume of dead zone, thus improving the mixing of melt. Both mean age and RTD methods can identify the small variance between the cases (MCE < 2 pct; dead volume fraction < 2 pct). Their conclusions are consistent, which means that mean age theory can be effectively used for the detailed design optimization of tundish.

  5. 5.

    Using the mean age theory, a large volume of dead zone is observed inside a recirculation loop in the outlet chamber of prototype tundish. Using slow mixing to define dead zone may be more appropriate considering the practical applications of the theory. The detailed information of dead zone, such as location and shape, can be used for the design optimization.

For the future work, it is important to mention that the mean age method is relatively new in the metallurgical applications and is still under development. More test cases are necessary to exam the applicability of the mean age method. Some advanced applications of tundish should also be considered, for instance, multi-strand casting, gas-stirring and the effect of thermal buoyancy. The validation of the mean age model by comparison with plant trial data are highly desirable, such as tracer experiments in the prototype tundish.

To sum up, mean age theory provides a substantial improvement over conventional RTD theory. It can provide detailed spatial distribution of mean age inside the tundish. In addition, the mean age can be computed with a much lower computing cost, especially for the tundish modelling with a very long-time scale. The results discussed in the present study demonstrated that the mean age method is a simple and precise way of quantitatively characterizing the mixing performance of tundish. The developed computational method can be a significant technology for the optimization practices of industrial design, which is meaningful for the digitalization of steel industry.