Electric Current Distribution During Electromagnetic Braking in Continuous Casting

Abstract

The electromagnetic brake (EMBr) is a well-known and widely applied technology for controlling the melt flow in the continuous casting (CC) of the steel. The effect of a steady (DC) magnetic field (0.31 T) in a CC mold is numerically studied based on the GaInSn experiment. The electrical boundary conditions are varied by considering a perfectly insulating/conductive mold or the presence of a conductive solid shell, which is experimentally modeled by 0.5 mm brass plates. An intense current density (up to 350 kA/m²) is induced by the EMBr magnetic field in the form of loops. The electric current loop tends to close either inside the liquid bulk or through the conductive solid. Based on the character of the induced current loop closures, the turbulent flow is affected as follows: (i) it becomes unstable in the insulated mold, forming 2D self-inducing vortex structures aligned with the magnetic field; (ii) it is strongly damped for the conductive mold; and (iii) it exhibits transitional behavior with the presence of a solid shell. The application of the obtained results for the real CC process is discussed and validated.

Introduction

Continuous casting (CC) technology is a constantly growing and developing branch of steel casting. Currently, more than 95 pct of the casted steel in the world is formed through continuous casting machines. With increasing casting speeds and production rates, more control is desired for the solidification process to increase the quality of the final products. One of the effective technologies to assist the continuous casting is the so-called electromagnetic braking (EMBr). It is applied by inducing an external magnetic field across the CC mold cavity normal to the casting direction to generate Lorentz forces, which slow down the liquid core motion and submeniscus velocities and reduce the turbulence level of the hot jets, which are formed due to the fresh melt feeding via a submerged entry nozzle (SEN). As was shown by the authors previously,[1,2,3] a highly turbulent flow is undesired due to the remelting of the solidified shell at the hot melt impingement areas; thereby EMBr is a favorable practice for the continuous casting process.

With the help of the numerical modeling, it is not only possible to understand but also to combat the formation of casting defects.

The long-time practical experience reveals that the electromagnetic brake (EMBr) can actually make the situation in the mold cavity even worse, for example, causing the entrapment of argon gas due to the weakening of the magnetic field towards the narrow faces.

As was recently reported by Tigrine et al.,[4] the applied magnetic field stabilizes and redistributes the melt core flow, suppressing the buoyancy effects as well; however, the Lorentz force accelerates the flow parallel to the magnetic field boundary layers, causing flow instability.

To avoid such situations, it is necessary to properly understand the effect of the magnetic field on the hydrodynamics inside the process.

Since the pioneering works of Takeuchi[5] on the EMBr process in the field of numerical simulation, a wide variety of numerical models have appeared. The requests for the numerical simulation approach have grown over the last decades, especially in the field of metallurgical applications, as reported by Thomas.[6]

A recent review by Yang, Vanka and Thomas[7] classifies the multiphase models for the CC of steel by summarizing the governing equations and discussing their advantages and drawbacks; the example applications and accuracy analysis aim to guide readers to the proper model choice.

The formation mechanisms of the multiphase flow-related defects, the corresponding high-resolution numerical models to quantify them and the control technique involving applying electromagnetic forces are discussed by Cho et al.[8]

A correct prediction of the multiphase flows strongly depends on the turbulence modeling. For numerical simulations on an industrial scale, a compromise between the accuracy and robustness of the algorithm is always desired. Some newly developed hybrid models offer an attractive alternative to the existing large eddy simulation (LES) approach for strongly unsteady multiphase flows, as reviewed by Liu et al.[9]

Han et al.[10] revealed the possible formation of severe meniscus fluctuations and excessive flow in the casting direction under electromagnetic stirring (EMS); they showed, that the proper combination of the static and traveling magnetic field helps to fight these phenomena.

Yin et al.[11] investigated the effects of the in-mold EMS on the flow and temperature distribution using a coupled MHD/solidification model. The optimal stirring settings to support a uniform shell growth were studied. It was also reported that severe meniscus fluctuations can develop under specific EMS conditions, which increase the risk of the slag entrapment.

As very recently reported by Schurmann et al.,[12] the applied magnetic field can either provide the desired flow structure or lead to the destabilization of the free surface when different SEN types are used.

Previously, Vakhrushev et al.[13] compared the capabilities of the commercial software ANSYS Fluent and the open-source CFD package OpenFOAM®[14] on the modeling of the MHD flow in the mold. Based on the long-time experience of the authors with the OpenFOAM®, an extended magnetohydrodynamics (MHD) model is developed based on the conservative formulation of the Lorentz force. A novel single mesh approach is suggested to simulate the turbulent flow inside the domain, including both the liquid melt and the stationary conductive solid. A verification based on both the experimental and numerical results reported elsewhere is performed.[15,16,17] Recently, the experimental results were improved with respect to the measurement technique and by varying the location of the EMBr system, as reported in Schurmann et al.,[18] providing unique data for the future MHD model developments.

It is well recognized that such flows are highly dependent on the CC mold electrical boundary conditions and that the MHD is directly controlled by the closure of the induced electric lines.

According to a rotating disk experiments of Deloffre et al.,[19] the corrosion of a 316 L austenitic steel in the presence of a liquid Pb-17Li melt is significantly reduced under a magnetic field. The flow conditions are changed towards meridian flow suppression by the Lorentz force, leading to the convection/diffusion reduction of the chemical elements in the hydrodynamic boundary layer of the conductive eroding disk.

Following the experiment,[19] an extended numerical study of the wall conductance was first presented by Kharicha et al.[20] It revealed that an insulated wall formulation cannot be applied to thin walls with a low conductance ratio. Moreover, the inverse value of the Hartmann number plays the role of the second conductivity; thereby, its product with the wall conductance defines the genesis of the current density generation, the boundary layers and the bulk structure and strongly affects the mass transfer during corrosion.

The numerical studies were in a good agreement with the ultrasonic Doppler velocimetry (UDV) of the rotating disk driven flow performed by the same authors for a wide range of the Reynolds (${\mathcal{R}}e \le 30000$) and Hartmann (${\mathcal{H}}a \le 260$) numbers.[21] As was previously predicted by the numerical study,[20] the conductance ratio of the tested disk materials fully defined the hydrodynamics and led to the formation or damping of the flow instabilities in specific regimes.

The modeling of a Helium-Cooled Lithium Lead (HCLL) blanket of a fusion reactor by Kharicha et al.[22] showed that due to the conductivity of thin walls, the distribution of the Lorentz force can either guide or block the flow in the connected ducts of a blanket. Consequently, the observed MHD instabilities strongly alter the hydrodynamics by breaking the closed recirculation loops; however, the temperature pattern is affected.

An application of the developed numeric technique for the electro slag remelting (ESR) process revealed that variations in the mold/slag skin conductivity affect the closure of the electric current lines.[23] The nonzero conductance ratio of the ESR mold results in a redistribution of the electric current and the Lorentz forces along the slag/melt interface, causing its significant distortion and leading, in the extreme case, to an electrical shortcut. Further studies showed that the resistivity of the slag at the high temperatures is insufficient to stop the current from entering into the mold; therefore, the insulation assumption of the slag skin can be only used in extreme cases.[24]

It is important to consider the presence of the conductive shell when searching for phenomena applicable for real casting situations. As was shown by the coauthors previously,[25] for the case of the attached highly conductive brass plates, the low frequency fluctuations of the jets are smoothed by the Lorentz force action, promoting a stable double-roll flow pattern. Conversely, when the cavity is fully electrically insulated, strong coherent vortex structures are generated and the flow is destabilized.

In contrast to the wide range of already published studies on the electromagnetic force applications, this work focuses on a very important topic, namely, the understanding of the steady (DC) magnetic field interaction with the turbulent flow in continuous casting. The detailed research presented in the paper aims at gaining valuable knowledge and answering the following questions: (i) how do the induced electric current loops behave in the liquid bulk depending on the electrical conductivity boundary conditions; (ii) how do they interact with the melt flow and turbulent structures; and (iii) what is the effect of the wall conductivity or presence of a thin conductive shell on the insulated mold cavity.

Numerical Model

In the presented studies, the MHD model is developed and implemented as an in-house finite volume method (FVM) solver based on the open-source CFD package OpenFOAM®.[14] A new solver was developed by the authors that combines the arbitrarily incompressible turbulent model and the electric potential method to calculated the induced electric current values and the Lorentz force acting in the fluid.

The following notations are used in the presented work: upright bold symbols are used to indicate vectors and tensors (e.g., velocity ${\mathbf{u}}$, stress ${\varvec{\uptau}}$); the notations in italics correspond to scalar variables (e.g., pressure p, electric potential $\varphi$); and symbols in the normal font are used to indicate the constants (e.g., laminar viscosity $\eta$, electrical conductivity of solid $\sigma_{\text{sol}}$).

General Equations of Motion

In the current work, an incompressible fluid is considered to represent the GaInSn alloy used in the physical experiment.[15] Thus, a turbulent flow that includes magneto-hydrodynamic effects can be described as a set of the incompressible Navier–Stokes equations, as follows:

$$ \nabla \bullet {\mathbf{u}} = 0 $$

(1)

$$ \frac{{\partial {\mathbf{u}}}}{\partial t} + \nabla \bullet \left( {{\mathbf{u}} \otimes {\mathbf{u}}} \right) = - \frac{1}{\rho }\nabla p + \nabla \bullet {\varvec{\uptau}}_{\text{lam}} - \nabla \bullet {\varvec{\uptau}}_{\text{SGS}} + \frac{1}{\rho }{\mathbf{F}}_{\text{L}} , $$

(2)

with velocity ${\mathbf{u}}$, liquid density $\rho$ and pressure $p$ characterizing the fluid flow.

The laminar stress tensor is defined by the kinematic viscosity $\eta$, as follows:

$$ {\varvec{\uptau}}_{\text{lam}} = 2\eta \cdot {\mathbf{D}} $$

(3)

and the rate-of-strain tensor ${\mathbf{D}}$, which is the symmetric part of the velocity gradient tensor, is defined as follows:

$$ {\mathbf{D}} = {\text{symm}}\left( {\nabla {\mathbf{u}}} \right) = \frac{1}{2}\left( {\nabla {\mathbf{u}} + \nabla^{\text{T}} {\mathbf{u}}} \right) $$

(4)

The tensor ${\varvec{\uptau}}_{\text{SGS}}$ is the traceless subgrid-scale (SGS) stress tensor, which is evaluated using a turbulence model. The latter is discussed in the corresponding section.

Magnetohydrodynamics Model

To include the influence of the magnetic field, the set of the Maxwell equations should be solved coupled with the fluid flow model, which is a complex task by itself. However, it can be significantly simplified for a low magnetic Reynolds number (${\mathcal{R}}m \ll 1$) by decoupling the total magnetic field from the flow.[26] Calculating the magnetic Reynolds number as follows:

$$ {\mathcal{R}}m = \frac{{\text{Induction}}}{{\text{Diffusion}}} = u_{0} \cdot L_{0} \cdot \mu_{0} \cdot \sigma_{0} $$

(5)

for a typical steel alloy flow with the characteristic velocity $u_{0} \approx 2 {\text{m}}/{\text{s}}$, the averaged half-thickness of the slab $L_{0} \approx 0.1 {\text{m}}$, with the electrical conductivity $\sigma_{0} \approx 770000\,{{\varOmega }}^{ - 1} {\text{m}}^{ - 1}$ and the magnetic permeability $\mu_{0} = 4\pi \times 10^{ - 7} {\text{H}}/{\text{m}}$ will give a value of ${\mathcal{R}}m_{\text{steel}} \approx 0.193$.

Thus, a low ${\mathcal{R}}m$ is typically the case for the continuous casting process when the induced magnetic field is weak in comparison to the imposed one and their interference can be neglected. Thus, by assuming the constant total magnetic field ${\mathbf{B}}$, the curl-less condition for the electric field ${\mathbf{E}}$ is obtained from the Faraday’s law of induction, as follows:

$$ \nabla \times {\mathbf{E}} = - \frac{{ \partial {\mathbf{B}}}}{\partial t} \mathop \Rightarrow \limits^{{{\text{with}} {\mathbf{B}} = {\mathbf{B}}_{0} }} \nabla \times {\mathbf{E}} \equiv 0 $$

(6)

Additionally, the solenoidal nature of the magnetic field ${\mathbf{B}}$ is inherited, such as $\nabla \bullet {\mathbf{B}}_{0} = 0$.

According to Eq. [6], the electric field ${\mathbf{E}}$ following a vector field rule can be rewritten using arbitrary scalar $\varphi$, called here the electric potential, in the form ${\mathbf{E}} = - \nabla \varphi$. Thus, to simulate the Lorentz force, a so-called electric potential method is applied.[26] Consistently, the induced current density is given by the modified Ohm’s law as follows:

$$ {\mathbf{j}} = \sigma \cdot \left( { - \nabla \varphi + {\mathbf{u}} \times {\mathbf{B}}_{0} } \right) $$

(7)

where $\sigma$ is the electrical conductivity.

The electric potential $\varphi$ distribution is predicted by solving the corresponding Poisson equation derived from the charge conservation equation ($\nabla \bullet {\mathbf{j}} = 0)$, as follows:

$$ \nabla \bullet \left( {\sigma \nabla \varphi } \right) = \nabla \bullet \left( {\sigma \cdot \left( {{\mathbf{u}} \times {\mathbf{B}}_{0} } \right)} \right) $$

(8)

The electric conductivity $\sigma$ is considered to be variable in the simulation domain to account for the presence of the highly conductive solid plates attached to the mold’s walls.

The Lorentz force introduced in Eq. [2] is defined as a cross product of the induced electric current density ${\mathbf{j}}$ and the applied magnetic field ${\mathbf{B}}_{0}$, as follows:

$$ {\mathbf{F}}_{\text{L}} = {\mathbf{j}} \times {\mathbf{B}}_{0} $$

(9)

Equation [9] represents a body force in a nondivergent form not taking into account the conservation of both the current density ${\mathbf{j}}$ and the applied magnetic field ${\mathbf{B}}_{0}$. A special numerical treatment of this term is used in the study and is further described in Section II−F.

Modeling a Conductive Solid

The novelty of the presented approach is that a single numerical mesh is used to model the induced current in the highly conductive solid plates, as well as for the liquid bulk. This technique allows the avoidance of complex multidomain coupling by the creation of so-called ‘shadow walls’ and the corresponding Neumann boundary conditions. Simultaneously, the convergence ratio increases since a sole set of equations is solved for the whole domain in a single run.

In the proposed method, a special porous-like zone is defined next to the geometry outer wall. The outer wall’s thickness is the thickness of the brass plates used in the experiment. The velocity field is set to zero by manipulating the coefficients of the linear system matrix for the momentum conservation law defined in Eq. [2].

The Poisson equation for the electric potential $\varphi$ Eq. [8] is split for the melt and the solid regions. For the liquid bulk it becomes the following:

$$ \nabla \bullet \left( {{{\sigma }}_{\text{liq}} \nabla \varphi } \right) = \nabla \bullet \left( {{{\sigma }}_{\text{liq}} \cdot \left( {{\mathbf{u}} \times {\mathbf{B}}_{0} } \right)} \right) $$

(10)

Inside the ‘solid shell’ it is reduced to a Laplacian form by canceling the right-hand side terms, as follows:

$$ \nabla \bullet \left( {\sigma_{\text{sol}} \nabla \varphi } \right) = 0 $$

(11)

The suggested approach should be carefully applied since it can influence the flow at the boundary layer close to the solid zone since no explicit wall is defined. Later, in this paper, the method is verified based on a flow simulation without the applied magnetic field.

Magnetic Boundary Layers

For the proper modeling of the MHD effects in the incompressible turbulent flow of a liquid alloy, there are several essential parameters of the simulated system. To express the ratio of the magnetic to viscous force in the fluid, a Chandrasekhar number is defined as follows:

$$ {\mathcal{Q}} = \frac{\text{Magnetic force}}{\text{Viscous force}} = \frac{{\left| {{\mathbf{B}}_{0} } \right|^{2} \cdot L_{0}^{2} \cdot \sigma_{\text{liq}} }}{\rho \cdot \eta } $$

(12)

where an additional characteristic $L_{0}$ stands for the domain’s length scale, which is typically half the size of the domain along the magnetic lines.[27]

The Chandrasekhar number ${\mathcal{Q}}$ is used to estimate the frequently used Hartmann number ${\mathcal{H}}a$ (${\mathcal{Q}} = {\mathcal{H}}a^{2}$). It reflects the deviation from the ordinary hydrodynamic behavior under the magnetic field applied, as follows:

$$ {\mathcal{H}}a = \sqrt {\mathcal{Q}} = \left| {{\mathbf{B}}_{0} } \right| \cdot L_{0} \cdot \sqrt {{{\sigma }}_{\text{liq}} /\rho \cdot \eta } $$

(13)

Another dimensionless number that is important for the MHD phenomenon is the so-called interaction number, which is calculated as follows:

$$ {\mathcal{N}} = \frac{{L_{0} }}{{u_{0} }} \cdot \frac{{\sigma_{0} \left| {{\mathbf{B}}_{0} } \right|^{2} }}{\rho } = \frac{{t_{\text{adv}} }}{{t_{\text{damp}} }} = \frac{{{\mathcal{H} }a^{2} }}{{{\mathcal{R}}e}} = \frac{{\mathcal{Q}}}{{{\mathcal{R}}e}} $$

(14)

which represents the ratio between the Joule damping time $t_{\text{damp}}$ to the characteristic advection time $t_{\text{adv}}$.

When the magnetic field is applied to the conductive fluid, in addition to the viscous sublayer, a magnetic sublayer is formed. The structure of the wall’s magnetic layers depends on their orientation with respect to the magnetic field. A so-called Hartmann layer with the thickness ${{\Delta }}_{\text{Ha}}$ is formed perpendicular to the ${\mathbf{B}}_{0}$ direction surfaces, whereas a Shercliff layer of the size ${{\Delta }}_{\text{Sh}}$ appears for the parallel ones.[28] The thicknesses of these layers can be estimated based on the Hartmann number according to the following expressions:[27]

$$ {{\Delta }}_{\text{Ha}} \cong {\text{L}}_{0} \cdot {\mathcal{H}}a^{ - 1} $$

(15)

$$ {{\Delta }}_{\text{Sh}} \cong {\text{L}}_{0} \cdot {\mathcal{H}}a^{ - 1/2 } $$

(16)

Generally, with the arbitrary alignment of the magnetic field relative to the bounding walls, the Hartmann layer is dominant wherever a nonzero normal component of the magnetic field exists at the considered surface.[29]

Turbulence Modeling

A large eddy simulation (LES) based on the subgrid-scale (SGS) models is successfully applied to the turbulent MHD flows, as discussed by Kabayashi[30] and verified in consequent studies that simulate single and multiphase flows elsewhere.[16,17,31,32] The basic aim is to estimate the SGS stress tensor ${\varvec{\uptau}}_{\text{SGS}}$ in the following form:

$$ {\varvec{\uptau}}_{\text{SGS}} = - 2 \cdot C_{\text{SGS}} \cdot \left( {{{\Delta }}_{\text{SGS}} } \right)^{2} \cdot \left| {\mathbf{D}} \right| \cdot {\mathbf{D}} $$

(17)

where the norm of the strain rate tensor is defined as follows:

$$ \left| {\mathbf{D}} \right| = \sqrt {2{\mathbf{D}}:{\mathbf{D}}} $$

(18)

$C_{\text{SGS}}$ and ${{\Delta }}_{\text{SGS}}$ are the model parameter and the filter width, respectively. In the presented work, the effect of the magnetic field on the subgrid turbulence is neglected. This can be justified by the fact that at the level of the grid size (~ 0.5 mm), the interaction number is small (${\mathcal{N}} \approx 0.024)$.

Traditionally, the standard Smagorinsky (SM) turbulence model[33] is used due to its robustness and efficiency. However, it is known for overpredicting the SGS viscosity in the wall shear flows and significant jumps in the mesh refinement regions.

The wall-adapting local eddy-viscosity (WALE) model is found among the popular LES models to be more reasonable and accurate for the complex geometry flows and is also robust for the mesh refinements.[34] The model is able to account for the strain effects and for the rate of rotation of the smallest resolved turbulent structures, which helps it naturally adapt to the Lorentz force in the case of MHD modeling. Moreover, WALE SGS is verified to correctly predict the build-up of coherent turbulent structures along the magnetic field lines.[30] It resolves the eddy viscosity with the cube of distance close to the wall and does not rely on expensive and complex algorithms or Van-driest damping based on y⁺ values. Since Chaudhary et al.[16] showed that the standard SM setup is far from the experimental measurements, which was also recently verified by authors,[13] the WALE SGS is employed for the presented studies. A standard setup is used; therefore, the details of the mathematical models are not disclosed in this report and can be found in the corresponding references.[16,30,34]

Discretization of the Equation System

It should be mentioned that for the discretization practice, a so-called Rhie–Chow interpolation is employed.[35] The OpenFOAM® package is based on the collocated unstructured mesh arrangement, which means that all the variables reside in the control volume centers. It should be remembered that to avoid a saw-oscillation pattern of the velocity field, which is notorious when employing collocated grids, the convective terms are obtained by cell-to-face interpolations.[36] The OpenFOAM® discretization of the main system for the turbulent flow including velocity–pressure coupling is performed in the conservative ‘out-of-the-box’ formulation; however, the implementation of the electric potential method to account for the MHD problem is performed by an in-house solver using the conservative formulation of the Lorentz force suggested elsewhere.[37,38,39]

Between the liquid and solid zones of the domain, the initial set of equations is naturally reduced by setting the cell-centered velocity values and velocity fluxes implicitly to be zero inside the solid. The interpolation of the electrical conductivity on the boundary between the melt and the solid is performed by taking a maximum value for the cell face owner/neighbor pair.

Model Applications

In the current section, both the melt flow and the MHD model are verified. First, the Hartmann and Shercliff verification cases were performed; the results are omitted here since they are fairly standard and carry no valuable information. However, the main focus on the comparison with the real experimental measurements during the liquid metal experiments related to the performed study.

Experimental Setup

The current study is based on and verified against the liquid metal experiment excluding and employing electromagnetic braking,[15] as well as against other numerical simulations of turbulent and MHD flows performed by other studies on the same geometry.[16,17] In the liquid metal experiment, the GaInSn alloy is used, which is in the liquid state at room temperature. The details of the experiment can be found in the corresponding references. The liquid metal properties of the Ga68In20Sn12 alloy used in the experiment are reported by Plevachuk.[40]

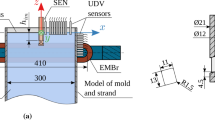
The applied static (DC) magnetic field ${\mathbf{B}}_{0}$ distribution of a single-ruler-type EMBr along the casting direction of the mold can be seen in Figures 1(b) and (c). Its maximum value corresponds to the SEN ports outlet position and reaches its maximum value of ~310 mT. The data correspond to the EMBr case positioned at 92 mm in Thomas et al.[17]

Fig. 1

Simulation domain: (a) LIMMCAST geometry details with monitor lines, as given by Chaudhary and Thomas;[16,17] (b) magnetic field profile along the vertical direction and (c) its volumetric distribution showing applied field direction with vectors

Referring to the GaInSn experiment performed at the HZDR Center,[15] a CAD drawing of the simulation domain is prepared using SALOME open-source software.[41] The mesh generation is performed by the OpenFOAM® meshing tool snappyHexMesh, which represents the hex-dominant numerical grid with an initially uniform cell size distribution, which is slightly distorted at the regions of high surface curvature. The region where the brass plates were attached was extruded using an ingenious in-house algorithm to keep it orthogonal and correctly aligned. The details of the numerical grid are presented in Figure 2.

Fig. 2

Details of the numerical mesh: (a) general overview; (b) details of the mesh refinement near the mold walls to resolve magnetic boundary layer and the attached brass plate zone (in red) (Color figure online)

Based on the Hartmann number definition in Eq. [13], the thicknesses of the Hartmann boundary layer for the wide walls and the Shercliff boundary layer for the narrow walls were estimated according to Eqs. [15] and [16], respectively. The length scaling factor $L_{0}$ for the mold cavity should be taken as a half-thickness in the magnetic field direction and corresponds to 17.5 mm. For the presented study, the estimated Hartmann’s number for the applied field of 310 mT is ${\mathcal{H}}a \approx 417$. The thickness of the Hartmann’s layer becomes ${{\Delta }}_{\text{Ha}} \approx 50 \mu {\text{m}}$ and the corresponding Shercliff’s layer is ${{\Delta }}_{\text{Sh}} \approx 1 {\text{mm}}$. Thus, refining the mesh to resolve the Hartmann layers can become a challenging task.

However, the wall conductance ratio, which is calculated as follows:

$$ C_{\text{wall}} = \frac{{\delta_{\text{wall}} \cdot \sigma_{\text{sol}} }}{{L_{0} \cdot \sigma_{\text{liq}} }} $$

(19)

is significant ($C_{\text{wall}} = 0.134$) for a brass wall with the thickness $\delta_{\text{wall}} = 0.5$ mm. Therefore, most of the induced current in the transversal direction will be conducted through the less resistive solid. Moreover, the transport of the induced current in the liquid bulk falls on the region of the parallel (insulated) walls.[27] Therefore, no dramatic resolution along the wide walls is required, and the criterion for the Shercliff boundary layer is much easier to fulfill.

Taking all this into account, the local mesh refinement was performed near the walls in regard to the magnetic boundary layers (see Figure 2). The total number of the finite volume elements in the performed study is ~ 5.15 million cells. The mesh studies were performed, and the mesh size was found to be reasonable both for the accuracy and for the computational performance of the simulations.

Next, the averaging time for the results comparison was selected. Since the LES simulation is always computational costly, all numerical simulations are performed for the characteristic time of the simulated process, which can be estimated as follows:

$$ t_{\text{charact}} = V/u_{\text{cast}} \cdot A_{\text{slab}} , $$

(20)

where ${\text{V}}$ stands for the volume of the simulated domain; $u_{\text{cast}} = 1.35$ m/min is the casting speed; $A_{\text{slab}}$ represents a slab cross-section area. For the presented studies, the characteristic time is $t_{\text{charact}} \approx 13 {\text{seconds}}$. Thus, hereinafter, the time averaging of the results is performed over a triple characteristic time interval of 39 sec. It should be mentioned that in the previous studies, a shorter time interval was used, which the authors found to be insufficient for the statistics collection.

Additionally, it should be mentioned that the developed solver and algorithm are very robust and effective for the parallel calculations. By using two Intel Xeon CPU E5-2690-v4 @ 2.60 GHz @ 128 GB nodes with 28 cores for each node (56 cores in total for a single run), each 39 physical seconds simulation takes 55 HPC hours. The stability criterion keeps the Courant number ${\text{Co}} \approx 0.15$, which is achieved based on the local cell size at the impingement area near the narrow walls (~ 0.1 mm) where the jet velocity reaches 0.3 m/s. Since the corresponding time integration step of $5 \times 10^{ - 5}$ seconds is very low and no drastic changes in either the hydrodynamic or electromagnetic fields appear, no underrelaxation is required to stabilize the numerical solution.

Fluid Flow and MHD Modeling Verification

Next, after the simulation domain and the numerical grid were set up, the fluid flow model was verified using published experimental data. All the discretization of the used turbulent flow/MHD model equation system is second order in time and space.

First, the single mesh approach was verified wherever the special treatment of the solid plate zones can cause the distortion of the melt flow inside the mold cavity. Therefore, two simulations were performed (excluding the EMBr) using exactly the same mold dimensions and mesh, as shown in Figure 2; one corresponds to the rigid outer walls and the second includes additional 0.5 mm solid plate zones, marked with red in Figure 2(b), where the velocities are set to zero by manipulating the momentum equation matrix.

The comparison results are presented in Figure 3; the time-averaged and the instantaneous flow patterns for the pure hydrodynamic test without EMBr are shown for both cases giving a perfect match. The details of the complex turbulent flow simulated using the WALE SGS model are shown for the SEN outer in Figure 4(a) and the internal region in Figures 4(b) through (d). The flow patter is observed to be very turbulent. Moreover, some pulsation is detected in the port region of the SEN cup; a symmetric flow, as observed in Figure 4(b), is distorted in a specific time instance, as indicated in Figure 4(c), and changes to a double vortex structure at the bottom of the internal port region (see Figure 4(d)). The described sequence repeats.

Fig. 3

Comparison of the fixed wall (a) and solid zone approaches (b) for the brass plates modeling: the pictures on the left display the time-averaged velocity magnitude and the pictures on the right show the instantaneous velocity field

Fig. 4

Submerged entry nozzle flow: (a) port exit area; (b)–(d) internal flow at the cup area displayed for different time instances

A good quantitative comparison was previously reported by the authors[13,25] based on the measurements in the LIMMCAST experiment in the HZDR lab,[15] which are also reported by Chaudhary[16] for a no EMBr flow and by Thomas[17] including an applied magnetic field. The verification results of the EMBr modeling, based on the time-averaged horizontal velocity from the experiment[17] and obtained by the simulations presented here, are shown in Figure 5; notice the reverse flow zones detected by the measurements and captured by the numerical model. It is worth mentioning that both the RANS[31] and LES models (even a tuned SGS reported by Chaudhary et al.[16]) are accurate in predicting the jet core and the bulk flow. However, none of them are capable of capturing the velocity field close to the SEN ports. In the future, extensions to the experimental studies and adjustments of the turbulent models (mentioned by Kabayashi[30]), including the MHD effect, are required.

Fig. 5

Verification of the MHD modeling results (solid lines) using the experimental measurements (dots) in Thomas et al.[17] EMBr position at 92 mm; semiconductive wide walls; probes locations 90, 100, and 110 mm below the meniscus

Simulation Results

Five cases are considered regarding the influence of the conductivity of the mold on the induced currents and the melt flow under the applied magnetic field. They are compared with the reference results for the melt flow (Case MF, Table I) without EMBr.

Table I Simulated Cases Based on the Wall Conductance Ratio ${\text{C}}_{\text{wall}}$ According to Eq. [19]

The electromagnetic brake simulations, as presented in Table I, correspond to the following variations of the electric boundary conditions: (i) the mold is electrically insulated (Case IM); (ii) the mold is perfectly conductive (Case CM); (iii) the wide walls of the mold are perfectly conductive (Case CW); (iv) partial conduction is provided in Case BPW along the wide (Hartmann) walls due to the attachment of the brass plates (~5 times more conductive than the melt); (v) in addition to the experimental setup in Case BPW, a highly conductive solid is considered at the narrow (Shercliff) walls (Case BPM) and is investigated by numerical modeling. In all simulations, a magnetic field of 310 mT (at the pole region) is applied for braking.

The time-averaged results (over 39 seconds of a physical process) are presented and analyzed hereafter apart from the instantaneous current density lines and turbulent structures.

Melt Flow Under the Applied EMBr

The instantaneous flow velocity without the magnetic field and for the cases with different electric boundary conditions in the CC mold are compared as shown in Figure 6. A logarithmic scale is used for the velocity magnitude to reveal more flow details. In the case without EMBr (Figure 6(a)), a highly turbulent flow is observed. When the magnetic field is applied, the flow is totally changed and differs from case to case, as follows: for the fully insulated mold (Figure 6(b)), strong instabilities are developed under the applied EMBr; with the perfectly or partially conductive mold (Figures 6(c) and (d)), the flow becomes quite stable, showing fluctuations at the jet, SEN and meniscus areas; when the brass plates are attached to the insulated mold, a transition regime between a plug-type and oscillating flow is observed (Figure 6(e)).

Fig. 6

Velocity magnitude $\left| {\mathbf{u}} \right|$ instantaneous distribution: (i) wide side mid-plane, (ii) top surface; (iii) narrow side mid-plane. The results are shown for the following cases: (a) no magnetic field applied; EMBr simulations (b) with all walls insulated; (c) all walls conductive; (d) with conductive wide walls; and (e) with attached brass plates

Since it is difficult to reveal the flow pattern based on the instantaneous velocities and compare its features for the different cases, a time averaging procedure was applied for the further studies, as seen in Figure 7. When the EMBr is applied for the flow inside an insulated mold (Case IM), strong coherent structures are generated that are aligned with the magnetic field. These vortices are self-inducing since the electric current loops can close through the melt bulk only. They destabilize the flow, which becomes totally unsteady; therefore, no final symmetric pattern is observed in Figure 7(b) after time averaging characteristic 39 seconds window (see Eq. [20]). The two vortices near the SEN ports are the upper rolls under the magnetic field (also in Figure 6(b)). As observed from the supplementary material “InsulatedMold.avi,” the jets and the upper rolls oscillate inside the insulated mold under the EMBr and take different shapes as time progresses.

Fig. 7

Time-averaged (39 seconds window) velocity magnitude $\left| {\mathbf{u}} \right|$: (i) wide side mid-plane, (ii) top surface; (iii) narrow side mid-plane. The results are shown for the following cases: (a) no magnetic field applied; EMBr simulations (b) with all walls insulated; (c) all walls conductive; (d) with conductive wide walls; and (e) with attached brass plates

According to previous work of the coauthors,[25] the low frequency (~1 Hz) oscillations of the jets and the induced vortex structures are detected both during the experiment and during the MHD simulation using the LES method. High velocity and instability of the meniscus is also detected (see Figure 6(b)).

For a perfectly conductive mold (Case CM), the flow is reduced to a plug-type below the SEN and jets region. The melt motion is damped along the mold walls in Figure 7(c), whereas the high velocities correspond to the jets and to the recirculation zones above and below them. The origin of these zones is explained by P.A. Davidson as follows:[26] the jet becomes elongated in the magnetic field direction; the mass conservation causes the melt entrainment from the bulk and leads to a reverse flow formation.

In the case of insulated mold sides (Case CW), the upward flow along the narrow walls is still low (see Figure 7(d)), but a strong downward melt motion is detected. As the narrow walls become electrically insulated, the flow load shifts towards the Shercliff boundary layer and the velocities at the central part of the mold below the SEN are reduced due to the mass conservation in comparison to Case CM in Figure 7(c).

It worth mentioning that in Cases CM and CW, the perfect conductivity of the wide walls causes an extreme braking effect at the top part of the mold cavity, which results in an almost stagnant zone. The latter is totally undesired during the CC process due to the risk of hook formation, low flux melting, etc.

Finally, in Case BPW, when the brass plates are attached to the wide walls of the insulated mold, the flow is significantly stabilized (see Figure 7(e)) in comparison to the chaotically oscillating jets without a conductive solid, as previously mentioned for Case IM in Figure 7(b). Simultaneously, a strong flow along the insulated narrow walls, meniscus and SEN is developed.

Distribution of Induced Electric Current

The distribution of the current density magnitude is compared for the different EMBr cases in Figure 8. In all occasions, most of the induced current is generated at the jet region.

Fig. 8

Electric current density $\left| {\mathbf{j}} \right|$ instantaneous distribution (i) in the wide mid-plane, (ii) at the meniscus and (iii) at the narrow mid-plane: (a) all walls insulated; (b) all walls conductive; (c) the wide walls of the mold are perfectly conductive; (d) brass plates are attached

When the mold is fully insulated (Figure 8(a)), the current density is mainly distributed in the upper part of the mold; the jets dispatching from the SEN ports (see Figure 6(b)) bend towards the meniscus and form the upper roll. Strong oscillation of the jets and instabilities inside the liquid bulk are observed. They are caused by the coherent structures generated under the EMBr and aligned with the magnetic field. These self-induced instabilities travel inside the mold cavity and are accompanied by the high electric current marked as the “e-current spots” in Figure 8(a).

For the perfectly conductive walls (see Figure 8(b)), more induced current is located at the lower part of the mold and almost none is found at the meniscus area. The electrical insulation of the narrow walls leads to a significant drop in the current concentration in the bulk, as observed in Figure 8(c).

The attachment of the brass plates (Figure 8(d)) causes a high current concentration inside the solid since it tends to go through a more highly conductive material to close the current loops, and a more uniform current density distribution is formed.

The current path lines are shown in Figure 9. In the case of the insulated walls, the electric current lines are concentrated along the Hartmann, as well as the Shercliff walls; as observed in Figure 9(a), the current density is high; however, the direction of the current density field is fully chaotic in the plane of the walls. The current density stream lines formed a star-like shape in Figure 9(a) that is colocated with the generated high current spots in Figure 8(a). These areas are later analyzed at the discussion section.

Fig. 9

Current density j stream lines for simulation cases: (a) all walls insulated; (b) all walls conductive; (c) the wide walls of the mold are perfectly conductive; (d) brass plates are attached

For the case of perfectly conductive walls, one observes that the current tends to flow parallel to the wide walls, which is consistent with the right-hand rule for the induced electric current (see Figure 9(b)). After reaching the narrow sides, the current immediately enters the conductive walls. In the jet area, the electric current lines are bended, either entering the conducting walls faster or sliding along the insulated SEN and meniscus. The current lines are generally ‘attached’ to the mold walls, which enhances the breaking effect from the magnetic field.

For the case of perfectly conductive wide walls and insulating narrow walls in Figure 9(c), we observe that the current also flows mainly parallel to the wide walls. However, after it reaches the insulating narrow walls, the current lines bend towards the wide wall and enter them, which results in the redistribution of the current density in comparison to the fully conductive mold. Another difference is that in the top region the current lines tend to go first to the meniscus rather than following the wide walls.

When the brass plates are introduced (Figure 9(d)), the current lines become arranged and are somewhat ‘fixed’ to the solid. The electric current tends to be conducted by the material with lower resistance. However, the current lines are still misaligned in the bulk, as well as along the Shercliff walls and at the meniscus. The detailed analysis of the results in Figures 7 through 9 reinforces that the case with the presence of the ‘solid shell’ gives a combination of the fully insulated and perfectly conductive molds, i.e., a plug-flow formation due to the breaking effect combined with more flow fluctuation in the Shercliff layers.

We encourage the readers to observe supplemental materials, including “InsulatedMold.avi” and “ConductiveMold.avi,” where all fields are demonstrated through animations for extreme cases with the electrically insulated molds (Case IM) and with the perfectly conductive molds (Case CM).

Discussion

In this section, the influence of the previously considered scenarios and some observed phenomena are discussed, starting with the changes, which the turbulence undergoes with the applied electromagnetic brake.

Turbulence Effects under the Applied Magnetic Field

As it known from the previous work on magnetohydrodynamics of the turbulent flows,[26,30] they are strongly influenced by the applied magnetic field; coherent structures aligned with the applied magnetic field are formed and the flow turbulence is reduced to a quasi-2D state. Applied to the melt flow in the continuous casting process, the turbulence is strongly damped in the core region of the mold, as reported previously.[25]

To analyze the change in the turbulent flow structure, it is visualized using so-called Q-criterion, which is the second invariant of the velocity gradient representing the local balance between the shear strain rate and vorticity, as follows:[42,43]

$$ {\mathcal{Q}}_{\text{crit}} = \frac{1}{2}\left[ {\left( {{\text{tr}} \left( {\nabla {\mathbf{u}}} \right) } \right)^{2} - {\text{tr}} \left( {\nabla {\mathbf{u}} \bullet \nabla {\mathbf{u}}} \right)} \right] $$

(21)

The simulated turbulent structures for a single flow without EMBr and for different scenarios involving an applied magnetic field, as well as the corresponding instantaneous meniscus velocities are shown in Figure 10.

Fig. 10

Turbulent flow structures displayed by ${\mathcal{Q}}_{\text{crit}} = 100$ iso-surface; the color map corresponds to the velocity magnitude $\left| {\mathbf{u}} \right|$; (a) flow simulation; (b) all walls insulated; (c) all walls conductive; (d) perfectly conductive wide walls; (e) attached brass plates

The general flow without the magnetic field shows rich turbulence, as displayed in Figure 10(a). The meniscus flow is quite unstable, showing high velocities, as well.

When the EMBr is applied to the fully insulated mold (see Figure 10(b)), strong vortex structures aligned with the magnetic field are generated. They disturb the bulk flow and the meniscus.

When all walls are conductive (Figure 10(c)) or just the sidewalls of the mold are insulated (Figure 10(d)), the turbulence is strongly suppressed and the meniscus becomes calm.

The attachment of the highly conductive brass plates (Figure 10(e)) increases the stability of the flow, while leaving some freedom for the flow oscillations and turbulence generation. A flow develops along the insulated sidewalls and the SEN surface. For the current EMBr setup, the meniscus flow is significantly higher than in the case of a flow without EMBr.

The electric current density is tightly connected with the coherent turbulent structures generated under the applied magnetic field. It is especially pronounced in the case of the electrically insulated mold when the created electric vortex is free to travel. A typical MHD vortex structure is shown in Figure 11. The electric current density in the liquid bulk crosses the turbulent structure without significant distortion of the current lines, as can be observed in Figure 11(a). However, close to the mold the electric current, a star-like shape forms, marked in Figure 9(a), which enters the Hartmann layer through the base side of the vortex (see Figure 11(b)) and flows along the wide walls. The magnitude of the induced current density is significantly higher (approximately 2 orders of magnitude) in the electromagnetic sublayer than in the bulk.

Fig. 11

Current density distribution lines in the vicinity of a vortex structure (a) in the liquid bulk; and (b) near the wide wall of the fully insulated mold

Influence of the Highly Conductive Solid

The detailed distribution of the induced current lines in the case of the attached brass plates is shown in Figure 12. As it can be observed, the dominant part of the current is concentrated in the solid plates, in the Shercliff layers and along the meniscus.

Fig. 12

Details of the current density distribution lines for the Case BPW with the brass plates attached to the wide walls of a nonconductive mold: (a) in the bulk around the SEN; (b) from the wide and narrow mold sides; and (c) from the top (meniscus) and bottom views

A closer look at the concentration of the induced electric current for the simulated case with the attached solid is given in Figure 13; both the magnitude of the current density (Figure 13(a)) and the actual electric current lines (Figure 13(b)) are shown, which indicates a strong concentration of the transmitted current inside the highly conductive solid.

Fig. 13

Electric current distribution for the Case BPW with the brass plates attached to the wide walls of a nonconductive mold: (a) current density magnitude; (b) current lines within the bulk (blue) and inside the plates (red); the semitransparent area marks the attached solid plates (Color figure online)

The simulated current density distribution inside the brass plates is presented in Figure 14. The first two subfigures show the magnitude of the current density inside the plate. As previously mentioned, 10 cell layers were used inside the plates subzone to resolve the current distribution, and each layer was 0.05 mm in thickness.

Fig. 14

Distribution of the current density in the brass plates: (a) liquid/solid interface; (b) next to the mold wall; (c) normal component of the current density on the liquid side of the brass plate surface; (d) areas of the entering (red) and leaving (blue) the electric current (Color figure online)

Figures 14(a) and (b) shows the very first and the last calculation cell layer inside the solid region. It can be observed that no significant change can be detected across the plate; thus, the rest of the cell layers are omitted in the plot. Since the solid shell is very thin, it is not surprising that the electric current distribution is almost two-dimensional inside the plates.

A high electric current is detected inside the more conductive solid in comparison to the liquid bulk, where it is more uniformly distributed and has significantly lower values.

One can observe that far from the jet and the SEN areas marked with white arrows and the rectangle in Figure 14(a), the current tends to enter the brass plates near the insulated narrow walls and at the meniscus area, which is indicated by the normal electric current component $j_{\text{n}}$ in Figure 14(c). The reason is that according to the right-hand rule at the lower part and the meniscus area, the current lines are dominantly parallel to the mold’s wide walls (see Figure 12(c)). Finally, they encounter resistive surfaces, which force them to bend towards the conductive ‘solid shell,’ which can be clearly detected in Figure 15(b). One can observe stronger normal components of the current density vector near the narrow walls and the meniscus in Figure 14(c), as well as the concentration of high electric current lines in Figure 15(b).

Fig. 15

Details of the induced current lines along the narrow walls with (a) insulating mold (Case IM); brass plates attached to (b) wide walls (Case BPW) and, (c) additionally, to the narrow walls (Case BPM)

The location of the current density entering (red color) or leaving (blue color) the brass plates is indicated in Figure 14(d), and the electric current lines are described in Figure 15. At the jets and SEN area, the entrance and exit spots of the induced currents are quite chaotic if one refers to Figures 12(a) and (b) and to the top part of Figures 14(c) and (d) due to the strong influence of the jets and the turbulent structures along the nonconductive nozzle walls.

The strong vertical flow along the insulated (Shercliff) narrow walls also initiates the current entering or leaving the brass plates next to the main areas of the concentration of current lines, as shown in Figure 14(d). However, according to the current lines in Figure 15(b), most of the current entering is concentrated next to the narrow walls, whereas the rest (marked in Figure 14(c) in blue-cyan color range) correspond to a weak current related to the flow perturbations along the insulated walls.

An interesting ‘current-free’ region is observed inside the brass plates just below the SEN bottom marked with a blue dash-line in Figures 14(a) and (b). This zone is related to a typical flow stagnation zone, and the insulated SEN ‘shadows’ it from the electric current.

The details of the comparison between the insulated and semiconductive mold cases are shown in Figure 15. In the case of the insulated walls, the current lines are very chaotically arranged in the bulk and at the meniscus area, destabilizing the flow at the meniscus, as in Figure 15(a). High electric current values are detected here as well.

When the attached brass plates are considered (see Figure 15(b)), the induced current enters the highly conductive media (see Figures 14(c) and (d)) close to the narrow walls and travels through (as in Figures 14(a) and (b)). The current path lines are closed in the loops and the simulated ‘solid shell’ plays a stabilizing role, as is clearly observed from Figure 15(b) in comparison to the insulated mold case in Figure 15(a).

In the real CC process, the solidified shell is formed along all the walls of the mold cavity. Therefore, a scenario when the brass plates are attached to the narrow walls of the fully insulated mold is presented in Figure 15(c). In comparison to the case in Figure 15(b), the electric current lines are also stabilized along the Shercliff (narrow) walls (see Figure 15(c)). In both cases, the top surface behavior remains, meaning that the induced electric current is free to move along the insulated meniscus.

Application to Continuous Casting

It is very important to analyze how the referenced GaInSn EMBr experiment (where the solid/liquid conductivity ratio is ~ 5) and the currently presented simulations relate to the real continuous casting process. As an illustration, some recent results of the thin slab casting modeling are briefly described in Figure 16.

Fig. 16

Solid shell conductance ratio for the thin slab casting: (a) averaged temperature-dependent ratio $\sigma_{\text{sol}} /\sigma_{\text{liq}}$ (from Chu and Ho 1978)[44] and surface temperature $T_{\text{surf}}$ for the 72-mm-thin slab (Vakhrushev et al.);[45,46] (b) simulated shell thickness (top); and its conductance ratio (bottom)

First, the averaged ratio between the liquid and solid electric conductivities is plotted in Figure 16(a) in the left curve, which is derived here from the extended data for different AISI steel grades, reported in 1978 by Chu and Ho.[44] The right curve in Figure 16(a) shows slab surface temperature along the mold’s wide face, simulated by Vakhrushev et al.[45,46] The corresponding thickness (100 pct of solid, top picture) and the conductance ratio (bottom picture) of the solid shell are plotted in Figure 16(b), which are obtained from the thin slab simulations[45,46] and calculated for the 72-mm-thick slab using Eq. [19] based on the temperature-dependent electric conductivity (see Figure 16(a)). The conductance ratio varies from very small values close to the meniscus where the solid shell is just formed up to 0.24 at the mold outlet. Despite a huge difference for the electrical conductivity ratio between the GaInSn/brass plates experiment and the liquid melt/solidifying solid shell for the steel alloys, the conductance ratio is of the same order. The experimental value[17] of $C_{\text{wall}} = 0.134$ is marked with a dashed horizontal line and qualitatively corresponds to an average value for the modeled thin slab case. Thus, with a high degree of confidence, the performed analysis of the induced electric current distribution and the influence of the highly conductive brass plates can be extended to the real CC process.

Conclusions

The turbulent flow of the GaInSn alloy was investigated in the presented study using an in-house solver based on the FVM open-source platform OpenFOAM®. A single mesh approach was introduced to simulate the presence of the highly conductive solid based on the conservative scheme for the Lorentz force. The single phase flow with and without the magnetic field from the single-ruler EMBr device were simulated and verified with the liquid metal experiment measurements. The WALE SGS model was chosen to be used within the large eddy approach since it was found to be a good match for both cases with and without electromagnetic braking applied.

It was observed that the perfect conductivity of the mold walls causes an extreme braking effect and the top part of the mold cavity become a stagnant zone, which should be avoided in the real CC process. Therefore, the role of the liquid slag film becomes not only important for the shell/mold gap lubrication and for the mold’s heat protection, but for the ‘controlled’ electrical insulation and partial reduction of the EMBr action.

When the brass plates are introduced, the current lines become arranged and are somewhat ‘fixed’ to the solid. The electric current tends to be conducted by the material with the lower resistance. However, the current lines are still misaligned in the bulk, as well as along the Shercliff walls and at the meniscus. The detailed analysis of the case with the presence of the ‘solid shell’ gives a combination of the fully insulated and perfectly conductive mold, i.e., plug-flow formation at the lower mold region due to the breaking effect combined with more flow fluctuations in the Shercliff layers. The closure of the induced electric current loops through the solidified shell plays the main role in allowing oscillations of the flow for the required melt mixing and mild turbulence level.

It was found that the presence of the highly conductive shell cannot be ignored in the real casting process. Assuming a fully insulated mold cavity, the numerical simulation predicts high instabilities and a totally unsteady mold flow. The application of the presented numerical study results to the real continuous casting process is qualitatively verified.

The expected performance of the electromagnetic brake is difficult if not impossible to achieve by plant trials, thereby the CFD modeling of the magnetohydrodynamics phenomena is vital for the continuous casting process. The presented results show the extreme importance of induced currents to properly understand the effects of EMBr in real continuous casting conditions.