Introduction

Metallurgical grade silicon (MG-Si) is produced in a submerged arc furnace by carbothermic reduction of silica (SiO2). The raw materials for this process, mainly quartz and a range of carbon materials, are not pure. Therefore, tapped MG-Si contains a range of impurities where the main ones are calcium and aluminum. An oxidative refining process is performed in a ladle by purging with an O2/air mixture in order to remove these impurities through formation of a CaO-Al2O3-SiO2 based slag.[1]

The refining result is determined by the thermodynamic equilibrium and the kinetics of mass transfer between slag and molten Si. The kinetics of the refining process has been described in an earlier publication.[2] In particular, the distribution of Ca and Al between molten Si and slag at equilibrium for a given temperature and composition is important for understanding the oxidative refining process. The reactions that determine the equilibrium condition are as follows:

$$ \underline{\text{Al}} + {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}\left( {{\text{SiO}}_{2} } \right) = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}\left( {{\text{Al}}_{2} {\text{O}}_{3} } \right) + {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}{\text{Si}} $$
(1)
$$ x_{\text{Al}} = \frac{{a_{{{\text{Al}}_{2} {\text{O}}_{3} }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \cdot a_{\text{Si}}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}}} }}{{K_{1} \cdot \gamma_{\text{Al}} \cdot a_{{{\text{SiO}}_{2} }}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}}} }} $$
(2)
$$ \underline{\text{Ca}} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}\left( {{\text{SiO}}_{2} } \right) = \left( {\text{CaO}} \right) + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}{\text{Si}} $$
(3)
$$ x_{\text{Ca}} = \frac{{a_{\text{CaO}}^{{}} \cdot a_{\text{Si}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{{K_{2} \cdot \gamma_{\text{Ca}} \cdot a_{{{\text{SiO}}_{2} }}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}, $$
(4)

where parentheses indicate components of the slag phase and underlining indicates elements dissolved in Si.

The equilibrium between Si and silicate slags has been measured by several researchers.[3–8] Weiss and Schwerdtfeger[3] investigated the chemical equilibria between molten Si and silica-saturated slags in the CaO-Al2O3-SiO2 system at 1773 K (1500 °C). Morita et al.[4] determined the thermodynamic activities in CaO-Al2O3-SiO2 slags by equilibrating slags with Si in graphite crucibles at 1823 K (1550 °C). Margaria et al.[5] and Wang et al.[6] reported equilibrium concentrations of Ca and Al in Si equilibrated with CaO-Al2O3-SiO2 slags at 1723 K (1450 °C) and 1823 K (1550 °C), respectively. Tuset et al.[7] estimated the concentrations of Ca and Al in Si equilibrated with CaO-Al2O3-SiO2 slags based on experimental data from 25 pct Fe - 75 pct Si and CaO-Al2O3-SiO2 slags. However, they did not determine Ca concentrations for slags with low CaO content. Fujiwara et al.[8] investigated the equilibrium between slag and Si for slags saturated with either Al6Si4O17, Al2O3, CaAl6O10, or CaAlO4 at 1873 K (1600 °C) using Al2O3 crucibles.

Knowledge of the equilibria also in the region with low CaO content in the slag is important for a better understanding of the refining process. The current study was hence aimed at determining the distribution of Ca and Al between molten Si and CaO-Al2O3-SiO2 slags containing 20 pct CaO at 1823 K (1550 °C) to complement the data from Tuset et al., Wang et al, and Morita et al. The experimental data are also compared with activity measurements and estimates from optimized thermodynamic models. All concentrations in this work are given in mass pct except for the values given in mole fraction in the thermodynamic evaluation.

Experimental

Apparatus and Procedure

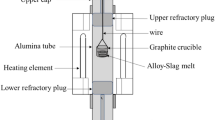
A graphite resistance tube furnace was used for the experiments in this work. The temperature was controlled at 1823 K (1550 °C) by a B-type thermocouple that was placed underneath the crucible. The set-up is illustrated in Figure 1. Four different mixtures were made from reagent grade SiO2, Al2O3, and CaCO3. The master slags were made by melting these mixtures three times in a Pt crucible at 1873 K (1600 °C). The slags were crushed between each melting cycle in order to produce homogeneous slags. In addition, granular polysilicon (8N), graphite crucibles, and silica crucibles were used for these experiments.

Fig. 1
figure 1

Graphite resistance tube furnace with two B-type thermocouples for accurate temperature control

Full size image

Each experiment was done by adding 10g of slag and 5g of Si in a crucible before holding at 1873 K (1600 °C) under a flow (5 L/hour) of 99.99 pct pure argon at atmospheric pressure. The furnace was shut off after the predetermined time and the system cooled to the melting point of Si in approximately two minutes where the temperature followed an exponential cooling trend towards room temperature. The graphite crucible was removed by grinding before slag and Si were carefully separated and crushed to powder. The Ca, Al, and Si contents of the resulting metal were analyzed in three replicate splits by both ICP-MS and ICP-OES. The SiO2, Al2O3, and CaO contents of the slags were determined by XRF. The XRF-measurements were calibrated against geological reference materials covering the composition range investigated in the present work. The master slags were analyzed to check purity and composition. A low impurity content was detected with <0.1 pct Fe2O3 and ≤0.05 pct MgO. The total content of other impurity oxides was detected to be ≤0.05 pct giving an overall purity with respect to CaO, Al2O3, and SiO2 of ≥99.8 pct.

Determination of Equilibrium Time

The present study is focused on the low-CaO region of the CaO-Al2O3-SiO2 system. Because of the high viscosity of these compositions,[9] it was expected that the rate of mass transfer between slag and Si would be slow. Prior to the main experiments, the change of concentration with reaction time was measured in order to determine the time to approach equilibrium. In these experiments, a silica-rich master slag and a silica crucible were used, and reaction times were varied from 6 to 24 hours. In this case, the crucible was removed by manually breaking it off piece by piece before separating slag and Si. A silica crucible was expected to give less change of slag composition with time than a graphite crucible since the composition was initially close to silica saturation.

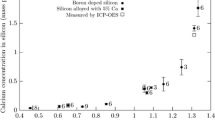
The experimental results are listed in Table I. The change in Ca and Al contents with reaction times is shown in Figure 2. Both concentrations approach asymptotically a constant value within 6 hours. The result at 9 hours appears to be an outlier and was not considered in the evaluation of the results. This result is also identified as an outlier for both Ca and Al by the one-sided Grubbs’ test at a 95 pct confidence level. In this test, all results for 6 hours and longer holding times were considered as equilibrium values. A possible cause of the outlier at 9 hours is that a slag inclusion was remaining in Si when it was crushed to a powder. To ensure that equilibrium was obtained, 15 hours was used as the reaction time for the main part of the study.

Table I Final Metal and Slag Compositions, in Mass Pct, for Experiments In Silica Crucibles at 1823 K (1550 °C)
Full size table
Fig. 2
figure 2

Ca and Al contents in Si as a function of reaction time with a 22CaO-9Al2O3-69SiO2 slag (compositions in mass pct) in silica crucibles at 1823 K (1550 °C)

Full size image

Results

All experiments were performed with ~20 pct CaO containing slags where the Al2O3 content was varied between 9 and 25 pct. The results from the main experiments are summarized in Table II. Chemical analysis was duplicated by ICP-MS and ICP-OES at two different laboratories to ensure accurate values. The analytical values from Table I and II are compared in Figure 3 and are seen to be in good agreement with each other. Hence, the average of these values was used.

Table II Metal and Slag Compositions, in Mass Pct, After Equilibration in Graphite Crucibles at 1823 K (1550 °C)
Full size table
Fig. 3
figure 3

Comparison of Ca and Al contents determined by ICP-MS and with ICP-OES

Full size image

The initial and final slag compositions are shown in Figure 4. The slag composition changes somewhat during the experiments because of reactions between the slag and the crucible. For the experiments in the graphite crucibles, SiO2 in the slag reacts with carbon to form SiO and CO gas. Therefore, the SiO2 content in the slags decreased somewhat during the experiments. A mass loss of about 0.8 grams was observed and is believed to be caused by the above reaction. The mean concentration of CaO was 22 pct after the experiments in graphite crucibles.

Fig. 4
figure 4

Initial and final slag compositions in the present work are shown together with Ca and Al concentrations in Si in equilibrium with CaO-Al2O3-SiO2 slags at 1823 K (1550 °C) estimated by Tuset et al.[7] An estimated iso-concentration line from the present work is also indicated

Full size image

A mass loss was also observed for the experiments performed in SiO2 crucibles. The mass loss in these experiments is believed to be caused by reaction between Si and SiO2 to form SiO gas. SiO2 can also dissolve from the crucible into the slag. The slag composition is, however, seen to be almost the same for all holding times and relatively far from the known liquidus line at 1823 K (1550 °C), as can be seen in Figure 4. This may indicate that the kinetics of dissolution of SiO2 was so slow that the slag did not reach equilibrium with the crucible. Iso-concentration curves for Ca and Al in Si at equilibrium CaO-Al2O3-SiO2 slags estimated by Tuset et al.[7] is also shown in Figure 4. It is seen that the Ca content in Si was not determined for low CaO contents in the slag.

Figure 5 shows the Ca and Al contents in Si equilibrated with 20 pct CaO-containing slags. The Ca concentration is nearly constant with changing slag composition. This means that the Ca content in Si is not significantly affected by the Al2O3/SiO2 ratio at constant CaO content in the slag. In contrast to this, the Al content increases with increasing Al2O3/SiO2 ratio. Both the Ca and Al concentrations were extrapolated to silica saturation to enable comparison with previous works along the liquidus line.

Fig. 5
figure 5

Effect of Al2O3 content in slag on the Ca and Al contents in Si equilibrated with CaO-Al2O3-SiO2 slags containing 20 pct CaO at 1823 K (1550 °C). Values extrapolated to the liquidus line at SiO2 saturation given by the Slag Atlas[24] are also indicated

Full size image

Discussion

Distribution of Ca and Al Between Molten Silicon and Slags Containing 22 pct CaO

Direct measurements

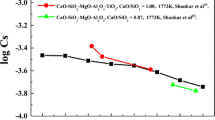
In Figure 6, the results of the present study are compared with results by Morita et al.,[4] Wang et al.,[6] Tuset et al.,[7] and Fujiwara et al.[8] with respect to Al. The present results are in relatively good agreement with Morita et al. and Tuset et al. The values found by Wang et al. are seen to be more scattered around the present work and the other previous works. Morita et al. used 18 hours, while Wang et al. used 4 hours equilibration time. Equilibrium may have been reached within 4 hours considering that the values found by Wang et al. are in the same magnitude as found in the present work and the other previous works, but the values are relatively scattered indicating that there may have been issues with the experiments or the analyses. The study by Fujiwara et al.[8] is for higher Al2O3 contents than the other studies and at a 50 K higher temperature. The measured Al contents are also seen to be a bit higher than the other results.

Fig. 6
figure 6

Concentration of Al in Si at 1823 K (1550 °C) as a function of Al2O3 content in the slag where the CaO concentration is 22.0 ± 2.5 pct

Full size image

The Ca concentrations in Si found in the present work are compared with previous works in Figure 7. The concentrations found by Morita et al.[4] are seen to be in good agreement with the present work while the values found by Wang et al.[6] are seen to be scattered and generally much higher. The values from Fujiwara et al.[8] are also seen to be higher than found in the present work and by Morita et al. with the exception of one value. The values from their work are also relatively scattered.

Fig. 7
figure 7

Concentration of Ca in Si at 1823 K (1550 °C) as a function of Al2O3 content in the slag where the CaO concentration is 22.0 ± 2.5 pct

Full size image

The Henrian activity coefficients of Ca and Al in Si

It is also interesting to compare the direct measurements of Ca and Al with activity measurements in slags. From Eqs. [2] and [4], it is seen that the activity coefficient of Ca and Al in Si has to be known in order to compare measurements with activities in the slag. The concentrations of Ca and Al are both well below one percent in Si, and it is therefore reasonable to assume that we are in the Henrian solute range. These activity coefficients are given with liquid Ca and Al as the reference state.

The Henrian activity coefficient of Al in Si 1823 K (1550 °C) was estimated to be 0.463 using the Factsage FTlite database which is relatively close to the value of 0.508 that can be estimated from the work by Gröbner et al.[10] The Modified Quasichemical Model[11] was used for the liquid solution of Si-Al in the Factsage database while Gröbner et al. used Redlich-Kister polynomials.[12] The relatively similar values of the Henrian activity coefficient from the two different models indicate that the predicted values should be relative close to the true value.

Jakobsson and Tangstad[21] have discussed the Henrian activity coefficient of Ca in Si in a previous article, and the different values found in literature are compared there. In the present work, the Henrian activity coefficient at 1823 K (1550 °C) was taken as the mean value of two direct determinations at this temperature,[5,22] which gives \( \ln \gamma_{\text{Ca}}^{0} = - 7.25 \). This value is also close to the estimate given in the book by Schei et al.[23]

Distribution of Ca and Al estimated from activity measurements of slags

Rein and Chipman[13] determined activities in CaO-Al2O3-SiO2 slags at 1823 K (1550 °C) by equilibration of slags and with graphite or silicon carbide-saturated Fe-Si-C alloys. Using the Henrian activity coefficient of 0.463 and activities of CaO and SiO2 from Rein and Chipman, an estimate was made from their data for the concentrations of Al in Si. Gibbs energies of Al2O3(corundum) and SiO2(β-cristobalite) were taken from Factsage, which are very close to the values given in the NIST-JANAF tables.[14] The estimated concentrations are shown in Figure 6 and they are seen to be somewhat on the low side of the measured values, but following the same trend as found in other works. The same procedure was used to estimate the concentrations of Al in Si using activities from Cameron et al.[15] and Zaitsev et al.[16] The values estimated from Zaitsev et al. are seen to be somewhat higher than the present work for slags with higher Al2O3 content while the estimate from Cameron et al. is relatively close to the values estimated from Rein and Chipman.

The work by Rein and Chipman[13] and by Tuset et al.[7] did not extend to the range investigated in the present work with respect to Ca. The concentrations estimated from Cameron et al. and Zaitsev et al. are seen in Figure 7 to be in relatively good agreement with the present work. The Henrian activity coefficient given as \( \ln \gamma_{\text{Ca}}^{0} = - 7.25 \) was used for these estimates while Gibbs energies of CaO(s) and SiO2(β-cristobalite) were taken from Factsage. The Gibbs energy of CaO(s) at 1823 K (1550 °C) from Factsage, with liquid Ca as reference state, was approximately 1 kJ less negative than the value from the NIST-JANAF tables. The calculated concentrations of Ca would be approximately 7 pct lower using the Gibbs energy from the NIST-JANAF tables.

There are at least two more works determining activities in the CaO-Al2O3-SiO2 system at 1823 K (1550 °C), one being the work by Kay and Taylor.[17] The work by Cameron et al. is however largely based on the work by Kay and Taylor by using activities of SiO2 from these authors. The second work determining activities is by Ohta and Suito,[18] who used the activity of SiO2 from Rein and Chipman. It was therefore considered sufficient to compare the present work with only two of these four works. Only the activity of SiO2 was determined experimentally in the above-mentioned works. The activities of CaO and Al2O3 were determined by Gibbs–Duhem integration of the activity of SiO2. It should be noted that the starting value of these integrals might be somewhat uncertain because of limited phase diagram and compound data.

Distribution of Ca and Al calculated from thermodynamic databases for slags

The Henrian activity coefficient of Al from above was also used to calculate the concentrations of Al in Si from slag databases. Activities of Al2O3 and SiO2 from thermodynamic optimizations done in the Factsage FToxid database and by Mao et al.[19] were used for this. The model in the Factsage FToxid database for the CaO-Al2O3-SiO2 system was originally done by Eriksson and Pelton.[20]

These estimates are seen in Figure 6 to be in relatively close agreement with each other even if two different liquid solution models were used. They are also seen to be in relatively close agreement with the experimental values. The Gibbs energies used in these estimates were the database values of Factsage.

The values for Ca in Si calculated from slag databases using the Henrian activity coefficient for Ca from above are shown in Figure 7. The values from the Factsage FToxid database and the model by Mao et al.[19] are seen to follow the same trend as the concentrations found in the present work. The values from the Factsage FToxid database are, however, somewhat closer to the values found in the present work.

Summary

The relatively close agreement between the trends for concentration of Ca and Al from the models and the experiments in the present work indicates that both the models and the experimental values are reasonable. In addition, the Henrian activity coefficients of Ca and Al used in the present work seem to be reasonable given the good agreement between measured concentrations and activities in the slag. Previous experimental activity measurements in the ternary CaO-Al2O3-SiO2 system are also in relatively good agreement with the present work.

Distribution of Ca and Al Between Molten Silicon and SiO2-Saturated Slags

Liquidus line at SiO2 saturation

The location of the liquidus line for SiO2 saturation from different works is compared in Figure 8 and is seen to be relatively scattered. This scatter indicates that there may be a challenge both to measure and to model this liquidus line. The SiO2 saturation lines from the Slag Atlas[24] are seen to be in best agreement with previous experimental works. The SiO2 saturation lines given in the Slag Atlas are in close agreement with the work by Osborn and Muan.[25] The work by Weiss and Schwerdtfeger at 1773 K (1500 °C) is seen to follow the estimated liquidus line from the Factsage FToxid database at 1823 K (1550 °C). The slag compositions found in the present work are in best agreement with the model by Berman and Brown[26] but the present authors are, as discussed above, not confident that the slag compositions are at SiO2 saturation.

Fig. 8
figure 8

Measured and modeled liquidus line for SiO2 saturation at 1773 K (1500 °C) and 1823 K (1550 °C)

Full size image

Distribution of aluminum

The concentrations of Al in Si follow an exponential trend along the liquidus line as can be seen in Figure 9. The extrapolated value from the present work is in relatively good agreement with previous works. The works by Weiss and Schwerdtfeger[3] and Morita et al.[4] are in relatively good agreement even if they have a 50 K temperature difference. This indicates that the Al content in equilibrium with SiO2-saturated CaO-Al2O3-SiO2 slags is relatively unaffected by temperature. The Al concentrations in Si in equilibrium with SiO2-saturated slags estimated by Tuset et al.[7] are also indicated in Figure 9 and are seen to be in relatively good agreement with the present work and other experimental works.

Fig. 9
figure 9

Concentration of Al in Si in equilibrium with slags along the SiO2-saturated liquidus line. (* 3 h experiment for slag with lowest CaO content omitted from curve fit because it may not be an equilibrium value, as discussed in the text)

Full size image

Calculated concentrations from the Factsage FToxid database and Mao et al.[19] are also shown in Figure 9. The calculated Al concentrations from the work by Mao et al. are seen to be significantly lower than experimental values in this study. This can to some extent be explained by the liquidus line for SiO2 saturation, which is somewhat closer to the binary CaO-SiO2 system than others have found, as can be seen in Figure 8. The calculated concentrations from the Factsage FToxid database are also seen to be somewhat lower than experimental values.

Distribution of calcium

The concentrations of Ca in Si found by Morita et al. and the extrapolated value in the present work at 1823 K (1550 °C) are seen in Figure 10. to be significantly higher than found by Weiss and Schwerdtfeger at 1773 K (1500 °C). This may indicate that the Ca content in equilibrium with SiO2-saturated CaO-Al2O3-SiO2 slags increases with increasing temperature. One of the measured values by Morita et al. is significantly lower than the linear trend of the other values, and it was therefore considered as an outlier. The extrapolated value from the present work is a bit lower than the linear trend found by Morita et al.

Fig. 10
figure 10

Concentration of Ca in Si in equilibrium with slags along the SiO2-saturated liquidus line. (* One data-point from the study by Morita et al. is seen to deviate significantly from the trend of the other measurements and was therefore deemed as an outlier.)

Full size image

The concentrations of Ca in Si calculated from the Factsage FToxid database and the model by Mao et al. are also shown in Figure 10. The values from the FToxid database are seen to follow the measured values by Weiss and Schwerdtfeger even if there is a 50 K temperature difference. This is correlated with the similarity of the liquidus lines seen in Figure 8. The values calculated from Mao et al. are less in agreement with experimentally measured values and trends.

Thermodynamic Evaluation of Measured Ca and Al Contents at SiO2 Saturation

Theory

The Gibbs–Duhem equation for the ternary CaO-Al2O3-SiO2 system is given by

$$ x_{\text{CaO}} d\ln a_{\text{CaO}} + x_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} d\ln a_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} + x_{{{\text{SiO}}_{2} }} d\ln a_{{{\text{SiO}}_{2} }} = 0. $$
(5)

Along the liquidus line for SiO2 saturation, we have a fixed activity of one relative to solid β-cristobalite. Weiss and Schwerdtfeger[4] have shown that the concentrations of Ca and Al in Si can be used to find the activity of CaO and Al2O3 by Gibbs–Duhem integration along the liquidus line.

As both Ca and Al behave as Henrian solutes in Si, the concentrations of Ca and Al are also directly related to the activities of CaO and Al2O3 through Eqs. [2] and [4] by the Henrian activity coefficients. Even without knowing the activities, we can calculate the concentrations of Ca along the liquidus line directly by Gibbs–Duhem integration of the concentrations of Al, provided we have one measurement value for Ca. The same can also be done the other way around in calculating the concentrations of Al from the concentrations of Ca. The derivation is given below.

First, we have

$$ a_{{{\text{SiO}}_{2} }} = 1 = {\text{const}} . { } \Rightarrow d\ln a_{{{\text{SiO}}_{2} }} = 0 $$
(6)

and we get

$$ x_{\text{CaO}} d\ln a_{\text{CaO}} + x_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} d\ln a_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} = 0. $$
(7)

With the ternary slag in contact with liquid Si, we have two exchange reactions between the two phases given by Reactions [2] and [4].

The Henrian activity coefficients are, by being constant, eliminated from the differentials in the Gibbs–Duhem equation. This gives

$$ d\ln a_{\text{CaO}} = d\ln \frac{{x_{\text{Ca}} }}{{x_{\text{Si}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} $$
(8)
$$ d\ln a_{{{\text{Al}}_{2} {\text{O}}_{3} }}^{{}} = 2 \cdot d\ln \frac{{x_{\text{Al}} }}{{x_{\text{Si}}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}}} }}. $$
(9)

Hence, we end up with

$$ x_{\text{CaO}} d\ln \frac{{x_{\text{Ca}} }}{{x_{\text{Si}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }} + 2x_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} d\ln \frac{{x_{\text{Al}} }}{{x_{\text{Si}}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0pt} 4}}} }} = 0. $$
(10)

The mole fraction of Si is very close to unity, which gives

$$ d\ln x_{\text{Ca}} = - \frac{{2x_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} }}{{x_{\text{CaO}} }}d\ln x_{\text{Al}}. $$
(11)

This equation can be integrated to find the concentrations of Ca from the concentrations from Al and vice a versa.

Thermodynamic evaluation of measurements

Weiss and Schwerdtfeger[3] and Morita et al.[4] measured both the concentrations of Ca and the concentrations of Al along the SiO2 saturation line. This allows a thermodynamic comparison between the measured Al concentrations and the measured Ca concentrations.

The measured concentrations of Al for 3 and 6 hours in the work by Weiss and Schwerdtfeger[3] are seen in Figure 9 to be in very good agreement except for the slag with lowest CaO content. Considering the very high viscosity of this slag, it is considered by the present authors that the measured value for 3 hours may not be the equilibrium value. The value for 3 hours was therefore omitted from the exponential fit to the data. The Al concentrations in Si were fitted as a function of concentration of CaO in the slag where the function had the following form:

$$ x_{\text{Al}} = \alpha \cdot \left( {\exp \left( {\beta \cdot \left( {x_{CaO} - x_{\text{CaO}}^{0} } \right)} \right) - 1} \right), $$
(12)

where \( x_{\text{CaO}}^{0} = 0.3611 \), which is the CaO concentration at SiO2 saturation in the binary CaO-SiO2 system according to Weiss and Schwerdtfeger. The values of α and β are given in Table III. This fit was used for the following integral:

Table III Coefficient Values for Functions [12] and [14]
Full size table
$$ \ln x_{\text{Ca}} = \int\limits_{{x_{{{\text{Al}}_{2} {\text{O}}_{3} }} = 0}}^{{x_{\text{CaO}} }} { - \frac{{2x_{{{\text{Al}}_{ 2} {\text{O}}_{ 3} }} }}{{x_{\text{CaO}} }}} d\ln x_{\text{Al}} + \ln x_{\text{Ca}}^{0}. $$
(13)

The concentration for \( x_{\text{Ca}}^{0} \)was chosen as the measured value by Weiss and Schwerdtfeger at SiO2 saturation in the binary CaO-SiO2 system. The integration path was a third degree polynomial fit to slag compositions along the liquidus line measured by Weiss and Schwerdtfeger. The polynomial had the following form:

$$ x_{{{\text{Al}}_{2} {\text{O}}_{3} }} = a \cdot \left( {x_{\text{CaO}} - x_{\text{CaO}}^{0} } \right) + b \cdot \left( {x_{\text{CaO}} - x_{\text{CaO}}^{0} } \right)^{2} + c \cdot \left( {x_{\text{CaO}} - x_{\text{CaO}}^{0} } \right)^{3} $$
(14)

with the same value of \( x_{\text{CaO}}^{0} \)as above (0.3611). The coefficients a, b and c are given in Table III. Using these functions, the concentrations of Ca could be determined by numerical integration of Eq. [13].

The concentrations of Ca found by this integral are seen in Figure 10 to have a sigmoid shape and follow the trend they found for the concentrations of Ca. The measured concentrations of Ca and Al by Weiss and Schwerdtfeger are in other words thermodynamically self-consistent. The integral does not have problems with divergence as \( x_{\text{Al}}^{{}} \)and \( x_{{{\text{Al}}_{2} {\text{O}}_{3} }}^{{}} \)approaches zero. This problem was mentioned by Weiss and Schwerdtfeger, but is in the present work overcome by using functions that makes the integral converge to zero

The Gibbs–Duhem integration procedure was also applied to the data for Al at SiO2 saturation found by Morita et al.[4] at 1823 K (1550 °C) to estimate the concentrations of Ca in Si. In this case \( x_{\text{Ca}}^{0} \)and \( x_{\text{CaO}}^{0} \)were taken from the study by Morita et al. at SiO2 saturation in the binary CaO-SiO2 system where \( x_{\text{Ca}}^{0} = 3.525 \cdot 10^{ - 4} \) and \( x_{\text{CaO}}^{0} \) = 0.355. The same polynomials [12] and [14], were used where the coefficient values are shown in Table III. The estimated concentrations of Ca in Si are shown in Figure 10 and the trend is seen to deviate somewhat from the experimentally determined linear trend by Morita et al.

The linear trend for Ca in Si found by Morita et al. was used to estimate the concentrations of Al in Si as a final check of the self-consistency between the concentrations of Ca and Al. The concentration \( x_{\text{Al}}^{0} \)was chosen to be the highest concentration measured by Morita et al. This estimate is seen in Figure 9 to have a less curved shape than measured experimentally.

Conclusion

The calcium and aluminum contents in molten silicon equilibrated with CaO-Al2O3-SiO2 slags containing 20 pct CaO were determined at 1823 K (1550 °C). The present work was found to be in good agreement with previous experimental measurements and estimates. The Henrian activity coefficients of calcium and aluminum were used to compare the experimental values with measured and modeled activities in the slag. A good agreement between activities in the slag and measured concentrations indicates that the Henrian activity coefficients used in the present work are reasonable. The modeled activities were found to be in better agreement with the present work than previous activity measurements.

The thermodynamic self-consistency of results at SiO2 saturation was evaluated using the Gibbs–Duhem equation and found to be relatively good. Modeled concentrations along the liquidus line were also compared with the experimental measurements. A wide scatter in the location of the liquidus line at SiO2 saturation from different models was seen. This also gave rise to differences in the estimated concentrations of calcium and aluminum in silicon. Further improvement of models with respect to the liquidus line for SiO2 saturation would therefore be advised.