1 Introduction

Advanced High Strength Steels (AHSSs) are under continuous development to meet various requirements, including combinations of strength, formability, and crashworthiness. In these steels, the combination of mechanical properties is achieved by a carefully designed multi-phase microstructure.[1] The volume fractions of the different microstructural constituents, such as ferrite, bainite, martensite, and austenite, determine the final properties.

During steel production and in sheet forming processes as well as joining processes like resistance spot welding, loading is applied that affects the behavior of the solid-state phase transformations in the steel. It has been reported that in hot pressing processes, non-isothermal deformation in austenite promotes ferrite and/or bainite formation prior to the martensitic transformation and that the martensite start temperature (M s) decreases.[2,3,4,5] If the austenite is plastically deformed, it will be strengthened. With an increase in yield strength of the austenite, M s decreases and this can be explained by a dislocation stabilization mechanism.[6,7,8,9] He et al. reported that M s increases with strain after small deformations and decreases with strain after large deformations of austenite in the plastic regime.[10]

In resistance spot welding, a constant load (stress range of 100–200 MPa) is applied by two electrodes. It is expected that this applied load will affect the solid-state phase transformations occurring after the formation of the weld. In-situ synchrotron diffraction is a suitable technique to study these solid-state phase transformations.[11,12,13,14,15,16,17] Dutta et al. observed that loading conditions below the yield strength of austenite lead to elastic strains upon martensitic transformation and M s increases with an increase in the applied external tensile load.[18]

From a thermodynamic point of view, a reduction in Gibbs free energy of a system indicates whether it is favorable for phase transformations to take place. The total Gibbs free energy is the sum of a chemical and a mechanical component. The chemical free energy component of austenite and martensite as a function of temperature is shown schematically in Figure 1. At T 0, both austenite and martensite have equal Gibbs free energies. At a certain temperature (M s) lower than T 0, martensite starts to form spontaneously. At temperatures between M s and T 0 (for example T 1), although the martensite Gibbs free energy is lower than that of austenite, the transformation does not occur, as there is a free energy barrier that must be overcome for the transformation to occur. To activate the martensitic transformation at temperatures between M s and T 0, the Gibbs free energy should be enhanced by applying an external load.[19]

Fig. 1
figure 1

Chemical component of the Gibbs free energy of austenite and martensite

Full size image

The effects of mechanical loading above the yield stress of austenite and the bcc phases on the microstructure development are not yet fully understood. In the present work, in-situ synchrotron X-ray diffraction experiments have been conducted to explore the effect of constant loading below and above the yield stress of austenite on the subsequent solid-state phase transformations. Time–temperature–load dependent diffraction patterns provide data to study the phase fractions and kinetics of transformations for different thermal–mechanical cycles.

2 Experimental Approach

The material studied is a 3rd generation 1 GPa AHSS with a thickness of 1.3 mm. The steel was received in a cold-rolled and galvanized condition (surface density of 50 gm−2). Material composition is listed in Table I. Small block samples were prepared from the as-received AHSS sheet. The coating was removed by an acid etch. The blocks were homogenized at 1523 K (1250 °C) for 3 days in a vacuum chamber. The material was then annealed in a salt bath at 1053 K (780 °C) for 30 minutes followed by water quenching to obtain a typical dual-phase ferritic martensitic microstructure (Figure 2).

Table I Material Composition
Full size table
Fig. 2
figure 2

Initial microstructure of the steel studied with in-situ synchrotron X-ray diffraction. Standard metallographic procedure with 2 pct Nital as an etchant was used

Full size image

Tensile specimens with a gage length of 16 mm and a cross section of 1.5 × 1.0 mm2 were electro-discharge machined from the homogenized and heat-treated samples. The loading axis was selected to be parallel to the transverse rolling direction (TD) and perpendicular to the rolling direction (RD).

In-situ synchrotron X-ray diffraction experiments were conducted at the ID11 beamline of the European Synchrotron Radiation Facility (ESRF) in Grenoble, France. A beam energy of about 80 keV (λ = 0.15582 Å) and a beam size of 300 ×300 μm2 were used. To obtain diffraction data, a 2D CCD detector (FReLoN—fast readout low noise) camera system[20] was employed. CeO2 calibrant was used on each sample to determine sample–detector distance, tilt of the detector, and the beam center. Corrections were applied to omit dark field, flat field, and detector distortion during data analysis.[21] An Instron/NPL electro-thermal mechanical testing (ETMT) machine was used to apply loads up to 3 kN. Thermal cycles were generated by Ohmic heating with a direct current passing through the sample. Temperature control was established by a type-R thermocouple discharge welded to the center of the specimen. The experimental configuration and a test specimen are shown in Figure 3. To prevent decarburization during heating and cooling, the ETMT was flushed with argon gas.

Fig. 3
figure 3

Experimental setup at the ID11 beamline of ESRF facility in Grenoble, France, (a) ETMT chamber, (b) vertically located sample, and (c) configuration of the sample with thermocouples attached and the CeO2 as a calibrant

Full size image

The specimens were heated up to 1273 K (1000 °C) at a heating rate of 10 Ks−1, kept for 10 seconds at that temperature to obtain a fully austenitic microstructure, and subsequently cooled at a rate of 40 Ks−1 to room temperature. According to previous dilatometric experiments for the steel studied, M s in the absence of loading is 600 K (327 °C). The cooling process was interrupted for 7 seconds at 823 K (550 °C) (i.e., above M s) to apply an axial force of 50, 100, 150, 250, and 400 N, which was held constant during further cooling to room temperature. The loads of 50, 100, and 150 are approximately equivalent to the stresses of 33, 67, and 100 MPa, which are below the yield stress of the material at 823 K (550 °C), while the 250 and 400 N loads (167 and 267 MPa) are equal to and higher than the yield stress, respectively. A schematic representation of the thermal–mechanical cycle is shown in Figure 4.

Fig. 4
figure 4

Schematic illustration of the thermal–mechanical cycles applied

Full size image

It should be mentioned that the martensitic transformation is known to occur very rapidly. Due to the experimental restrictions such as detector frequency for collecting diffraction images and the high cooling rates required for martensitic transformation, diffraction patterns were recorded at 0.7 second intervals for each temperature–load treatment. The martensite start temperatures were estimated from the experimental data.

Data analysis was conducted with Fit2D image processing software developed at ESRF.[22] A typical 2D X-ray diffraction pattern is shown in Figure 5. To convert the 2D data to 1D diffraction patterns, integration over the azimuthal angles at a constant scattering angle was performed. From the 1D patterns, a fit of each reflection to a pseudo-Voigt profile over the azimuthal angles was carried out. Volume fractions of the phases and austenite lattice parameters were acquired from the integrated intensities and the scattering angles of two austenite (γ(200) and γ(220)) and two bcc (α(200) and α(211)) phase rings.[23] Typical intensity–2θ patterns of γ(220) and α(211) at different times during cooling are shown in Figure 6, and these were used for volume fraction calculations. The bcc phases include several ferrite products such as grain boundary ferrite, Widmanstätten ferrite, bainitic ferrite, and also martensite. Although martensite has a BCT structure, considering the low carbon content of the steel, diffraction peaks of this phase cannot be distinguished from the bcc phase using X-ray diffraction, due to the line broadening of the martensite peaks.

Fig. 5
figure 5

2D X-ray diffraction pattern. LD indicates the loading direction

Full size image
Fig. 6
figure 6

Intensity–2θ patterns for the sample subjected to 400 N load during cooling. The austenite peak (γ(220)) intensity decreases and the bcc peak (α(211)) intensity increases during cooling

Full size image

The transformation temperatures and kinetics were derived from the volume fraction data.

3 Results

3.1 Phase Transformations During Cooling

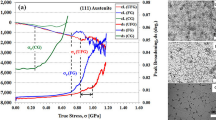
The bcc phase volume fractions as a function of temperature during cooling for different applied loads are shown in Figure 7. The bcc volume fraction as a function of time between 873 K and 473 K (600 °C and 200 °C) is also presented in the inset.

Fig. 7
figure 7

bcc phase volume fraction as a function of temperature during cooling for different heat treatment cycles

Full size image

3.1.1 Initial bcc phase transformation (isothermal holding)

The initial bcc phase transformation occurs at 823 K (550 °C), where the load is applied (Figure 7). As can be seen, by increasing the load, the bcc phase volume fraction at a constant temperature of 823 K (550 °C) increases. In the sample subjected to a 400 N load, 2 pct bcc phase is present before applying the load [at 823 K (550 °C)]. After applying the load, the bcc phase fraction has increased to around 27 pct.

3.1.2 Phase transformation during subsequent cooling (martensitic transformation)

Upon subsequent cooling, the bcc volume fraction gradually increases for each of the loads. A steep increase in the bcc phase fraction when cooling below around 723 K (450 °C), especially for small loads, provides evidence that the martensitic transformation takes place (Figure 7). It should be noted that the martensitic phase is included in the bcc fraction as mentioned before.

The estimated M s from the available data for the 50, 100, 150, 250, and 400 N samples are 636 K, 670 K, 695 K, 623 K, and 663 K (363 °C, 397 °C, 422 °C, 350 °C, and 390 °C), respectively. M s increases with increasing applied stress below the yield stress. In the case of a 250 N load, the applied stress is approximately at the yield stress of the material, whereas at 400 N it is higher than the yield stress. In these loading cases, M s is reduced in comparison to the value obtained from samples loaded in the elastic regime.

3.2 Kinetics of Phase Transformations During Cooling

The kinetics of the phase transformation during cooling are presented in Figure 8. The curves show the transformation rate as a function of temperature. The kinetics of the bcc phase transformation vs time in the temperature range between 873 K and 473 K (600 °C and 200 °C) is also presented in this figure.

Fig. 8
figure 8

Kinetics of bcc phase transformations during cooling for heat treatment cycles

Full size image

The kinetics of the initial bcc phase transformation at 823 K (550 °C) is higher for the sample subjected to 400 N in comparison with the other thermal–mechanical cycles.

The maximum transformation rate in each load case is related to the martensitic transformation and it is achieved at different temperatures. In the sample subjected to a 50 N load, the highest martensite transformation kinetics was obtained. For higher loads of 100, 150, 250, and 400 N, the martensitic transformation kinetics become slower. The slowest martensitic transformation is related to the sample subjected to a load of 400 N.

3.3 Austenite Lattice Parameter

The austenite lattice parameter for different thermal mechanical cycles is shown in Figure 9. The austenite lattice parameter decreases during cooling. Under constant load at 823 K, the austenite lattice parameter increases. Applying higher loads results in a larger increase in the austenite lattice parameter. Upon further cooling, again a reduction in austenite lattice parameter is found.

Fig. 9
figure 9

Austenite lattice parameter vs temperature for different thermal–mechanical cycles

Full size image

3.4 Retained Austenite

The bcc phase volume fraction at room temperature, and thus the retained austenite volume fraction, differs for each temperature–load history (Figure 7). Extracted data on retained austenite volume percent and lattice parameter at room temperature after unloading are presented in Table II. The fraction shows an increase with increasing applied load. The sample subjected to 400 N load contains the highest retained austenite volume fraction, of approximately 7.6 pct. The retained austenite lattice parameter also shows higher levels with increasing applied load.

Table II Retained Austenite Volume Percent and Lattice Parameter at RT for Different Samples
Full size table

The carbon concentration (C γ) of retained austenite is obtained from Eq. [1][23,24,25,26]:

$$ a_{\gamma } = a_{0} + k_{\text{C}} X_{\text{C}} + k_{\text{Mn}} X_{Mn} \ldots, $$
(1)

where \( {\text{a}}_{0} \) is the theoretical austenite lattice parameter (at 20 °C) for pure iron, being 3.556 Å,[23] \( X_{\text{C}} \) is the concentration of carbon in wt pct, \( X_{\text{Mn}} \) is the concentration of manganese in wt pct, and \( k_{\text{C}} \) and \( k_{\text{Mn}} \)are determined to be 0.00453 nm/(wt pct) C and 0.000095 nm/(wt pct) Mn as indicated in Reference 23, respectively.

The calculated carbon content of retained austenite is higher within the samples subjected to higher loads (Table III).

Table III Carbon Content of Retained Austenite
Full size table

3.5 Microstructural Characterization

The color-etched microstructures of different samples are shown in Figure 10. The samples are etched with LePera etchant. This etching changes the colors of retained austenite/martensite into whitish blue, bainite into brown, and ferrite into a tan color.[27,28] The sample subjected to a load of 50 N is almost fully martensitic (Figure 10(a)). By increasing the load to 100 N, ferrite decorates the prior austenite grain boundaries (Figures 10(b) through (d)). In the thermo–mechanically treated sample subjected to a 400 N load, the highest volume fraction of ferrite is shown. Furthermore, the micrograph shows a heavily deformed microstructure (Figure 10(e)).

Fig. 10
figure 10

Microstructures of samples subjected to the loads of (a) 50 N, (b) 100 N, (c) 150 N, (d) 250 N, and (e) 400 N

Full size image

4 Discussion

In the bcc phase volume fraction diagram during cooling (Figure 7), high temperature range indicates the increase in bcc phase fraction, which is related to the ferrite transformation at 823 K (550 °C). From the results obtained, it can be seen that loading has a remarkable effect on the fraction of the initial bcc phase formed isothermally. It seems that the ferrite transformation is a stress-enhanced transformation as with an increase in load (stress) at a constant temperature of 823 K (550 °C), the volume fraction of ferrite increases. Matsuzaki et al. have also reported that in a FeCSiMn alloy bainitic ferrite transformation kinetics in isothermal condition have been accelerated by applying external loads.[29]

At lower temperatures, martensite forms at a high transformation rate. In the 50, 100, and 150 N thermal–mechanical cycles, the applied stress is lower than the yield stress of the material, and by increasing the load from 50 to 100 and 150 N, M s increases and the volume fraction of the ferrite phase before reaching M s is relatively low. This is in agreement with the work of Dutta et al.[18] for loads in the elastic region. However, in samples subjected to 250 N (approximately at the yield stress) and 400 N load, a decrease in M s is observed. Applying loads higher than the yield stress of austenite will change the austenite morphology. The austenite in the sample subjected to 400 N is elongated in the tensile loading direction and the morphology resembles a film-like austenite. This austenite morphology shows a higher stability than blocky austenite.[30] Furthermore, an increase in dislocation density of austenite associated with plastic deformation (work hardening) can also result in austenite stabilization.[31]

Another potentially important mechanism that can contribute to austenite stability is carbon enrichment due to diffusion from transformed stress-induced ferritic phases into the austenite.[32] As shown in Figure 9, when the constant load is applied at 823 K, an increase in austenite lattice parameter is observed. This increase can be attributed to the application of mechanical loading and the chemical effect, i.e., carbon redistribution. The elastic component of the mechanical loading can be obtained from the peak shift in the XRD data. However, the plastic strain cannot be calculated from the peak shift. Given that 250 N is at the elastic limit, the mechanical contribution on the lattice parameter change is expected to be the same at 400 N as in the case of 250 N. The austenite lattice parameter at 823 K after applying load is 3.61195 Å for the 250 N sample and 3.61459 Å for the 400 N sample. The larger austenite lattice parameter in the 400 N sample indicates a higher austenite carbon content, leading to austenite stabilization. Indeed, the higher ferrite transformation in the 400 N sample leads to higher carbon content in austenite in this sample.

When the samples have reached room temperature, the mechanical loading is released. At this temperature, the remaining contribution to the variation in lattice parameter results from the carbon concentration of austenite as indicated in Table III. Carbon stabilizes the retained austenite. The 400 N sample has the highest retained austenite carbon content and volume fraction.

The Gibbs free energies of austenite, martensite, and carbon-enriched austenite are shown in Figure 11. Carbon-enriched austenite shows a lower free energy. Austenite carbon enrichment, stabilization with plastic deformation, and change in morphology increase the yield stress for austenite, thereby retarding the martensitic transformation. These mechanisms can explain the decrease in M s for samples subjected to the 250 N and 400 N loads. Comparing the two samples of 250 and 400 N, M s has increased with enhancing load. This could be related to the limited set of data points available to determine M s, since there is a temperature change of 28 K between consecutive data points.

Fig. 11
figure 11

Schematic illustration of M s changes under different loading conditions studied in this work

Full size image

The microstructures of different samples are in good agreement with the bcc phase volume fraction–temperature diagrams. As expected from the phase fraction diagram (Figure 7), the 50 N sample has the highest volume fraction of martensite, and the 400 N sample contains a high volume fraction of ferrite and thus a lower fraction of martensite. As shown in Figure 10, the ferrite phase has decorated the prior austenite grain boundaries. The micrograph of the sample subjected to 400 N load shows elongated grains, which is related to the high external load applied to this sample.

The sample subjected to 400 N load shows the highest retained austenite at room temperature. As reported by Xiong et al.,[30] the stability of retained austenite is affected by the carbon content and the morphology. The increase in the retained austenite volume fraction with increased load can be related to the more stabilized austenite due to the mechanisms discussed.

The effect of loading magnitude and carbon content of austenite on the martensitic transformations according to the results obtained in this study is summarized in Figure 11. Increasing the loads below the yield stress (i.e., the elastic regime), increases the M s. However, applying a load higher than the yield stress, accompanied by carbon enrichment of the austenite due to former ferrite transformation, results in a decrease in M s.

5 Conclusions

Based on the results obtained in the current work, the following conclusions can be drawn:

  1. 1.

    At a constant temperature of 823 K (550 °C), applying a load increases the bcc phase volume fraction. The bcc phase volume fraction increases with an increase in load.

  2. 2.

    Applying stresses lower than the yield stress of the material increases M s, and conversely applying loads higher than the yield stress decreases M s, possibly due to an increase in austenite dislocation density, change in morphology, and carbon enrichment.

  3. 3.

    The samples subjected to higher loads show higher retained austenite volume fractions and a larger retained austenite lattice parameter as a result of change in austenite morphology and austenite carbon enrichment.