Evolution of Martensite Tetragonality in High-Carbon Steels Revealed by In Situ High-Energy X-Ray Diffraction

Abstract

The martensitic transformation was studied by in situ and ex situ experiments in two high-carbon, 0.54 and 0.74 wt pct C, steels applying three different cooling rates, 15 °C/s, 5 °C/s, and 0.5 °C/s, in the temperature range around Ms, to improve the understanding of the evolution of martensite tetragonality c/a and phase fraction formed during the transformation. The combination of in situ high-energy X-ray diffraction during controlled cooling and spatially resolved tetragonality c/a determination by electron backscatter diffraction pattern matching was used to study the transformation behavior. The cooling rate and the different Ms for the steels had a clear impact on the martensitic transformation with a decrease in average tetragonality due to stronger autotempering for a decreasing cooling rate and higher Ms. A slower cooling rate also resulted in a lower fraction of martensite at room temperature, but with an increase in fraction of autotempered martensite. Additionally, a heterogeneous distribution of martensite tetragonality was observed for all cooling rates.

1 Introduction

Martensite is a key constituent in steels,^[1] where its high hardness and strength improve performance in, for example, automotive and tooling applications. A simple quenching heat treatment can be used to achieve martensite formation, but in order to obtain the final properties with sufficient toughness, additional treatments such as tempering or partitioning^[1,2,3,4] are applied in industrial processes. These processes can also occur spontaneously during cooling, i.e., autotempering or autopartitioning.^{[5,6,7,8,9,10,11,12,13,14,15]} Buffum et al.^[7] studied the tempering kinetics of high-carbon martensite and concluded that autotempering should occur during cooling after formation of martensite for sufficiently high Ms. Following this, the carbide precipitation due to autotempering in low carbon steels was observed by Kelly et al.,^[5] but no indications of autotempering in high-carbon steels were observed in that work. Sarikaya et al.^[6] found a clear partitioning of carbon from martensite to austenite during cooling with strong agglomeration at the phase interface for low and medium carbon steels leading to a stabilization of retained austenite. The development of modern characterization techniques like atom-probe tomography and high-energy X-ray diffraction (HEXRD) have opened new possibilities for in-depth studies on autotempering/partitioning in the last 15 years.^{[8,9,11,12,13,14,15]} The degree of autotempering in medium carbon steels has been shown to depend on the cooling rate and transformation temperatures.^[8,16] Furthermore, the impact of the cooling rate on autotempering in high-carbon steels has been studied by Van Bohemen et al.^[17] with dilatometer experiments. The results showed a stronger autotempering for slower cooling rates, but a distinction of the contribution from changes in local carbon distribution and the connected martensite tetragonality as well as the phase fraction was not possible.^[17] Additionally, the cooling rate has been shown to impact the final phase fraction, while there have been conflicting reports on its impact on the Ms temperature.^{[8,12,13,18,19]}

The study of autotempering or -partitioning in high-carbon steels and how it is affected by different cooling rates is of special interest due to the strong supersaturation of carbon in martensite and the resulting high tetragonality,^{[11,20,21,22,23]} which in turn can impact the final mechanical properties. A better understanding of the impact of the cooling rate is important for case-hardening of gears by low-pressure carburizing and subsequent high-pressure gas quenching (HPGQ). The use of HPGQ allows a high control over the cooling rate in the low-temperature region, which enables the design of new improved heat treatments.^[24,25] For instance, it has been shown that slower cooling around Ms results in a significant increase of the fatigue strength in case-hardened gears.^[24] Case-hardened gears have a decreasing carbon content from typically 0.75 wt pct C at the surface to 0.2 wt pct C in the core.

The impact of different cooling rates on the martensitic transformation in two high-carbon steels is here investigated to better understand the processes during the transformation. The two steels have the same overall composition except for the carbon content to simulate the behavior in the high-carbon region of case-hardened gears. The martensite evolution during the complete transformation is studied by in situ HEXRD due to the excellent time resolution with a focus on the average bulk tetragonality of martensite. It is complemented with spatially resolved tetragonality determination by electron backscatter diffraction (EBSD) after the transformation. This combination of bulk average and local characterization methodologies allows the separation of evolution of martensite tetragonality and phase fraction during the transformation.

2 Experimental Methods

2.1 Material

Two materials with the same overall composition of 1.2Mn–1.1Cr-0.2Si-Fe in weight percent and different carbon contents, 0.54 wt pct C and 0.74 wt pct C, were studied. The materials will be called C54 and C74 from here on. Both materials were cast, hot rolled at 900 °C and homogenized under vacuum at 1200 °C for 24 hours. Cylindrical (C54, 10 × $\varnothing$ 4 mm) and rectangular (C74, 10 × 5 × 2 mm) dilatometer specimens were manufactured after homogenization.

2.2 Heat Treatment

The impact of different cooling rates on the martensitic transformation was studied by dilatometry in a DIL 805 A/D from TA Instruments. The complete heat treatments for both materials are shown in Figure 1. The austenization and start of cooling were the same for all heat treatments and consisted of heating to 960 °C with 10 °C/s, holding for 30 seconds followed by cooling with 30 °C/s to 550 °C and 15 °C/s to 300 °C (C54) or 250 °C (C74). At these temperatures, the cooling rate was changed to one of the three studied rates: 15 °C/s, 5 °C/s, or 0.5 °C/s. At the end of the heat treatment of interest, another cooling treatment was applied to ensure that the sample reached room temperature during the measurement. This additional cooling resulted in deviations from the constant cooling rate in the low-temperature region at around 50 °C, this can be seen in all heat treatment curves in Figure 1.

Fig. 1

Heat treatments for (a) C54 and (b) C74 samples with austenization at 960 °C and cooling rates of 15 °C/s, 5 °C/s or 0.5 °C/s from 300 (C54) or 250 °C (C74) to room temperature

2.3 In situ HEXRD

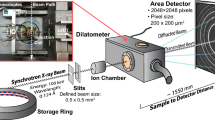
In situ HEXRD experiments in combination with a dilatometer setup were carried out at the P07b beamline operated by the Helmholtz-Zentrum Hereon at DESY,^[26] Hamburg, Germany. The detailed description of the used experimental setup can be found in Reference 27. HEXRD measurements were conducted in transmission geometry with two acquisition rates of approximately 0.25 and 5 Hz during the heat treatments described in Section II–B. To ensure a temperature step of 1 °C/pattern or 3 °C/pattern for all heat treatments and to improve the overall diffraction pattern intensity, 10 diffraction patterns were summed up for the 5 Hz measurements for 0.5 °C/s. This resulted in a temperature resolution of 3 °C/pattern for 15 °C/s and 1 °C/pattern for 5 and 0.5 °C/s for the 5 Hz measurements. The X-ray beam energy was 87.1 keV (0.14236 Å) and a 2D Perkin Elmer detector placed at a distance of 1392 mm behind the sample was used to record the 2D diffraction patterns. This allowed the detection of the first 5 austenite and 4 martensite full Debye–Scherrer rings. The software Fit2D^[28] was used to integrate the 2D patterns over 360 deg to obtain 1D diffraction patterns to analyze the average bulk behavior of the materials. A measurement on a $\text {LaB}_{6}$ powder was used for calibration.

The resulting 1D diffraction patterns were analyzed in two different ways: single-peak fitting of the $a_{200}$ and $c_{002}$ martensite peaks and Rietveld refinement for the first 3 austenite and 2 martensite peaks. The {200} martensite peaks were selected for single-peak fitting using the Lipras software^[29] since they exhibit the strongest splitting of c and a in the diffraction patterns. The combination of an asymmetric ($c_{002}$) and a symmetric ($a_{200}$) Pearson VII function was chosen to fit both peaks and a typical peak fit is shown in Figure 2(a) for the 15 °C/s sample (C74) at room temperature. The $c_{002}$ peak was selected as the asymmetric peak since there is a stronger impact of changes in carbon content on the $c_{002}$ lattice parameter in comparison to $a_{200}$, which was shown by Cheng et al.^[22] for varying mole fraction of carbon $x_C$:

$$\begin{aligned} a&= 2.8664 - 0.0027 \cdot x_{C}\,[{\text{\AA }}] \end{aligned},$$

(1)

$$\begin{aligned} c&= 2.8664 + 0.0243 \cdot x_{C}\, [ {\text{\AA }}]. \end{aligned}$$

(2)

The maximum of the full width half maximum (FWHM) of the $c_{002}$ peak function was limited to 0.126 to suppress too strong asymmetric peak shapes in Lipras.^[29] The value of 0.126 was chosen based on qualitative analysis of the peak fitting for all datasets. Additionally, the peak shape factor m was constrained to have the same value for both peaks, but the exact value was optimized in the fitting procedure. The average lattice parameter ratio $c_{002}/a_{200}$, intensity ratio $I_{a_{200}}/I_{c_{002}}$ as well as the asymmetry $I_{c_{002},R}/I_{c_{002},L}$ of the $c_{002}$ peak were determined from the single-peak fitting and used to describe the martensite transformation. The average $c_{002}/a_{200}$ ratio was calculated from the lattice parameters $a_{200}$ and $c_{002}$ of the 200 and 002 martensite peak after thermal contraction correction and showed the evolution of the martensite tetragonality. The intensity ratio $I_{a_{200}}/I_{c_{002}}$ was determined from the integrated peak intensities of the $a_{200}$ and $c_{002}$ peaks while the asymmetry $I_{c_{002},R}/I_{c_{002},L}$ describes the intensity ratio of the right- and left-hand side of the asymmetric $c_{002}$ peak and thereby the deviation from a symmetric peak shape. The intensity ratio $I_{a_{200}}/I_{c_{002}}$ and asymmetry $I_{c_{002},R}/I_{c_{002},L}$ were used to describe the heterogeneous distribution of $c_{002}/a_{200}$ and to estimate the deviation from the case of a martensitic structure with a single tetragonality value. The thermal contraction correction and further details of the used method can be found in Appendix A.1.

In addition, theoretical diffraction patterns were simulated for multiple carbon contents based on Eqs. [1] and [2] in the powder diffraction module in Vesta.^[30] They show the overlap of $c_{002}$ peaks with low tetragonality with the $a_{200}$ peak in Figure 2(b) under consideration of the experimental broadening observed in Figure 2(a). The theoretical intensity ratio $I_{a_{200}}/I_{c_{002}}$ was assumed to be 2 based on the ratio of multiplicities for the {200} peak, 4, and {002} peak, 2. It is noteworthy that higher values for the intensity ratio due to changes in the Fe atom position have been reported.^[31,32,33]

Fig. 2

(a) HEXRD pattern of 002/200 martensite peak with asymmetric and symmetric Pearson VII fit for $c_{002}$ and $a_{200}$ for 15 °C/s C (C74) at room temperature. The integrated peak intensities $I_{a_{200}}$ (green), $I_{c_{002},L}$ (orange), and $I_{c_{002},R}$ (red) are highlighted; (b) Theoretically calculated diffraction patterns of $c_{002}$ and $a_{200}$ peaks for varying carbon contents of 0, 0.3, 0.54, and 0.74 wt pct (Color figure online)

The Rietveld refinement of the patterns was done in GSAS-II^[34] with refinement of intensity, lattice parameter as well as microstrain. Two different phase setups were used for the refinement, with austenite (fcc) in both, martensite (bct) in one and ‘fresh’ (bct) and tempered martensite (bcc) in the other. The bcc structure is used to estimate the fraction of tempered martensite with low carbon content. The second approach was chosen since it resulted in an improvement of the overall fit and provided insights into the separate evolution of bct and bcc phase fractions during the transformation. In addition, the phase fraction of austenite shows only a maximal deviation of 0.7 pct between the two methods with a consistent shift to lower values for all samples for the second approach due to the better fit of the martensite compared to the first. The Rietveld refinement was limited to the first 3 austenite and 2 martensite peaks due to overlap of strong peak tails between the {220} and {311} austenite peaks. This overlap resulted in an additional background that impacted the Rietveld refinement, see Appendix A.2.3. Additionally, the microstrain was limited to values between 100 and 50,000 to avoid unphysical peak broadening for low peak intensities at the transformation start. The overlap of bcc and bct peaks resulted in discontinuities in their phase fraction at the start of the transformation due to the low peak intensities. These discontinuities had no impact on the sum of the two phase fractions (bct + bcc) $PF_{\rm BCT+BCC}$, which corresponds to the total martensite phase fraction.

The evolution of bct and bcc martensite with respect to each other can be demonstrated by the ratio of their phase fractions $PF_{\rm BCT}/PF_{\rm BCC}$, where a value of 1 represents a 50:50 split in phase fraction. Values below 1 show a dominance of bcc while values above 1 show a dominance of bct.

The kinetics of the martensitic transformation was determined from the change in phase fraction of martensite $PF_{\rm BCT+BCC}$ over temperature $-dPF_{\rm BCT+BCC}/dT$. The negative definition was chosen to describe the transformation with positive values since dT is negative during cooling and $dPF_{\rm BCT+BCC}$ is positive. The values were calculated with a step size of 6 °C between data points for all cooling rates to facilitate a comparison between them.

The dilatometer data recorded during the in situ HEXRD experiment were also used to determine the martensite fraction with the lever rule under consideration of the non-linear expansion of martensite and austenite.^[17,35] The phase fraction of martensite was calibrated using the results from the Rietveld refinement for the 15 °C/s sample at room temperature after the heat treatment for both materials. This allowed the determination of the transformation behavior averaged over the complete samples and the comparison with the in situ HEXRD results.

2.4 Local Tetragonality c/a

The final microstructure of the samples after the heat treatment was studied with electron backscatter diffraction (EBSD). The samples were mechanically grinded and polished (9, 3, and 1 μm) followed by a final electropolishing at 12 V and 10 °C for 60 seconds in Struers A3 electrolyte.

For the EBSD study, a FEI Nova 600 NanoLab dual-beam system with an Oxford Instruments Symmetry CMOS detector was used. The EBSD analysis was focused on the local tetragonality c/a to correlate it with the in situ HEXRD results. The local tetragonality c/a was determined by the projective Kikuchi pattern matching algorithm from Winkelmann et al.^[36,37] and subsequently analyzed in the MTEX toolbox.^[38,39] The raw EBSD patterns were recorded at 20 kV and 9.5 nA with an acquisition time of 10 ms and a resolution of 156 $\times$ 128 pixels. A minimum value of $r=0.5$ of the normalized cross-correlation coefficient r defined in References 36 and 37 was chosen as the threshold to exclude poorly matching experimental and simulated patterns. The analysis was done for the fastest (15 °C/s) and the slowest (0.5 °C/s) cooling rates for both materials. To obtain sufficient statistical data, 3 (C54) or 4 (C74) EBSD maps of size 100 × 80 μm were recorded and analyzed for each sample with a step size of 150 nm.

3 Results

3.1 Evolution of Tetragonality $c_{002}/a_{200}$

The evolution of the average tetragonality $c_{002}/a_{200}$, peak intensity ratio $I_{a_{200}}/I_{c_{002}},$ and asymmetry $I_{c_{002},R}/I_{c_{002},L}$ during cooling are shown for both materials in Figure 3.

Fig. 3

Single-peak fitting results for (a, b) thermal contraction corrected tetragonality $c_{002}/a_{200}$, (c, d) intensity ratio $I_{a_{200}}/I_{c_{002}},$ and (e, f) asymmetry $I_{c_{002},R}/I_{c_{002},L}$ for 15 °C/s, 5 °C/s, and 0.5 °C/s for C54 (a, c, e) and C74 (b, d, f)

All C54 and the C74 sample cooled with 0.5 °C/s show the same overall behavior in tetragonality $c_{002}/a_{200}$ determined from the 002 and 200 peak position (Figures 3(a) and (b)) with a minimum at the onset of transformation around 210 °C to 230 °C and 170 °C, respectively. For C54, the 0.5 °C/s sample has the lowest value followed by 5 °C/s and 15 °C/s. The position of the minimum is shifted for 15 °C/s to a slightly higher temperature than for 5 °C/s and 0.5 °C/s, which are at similar values between 210 °C and 220 °C. Furthermore, it can be seen that the minimum of 0.5 °C/s is broader than for the other two cooling rates. After reaching the minimum, $c_{002}/a_{200}$ sharply increases. The 15 °C/s sample shows a constant value from approximately 160 °C while the other three continue to increase slowly. In contrast to this, the 15 °C/s and 5 °C/s samples for C74 show an almost constant tetragonality $c_{002}/a_{200}$ over the complete temperature range with a small scatter at the start with the 5 °C/s sample having a slightly lower $c_{002}/a_{200}$ value. The C54 sample cooled with 0.5 °C/s has a discontinuity around 70 °C, which is a result of the change in acquisition rate from 5 to 0.25 Hz and an associated change in intensity. This discontinuity can also be seen in Figures 3(c) and (e).

The ratio of the integrated peak intensities $I_{a_{200}}/I_{c_{002}}$ shows a similar overall behavior for both materials and all cooling rates, see Figures 3(c) and (d). The total value has a maximum at the start of the transformation and continuously decreases until reaching a constant value. The exact position of the maximum varies, it is either directly at the start of the transformation (15 °C/s (both), 5 °C/s (C74)) or at slightly lower temperatures (5 °C/s (C54), 0.5 °C/s (both)). The C74 samples have very similar maximum and final values for all cooling rates while the C54 samples show significant differences with 0.5 °C/s having the highest value, followed by 5 °C/s and 15 °C/s. The C54 values for 15 °C/s are similar to the C74 values.

The asymmetry $I_{c_{002},R}/I_{c_{002},L}$ of the $c_{002}$ peak is presented in Figures 3(e) and (f). The C54 samples have an $I_{c_{002},R}/I_{c_{002},L}$ value below 1 for all cooling rates at the start of the transformation and show an increase during further cooling. For 15 °C/s and 5 °C/s, it reaches a constant value after an initial sharp increase with a slightly stronger increase in the 15 °C/s sample. The 0.5 °C/s sample slowly increases to 1 and jumps to 1.5 due to the change in acquisition rate. The 15 °C/s and 5 °C/s samples for C74 show a similar behavior at low temperatures with a weaker asymmetry compared to the 0.5 °C/s sample. For higher temperatures close to Ms, they show clear differences with a significantly stronger asymmetry in the 5 °C/s with a maximum around 170 °C. The 0.5 °C/s sample shows a decrease in asymmetry at the start of the transformation reaching a symmetric peak shape around 170 °C. Upon further cooling, the asymmetry increases and reaches a near constant value from around 100 °C down to room temperature. The contribution of the instrument to the asymmetry is estimated by single-peak fitting of the $\mathrm {LaB_6}$ reference sample in the 5.3 to 6.0 deg range used for the analysis, see Appendix A.2.1, and determined to be negligible compared to the observed values in Figures 3(e) and (f).

An additional approach for the single-peak fitting with 2 asymmetric Pearson VII (2A) was used to assess the influence of different fitting methods on the average $c_{002}/a_{200}.$ This method was only used for the C74 samples since it was not possible to get satisfactory fitting results for the 0.5 °C/s (C54) sample due to weak intensities of the $c_{002}$ peak. The results can be seen in Figure 4.

Fig. 4

Single-peak fitting results for 2A (a) thermal contraction corrected tetragonality $c_{002}/a_{200}$, (b) intensity ratio $I_{a_{200}}/I_{c_{002}},$ and (c) asymmetry $I_{c_{002},R}/I_{c_{002},L}$ and $I_{a_{200},L}/I_{a_{200},R}$ for 15 °C/s, 5 °C/s, and 0.5 °C/s for C74

The average tetragonality $c_{002}/a_{200}$ (Figures 3(b) and 4(a)) and intensity ratio $I_{a_{200}}/I_{c_{002}}$ (Figures 3(d) and 4(b)) are nearly identical for 15 °C/s and 5 °C/s while there are differences in the asymmetry $I_{c_{002},R}/I_{c_{002},L}$ (Figures 3(f) and 4(c)) especially for 5 °C/s at the start of the transformation. The 0.5 °C/s sample shows overall similar trends for both methods, but the absolute values vary strongly with a significantly higher $c_{002}/a_{200}$ and $I_{a_{200}}/I_{c_{002}}$ for the 2A method at the start of the transformation. The differences between the two methods can mainly be explained by the additional asymmetry $I_{a_{200},L}/I_{a_{200},R}$ of $a_{200}$. 15 °C/s and 5 °C/s only have a weak asymmetry while 0.5 °C/s has a significant asymmetry especially at the start of the transformation. This asymmetry of $a_{200}$ leads to the shift to higher $I_{a_{200}}/I_{c_{002}}$ as well as higher $c_{002}/a_{200}$ values at the minima. This is supported by the similar values at low temperature, where only a low asymmetry is observed.

The comparison of the two methods applied for the C74 samples (Figures 3(a), (c), (e) and 4) shows that the absolute average tetragonality $c_{002}/a_{200}$ values depend heavily on the chosen fitting method. However, the observed minimum of tetragonality $c_{002}/a_{200}$ for 0.5 $^\circ$C/s (C74) is reproduced using both methods and confirms that the general trends observed for $c_{002}/a_{200}$ are reliable, but they need to be discussed considering $I_{a_{200}}/I_{c_{002}}$ and $I_{c_{002},R}/I_{c_{002},L}$.

3.2 Evolution of Phase Fraction

The transformation kinetics of the C54 and C74 samples are analyzed by the evolution of martensite phase fraction from the volume expansion determined with dilatometer and from Rietveld refinement. Additionally, the phase fraction change over temperature $-dPF_{\rm BCT+BCC}/dT$ is presented in Figure 5, and the separate evolution of bct and bcc determined by comparing the ratio of phase fractions of both phases $PF_{{\rm BCT}}/PF_{\rm BCC}$ is shown in Figure 6.

Fig. 5

(a, b) Martensite phase fraction vs temperature from dilatometer, (c, d) Sum of bct and bct martensite phase fraction $PF_{\rm BCT+BCC}$ vs temperature from Rietveld refinement and (e, f) phase fraction change over temperature $-dPF_{\rm BCT+BCC}/dT$ vs temperature from Rietveld refinement for 15, 5, and 0.5 $^\circ$C/s for C54 (a, c, e) and C74 (b, d, f)

The dilatometer results show the same trends in both materials, but clear differences between the different cooling rates can be seen in Figures 5(a) and (b). The bulk transformation starts with a strong phase fraction increase around 240 (C54) and 180 °C (C74) followed by a decline in transformation rate. The early transformation behavior is very similar for all cooling rates and at room temperature 15 $^\circ$C/s samples have the highest phase fraction, followed by 5 $^\circ$C/s and 0.5 $^\circ$C/s. The dilatometer results show an abnormality around 40 $^\circ$C or 50 $^\circ$C with a strong phase fraction increase that can be correlated with the artifacts observed in the heat treatments, see Figure 1. The same kinds of artifacts as in Figures 5(a) and (b) are also observed for the martensite phase fraction $PF_{\rm BCT+BCC}$ from Rietveld refinement in Figures 5(c) and (d).

According to the Rietveld refinement in Figure 5(c), the main transformation in the C54 samples starts at similar temperatures as observed in the dilatometer results. All cooling rates show overall a similar behavior with only small deviations over the complete temperature range. The final martensite phase fractions at room temperature are $88.5\pm 0.3$ pct (15 $^\circ$C/s), $87.8\pm 0.3$ pct (5 $^\circ$C/s) and $86.0\pm 0.3$ pct (0.5 $^\circ$C/s). The errors are determined from the Rietveld refinement. For C74, the 5 $^\circ$C/s and 0.5 $^\circ$C/s samples have overall very similar behaviors and have a slightly higher $PF_{\rm BCT+BCC}$ than 15$^\circ$C/s down to approx. 80 $^\circ$C where the curves intersect, see Figure 5(d). The final phase fraction of martensite at room temperature is $81.0\pm 0.4$ pct (15 $^\circ$C/s), $79.5\pm 0.3$ pct (5 $^\circ$C/s) and $78.3\pm 0.3$ pct (0.5 $^\circ$C/s). The corresponding weighted profile R-factor $R_{\rm wp}$ lie between 11.7 and 13.7 for all samples.

The 15 $^\circ$C/s and 5 $^\circ$C/s samples of C54 show a near constant martensite fraction before the onset of the transformation in Figure 5(c), which can be explained by an early transformation that is most likely connected to a decarburized surface layer. The corresponding patterns can be found in Appendix A.2.3. The dilatometer results also show an early transformation for all cooling rates (Figure 5(a)), but with lower values compared to the Rietveld results. Additionally, this effect, although weaker, is observed for the C74 samples in Figure 5(b).

The overall behavior of the phase fraction change over temperature $-dPF_{\rm BCT+BCC}/\text {d}T$ is similar for all cooling rates in both materials, see Figures 5(e) and (f). $-dPF_{\rm BCT+BCC}/dT$ shows an increase at the start of transformation with a maximum around 170 $^\circ$C to 190 $^\circ$C (C54) and 130 $^\circ$C to 150 $^\circ$C (C74) followed by a continuous reduction. Small differences in the position and the value of the maximum rate between the cooling rates for C74 are observed. The 0.5 $^\circ$C/s sample shows a lower value at a higher temperature in comparison to 5 $^\circ$C/s and 15 $^\circ$C/s. This analysis was stopped at 50 $^\circ$C due to the artifacts observed in $PF_{\rm BCT+BCC}$ (Figures 5(c) and (d)).

Fig. 6

Ratio of bct and bcc phase fraction $PF_{{\rm BCT}}/PF_{\rm BCC}$ determined by Rietveld refinement with a combination of bct and bcc phase to describe martensite vs temperature for 15 $^\circ$C/s, 5 $^\circ$C/s, and 0.5 $^\circ$C/s for C54 (a) and C74 (b)

The $PF_{\rm BCT}/PF_{\rm BCC}$ shows similar trends for both materials regardless of cooling rates, but there are clear differences in their total values, see Figures 6(a) and (b). The ratio $PF_{\rm BCT}/PF_{\rm BCC}$ starts at a low value, in most cases close to 0 and increases upon cooling. At the final temperature, the 15 $^\circ$C/s samples have the highest value, followed by 5 $^\circ$C/s and 0.5 $^\circ$C/s. The C54 samples have overall significantly lower values compared to the C74 samples. Most curves show strong variations at the start of the transformation due to discontinuities in the bct and bcc phase fraction from peak overlap and low peak intensities. The 15 $^\circ$C/s sample for C74 shows an additional clear change in its behavior around 110 $^\circ$C where the increase stops and a slight decrease is observed for lower temperatures.

$PF_{\rm BCT}/PF_{\rm BCC}$ can also be used to determine the fraction of low tetragonality, bcc, martensite at room temperature. The corresponding bcc fractions $PF_{\rm BCC}/(PF_{\rm BCT}+PF_{\rm BCC})$ are 0.43, 0.51, and 0.66 for the C54 15 $^\circ$C/s, 5 $^\circ$C/s, and 0.5 $^\circ$C/s samples, respectively, as well as 0.21, 0.27, and 0.39 for C74.

3.3 Local Tetragonality c/a

The overall microstructure of the two materials cooled with cooling rates of 15 $^\circ$C/s and 0.5 $^\circ$C/s, is very similar and consists of a mixture of larger and smaller martensite units, see Figure 7. The dimensions of the larger units can be up to several tens of μm’s while the smallest observed units are limited by the step size and cannot reliably be determined. There are no clear differences in average unit size distribution for the two cooling rates in both materials.

Fig. 7

Orientation map with inverse pole figure [001] coloring overlayed with calculated unit boundaries for C54 (a) 15 and (c) 0.5 $^\circ$C/s as well as for C74 (b) 15 and (d) 0.5 $^\circ$C/s samples

The spatially resolved tetragonality c/a is shown for the different cooling rates in the two materials in Figure 8. The C54 samples show a similar distribution of low tetragonality c/a with a tendency to higher values for smaller martensite units for 15 $^\circ$C/s, see Figures 8(a) and (c). The C74 samples have overall a higher tetragonality c/a with a broader distribution in comparison to the C54 samples. The differences between the cooling rates can be clearly seen for the larger units, where 0.5 $^\circ$C/s (Figure 8(d)) has low c/a values for large units while a mixture of lower and higher c/a values is observed for 15 $^\circ$C/s (Figure 8(b)).

Fig. 8

Local tetragonality c/a EBSD maps determined via projective Kikuchi pattern matching^[36,37] of C54 (a) 15 and (b) 0.5 $^\circ$C/s as well as for C74 (c) 15 and (d) 0.5 $^\circ$C/s samples. The white areas have a normalized cross-correlation below 0.5 or are retained austenite

The success rate of the tetragonality c/a determination varies significantly between EBSD scans, which can be clearly seen in Figure 8. The success rate is defined as the ratio of martensite pixels with a normalized cross-correlation coefficient $r>0.5$ and thereby successful c/a determination, divided by the total amount of martensite pixels. The success rate is higher for the C54 samples with values between 42 and 56 pct compared to the C74 samples with values between 28 and 38 pct. The success rate depends mainly on the quality of the recorded patterns and is in general better for larger units, probably due to less overlap from neighboring crystal orientations or phases and lower defect density.

The normalized tetragonality c/a frequency was calculated from the sum of 3 (C54) and 4 (C74) EBSD scans for each sample and is shown in Figure 9. There is a clear difference in c/a between the cooling rates for both materials with a higher frequency of low c/a ratios for 0.5 $^\circ$C/s compared to the 15 $^\circ$C/s samples. The 15 $^\circ$C/s samples have also a higher frequency of larger c/a ratios. These differences are more pronounced in the C74 samples (Figure 9(b)) where a clear shift in the maximum between the two cooling rates and a stronger heterogeneous distribution of c/a ratios for 15 $^\circ$C/s is shown.

Fig. 9

Normalized frequency of tetragonality c/a for C54 (a) and C74 (b) determined by EBSD

4 Discussion

4.1 Evolution of Tetragonality $c_{002}/a_{200}$

Both materials show an impact of the cooling rate on the average tetragonality $c_{002}/a_{200}$ with a stronger minimum in $c_{002}/a_{200}$ for the slower cooling rate, see Figures 3(a) and (b). This impact is more pronounced in the C54 samples with a clear trend of decreasing minima values for a slower cooling rate compared to the C74 samples. These changes can be related to the carbon content of the martensite by the Honda–Nishiyama^[11,20] equation:

$$\begin{aligned} c/a (\mathrm {wt\,pct\,C}) = 1 + 0.045 \cdot \mathrm {wt\,pct\,C} \end{aligned}.$$

(3)

The minimum in tetragonality $c_{002}/a_{200}$ at the start of the transformation, which is also reported for a similar composition for a single cooling rate,^[40] can therefore be connected to a reduction or heterogeneous distribution of the carbon content in martensite. This indicates diffusion of carbon in the martensite matrix due to autotempering with carbon segregation at lattice defects and subsequent carbide formation^[11] or autopartitioning with diffusion of carbon to austenite boundaries as reported for medium and low carbon steels.^[8,12,15] The carbon diffusion distance during cooling from different martensite formation temperatures to room temperature is presented in Figure 10 for the three cooling rates, 15 $^\circ$C/s, 5 $^\circ$C/s and 0.5 $^\circ$C/s, to better understand the impact of the cooling rate and Ms. The diffusion distances are calculated by stepwise summation of diffusion distances determined at each temperature by the Einstein equation $\bar{x}=\sqrt{2Dt}$ in an approach similar to Hutchinson et al.^[9] and Morsdorf et al.^[41] The carbon diffusion coefficient $D= 2 \times 10^{-6} \cdot {\rm exp}(-109600/RT)$ m$^2$s$^{-1}$ from Hutchinson et al.^[9] is used. The absolute values heavily depend on the chosen diffusion coefficient and there are strong variations in reported literature values,^{[9,42,43,44,45,46]} but the general trends are not impacted by this. The slowest cooling rate, 0.5 $^\circ$C/s, significantly increases the carbon diffusion distance in Figure 10, which can explain the observed stronger reduction of $c_{002}/a_{200}$ for slower cooling due to a stronger autotempering/-partitioning. Additionally, the stronger effect for C54 compared to C74 can be explained with the higher Ms and longer diffusion distances in the temperature range from 200 $^\circ$C to 250 $^\circ$C compared to lower temperatures. Overall, the tetragonality of a single martensite unit is governed by its formation temperature and the used cooling rate since this decides the degree of autotempering/-partitioning.

Fig. 10

Calculated carbon diffusion distance during cooling from varying martensite formation temperatures to room temperature. The inset shows the temperature range from 0 $^\circ$C to 200 $^\circ$C and diffusion distance range 0 to 50 nm

The degree of autotempering and -partitioning during cooling can be separately estimated from the HEXRD diffraction patterns at room temperature in combination with the local tetragonality c/a. The presence of autotempering in all C54 samples is indicated by the weak additional diffraction peaks at 3.5 and 5 deg, which are consistent with carbide peaks, in the room temperature HEXRD pattern shown in Appendix A.2.2 Figure A.3, while no clear additional peaks are observed for C74. Additionally, the presence of autotempering in both C54 and C74 is supported by the observation of varying local tetragonality c/a values determined by EBSD in Figures 8 and 9. This heterogeneous c/a distribution is in good agreement with previous spatially resolved tetragonality studies,^[23,36,37] but the presented results are from a significantly larger area. A separate investigation of the local correlation of c/a values with the carbon distribution determined by APT for the 15 $^\circ$C/s and 0.5 $^\circ$C/s C74 samples showed clear autotempering effects with carbon segregation.^[47] The carbon segregation was more pronounced for low c/a regions compared to high c/a^[47] probably due to a stronger autotempering after formation at higher temperatures or slower cooling. The effect of autopartitioning can be estimated from the austenite peak position at room temperature and a small shift of the 311 austenite peak to lower $2\theta$ values is observed for the 0.5 $^\circ$C/s C54 sample compared to the faster cooling rates in Figure A.2(c). This shift is consistent with an increase in lattice parameter due to a higher carbon content. However, the shift is very small and in the same order as the experimental error. Therefore, the observed changes in tetragonality are mainly attributed to autotempering effects, but a weak autopartitioning effect limited to the region close to the martensite–austenite interface is possible. Accordingly, autotempering will be used instead of autotempering/-partitioning from here on.

The strong increase in tetragonality $c_{002}/a_{200}$ (Figures 3(a) and (b)) after the minima in both materials (C74 only 0.5 $^\circ$C/s) can be explained by a combination of continuous formation of ‘fresh’ martensite, autotempering of the formed ‘fresh’ martensite and amount of previously formed autotempered martensite. The $c_{002}/a_{200}$ of the 5 $^\circ$C/s and 0.5 $^\circ$C/s C54 samples increases around 200 $^\circ$C, where the carbon diffusion is reduced significantly compared to at higher temperatures, see Figure 10. Additionally, the increase in $c_{002}/a_{200}$ coincides with the maxima in transformation rate $-dPF_{\rm BCT+BCC}/dT$ in Figure 5(e) for the two samples. The influence of the faster carbon diffusion and resulting stronger autotempering can be seen in the slower increase of $c_{002}/a_{200}$ for the 0.5 $^\circ$C/s sample compared to 5 $^\circ$C/s. The $c_{002}/a_{200}$ value for 15 $^\circ$C/s C54 and 0.5 $^\circ$C/s C74 starts to increase at a higher temperature, where $-dPF_{\rm BCT+BCC}/\text {d}T$ is still increasing and the maximum of $-dPF_{\rm BCT+BCC}/\text {d}T$ is approximately around the respective inflection point of $c_{002}/a_{200}$ for both samples. This shift to a higher temperature is probably due to significantly less carbon diffusion for the 15 $^\circ$C/s sample compared to the 5 $^\circ$C/s and 0.5 $^\circ$C/s C54 samples. However, this cannot explain the shift for the 0.5 $^\circ$C/s C74 sample since the expected diffusion distance is still longer than for 5 $^\circ$C/s C54 in Figure 10, but the amount of previously autotempered martensite is significantly lower due to the lower Ms. This indicates that the $c_{002}/a_{200}$ value is heavily influenced by the carbon diffusion since it controls the autotempering kinetics, but the amount of formed ‘fresh’ martensite and previously autotempered martensite seem to play a significant role.

The general behavior of tetragonality can be well described by $c_{002}/a_{200}$, but the direct comparison of the C54 and C74 results as well as the interpretation of the 15 $^\circ$C/s and 5 $^\circ$C/s (C74) $c_{002}/a_{200}$ needs a more detailed look at the limitations of the used single-peak fitting model. The differences of the absolute values for the two fitting approaches in Figures 3(b), (d), (f) and 4 are a consequence of the chosen model with only 2 peaks, while in reality, it is a combination of multiple tetragonality $c_{002}/a_{200}$ values and thereby carbon contents. The simple model makes a compromise between the possibility to determine an average tetragonality $c_{002}/a_{200}$ and the accuracy of the determined values. The deviations from reality can be estimated from the intensity ratio $I_{a_{200}}/I_{c_{002}}$ and the asymmetry $I_{c_{002},R}/I_{c_{002},L}$. $I_{a_{200}}/I_{c_{002}}$ in Figures 3(c) and (d) are higher than the theoretical value of 2 indicating the presence of low carbon bct structures since the overlap of low carbon $c_{002}$ with $a_{200}$ peaks (Figure 2(b)) would result in a shift to higher $I_{a_{200}}/I_{c_{002}}$ values. In addition, deviations from symmetric behavior ($I_{c_{002},R}/I_{c_{002},L}\ne 1$), which are observed for most of the transformation in Figures 3(e) and (f), show that a model for a bct structure with a single carbon content described by 2 symmetric peaks is not ideal. Furthermore values of $I_{c_{002},R}/I_{c_{002},L}>1$ indicate the presence of lower $c_{002}$, which result in lower tetragonality $c_{002}/a_{200}$ than average and therefore even lower carbon content in the martensite.

Therefore, it is necessary to combine the average tetragonality $c_{002}/a_{200}$ with $I_{a_{200}}/I_{c_{002}}$ and $I_{c_{002},R}/I_{c_{002},L}$ for a more complete understanding of the processes during the transformation. The strong deviations of the $I_{a_{200}}/I_{c_{002}}$ values in Figures 3(c) and (d) from the theoretical value show that there is a significant part of martensite with a tetragonality lower than the determined average. The differences in $I_{a_{200}}/I_{c_{002}}$ also clearly show that the tetragonality $c_{002}/a_{200}$ is much lower in the 0.5 $^\circ$C/s sample for C54 in comparison to C74 even though their minima in $c_{002}/a_{200}$ are nearly the same (Figures 3(a) and (b))

This tendency is also shown in the phase fraction ratios of bct and bcc $PF_{\rm BCT}/PF_{\rm BCC}$ in Figures 6(a) and (b). The C54 samples have a significantly stronger bcc character over the complete transformation range than C74 and should therefore have a lower average martensite tetragonality. $PF_{\rm BCT}/PF_{\rm BCC}$ also clearly shows that a slower cooling rate leads to stronger autotempering with a lower tetragonality due to their stronger bcc character in both materials.

The average tetragonality $c_{002}/a_{200}$ for 5 $^\circ$C/s and 15 $^\circ$C/s in C74 is constant in Figure 3(b), but $I_{a_{200}}/I_{c_{002}}$, $I_{c_{002},R}/I_{c_{002},L}$ and $PF_{\rm BCT}/PF_{\rm BCC}$ (Figures 3(d) through (f) and 6(b)) show a clear indication of a heterogeneous tetragonality distribution due to autotempering of martensite for these cooling rates as well. Furthermore, there are clear indications from $I_{c_{002},R}/I_{c_{002},L}$ and $PF_{\rm BCT}/PF_{\rm BCC}$ that the effect is stronger for the slower cooling rate 5 $^\circ$C/s compared to 15 $^\circ$C/s. This shows the necessity to combine all parameters to understand the complex tetragonality $c_{002}/a_{200}$ behavior.

The overall trends of average $c_{002}/a_{200}$ determined by in situ HEXRD in Figure 3(a) and (b) and local c/a from EBSD in Figures 8 and 9 agree well with each other, but there are significant differences in the quantitative c/a values between the two methods as seen in Figures 3(a), (b) and 9. These differences can mainly be attributed to the success rate of c/a determination in EBSD and the uncertainty of the average $c_{002}/a_{200}$ from single-peak fitting. The success rate for c/a in EBSD lies between 28 and 56 pcts for all samples and large units are preferentially successfully determined. This leads to a bias in the c/a values since large units generally have a lower tetragonality c/a in all samples, see Figure 8. This lower c/a can be best explained by the early formation of large units due to volume restrictions at later stages^[48] and subsequent stronger autotempering. The values agree well with the martensite formed at the early stages of the transformation (Figures 3(a) and (b)) except for the 15 $^\circ$C/s sample for C74. This difference can at least partially be explained by the uncertainty of $c_{002}/a_{200}$ since $I_{a_{200}}/I_{c_{002}}$ and/or $I_{c_{002},R}/I_{c_{002},L}$ clearly indicate that there is a significant amount of martensite with a lower $c_{002}/a_{200}$ than average at the final temperature for all samples, see Figures 3(c) through (f).

Overall, this work gives an in-detail view into the evolution and final heterogeneous distribution of martensite tetragonality and carbon content due to different degrees of autotempering for the three cooling rates, 15 $^\circ$C/s, 5 $^\circ$C/s and 0.5 $^\circ$C/s. The average martensite tetragonality is a balance of carbon diffusion kinetics controlling the degree of autotempering as well as the amount of ‘freshly’ formed and previously tempered martensite. Autotempering is the dominant effect during cooling, but weak autopartitioning limited to region close to austenite–martensite interface is possible.

4.2 Evolution of Phase Fraction

The phase fraction analysis by Rietveld refinement can directly determine the martensite fraction, while it can be indirectly determined using dilatometry. The measured volume expansion in dilatometer during the transformation can mainly be explained and correlated to an increase in martensite fraction. It is important to note that other effects like stresses, carbide formation, or loss of tetragonality can influence the expansion behavior and should be considered for an exact determination.^[49,50]

The martensite phase fraction from Rietveld and dilatometer at the final temperature in Figures 5(a) through (d) show the same overall trend, a higher cooling rate results in a higher martensite phase fraction, though there are differences in the absolute values. This trend agrees with the reported results for the impact of the cooling rate on the final phase fraction for medium carbon steels^[8,12] for significantly higher cooling rates and Ms. The difference was mainly attributed to different degrees of autopartitioning and the resulting stabilization of austenite.^[8,12] A shallow autopartitioning, which is limited to region close to the austenite–martensite interface, is reasonable for C54 based on the results in Figure A.3(c) discussed in the previous section. This increase in carbon content in the interface would locally decrease Ms resulting in a slower transformation, which is even more impactful since clear indications for autocatalysis have been found in the C74 steel.^[51]

The largest difference in the final phase fraction between Rietveld and dilatometry is observed for 0.5 $^\circ$C/s (C54), Figures 5(a) and (c). This difference can be explained by the stronger autotempering with loss of tetragonality (Figure 3(a)) and the resulting volume loss, which is not corrected for in the dilatometer phase fraction determination.

The overall transformation kinetics show significantly different behavior for the Rietveld and dilatometer method for the C54 samples, while they have a similar behavior for C74, see Figures 5(a) through (d). The comparison for C54 is complicated by the early transformation observed for 15 $^\circ$C/s and 5 $^\circ$C/s (Figure 5(c)) and the resulting additional martensite fraction. This early transformation occurs most likely in a decarburized surface layer. The dilatometer data show an early transformation as well (Figure 5(a)), but this is significantly smaller and could be attributed to experimental artifacts due to the change in cooling rate. A decarburized surface layer could also have an impact, but since the dilatometer results take the whole sample volume into account, it is less sensitive for surface effects, and therefore, the following discussion will be based on the dilatometer results.

The evolution of the phase fraction is very similar for the early transformation stages while strong differences are observed below 170 $^\circ$C for C54 and 130 $^\circ$C for C74 in Figures 5(a) and (b). The higher phase fraction for faster cooling rates could be explained by a stronger stabilization of austenite due to autopartitioning for slower cooling rates as described above and therefore slower transformation. Other possible effects could be changes in stress states^{[52,53,54,55,56]} and mechanical stabilization of austenite^{[57,58,59,60,61]} due to the difference in cooling rate in combination with the corresponding change in tetragonality. This behavior is supported by the phase fraction change over temperature $-dPF_{\rm BCT+BCC}/dT$ in the C74 samples (Figure 5(f)) while the differences between cooling rates are not as clear for the C54 samples. For C74, 15 $^\circ$C/s has a higher $-dPF_{\rm BCT+BCC}/\text {d}T$ for lower temperatures as well as a higher maximum compared to 0.5 $^\circ$C/s.

The impact of cooling rate and Ms on the fraction of autotempered martensite can be clearly seen in Figure 6 with a significantly higher fraction for a higher Ms or slower cooling rate. This behavior can mainly be explained by different degrees of carbon diffusion described in Figure 10. The similar fractions of autotempered, bcc, martensite for 0.5 $^\circ$C/s C74 and 15 $^\circ$C/s C54 is surprising based on the larger expected diffusion distances from Figure 10, but it could be partially explained by the uncertainty of the diffusion coefficient D.^{[9,42,43,44,45,46]} Additionally, the overlap of the bct and bct peak results in uncertainties as discussed in Section II–C.

Overall, there is a clear correlation between the cooling rate and final martensite fraction for Rietveld and dilatometer results. A faster cooling rate results in a higher martensite fraction, which agrees with the literature reports.^[8,12] Additionally, the amount of autotempered martensite depends on the cooling rate and Ms with a higher fraction for a slower cooling rate and higher Ms.

5 Conclusion

The impact of different cooling rates on the martensitic transformation was studied in two steel grades with different carbon contents, 0.54 and 0.74 wt pct C.

The cooling rate and Ms were shown to have a strong impact on the observed tetragonality c/a in martensite and thereby the carbon content in martensite with a slower cooling and higher Ms resulting in a stronger autotempering effect. The average tetragonality is determined by a balance of the carbon diffusion kinetics with the amounts of formed ‘fresh’ and previously autotempered martensite.

The spatially resolved tetragonality determination via EBSD showed the clear presence of multiple tetragonality values and thereby a heterogeneous carbon distribution in martensite. Furthermore, it showed that larger units have preferentially a lower tetragonality c/a.

The final martensite fraction was shown to be dependent on the cooling rate in both materials with faster cooling rates resulting in higher martensite fractions. Additionally, the fraction of autotempered martensite increases for slower cooling and a higher Ms.

Appendix A: In-situ HEXRD

1.1 A.1 Methods Single Peak Fitting

The peak positions, integrated intensities and asymmetry were determined from single peak fitting and used to describe the martensite during the transformation. The average lattice parameters a₂₀₀ (200/020) and c₀₀₂ (002) were determined from the peak positions with Bragg’s law. The lattice parameters a₂₀₀ and c₀₀₂ were corrected for thermal contraction during cooling to separate the thermal behaviour from other effects. This was done by fitting a linear equation to the determined a₂₀₀ lattice parameters for 15 °C/s at low temperatures between 50 °C and 100 °C for both alloys, see Figures A.1(a) and (b). The a₂₀₀ lattice parameters were used for fitting under the assumption of isotropic thermal expansion and that the effects of changed carbon content are less intense for a₂₀₀, see Eqs. [1] and [2]. Only the samples cooled with 15 °C/s were fitted and the results were transferred to the other measurements since some samples with lower cooling rates showed a different behaviour at low temperatures. This indicates that the average lattice parameter is still changing in these samples and is not showing the pure thermal contraction. The 15 °C/s samples could also exhibit other changes than thermal contraction, but the effect should be smallest for the fastest cooling rate, which thereby describes the thermal contraction best. The resulting contraction for C54 is $3.74 \times 10^{-5}\,{\text{\AA /K}}$ and $4.64\times 10^{-5}\,{\text{\AA /K}}$ for C74. The corrected lattice parameters are shown in Figures A.1(c) through (f).

Fig. A.1

a₂₀₀ with linear fit of 15 °C/s in the range from 50 °C to 100 °C vs temperature T for (a) C54 and (b) C74; Thermal contraction corrected lattice parameters a₂₀₀ and c₀₀₂ for (c + e) C54 and for (d + f) C74

The ratio of lattice parameters c₀₀₂/a₂₀₀ describes the tetragonality of martensite and was calculated from the for thermal contraction corrected lattice parameters to determine the degree of tetragonality during the transformation.

The ratio $I_{a_{200}}/I_{c_{002}}$ in peak intensity of a₂₀₀ and c₀₀₂ was used to estimate how well the patterns are described by a bct structure with a single carbon content or if there is a superposition of multiple carbon contents. This analysis is based on the comparison of the experimental determined $I_{a_{200}}/I_{c_{002}}$ and theoretically calculated $I_{a_{200}}/I_{c_{002}}$. It is assumed that a superposition of multiple bct structures with varying carbon contents is the most likely explanation for differences between both values. This assumption is based on the strong impact of carbon content on c₀₀₂ in comparison to a₂₀₀ (Eqs. [1] and [2]) and theoretical calculations of peak positions in VESTA^[30] for multiple carbon contents shown in Figure 2(b). The position of a₂₀₀ shows only slight variations while c₀₀₂ exhibits strong position changes. A superposition of multiple carbon contents in combination with a typical peak broadening that is observed in the experiments (see Figure 2(a)) would therefore result in an overlap of low carbon c₀₀₂ with a₂₀₀ peaks. This overlap would result in a higher intensity for a₂₀₀ in comparison to c₀₀₂ and therefore a deviation from the expected theoretical $I_{a_{200}}/I_{c_{002}}$. In addition a stronger peak broadening for c₀₀₂ would be expected. As a consequence, the determined $c_{002}/a_{200}$ should be referred to as an average in the case of strong deviations between both values and therefore presence of multiple carbon contents.

The asymmetry $I_{c_{002},R}/I_{c_{002},L}$ of the $c_{002}$ peak is an additional method to estimate how well the data is represented by the average $c_{002}/a_{200}$ ratio. An example of the asymmetry can be seen in Figure 2(a). The asymmetric Pearson VII function of $c_{002}$ has a value of $I_{c_{002},R}/I_{c_{002},L} > 1$ since the right hand side clearly has a higher intensity. This asymmetry would indicate that there is additional martensite with a lower $c_{002}/a_{200}$ ratio than the determined average to describe this deviation from symmetric peak shape, see Figure 2(b). Respectively $I_{c_{002},R}/I_{c_{002},L} < 1$ would indicate that there is a part with a higher $c_{002}/a_{200}$ ratio. Additionally a strong asymmetry shows that the data cannot be well described by 2 symmetric peaks and therefore not as a bct structure with only one carbon content.

Overall, a strong asymmetry $I_{c_{002},R}/I_{c_{002},L}$ and/or difference between $I_{a_{200}}/I_{c_{002}}$ and theoretical values indicates that the martensite pattern cannot be well described by a bct structure with a single carbon content and that there is a distribution of $c_{002}/a_{200}$ ratios. This distribution would indicate the presence of multiple carbon contents in the martensite

1.2 A.2 Raw HEXRD Patterns

1.2.1 A.2.1 Reference sample pattern

The HEXRD pattern of the reference sample $\text{LaB}_{6}$ is shown in Figure A.2 for the same $2\theta$ region that is studied in the single peak fitting in Figure 2(a). The two visible peaks are fitted with an asymmetric Pearson VII function to estimate the contribution of the instrumental setup to the observed asymmetry. The ratio of the left and right integrated peak intensities $I_{\rm L}/I_{\rm R}$ is 1.04 and 1.01, respectively. This shows that the contribution of the instrumental setup is negligible compared to the observed values in Figures 3(e) and (f).

Fig. A.2

HEXRD diffraction pattern of reference sample $\text{LaB}_{6}$ with asymmetric Pearson VII fits for region of interest of single peak fitting

1.2.2 A.2.2 Room temperature patterns

The HEXRD pattern of the C54 samples at room temperature show weak additional peaks around 3.5 and 5 deg that could be possible carbides due to autotempering, see Figure 13a. The 0.5 °C/s sample shows a stronger peak at 5 deg compared to the faster cooled samples, 15 and 5 °C/s, indicating a stronger autotempering. No clear indications of carbide peaks are observed for the C74 samples at room temperature in Figure A.3(b). The 311 austenite peak of the C54 samples at room temperature is shown in Figure A.3(c) and a small shift of the peak position to lower $2\theta$ values is observed for slower cooling with 0.5 °C/s compared to 15 and 5 °C/s. The lattice parameters determined based on the peak position have a maximum difference in the order of $10^{-4}$ Å, which is similar to the experimental accuracy.

Fig. A.3

HEXRD diffraction pattern recorded at room temperature after quenching for (a) C54, (b) C74 samples for the three cooling rates 15, 5 and 0.5 °C/s, (c) 311 austenite peak of C54 at room temperature with magnification of peak maximum in inset

1.2.3 A.2.3 Early transformation onset C54

The HEXRD patterns of 15 and 5 °C/s samples for C54 show an early onset with bcc/bct phase fractions before the onset of the bulk austenite to martensite transformation. This is connected to an early transformation below 650 °C, which is most likely related to decarburized surface areas that have not been sufficiently removed before the experiments. The corresponding HEXRD patterns can be seen in Figure A.4 and they show clear bcc peaks at 603 °C for 15 °C/s while a typical {110} bcc peak shoulder can be seen in the {111} fcc peak around 513 °C for 5 °C/s in Figure A.4(b). The diffraction patterns also show the strong tails of the austenite peaks. The overlap of the tails results in an additional intensity between the {220} and {311} austenite peak compared to the range between {200} and {220}, see Figures A.4(a) (inset) and (b). This difference impacts the Rietveld refinement of the martensite peaks {200} and {211} negatively.

Fig. A.4

HEXRD diffraction pattern for C54 samples (a) 15 °C/s at 603 °C with early bcc/bct transformation; inset focus on lower intensity region (b) 5 °C/s at 513 °C for C54