Introduction

Multidisciplinary laboratory measurements on geological material give the challenging possibility to discover and combine information from different resolutions and physical background. It is extremely important to look closely at the rock by reading petrophysical properties and creating a full image as a one body. Hence, several methods are combined together to check how pore system can behave in low-porous and low-permeable gas-bearing formations. Computed X-ray tomography (CT) is safe and high-resolution laboratory technique for 3D pore network examination (Ketcham and Carlson 2001; Cnudde and Boone 2013; Cubit et al. 2009; Adeleye and Akanji 2022). Moreover, it is a matter of scale: do we want to look at the rock in low or high resolution and thus look at the rock in centimeters or nanometers (Cnudde et al. 2011; Liu et al. 2018)? In both cases, some of the information is missing. The first example does not concentrate on the small pores and in case of tight formation it is not acceptable because we lose a huge amount of useful data. The advantage of this resolution is that rock examination is on the core or core plus. The second example looks deeply into the small pores, but we read the information from the small piece of rock; often the rock is the size of a crumb.

Tortuosity of the pore ganglia is one of the crucial geometric parameters of pore structure and can be evaluated based on CT (Backeberg et al. 2017; Mohan et al. 2023). There are several methods in tortuosity estimation (Ribeiro et al. 2022; Mahmood et al. 2023), but only CT gives the chance to conduct the measurement in 3D. Moreover, tortuosity influences electrical parameters (EPM), such as formation factor, saturation exponent, and intrusion parameters from mercury porosimetry (MICP).

The article presents a new method in tortuosity calculations from the 3D CT images. An attempt was also made to determine the relationship between tortuosity and electrical parameters. Moreover, absolute permeability was evaluated based on the multilinear regression analysis and mentioned parameters. Tortuosity has an enormous impact on rock ability to fluid flow, so the idea of connecting the tortuosity with absolute permeability is significant (Javadpour 2009; Berg 2014; Kaczmarek et al. 2017). Permeability is a challenging parameter, in both measurement and results interpretation (Soulaine et al. 2016; Ghanizadeh et al. 2017). Many researches were devoted to the permeability determination, often through the pore network modeling, as well as advanced statistical methods (Mostaghimi et al. 2013; Krakowska 2019; Al Balushi and Taleghani 2022). Certainly, the tortuosity parameter enriches and adds credibility to the obtained results.

Methods and materials

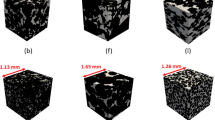
The subject of the analysis were tight, low-porosity and low-permeability rocks cored from the present depth of deposition below 3000 m, containing different lithologies, such as sandstones, mudstones, limestones and dolomites. The most important link in the research material is connected with the low values of porosity and permeability, meeting the condition of tight, gas-bearing reservoirs. We can expect simplified pore network, revealed in not tortuous pore paths. An example image of the pore space is shown in Fig. 1. CT images were processed using Feldkamp (1984) back-projection algorithm. Colors refer to the size of the pores. The pore sizes are given in voxels and thus a pixel in 3D with the size of 0.5 × 0.5 × 0.5 µm. Lots of small objects are visible in the 3D CT image, from red (pores below 99 voxels) to green (pores below 99,999 voxels). Often in tight formations, only few objects are present from the highest volume class (blue color). It is quite typical in tight formations that single extensive pore networks (dark and light blue) can occur in the whole pore system and simple pore networks (red, orange, yellow, and green) predominate.

Fig. 1
figure 1

Exemplary 3D image of pore space of tight, low-porosity, and low-permeability carbonates. Colors refer to the pore sizes in voxels (pixel in 3D with the size of 0.5 × 0.5 × 0.5 µm) detected in the pore space: red—832 pores, orange—706, yellow—366, green—175, light blue—18, and dark blue—1

Full size image

Tortuosity analysis needs to connect data from different laboratory methods. First and most precious 3D imaging method is computed X-ray tomography (CT). CT allows to estimate porosity, pore channel size, and the most important from the research point—tortuosity. Often tortuosity is determined from the capillary pressure data or petrographic image analysis. CT definitely gives better insight into all pore channels and overview on pore system in 3D (Rabbani et al. 2016; Krakowska-Madejska 2022; Moosavi et al. 2023). High-resolution CT was performed on the crumb-size sample for the research purposes in the form of the nano-CT. The most popular are the micro-CT (microresolution) and medical CT scanning (macroresolution) (Dohnalik and Ziemianin 2020; Drabik et al. 2021).

Mercury injection capillary pressure data (MICP) answers the question about the potential pore connectivity by mercury injection with the high pressure into the pore space. It appeared that tortuosity can be associated the MICP data, specifically with effective porosity, percentage of pores with diameters above 0.1 µm, percentage of pores with diameters above 1 µm, and Swanson parameter (Swanson 1981; Thomeer 1983; Mao et al. 2013). Swanson parameter is directly related to rock permeability and indirectly to tortuosity, because it refers to main point in the injection saturation of mercury, which controls the fluid flow.

Pressure- and pulse-decay methods (PDP) in permeability estimation are crucial in tight rock analysis (Handwerger et al. 2011). PDP delivers absolute permeability for low-porous and low-permeable formations. The last important laboratory analysis is connected with the electrical parameters measurement (EPM). It is carried out on core plugs and determined the electrical resistivity of formation, formation factor, cementation exponent and saturation exponent. This mentioned electrical parameters are directly linked with tortuosity. The more tortuous is the pore network, the worse environment for current flow. Scheme of laboratory measurements on geological materials, as well as equipment description, is presented in Fig. 2. CT, MICP and PDP pressure-decay measurements were performed on crushed material, while EPM and pulse-decay method on core plugs. MICP was the last measurement because crushed material became contaminated.

Fig. 2
figure 2

List of laboratory measurements on geological materials. Symbols of methods: CT—computed X-ray tomography, MICP—mercury injection capillary pressure (mercury porosimetry), PDP—pulse-/pressure-decay methods for absolute permeability, and EPM—electrical parameters laboratory measurement

Full size image

Tortuosity is a significant parameter in the fluid dynamics. The more pore space is complex, the greater the difficulty of fluid flow. That is why tortuosity cannot be omitted in the tight reservoirs analysis, in which all difficulties count in hydrocarbon exploitation. The geometrical tortuosity is the ratio of the actual flow path or simply saying actual length of pore channel and straight-line distance between the beginning and the end of the pore channel (Thovert et al. 1993; Lindquist et al. 1996; Ghanbarian et al. 2013; Sobieski et al. 2018).

The novelty in the presented approach is connected with the identification and analysis of the main pore channels. Skeleton is retrieved from the pore space; hence, the pore space is divided into the branches (pore channel) and the junctions (branches connection point). Most algorithms divide the main pore channel info set of branches. Algorithm of the central axis, which is implemented in the poROSE software (Madejski et al. 2018), does not divide the main pore channel into smaller sections but identifies and analyzes the whole main flow path. poROSE software is dedicated for 3D images analysis, especially from CT or 3D FIB SEM (focused ion beam scanning electron microscopy) and is delivered by AGH University of Krakow in the licensing form. Figure 3 shows main pore channel marked in red and branches marked in green. Often branches are complex, well-built and create flow paths, but sometimes are the dead ends. The algorithm works for 21-neigbourhood connectivity.

Fig. 3
figure 3

Products of skeleton analysis on 3D CT images, sketch of main pore channel and pore space components

Full size image

The definition of geodesic tortuosity was described by Hormann et al. (2016), which is defined by the shortest path between two pores that does not intersect the skeleton. Dijkstra's algorithm is most often used for this case (Roque and Costa 2020; Pheng et al. 2023), while start and end points are defined by centroid coordinates.

The main advantage in the presented approach is identification of main pore channels, without taking into consideration blind pores. The main pore channel is, among other things, identified by searching for the thickest and longest pore channel, by inscribing a 3D sphere into the path. After main pore channel detection, the algorithm calculates tortuosity, as presented in Fig. 4. Thousands of main channels can be found in the pore system depending on the number of separate pore networks. It is the effect of the pore space complexity.

Fig. 4
figure 4

Sketch of the tortuosity definition based on 3D CT images. Symbols: τ—tortuosity of the main pore channel, La—actual flow path (actual length of pore channel), L—straight-line distance between the beginning and the end of the pore channel

Full size image

Multilinear regression (MLR) was implemented in the research to estimate absolute permeability based on variables (parameters) from CT, MICP, PDP and EPM data. MLR allows finding the relationship between several independent variables and one dependent, in this case absolute permeability (Freund et al. 2006):

$$K = b_{0} + b_{1} X_{1} + b_{2} X_{2} + b_{3} X_{3} + \cdots + b_{n} X_{n},$$
(1)

where K is the dependent variable (absolute permeability); b0, b1, b2, b3, …, bn—regression coefficients; X1, X2, X3, …, Xn—independent variables; and n—number of independent variables.

The data were divided into the calibration, validation and testing data sets. Results from MLR can be treated as generalized estimation for tight, low-porosity and low-permeability rocks. Calculation was carried out in Statistica software (TIBCO 2017).

Results and discussion

Images from computed X-ray tomography were transferred into skeleton, which consists of branches (pore channels) and junctions (pore connection point). Basic statistics for parameters from the CT skeleton analysis, performed in the poROSE software, are depicted in Table 1 and Fig. 5. Research material varies in the branches number (pore channels), analyzing mean and standard deviation value, what points to diversity in poorly developed pore space. However, this number is still relatively low. On average, five junctions create pore network and three branches merge into the pore junction.

Table 1 Basic statistics for parameters from the CT skeleton analysis
Full size table
Fig. 5
figure 5

Box plots for the average number of junctions and the average coordination number in the samples from CT. Description: center line—median, box edges—quartiles, and whiskers—percentiles

Full size image

Coordination number parameter describes how many branches connect and end in one junction (Wayne 2008).

Figure 5 shows variety in average number of junctions in the single pore network and consistency in coordination number. Both average number of junctions and coordination number have similar median value and indicates poorly developed pore system.

Table 2 and Figs. 6, 7, 8 present basic statistics for parameters from the CT, MICP, PDP and EPM for the analyzed rock samples. Tortuosity is around 1.3 (median similar to the average value) for the all analyzed samples. It indicates a poorly developed pore space in the all research material. Moreover, average pore diameter from CT is not high, because is around 2 µm. Effective porosity from MICP is quite low, around 3% what is consistent with the information about the percentage of pores with diameters higher than 0.1 µm (important threshold for gas flow regarding gas molecule size) and 1 µm (important threshold for oil flow regarding oil drop size). Swanson parameter is defined as the maximum value of mercury saturation per pressure. Swanson parameter was determined for the pore system, not for crack system and is characteristic for the low-porous and low-permeable rocks. Absolute permeability is typical as for the tight formations and corresponds with the other parameters from the MICP and CT data. Thus, electrical parameters, such as rock formation resistivity, formation factor, cementation exponent and saturation exponent, also assume values reflecting tight rocks. Formation electrical resistivity varies diametrically. Average value and median are not consistent, while standard deviation is quite high. Similarly, formation factor behaves, with one difference; the spread in values is even greater than that in the rock resistivity.

Table 2 Basic statistics for parameters from the CT, MICP, PDP and EPM
Full size table
Fig. 6
figure 6

Tortuosity distribution for all samples

Full size image
Fig. 7
figure 7

Box plots for the logarithm of rock electrical resistivity Rt, formation factor F, absolute permeability K. Description: center line—median, box edges—quartiles, whiskers—minimum and maximum value

Full size image
Fig. 8
figure 8

Box plots for the tortuosity τ and cementation factor m (unitless) Description: center line—median, box edges—quartiles, whiskers—minimum and maximum value

Full size image

Distribution of pore tortuosity is presented in Fig. 6. Mostly, the tortuosity is in the range of 1.14–1.19. All values of tortuosity can be validated by analyzing 3D CT images. In this case, great portion of analyzed pore channels have simplified structure, which is connected with the poorly developed pore space and process of deposit sedimentation and consolidation.

Lala (2020) presented micromechanical theory approach to create a novel formula and to estimate the tortuosity in the model from precise experimental measurements. Tortuosity varies from 1.25 to 1.77 for the samples with porosity in the range of 29–44%. Zakirov and Khramchenkov (2020) found a meaningful effect of pore-level heterogeneity on permeability and tortuosity by investigating fluid flow using lattice Boltzmann simulations. They established the tortuosity in the range of 1.18–1.36 for different types of simulated porous media (nearly round grains). Moreover, Fu et al. (2021), using 3D CT images of Fontainebleau sandstone, described tortuosity between 1.28 for 24.5% porosity and 1.91 for 8.61% porosity.

Figure 7 collectively shows box plots for the logarithm of rock electrical resistivity Rt, formation factor F and absolute permeability K, described by center line as median, box edges as quartiles and whiskers as minimum and maximum values. Meanwhile, Fig. 8 presents box plots for the tortuosity τ and cementation factor m in the same box manner. It is worth mentioning that cementation factor has low values as expected. Tight formations can be characterized by cementation factor even greater than 2 (around 2.2).

Tortuosity corresponds with the amount of pores above 1 µm in diameter from MICP data (Fig. 9). There is visible positive relation between the tortuosity and percentages of pores above 1 µm, and this relationship indicates that the more pores with diameters greater than 1 µm we observe in the tight rock sample, the more tortuous the pore channels can be expected. The points with the outstanding data (below the correlation line) represent limestones and dolomites.

Fig. 9
figure 9

Relation between the tortuosity from CT and percentage of pores with dimeter above 1 µm in diameter from MICP

Full size image

Moreover, high correlation is determined between the tortuosity and Swanson parameter (Fig. 10). Tortuosity and Swanson parameter are connected with rock ability to fluid flow. Swanson parameter controls the fluid flow because it is main point in the injection saturation of mercury and is estimated in the point at the MICP data curve in which pressure rises rapidly and the mercury fills ever narrower pore channels. Figure 10 shows interesting relationship for low-porous and low-permeable rocks. The tortuosity increases with an increase in the Swanson parameter. Swanson parameter is higher when amount of mercury is higher for the lower pressure, which indicates that in low-porous and low-permeable rocks tortuosity plays a key role. Tortuosity in tight rocks refers to the development of pore network. It is more complicated in conventional deposits. Here, in case of low-porosity and low-permeability rocks it is an indicator of the more extensive pore network, if the pore network of tight rocks can be qualified as extensive at all. This relation depicts challenging relationship and can be used as an initial estimation of tortuosity from MICP data in tight rocks. The two outstanding points are dolomites and represent the same dolomites as in Fig. 9.

Fig. 10
figure 10

Relation between the tortuosity from CT and Swanson parameter from MICP

Full size image

Research was also concentrated on analysis of the connection between the tortuosity from CT and electrical parameters from laboratory measurements on core plugs. Both tortuosity and electrical parameters are associated with “flow”. The high correlation is observed between the tortuosity and saturation exponent in analyzed tight deposits (Fig. 11). Saturation exponent matches dependency on hydrocarbons in the pore system, simply saying it reflects the effect on the resistivity of the sample desaturation process. High values of saturation exponent refer to the oil-wet pore system. Sometimes, the saturation exponent is analyzed qualitatively as a measure of the efficiency for the electrical flow ability within the brine filling a partially saturated rock (Han et al. 2021). Tortuosity and saturation exponent in a sense correspond to each other in the way that high tortuosity leads to complicated flow path and high formation factor; on the other hand, high values of saturation exponent are characteristic for uniform hydrocarbon-wet system described by high values of rock resistivity.

Fig. 11
figure 11

Relation between the tortuosity from CT on the crushed material and saturation exponent from electrical measurements on core plugs

Full size image

Multilinear regression was conducted to estimate absolute permeability taking all parameters into consideration. Absolute permeability from PDP methods was used as a reference. Depending on the data set size, one dependent variable—absolute permeability from pulse- or pressure-decay methods was considered in terms of several independent variables from CT, MICP and EPM. Four different models were obtained including effective porosity from MICP, logarithm of formation factor from EPM, logarithm of rock electrical resistivity from EPM, cementation factor from EPM, saturation exponent from EPM and tortuosity from CT (Table 3). Summary results are collected in Table 3 including parameter used in MLR analysis and determination coefficient for the fit with absolute permeability from PDP. The more weak relation was obtained using effective porosity, logarithm of rock electrical resistivity and tortuosity (R2 = 0.51), while the most strong for the saturation exponent and tortuosity (R2 = 0.77). Moreover, one relationship is worth discussing, namely that consisting of effective porosity, logarithm of formation factor and tortuosity (R2 = 0.72) and presented in Eq. 1 (Table 3) (1). Usually mercury porosimetry as well as electrical parameters measurement is carried out on every crushed material or/and core plug as routine or special core analysis (SCAL). Tortuosity is estimated based on CT measurement and is not a standard laboratory measurement. Combination of these parameters in one equation with quite high determination coefficient gives credence in estimating preliminary absolute permeability based on the data which is executed as standard (MICP and EPM) and data from the non-invasive method (CT).

$$\log K = - 22.1295 + \left( {19.5795*\varphi_{{{\text{eff}}}} } \right) + \left( {0.1541*\log F} \right) + \left( {14.6972*\tau } \right).$$
(2)
Table 3 Results for MLR analysis based on rock electrical parameters and tortuosity from CT
Full size table

The best solution was obtained for Eq. 4 (Table 3), based on tortuosity and saturation exponent (2). Absolute permeability can be easily estimated using these two parameters. Detail results of MLR analysis for the best solution are presented in Table 4 including standardized partial regression coefficient and partial regression coefficient.

$$\log K = - 4.18069 + \left( { - 0.00712*\tau } \right) + \left( { - 0.03334*n} \right).$$
(3)
Table 4 Results of MLR analysis for the best solution—Eq. 4 (2)
Full size table

Figure 12 illustrates the comparison between the logarithm of absolute permeability form PDP (logK) and estimated absolute permeability based on MLR (logK MLR). Relationship is good taking into consideration heterogeneous material as tight low-porosity and low-permeability rocks and different lithologies. One point is outstanding (low value of logK and logMLR) and is connected with the lithology (dolomite).

Fig. 12
figure 12

Logarithm of absolute permeability from PDP (logK) versus logarithm of absolute permeability from MLR, Eq. 4 (2)

Full size image

Al-Anazi and Gates (2010) presented the result of permeability estimation from well logs using core clustering and BPNN (a nonparametric, nonlinear statistical models for both regression and classification purposes), GRNN (a single-pass nonlinear learning algorithm in a neural network architecture for continuous variables estimation) and SVM (support vector machines) methods. They obtained correlation coefficient for permeability prediction as follows: BPNN—0.71, for GRNN—0.73 and for SVM—0.74. It is worth mentioning that it is quite high correlation taking into consideration comparison between the core and well logs results. Performed calculations on core samples allowed receiving correlation coefficient equal to 0.88 using only MLR analysis and only core data.

Gholami et al. (2014) showed applications of artificial intelligence methods in prediction of permeability in hydrocarbon reservoirs. Two methods were used to predict permeability in this case: RVR (relevance vector regression) and SVR (support vector regression). They compared the result of permeability estimation with the core permeability and obtained determination coefficient of about 0.9 for both methods. Tight, low-porosity and low-permeability gas-saturated rocks, cored from the present depth of deposition below 3000 m, are unique and quite difficult geological material; hence, the prediction in permeability in the presented MLR case is lower than in mentioned paper.

Presented formulas have a limitation and can be tested on tight, gas-bearing formations. Moreover, the equations were calibrated, validated and tested on data from four different lithologies; hence, it can have a positive or negative influence.

Conclusions

The research presents the novel approach in the identification and analysis of the main pore channels based on 3D CT images. Algorithm of the central axis, which was implemented in the research, identifies and analyzes the whole main flow path and calculates tortuosity. The main flow path plays a key role in hydrocarbons and water exploitation.

Tight, low-porosity and low-permeability gas-saturated rocks are extremely difficult geological material because the variability of petrophysical parameters in the borehole geological profile is significant. 3D CT images, together with mercury porosimetry data, pulse- and pressure-decay permeability data, as well as electrical parameters, can give detailed information about the specific parameter distribution.

Calculated geometrical tortuosity is around 1.3 for the all analyzed core samples. It indicates a poorly developed pore space in the all research material. Mostly, the detected tortuosity is in the range of 1.14–1.19.

High correlation was observed between the tortuosity and Swanson parameter from mercury porosimetry data. Tortuosity and Swanson parameters are connected with rock ability to fluid flow. Moreover, the high correlation was detected between the tortuosity and saturation exponent from electrical parameter measurement in analyzed tight low-porosity and low-permeability deposits.

Multilinear regression allows estimating absolute permeability taking CT, MICP and EPM parameters into consideration. Four different models were obtained including effective porosity from MICP, logarithm of formation factor from EPM, logarithm of rock electrical resistivity from EPM, cementation factor from EPM, saturation exponent from EPM and tortuosity from CT. Combination of these parameters in one Eq. 4 (2), using tortuosity from CT and saturation exponent from EPM, with high determination coefficient gives credence in estimating preliminary absolute permeability based on the data which is executed as standard core analysis (MICP and EPM) and data from the non-invasive method (CT).