Introduction

The mechanical behavior of rock is a key issue in many geological environments, where the elastic moduli of rock are key parameters for accurate analyses. For instance, the interpretation of elastic wave velocity is of great significance for determining the crustal rock structure, which requires important rock mechanical parameters: elastic moduli. Elastic moduli control the deformation behavior of rock under a specific pressure, which can be classified into static elastic moduli and dynamic elastic moduli according to loading conditions. In geophysical measurements, the elastic moduli obtained by static and dynamic approaches are different (e.g., Simmons and Brace 1965; Cheng and Johnston 1981; Tutuncu et al. 1998). Taking deep geothermal engineering as an example, the static elastic moduli of the reservoir rock are related to the performance of the fracture network. Therefore, an accurate and rapid determination method of static elastic moduli has substantial significance for deep geothermal energy exploitation.

Rapid and non-destructive methods for the static moduli of rock are a continuous research topic, where the method using elastic wave velocity is commonly used. In some extreme environments, such as deep mining, tunneling, and seismic zone (Kurlenya et al. 2015; Shreedharan and Kulatilake 2015; Catalán et al. 2017), rock specimens are very difficult to obtain. In those cases, obtaining the static elastic moduli of rock by wave velocity may be the best choice since the wave propagation test is a rapid, nondestructive, and in-situ measurement. Although many signs of progress have been made on the elastic wave method, some issues still restrict the accurate extraction and its applications. A review of this method and its further research prospect is urgently needed.

The empirical correlations proposed by previous researchers provide convenient and feasible methods. Nevertheless, the results obtained from multiple correlations are different (sometimes with a large difference), which presents a large application obstacle for the prediction of the static modulus. In addition, empirical correlations were only obtained by fitting experimental data. It lacks a theoretical basis, and its rationality does not answer scientific questions. Under different frequencies, the wave velocities of rock are different, leading to the difference in the calculated dynamic elastic moduli, which brings greater error to predict the static elastic modulus by empirical correlations. What is the representative frequency to obtain dynamic elastic modulus (or how to get the representative modulus based on frequency dependence)? The results under the uniaxial compressive condition reveal that the static modulus of rock is nonlinear (e.g. Hilbert et al. 1994; Kurlenya et al. 2015; Sebastian and Sitharam 2018; Wu et al. 2020). What stage does the modulus obtained by elastic waves represent (or under what strain condition)? To date, these questions are still unknown and require further studies.

In this paper, we review the relationship and empirical correlations between the static and dynamic elastic moduli, the frequency dependence of the P- and S-wave velocities, and dynamic Young’s and bulk moduli of rock. By summarizing the experimental data published in previous literature, the research status of the elastic wave method for obtaining the static elastic moduli of rock is presented. Finally, existing problems and further prospects are pointed out for better development of the elastic wave method.

Static and dynamic elastic moduli of rock

Static elastic modulus

The elastic moduli of rocks are the deformation characteristics during the elastic deformation stage. The static elastic moduli reflect the deformation characteristics of rocks under static loading conditions which include Young’s modulus, bulk modulus, and shear modulus. The methods for obtaining the static elastic moduli of rock include two categories: static and dynamic methods. This section mainly introduces static methods, where static elastic moduli could be obtained using static mechanical tests.

Young’s modulus was originally defined in steel deformation. During the elastic stage, the stress-strain curve is nearly linear, hence Young’s modulus of steel is a constant. However, the stress-strain curve of rocks varies with strain since rock deformation is nonlinear. According to stain level, Young’s modulus includes the initial Young’s modulus and Young’s modulus. Initial Young’s modulus is calculated at the original stage where the rock is loaded with a small force, which reflects the initial deformation characteristic. Young’s modulus is calculated when rock enters the elastic deformation stage from the fracture closure stage.

The most used test method in static methods is the uniaxial compressive test (UCT), where cylindrical specimens are generally used. Generally, three calculation approaches were used for Young’s modulus of rock:

  1. i.

    Tangent modulus. The choice of stress level can be a few percent of uniaxial compressive strength (UCS, \(\sigma_{c}\)), and the general value is taken as 0.5 \(\sigma_{c}\). This calculation is the most common method.

  2. ii.

    The average slope of a stress-strain curve in the elastic stage (straight section).

  3. iii.

    The secant modulus from the original point to a specific stress level can be Young’s modulus, where the stress level is generally taken as 0.5 \(\sigma_{c}\).

The bulk modulus of rock is the ratio of volume stress and volume strain and can be obtained by uniaxial compressive test and triaxial compressive test. The shear modulus of rock is the ratio of shear stress and shear stain and can be obtained by triaxial compressive test, direct shear test, and compression shear test. In addition, in-situ loading tests can also obtain the deformation characteristics of rock, such as the plate load (ISRM 1979), flat jack (ISRM 1986), and Goodman jack test (Selig and Heuze 1984).

The static elastic moduli of a rock specimen obtained by different calculation methods are generally different. The results of Al-Shayea (2004) show that the difference between static elastic moduli from different calculation methods can reach 20%. Besides, the static method is time-consuming and expensive, and the results are discrete.

Dynamic elastic modulus

Similar to static elastic moduli, dynamic elastic moduli are composed of dynamic Young’s modulus, bulk modulus, and shear modulus. The main methods to obtain dynamic elastic moduli are wave velocity tests, dynamic experiments (force deformation), and resonant techniques. Wave velocity measurement is the most widely used method to determine dynamic elastic moduli, which needs the P- and S-wave velocities of rock and then determines the dynamic elastic moduli according to elastic wave propagation theory, where the rock is assumed as a continuous, isotopic, and homogenous medium with small strain and no initial stress.

In terms of the P- and S-wave velocities, dynamic Young’s modulus can be calculated by (Goodman 1989):

$$E_{{\text{d}}} = \frac{{\rho c_{{\text{s}}}^{2} \left( {3c_{{\text{p}}}^{2} - 4c_{{\text{s}}}^{2} } \right)}}{{c_{{\text{p}}}^{2} - c_{{\text{s}}}^{2} }},$$
(1)

where \(E_{{\text{d}}}\) is dynamic Young’s modulus, \(\rho\) is density, and \(c_{{\text{p}}}\) \(c_{{\text{s}}}\) are the P- and S-wave velocities, respectively.

The dynamic bulk modulus of rock can be calculated by:

$$K_{{\text{d}}} = \rho \left( {c_{{\text{p}}}^{2} - \frac{4}{3}c_{{\text{s}}}^{{2}} } \right).$$
(2)

The dynamic shear modulus of rock is as follows:

$$G_{{\text{d}}} = \rho c_{{\text{s}}}^{{2}}.$$
(3)

The conventional wave velocity test processes the rock specimen into a certain shape and measures P- and S-wave velocities in laboratory experiments. By a detector, a seismograph, or other equipment, in situ tests of large-scale rock can also be carried out for determining the dynamic elastic moduli of rock. Although moduli obtained by a static method have a larger dispersion, it can obtain the static moduli under a high strain level (it can reach 10–2). The dynamic method has a smaller dispersion, but the measured strain level (\(<\) 10–5) is also low (Al-Shayea 2004).

The dynamic experiment could be also conducted to determine the dynamic elastic modulus by applying an impact load to a rock specimen. During this process, the deformation parameters of the specimen are determined by a high-speed camera or strain gauges (Fan et al. 2017). The main purpose of this paper is to focus on the wave velocity test. Many works show the dynamic experiment. Readers can refer to published literature (e.g. Peng et al. 2019; Liu et al. 2021).

Methods for the determination of wave velocities

The determination method for accurate arrival times of P- and S-waves is a premise for calculating P- and S-wave velocities. At low-frequency range (generally below 100 Hz), a seismic experiment was usually used. At a high-frequency range (thousands of Hz), an ultrasonic test was usually used. Based on a time-domain analysis, a frequency-domain analysis, and mathematical models, researchers have proposed many methods for the determination of arrival times of elastic waves (including AE wave, ultrasonic wave, and seismic wave). Revised or new methods are also being improved or proposed. In terms of the differences in the degree of automation and algorithm, these methods can be classified into three categories.

Category 1: manual identification or semi-automatic method

This category includes the direct observation method, the start-to-start distance method in the time domain, and the peak-to-peak distance method in the time domain (Ogino et al. 2015). If the arrival time of the start vibration is easy to identify, direct observation can be used. This method is suitable for the P-waveform with a high signal-to-noise ratio (SNR). A large error may be caused by manual operation on the S-waveform because the arrival time of the S-wave is difficult to be observed. The start-to-start distance is a widely used method for P-wave. The linear regression method is used to make a tangent at a point after the start vibration point of the waveform, where the tangent point can be taken as a point whose voltage is about one-third of the first peak. The intersection point between the tangent and the time axis is considered the arrival time. The peak-to-peak distance in the time domain is taken as the travel time where the first peak is that of the excitation signal, and the second peak is that of the received wave. This method is widely used in waveforms whose arrival time is difficult to be identified, such as S-wave.

Category 2: the threshold method

This category determines the arrival time in terms of a threshold value and can be further classified into two types. If the voltage of a waveform exceeds a threshold value, the wave is considered to arrive. In type 1, the threshold value is fixed. This type is suitable for the waveform with high SNR or high amplitude. For a waveform with low amplitude or low SNR, the noise before the arrival of the wave may be sometimes regarded as the arrival, resulting in a large error in wave velocity calculation. In type 2, the arrival time can be determined by a dynamic threshold value and a characteristic function. This type of method can be also called the short-term average/long-term average method and has been widely applied in seismic waves (Allen 1978; Allen 1982; Earle and Shearer 1994; Dai H and MacBeth 1995; Leonard and Kennett 1999).

Category 3: a method based on statistics

This category determines the travel time by automatic regression analysis based on mathematical statistics (Sleeman and van Eck 1999; Leonard 2000; Zhang et al. 2003; Bai et al. 2016). The Akaike information criterion (AIC) is well-known in this category and is an efficient method suitable for in situ and laboratory tests. The arrival time is regarded as the minimum of the AIC function. The AIC function can effectively separate the noise in front of the real arrival time. For an array of waveform data composed of N points, the AIC value of each point could be determined by (Maeda 1985):

$${\text{AIC}}(k) = k\log \left[ {{\text{var}} (V_{i} [1, \, k])} \right] + (N - k - 1)\log \left[ {{\text{var}} (V_{i} [k + 1, \, N])} \right],$$
(4)

where k is the No. of the point in a discrete signal and \({\text{var}} ( \bullet )\) is the variance of the voltages of the discrete signal in the voltage range of [1, k] or [k + 1, N]. The minimum of the AIC value is the arrival time (\(t_{{\text{P}}}\) for P-wave and \(t_{{\text{S}}}\) for S-wave). By choosing an appropriate time window we can accurately obtain the ultrasonic wave velocities.

Extracting static elastic modulus according to empirical correlation

Besides static mechanical tests, dynamic Young’s modulus is often used to predict the static Young’s modulus of rock (dynamic method). Since the 1930s, due to the application of wave propagation testing technology in mining, petroleum, and civil engineering, scholars began to study the relationship between dynamic and static elastic moduli. A large amount of measured data were obtained. The dynamic and static Young’s moduli of rock generally differ. Using the dynamic-static ratio, their relationship can be described:

$$k_{{\text{d/s}}} = \frac{{E_{{\text{d}}} }}{{E_{{\text{s}}} }},$$
(5)

where \(E_{{\text{d}}}\) and \(E_{{\text{s}}}\) are the dynamic and static Young’s moduli, respectively.

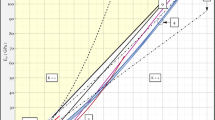
A scatter diagram of the dynamic and static Young’s and bulk modulus of rock is given in Fig. 1. In most cases, the dynamic-static ratio is greater than 1. In the low modulus range (< 70 GPa), the dynamic-static ratio is different. In some cases, this parameter is less than 1. By summarizing ten kinds of rocks, van Heerden (1987) revealed that the dynamic-static ratio reduces with increasing Young’s modulus. At a high Young’s modulus level (still in the elastic stage), the dynamic-static ratio is a little less than 1. Al-Shayea (2004) revealed that the dynamic-static ratio would be equal for dense rock. van Heerden (1987) revealed that the dynamic Young’s moduli of low modulus (< 100 GPa) samples were greater than the static Young’s modulus, whereas the static Young’s modulus of high modulus (> 100 GPa) samples is larger than the dynamic Young’s modulus.

Fig. 1
figure 1

Relationship between the dynamic and static elastic moduli of rocks

Full size image

Through regression analysis, scholars have proposed many empirical correlations between dynamic and static Young’s moduli. Table 1 lists the current empirical correlations of Young’s modulus, and Table 2 lists the current empirical correlations of bulk and shear moduli. According to the expression form of the empirical correlations, they can be divided into linear relations and nonlinear relations, in which the nonlinear relations include logarithms, power functions, binomial functions, and so on. Some scholars established their relationship by introducing other parameters, such as density and porosity. Through these formulas, a mutual prediction can be made.

Table 1 Empirical correlations between the dynamic and static Young’s moduli of rocks
Full size table
Table 2 Empirical correlations between the dynamic and static bulk and shear moduli of rocks
Full size table

Savich (1984) found that the relationship is related to the stress state. van Heerden (1987) established an empirical correlation by testing Young’s modulus of different rock specimens under the stress of 10, 20, 30, and 40 MPa:

$$E_{{\text{s}}} = aE_{{\text{d}}}^{b},$$
(6)

where a and b are the parameters related to the rock stress state.

Based on the summary of the test data of more than 40 rocks, Davarpanah et al. (2020) systematically studied the relationship, which was fitted by a linear function, a power function, and a logarithmic function. The empirical correlations were also related to rock type. Igneous rock and metamorphic rock were more suitable for logarithmic and power functions. Sedimentary rocks are more suitable for a linear function.

Although many empirical correlations have been proposed, the prediction results by different correlations often vary, and some of them are quite different (see Fig. 2). Therefore, the empirical correlations can be used for rough prediction. Accurate determination by the dynamic method still requires further studies.

Fig. 2
figure 2

Empirical correlations of the dynamic and static Young’s moduli of rock

Full size image

Extracting static elastic modulus according to frequency dependence

Frequency-dependent wave velocity

The frequency dependence of wave velocities (also known as wave velocity dispersion) refers to differences in wave velocities at different frequencies of stress wave (including P- and S-wave velocities). In other words, the P- and S-wave velocities vary with the change in frequency. Many experiments demonstrated that the P- and S-wave velocities of rocks increase with increasing frequency. For example, from 5 Hz to 800 kHz, the P- and S-wave velocities of carbonatite and sandstone have strong frequency dependences, and both increase with a rise in frequency (Batzle et al. 2006). Although different scholars reached different results based on different rocks, the frequency dependence of rock wave velocities has been widely confirmed and recognized. This law applies to soft rock, quartzite, low frequency, and high frequency. Figure 3 shows the variations in the P- and S-wave velocities of typical rocks with frequency.

Fig. 3
figure 3

Frequency dependences of P- and S-wave velocities of typical rocks

Full size image

Frequency-dependent elastic modulus

Since dynamic elastic moduli can be calculated from wave velocities, the frequency dependence of dynamic moduli is also frequency dependence, which is widely studied in the seismic field, mainly in the range of 0.1–200 Hz. In addition, some researchers have also tested the wave velocities under an ultrasonic wave and found that there is also a frequency dependence. James and Spencer (1981) measured that the dynamic Young’s modulus of Navajo Sandstone gradually increases with increasing frequency in 2–200 kHz. Lozovyi and Bauer (2019a) measured the P- and S-wave velocities of three kinds of shale and one kind of mudstone at frequencies of 1–150 Hz (belonging to seismic wave frequency) and 500 Hz. The dynamic Young’s modulus obtained at low frequency is different from that obtained at high frequency. From low frequency to high frequency, the dynamic Young’s modulus increases by 70%. The dispersion of the S-wave velocity with frequency (15–44%) is more obvious than that of the P-wave velocity (2–25%). Subsequently, Lozovyi and Bauer (2019b) measured the dynamic Young’s modulus of shale at 0.5–150 Hz. The results show that with the increase in frequency in the test range, the dynamic Young’s modulus gradually increases from ~ 4.8 to ~ 5.4 GPa, increasing by 13%. Szewczyk et al. (2016) measured the dynamic Young’s modulus of shale under confining pressure, showing that the dynamic Young’s modulus gradually increases with increasing frequency. The dynamic Young’s moduli of shales at high frequencies are much more than those of seismic waves. They attributed this difference to the strain level and frequency dependence. Under different hydrostatic loading (3.5, 1.35, 23.5 MPa), the change laws of frequency dependence are similar, but the dynamic Young’s modulus increase with increasing hydrostatic loading. Pimienta et al. (2015, 2016) measured the change in the dynamic Young’s and bulk moduli of sandstone with frequency in the range of 0.01 Hz–300 kHz, showing that the dynamic Young’s and bulk modulus increases slowly in the range of 0.01–2 Hz and increases rapidly with increasing frequency in the range of 2 Hz–300 kHz. Figure 4 shows the frequency dependence of dynamic Young’s modulus and bulk modulus of rocks. All results demonstrate that, in a wide frequency range (10–2–106 Hz), the dynamic Young’s modulus of rocks increases with increasing frequency.

Fig. 4
figure 4

Frequency dependence of dynamic Young’s modulus and bulk modulus of rocks

Full size image

Frequency-dependent attenuation

Attenuation (Q−1) describes the change rate of frequency dependence, whose peak is at a relation frequency, where velocity/elastic modulus increases rapidly. Attenuation could be classified as velocity attenuation, Young’s attenuation, bulk attenuation, and so on. In a linear viscoelastic medium, the velocity/modulus dependence and attenuation are related (Cole and Cole 1941; Bourbie et al. 1987). For a single relaxation mechanism, velocity/elastic modulus increases with a sigmoidal character. Figure 5 shows a sketch map of the frequency dependence of wave velocity and its related attenuation. The attenuation peaks at the relation frequency. Figure 5 also shows the influence of fluid on frequency dependence. Dry rock and saturated rock show different peaks. The peak frequency will be lower if the rock is saturated. And, the rock saturated with lower mobility fluid has a lower peak frequency. Young’s and bulk attenuations have a similar change to velocity attenuation. Figure 6 shows the bulk and Young’s attenuations of saturated limestone and sandstones, revealing different peak frequencies with different rocks.

Fig. 5
figure 5

Frequency dependence of wave velocity and its related attenuation (revised after Batzle et al. 2006)

Full size image
Fig. 6
figure 6

Bulk and Young’s attenuations of saturated limestone and sandstones. Different peak frequencies are observed from different testing. The rocks are saturated with glycerine, water, and brine, respectively. Due to data acquisition, there are few data in a high-frequency range of the brine-saturated sandstone

Full size image

Influence of fluid and pressure on the frequency dependence

Fluid influences the frequency dependence of wave velocity and elastic moduli. Rock is a porous medium. Fluid in its pores will change its properties. Figure 7 shows the frequency dependence of wave velocities and bulk modulus of dry and saturated sandstones. The existence of fluid could increase the P- and S-wave velocities and bulk modulus. Given the change rate of frequency dependence, fluid may make the frequency dependence more obvious. For instance, the increase rate of glycerine-saturated sandstone at 4 × 10–2 Hz obtained from Pimienta et al. (2015) is much higher than that of water-saturated and dry sandstone specimens.

Fig. 7
figure 7

Influence of fluid on the frequency dependence of wave velocity and dynamic bulk modulus

Full size image

Pressure also influences the frequency dependence of wave velocity and elastic moduli. Different from static loading, ultrasonic loading is applied with a specific frequency and amplitude, where the amplitude is the maximum loading of the applied excitation force. Figure 8 shows the influence of amplitude on the frequency dependence of dynamic Young’s modulus, indicating that the dynamic Young’s modulus increases with increased amplitude. If the tested specimen is under confining pressure, the dynamic Young’s modulus will differ. As is shown in Fig. 9, hydrostatic loading increases the dynamic Young’s modulus of Pierre shale.

Fig. 8
figure 8

Influence of amplitude on the frequency dependence of dynamic Young’s modulus

Full size image
Fig. 9
figure 9

Frequency dependence of dynamic Young’s modulus with various hydrostatic loadings

Full size image

It should be noticed that there are many factors influencing frequency dependence, such as humidity and rock structures (fractures). The influence of fractures will be introduced in the next section. Figure 10 shows the dynamic Young’s modulus of Mancos shale with increased frequency under different relative humidity. The specimens tested at 11% and 100% relative humidity have a large difference in Young’s modulus. Large relative humidity may increase the change rate of frequency dependence. However, why this phenomenon is not revealed.

Fig. 10
figure 10

Dynamic Young’s modulus of Mancos shale with increased frequency under different relative humidity

Full size image

Multifrequency ultrasonic approach

According to the frequency-dependence wave velocities, we have proposed a multifrequency ultrasonic approach to extracting the static initial Young’s modulus of rock (Zhang et al. 2021). In a dynamic test, if the frequency of the excitation wave becomes increasingly lower, the loading condition will be the same as that in the static test when the frequency nears zero. Under this condition, the wave velocity can be regarded as the critical wave velocity (it does not exist in reality). Based on this idea, the modulus should be the real static modulus of rock. By determining the critical P- and S-wave velocities through the change law of the frequency dependence in experiments (Fig. 11a, b), the static modulus from UT can be obtained by:

$$E_{{\text{s}}}^{{{\text{UT}}}} = \rho \psi_{{\text{s}}}^{{2}} (f)\frac{{3\psi_{{\text{p}}}^{{2}} (f) - 4\psi_{{\text{s}}}^{{2}} (f)}}{{\psi_{{\text{p}}}^{{2}} (f) - \psi_{{\text{s}}}^{{2}} (f)}}\left| {f \to 0^{ + } }, \right.$$
(7)

where \(E_{{\text{s}}}^{{{\text{UT}}}}\) is static modulus obtained from the ultrasonic test, \(\psi_{{\text{p}}} ( \cdot )\) and \(\psi_{{\text{s}}} ( \cdot )\) are the functions of P-wave velocity and S-wave velocity with frequency, respectively, and f is frequency. Figure 11c shows the comparison between the static initial Young’s moduli obtained from static and ultrasonic methods, which experimentally demonstrate the rationality of the multifrequency approach. We also validate the proposed method by using the distinct lattice spring model and found that increased fracture length in rock could lead to an increase in the standard deviation. Therefore, the characteristics of cracks during thermal damage can be preliminarily estimated. Detailed information about this method sees Zhang et al. (2021).

Fig. 11
figure 11

Multifrequency ultrasonic approach to extracting static initial Young’s modulus of granite with various temperature treatments (Zhang et al. 2021)

Full size image

Discussion

Empirical correlation method

Using P- and S-wave velocities, the dynamic elastic moduli of rocks can be calculated. Through regression analysis, all kinds of empirical correlations have been established to quickly achieve in situ tests or ultrasonic acquisition of the static Young’s modulus of rock. An accurate method using ultrasonic waves for the determination of the static Young’s modulus of rock still has great difficulty. Empirical correlation methods have three challenges. One is the choice of a proper correlation. Selecting a suitable correlation is very difficult from so many correlations since different correlations have different results, and some of them are even far from each other. Such a large difference makes it difficult to choose a proper empirical method for accurate determination. The second one is that the relationship between the dynamic Young’s modulus and static Young’s modulus is not fixed. There is no specific relationship between the dynamic and static moduli of different rocks (or specimens). The third one is the theoretical basis of the relationship between dynamic and static parameters. Currently, most of the work has focused on the mathematical relationship between dynamic and static parameters, which aims to realize the mutual prediction of dynamic and static parameters from the mathematical relationship. However, there are still some deficiencies in the research on the internal relationship and the mechanism of dynamic and static Young’s moduli. Although different scholars have explained the dynamic-static relationship, these explanations lack quantitative analysis, and the theoretical basis of the dynamic-static relationship is still unclear. There is no unified understanding of it.

Multifrequency ultrasonic method

Explanations for the difference between dynamic and static moduli can be classified into three aspects: the nonlinear elastic response of strain, the strain level, and strain rate, and the influences of pores and cracks. However, according to the dynamic and static test results in the experimental results (Zhang et al. 2021), the dynamic and static moduli of granite are the same when the compaction stage finishes, while the dynamic modulus of sandstone near the elastic stage is always higher than the static modulus, which cannot be explained by the nonlinear elastic response of rock. The difference between the dynamic and static parameters of rock is also caused by the difference in the strain level and strain rate (Hilbert et al. 1994; Martin and Haupt 1994; Tutuncu et al. 1994; Al-Shayea 2004). The frequency dependence of the dynamic Young’s modulus of rock leads to the fact that the dynamic Young’s modulus obtained at different frequencies is not a constant. Static Young’s modulus and dynamic Young’s modulus are variables. Without knowing the influencing factors and changing rules of the rock modulus, we can only obtain some general conclusions. It is not enough to determine the exact relationship between them. Elastic wave propagation theory was established by assuming that material is of continuum, elasticity, small strain, isotropy, homogeneity, and no initial stress. For a material, if it is an intact crystal, its dynamic and static moduli are equal. However, there are many cracks in rock structures. Wave velocity is largely dependent on frequency (e.g. Ciccotti and Mulargia 2004; Borgomano et al. 2019). According to the result of Zhang et al. (2021), the wave velocity of a homogenous model is larger than that of the cracked model. This reveals that cracks have significant influences. The wave velocity of rock trends to be the velocity of mineral grains with increasing frequency. Therefore, wave velocity has an increasing trend with the increase in frequency. In addition, if the frequency of the ultrasonic wave decreases gradually to zero, the loading condition is similar to the static loading. According to the nonlinear response of rock elasticity, the modulus calculated by the critical wave velocity is, theoretically, the static Young’s modulus of rock under the condition of a low strain level. The dynamic modulus of rock is larger than the static modulus because cracks exist in the rock interior. If there are fewer cracks in a rock (namely its stiffness is large), the dynamic modulus is close to the static modulus. Considering this, the multifrequency ultrasonic method provides a potential approach for accurate static Young’s modulus.

Frequency dependence of rock exists in a large frequency range (see Fig. 5). Theoretically, the static modulus obtained by a full frequency range (including seismic region and ultrasonic region) is conducive to an accurate result. However, full-frequency measurement is difficult and has large application limitations in practice. Ultrasonic measurement is easy for laboratory tests with small rock specimens (10 cm length is enough). Our experimental results demonstrated this method is reasonable. But, wave velocity has large dispersion in the ultrasonic region, and the attenuation of the ultrasonic wave is large. Low-frequency wave velocity can be tested by seismic experiments. Wave velocity has low dispersion in the low-frequency velocity range (Wei et al. 2015; Yin et al. 2017; Sun et al. 2018). In practice application, the seismic wave can propagate far with lower attenuation than the ultrasonic wave.

Factors influencing dynamic and static moduli

The value of the static modulus of rock is related to the calculation methods. Due to the nonlinear elastic response of rock, the static elastic moduli based on different methods must differ (see “Static elastic modulus” section). For the dynamic elastic modulus, besides the influence of cracks on dynamic and static elastic moduli, fluid in pores and cracks (Yurikov et al. 2018; Sun and Gurevich 2020), density, pores (Moos et al. 1997; Yan et al. 2017), mineral grains (Yin et al. 1995; Blake and Faulkner 2016; Li et al. 2017; Brotons et al. 2016; Wang et al. 2020a, b), and loading conditions (Muqtadir et al. 2020) also have effects on the difference between dynamic and static moduli. For example, cracks have larger effects on static modulus than dynamic modulus (Blake and Faulkner 2016). These influencing factors may cause different static or dynamic responses, leading to differences in dynamic and static results. Furthermore, the dynamic modulus is related to measuring frequency. At different wave frequencies, the dynamic moduli must be different.

Rock is an anisotropic material due to oriented crack networks or foliation, showing a difference in properties in different directions. For instance, the anisotropy of P-wave velocity is higher than S-wave velocity in the Naparima Hill Formation mudstones (Blake et al. 2020). Different lithofacies have different anisotropy (Blake et al. 2020). The Young’s moduli in different direction may differ several times, and the change amplitudes between dynamic and static moduli are also different. The results of Condon et al. (2020) show that the change law of static and dynamic Young’s moduli of different samples may be different (see Fig. 12). However, many researchers did not take anisotropy considerations when determining the dynamic elastic properties. The dynamic elastic properties calculated by elastic wave velocity present that in the wave propagation direction. This result may have large differences with that in other direction. Therefore, this factor may cause large error between the dynamic and static moduli. The extent of how anisotropy affects the results for the static and dynamic elastic properties is now still uncertain. Further work should be carried out.

Fig. 12
figure 12

Influence of anisotropy on the static and dynamic Young’s moduli of rock (data from Condon et al. 2020). P and I denote the samples are obtained from boreholes P and I

Full size image

Further research prospect

Obtaining the static elastic moduli of rock is a premise for accurate mechanical analyses. Although many signs of progress on the elastic wave method have been made over the past few decades, some significant issues still exist to be addressed. These include:

In the empirical correlation method, much work should be done to accurately predict static Young’s modulus by using dynamic Young’s modulus, which mainly includes two aspects. One is the expansion of correlation equations. As we know, rock is a complex material. Different rocks have different dynamic-static relationships. In empirical correlations, only is there a proper correlation for the specific rock, and can we obtain the true static value. Another is the choice of a proper empirical correlation. How to choose a proper correlation is very difficult. For example, even though two specimens with the same lithology, may have different dynamic-static relationships. To date, the influencing factors of the dynamic-static relationship are still unknown, which include rock structure, lithology, fluid, and so on. Finding out the factor, and revealing the mechanism and reaction rule of the factor on the dynamic-static relationship is meaningful.

The multifrequency ultrasonic method is newly proposed. Four aspects should be focused on in future research. One is the further demonstration of its wide application to all kinds of rocks. We have tested three types of granite and three types of sandstone, demonstrating the reasonability of this method (detailed information see Zhang et al. 2021). This method is also suitable for thermally-damaged granite (Fig. 11) Another is to accurately determine the critical P- and S-wave velocities. The current determination uses the fitting method in the frequency range of 30 to 425 kHz. Literature has shown that the frequency dependence of wave velocities has a wide frequency range (10–3–106 Hz). Few studies were conducted in such a wide frequency range. Further research should be conducted to reveal the full frequency dependence law and find an effective frequency range. By doing so, a more accurate determining method can be proposed, where we can determine the critical P- and S-wave velocities without testing a full frequency dependence curve. The third one is the prediction of Young’s modulus at each strain level. The multifrequency ultrasonic method can extract the static initial Young’s modulus of rock since the applied ultrasonic amplitude is low. However, Young’s modulus of rock varies with strain level. Wave velocities and their frequency dependence are the comprehensive results of rock structure, minerals, and so on. How to use the wave information to extract Young’s modulus at each strain level is a meaningful subject. The last one is the influence of fluid and fractures in the rock. The multifrequency ultrasonic method was obtained in the condition of dry rock. Whether it is reasonable for the rock with various water content is unknown. And, what is the influence of fractures on frequency dependence is not completely revealed.

Conclusions

Obtaining the static elastic moduli of rock by elastic wave velocities is a rapid and convenient approach, which is also a significant method in geophysical prospecting to capture the crustal rock’s static elastic moduli. This paper reviews the published work on this approach. Some conclusions are as follows.

  1. 1.

    According to P- and S-wave velocities, there are two methods to extract static elastic moduli: empirical correlation method and multifrequency ultrasonic method. Through P- and S-wave velocities, dynamic elastic moduli (including Young’s modulus, bulk modulus, and shear modulus) can be calculated based on elastic wave propagation theory. By establishing correlation equations between the static and dynamic Young’s moduli of all kinds of rocks, the empirical correlation method can obtain the static Young’s modulus of rock by P- and S-wave velocities. Up to now, many correlation equations have been made, such as linear, power/logarithm, quadratic, and other equations. These equations could achieve relatively accurate calculations for specific rock types and structures. Different from the empirical correlation method, the multifrequency ultrasonic method uses frequency dependence to calculate the static initial Young’s modulus base on elastic wave propagation theory. This method has been demonstrated reasonable for three kinds of sandstone and granite.

  2. 2.

    The frequency dependences of the wave velocity and dynamic elastic moduli of rock are summarized. P- and S-wave velocities, Young’s modulus, and bulk modulus of rock, especially the saturated rock, have strong frequency dependence in a wide range of 10–6 to 106 Hz. With the increase in frequency, these four parameters increase. However, in different rocks or conditions, the increased characteristics are different. For instance, the attenuations (Q−1) and the peak frequencies of different rocks are different. The peak frequency of saturated rock is lower than that of dry rock. Saturated rock has stronger frequency dependence. Besides, amplitude and pressure also have influences on frequency dependence.

  3. 3.

    Three reasons can be used to explain the difference between the dynamic and static moduli: nonlinear elastic response, strain level/rate, and pores and cracks in rock material. According to the multifrequency dependence, the critical P- and S-wave velocities are closed to static loading with low amplitude. Therefore, the result obtained from the multifrequency ultrasonic approach is the static initial Young’s modulus, which provides a potential method for the quick and convenient acquisition of the static elastic modulus of rock.

  4. 4.

    Existing problems and prospects for the two methods are also pointed out. For the empirical correlation method, more correlation equations should be established for all kinds of rocks through extensive tests, and the choice of a proper empirical correlation is a key issue. For the multifrequency ultrasonic method, much work should be done: more demonstration cases with various rocks, accurate determination of the critical P- and S-wave velocities, the prediction of Young’s modulus at each strain level, and the reasonability of the method under complex water contents and fracture structures.