1 Introduction

The facility layout problem (FLP) is concerned with finding an arrangement of non-overlapping indivisible departments within a facility so as to minimize the total expected cost of flows. This cost between two departments is measured as the rectilinear distance between their centroids multiplied by the projected flow between them. We refer the reader to [9, 21] for recent reviews of the state-of-the-art in FLP.

In this paper we consider the special case of the FLP in which all the departments are to be placed in three or more rows. This case is referred to as multi-row facility layout problem (MRFLP) [9]. Instances of the MRFLP arise in various practical contexts. One such context is in manufacturing where the machines (equivalent to departments) are to be placed in rows with a predetermined separation between the rows to accommodate movement of people and/or materials. A related application of row FLPs is in the design of application-specific integrated circuits for which the layout of the components is organized in rows (called base layers), the objective is to minimize the total wirelength required to connect the components, and the separation between rows is used for the wires connecting the components. A review of the recent trends of layout in reconfigurable manufacturing systems is given in [29].

Our interest here in the MRFLP with three or more rows because first, the cases of one row and two rows have already been well studied in the literature, and second, the practical contexts mentioned above often require layouts with more than two rows. Furthermore, in manufacturing systems, the material handling devices determine the type of layout [18, 20]. The most common material handling devices are: a) handling robot; b) automated guided vehicle (AGV); and c) gantry robot. The first device determines a circular machine layout, the second one determines single-row or double-row layout, where the available space may determine which one should be used. The third device determines multi-row layout with more than 2 rows. When gantry robots are used to transfer parts among the machines, for instance when space is a limiting factor, multi-row layout plays an important role. Thus, the multi-row layout is a layout variant with its own applicability different from that of single or double-row layout, and from a mathematical optimization point of view, multi-row layout required specialized models.

Our contribution is mainly on providing solutions for medium- and large-scale instances of the MRFLP, for which we are not able to obtain the optimal solutions. We first propose a new mixed integer linear programming formulation that uses continuous variables to represent the departments’ location in both x and y coordinates, where x represents the position of a department within a row and y represents the row assigned to the department. We prove that this formulation always achieves an optimal solution with integer values of y, even though y is continuous. Because our fomulation, like other exact global optimization approaches in the literature, is limited to solving instances with up to 13 departments, we use it as the basis for a new two-stage optimization algorithm. The algorithm combines two mathematical optimization models by taking the output of the first-stage model as the input of the second-stage model. Our computational experiments show that this algorithm is, to the best of our knowledge, the first one in the literature reporting solutions for instances with up to 100 departments in reasonable time.

This paper is structured as follows. In Sect. 2 we review the problem and the relevant literature, with a focus on previous mathematical optimization approaches. Our new mixed integer linear programming formulation is presented in Sect.  3, and its theoretical integrality properties are proved in Sect. 4. Section 5 describes the two-stage optimization algorithm. We describe it explicitly as an algorithm (for the first time), and report results (Sect. 6) showing that it can efficiently find solutions for large-scale problems. Finally, Sect. 7 concludes the paper.

2 Literature review

The FLP on rows can be stated in the following general form: given a number of rows, a set of departments represented by rectangles, each of a given length, and a non-negative weight for each pair of departments, determine an assignment of departments to rows, and the positions of the departments in each row, so that the sum of weighted center-to-center distances is minimized. We assume that the rows and the departments all have the same height, that any department can be assigned to any row, and that the distances between adjacent rows are equal.

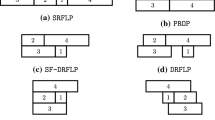
The row FLP most studied in the literature is the Single-Row FLP (SRFLP). We refer the reader to the recent survey papers [27] and [26] for the state-of-the-art on SRFLP, including extensions, meta-heuristics, and exact approaches. The Double-Row FLP (DRFLP) allows departments to be placed on both sides of a central corridor. Because there are only two rows, it is sufficient to determine which departments are placed in one of the rows, as the remaining departments must be in the other row. This property is explicitly exploited in the model presented in [2]. To the best of our knowledge, the earliest formulation of the DRFLP is a nonlinear optimization model proposed in [18] and used to find locally optimal solutions. Most of the subsequent mathematical optimization approaches in the literature use either mixed integer linear programming (MILP), see [2, 12, 36], or semidefinite programming (SDP) [24]. Among the most recent publications on the DRFLP are [3, 11, 32] that present MILP models for DRFLP; we note that [32] makes use of the concept of betweenness from [1]. New combinatorial lower bounds for the DRFLP that can be computed very fast are presented in [13]. Problems related to the DRFLP that are also the focus of current research are the corridor allocation problem, see [17, 35], and the parallel row ordering problem [34].

An important class of instances of the MRFLP arises in situations where gantry robots are used, for example in flexible manufacturing systems and in pick and place applications. Gantry robots have linear axes of control and move up/down and left/right with the movement directions at right angles, as illustrated in Fig.  1. This makes multi-row layouts particularly suitable, and so the total weighted sum of the center-to-center rectilinear distances is a good measure of the total displacement of such a robot to complete a given task.

Fig. 1
figure 1

Operational setup of a gantry robot

Full size image

The MRFLP has received very limited attention in the operations research literature to date. The MRFLP was formulated as a two-dimensional continuous space allocation problem in [18], using a nonlinear optimization approach. However, in many practical problems, the departments are arranged in well-defined rows because the separation between the rows is predetermined according to the features of the material-handling system; that is, this problem can be viewed as discrete in one dimension and continuous in the other. Heuristic algorithms were proposed in [18], and a nonlinear formulation was given in [16] and solved using a genetic algorithm (GA). A GA was also proposed by [31] but they do not enforce the strict row structure as we do here. An SDP-based approach was introduced in [24], and to the best of our knowledge, this is the only global optimization approach for the general row FLP with more than two rows. However, their approach only provided lower bounds for instances with up to 9 departments.

The most recent results on the MRFLP are reported in [15, 37]. The first of these papers is specialized to the space-free version of MRFLP, while the second considers a variant of the MRFLP to handle groups of machines. The work presented here is therefore not directly comparable with either of these.

3 A new MILP formulation

In this section we present our proposed new MILP formulation for row FLPs with three or more rows. Like the models reviewed in Sect.  2 and most other mathematical optimization models in the literature, our proposed model uses binary variables to prevent overlap. Unlike most other models however, it uses continuous variables for the assignment of departments to rows, and we prove that these variables have integer values at optimality, so that departments are assigned to rows without the need for rounding or other similar operation.

We assume that we are given the following parameters: n is the number of departments; m is the maximum number of rows allowed for the layout; d is the row width; \(c_{ij}\) is the pairwise connection cost between departments i and j; \(\ell _i\) is the length of department i; and \(L=\sum _{i=1}^n \ell _i\) is the sum of the lengths of all the departments.

For each department i we use the variable \(x_i\) to represent the horizontal position of department i (within the row assigned to it), and \(y_i\) to represent the vertical position of i (the row it is assigned to). For each pair of departments i and j, we use the following binary variables to encode their relative position: \(\alpha _{ij}=1\) if i is placed to the left of j in the same row and 0 otherwise; \(\beta _{ij}=1\) if i and j are placed in different rows and i is below j, 0 otherwise. We use the total distance in our objective function, and let \(d^x_{ij}\) and \(d^y_{ij}\) equal the horizontal and vertical distances between i and j.

Using the above parameter and variable definitions, the proposed formulation for the double- and multi-row FLP is:

$$\begin{aligned} \min \quad&\sum _{1\le i<j\le n} c_{ij}(d_{ij}^x+d^y_{ij}) \end{aligned}$$
(1)
$$\begin{aligned} \text {s.t.} \quad&d_{ij}^x\ge x_i-x_j, \ d_{ij}^x\ge x_j-x_i,\ 1\le i<j\le n \end{aligned}$$
(2)
$$\begin{aligned}&d_{ij}^y\ge y_i-y_j, \ d_{ij}^y\ge y_j-y_i,\ 1\le i<j\le n \end{aligned}$$
(3)
$$\begin{aligned}&x_j-x_i\ge \frac{1}{2}(\ell _i+\ell _j)-L(1-\alpha _{ij}),\ 1\le i<j\le n, \end{aligned}$$
(4)
$$\begin{aligned}&x_i-x_j\ge \frac{1}{2}(\ell _i+\ell _j)-L(1-\alpha _{ji}),\ 1\le i<j\le n, \end{aligned}$$
(5)
$$\begin{aligned}&y_j-y_i\ge d-md(1-\beta _{ij}),\ 1\le i<j\le n, \end{aligned}$$
(6)
$$\begin{aligned}&y_i-y_j\ge d-md(1-\beta _{ji}),\ 1\le i<j\le n, \end{aligned}$$
(7)
$$\begin{aligned}&y_i-y_j \le (1-\alpha _{ij}-\alpha _{ji})(m-1)d,\ 1\le i<j\le n, \end{aligned}$$
(8)
$$\begin{aligned}&y_j-y_i\le (1-\alpha _{ij}-\alpha _{ji})(m-1)d,\ 1\le i<j\le n, \end{aligned}$$
(9)
$$\begin{aligned} \quad&0 \le y_i\le d(m-1),\ 1\le i\le n, \end{aligned}$$
(10)
$$\begin{aligned}&\frac{1}{2} \ell _i \le x_i\le L-\frac{1}{2} \ell _i,\ 1\le i\le n, \end{aligned}$$
(11)
$$\begin{aligned}&\alpha _{ij}+\alpha _{ji}+\beta _{ij}+\beta _{ji}=1,\ 1\le i<j\le n, \end{aligned}$$
(12)
$$\begin{aligned}&\alpha _{ij}+\alpha _{jk}\le 1 +\alpha _{ik},\ \beta _{ij}+\beta _{jk}\le 1 +\beta _{ik},\ 1\le i<j\le n \end{aligned}$$
(13)
$$\begin{aligned}&\alpha _{ij},\beta _{ij}\in \{0,1\},\ 1\le i,j\le n. \end{aligned}$$
(14)

Constraints (2)-(3) establish the horizontal and vertical distances between departments. Constraints (4)-(5) prevent any two departments from overlapping. Constraints (6)-(7) avoid the overlapping of rows, and simultaneously create the rows. Constraints (8) and (9) ensure that \(y_i=y_j\) when departments i and j are placed in the same row. Constraints (10) limit the number of rows to m rows (each of width d). Constraints (11) provide basic bounds on the variables \(x_i\). Constraints (12) require the separation of i and j in only one dimension (though they may be separated in both dimensions). Constraints (13) are triangle inequalities.

4 Integrality properties of the model

As mentioned above, the formulation presented in Sect.  3 uses continuous variables to represent the assignment of departments to rows. In this Section, we give the proof that we can always achieve an optimal solution with integer values for these variables, meaning that the rows are well defined.

Theorem 1

For every feasible instantiation of the variables \(\alpha _{ij}\) and \(\beta _{ij}\), i.e., which satisfy constraints (12)–(14), the matrix of the constraints (4)–(11) is totally unimodular.

Proof

Let A be the system matrix of the constraints (4)–(11). We prove that A is totally unimodular. Observe that every element in \(A^T\) is \(-1,0\) or \(+1\), this is, the coefficients of the variables \(x_i\) or \(y_i\) are \(-1,0\) or \(+1\). Since every column of \(A^T\) corresponds to the coefficients of \(x_i, x_j\) or \(y_i, y_j\) in each constraint, then it contains at most two non-zero elements. For each column of \(A^T\) with two non-zero elements, these are of opposite sign. Therefore by Proposition 2.6, chapter III.1 of [30], \(A^T\) is totally unimodular. Thus, A is also totally unimodular. The result follows. \(\square \)

Corollary 1

For every feasible instantiation of the variables \(\alpha _{ij}\) and \(\beta _{ij}\), if d is integer, the y-components of every extreme point of (4)–(11) are integer.

Proof

For integer d, the right hand side of the constraints (6)–(10) is integer. The result follows by Theorem 1. \(\square \)

5 Two-stage optimization algorithm

The exact MILP model proposed in Sect. 3 can only obtain global optimal solutions for instances with up to 13 departments. To obtain solutions for larger instances, we propose a two-stage algorithm to compute solutions but without the guarantee of global optimality.

Two-stage approaches have been successfully used for unequal-area facility layout problems, see [9]. A two-stage approach based on the attractor-repeller (AR) technique for VLSI floorplanning was introduced in [5]. The first-stage uses the Attractor-Repeller technique to establish the relative positions of the departments, and the second-stage finds a feasible layout satisfying the relative positions specified by the solution to the first-stage via a mathematical optimization model.

A nonconvex model with the repeller function \(\frac{1}{z} -1\) was proposed in [5]; this model was modified in [6] to achieve convexity, but then the addition of a new penalty term resulted again in a loss of convexity, though in a more controlled manner. Significant improvements to this approach were carried out in [25], and most recently in [8]. We follow the same ideas as in [8] with the additional improvement of an automatic strategy for adjusting the parameters.

5.1 First-stage model

The first-stage model minimizes a nonlinear and non-convex function over a box to estimate the desired relative positions of the departments. To achieve this, we relax constraints (4)-(9) and (12) and penalize overlapping in the objective function via the penalty function

$$\begin{aligned} f(t)=\frac{1}{t} -1,~t>0. \end{aligned}$$

This barrier was originally used for VLSI floorplanning in [14], further tested in that context in [5], and used in convexified form in [6] for the unequal-areas FLP and in [28] for floorplanning. It was also used without convexification or other modifications in a two-stage framework for the unequal-areas FLP in [8].

We give a short description of the technique to make this paper self-contained. The distance between departments i and j is measured with the squared Euclidean distance. \(D_{ij}^2=(x_i-x_j)^2+(y_i-y_j)^2.\) To establish a threshold for this distance a (squared) target distance between departments i and j is defined in terms of their lengths: \(T_{ij}^2 = 1/4 \left( (l_i+l_j)^2+4\right) .\) We penalize overlap using the scaled squared Euclidean distance by adding the following term to objective function:

$$\begin{aligned} f\left( \frac{D^2_{ij}}{\log T^2_{ij}}\right) . \end{aligned}$$
(15)

The idea of using \(\log T_{ij}\) (instead of \(T_{ij}\)) to scale the distance \(D_{ij}\) differs from the one presented in [8, 25]. Although it has the same role, the magnitude of the lengths of some instances is quite different (in some instances the lengths are 10 times bigger than others) and the logarithm gives some amount of uniformization to the target distance. In addition, it improves the adjusting of parameter \(\mu \). In this way, we develop a two-stage strategy where adjusting the only parameter is straightforward, as we will explain later.

The first-stage model is thus:

$$\begin{aligned} \min \quad&\sum _{1\le i<j\le n} c_{ij}D_{ij}^2+ K \sum _{1\le i<j\le n}\left( \frac{\log (T_{ij}^2)}{D_{ij}^2}-1\right) \\ \text {s.t.} \quad&0 \le y_i\le d(m-1),\ 1\le i\le n,\\&\frac{1}{2} \ell _i \le x_i\le L-\frac{1}{2} \ell _i,\ 1\le i\le n,\\ \end{aligned}$$

The objective function combines the total connectivity cost between departments, and the penalty term (15) for overlap. To appropriately balance these terms, we scale the penalty term by the parameter:

$$\begin{aligned} K = \mu 10^{-1}\sum _{1\le i<j\le n} c_{ij}, \quad \text {with} \quad 0<\mu \le 1. \end{aligned}$$
(16)

Unlike the first-stage models in [6, 25], this objective function is not convex; nevertheless we can compute local optimal solutions and if we appropriately tradeoff the connectivity cost with the overlap penalty, these solutions will give information about the relative positions between departments that are passed on to the second stage via the non-overlapping constraints, and contribute to the quality of the layouts computed by the second-stage model. The parameter \(\mu \) acts by increasing or decreasing the weight of the barrier term against the connectivity cost, in order to balance the weight of both terms in the objective function. For each value of \(\mu \), we find a local optimum of the first stage model.

Figure 2 shows a typical local optimum for the first-stage model applied to the HeKu12 benchmark problem. We allow departments to overlap because in the first-stage our objective is not to find a feasible layout but rather to obtain information about the relative positions of departments. The relative position is determined by the position of the departments’ centroids. Strict non-overlap is enforced in the second stage (Sect.  5.2).

Fig. 2
figure 2

Instance HeKu12, with \(\mu =0.193\)

Full size image

5.2 Second-stage model

The second-stage model produces a feasible layout by using the model in Sect. 3 with the binary variables fixed according to the optimal solution of the first stage. The resulting linear programming model can be efficiently solved and provides the final layout:

$$\begin{aligned} \min \quad&\sum _{1\le i<j\le n} c_{ij}(d_{ij}^x+d^y_{ij})\\ \text {s.t.} \quad&d_{ij}^x\ge x_i-x_j, \ d_{ij}^x\ge x_j-x_i,\ 1\le i<j\le n\\&d_{ij}^y\ge y_i-y_j, \ d_{ij}^y\ge y_j-y_i,\ 1\le i<j\le n\\&0 \le y_i\le d(m-1),\ 1\le i\le n,\\&\frac{1}{2} \ell _i \le x_i\le L-\frac{1}{2} \ell _i,\ 1\le i\le n,\\&\text {a subset of non-overlapping constraints from} (4)-(7). \end{aligned}$$

The constraints (4)-(7) are selected by applying the following rule to the first-stage solution. Let \(({\bar{y}}_i,{\bar{x}}_i)\) be a solution of the first-stage model. For each pair of departments i and j, if the rounded values of \({\bar{y}}_i\) and \({\bar{y}}_j\) are equal we force horizontal separation. In this case, if \({\bar{x}}_i\ge {\bar{x}}_j\) we separate these two departments horizontally, by adding the non-overlapping constraint \(x_i-x_j\ge \frac{1}{2}(l_i+l_j);\) otherwise, we add \(x_j-x_i\ge \frac{1}{2}(l_i+l_j).\) For each pair of departments i and j, if the rounded values of \({\bar{y}}_i\) and \({\bar{y}}_j\) are different we force vertical separation. In this case, if \(\bar{y}_i\ge {\bar{y}}_j\) we add constraint \(y_i-y_j\ge d\); otherwise we add \(y_j-y_i\ge d\).

The strategy of rounding the row position variables works well, which is concordant with Corollary 1.

5.3 Two-stage optimization algorithm

The two-stage optimization algorithm (2SOA) that we propose is directly based on the two-stage optimization framework presented in [8]. However, we give here a straightforward way of setting the parameter \(\mu \), which allows the algorithm to tune itself automatically for every instance.

The data of instances vary significantly, for example the length of the largest department for instance KeHu12 is 80, while for instance HuAn13 is 10. Therefore, it would be difficult to tune the parameter \(\mu \) homogenously, i.e., keeping the same small interval for \(\mu \), independently of the instance data. To this matter, instead of scaling \(D_{ij}\) with \(T_{ij}\), we scaled with \(\log T_{ij}\) and we were able to empirically prove that the best layouts are obtained with \(\mu \) varying between 0 and 1. Thus, in 2SOA we take values of \(\mu \) as a finite set of values between 0 and 1, and choose the best layout among all those obtained. Specifically, we consider \(\mu \in G=\{0.001+0.001i\ | i=0,1,\dots ,999 \}\).

An explicit statement of the algorithm follows.

figure a

For each instance the interval for values of \(\mu \) can be specialized and made shorter. Figures 3 and 4 show the layouts obtained by the first-stage model for the smallest and the largest values of \(\mu \). Note that the departments’ centroids almost coincide in Fig.  3, therefore the value of \(\mu \) should be increased. On the other hand, Fig. 4 shows departments being pushed apart, as they seem to need fewer rows, therefore \(\mu \) should be reduced.

Fig. 3
figure 3

HeKu12, \(\mu =0.001\)

Full size image
Fig. 4
figure 4

HeKu12, \(\mu =1\)

Full size image

After running 2SOA, we can visualize the solutions obtained using a graph of the layout cost versus the corresponding value of \(\mu \), as shown in Fig. 5. While this curve has large jumps, a sub-interval of (0, 1] can typically be identified where the smallest cost layouts are obtained. One can them run 2SOA using only this sub-interval to search for better layouts.

Fig. 5
figure 5

Layout costs versus \(\mu \)

Full size image

6 Computational results for the two-stage algorithm

In this section, we report our computational results using 2SOA. We implemented the new formulation in (3) using the modeling language AMPL and solved them using CPLEX (version 12.5.1.0). We tested the proposed algorithm using the nonlinear optimization solver SNOPT 7.2-8 for the first-stage model, and the solver CPLEX 12.5.1.0 for the second-stage model, both accessed via the modeling language AMPL. The computations were performed on a dual core Intel(R) Xeon(R) X5675 @ 3.07 GHz with 12 Gb of memory.

Table 1 2SOA results for small instances
Full size table

We start by comparing its results for small instances, where the optimal solutions are obtained using the MILP model. After this, we analyze the behaviour of the algorithm for large instances. All the results were obtained using the default set \(G=\{0.001+0.001i\ | i=0,1,\dots ,999 \}\) for the values of \(\mu \).

The algorithm is able to find solutions for instances up to size 13, in less than 600 s. All the solutions are within \(10\%\) or less of the corresponding optimal values. Moreover, more than half of the solutions are within \(5\%\), as shown by the results emphasized in bold in Table 1 (the number of departments is indicated in the instance name). For small instances, as the size increases, the MILP model requires an increasing amount of computational time to obtain the optimal solutions. On the other hand, for small instances, the proposed algorithm obtains solutions close to the optimum and the computational time is in general stable. These results demonstrate that the 2SOA is able to quickly compute solutions within a small gap of global optimality. More importantly, we see that the gaps do not seem to increase with increasing problem size. Thus, these results provide us with confidence that the 2SOA may be able to reach good solutions for larger instances, for which not even lower bounds can be computed. Such large instances are considered next.

We further tested 2SOA on the set of large instances \((n\ge 14)\) which is presented in Table 2. We obtained solutions for instances with up to 100 departments in less than 40 min per instance. More precisely, for the largest instance sko100-05, we obtained a solution arranged within 7 rows in 2352.8 s.

Table 2 2SOA results for medium- and large-size instances
Full size table

7 Conclusion

In this paper, we consider the special case of multi-row layout in which all the departments are to be placed in several rows, as happens for example in the context of flexible manufacturing and in the design of application-specific integrated circuits. We proposed a new mixed integer linear programming formulation with the interesting property that the optimal solutions achieve integer row assignments even though the corresponding variable in the model is continuous.

To address larger instances, we proposed a two-stage optimization algorithm that combines two mathematical optimization models by taking the output of the first-stage model as the input of the second-stage model. Our computational tests suggest that this new algorithm finds, for the first time, solutions for instances with up to 100 departments.