1 Introduction

Bi-disperse convection is the analysis of the onset of convection in dual porosity materials, called bi-disperse porous media. A bi-disperse porous medium (BDPM) is a material characterized by two types of pores called macropores—with porosity \(\phi \)—and micropores—with porosity \(\epsilon \). Therefore, \((1-\phi ) \epsilon \) is the fraction of volume occupied by the micropores, \(\phi + (1- \phi ) \epsilon \) is the fraction of volume occupied by the fluid, \((1- \epsilon )(1-\phi )\) is the fraction of volume occupied by the solid skeleton. In particular, the macropores are referred to as f-phase (fractured phase), while the remainder of the structure is referred to as p-phase (porous phase). The first refined mathematical model describing the onset of bi-disperse convection was proposed by Nield and Kuznetsov in [1,2,3], where the authors analysed the onset of convection in a horizontal layer of BDPM saturated by a non-isothermal incompressible fluid heated from below, proposing a model with two seepage velocities \({\textbf {v}}^f\) and \({\textbf {v}}^p\), two pressures \(p^f\) and \(p^p\) and two temperature fields \(T^f\) and \(T^p\). Nield and Kuznetsov proved that the critical Rayleigh number for the onset of bi-disperse convection is higher with respect to the critical Rayleigh number for the single porosity case, therefore dual porosity materials are better suited for insulation problems and thermal management problems. Hence, bi-disperse porous materials offer much more possibilities to design man-made materials for heat transfer problems and for this reason the onset of bi-disperse convection has recently attracted the attention of many researchers [4,5,6]. In this paper, we will focus the attention on single-temperature bi-disperse porous media (i.e. \(T^f=T^p\)), since a single-temperature model may suffice to represent many real situations and the resulting mathematical model is consistent with experiments related to heat transfer and thermal dispersion in bi-disperse porous media [7, 8].

The relevance of the analysis of non-isothermal steady flow of fluids through porous materials called throughflow is due to the effect that such flow has on convective instabilities. When a vertical net mass flow (throughflow) is present across a horizontal layer heated from below, the problem to determine until this motion is stable is of fundamental importance, due to the possibility of controlling the convective instabilities by adjusting the strength of the throughflow, especially in applications involving cloud physics, hydrological/geophysical studies, seabed hydrodynamics, subterranean pollution, and many industrial and technological processes [9,10,11]. Keeping in mind these applications, the use of dual porosity materials for thermal management problems and the relevance of regulating convective instabilities for thermal and engineering sciences, in this paper the onset of convective instability in a fluid-saturated bi-disperse porous layer heated from below is analysed, assuming that there is a vertical net mass flow across the layer. The paper is organized as follows. In Sect. 2 the mathematical model is presented, along with the equations governing the evolutionary behaviour of the perturbation to the throughflow solution. In Sect. 3 the linear instability analysis of the throughflow solution is performed, in order to find the instability threshold for the onset of convective instabilities and the effect of the vertical constant throughflow on the instability threshold is numerically analysed. In Sect. 4, the nonlinear stability analysis of the throughflow solution is performed via the differential constraints approach and the weighted energy method in order to catch the method that better describes the physics of the problem. Via numerical simulations, the stability thresholds are compared to the instability ones and analysed as functions of the Peclet number. Section 5 is a concluding section that recaps the obtained results.

2 Mathematical model

Introducing a reference frame Oxyz with fundamental unit vectors \(\textbf{i},\textbf{j},\textbf{k}\) (\(\textbf{k}\) pointing vertically upward), let us consider a plane layer \(L=\mathbb {R}^2 \times [0,d]\) of bi-disperse porous medium saturated by a non-isothermal fluid and uniformly heated from below. Let us employ a single temperature bi-disperse porous medium, i.e. \(T^f=T^p=T\). A Oberbeck-Boussinesq approximation is assumed: the fluid density \(\rho \) is constant in all terms of the governing equations, except in the body force term (due to the gravity \(\textbf{g}=-g \textbf{k}\)), where we choose a linear dependence on temperature, i.e. \(\rho =\rho _0[1-\alpha (T-T_0)]\), \(\alpha \) being the thermal expansion coefficient and \(\rho _0\) being the constant fluid density at the reference temperature \(T_0\). Let us underline that this assumption is experimentally and thermodynamically consistent if \( p \ll p_{CR}=\dfrac{c_p \rho _0}{\alpha },\) p being the pressure field, while \(c_p\) is the specific heat at constant pressure. In particular, in [12] the authors proved that if \(p \ll p_{CR}\), the Oberbeck-Boussinesq approximation is compatible with the entropy principle. Therefore, the governing equations, according to the Darcy’s model, are, cf. [8],

$$\begin{aligned} {\left\{ \begin{array}{ll} - \dfrac{\mu }{K_f} \textbf{v}^f - \zeta (\textbf{v}^f \! - \! \textbf{v}^p) \! - \! \nabla p^f \! + \! \rho _0 \alpha g T \textbf{k} = {\textbf {0}}, \\ - \dfrac{\mu }{K_p} \textbf{v}^p - \zeta (\textbf{v}^p \! - \! \textbf{v}^f) \! - \! \nabla p^p \! + \! \rho _0 \alpha g T \textbf{k} = {\textbf {0}}, \\ \nabla \cdot \textbf{v}^f = 0, \\ \nabla \cdot \textbf{v}^p = 0, \\ (\rho c)_m \dfrac{\partial T}{\partial t} + (\rho c)_f (\textbf{v}^f + \textbf{v}^p) \cdot \nabla T = k_m \Delta T, \end{array}\right. } \end{aligned}$$
(1)

where \(\textbf{x}=(x,y,z)\), T is the temperature field, \(p^s\) and \(\textbf{v}^s\) are pressure field and seepage velocity for \(s=\{f,p\}\), respectively, \(\zeta \) is the interaction coefficient between the f-phase and the p-phase, \(\mu \) is the fluid viscosity, \(K_s\) are the permeabilities for \(s=\{f,p\}\), \(k_m\) is the thermal conductivity, respectively. Moreover, \((\rho c)_m=(1-\phi )(1-\epsilon )(\rho c)_{sol}+\phi (\rho c)_f+\epsilon (1-\phi )(\rho c)_p\), \(k_m=(1-\phi )(1-\epsilon )k_{sol}+\phi k_f+\epsilon (1-\phi )k_p\) (the subscript sol is referred to the solid skeleton). Since we are confining ourselves in the case of a single temperature BDPM and macropores and micropores are saturated by the same fluid, we expect \((\rho c)_f\) and \((\rho c)_p\) to be the same, hence \((\rho c)_m=(1-\phi )(1-\epsilon )(\rho c)_{sol}+[\phi +\epsilon (1-\phi )](\rho c)_f\), see [13].

We are interested in the stability analysis of a vertical throughflow present across the layer L, therefore to (1) we append the following boundary conditions

$$\begin{aligned} {\textbf {v}}^s = Q^s {\textbf {k}}, \ \text {on} \ z=0,d \quad \text {for} \ s=\{f,p \}, \quad T=T_L \ \text {on} \ z=0, \ T=T_U \ \text {on} \ z=d \end{aligned}$$
(2)

where \(T_L>T_U\), since the layer is heated from below, and \(Q^s\) are constants (\(s=\{f,p \}\)).

The steady constant non-isothermal fluid flow solution to (1)–(2) called throughflow is given by

$$\begin{aligned} \begin{aligned}&\bar{{\textbf {v}}}^f=Q^f {\textbf {k}}, \quad \bar{{\textbf {v}}}^p=Q^p {\textbf {k}}, \quad \bar{T}=\dfrac{T_U - T_L e^{\bar{Q}d/k} + (T_L-T_U) e^{\bar{Q}z/k}}{1-e^{\bar{Q}d/k}} \end{aligned} \end{aligned}$$
(3)

where \(\bar{Q}=Q^f+Q^p\), while \(k=\frac{k_m}{(\rho c)_f}\) is the thermal diffusivity. Let us introduce a generic perturbation \(\{ \textbf{u}^f, \textbf{u}^p, \theta , \gamma , \pi ^f, \pi ^p \}\) to the throughflow solution, with \(\textbf{u}^f=(u^f,v^f,w^f)\) and \(\textbf{u}^p=(u^p,v^p,w^p)\). The equations describing the behaviour of the perturbations fields are

$$\begin{aligned} {\left\{ \begin{array}{ll} - \dfrac{\mu }{K_f} \textbf{u}^f - \zeta (\textbf{u}^f - \textbf{u}^p) - \nabla \pi ^f + \rho _0 \alpha g \theta \textbf{k} = \textbf{0}, \\ - \dfrac{\mu }{K_p} \textbf{u}^p - \zeta (\textbf{u}^p - \textbf{u}^f) - \nabla \pi ^p + \rho _0 \alpha g \theta \textbf{k} = \textbf{0}, \\ \nabla \cdot \textbf{u}^f = 0, \\ \nabla \cdot \textbf{u}^p = 0, \\ (\rho c)_m \dfrac{\partial \theta }{\partial t} + (\rho c)_f (\textbf{u}^f {+} \textbf{u}^p) \cdot \nabla \theta {=} \,{-}(\rho c)_f (w^f+w^p) \dfrac{\partial \bar{T}}{\partial z} {-} (\rho c)_f \bar{Q} \dfrac{\partial \theta }{\partial z} {+} k_m \Delta \theta , \end{array}\right. } \end{aligned}$$
(4)

under the boundary conditions

$$\begin{aligned} w^f=w^p=\theta =0, \quad \text {on} \ z=0,d. \end{aligned}$$
(5)

To derive the dimensionless perturbation equations, we introduce the following non-dimensional parameters:

$$\begin{aligned}{} & {} \textbf{x}^{*} = \dfrac{\textbf{x}}{d}, \ t^{*}=\dfrac{t}{t^{\#}}, \ \theta ^{*} = \dfrac{\theta }{T^{\#}}, \ \gamma _1=\dfrac{\mu }{K_f \zeta }, \ \gamma _2=\dfrac{\mu }{K_p \zeta }, \ \textbf{u}^{s*} = \dfrac{\textbf{u}^s}{U}, \ \pi ^{s*} = \dfrac{\pi ^s}{P^{\#}}, \text {for} \ s=\{ f,p \} \end{aligned}$$

with the following scales

$$\begin{aligned} U=\frac{\zeta k_m}{(\rho c)_f d}, \ t^{\#} = \frac{d^2 (\rho c)_m}{k_m}, \ P^{\#} = \frac{k_m \zeta }{(\rho c)_f}, \ T^{\#} = \sqrt{\frac{\beta k_m \zeta }{(\rho c)_f \rho _0 \alpha g}}, \end{aligned}$$

and define the Darcy-Rayleigh number \(\mathcal {R}\) and the Peclet number Pe as

$$\begin{aligned} \mathcal {R}= \sqrt{ \dfrac{\beta d^2 (\rho c)_f \rho _0 \alpha g}{\zeta k_m}}, \qquad Pe = \dfrac{\bar{Q} d}{k}. \end{aligned}$$

The dimensionless equations governing the perturbation fields, dropping the asterisks, are

$$\begin{aligned} {\left\{ \begin{array}{ll} - \gamma _1 \textbf{u}^f - (\textbf{u}^f - \textbf{u}^p) - \nabla \pi ^f + \mathcal {R}\theta \textbf{k} = \textbf{0}, \\ - \gamma _2 \textbf{u}^p - (\textbf{u}^p - \textbf{u}^f) - \nabla \pi ^p + \mathcal {R}\theta \textbf{k} = \textbf{0}, \\ \nabla \cdot \textbf{u}^f = 0, \\ \nabla \cdot \textbf{u}^p = 0, \\ \dfrac{\partial \theta }{\partial t} + (\textbf{u}^f + \textbf{u}^p) \cdot \nabla \theta = -\mathcal {R}f(z) (w^f+w^p) - Pe \dfrac{\partial \theta }{\partial z} + \Delta \theta , \end{array}\right. } \end{aligned}$$
(6)

where

$$\begin{aligned} f(z)=\dfrac{Pe \ e^{Pe z}}{1-e^{Pe}} \end{aligned}$$

is the dimensionless basic temperature gradient.

Remark 1

Due to the specific non-dimensionalization we used, as \(Pe\rightarrow 0\) (which is equivalent to consider the conduction solution in a bi-disperse layer), all singularities are removable, allowing (6) to tend to the standard system where no throughflow is present (see [8]). This follows as, utilizing De L’Hospital’s rule, one gets

$$\begin{aligned} \lim _{Pe \rightarrow 0} f(z) = -1. \end{aligned}$$

The initial conditions and the boundary conditions appended to system (6) are

$$\begin{aligned} \textbf{u}^s(\textbf{x},0)=\textbf{u}^s_0(\textbf{x}), \quad \pi ^s(\textbf{x},0)=\pi ^s_0(\textbf{x}), \quad \theta (\textbf{x},0)=\theta _0(\textbf{x}), \end{aligned}$$

with \(\nabla \cdot \textbf{u}^s_0=0\), for \(s=\{f,p\}\), and

$$\begin{aligned} w^f=w^p=\theta =0 \quad \text {on} \ z=0,1, \end{aligned}$$
(7)

respectively. According to experimental results, we will assume that \(\textbf{u}^s,\theta \in W^{1,2}(V), \ \forall t \in \mathbb {R}^{+}\), with \(s=\{f,p\}\), are periodic functions in the (x, y) directions of period \(2 \pi / l\) and \(2 \pi / m\), \(V=\Big [ 0,\frac{2 \pi }{l} \Big ] \times \Big [ 0,\frac{2 \pi }{m} \Big ] \times [0,1]\) being the periodicity cell.

Let us consider the third components of the double curl of the momentum equations (6)\(_1\) and (6)\(_2\), hence the linear and the nonlinear stability analyses of the throughflow solution will be performed on the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} (1+ \gamma _1) \Delta w^f - \Delta w^p - \mathcal {R}\Delta _1 \theta = 0, \\ - \Delta w^f + (1+ \gamma _2) \Delta w^p - \mathcal {R}\Delta _1 \theta = 0, \\ \nabla \cdot \textbf{u}^f = 0, \\ \nabla \cdot \textbf{u}^p = 0, \\ \dfrac{\partial \theta }{\partial t} + (\textbf{u}^f + \textbf{u}^p) \cdot \nabla \theta = -\mathcal {R}f(z) (w^f+w^p) - Pe \dfrac{\partial \theta }{\partial z} + \Delta \theta , \end{array}\right. } \end{aligned}$$
(8)

where \(\Delta _1=\partial ^2/ \partial x^2 + \partial ^2/ \partial y^2\) is the horizontal Laplacian.

3 Linear instability analysis

Since system (6) is autonomous, let us seek for perturbed solutions with exponential time dependence (i.e. \(e^{\sigma t}\), \(\sigma \in \mathbb {C}\) being the growth rate of the system) in the linearised perturbations system. Therefore, the linear instability threshold is to recover from the analysis of the linearised version of system (8), i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} (1+ \gamma _1) \Delta w^f - \Delta w^p - \mathcal {R}\Delta _1 \theta = 0, \\ - \Delta w^f + (1+ \gamma _2) \Delta w^p - \mathcal {R}\Delta _1 \theta = 0, \\ \sigma \theta = -\mathcal {R}f(z) (w^f+w^p) - Pe \dfrac{\partial \theta }{\partial z} + \Delta \theta , \end{array}\right. } \end{aligned}$$
(9)

under the boundary conditions \(w^f=w^p=\theta =0\) on \(z=0,1\). System (9) is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta w^f = \dfrac{2+\gamma _2}{\gamma _1+\gamma _2+\gamma _1 \gamma _2} \mathcal {R}\Delta _1 \theta , \\[3mm] \Delta w^p = \dfrac{2+\gamma _1}{\gamma _1+\gamma _2+\gamma _1 \gamma _2} \mathcal {R}\Delta _1 \theta , \\[3mm] \sigma \theta = -\mathcal {R}f(z) (w^f+w^p) - Pe \dfrac{\partial \theta }{\partial z} + \Delta \theta . \end{array}\right. } \end{aligned}$$
(10)

Let us denote by \(<\cdot ,\cdot>\), \(\Vert \cdot \Vert \) and \(^*\), inner product and norm on the Hilbert space \(L^2(V)\) and the complex conjugate of a field, respectively.

Theorem 1

The principle of exchange of stabilities holds for system (7)–(10), therefore convective instabilities can arise only through steady motions.

Proof

Let us employ the following transformation

$$\begin{aligned} \theta =e^{\frac{Pe}{2}z} \Phi \end{aligned}$$
(11)

in system (10), which becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta w^f = \mathcal {R}\ c_1 e^{\frac{Pe}{2}z} \Delta _1 \Phi , \\ \Delta w^p = \mathcal {R}\ c_2 e^{\frac{Pe}{2}z} \Delta _1 \Phi , \\ \sigma e^{\frac{Pe}{2}z} \Phi = -\mathcal {R}f(z) (w^f+w^p) - \dfrac{Pe^2}{4} e^{\frac{Pe}{2}z} \Phi + e^{\frac{Pe}{2}z} \Delta \Phi , \end{array}\right. } \end{aligned}$$
(12)

where we set \(c_1=\dfrac{2+\gamma _2}{\gamma _1+\gamma _2+\gamma _1 \gamma _2}\) and \(c_2=\dfrac{2+\gamma _1}{\gamma _1+\gamma _2+\gamma _1 \gamma _2}\). Employing the periodicity of the perturbation fields in the horizontal directions x and y and according to the boundary conditions (7), we can assume the solutions be two-dimensional periodic waves of assigned wavenumber:

$$\begin{aligned} \phi (x,y,z)= \bar{\phi }(z) e^{ i(lx+my)} \quad \forall \phi \in \{ w^f,w^p,\Phi \}. \end{aligned}$$
(13)

Since \(f(z)=\displaystyle \frac{Pe \ e^{Pe z}}{1-e^{Pe}}\), by virtue of (13), we get

$$\begin{aligned} {\left\{ \begin{array}{ll} (D^2- a^2) \bar{w}^f = -c_1 \mathcal {R}\ a^2 e^{\frac{Pe}{2}z} \bar{\Phi }, \\ (D^2- a^2) \bar{w}^p = -c_2 \mathcal {R}\ a^2 e^{\frac{Pe}{2}z} \bar{\Phi }, \\ \sigma e^{\frac{Pe}{2}z} \bar{\Phi } = - \mathcal {R}\dfrac{Pe}{1-e^{Pe}} e^{Pe z} (\bar{w}^f+\bar{w}^p) - \dfrac{Pe^2}{4} e^{\frac{Pe}{2}z} \bar{\Phi } + e^{\frac{Pe}{2}z} (D^2-a^2) \bar{\Phi }, \end{array}\right. } \end{aligned}$$
(14)

where \(D=\frac{d}{dz}\), while \(a^2=l^2+m^2\) is the overall wavenumber. Multiplying (14)\(_3\) by \(e^{-\frac{Pe}{2}z}\), we get

$$\begin{aligned} \sigma \bar{\Phi } = - \mathcal {R}\dfrac{Pe}{1-e^{Pe}} e^{\frac{Pe}{2}z} (\bar{w}^f+\bar{w}^p) - \dfrac{Pe^2}{4} \bar{\Phi } + (D^2-a^2) \bar{\Phi }. \end{aligned}$$
(15)

Let us multiply (14)\(_1\) by \(\bar{w}^{f*}\), (14)\(_2\) by \(\bar{w}^{p*}\), (15) by \(\bar{\Phi }^{*}\) and let us integrate the resulting equations over [0, 1], hence we obtain

$$\begin{aligned} \begin{aligned} \frac{1}{c_1} \left( \Vert D \bar{w}^f \Vert ^2_{L^2(0,1)} + a^2 \Vert \bar{w}^f \Vert ^2_{L^2(0,1)} \right) =&\,\mathcal {R}\ a^2 \int _0^1 e^{\frac{Pe}{2}z} \bar{\Phi } \bar{w}^{f*} \ dz, \\ \frac{1}{c_2} \left( \Vert D \bar{w}^p \Vert ^2_{L^2(0,1)} + a^2 \Vert \bar{w}^p \Vert ^2_{L^2(0,1)} \right) =&\,\mathcal {R}\ a^2 \int _0^1 e^{\frac{Pe}{2}z} \bar{\Phi } \bar{w}^{p*} \ dz, \\ \sigma \Vert \bar{\Phi } \Vert ^2_{L^2(0,1)} =&\,- \mathcal {R}\dfrac{Pe}{1-e^{Pe}} \int _0^1 e^{\frac{Pe}{2}z} \bar{\Phi }^* (\bar{w}^f+\bar{w}^{p}) \ dz \\ {}&- \frac{Pe^2}{4} \Vert \bar{\Phi } \Vert ^2_{L^2(0,1)} \\ {}&-( \Vert D \bar{\Phi } \Vert ^2_{L^2(0,1)} +a^2 \Vert \bar{\Phi } \Vert ^2_{L^2(0,1)}). \end{aligned}\nonumber \\ \end{aligned}$$
(16)

By virtue of (16)\(_{1,2}\) one has that \(\int _0^1 e^{\frac{Pe}{2}z} \bar{\Phi }^* (\bar{w}^f+\bar{w}^{p}) \ dz \in \mathbb {R}\), therefore from (16)\(_{3}\) it follows \(Im(\sigma ) \Vert \bar{\Phi } \Vert ^2_{L^2(0,1)}=0 \ \Rightarrow \ Im(\sigma )=0\), i.e. \( \sigma \in \mathbb {R}\). \(\square \)

Let us assume \(\sigma =0\) in (10). Using solutions (13) in system (10), one obtains

$$\begin{aligned} {\left\{ \begin{array}{ll} D^2 \bar{w}^f = a^2 \bar{w}^f - c_1 \mathcal {R}\ a^2 \bar{\theta }, \\ D^2 \bar{w}^p = a^2 \bar{w}^p - c_2 \mathcal {R}\ a^2 \bar{\theta }, \\ D^2 \bar{\theta } = a^2 \bar{\theta } + Pe \ D \bar{\theta } + \mathcal {R}\ f(z) (\bar{w}^f+\bar{w}^p). \end{array}\right. } \end{aligned}$$
(17)

In order to find the instability threshold for the onset of steady convective instabilities, that is

$$\begin{aligned} \mathcal {R}_L = \min _{a^2 \in \mathbb {R}^+} \{ \mathcal {R}^2(a^2) \vert \mathcal {R}^2 \ \text {verifies} \ (17) \}, \end{aligned}$$
Fig. 1
figure 1

\(\gamma _1=2,\gamma _2=0.2\). Stationary instability threshold as function of the Peclet number Pe

Full size image
Fig. 2
figure 2

\(\gamma _1=2,\gamma _2=0.2\) a Stationary instability thresholds for positive quoted values of the Peclet number Pe. b Stationary instability thresholds for negative quoted values of the Peclet number Pe

Full size image

system (17) needs to be solved. Let us underline that (7)–(17) is a boundary value problem of second order ODEs in the variable z and it has been numerically solved via MatLab software, employing a user-written code based on a combination of the Shooting Method and the Newton–Raphson Method.

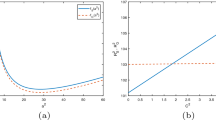
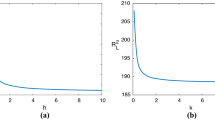
The overall behaviour of the steady instability threshold as function of the Peclet number is shown in Fig. 1. Solving the boundary value problem (7)–(17) for quoted values of the Peclet number, we obtain the thresholds depicted in Fig. 2: in Fig. 2a the thresholds are plotted for \(Pe>0\) and it is shown the stabilizing effect of a vertical constant upward throughflow on system dynamics, while the thresholds in Fig. 2b are depicted for \(Pe<0\) and show that a vertical constant downward throughflow has a destabilizing effect on system dynamics.

Finally, in Fig. 3 the convective rolls and the isotherms are plotted for quoted value of the Peclet number. As \(\vert Pe \vert \) increases, the convective rolls lose the symmetry that characterizes the limit case \(Pe \rightarrow 0\). In particular, for high positive Peclet numbers, we can observe a progressive detachment of the kinematic and temperature fields from the lower surface, hence the convective motion is confined near the surface toward which the throughflow is directed. Similarly, for high negative Peclet numbers, there is a detachment of the kinematic and temperature fields from the upper surface.

Fig. 3
figure 3

\(\gamma _1=2,\gamma _2=0.2\) Convective rolls and isotherms for quoted value of the Peclet number

Full size image

4 Nonlinear stability analysis

The aim of this Section is to analyse the stability of the throughflow solution (3) considering the full nonlinear system (8).

4.1 Differential constraint approach

In the present Section the differential constraint approach (see [14]) will be applied to system (8). Therefore, retaining (8)\(_{1,2}\) as constraints, let us define

$$\begin{aligned} \begin{aligned} \hat{E}&= \frac{1}{2} \Vert \theta \Vert ^2, \quad \\ \hat{I}&= -<f(z)(w^f+w^p),\theta >, \quad \hat{D}&= \Vert \nabla \theta \Vert ^2, \end{aligned} \end{aligned}$$
(18)

therefore, multiplying (8)\(_5\) by \(\theta \) and integrating over the periodicity cell V, we get

$$\begin{aligned} \dfrac{d \hat{E}}{dt} = \mathcal {R}\hat{I} - \hat{D} \le - \hat{D} \left( 1-\frac{\mathcal {R}}{\mathcal {R}_N} \right) , \end{aligned}$$
(19)

where

$$\begin{aligned} \frac{1}{\mathcal {R}_N} = \max _{\mathcal {H}^{*}} \frac{\hat{I}}{\hat{D}} \end{aligned}$$
(20)

and

$$\begin{aligned} \begin{aligned} \mathcal {H}^{*} = \{&(w^f,w^p,\theta ) \in (H^1)^3 | w^f=w^p=\theta =0 \ \text {on} \ z=0,1; \text {periodic in} \ x,y \\ {}&\text {with periods} \ 2 \pi /l, 2 \pi /m;\hat{D}<\infty ; \text {verifying} \ (8)_{1,2} \}. \end{aligned} \end{aligned}$$

Remark 2

Let us observe that the boundedness of \( \frac{\hat{I}}{\hat{D}}\) in \(\mathcal {H}^{*}\) is guaranteed by (8)\(_{1}\) and (8)\(_{2}\). In fact, multiplying (8)\(_{1}\) and (8)\(_{2}\) by \(w^f\) and \(w^p\), respectively, integrating over the periodicity cell and adding the resulting equations, we get

$$\begin{aligned} c_P \left( \gamma _1 \Vert w^f \Vert ^2 + \gamma _2 \Vert w^p \Vert ^2 \right) \le \mathcal {R}^2 \Bigl ( \frac{1}{\gamma _1} + \frac{1}{\gamma _2} \Bigr ) \Vert \theta \Vert ^2, \end{aligned}$$
(21)

where the arithmetic–geometric mean, the Cauchy-Schwartz and the Poincaré inequalities were used, and where \(c_P(V)\) is the Poincaré constant. Accounting for the definitions of \(\hat{I}\) and \(\hat{D}\) and since f(z) is bounded in [0, 1], by virtue of (21) it immediately follows that the ratio \( \frac{\hat{I}}{\hat{D}}\) is bounded in \(\mathcal {H}^{*}\).

The variational problem (20) is actually equivalent to

$$\begin{aligned} \frac{1}{\mathcal {R}_N}= \max _{\mathcal {H}} \frac{\hat{I} + \int _V \lambda ^{'} f_1 \ dV + \int _V \lambda ^{''} f_2 \ dV }{\hat{D}}, \end{aligned}$$
(22)

where \(\lambda ^{'}(\textbf{x})\) and \(\lambda ^{''}(\textbf{x})\) are suitable Lagrange multipliers and

$$\begin{aligned} \begin{aligned} f_1&= (1+ \gamma _1) \Delta w^f - \Delta w^p - \mathcal {R}\Delta _1 \theta , \quad f_2&= - \Delta w^f + (1+ \gamma _2) \Delta w^p - \mathcal {R}\Delta _1 \theta , \end{aligned} \\ \begin{aligned} \mathcal {H} = \{&(w^f,w^p,\theta ) \in (H^1)^3 | w^f=w^p=\theta =0 \ \text {on} \ z=0,1; \text {periodic in} \ x,y \\ {}&\text {with periods} \ 2 \pi /l, 2 \pi /m, \ \text {respectively}; \hat{D} < \infty \}. \end{aligned} \end{aligned}$$

Theorem 2

Condition \(\mathcal {R}< \mathcal {R}_N\) guarantees the global, nonlinear, asymptotic, exponential stability in the \(\hat{E}\)-norm of the throughflow solution (3).

Proof

Applying the Poincaré inequality one obtains that \(\hat{D} \ge \pi ^2 \Vert \theta \Vert ^2\), hence from the energy equation (19) it follows that the condition \(\mathcal {R}<\mathcal {R}_N\) implies \(\hat{E}(t) \rightarrow 0\) at least exponentially. Moreover, multiplying the momentum equations (6)\(_{1}\) and (6)\(_{2}\) by the kinematic fields \({\textbf {u}}^f\) and \({\textbf {u}}^p\), integrating over the periodicity cell and adding the resulting equations, by virtue of the arithmetic–geometric mean inequality and Cauchy-Schwartz inequality we get

$$\begin{aligned} \gamma _1 \Vert {\textbf {u}}^f \Vert ^2 + \gamma _2 \Vert {\textbf {u}}^p \Vert ^2 \le \mathcal {R}^2 \Bigl ( \frac{1}{\gamma _1} + \frac{1}{\gamma _2} \Bigr ) \Vert \theta \Vert ^2. \end{aligned}$$
(23)

Therefore, by virtue of estimate (23), we can conclude that condition \(\mathcal {R}<\mathcal {R}_N\) guarantees the exponential stability of the throughflow solution with respect to the \(\hat{E}\)-norm. \(\square \)

The Euler-Lagrange equations associated to the maximum problem (22) are

$$\begin{aligned} {\left\{ \begin{array}{ll} (1+ \gamma _1) \Delta w^f - \Delta w^p - \mathcal {R}_N \Delta _1 \theta = 0, \\ - \Delta w^f + (1+ \gamma _2) \Delta w^p - \mathcal {R}_N \Delta _1 \theta = 0, \\ -\mathcal {R}_N f(z) (w^f+w^p) -\mathcal {R}_N^2 \Delta _1( \lambda ^{'} + \lambda ^{''}) +2 \Delta \theta =0, \\ -f(z) \theta +(1+\gamma _1) \Delta \lambda ^{'} - \Delta \lambda ^{''} =0, \\ -f(z) \theta -\Delta \lambda ^{'} + (1+\gamma _2) \Delta \lambda ^{''}=0. \end{array}\right. } \end{aligned}$$
(24)

Assuming solutions (13) in (24), we obtain

$$\begin{aligned} {\left\{ \begin{array}{ll} D^2 \bar{w}^f = a^2 \bar{w}^f - c_1 \mathcal {R}_N a^2 \bar{\theta }, \\[1.5mm] D^2 \bar{w}^p = a^2 \bar{w}^p - c_2 \mathcal {R}_N a^2 \bar{\theta }, \\[1.5mm] D^2 \bar{\theta } = a^2 \bar{\theta } + \dfrac{\mathcal {R}_N}{2} f(z) (\bar{w}^f+\bar{w}^p) - \dfrac{\mathcal {R}_N^2}{2} a^2 (\bar{\lambda }^{'}+\bar{\lambda }^{''}), \\[1.5mm] D^2 \bar{\lambda }^{'} = a^2 \bar{\lambda }^{'} + c_1 f(z) \bar{\theta }, \\[1.5mm] D^2 \bar{\lambda }^{''} = a^2 \bar{\lambda }^{''} + c_2 f(z) \bar{\theta }. \end{array}\right. } \end{aligned}$$
(25)

The critical nonlinear threshold \(\mathcal {R}_N\) has been numerically found solving the boundary value problem (7)–(25), employing the same technique described in the previous Section. In the following numerical simulations, our results were tested for the dimensionless physical parameters \(\gamma _1=2\) and \(\gamma _2=0.2\) (see [15, 16]). In Fig. 4 the linear instability threshold \(\mathcal {R}_L\) and the nonlinear stability threshold with respect to \(\hat{E}\)-norm \(\mathcal {R}_N\) are depicted for quoted values of the Peclet number (for \(Pe \rightarrow 0\) in 4a and for \(Pe=3\) in 4b). For \(Pe \rightarrow 0\) the coincidence between \(\mathcal {R}_L\) and \(\mathcal {R}_N\) is recovered, but as \(\vert Pe \vert \) increases, the gap between the linear threshold and the nonlinear threshold increases, as clearly depicted in Fig. 5, where the instability threshold \(\mathcal {R}_L\) and the nonlinear stability threshold \(\mathcal {R}_N\) are plotted as functions of the Peclet number Pe.

Fig. 4
figure 4

a \(\mathcal {R}_L\) and \(\mathcal {R}_N\) for \(Pe=0\) and \(\gamma _1=2,\gamma _2=0.2\). b \(\mathcal {R}_L\) and \(\mathcal {R}_N\) for \(Pe=3\) and \(\gamma _1=2,\gamma _2=0.2\)

Full size image
Fig. 5
figure 5

Linear instability threshold \(\mathcal {R}_L\), nonlinear stability threshold \(\mathcal {R}_N\) as function of the Peclet number Pe, for \(\gamma _1=2,\gamma _2=0.2\)

Full size image

Remark 3

In [8], the onset of convection for a single temperature bi-disperse porous medium was analysed, the instability threshold is:

$$\begin{aligned} \mathcal {R}_c= \min _{n,a^2} \dfrac{(n^2 \pi ^2 + a^2)^2}{a^2} \dfrac{\gamma _1 \gamma _2 + \gamma _1 + \gamma _2}{\gamma _1 + \gamma _2 +4} \end{aligned}$$

Let us underline that if the throughflow is not considered (i.e. \(Pe \rightarrow 0\)), we found \(\mathcal {R}_c=\mathcal {R}_L=\mathcal {R}_N=16.5555\) (with \(\gamma _1=2,\gamma _2=0.2\)), hence the stability results found in [8] are recovered.

4.2 Weighted energy method

In this Section, we will perform the nonlinear stability analysis applying the weighted energy method to the nonlinear boundary value problem (8)\(_1\), (8)\(_2\), (8)\(_5\) in \(w^f,w^p,\theta \), i.e.

$$\begin{aligned} \begin{aligned}&{\left\{ \begin{array}{ll} (1+ \gamma _1) \Delta w^f - \Delta w^p - \mathcal {R}\Delta _1 \theta = 0, \\ - \Delta w^f + (1+ \gamma _2) \Delta w^p - \mathcal {R}\Delta _1 \theta = 0, \\ \dfrac{\partial \theta }{\partial t} + (\textbf{u}^f + \textbf{u}^p) \cdot \nabla \theta = -\mathcal {R}f(z) (w^f+w^p) - Pe \dfrac{\partial \theta }{\partial z} + \Delta \theta , \end{array}\right. } \\&\quad w^f=w^p=\theta =0 \quad \text {on} \ z=0,1. \end{aligned} \end{aligned}$$
(26)

The following result holds true.

Theorem 3

(Weighted Poincaré Inequality) If \(\Phi \in \mathcal {H}\), with

$$\begin{aligned}{} & {} \mathcal {H} = \{\phi \in H^1(V) | \phi =0 \ \text {on} \ z=0,1; \text {periodic in} \ x,y \ \text {with periods} \ 2 \pi /l, 2 \pi /m,\\{} & {} \text {respectively} \}\,, \end{aligned}$$

then

$$\begin{aligned} \left\langle e^{Pez},\Phi ^2\right\rangle \le \displaystyle \frac{4}{4 \pi ^2 + Pe^2} \left\langle e^{Pez},\vert \nabla \Phi \vert ^2\right\rangle . \end{aligned}$$
(27)

Proof

Since \(\theta =e^{\frac{Pe}{2}z} \Phi \) is periodic on the x and y directions and vanishes on \(z=0,1\), one gets (see [17,18,19])

$$\begin{aligned} \int _V \left( e^{\frac{Pe}{2}z} \Phi \right) ^2 dV \le \dfrac{1}{\pi ^2} \int _V \left[ \dfrac{\partial }{\partial z} \left( e^{\frac{Pe}{2}z} \Phi \right) \right] ^2 dV. \end{aligned}$$
(28)

In view of the identity

$$\begin{aligned} \int _V \left[ \dfrac{\partial }{\partial z} \left( e^{\frac{Pe}{2}z} \Phi \right) \right] ^2 dV = -\dfrac{Pe^2}{4} \int _V e^{Pez} \Phi ^2 dV + \int _V e^{Pez} \left( \dfrac{\partial \Phi }{\partial z} \right) ^2 dV, \end{aligned}$$
(29)

from (28), it follows

$$\begin{aligned} \left( 1 + \dfrac{Pe^2}{4 \pi ^2} \right) \int _V e^{Pez} \Phi ^2 dV \le \dfrac{1}{\pi ^2} \int _V e^{Pez} \vert \nabla \Phi \vert ^2 dV, \end{aligned}$$
(30)

therefore, one obtains (27). \(\square \)

Now, considering the transformation (11), (26) becomes

$$\begin{aligned} \begin{aligned}&{\left\{ \begin{array}{ll} (1+ \gamma _1) \Delta w^f - \Delta w^p - \mathcal {R}\ e^{\frac{Pe}{2}z} \Delta _1 \Phi = 0, \\[2mm] - \Delta w^f + (1+ \gamma _2) \Delta w^p - \mathcal {R}\ e^{\frac{Pe}{2}z} \Delta _1 \Phi = 0, \\[2mm] e^{\frac{Pe}{2}z} \dfrac{\partial \Phi }{\partial t} \!+\! (\textbf{u}^f \!+\! \textbf{u}^p) \cdot \nabla \left( e^{\frac{Pe}{2}z} \Phi \right) = -\mathcal {R}f(z) (w^f\!+\!w^p) - \frac{Pe^2}{4} e^{\frac{Pe}{2}z} \Phi \!+\! e^{\frac{Pe}{2}z} \Delta \Phi , \end{array}\right. } \\&\quad w^f=w^p=\Phi =0 \quad \text {on} \ z=0,1. \end{aligned} \hspace{-5.0pt}\end{aligned}$$
(31)

Let us multiply (31)\(_1\) by \(w^f\), (31)\(_2\) by \(w^p\) and (31)\(_3\) by \(e^{\frac{Pe}{2}z} \Phi \), integrating each equation over the periodicity cell V and adding the resulting equations one obtains

$$\begin{aligned} \dfrac{d \mathcal {E}}{dt} = \mathcal {R}\mathcal {I} - \mathcal {D} + \dfrac{Pe^2}{2} \mathcal {E}, \end{aligned}$$
(32)

where

$$\begin{aligned} \begin{aligned} \mathcal {E}&= \dfrac{\mu }{2} \left\langle e^{Pe z},\Phi ^2\right\rangle , \\ \mathcal {I}&= - \left\langle e^{\frac{Pe}{2}z} \Delta _1 \Phi , w^f + w^p\right\rangle - \mu \left\langle e^{\frac{Pe}{2}z} f(z) \Phi ,w^f+w^p\right\rangle , \\ \mathcal {D}&= \gamma _1 \Vert \nabla w^f \Vert ^2 + \gamma _2 \Vert \nabla w^p \Vert ^2 + \Vert \nabla w^f - \nabla w^p \Vert ^2 + \mu \left\langle e^{Pe z},\vert \nabla \Phi \vert ^2\right\rangle , \end{aligned} \end{aligned}$$
(33)

and \(\mu \) a positive coupling parameter to be suitably chosen later. Setting

$$\begin{aligned} \dfrac{1}{\mathcal {R}_W} = \max _{\mathcal {H}} \frac{\mathcal {I}}{\mathcal {D}}, \end{aligned}$$
(34)

the following theorem holds.

Theorem 4

Let us set

$$\begin{aligned} \mathcal {E}_1=e^{-\frac{Pe^2}{2}t}\mathcal {E}, \end{aligned}$$
(35)

then the condition

$$\begin{aligned} \mathcal {R}< \mathcal {R}_W \end{aligned}$$
(36)

guarantees the global, nonlinear, asymptotic, exponential stability of the throughflow solution (3) with respect to the \(\mathcal {E}_1\)-norm.

Proof

By virtue of (35), from (32) one obtains

$$\begin{aligned} \dfrac{d \mathcal {E}_1}{dt} = \mathcal {D}\left( \mathcal {R}\displaystyle \frac{\mathcal {I}}{\mathcal {D}}-1\right) e^{-\frac{Pe^2}{2}t}, \end{aligned}$$
(37)

where by virtue of (27)

$$\begin{aligned} \mathcal {D} \ge \displaystyle \frac{4 \pi ^2 + Pe^2}{2} \mathcal {E}. \end{aligned}$$
(38)

Moreover, accounting for (34) and (36), from (37) it follows that

$$\begin{aligned} \dfrac{d \mathcal {E}_1}{dt} \le \displaystyle \frac{4 \pi ^2 + Pe^2}{2}\left( \dfrac{\mathcal {R}}{\mathcal {R}_W} -1\right) \mathcal {E}_1, \end{aligned}$$
(39)

hence, integrating with respect to time t, one gets

$$\begin{aligned} \mathcal {E}_1(t) \le \mathcal {E}_1(0) \exp \left[ {\displaystyle \frac{(4 \pi ^2 + Pe^2)(R-R_W)}{2R_W}t} \right] , \qquad \forall \,\,t\ge 0 \end{aligned}$$
(40)

and hence the global, nonlinear, asymptotic, exponential stability of the throughflow solution (3) with respect to the \(\mathcal {E}_1\)-norm is obtained. \(\square \)

Remark 4

Let us underline that in the limit case \(Pe \rightarrow 0\), from (35) we get that \( \mathcal {E}_1= \mathcal {E}\) coincides with \(\hat{E}\) defined in (18) choosing \(\mu =1\). Therefore, in the limit case for vanishing throughflow, one has to refer to the stability results obtained in [8] (as stated in Remark 3).

The Euler-Lagrange equations associated to the maximum problem (34), assuming solutions (13), are:

$$\begin{aligned} {\left\{ \begin{array}{ll} D^2 \bar{w}^f = a^2 \bar{w}^f + \frac{c_1}{2} \mathcal {R}_W e^{\frac{Pe}{2}z} [\mu f(z)-a^2] \bar{\Phi }, \\ D^2 \bar{w}^p = a^2 \bar{w}^p + \frac{c_2}{2} \mathcal {R}_W e^{\frac{Pe}{2}z} [\mu f(z)-a^2] \bar{\Phi }, \\ D^2 \bar{\Phi } = a^2 \bar{\Phi } - Pe \ D \bar{\Phi } + \frac{1}{2 \mu } e^{-\frac{Pe}{2}z} \mathcal {R}_W [\mu f(z)-a^2] (\bar{w}^f+\bar{w}^p). \end{array}\right. } \end{aligned}$$
(41)

We numerically solved (41) under the boundary conditions \(\bar{w}^f=\bar{w}^p=\bar{\Phi }=0\) on \(z=0,1\), in order to determine the critical threshold

$$\begin{aligned} \mathcal {R}_W = \max _{\mu } \min _{a^2} \{ \mathcal {R}^2(a^2,\mu ) \vert \mathcal {R}^2 \ \text {verifies} \ (41) \}. \end{aligned}$$

In Fig. 6 all the stability thresholds we found are depicted as functions of the Peclet number Pe. From Fig. 6 we found that, while for \(Pe \rightarrow 0\) the coincidence between the thresholds is recovered, for increasing Peclet numbers the weighted energy method significantly reduces the region of subcritical instabilities.

Fig. 6
figure 6

Linear instability threshold \(\mathcal {R}_L\), nonlinear stability thresholds \(\mathcal {R}_N\) and \(R_W\) as function of the Peclet number Pe, for \(\gamma _1=2,\gamma _2=0.2\)

Full size image

5 Conclusions

In this paper the effect of a vertical constant steady net mass flow (throughflow) on the onset of convective instabilities is analysed in a horizontal layer of fluid-saturated bi-disperse porous medium heated from below. We proved the validity of the principle of exchange of stabilities, therefore convective instabilities can arise only via steady motions. Via linear instability analysis of the throughflow solution, we determined the critical Rayleigh number for the onset of stationary convective instabilities and studied the behaviour of the critical Rayleigh number with respect to the Peclet number, proving that the throughflow has a stabilizing effect on the onset of convective instabilities when \(Pe>0\), destabilizing when \(Pe<0\). By mean of the differential constraints approach and the weighted energy method, we performed the nonlinear stability analysis of the throughflow solution, in order to catch the method that better describes the physics of the problem. We found that there is not coincidence between the linear and the nonlinear thresholds, therefore a region of subcritical instabilities is present, but, for increasing Peclet numbers, the thickness of the region of subcritical instabilities is significantly reduced by the weighted energy method.