Envelope theorems in Banach lattices and asset pricing

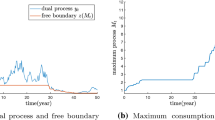
Abstract

We develop envelope theorems for optimization problems in which the value function takes values in a general Banach lattice. We consider both the special case of a convex choice set and a concave objective function and the more general case case of an arbitrary choice set and a general objective function. We apply our results to discuss the existence of a well-defined notion of marginal utility of wealth in optimal discrete-time, finite-horizon consumption-portfolio problems with an unrestricted information structure and preferences allowed to display habit formation and state dependency.

Differentiability and concavity in normed vector spaces

In this section we summarize the main definition and results for cone-concave functions on vector spaces and, in particular, on the relation between concavity and differentiability. Let $X$, $Y$ be normed vector spaces and $G$ a mapping defined on an open domain $U\subset X$, with values in $Y$.

Definition 4

We say that $G$ admits derivative at a point $u\in U$ in a direction $x\in X$ if the limit:

$$\begin{aligned} G^{\prime }(u;x):=\lim _{h\rightarrow 0^{+}}\dfrac{G(u+hx)-G(u)}{h} \end{aligned}$$

(5.1)

exists, where the limit is meant in $Y$-norm.

The function $G$ is said to be Gateaux differentiable at $u$ if it is directional differentiable at $u$ in every direction $x\in X$ and the directional derivative $G^{\prime }(u;\, \cdot \,):X\rightarrow Y$ is a continuous and linear operator. In this case, we denote this operator with $DG(u)$ (namely, $DG(u)(x) = G^{\prime }(u;x)$) and call it the Gateaux differential of $G$ at $u$.

Definition 5

We say that $G$ is Fréchet-differentiable at $u$ if there exists a continuous and linear operator $DG(u):X\rightarrow Y$ such that

$$\begin{aligned} \lim _{\Vert x\Vert _{X}\rightarrow 0}\dfrac{\left\| G(u+x)-G(u)-DG(u)(x)\right\| _{Y}}{\left\| x\right\| _{X}}=0 \end{aligned}$$

(5.2)

The operator $DG(u)$ is called the Fréchet differential of $G$ at $u$.

The results which follow can be found in [6, 16, 21]. Usually, definition and results are stated for convex function. Since we work under a concavity assumption, we reformulated them in the appropriate form for concave functions with values in the order complete Banach lattice $(Y,C,\ge ),$ where $C$ is the positive cone of $Y$.

Definition 6

A function $F:X \rightarrow Y$ is $C$ -concave (or simply concave) if for all $x,y\in X$, $\lambda \in [0,1]$

$$\begin{aligned} F(\lambda x + (1-\lambda ) y) \ge \lambda F(x) + (1-\lambda ) F(y), \end{aligned}$$

namely, $F(\lambda x + (1-\lambda ) y) - \lambda F(x) + (1-\lambda ) F(y) \in C$.

The sets of points at which $F$ is finite is called the essential domain of $F$ and denoted by $domF$. The algebraic interior of $F$ is denoted $coreF$.

Proposition 8

(Borwein [6], Proposition 2.3) Let $G:X \rightarrow \bar{Y}$ be concave. Assume that there exists a function $F:X \rightarrow \bar{Y}$ such that $G(x) \ge F(x)$ for all $x\in X$. If $F$ is continuous at some point $x_0 \in X$, then $G$ is continuous at $x_0$.

Let now $\mathcal {L}(X,Y)$ denote the set of continous and linear operators between $X$ and $Y$ and let $F$ be a concave function from $X$ to $\bar{Y}$.

Definition 7

An operator $L\in \mathcal {L}(X,Y)$ is called a superdifferential for $F$ at $x_0$ if for all $x \in X$

$$\begin{aligned} L(x) \ge F(x_0 + x) - F(x_0). \end{aligned}$$

The superdifferential set is denoted by $\partial F(x_0)$.

Proposition 9

(Borwein [6], Proposition 3.2 (a) and Proposition 3.7 (a)) If $F: X \rightarrow \bar{Y}$ is concave, with $x_0 \in core F$, then

$$\begin{aligned} F^> (x_0,x) = \sup _{h>0} \frac{F(x_0 + hx) - F(x_0)}{h} \end{aligned}$$

exists and is everywhere finite and superlinear.

Proposition 10

(Valadier [21], Proposition 4 and Théorème 6) If $F:X \rightarrow \bar{Y}$ is concave and $x_0 \in core F$ then:

• (i) $L\in \mathcal {L}(X,Y)$ is a superdifferential for $F$ at $x_0$ if and only if $L(x) \ge F^> (x_0,x)$ for all $x \in X$;

• (ii) if in addition $F$ is continuous at $x_0$, then $\partial F(x_0)$ is non-empty, convex and equicontinuous in $\mathcal {L}(X,Y)$ and

  $$\begin{aligned} F^> (x_0,x) = \min \{L(x): L \in \partial F(x_0)\}. \end{aligned}$$

Proposition 11

(Papageorgiou [16], Theorem 4.6) Let $F:X \rightarrow \bar{Y}$ be a concave function. If $F$ is continuous at $x_0$, then $F$ is Gateaux-differentiable at $x_0$ if and only if $\partial F(x_0)$ is a singleton.