K-stability of Fano 3-folds of Picard rank 3 and degree 20

Abstract

We prove K-stability of smooth Fano 3-folds of Picard rank 3 and degree 20 that satisfy very explicit generality condition.

1 Introduction

Let $S={\mathbb {P}}^1\times {\mathbb {P}}^1$, let C be a smooth curve in S of degree (5, 1), and let $\epsilon :C\rightarrow {\mathbb {P}}^1$ be the morphism induced by the projection $S\rightarrow {\mathbb {P}}^1$ to the first factor. Then $\epsilon$ is a finite morphism of degree five, and we may assume that the points ([1 : 0], [0 : 1]) and ([0 : 1], [1 : 0]) are among its ramifications points. This assumption implies that the curve C is given by

$$\begin{aligned} u\big (x^5+a_1x^{4}y+a_2x^{3}y^2+a_3x^{2}y^3\big )=v\big (y^5+b_1xy^4+b_2x^{2}y^3+b_3x^{3}y^2\big ) \end{aligned}$$

for some $a_1$, $a_2$, $a_3$, $b_1$, $b_2$, $b_3$, where ([u : v], [x : y]) are coordinates on S. Note that the ramification index of the point ([1 : 0], [0 : 1]) can be computed as follows:

$$\begin{aligned} \left\{ \begin{aligned}&2\ \text {if }a_3\ne 0,\\&3\ \text {if }a_3=0\text { and }a_2\ne 0,\\&4\ \text {if }a_3=a_2=0\text { and }a_1\ne 0,\\&5\ \text {if }a_3=a_2=a_1=0. \end{aligned} \right. \end{aligned}$$

Likewise, we can compute the ramification index of the point ([0 : 1], [1 : 0]). We may assume that

• ([1 : 0], [0 : 1]) has the largest ramification index among all ramifications points of $\epsilon$

• the ramification index of the point ([0 : 1], [1 : 0]) is the second largest index.

If both these indices are 5, then $a_1=a_2=a_3=b_1=b_2=b_3=0$, the morphism $\epsilon$ does not have other ramification points, and the equation of the curve C simplifies as

$$\begin{aligned} ux^5=vy^5. \end{aligned}$$

In this case, we have $\textrm{Aut}(S,C)\cong {\mathbb {C}}^*\rtimes {\mathbb {Z}}/2{\mathbb {Z}}$. In all other cases, this group is finite [5, Corollary 2.7].

Now, we consider embedding $S\hookrightarrow {\mathbb {P}}^1\times {\mathbb {P}}^2$ given by

$$\begin{aligned} \big ([u:v],[x:y]\big )\mapsto \big ([u:v],[x^2:xy:y^2]\big ), \end{aligned}$$

and identify S and C with their images in ${\mathbb {P}}^1\times {\mathbb {P}}^2$. Let $\pi :X\rightarrow {\mathbb {P}}^1\times {\mathbb {P}}^2$ be the blow up of the curve C. Then X is a smooth Fano threefold in the deformation family № 3.5 in the Mori–Mukai list and every smooth member of this family can be obtained in this way. We know from [2, Section 5.14], that

• X is K-stable if the numbers $a_1$, $a_2$, $a_3$, $b_1$, $b_2$, $b_3$ are general enough,

• X is K-polystable if $a_1=a_2=a_3=b_1=b_2=b_3=0$.

However, for some $a_1$, $a_2$, $a_3$, $b_1$, $b_2$, $b_3$, the threefold X is not K-polystable.

Example 1

If $(a_1,a_2,a_3)=(0,0,0)\ne (b_1,b_2,b_3)$, then X is not K-polystable [2, Lemma 7.6].

Note also that it follows from the proof of [5, Lemma 8.7] that $\textrm{Aut}(X)\cong \textrm{Aut}(S,C)$. In particular, we conclude the group $\textrm{Aut}(X)$ is finite if and only if $(a_1,a_2,a_3,b_1,b_2,b_3)\ne (0,0,0,0,0,0)$. In this case, the threefold X is K-polystable if and only if it is K-stable. Moreover, we have

Conjecture 1

([2]) The Fano threefold X is K-stable if and only if $(a_1,a_2,a_3)\ne (0,0,0)$.

Geometrically, this conjecture says that the following two conditions are equivalent:

• (1) the threefold X is K-stable,

• (2) the morphism $\epsilon :C\rightarrow {\mathbb {P}}^1$ does not have ramification points of ramification index five.

The goal of this paper is to prove the following (slightly weaker) result:

MainTheorem

If all ramification points of $\epsilon$ have ramification index two, then X is K-stable.

Let $\textrm{pr}_1: {\mathbb {P}}^1\times {\mathbb {P}}^2 \rightarrow {\mathbb {P}}^1$ be the projection to the first factor and $\phi _1=\textrm{pr}_1\circ \pi$. Then $\phi _1$ is a fibration into del Pezzo surfaces of degree four, and every singular fiber of this fibration has Du Val singular points of types ${\mathbb {A}}_1$, ${\mathbb {A}}_2$, ${\mathbb {A}}_3$ or ${\mathbb {A}}_4$, and we have the following possibilities for the singularities of a given singular fiber

• (1) one singular point of type ${\mathbb {A}}_1$,

• (2) two singular points of type ${\mathbb {A}}_1$,

• (3) one singular point of type ${\mathbb {A}}_2$,

• (4) one singular point of type ${\mathbb {A}}_1$ and one singular point of type ${\mathbb {A}}_2$,

• (5) one singular point of type ${\mathbb {A}}_3$,

• (6) one singular point of type ${\mathbb {A}}_4$.

Note that $\phi _1$ has at most two singular fibers that have singular points of type ${\mathbb {A}}_4$. Moreover, if $\phi _1$ has two singular fibers with singular points of type ${\mathbb {A}}_4$ then all numbers $a_i$ and $b_j$ vanish, so that X is K-polystable. Vice versa, if $\phi _1$ has exactly one singular fiber with a point type ${\mathbb {A}}_1$, then the authors of [2] proved that X is not K-polystable. Moreover, they conjectured that X is K-stable in all remaining cases. Now Main Theorem and Conjecture 1 can be restated as follows:

MainTheorem

If every singular fiber of $\phi _1$ has only singular points of type ${\mathbb {A}}_1$, then X is K-stable.

Conjecture 2

The Fano threefold X is K-stable if and only if every singular fiber of $\phi _1$ has only singular points of type ${\mathbb {A}}_1$, ${\mathbb {A}}_2$ or ${\mathbb {A}}_3$.

2 The Proof

To prove Main Theorem, we suppose that each singular fiber of the fibration $\phi _1$ has one or two singular points of type ${\mathbb {A}}_1$. Note that this fiber is a del Pezzo surface of degree 4 with Du Val singularities. We know ( [7, 9]) that the Fano threefold X is K-stable if and only if for every prime divisor ${\textbf{F}}$ over X we have

$$\begin{aligned} \beta ({\textbf{F}})=A_X({\textbf{F}})-S_X({\textbf{F}})>0 \end{aligned}$$

where $A_X({\textbf{F}})$ is the log discrepancy of the divisor ${\textbf{F}}$, and

$$\begin{aligned} S_X\big ({\textbf{F}}\big )=\frac{1}{(-K_X)^3}\int \limits _0^{\infty }\textrm{vol}\big (-K_X-u{\textbf{F}}\big )du. \end{aligned}$$

To show this, we fix a prime divisor ${\textbf{F}}$ over X. Then we set $Z=C_{X}({\textbf{F}})$. If Z is an irreducible surface, then it follows from [8] that $\beta ({\textbf{F}})>0$, see also [2, Theorem 3.17]. Therefore, we may assume that

• either Z is an irreducible curve in X,

• or Z is a point in X.

In both cases, we fix a point $O\in Z$. Let ${\overline{T}}$ be the fiber of $\phi _1$ which contains O. Then ${\overline{T}}$ is a del Pezzo surface with at most Du Val singularities. Set

$$\begin{aligned} \tau ({\overline{T}}) = \textrm{sup}\Big \{u\in {\mathbb {R}}_{>0}\big |\text { the divisor }-K_X - u{\overline{T}} \text { is pseudo-effective}\Big \} \end{aligned}$$

For $u \in [0, \tau ({\overline{T}}) ]$ let P(u) be the positive part of the Zariski decomposition of the divisor $-K_X-u{\overline{T}}$, and let N(u) be its negative part. We denote ${\widetilde{S}}$ to be the proper transform on X of the surface S. Then we have

$$\begin{aligned}&P(u)=\left\{ \begin{aligned}&-K_X-u{\overline{T}} \ \text { if } u\in [0,1], \\&-K_X-u{\overline{T}}-(u-1){\widetilde{S}}\ \text { if } u\in [1,2], \end{aligned} \right. \text { and }\\&N(u)= \left\{ \begin{aligned}&0\ \text { if } u\in [0,1], \\&(u-1){\widetilde{S}}\ \text { if } u\in [1,2], \end{aligned} \right. \end{aligned}$$

which gives

$$\begin{aligned} S_{X}({\overline{T}})=\frac{1}{20}\int \limits _{0}^{2}P(u)^3du=\frac{69}{80}<1 \end{aligned}$$

Now, for every prime divisor F over the surface ${\overline{T}}$, we set

$$\begin{aligned} S\big (W^{{\overline{T}}}_{\bullet ,\bullet };F\big )= & {} \frac{3}{(-K_X)^3}\int \limits _0^{\tau }\textrm{ord}_F \big (N(u)\vert _{{\overline{T}}}\big )\big (P(u)\vert _{{\overline{T}}}\big )^2du\\{} & {} +\frac{3}{(-K_X)^3}\int \limits _0^\tau \int \limits _0^{\infty }\textrm{vol}\big (P(u)\big \vert _{{\overline{T}}}-vF\big )dvdu. \end{aligned}$$

Then, following [1, 2], we let

$$\begin{aligned} \delta _O\big ({\overline{T}},W^{{\overline{T}}}_{\bullet ,\bullet }\big )=\inf _{\begin{array}{c} F/{\overline{T}}\\ O\in C_{{\overline{T}}}(F) \end{array}}\frac{A_T(F)}{S\big (W^{{\overline{T}}}_{\bullet ,\bullet };F\big )}, \end{aligned}$$

where the infimum is taken by all prime divisors over the surface ${\overline{T}}$ whose center on ${\overline{T}}$ contains O. Then it follows from [1, 2] that

$$\begin{aligned} \frac{A_X({\textbf{F}})}{S_X({\textbf{F}})}\geqslant \min \Bigg \{\frac{1}{S_X({\overline{T}})},\delta _O\big ({\overline{T}},W^{{\overline{T}}}_{\bullet ,\bullet }\big )\Bigg \}. \end{aligned}$$

Therefore, if $\beta ({\textbf{F}})\leqslant 0$, then $\delta _O({\overline{T}},W^{{\overline{T}}}_{\bullet ,\bullet })\leqslant 1$.

Let’s prove that $\delta _O({\overline{T}},W^{{\overline{T}}}_{\bullet ,\bullet }) > 1$. To estimate $\delta _O(T,W^{{\overline{T}}}_{\bullet ,\bullet })$, we set ${\overline{D}}=P(u)\vert _{{\overline{T}}}$. We have

$$\begin{aligned} {\overline{D}}=\left\{ \begin{aligned}&-K_{{\overline{T}}} \ \text { if } u\in [0,1], \\&-K_{{\overline{T}}}-(u-1){\overline{C}}_2\ \text { if } u\in [1,2], \end{aligned} \right. \end{aligned}$$

where ${\overline{C}}_2:={\widetilde{S}}|_{{\overline{T}}}$. Then ${\overline{D}}$ is ample for $u\in [0,2)$, and

$$\begin{aligned} {\overline{D}}^2=\left\{ \begin{aligned}&4\ \text { if } u\in [0,1], \\&5-u^2 \ \text { if } u\in [1,2]. \end{aligned} \right. \end{aligned}$$

By [2, Lemma 5.68] and [2, Lemma 5.69] we have

Lemma 1

If $O\in {\widetilde{S}}$ then $\delta _O(X) > 1$.

Lemma 2

If ${\overline{T}}$ is smooth then $\delta _O(X)>1$.

Thus, to prove Main Theorem, we may assume that $O\not \in {\widetilde{S}}$ and ${\overline{T}}$ is singular. Recall that

$$\begin{aligned} \delta _O\big ({\overline{T}},{\overline{D}}\big )=\inf _{\begin{array}{c} F/{\overline{T}}\\ O\in C_{{\overline{T}}}(F) \end{array}}\frac{A_{{\overline{T}}}(F)}{S_{{\overline{D}}}\big (F\big )}\end{aligned}$$

where the infimum is taken by all prime divisors over ${\overline{T}}$ whose center on ${\overline{T}}$ contain O, and $S_{{\overline{D}}}(F)~=~\frac{1}{{\overline{D}}^2}\int \limits _0^{\infty }\textrm{vol}\big ({\overline{D}}-vF\big )dv$. Usually $\delta _O({\overline{T}},-K_{{\overline{T}}})$ is denoted by $\delta _O({\overline{T}})$.

Note that since $O\not \in {\widetilde{S}}$ then for any divisor F over ${\overline{T}}$ then we get

$$\begin{aligned} S\big (W^{{\overline{T}}}_{\bullet ,\bullet };F\big )&=\frac{3}{(-K_X)^3}\Bigg (\int _0^\tau \big (P(u)^{2}\cdot {\overline{T}}\big )\cdot \textrm{ord}_{O}\Big (N(u)\big \vert _{{\overline{T}}}\Big )du\\&\quad +\int _0^\tau \int _0^\infty \textrm{vol}\big (P(u)\big \vert _{{\overline{T}}}-vF\big )dvdu\Bigg )\\&= \frac{3}{20}\int _0^\tau \int _0^\infty \textrm{vol}\big (P(u)\big \vert _{{\overline{T}}}-vF\big )dvdu\\&= \frac{3}{20}\Bigg (\int _0^1\int _0^\infty \textrm{vol}\big (-K_{{\overline{T}}}-vF\big )dvdu\\&\quad +\int _1^2\int _0^\infty \textrm{vol}\big (-K_{{\overline{T}}}-(u-1){\overline{C}}_2-vF\big )dvdu\Bigg )\\&= \frac{3}{20}\Bigg (\int _0^\infty \textrm{vol}\big (-K_{{\overline{T}}}-vF\big )dv\\&\quad +\int _0^\infty \textrm{vol}\big (-K_T-(u-1){\overline{C}}_2-vF\big )dv\Bigg )\\&= \frac{3}{20}\Bigg (\int _0^\infty \textrm{vol}\big (-K_{{\overline{T}}}-vF\big )dv+\int _0^\infty \textrm{vol}\big (-K_{{\overline{T}}}-vF\big )dv\Bigg )\\&= \frac{3}{10}\Bigg (\int _0^\infty \textrm{vol}\big (-K_{{\overline{T}}}-vF\big )dv\Bigg )\\&=\frac{6}{5}\Bigg (\frac{1}{4}\int _0^\infty \textrm{vol}\big (-K_{{\overline{T}}}-vF\big )dv\Bigg )\\&=\frac{6}{5}S_{{\overline{T}}}(F)\le \frac{6}{5}\cdot \frac{A_{{\overline{T}}}(F)}{\delta _O({\overline{T}})} \end{aligned}$$

Thus, if $\delta _O({\overline{T}})>6/5$, then $\delta _O({\overline{T}},W^{{\overline{T}}}_{\bullet ,\bullet })>1$. To estimate $\delta _O({\overline{T}},W^{{\overline{T}}}_{\bullet ,\bullet })$ in the case when $\delta _O({\overline{T}})\le 6/5$, we define the following positive continuous function on [1, 2]:

$$\begin{aligned}f(u):= \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { if }u\in [1,a],\\&\frac{15 - 3 u^2}{11 - u^3}\text { if }u\in [a,2] \end{aligned} \right. \end{aligned}$$

where a is a root of $3u^3 - 9u^2 + 3u + 5$ on [1, 2]. More precisely, $a\in [1.355,1.356]$. In the appendix we prove that for each O such that $\delta _O({\overline{T}})\le \frac{6}{5}$ we have $\delta _{O}({\overline{T}},{\overline{D}})\ge f(u)$ for every $u\in [1,2]$. So we obtain

$$\begin{aligned} S\big (W^{{\overline{T}}}_{\bullet ,\bullet };F\big )&=\frac{3}{(-K_X)^3}\int \limits _1^{2} \int \limits _0^{\infty }\textrm{vol}\big (P(u)\big \vert _{{\overline{T}}}-vF\big )dvdu\\&\quad +\frac{3}{(-K_X)^3}\int \limits _0^{1}\int \limits _0^{\infty }\textrm{vol}\big (P(u)\big \vert _{{\overline{T}}}-vF\big )dvdu\\&\le \frac{3}{20} \Bigg (\int \limits _1^{2}\frac{(5-u^2)}{\delta _O({\overline{T}},{\overline{D}})}du\Bigg )A_{{\overline{T}}}(F) +\frac{3}{20}\cdot \frac{4A_{{\overline{T}}}(F)}{\delta _O({\overline{T}})}\\&\le \frac{3}{20} \Bigg (\int \limits _1^{2}\frac{(5-u^2)}{f(u)}du\Bigg )A_{{\overline{T}}}(F)+\frac{3}{5}A_{{\overline{T}}}(F)\\&\le \frac{3}{20} \Bigg (\int \limits _1^{1.356}(5-u^2)\frac{16 + 3 u - 9 u^2 + 2 u^3}{15 - 3 u^2} du\\&\quad +\int \limits _{1.355}^{2}(5-u^2)\frac{11 - u^3}{15 - 3 u^2} du\Bigg )A_{{\overline{T}}}(F)+\frac{3}{5}A_{{\overline{T}}}(F)\le \frac{99}{100}A_{{\overline{T}}}(F) \end{aligned}$$

Thus $\frac{A_{{\overline{T}}}(F)}{S\big (W^{{\overline{T}}}_{\bullet ,\bullet };F\big )}\ge \frac{100}{99}$ for every prime divisor F over ${\overline{T}}$ whose support on F contains O, so that $\delta _O(W^{{\overline{T}}},F)\ge \frac{100}{99}$, which implies $\beta ({\textbf{F}})>0$ and X is K-stable.

Remark 1

If O were a singular point of type ${\mathbb {A}}_2$ in ${\overline{T}}$, this approach would not work, because as is shown in Appendix A.3 we have $\delta _O({\overline{T}}, {\overline{D}}) = \frac{15-3u^2}{u^3 - 6u^2 + 19}$ and there is prime divisor F over ${\overline{T}}$ such that $A_{{\overline{T}}}(F) = 1$ and $S(W^{{\overline{T}}}_{\bullet ,\bullet }; F) = \frac{83}{80}$, which implies that $\delta _O({\overline{T}},W^{{\overline{T}}}_{\bullet ,\bullet }) \le \frac{80}{83}$.

Appendix A. Polarized \(\delta \)-invariant via Kento Fujita’s formulas

Let us use notations from Section 2. Recall that ${\overline{T}}$ is a Du Val del Pezzo surface, and the blow up $\pi$ induces a birational morphism $\upsilon :{\overline{T}}\rightarrow {\mathbb {P}}^2$. We assume that ${\overline{T}}$ is singular. We have the following commutative diagram

Suppose that $u\in [1,2]$. Recall that ${\overline{D}}=-K_{{\overline{T}}}-(1-u){\overline{C}}_2$. Observe that ${\overline{C}}_2$ is contained in the smooth locus of the surface ${\overline{T}}$. Let $C_2$ be the strict transform of the curve ${\overline{C}}_2$ on the surface T, set $D=-K_T-(1-u)C_2$. Note that $D=\sigma ^*({\overline{D}})$ so the divisor D is big and nef for $u\in [1,2]$. Recall

$$\begin{aligned} \delta _O({\overline{T}},{\overline{D}})=\inf _{\begin{array}{c} F/{\overline{T}}\\ O\in C_{{\overline{T}}}(F) \end{array}}\frac{A_{{\overline{T}}}(F)}{S_D(F)} \end{aligned}$$

where the infimum is run over all prime divisor F over ${\overline{T}}$ such that $O\in C_{{\overline{T}}}(F)$. For every point $P\in T$, we also define

$$\begin{aligned} \delta _P(T,D)=\inf _{\begin{array}{c} E/T\\ P\in C_T(E) \end{array}}\frac{A_T(E)}{S_D\big (E\big )} \end{aligned}$$

where the infimum is run over all prime divisor E over T such that $P\in C_T(E)$. Since $D=\sigma ^*({\overline{D}})$ and $K_T=\sigma ^*(K_{{\overline{T}}}),$ we have

$$\begin{aligned} \delta _O({\overline{T}},{\overline{D}})=\inf _{\begin{array}{c} P\in T\\ O=\sigma (P) \end{array}}\delta _P(T,D) \end{aligned}$$

So, to estimate $\delta _O({\overline{T}},{\overline{D}})$ it is enough to estimate $\delta _P(T,D)$ for P all points P such that $\sigma (P)=O$.

Let ${\mathcal {C}}$ be a smooth curve on T containing P. Set

$$\begin{aligned} \tau ({\mathcal {C}})=\textrm{sup}\Big \{v\in {\mathbb {R}}_{\geqslant 0}\ \big \vert \ \text {the divisor }-K_T-v{\mathcal {C}}\text { is pseudo-effective}\Big \}. \end{aligned}$$

For $v\in [0,\tau ]$, let P(v) be the positive part of the Zariski decomposition of the divisor $-K_T-{\mathcal {C}}$, and let N(v) be its negative part. Then we set

$$\begin{aligned} S\big (W^{{\mathcal {C}}}_{\bullet ,\bullet };P\big )=\frac{2}{D^2}\int _0^{\tau ({\mathcal {C}})} h_D(v) dv, \end{aligned}$$

where

$$\begin{aligned} h_D(v)=\big (P(v)\cdot {\mathcal {C}}\big )\times \big (N(v)\cdot {\mathcal {C}}\big )_P+\frac{\big (P(v)\cdot {\mathcal {C}}\big )^2}{2}. \end{aligned}$$

It follows from [1, 2] that:

$$\begin{aligned} \delta _P(T,D)\geqslant \textrm{min}\Bigg \{\frac{1}{S_D({\mathcal {C}})},\frac{1}{S(W_{\bullet ,\bullet }^{{\mathcal {C}}},P)}\Bigg \}. \end{aligned}$$

We will estimate $\delta _P(T,D)$ in the following using the notations above for a suitable choice of the curve ${\mathcal {C}}$, $\tau ({\mathcal {C}})$, P(v) and N(v) later in special cases.

A similar approach was taken in [3] and [4].

1.1 Polarized $\delta$-invariant on Del Pezzo surface of degree 4 with ${\mathbb {A}}_1$ singularity.

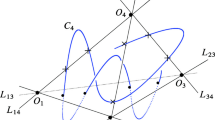
Suppose that ${\overline{T}}$ has one singular point and this point is a singular point of type ${\mathbb {A}}_1$. Then $\eta$ is a blow up of ${\mathbb {P}}^2$ at points $P_1$, $P_2$, $P_3$ and $P_4$ in general position and a point $P_5$ which belongs to the exceptional divisor corresponding to $P_4$ and no other negative curve. Suppose ${\textbf{E}}:=L_{14}\cup L_{24}\cup L_{24}\cup E_5$. By [6, Section 6.2] we have:

$$\begin{aligned}\delta _P(T)=\left\{ \begin{aligned}&1\text { if }P\in E_4,\\&6/5\text { if }P\in {\textbf{E}}\backslash E_4,\\&4/3\text { if }P \text { belongs to two curves in }\{E_1,E_2,E_3,L_{12},L_{13},L_{23},L_{45},C_2\},\\&18/13\text { if }P\text { belongs to exactly one curve in } \{E_1,E_2,E_3,L_{12},L_{13},L_{23},\\&L_{45},C_2\}\backslash {\textbf{E}},\\&3/2,\text { otherwise} \end{aligned} \right. \end{aligned}$$

where $E_1$, $E_2$, $E_3$, $E_4$, $E_5$ are exceptional divisors corresponding to $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ respectively, $C_{2}$ is a strict transform of a $(-1)$-curve coming from the conic on ${\mathbb {P}}^2$, $L_{ij}$ are strict transforms of the lines passing through $P_i$ and $P_j$ for $(i,j)\in \{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)\}$ and $L_{45}$ a strict transform of a $(-1)$-curve coming from a line on ${\mathbb {P}}^2$. The dual graph of $(-1)$ and $(-2)$-curves is given in the following picture:

Lemma A.1

Suppose P is a point on T and $D=-K_{T}-(u-1)C_2$ with $D^2=5-u^2$ then

$$\begin{aligned}\delta _{P}(T,D)= \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3} \ \text { for }P\in E_4\backslash E_5 \text { and }u\in [1,2]\\&\frac{15 - 3 u^2}{11 - u^3}\text { for }P\in E_5\backslash E_4\text { and }u\in [1,2]\\&\frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\ \text { for }P\in L_{14}\backslash (E_4\cup E_5 \cup E_1)\ \text { and }u\in [1,2]\\ \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13} \ \text { for }P=E_4\cap E_5 \text { and }u\in [1,a]\\&\frac{15 - 3 u^2}{11 - u^3}\ \text { for }P= E_4\cap E_5 \text { and }u\in [a,2]\\ \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\ \text { for }P=L_{14}\cap E_1 \text { and }u\in [1,b]\\&\frac{2(15 - 3 u^2)}{19 - 2u^3}\ \text { for }P=L_{14}\cap E_1 \text { and }u\in [b,3/2]\\&\frac{15 - 3 u^2}{3u^3 - 18u^2 + 27u - 4}\text { for }P=L_{14}\cap E_1 \text { and }u\in [3/2,2] \end{aligned} \right. \end{aligned}$$

where a is a root of $3u^3 - 9u^2 + 3u + 5$ on [1, 2], b is a root of $8u^3 - 24u^2 + 12u + 7$ on [1, 3/2]. Note that $a\in [1.355,1.356]$, $b\in [1.261,1.262]$.

Proof

Step 1. Suppose $P\in E_4$. In this case we set ${\mathcal {C}}= E_4$. Then $\tau ({\mathcal {C}})=3-u$. The Zariski Decomposition of the divisor $D-vE_4$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}-K_{T}-(u-1)C_2-vE_4\text { for }v\in [0,2-u]\\ -K_{T}-(u-1)C_2-vE_4-(u+v-2)E_5\text { for }v\in [2-u,1]\\ -K_{T}-(u-1)C_2-vE_4-(u+v-2)E_5-(v-1)(L_{14}+L_{24}+L_{34})\\ \text {for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll} 0\text { for }v\in [0,2-u]\\ (u+v-2)E_5\text { for }v\in [2-u,1]\\ (u+v-2)E_5+(v-1)(L_{14}+L_{24}+L_{34})\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

Moreover,

$$\begin{aligned}P(v)^2={\left\{ \begin{array}{ll}5 -u^2 - 2v^2 \text { for }v\in [0,2-u]\\ 9+ 2uv - 4u - 4v - v^2\text { for }v\in [2-u,1]\\ 2(2 -v)(3 - u - v)\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}={\left\{ \begin{array}{ll} 2v\text { for }v\in [0,2-u]\\ 2-u+v\text { for }v\in [2-u,1]\\ 5-u-2v\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{2-u} 5 -u^2 - 2v^2 dv+\int _{2-u}^1 9+ 2uv - 4u - 4v - v^2 dv\\&\quad +\int _{1}^{3-u} 2(2 -v)(3 - u - v) dv\Big )=\frac{16 + 3 u - 9 u^2 + 2 u^3}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}$ for $P\in E_4$. Note that we have:

• if $P\in E_4\backslash (E_5\cup L_{14}\cup L_{24}\cup L_{34})$

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll}2v^2\text { for }v\in [0,2-u]\\ \frac{(2-u+v)^2}{2}\text { for }v\in [2-u,1]\\ \frac{(5-u-2v)^2}{2}\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P=E_4\cap E_5$

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll}2v^2\text { for }v\in [0,2-u]\\ \frac{(2 - u + v) (u + 3 v - 2)}{2}\text { for }v\in [2-u,1]\\ \frac{(u + 1) (5-u - 2 v)}{2}\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P\in E_4\cap (L_{14}\cup L_{24}\cup L_{34})$

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll}2v^2\text { for }v\in [0,2-u]\\ \frac{(2-u+v)^2}{2}\text { for }v\in [2-u,1]\\ \frac{(3 - u) (5-u - 2 v)}{2}\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

So we have

• if $P\in E_4\backslash (E_5\cup L_{14}\cup L_{24}\cup L_{34})$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} 2v^2 dv\\&\quad +\int _{2-u}^1 \frac{(2-u+v)^2}{2} dv+\int _{1}^{3-u} \frac{(5-u-2v)^2}{2} dv\Big )\\&=\frac{9 + 6 u - 9 u^2 + 2 u^3}{15 - 3 u^2}\le \frac{16 + 3 u - 9 u^2 + 2 u^3}{15 - 3 u^2} \end{aligned}$$

• if $P=E_4\cap E_5$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} 2v^2 dv+\int _{2-u}^1\frac{(2 - u + v) (u + 3 v - 2)}{2} dv\\&\quad +\int _{1}^{3-u} \frac{(u + 1) (5-u - 2 v)}{2} dv\Big )=\frac{11 - u^3}{15-3u^2} \end{aligned}$$

• if $P\in E_4\cap (L_{14}\cup L_{24}\cup L_{34})$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} 2v^2 dv+\int _{2-u}^1 \frac{(2-u+v)^2}{2} dv\\&\quad +\int _{1}^{3-u} \frac{(3 - u) (5-u - 2 v)}{2}dv\Big )\\&=\frac{13 + 3 u^3 - 12 u^2 + 6 u}{15 - 3u^2}\\ {}&\le \frac{16 + 3 u - 9 u^2 + 2 u^3}{15 - 3 u^2} \end{aligned}$$

We obtain that

$$\begin{aligned} \delta _{P}(T,D)= \frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }P\in E_4\backslash E_5 \text { and }u\in [1,2] \end{aligned}$$

and

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }P=E_4\cap E_5 \text { and }u\in [1,a]\\&\frac{15 - 3 u^2}{11 - u^3}\text { for }P= E_4\cap E_5 \text { and }u\in [a,2] \end{aligned} \right. \end{aligned}$$

where a is a root of $3u^3 - 9u^2 + 3u + 5$ on [1, 2]. Note that $a\in [1.355,1.356]$.

Step 2. Suppose $P\in E_5$. In this case we set ${\mathcal {C}}= E_5$. Then $\tau ({\mathcal {C}})=2$. The Zariski Decomposition of the divisor $D-vE_5$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}-K_{T}-(u-1)C_2-vE_5-\frac{v}{2}E_4\text { for }v\in [0,1]\\ -K_{T}-(u-1)C_2-vE_5-\frac{v}{2}E_4-(v-1)L_{45}\text { for }v\in [1,u]\\ -K_{T}-(u-1)C_2-vE_5-\frac{v}{2}E_4-(v-1)L_{45}-(v-u)C_2\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll}\frac{v}{2}E_4\text { for }v\in [0,1]\\ \frac{v}{2}E_4+(v-1)L_{45}\text { for }v\in [1,u]\\ \frac{v}{2}E_4+(v-1)L_{45}+(v-u)C_2\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

Moreover,

$$\begin{aligned}P(v)^2= {\left\{ \begin{array}{ll} 5 - 4v + 2uv - u^2 - \frac{v^2}{2} \text { for }v\in [0,1]\\ 6 - 6v + \frac{v^2}{2} + 2uv - u^2\text { for }v\in [1,u]\\ \frac{3(2 - v)^2}{2}\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}={\left\{ \begin{array}{ll} 2-u+v/2\text { for }v\in [0,1]\\ 3-u-v/2\text { for }v\in [1,u]\\ 3-3v/2\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{1} 5 - 4v + 2uv - u^2 - \frac{v^2}{2} dv\\&\quad +\int _{1}^{u} 6 - 6v + \frac{v^2}{2} + 2uv - u^2 dv\\&\quad +\int _{u}^{2} \frac{3(2 - v)^2}{3} dv\Big )=\frac{11 - u^3}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{11 - u^3}$ for $P\in E_5$. Note that we have:

• if $P\in E_5\backslash (E_4\cup C_2\cup L_{45})$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(2-u+v/2)^2}{2}\text { for }v\in [0,1]\\ \frac{(3-u-v/2)^2}{2}\text { for }v\in [1,u]\\ \frac{(3-3v/2)^2}{2}\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

• if $P=E_5\cap C_2$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(2-u+v/2)^2}{2}\text { for }v\in [0,1]\\ \frac{(3-u-v/2)^2}{2}\text { for }v\in [1,u]\\ \frac{ 3 (2 - v) (6 -4 u + v)}{8}\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

• if $P= E_5\cap L_{45}$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(2-u+v/2)^2}{2}\text { for }v\in [0,1]\\ \frac{(6-2 u - v) (2-2 u + 3 v)}{8}\text { for }v\in [1,u]\\ \frac{3(2 - v) (v + 2)}{8}\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

So we have

• if $P\in E_5\backslash (E_4\cup C_2\cup L_{45})$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{1} \frac{(2-u+v/2)^2}{2} dv+\int _{1}^u \frac{(3-u-v/2)^2}{2} dv\\&\quad +\int _{u}^{2} \frac{(3-3v/2)^2}{2} dv\Big )=\frac{21 + 6 u - 18 u^2 + 5 u^3}{2(15 - 3 u^2)}\le \frac{11 - u^3}{15 - 3 u^2} \end{aligned}$$

• if $P= E_5\cap C_2$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{1} \frac{(2-u+v/2)^2}{2} dv+\int _{1}^u \frac{(3-u-v/2)^2}{2} dv\\&\quad +\int _{u}^{2} \frac{ 3 (2 - v) (6 -4 u + v)}{8} dv\Big )=\frac{45 - 30 u + 2 u^3}{2(15 - 3 u^2)}\le \frac{11 - u^3}{15 - 3 u^2} \end{aligned}$$

• if $P= E_5\cap L_{45}$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{1} \frac{(2-u+v/2)^2}{2} dv\\&\quad +\int _{1}^u \frac{(6-2 u - v) (2-2 u + 3 v)}{8}dv\\&\quad +\frac{3(2 - v) (v + 2)}{8} dv\Big )=\frac{26 - 12 u^2 + 3 u^3}{2(15 - 3 u^2)}\le \frac{11 - u^3}{15 - 3 u^2} \end{aligned}$$

We obtain that

$$\begin{aligned} \delta _P(T,D)= \frac{15 - 3 u^2}{11 - u^3}\text { for }P\in E_5\backslash E_4\text { and }u\in [1,2]. \end{aligned}$$

Step 3.1. Suppose $P\in L_{14}\cup L_{24}\cup L_{34}$ and $u\in [1,3/2]$. Without loss of generality, we can assume that $P\in L_{14}$. In this case we set ${\mathcal {C}}= L_{14}$. Then $\tau ({\mathcal {C}})=3-u$. The Zariski Decomposition of the divisor $D-vL_{14}$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}D-vL_{14}-\frac{v}{2}E_4\text { for }v\in [0,2-u]\\ D-vL_{14}-\frac{v}{2}E_4-(u+v-2)E_1\text { for }v\in [2-u,1]\\ D-vL_{14}-\frac{v}{2}E_4-(u+v-2)E_1-(v-1)L_{23}\text { for }v\in [1,4-2u]\\ D-vL_{14}-(u+v-2)(E_1+E_4)-(v-1)L_{23}-(2u+v-4)E_5\\ \text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll}\frac{v}{2}E_4\text { for }v\in [0,2-u]\\ \frac{v}{2}E_4+(u+v-2)E_1\text { for }v\in [2-u,1]\\ \frac{v}{2}E_4+(u+v-2)E_1+(v-1)L_{23}\text { for }v\in [1,4-2u]\\ (u+v-2)(E_1+E_4)+(v-1)L_{23}+(2u+v-4)E_5\\ \text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

Moreover

$$\begin{aligned}P(v)^2= {\left\{ \begin{array}{ll}5 - 2v - \frac{v^2}{2} - u^2\text { for }v\in [0,2-u]\\ 9 - 4u - 6v + \frac{v^2}{2} + 2uv\text { for }v\in [2-u,1]\\ \frac{(v - 2)(3v + 4u - 10)}{2}\text { for }v\in [1,4-2u]\\ 2( u + v-3)^2\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}= {\left\{ \begin{array}{ll} v/2 + 1\text { for }v\in [0,2-u]\\ 3 - u - v/2\text { for }v\in [2-u,1]\\ 4 - u - 3v/2\text { for }v\in [1,4-2u]\\ 2(3 - u - v)\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{2-u} 5 - 2v - \frac{v^2}{2} - u^2 dv +\int _{2-u}^{1} 9 - 4u - 6v + \frac{v^2}{2} + 2uv dv\\&\quad +\int _{1}^{4-2u} \frac{(v - 2)(3v + 4u - 10)}{2} dv\\&\quad +\int _{4-2u}^{3-u} 2( u + v-3)^2 dv\Big )=\frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}$ for $P\in L_{14}$. Note that we have:

• if $P\in L_{14}\backslash (E_4\cup E_1\cup L_{23}\cup E_5)$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(v/2 + 1)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(3 - u - v/2)^2}{2}\text { for }v\in [2-u,1]\\ \frac{(4 - u - 3v/2)^2}{2}\text { for }v\in [1,4-2u]\\ 2(3 - u - v)^2\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

• if $P = L_{14} \cap E_1$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(v/2 + 1)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(6 - 2 u - v ) (2 u + 3 v - 2)}{8}\text { for }v\in [2-u,1]\\ \frac{(8 -2 u - 3 v) (2 u + v)}{8}\text { for }v\in [1,4-2u]\\ (3-u - v)\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

• if $P = L_{14}\cap L_{23}$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(v/2 + 1)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(3 - u - v/2)^2}{2}\text { for }v\in [2-u,1]\\ \frac{(8 -2 u - 3 v) (4 -2 u + v)}{8}\text { for }v\in [1,4-2u]\\ 2 (2 - u) (3 - u - v)\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

So we have

• if $P\in L_{14}\backslash (E_4\cup E_1\cup L_{23}\cup E_5)$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv+\int _{2-u}^1 \frac{(3 - u - v/2)^2}{2} dv\\&\quad +\int _{1}^{4-2u} \frac{(4 - u - 3v/2)^2}{2} dv+ \int _{4-2u}^{3-u} 2(3 - u - v)^2 dv\Big )\\&=\frac{21-u^3 - 6u}{2(15 - 3 u^2)}\le \frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

• if $P = L_{14}\cap E_1$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv\\&\quad +\int _{2-u}^1 \frac{(6 - 2 u - v ) (2 u + 3 v - 2)}{8} dv \\&\quad +\int _{1}^{4-2u} \frac{(8 -2 u - 3 v) (2 u + v)}{8} dv\\&\quad + \int _{4-2u}^{3-u}(3-u - v) dv\Big )=\frac{19 - 2u^3}{2(15 - 3 u^2)} \end{aligned}$$

• if $P = L_{14}\cap L_{23}$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv+\int _{2-u}^1\frac{(3 - u - v/2)^2}{2} dv\\&\quad +\int _{1}^{4-2u} \frac{(8 -2 u - 3 v) (4 -2 u + v)}{8} dv\\&\quad + \int _{4-2u}^{3-u} 2 (2 - u) (3 - u - v) dv\Big )\\&=\frac{26 - 12u^2 + 3u^3}{2(15 - 3 u^2)}\le \frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

We obtain that

$$\begin{aligned}\delta _{P}(T,D)= \frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\text { for }P\in L_{14}\backslash (E_4\cup E_5 \cup E_1) \text { and }u\in [1,3/2]\end{aligned}$$

and

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\text { for }P=L_{14}\cap E_1 \text { and }u\in [1,b]\\&\frac{2(15 - 3 u^2)}{19 - 2u^3}\text { for }P=L_{14}\cap E_1 \text { and }u\in [b,3/2] \end{aligned} \right. \end{aligned}$$

where b is a root of $8u^3 - 24u^2 + 12u + 7$ on [1, 3/2]. Note that $b\in [1.261,1.262]$.

Step 3.2. Suppose $P\in L_{14}\cup L_{24}\cup L_{34}$ and $u\in [3/2,2]$. Without loss of generality, we can assume that $P\in L_{14}$. In this case we set ${\mathcal {C}}= L_{14}$. Then $\tau ({\mathcal {C}})=3-u$. The Zariski Decomposition of the divisor $D-vL_{14}$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}D-vL_{14}-\frac{v}{2}E_4\text { for }v\in [0,2-u]\\ D-vL_{14}-\frac{v}{2}E_4-(u+v-2)E_1\text { for }v\in [2-u,4-2u]\\ D-vL_{14}-(u+v-2)(E_1+E_4)-(2u+v-4)E_5\text { for }v\in [4-2u,1]\\ D-vL_{14}-(u+v-2)(E_1+E_4)-(v-1)L_{23}-(2u+v-4)E_5\\ \text { for }v\in [1, 3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll} \frac{v}{2}E_4\text { for }v\in [0,2-u]\\ \frac{v}{2}E_4+(u+v-2)E_1\text { for }v\in [2-u,4-2u]\\ (u+v-2)(E_1+E_4)+(2u+v-4)E_5\text { for }v\in [4-2u,1]\\ (u+v-2)(E_1+E_4)+(v-1)L_{23}+(2u+v-4)E_5\text { for }v\in [1, 3-u] \end{array}\right. }\end{aligned}$$

Moreover

$$\begin{aligned}P(v)^2= {\left\{ \begin{array}{ll}5 - 2v -\frac{v^2}{2} - u^2\text { for }v\in [0,2-u]\\ 9 - 4u - 6v + \frac{v^2}{2} + 2uv\text { for }v\in [2-u,4-2u]\\ 2u^2 + 4uv + v^2 - 12u - 10v + 17\text { for }v\in [4-2u,1]\\ 2(u + v-3)^2\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}= {\left\{ \begin{array}{ll} 1 + v/2\text { for }v\in [0,2-u]\\ 3 - u - v/2\text { for }v\in [2-u,4-2u]\\ 5 - 2u - v\text { for }v\in [4-2u,1]\\ 2(3 - u - v)\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{2-u} 5 - 2v - \frac{v^2}{2} - u^2 dv +\int _{2-u}^{4-2u} 9 - 4u - 6v + \frac{v^2}{2} + 2uv dv\\&\quad +\int _{4-2u}^1 2u^2 + 4uv + v^2 - 12u - 10v + 17 dv+\int _{1}^{3-u} 2( u + v-3)^2 dv\Big )\\&=\frac{3u^3 - 12u^2 + 6u + 13}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{3u^3 - 12u^2 + 6u + 13}$ for $P\in L_{14}$. Note that we have:

• if $P\in L_{14}\backslash (E_4\cup E_1\cup L_{23}\cup E_5)$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(1+ v/2)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(3 - u - v/2)^2}{2}\text { for }v\in [2-u,4-2u]\\ \frac{(5 - 2u - v)^2}{2}\text { for }v\in [4-2u,1]\\ 2(3 - u - v)^2\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P = L_{14} \cap E_1$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(1+ v/2)^2}{2}\text { for }v\in [0,2-u]\\ \frac{ (6 -2 u - v ) (2 u + 3 v - 2)}{8}\text { for }v\in [2-u,4-2u]\\ \frac{(v + 1) (5 -2 u - v)}{2}\text { for }v\in [4-2u,1]\\ 2 (3-u - v)\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P= L_{14}\cap L_{23}$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(1+ v/2)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(3 - u - v/2)^2}{2}\text { for }v\in [2-u,4-2u]\\ \frac{(5 - 2u - v)^2}{2}\text { for }v\in [4-2u,1]\\ 2 (2 - u) (3 -u - v)\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P\in L_{14}\backslash (E_4\cup E_1\cup L_{23}\cup E_5)$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv+\int _{2-u}^{4-2u} \frac{(3 - u - v/2)^2}{2} dv\\&\quad +\int _{4-2u}^1 \frac{(5-2u-v)^2}{2} dv+ \int _{1}^{3-u} 2(3 - u - v)^2 dv\Big )\\&=\frac{7u^3 - 36u^2 + 48u - 6}{2(15 - 3 u^2)}\le \frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

• if $P = L_{14}\cap E_1$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv\\&\quad +\int _{2-u}^{4-2u} \frac{ (6 -2 u - v ) (2 u + 3 v - 2)}{8} dv\\&\quad +\int _{4-2u}^1 \frac{(v + 1) (5 -2 u - v)}{2} dv+ \int _{1}^{3-u} 2 (3-u - v) dv\Big )\\&=\frac{3u^3 - 18u^2 + 27u - 4}{15 - 3 u^2} \end{aligned}$$

• if $P = L_{14}\cap L_{23}$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv+\int _{2-u}^{4-2u} \frac{(3 - u - v/2)^2}{2} dv\\&\quad +\int _{4-2u}^1 \frac{(5-2u-v)^2}{2} dv+ \int _{1}^{3-u} 2 (2 - u) (3 -u - v) dv\Big )\\&=\frac{3u^3 - 12u^2 + 26}{2(15 - 3 u^2)}\le \frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

We obtain that

$$\begin{aligned} \delta _{P}(T,D)= \frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\text { for }P\in L_{14}\backslash (E_1\cup E_4 \cup E_5) \text { and }u\in [3/2,2] \end{aligned}$$

and

$$\begin{aligned} \delta _{P}(T,D)\ge \frac{15 - 3 u^2}{3u^3 - 18u^2 + 27u - 4}\text { for }P=L_{14}\cap E_1 \text { and }u\in [3/2,2] \end{aligned}$$

$\square$

Corollary A.1

Let P be a point in T that is contained in $L_{12}\cup L_{24}\cup L_{34}\cup E_4 \cup E_5$ then

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }u\in [1,a],\\&\frac{15 - 3 u^2}{11 - u^3}\text { for }u\in [a,2] \end{aligned} \right. \end{aligned}$$

Corollary A.2

Suppose O is a point on a del Pezzo surface ${\overline{T}}$ with ${\mathbb {A}}_1$ singularity and $\delta _O(T)\le \frac{6}{5}$ then

$$\begin{aligned}\delta _{O}({\overline{T}},{\overline{D}})\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }u\in [1,a],\\&\frac{15 - 3 u^2}{11 - u^3}\text { for }u\in [a,2] \end{aligned} \right. \end{aligned}$$

1.2 Polarized $\delta$-invariant on Del Pezzo surface of degree 4 with two ${\mathbb {A}}_1$ singularities.

Suppose that ${\overline{T}}$ has two singular points and these points are singular point of type ${\mathbb {A}}_1$. Then $\eta$ is a blow up of ${\mathbb {P}}^2$ at points $P_1$, $P_2$, and $P_4$ in general position and after that blowing up a point $P_3$ which belongs to the exceptional divisor corresponding to $P_2$ and a point $P_5$ which belongs to the exceptional divisor corresponding to $P_4$ and no other negative curve. By [6, Section 6.2] we have:

$$\begin{aligned}\delta _P(T)= \left\{ \begin{aligned}&1\text { if }P\in (E_2\cup E_4\cup L_{24}),\\&6/5\text { if }P\in (E_3\cup E_5\cup L_{12}\cup L_{14})\backslash (E_2\cup E_4),\\&4/3\text { if }P\in (C_2\cap E_1)\cup (L_{23}\cap L_{45}),\\&18/13\text { if }P\in (C_2\cup E_1\cup L_{23}\cup L_{45})\backslash \big ((C_2\cap E_1)\cup (L_{23}\cap L_{45})\\&\cup (E_3\cup E_5\cup L_{12}\cup L_{14})\big ),\\&3/2,\text { otherwise } \end{aligned} \right. \end{aligned}$$

where $E_1$, $E_2$, $E_3$, $E_4$, $E_5$ are exceptional divisors corresponding to $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ respectively, $C_{2}$ is a strict transform of a $(-1)$-curve coming from the conic on ${\mathbb {P}}^2$, $L_{ij}$ are strict transforms of the lines passing through $P_i$ and $P_j$ for $(i,j)\in \{(1,2),(1,4)\}$ and $L_{45}$ and $L_{23}$ are strict transforms of a $(-1)$-curve coming from lines passing through $P_2$ and $P_4$ respectively on ${\mathbb {P}}^2$. The dual graph of $(-1)$ and $(-2)$-curves is given in the following picture:

Lemma A.2

Suppose P is a point on T and $D=-K_{T}-(u-1)C_2$ with $D^2=5-u^2$ then

$$\begin{aligned}\delta _{P}(T,D)= \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }P\in (E_2\cup E_4)\backslash (E_3\cup E_5) \text { and }u\in [1,2],\\&\frac{15 - 3 u^2}{11 - u^3}\text { for }P\in (E_3\cup E_5)\backslash (E_2\cup E_4)\text { and }u\in [1,2],\\&\frac{15 - 3 u^2}{u^3 - 6u^2 + 6u + 5}\text { for }P\in L_{24}\backslash (E_2\cup E_4)\text { and }u\in [1,2],\\&\frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\text { for }P\in L_{14}\backslash (E_4\cup E_5 \cup E_1) \text { and }u\in [1,2], \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }P\in \{E_2\cap E_3,E_4 \cap E_5\} \text { and }u\in [1,a],\\&\frac{15 - 3 u^2}{11 - u^3}\text { for }P\in \{E_2\cap E_3,E_4 \cap E_5\} \text { and }u\in [a,2] \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\text { for }P=L_{14}\cap E_1 \text { and }u\in [1,b],\\&\frac{2(15 - 3 u^2)}{19 - 2u^3}\text { for }P=L_{14}\cap E_1 \text { and }u\in [b,3/2],\\&\frac{15 - 3 u^2}{3u^3 - 18u^2 + 27u - 4}\text { for }P=L_{14}\cap E_1 \text { and }u\in [3/2,2], \end{aligned} \right. \end{aligned}$$

where a is a root of $3u^3 - 9u^2 + 3u + 5$ on [1, 2], b is a root of $8u^3 - 24u^2 + 12u + 7$ on [1, 3/2]. Note that $a\in [1.355,1.356]$, $b\in [1.261,1.262]$.

Proof

Step 1. Suppose $P\in E_2\cup E_4$. Without loss of generality we can assume that $P\in E_4$. In this case we set ${\mathcal {C}}= E_4$. Then $\tau ({\mathcal {C}})=3-u$. The Zariski Decomposition of the divisor $D-vE_4$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}-K_{T}-(u-1)C_2-vE_4\text { for }v\in [0,2-u]\\ -K_{T}-(u-1)C_2-vE_4-(u+v-2)E_5\text { for }v\in [2-u,1]\\ -K_{T}-(u-1)C_2-vE_4-(u+v-2)E_5-(v-1)(L_{14}+2L_{24}+E_2)\\ \text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll} 0\text { for }v\in [0,2-u]\\ (u+v-2)E_5\text { for }v\in [2-u,1]\\ (u+v-2)E_5+(v-1)(L_{14}+2L_{24}+E_2)\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

Moreover,

$$\begin{aligned}P(v)^2={\left\{ \begin{array}{ll}5 -u^2 - 2v^2 \text { for }v\in [0,2-u]\\ 9+ 2uv - 4u - 4v - v^2\text { for }v\in [2-u,1]\\ 2(2 -v)(3 - u - v)\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}={\left\{ \begin{array}{ll} 2v\text { for }v\in [0,2-u]\\ 2-u+v\text { for }v\in [2-u,1]\\ 5-u-2v\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{2-u} 5 -u^2 - 2v^2 dv+\int _{2-u}^1 9+ 2uv - 4u - 4v - v^2 dv\\&\quad +\int _{1}^{3-u} 2(2 -v)(3 - u - v) dv\Big )=\frac{16 + 3 u - 9 u^2 + 2 u^3}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}$ for $P\in E_4$. Note that we have:

• if $P\in E_4\backslash (E_5\cup L_{14}\cup L_{24}\cup L_{34})$

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll}2v^2\text { for }v\in [0,2-u]\\ \frac{(2-u+v)^2}{2}\text { for }v\in [2-u,1]\\ \frac{(5-u-2v)^2}{2}\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P=E_4\cap E_5$

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll}2v^2\text { for }v\in [0,2-u]\\ \frac{(2 - u + v) (u + 3 v - 2)}{2}\text { for }v\in [2-u,1]\\ \frac{(u + 1) (5-u - 2 v)}{2}\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P\in E_4\cap (L_{14}\cup L_{24})$

  $$\begin{aligned}h_D(v)\le {\left\{ \begin{array}{ll}2v^2\text { for }v\in [0,2-u]\\ \frac{(2-u+v)^2}{2}\text { for }v\in [2-u,1]\\ \frac{(5-u - 2 v) (1 -u + 2 v)}{2}\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

So we have

• if $P\in E_4\backslash (E_5\cup L_{14}\cup L_{24}\cup L_{34})$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} 2v^2 dv+\int _{2-u}^1 \frac{(2-u+v)^2}{2} dv\\&\quad +\int _{1}^{3-u} \frac{(5-u-2v)^2}{2} dv\Big )\\&=\frac{9 + 6 u - 9 u^2 + 2 u^3}{15 - 3 u^2}\le \frac{16 + 3 u - 9 u^2 + 2 u^3}{15 - 3 u^2} \end{aligned}$$

• if $P=E_4\cap E_5$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} 2v^2 dv+\int _{2-u}^1\frac{(2 - u + v) (u + 3 v - 2)}{2} dv\\&\quad +\int _{1}^{3-u} \frac{(u + 1) (5-u - 2 v)}{2} dv\Big )=\frac{11 - u^3}{15-3u^2} \end{aligned}$$

• if $P\in E_4\cap (L_{14}\cup L_{24})$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} 2v^2 dv+\int _{2-u}^1 \frac{(2-u+v)^2}{2} dv\\&\quad +\int _{1}^{3-u} \frac{(5-u - 2 v) (1 -u + 2 v)}{2}dv\Big )\\&=\frac{2u^3 - 6u^2 + 8}{15 - 3u^2}\le \frac{16 + 3 u - 9 u^2 + 2 u^3}{15 - 3 u^2} \end{aligned}$$

We obtain that

$$\begin{aligned} \delta _{P}(T,D)= \frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }P\in E_4\backslash E_5 \text { and }u\in [1,2] \end{aligned}$$

and

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }P=E_4\cap E_5 \text { and }u\in [1,a]\\&\frac{15 - 3 u^2}{11 - u^3}\text { for }P= E_4\cap E_5 \text { and }u\in [a,2] \end{aligned} \right. \end{aligned}$$

where a is a root of $3u^3 - 9u^2 + 3u + 5$ on [1, 2]. Note that $a\in [1.355,1.356]$.

Step 2. Suppose $P\in E_3\cup E_5$. Without loss of generality we can assume that $P\in E_5$. In this case we set ${\mathcal {C}}= E_5$. Then $\tau ({\mathcal {C}})=2$. The Zariski Decomposition of the divisor $D-vE_5$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}-K_{T}-(u-1)C_2-vE_5-\frac{v}{2}E_4\text { for }v\in [0,1]\\ -K_{T}-(u-1)C_2-vE_5-\frac{v}{2}E_4-(v-1)L_{45}\text { for }v\in [1,u]\\ -K_{T}-(u-1)C_2-vE_5-\frac{v}{2}E_4-(v-1)L_{45}-(v-u)C_2\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll}\frac{v}{2}E_4\text { for }v\in [0,1]\\ \frac{v}{2}E_4+(v-1)L_{45}\text { for }v\in [1,u]\\ \frac{v}{2}E_4+(v-1)L_{45}+(v-u)C_2\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

Moreover,

$$\begin{aligned}P(v)^2= {\left\{ \begin{array}{ll} 5 - 4v + 2uv - u^2 - \frac{v^2}{2} \text { for }v\in [0,1]\\ 6 - 6v + \frac{v^2}{2} + 2uv - u^2\text { for }v\in [1,u]\\ \frac{3(2 - v)^2}{2}\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}={\left\{ \begin{array}{ll} 2-u+v/2\text { for }v\in [0,1]\\ 3-u-v/2\text { for }v\in [1,u]\\ 3-3v/2\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{1} 5 - 4v + 2uv - u^2 - \frac{v^2}{2} dv\\&\quad +\int _{1}^{u} 6 - 6v + \frac{v^2}{2} + 2uv - u^2 dv\\&\quad +\int _{u}^{2} \frac{3(2 - v)^2}{3} dv\Big )=\frac{11 - u^3}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{11 - u^3}$ for $P\in E_5$. Note that we have:

• if $P\in E_5\backslash (E_4\cup C_2\cup L_{45})$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(2-u+v/2)^2}{2}\text { for }v\in [0,1]\\ \frac{(3-u-v/2)^2}{2}\text { for }v\in [1,u]\\ \frac{(3-3v/2)^2}{2}\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

• if $P=E_5\cap C_2$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(2-u+v/2)^2}{2}\text { for }v\in [0,1]\\ \frac{(3-u-v/2)^2}{2}\text { for }v\in [1,u]\\ \frac{ 3 (2 - v) (6 -4 u + v)}{8}\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

• if $P= E_5\cap L_{45}$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(2-u+v/2)^2}{2}\text { for }v\in [0,1]\\ \frac{(6-2 u - v) (2-2 u + 3 v)}{8}\text { for }v\in [1,u]\\ \frac{3(2 - v) (v + 2)}{8}\text { for }v\in [u,2] \end{array}\right. }\end{aligned}$$

So we have

• if $P\in E_5\backslash (E_4\cup C_2\cup L_{45})$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{1} \frac{(2-u+v/2)^2}{2} dv+\int _{1}^u \frac{(3-u-v/2)^2}{2} dv\\&\quad +\int _{u}^{2} \frac{(3-3v/2)^2}{2} dv\Big )=\frac{21 + 6 u - 18 u^2 + 5 u^3}{2(15 - 3 u^2)}\le \frac{11 - u^3}{15 - 3 u^2} \end{aligned}$$

• if $P= E_5\cap C_2$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{1} \frac{(2-u+v/2)^2}{2} dv+\int _{1}^u \frac{(3-u-v/2)^2}{2} dv\\&\quad +\int _{u}^{2} \frac{ 3 (2 - v) (6 -4 u + v)}{8} dv\Big )=\frac{45 - 30 u + 2 u^3}{2(15 - 3 u^2)}\le \frac{11 - u^3}{15 - 3 u^2} \end{aligned}$$

• if $P= E_5\cap L_{45}$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{1} \frac{(2-u+v/2)^2}{2} dv\\&\quad +\int _{1}^u \frac{(6-2 u - v) (2-2 u + 3 v)}{8}dv\\&\quad +\frac{3(2 - v) (v + 2)}{8} dv\Big )=\frac{26 - 12 u^2 + 3 u^3}{2(15 - 3 u^2)}\le \frac{11 - u^3}{15 - 3 u^2} \end{aligned}$$

We obtain that

$$\begin{aligned} \delta _P(T,D)= \frac{15 - 3 u^2}{11 - u^3}\text { for }P\in (E_3\cup E_5)\backslash (E_2\cup E_4)\text { and }u\in [1,2]. \end{aligned}$$

Step 3. Suppose $P\in L_{24}$. In this case we set ${\mathcal {C}}= L_{24}$. Then $\tau ({\mathcal {C}})=3-u$. The Zariski Decomposition of the divisor $D-vL_{24}$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}D-vL_{24}-\frac{v}{2}(E_2+E_4)\text { for }v\in [0,4-2u]\\ D-vL_{24}-(u+v-2)(E_2+E_4)-(2u+v-4)(E_3+E_5)\\ \text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll}\frac{v}{2}(E_2+E_4)\text { for }v\in [0,4-2u]\\ (u+v-2)(E_2+E_4)+(2u+v-4)(E_3+E_5)\text { for }v\in [4-2u, 3-u] \end{array}\right. }\end{aligned}$$

Moreover,

$$\begin{aligned}P(v)^2= {\left\{ \begin{array}{ll} -u^2 - 2v + 5 \text { for }v\in [0,4-2u]\\ (u + v - 3)(3u + v - 7)\text { for }v\in [4-2u,3-v] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}={\left\{ \begin{array}{ll} 1\text { for }v\in [0,4-2u]\\ 5 - 2u - v\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{4-2u} -u^2 - 2v + 5 dv+\int _{4-2u}^{3-uu} (u + v - 3)(3u + v - 7) dv\Big )\\&=\frac{4u^3 - 15u^2 + 6u + 17}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{4u^3 - 15u^2 + 6u + 17}$ for $P\in L_{24}$. If $P\in L_{24}\backslash (E_2\cup E_4)$ then

$$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{1}{2}\text { for }v\in [0,4-2u]\\ \frac{(5 - 2u - v)^2}{2}\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

So for $P\in L_{24}\backslash (E_2\cup E_4)$ we have

$$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{4-2u} \frac{1}{2} dv+\int _{4-2u}^{3-u} \frac{(5 - 2u - v)^2}{2} dv\\&=\frac{u^3 - 6u^2 + 6u + 5}{15 - 3 u^2}\le \frac{4u^3 - 15u^2 + 6u + 17}{15 - 3 u^2} \end{aligned}$$

We obtain that

$$\begin{aligned} \delta _P(T,D)= \frac{15 - 3 u^2}{u^3 - 6u^2 + 6u + 5}\text { for }P\in L_{24}\backslash (E_2\cup E_4)\text { and }u\in [1,2]. \end{aligned}$$

Step 4.1. Suppose $P\in L_{12}\cup L_{14}$ and $u\in [1,3/2]$. Without loss of generality, we can assume that $P\in L_{14}$. In this case we set ${\mathcal {C}}= L_{14}$. Then $\tau ({\mathcal {C}})=3-u$. The Zariski Decomposition of the divisor $D-vL_{14}$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}D-vL_{14}-\frac{v}{2}E_4\text { for }v\in [0,2-u]\\ D-vL_{14}-\frac{v}{2}E_4-(u+v-2)E_1\text { for }v\in [2-u,1]\\ D-vL_{14}-\frac{v}{2}E_4-(u+v-2)E_1-(v-1)L_{23}\text { for }v\in [1,4-2u]\\ D-vL_{14}-(u+v-2)(E_1+E_4)-(v-1)L_{23}-(2u+v-4)E_5\\ \text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll}\frac{v}{2}E_4\text { for }v\in [0,2-u]\\ \frac{v}{2}E_4+(u+v-2)E_1\text { for }v\in [2-u,1]\\ \frac{v}{2}E_4+(u+v-2)E_1+(v-1)L_{23}\text { for }v\in [1,4-2u]\\ (u+v-2)(E_1+E_4)+(v-1)L_{23}+(2u+v-4)E_5\\ \text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

Moreover

$$\begin{aligned}P(v)^2= {\left\{ \begin{array}{ll}5 - 2v - \frac{v^2}{2} - u^2\text { for }v\in [0,2-u]\\ 9 - 4u - 6v + \frac{v^2}{2} + 2uv\text { for }v\in [2-u,1]\\ \frac{(v - 2)(3v + 4u - 10)}{2}\text { for }v\in [1,4-2u]\\ 2( u + v-3)^2\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}= {\left\{ \begin{array}{ll} v/2 + 1\text { for }v\in [0,2-u]\\ 3 - u - v/2\text { for }v\in [2-u,1]\\ 4 - u - 3v/2\text { for }v\in [1,4-2u]\\ 2(3 - u - v)\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{2-u} 5 - 2v - \frac{v^2}{2} - u^2 dv +\int _{2-u}^{1} 9 - 4u - 6v + \frac{v^2}{2} + 2uv dv\\&\quad +\int _{1}^{4-2u} \frac{(v - 2)(3v + 4u - 10)}{2} dv+\int _{4-2u}^{3-u} 2( u + v-3)^2 dv\Big )\\&=\frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}$ for $P\in L_{14}$. Note that we have:

• if $P\in L_{14}\backslash (E_4\cup E_1\cup L_{23}\cup E_5)$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(v/2 + 1)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(3 - u - v/2)^2}{2}\text { for }v\in [2-u,1]\\ \frac{(4 - u - 3v/2)^2}{2}\text { for }v\in [1,4-2u]\\ 2(3 - u - v)^2\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

• if $P = L_{14} \cap E_1$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(v/2 + 1)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(6 - 2 u - v ) (2 u + 3 v - 2)}{8}\text { for }v\in [2-u,1]\\ \frac{(8 -2 u - 3 v) (2 u + v)}{8}\text { for }v\in [1,4-2u]\\ (3-u - v)\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

• if $P = L_{14}\cap L_{23}$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(v/2 + 1)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(3 - u - v/2)^2}{2}\text { for }v\in [2-u,1]\\ \frac{(8 -2 u - 3 v) (4 -2 u + v)}{8}\text { for }v\in [1,4-2u]\\ 2 (2 - u) (3 - u - v)\text { for }v\in [4-2u,3-u] \end{array}\right. }\end{aligned}$$

So we have

• if $P\in L_{14}\backslash (E_4\cup E_1\cup L_{23}\cup E_5)$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv+\int _{2-u}^1 \frac{(3 - u - v/2)^2}{2} dv\\&\quad +\int _{1}^{4-2u} \frac{(4 - u - 3v/2)^2}{2} dv\\&\quad + \int _{4-2u}^{3-u} 2(3 - u - v)^2 dv\Big )\\&=\frac{21-u^3 - 6u}{2(15 - 3 u^2)}\le \frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

• if $P = L_{14}\cap E_1$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv\\&\quad +\int _{2-u}^1 \frac{(6 - 2 u - v ) (2 u + 3 v - 2)}{8} dv\\&\quad +\int _{1}^{4-2u} \frac{(8 -2 u - 3 v) (2 u + v)}{8} dv+ \int _{4-2u}^{3-u}(3-u - v) dv\Big )\\&=\frac{19 - 2u^3}{2(15 - 3 u^2)} \end{aligned}$$

• if $P = L_{14}\cap L_{23}$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv+\int _{2-u}^1\frac{(3 - u - v/2)^2}{2} dv\\&\quad +\int _{1}^{4-2u} \frac{(8 -2 u - 3 v) (4 -2 u + v)}{8} dv\\&\quad + \int _{4-2u}^{3-u} 2 (2 - u) (3 - u - v) dv\Big )\\&=\frac{26 - 12u^2 + 3u^3}{2(15 - 3 u^2)}\le \frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

We obtain that

$$\begin{aligned}\delta _{P}(T,D)= \frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\text { for }P\in L_{14}\backslash (E_4\cup E_5 \cup E_1) \text { and }u\in [1,3/2]\end{aligned}$$

and

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\text { for }P=L_{14}\cap E_1 \text { and }u\in [1,b]\\&\frac{2(15 - 3 u^2)}{19 - 2u^3}\text { for }P=L_{14}\cap E_1 \text { and }u\in [b,3/2] \end{aligned} \right. \end{aligned}$$

where b is a root of $8u^3 - 24u^2 + 12u + 7$ on [1, 3/2]. Note that $b\in [1.261,1.262]$.

Step 4.2. Suppose $P\in L_{12}\cup L_{14}$ and $u\in [3/2,2]$. Without loss of generality, we can assume that $P\in L_{14}$. In this case we set ${\mathcal {C}}= L_{14}$. Then $\tau ({\mathcal {C}})=3-u$. The Zariski Decomposition of the divisor $D-vL_{14}$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}D-vL_{14}-\frac{v}{2}E_4\text { for }v\in [0,2-u]\\ D-vL_{14}-\frac{v}{2}E_4-(u+v-2)E_1\text { for }v\in [2-u,4-2u]\\ D-vL_{14}-(u+v-2)(E_1+E_4)-(2u+v-4)E_5\text { for }v\in [4-2u,1]\\ D-vL_{14}-(u+v-2)(E_1+E_4)-(v-1)L_{23}-(2u+v-4)E_5\\ \text { for }v\in [1, 3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll} \frac{v}{2}E_4\text { for }v\in [0,2-u]\\ \frac{v}{2}E_4+(u+v-2)E_1\text { for }v\in [2-u,4-2u]\\ (u+v-2)(E_1+E_4)+(2u+v-4)E_5\text { for }v\in [4-2u,1]\\ (u+v-2)(E_1+E_4)+(v-1)L_{23}+(2u+v-4)E_5\text { for }v\in [1, 3-u] \end{array}\right. }\end{aligned}$$

Moreover

$$\begin{aligned}P(v)^2= {\left\{ \begin{array}{ll}5 - 2v - \frac{v^2}{2} - u^2\text { for }v\in [0,2-u]\\ 9 - 4u - 6v + \frac{v^2}{2} + 2uv\text { for }v\in [2-u,4-2u]\\ 2u^2 + 4uv + v^2 - 12u - 10v + 17\text { for }v\in [4-2u,1]\\ 2(u + v-3)^2\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}= {\left\{ \begin{array}{ll} 1 + v/2\text { for }v\in [0,2-u]\\ 3 - u - v/2\text { for }v\in [2-u,4-2u]\\ 5 - 2u - v\text { for }v\in [4-2u,1]\\ 2(3 - u - v)\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{2-u} 5 - 2v - \frac{v^2}{2} - u^2 dv\\&\quad +\int _{2-u}^{4-2u} 9 - 4u - 6v + \frac{v^2}{2} + 2uv dv\\&\quad +\int _{4-2u}^1 2u^2 + 4uv + v^2 - 12u - 10v + 17 dv\\&\quad +\int _{1}^{3-u} 2( u + v-3)^2 dv\Big )=\frac{3u^3 - 12u^2 + 6u + 13}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{3u^3 - 12u^2 + 6u + 13}$ for $P\in L_{14}$. Note that we have:

• if $P\in L_{14}\backslash (E_4\cup E_1\cup L_{23}\cup E_5)$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(1+ v/2)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(3 - u - v/2)^2}{2}\text { for }v\in [2-u,4-2u]\\ \frac{(5 - 2u - v)^2}{2}\text { for }v\in [4-2u,1]\\ 2(3 - u - v)^2\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P = L_{14} \cap E_1$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(1+ v/2)^2}{2}\text { for }v\in [0,2-u]\\ \frac{ (6 -2 u - v ) (2 u + 3 v - 2)}{8}\text { for }v\in [2-u,4-2u]\\ \frac{(v + 1) (5 -2 u - v)}{2}\text { for }v\in [4-2u,1]\\ 2 (3-u - v)\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P= L_{14}\cap L_{23}$ then

  $$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{(1+ v/2)^2}{2}\text { for }v\in [0,2-u]\\ \frac{(3 - u - v/2)^2}{2}\text { for }v\in [2-u,4-2u]\\ \frac{(5 - 2u - v)^2}{2}\text { for }v\in [4-2u,1]\\ 2 (2 - u) (3 -u - v)\text { for }v\in [1,3-u] \end{array}\right. }\end{aligned}$$

• if $P\in L_{14}\backslash (E_4\cup E_1\cup L_{23}\cup E_5)$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv+\int _{2-u}^{4-2u} \frac{(3 - u - v/2)^2}{2} dv\\&\quad +\int _{4-2u}^1 \frac{(5-2u-v)^2}{2} dv+ \int _{1}^{3-u} 2(3 - u - v)^2 dv\Big )\\&=\frac{7u^3 - 36u^2 + 48u - 6}{2(15 - 3 u^2)}\le \frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

• if $P = L_{14}\cap E_1$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv\\&\quad +\int _{2-u}^{4-2u} \frac{ (6 -2 u - v ) (2 u + 3 v - 2)}{8} dv\\&\quad +\int _{4-2u}^1 \frac{(v + 1) (5 -2 u - v)}{2} dv+ \int _{1}^{3-u} 2 (3-u - v) dv\Big )\\&=\frac{3u^3 - 18u^2 + 27u - 4}{15 - 3 u^2} \end{aligned}$$

• if $P = L_{14}\cap L_{23}$ then

  $$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{(v/2 + 1)^2}{2} dv+\int _{2-u}^{4-2u} \frac{(3 - u - v/2)^2}{2} dv\\&\quad +\int _{4-2u}^1 \frac{(5-2u-v)^2}{2} dv+ \int _{1}^{3-u} 2 (2 - u) (3 -u - v) dv\Big )\\&=\frac{3u^3 - 12u^2 + 26}{2(15 - 3 u^2)}\le \frac{3 u^3 - 12 u^2 + 6 u + 13}{15 - 3 u^2} \end{aligned}$$

We obtain that

$$\begin{aligned} \delta _{P}(T,D)= \frac{15 - 3 u^2}{3 u^3 - 12 u^2 + 6 u + 13}\text { for }P\in L_{14}\backslash (E_1\cup E_4 \cup E_5) \text { and }u\in [3/2,2] \end{aligned}$$

and

$$\begin{aligned} \delta _{P}(T,D)\ge \frac{15 - 3 u^2}{3u^3 - 18u^2 + 27u - 4}\text { for }P=L_{14}\cap E_1 \text { and }u\in [3/2,2] \end{aligned}$$

$\square$

Corollary A.3

Let P be a point in T that is contained in $L_{12}\cup L_{14}\cup L_{24}\cup E_2\cup E_3\cup E_4\cup E_4$ then

$$\begin{aligned}\delta _{P}(T,D)\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }u\in [1,a],\\&\frac{15 - 3 u^2}{11 - u^3}\text { for }u\in [a,2] \end{aligned} \right. \end{aligned}$$

Corollary A.4

Suppose O is a point on a del Pezzo surface ${\overline{T}}$ with two ${\mathbb {A}}_1$ singularities and nine lines such that $\delta _O(T)\le \frac{6}{5}$ then

$$\begin{aligned}\delta _{O}({\overline{T}},{\overline{D}})\ge \left\{ \begin{aligned}&\frac{15 - 3 u^2}{16 + 3 u - 9 u^2 + 2 u^3}\text { for }u\in [1,a],\\&\frac{15 - 3 u^2}{11 - u^3}\text { for }u\in [a,2] \end{aligned} \right. \end{aligned}$$

1.3 Polarized $\delta$-invariant on Del Pezzo surface of degree 4 with ${\mathbb {A}}_2$ singularity

Now, let us use the notations and assumptions of Section 2 with a minor difference: we assume that ${\overline{T}}$ has a singular point of type ${\mathbb {A}}_2$. Let us show that in the case when O is the singular point of the surface ${\overline{T}}$ we have

$$\begin{aligned} \delta _O({\overline{T}},{\overline{D}})=\frac{15-3u^2}{u^3 - 6u^2 + 19} \end{aligned}$$

which immediately implies that $\delta _O({\overline{T}},W^{{\overline{T}}}_{\bullet ,\bullet })\le \frac{80}{83}$. In this case, the morphism $\eta$ is a blow up of ${\mathbb {P}}^2$ at points $P_1$, $P_2$, and $P_3$ in general position; after that blowing up a point $P_4$ which belongs to the exceptional divisor corresponding to $P_3$ and no other negative curve and after that a point $P_5$ which belongs to the exceptional divisor corresponding to $P_4$ and no other negative curve. By [6, Section 6.5] we have:

$$\begin{aligned}\delta _P(T)= \left\{ \begin{aligned}&6/7\text { if }P\in E_3\cup E_4,\\&8/7\text { if }P\in (L_{13}\cup L_{23}\cup L_{34}\cup E_5)\backslash (E_3\cup E_4),\\&4/3 \text { if }P\in (L_{12}\cup C_2)\cap (E_1\cup E_2),\\&18/13\text { if }P\in (L_{12}\cup C_2\cup E_1\cup E_2)\backslash ((L_{12}\cup C_2)\cap (E_1\cup E_2)),\\&3/2,\text { otherwise } \end{aligned} \right. \end{aligned}$$

where $E_1$, $E_2$, $E_3$, $E_4$, $E_5$ are exceptional divisors corresponding to $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ respectively, $C_{2}$ is a strict transform of a $(-1)$-curve coming from the conic on ${\mathbb {P}}^2$, $L_{ij}$ are strict transforms of the lines passing through $P_i$ and $P_j$ for $(i,j)\in \{(1,2),(1,3),(2,3)\}$ and $L_{34}$ is a strict transform of a $(-1)$-curve coming from a line passing through $P_3$ on ${\mathbb {P}}^2$. The dual graph of $(-1)$ and $(-2)$-curves is given in the following picture:

Now let’s prove that:

Lemma A.3

Suppose P is a point on T and $D=-K_{T}-(u-1)C_2$ with $D^2=5-u^2$ then

$$\begin{aligned} \delta _{P}(T,D)= \frac{15-3u^2}{u^3 - 6u^2 + 19}\text { for }P\in E_4\backslash (L_{34}\cup E_5) \end{aligned}$$

Proof

Suppose $P\in E_4\backslash (L_{34}\cup E_5)$. In this case we set ${\mathcal {C}}= E_4$. Then $\tau ({\mathcal {C}})=2$. The Zariski Decomposition of the divisor $D-vE_4$ is given by:

$$\begin{aligned}P(v)= {\left\{ \begin{array}{ll}-K_{T}-(u-1)C_2-vE_4-\frac{v}{2}E_3\text { for }v\in [0,2-u]\\ -K_{T}-(u-1)C_2-vE_4-\frac{v}{2}E_3-(u+v-2)E_5\text { for }v\in [2-u,1]\\ {-}K_{T}{-}(u{-}1)C_2{-}vE_4{-}\frac{v}{2}E_3-(u{+}v-2)E_5{-}(v{-}1)L_{34}\text { for }v\in [1,2] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}N(v)= {\left\{ \begin{array}{ll} \frac{v}{2}E_3\text { for }v\in [0,2-u]\\ \frac{v}{2}E_3+(u+v-2)E_5\text { for }v\in [2-u,1]\\ \frac{v}{2}E_3+(u+v-2)E_5+(v-1)L_{34}\text { for }v\in [1,2] \end{array}\right. }\end{aligned}$$

Moreover,

$$\begin{aligned}P(v)^2={\left\{ \begin{array}{ll}5 -u^2 - \frac{3v^2}{2} \text { for }v\in [0,2-u]\\ 9 - 4u - 4v + 2uv - 1/2v^2\text { for }v\in [2-u,1]\\ \frac{(v - 2)(v + 4u - 10)}{2}\text { for }v\in [1,2] \end{array}\right. }\end{aligned}$$

and

$$\begin{aligned}P(v)\cdot {\mathcal {C}}={\left\{ \begin{array}{ll} 3v/2\text { for }v\in [0,2-u]\\ 2-u+v/2\text { for }v\in [2-u,1]\\ 3-u-v/2\text { for }v\in [1,2] \end{array}\right. }\end{aligned}$$

Thus,

$$\begin{aligned} S_D({\mathcal {C}})&=\frac{1}{5-u^2}\Big (\int _0^{2-u} 5 -u^2 - \frac{3v^2}{2} dv+\int _{2-u}^1 9 - 4u - 4v + 2uv - 1/2v^2 dv\\&\quad +\int _{1}^{2} \frac{(v - 2)(v + 4u - 10)}{2} dv\Big )=\frac{19+u^3 - 6u^2}{15 - 3 u^2} \end{aligned}$$

Thus, $\delta _P(T,D)\le \frac{15 - 3 u^2}{19+u^3 - 6u^2}$ for $P\in E_4$. Note that for $P\in E_4\backslash (E_5\cup L_{34})$ we have:

$$\begin{aligned}h_D(v)={\left\{ \begin{array}{ll} \frac{9v^2}{8}\text { for }v\in [0,2-u]\\ \frac{(2-u+v/2)^2}{2}\text { for }v\in [2-u,1]\\ \frac{(3-u-v/2)^2}{2}\text { for }v\in [1,2] \end{array}\right. }\end{aligned}$$

So we have

$$\begin{aligned} S_D(W_{\bullet ,\bullet }^{{\mathcal {C}}};P)&=\frac{2}{5-u^2}\Big (\int _0^{2-u} \frac{9v^2}{8} dv+\int _{2-u}^1 \frac{(2-u+v/2)^2}{2} dv\\&\quad +\int _{1}^{2} \frac{(3-u-v/2)^2}{2} dv\Big )\\&=\frac{21 + 6 u - 18 u^2 + 5 u^3}{2(15 - 3 u^2)}\le \frac{19+u^3 - 6u^2}{15 - 3 u^2} \end{aligned}$$

So we obtain that

$$\begin{aligned} \delta _{P}(T,D)= \frac{15-3u^2}{u^3 - 6u^2 + 19}\text { for }P\in E_4\backslash (L_{34}\cup E_5). \end{aligned}$$

$\square$

Corollary A.5

We have $S(W^{{\overline{T}}}_{\bullet ,\bullet }; E_4) = \frac{83}{80}$, which implies that $\delta _O({\overline{T}}, W^{{\overline{T}}}_{\bullet ,\bullet }) \le \frac{80}{83}$.

Proof

$$\begin{aligned} S\big (W^{{\overline{T}}}_{\bullet ,\bullet };E_4\big )&=\frac{3}{(-K_X)^3}\int \limits _1^{2}\int \limits _0^{\infty } \textrm{vol}\big (P(u)\big \vert _{{\overline{T}}}-vE_4\big )dvdu\\&\quad +\frac{3}{(-K_X)^3}\int \limits _0^{1}\int \limits _0^{\infty }\textrm{vol}\big (P(u)\big \vert _{{\overline{T}}}-vE_4\big )dvdu\\&=\frac{3}{20}\int \limits _1^{2}(5-u^2)S_D(E_4)du+\frac{3}{5}\\&=\frac{3}{20}\int \limits _1^{2}(5-u^2)\frac{19+u^3 - 6u^2}{15 - 3 u^2}du+\frac{3}{5}=\frac{83}{80} \end{aligned}$$

$\square$